SAR image despeckling via Lp norm regularization①

HAN Chengde(韩成德), CUI Yingzi, HUANG Ying∗, GUO Mingqiang②,LIU Zheng, WU Liang

(∗Key Laboratory of Urban Land Resources Monitoring and Simulation, Ministry of Natural Resources, Shenzhen 518034, P.R.China)

(∗∗School of Geography and Information Engineering, China University of Geosciences, Wuhan 430074, P.R.China)

(∗∗∗Hubei Geomatics Technology Group Stock Co., Ltd., Wuhan 430074, P.R.China)

(∗∗∗∗Wuhan Zondy Advanced Technology Institute Co., Ltd., Wuhan 430074, P.R.China)

(∗∗∗∗∗National Engineering Research Center of Geographic Information System, Wuhan 430074, P.R.China)

Abstract Synthetic aperture radar (SAR) image despeckling has been an attractive problem in remote sensing. The main challenge is to suppress speckle while preserving edges and preventing unnatural artifacts (such as annoying artifacts in homogeneous regions and over-smoothed edges). To address these problems, this paper proposes a new variational model with a nonconvex nonsmooth Lp (0 ＜p＜1) norm regularization. It incorporates Lp (0 ＜p ＜1) norm regularization and I-divergence fidelity term. Due to the nonconvex nonsmooth property, the regularization can better recover neat edges and homogeneous regions. The I-divergence fidelity term is used to suppress the multiplicative noise effectively. Moreover, based on variable-splitting and alternating direction method of multipliers(ADMM) method, an efficient algorithm is proposed for solving this model. Intensive experimental results demonstrate that nonconvex nonsmooth model is superior to other state-of-the-art approaches qualitatively and quantitatively.

Key words:synthetic aperture radar (SAR) image,speckle,nonconvex nonsmooth regularization, variational method, alternating direction method of multiplier (ADMM)

0 Introduction

Synthetic aperture radar (SAR) is an active remote sensing system, which is widely used in military,agricultural, and disaster relief. Compared with other imaging systems (optical and infrared), the all-day and all-weather imaging capability of SAR is unique.However, as coherent imaging systems, speckle noise inevitably appears in SAR images. Over the years,many methods have been proposed to suppress speckle in SAR images, which can be classified into three major categories: the filtering methods, the variational methods, and the data-driven methods.

The filtering method is a classical speckle reduction strategy. Early filters were proposed to suppress speckle in the spatial domain, for example, Lee filter[1], Kuan filter[2], Frost filter[3]. The above methods were based on maximum a posteriori (MAP),while these methods may lose features in the speckle suppression result. Therefore, filters in the wavelet domain were proposed to preserve signal resolution well so as to get the most suitable prior for the SAR image[4-5]. Recently, the nonlocal filtering methods,e.g., nonlocal mean (NLM)[6], block matching 3D(BM3D)[7], KSVD[8], overlapping group sparsity[9],and low rank recovery[10], are extended to suppress speckle in SAR image. Due to the mechanism of selfsimilarity search, nonlocal filters can usually obtain the breakthrough speckle reduction results, such as PPBit[11], SARBM3D[12], FANS[13].

The variational method is another popular speckle suppression approach due to the favorable ability for recovering edges and homogeneous regions. The variational model usually incorporates a regularization and a fidelity term. The fidelity term generally simulates the random distribution of speckle noise, while the regularization usually contains the prior information of SAR image. Aubert and Aujol[14]proposed a variational model based on MAP to suppress speckle well, abbreviated as the AA model. However, due to the nonconvex AA fidelity term, the global minimum of the AA model is difficult to obtain by the common solving method, such as gradient descent approach. For tackling this problem, some studies were proposed, which can be classified into two categories: the convex approximation and the logarithmic transformation of AA model. In the first category, they usually add a penalty function to the original AA model so as to transform the nonconvex model into a convex model[15-17]. The second category is logarithmic transformation of the AA model[18-20]. By using logarithmic transformation, the nonconvex AA model can transform to a convex one.

More recently, several deep learning methods[21-23]have attracted more attention. Chierchia et al.[22]used log-transformed and residual learning of SAR images for a convolutional neural network (SAR-CNN),which are trained in the log-transformed original image. Once the speckle-free log-transformed SAR image is obtained, the restored image of the original domain is mapping back through the exponential function. Wang et al.[23]proposed a convolutional neural network in the original domain of the image, where a componentwise division-residual layer is used for recovering the filtered image. The above methods can effectively suppress speckle noise,while they highly rely on the training data set.

Motivated by these issues, a nonconvex nonsmooth model is proposed to suppress speckle noise for SAR image in this paper. The core idea of this work is to use a nonconvex nonsmoothLp(0 ＜p＜1) norm regularization for getting the most suitable sparsity with SAR image, which can better recover neat edges and homogeneous regions. The I-divergence fidelity term is used to suppress the speckle noise effectively. Moreover, an efficient algorithm based on alternating direction method of multiplier (ADMM) method is proposed for solving this model. Specifically, the contributions are summarized as follows.

(1) A new variational model with a nonconvex nonsmoothLp(0＜p ＜1) norm regularization is proposed for recovering neat edges and homogeneous regions well.

(2) An efficient algorithm based on variablesplitting and ADMM method is proposed for solving the propose nonconvex nonsmooth model.

(3) Intensive experimental results demonstrate that the new model is superior to other state-of-the-art approaches in recovering neat edges and homogeneous regions.

1 Variational methods for speckle reduction

In this section, firstly the basic notations are defined, then the major variational methods for suppressing multiplicative noise are described. Finally,the motivations of the new nonconvex nonsmooth variational model are expressed.

1.1 Basic notation

For generality,SAR image intensityuis represented as anM×Nmatrix. The Euclidean space RM×Nis denoted asV, and the discrete gradient operator is a mapping ∇:V→Q, whereQ=V×V. Foru∈V, ∇uis given by

1.2 Variational methods for speckle reduction

Speckle noise is usually regarded as multiplicative noise in SAR image as follows.

whereα ＞0 is a convex approximation parameter. To cope with the staircase artifacts produced by Eq.(9),Shama et al.[15]replaced the TV regularizer in Eq.(9)with TGV regularization. Li et al.[16]applied a difference of convex algorithm (DCA) to solve the original AA model Eq.(8), which can split the AA model into a difference of two convex functions.

The second category is logarithmic transformation of the AA model. By using logarithmic transformation,the nonconvex AA model can transform to a convex one. Feng et al.[18]adopted this strategy with a TGV regularizer, but this method will result in low value pixels weakeness due to nonlinear logarithmic transform. To tackle this problem, Steidl and Teuber[24]proposed a variational model with I-divergence fidelity term which is convex and not require the deficiency of logarithmic transformation. The proposed model is formulated as

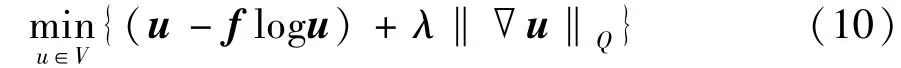
Feng et al.[18]also modified the model Eq.(10)with TGV regularization term for reducing staircase effects. However, due to the using of high-order operator in their model, the results produced by their method also are over-blurring in edges and corners.

The regularizer of the aforementioned models are all convexL1 norm regularizer. However, for many problems based on recovery of sparse and discontinuous signals, using nonconvex regularizer (Lpnorm) can usually obtain better results than the convex regularizer(L1 norm), which is verified by numerical experiments in numerous papers[25-28]. Inspired by these studies, this paper proposes a new variational model with a nonconvex nonsmoothLp(0＜p ＜1) norm regularization.

2 Lp-regularized model and corresponding numerical algorithm

As coherent imaging systems, speckle noise inevitably appears in SAR images. Compared with Gaussian noise of natural images, multiplicative speckle noise can seriously blur geometry features, especially in SAR images with intensity format. In order to recovery neat edges and homogeneous regions well, this paper proposes a new variational model with a nonconvex nonsmoothLp(0＜p ＜1) norm regularization as follows.

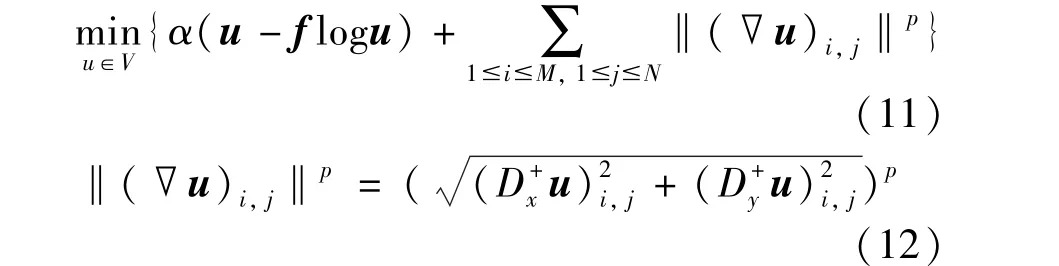
here,α ＞0 is a regularization parameter, which is used to balance the weight between the fidelity term and the regularizer.p∈[0,1] is a parameter for controlling the nonconvexity of theLpregularizer.

Because of the minimization problem Eq.(11) is nonconvex, it is difficult to find the global minimum.Inspired by Ref.[29], this paper uses variable-splitting and ADMM to solve this nonconvex model. Firstly, two auxiliary variableswandtare introduced in the problem Eq.(11),and then it is reformulated as follows.

3 Experiments and analysis

In this section,the proposed model is evaluated on three real SAR images, which are presented in the first row of Fig.1(a), Fig.2(a), and Fig.3(a). The real SAR images are accessed from https:/ /www. intelligence-airbusds. com/. The proposed SAR image despeckling method is abbreviated as IDIVLP,which is compared with the corresponding state-of-the-art methods, such as SARBM3D[12], PPBit[11], DCA[16], and TGV[18]. All the methods tested in this paper are implemented by using the code provided by their authors,except TGV[18]according to the published paper. All of the examples are run on a laptop with an AMD Ryzen7 core 2. 9 GHz processor and 16 GB RAM by using Matlab R2016a.

3.1 Parameters tuning

Most SAR image despeckling methods have parameters, which need to be manually tuned to produce satisfactory results. The proposed variational model Eq.(11) has two parameters:αandp. αis a weight between the fidelity term and the regularization, which is used to prevent the output deviating far from the input. Ifαis too large, the speckle noise cannot be suppressed fully; ifαis too small, the fine features will be oversmoothed. To obtain satisfactory despeckling results, this paper empirically gives the following parameter setting guidance:L≤4,α∈[0.1,20];L ＞4,α∈[10,100]. p∈[0,1] is a parameter for controlling the nonconvexity of theLpregularizer. The smaller ofpmeans that the nonconvexity of the new proposed model is stronger. Ifpis too small for the SAR image,staircase effects and other annoying artifacts appear in recovering results.

On the contrary, too largepwill blur edges and leave some speckles. Therefore,pis suggested to be set a suitable value. For cartoon images,p∈[0.1,0.6];for images with rich details,p∈[0.5,0.9].

3.2 Qualitative comparisons

In this subsection, some visual experiments are executed to compare the new model IDIVLP with the state-of-the-art methods including SARBM3D, PPBit,DCA, and TGV. All the parameters used in these methods are elaborately tuned for yielding visually best speckle suppression results. In addition,to better evaluate the ability of edges recovery visually, ratio images are adopted in the tests (see the second row of Figs1,2, and 3). More structures appear in the ratio images,which means that this method loses more features and flattens more edges in the recover results.

Fig.1 demonstrates and compares results of SAR1, which has sharp features and homogeneous areas. All of the methods are capable of removing speckle. However, it can be seen that, except the new method, all the other methods smooth some sharp edges and over-blur homogeneous regions more or less,especially for TGV (see the first row of Fig.1(e)). At the same time, the ratio image of TGV leaves the most structures (see the second row of Fig.1(e)). This is because that it uses the second derivative in its model,which tends to produce over-blurring results. DCA produces better results than TGV, but it also loses more features (see Fig.1(d)). In addition, it yields some staircase artifacts in homogeneous regions. Compared the new method with the non-local methods PPBit and SARBM3D, they usually yield better results than DZ and DCA. In ratio images, they leave fewer structures(see the second row of Fig.1(b), (c)). However,because of the attempt to recognize structures even when these structures are absent, the despeckling result of SARBM3D suffers from ghost artifacts in the homogeneous regions (see Fig.1(b) for example).For the same reason as SARBM3D, PPBit tends to produce some brushstrokes in homogeneous regions as shown in the first row of Fig.1(c). These unnatural artifacts produced by PPBbit and SARBM3D reduce the quality of the despeckling results evidently. In contrast to these methods, the new method IDIVLP yields the more attractive result with neat edge preserving and homogeneous regions recovery (see the first row of Fig.1(f)). In addition, IDIVLP also produces the fewest structures in ratio images (see the second row of Fig.1(f)).

Fig.2 shows despeckling results on SAR2 containing city scene. TGV over-blurs weak edges and homogeneous regions in various degrees, and it leaves the most structures in ratio image (see the second row of Fig.2(e)). DCA produces better results than TGV in preserving edges, but it also produces staircase artifacts (see the second row of Fig.2(d)). Again,PPBit suffers from serious brushstrokes, and SARBM3D shows severe ghost artifacts (see the first rows of Fig.2(b)and (c)). In contrast, IDIVLP preserves clearer edges and recovers homogeneous regions better, and it yields the fewest structures in ratio images (Fig.2(f)).

Fig.1 Despeckling results of SAR1 (the first row is: (a) noisy image, denoising results produced by (b) SARBM3D, (c) PPBit,(d) DCA, (e) TGV, (f) IDIVLP ( α = 6, p = 0.7 ), respectively, the second row is the corresponding ratio images)

Fig.2 Despeckling results of SAR2 (the first row is: (a) noisy image, denoising results produced by (b) SARBM3D, (c) PPBit,(d) DCA, (e) TGV, (f) IDIVLP ( α = 11, p = 0.4 ), respectively, the second row is the corresponding ratio images)

To further testify the validity of the new method IDIVLP, some tests are executed on SAR3 containing hill scene in Fig.3. DCA produces slight staircase effects in homogeneous regions,but it is superior in preserving edges compared with other tested despeckling methods.Moreover, the new method IDIVLP produces the least structures in ratio image (see the second rows of Fig.3(d)). TGV smoothes more sharp edges and homogeneous regions. PPBit and SARBM3D suffers from the annoying artifacts in homogeneous areas. In contrast, the new method preserves features well and outperforms the best structure recovery ability.

Fig.3 Despeckling results of SAR3 (the first row is: (a) noisy image, denoising results produced by (b) SARBM3D, (c) PPBit,(d) DCA, (e) TGV, (f) IDIVLP ( α = 7, p = 0.7 ), respectively, the second row is the corresponding ratio images)

3.3 Quantitative comparisons

For demonstrating more objective comparisons,two indexes are adopted to further evaluate the performances of the despekling methods quantitatively. Specifically, equivalent number of looks (ENL) and edge preservation index (EPI) are used to respectively measure the ability of speckle suppression and edge preservation, which are widely suggested in previous work[21,30-32]. The ENL of tested SAR image were estimated from the homogenous regions in the rectangles in the first row of Figs1(a),2(a) and 3(a). The higher of ENL means that this method can suppress speckle more thoroughly. The value of EPI is in the range of[0,1] and EPI is close to 1 means that this method yields a favorable despeckling results in edges preserving. These assessment results of SAR1, SAR2, and SAR3 by using the two indexes are listed in Table 1.

Table 1 Numerical evaluation results

As shown in Table 1, for all tested SAR image,the values of ENL and EPI of the new method IDIVLP are consistently superior to the compared methods.These show that IDIVLP not only suppresses speckle noise effectively but also recovers neat edges well. In the compared methods, the nonlocal methods (PPBit and SARBM3D) usually can obtain better EPI but worse ENL. This is because that the nonlocal methods adopt the similar structures searching mechanism, so they can recover features well. However, in the same time, this mechanism produces the annoying artifacts in homogeneous regions, which results in the lower ENL than the tested variational methods. The computation time of all the tested methods is recorded in Table 1. As can be seen, for all scenes SAR images, the proposed method has the least time costs in the tested methods.

4 Conclusions

A variational model with a nonconvex nonsmoothLpnorm regularization is, introduced to suppress speckle noise for SAR image. By using theLp(0＜p ＜1)regularizer, the proposed model can obtain the most suitable sparsity with SAR image. Compared with existing depeckling methods, the proposed model is more robust in preserving neat edges and recovering homogeneous regions. An effective algorithm based on variable-splitting and ADMM is also proposed to solve the model, which has smaller computational complexity.Intensive experimental results demonstrate that the new nonconvex nonsmooth model is superior to other stateof-the-art approaches qualitatively and quantitatively.In the future, more application withLpregularizer in other fields will be explored. For example,Lpregularizer is extended for mesh and point cloud denoising.