Directional nearest neighbor query method for specified geographical direction space based on Voronoi diagram①

LI Song(李 松), SONG Shuang, HAO Xiaohong, ZHANG Liping

(College of Computer Science and Technology, Harbin University of Science and Technology, Harbin 150080, P.R.China)

Abstract The existing nearest neighbor query methods cannot directly perform the nearest neighbor query of specified geographical direction space. In order to compensate the shortcomings of the existing methods, a directional nearest neighbor query method in specific direction space based on Voronoi diagram is put forward. This work studies two cases, i.e. the query point is static and the query point moves with a constant velocity. Under the static condition, the corresponding pruning method and the pruning algorithm of the specified direction nearest neighbor (pruning SDNN algorithm)are proposed by combining the plane right-angle coordinate system with the north-west direction,and then according to the smallest external rectangle of Voronoi polygon, the specific query is made and the direction nearest neighbor query based on Voronoi rectangle (VR-DNN) algorithm is given. In the case of moving with a constant velocity, first of all, the combination of plane right angle coordinate system, geographical direction and circle are used, the query range is determined and pruning methods and the pruning algorithm of the direction nearest neighbor based on decision circle (pruning DDNN algorithm) are put forward. Then, according to the different position of motion trajectory and Voronoi diagram, a specific query through the nature of Voronoi diagram is given. At last,the direction nearest neighbor query based on Voronoi diagram and motion trajectory (VM-DNN) algorithm is put forward. The theoretical research and experiments show that the proposed algorithm can effectively deal with the problem of the nearest neighbor query for a specified geographical direction space.

Key words: nearest neighbor query, direction, Voronoi diagram, rectangular plane coordinate system

0 Introduction

The spatial nearest neighbor query has important application value. Some important research results have been achieved in the field of nearest neighbor query,such as nearest neighbor (NN) query[1-2],continuous nearest neighbor (CNN) query[3-4]and other basic query algorithms. Nearest neighbor query is widely used in real life, such as finding the nearest convenience store, recommending the best tour route for a scenic spot, and finding the best temperature for a species. Further, according to the different query requirements and different query objects, some researchers propose the nearest neighbor query between points and points, the nearest neighbor query between line segments and line segments, and the nearest neighbor query between points and line segments. Then according to different query environments, researchers propose the nearest neighbor query in the obstacle environment, the nearest neighbor query in the high-dimensional environment, and the nearest neighbor query in the road network environments. The existing researches mainly focus on reverse nearest neighbor (RNN)query[5-6], group nearest neighbor (GNN) query[7-8],K-nearest neighbor (KNN) query[9-10], moving view field nearest neighbor (MVFNN) query[11], reverse Knearest neighbor (RKNN) query[12-13],dependent nearest neighbor (dNN)[14-15], K-aggregate nearest neighbor (K-ANN) query[16]and so on.

In practical application, the direction nearest neighbor query has the vital significance. For example,when a vehicle is driving on a highway and needs to find a nearest gas station, if the traditional nearest neighbor inquiry is used,it maybe show the nearest gas station on the other side of the driving direction. If the vehicle turns around or goes retrograde on the highway at this time, there will be great danger. According to the actual demand, the nearest neighbor query problem with direction in the spatial database is an important issue. Therefore, the nearest gas station can be quickly judged in the direction of vehicles by adding geographic direction to the query of the nearest neighbor. The existing methods of the directional nearest neighbor queries have some limitations,and cannot be better applied in a given geographic direction. At the same time, continuous nearest neighbor queries cannot be conducted in a designated geographic direction when the query point is moving.

The method proposed in this paper is able to effectively reduce the redundant data, reduce the period for complicated calculation and receive more accurate searching results. The main contributions of this paper are as follows.

(1) In view of the data redundancy, when the query point is static, a method of combining geographical direction with the plane right-angle coordinate system is proposed. According to the positive and negative nature of the four quadrant symbols in the plane rightangle coordinate system, the pruning method can be proposed, which can effectively remove the data set points other than the query direction before the query is carried out.

(2) For the data redundancy when moving with constant velocity, on the basis of combining with the plane right angle coordinate system, a judgment circle is generated. And according to the different position of the determination circle and the plane right angle coordinate system, two pruning methods are proposed. The judgment circle can narrow the scope of the query and reduce the searching time complexity.

(3) By utilizing the nature of the Voronoi diagram and the nature of the Voronoi polygon minimum circumscribed rectangle, a specific search is made in the data set after the pruning, and the corresponding algorithm is put forward, which can make efficient query in a specific direction.

1 Related wor k

Ref.[19] introduced a novel type of spatial query called the reverse view field nearest neighbor (RVFNN)query. To process the query, Ref. [19] proposed two query processing methods on an R∗-tree,i.e. RVFNN query processing on a sector-based R∗-tree and RVFNN query processing on an origin-based R∗-tree.In addition, Ref.[19] proposed a new type of spatial data index structure called the view field R-tree (VFRtree) and a search method for RVFNN queries on the VFR-tree. Based on the definition of influence,Ref.[20] proposed reverse approximate nearest neighbors (RANN) queries. Ref.[21] presented a progressive algorithm for approximate nearest neighbor indexing and querying, which is a novel algorithm for progressive approximate K-nearest neighbors, enabling fast KNN queries while continuously indexing new batches of data. In Ref.[22], a shared execution-based approach called standard clustered loop (SCL) was proposed that allows efficient processing of all nearest neighbor (ANN) queries on a dynamic road network.The key concept behind the shared execution technique is to exploit the coherence property of road networks by clustering objects that share common paths and processing the cluster as a single path.

In the existing research on directional-related nearest neighbor queries, the directional-aware index structure was proposed in Ref.[23]. It first groups the points of interest (POI) according to the distance from the query point to the lower left corner of the smallest bounding rectangle containing all nearest POIs. Then,POI is sorted in each group according to the direction of the lower left corner, and the effective region-based pruning techniques and direction-based pruning techniques are further proposed. Meanwhile, an effective algorithm is put forward to solve the direction-aware spatial keyword query problem. Ref.[24] proposed a new spatial data query,that is,the direction-constrained continuous nearest neighbor (DCNN) query. DCNN query finds the nearest POI that satisfies the direction constraint. The direction constraint is an angular range that depends on the direction of the user’s speed,and the range of angles is determined by the user.

During the past years, direction nearest neighbor query has gained further research. The direction-aware nearest neighbor ( DNN) query was proposed in Ref.[25]. Given the query pointqand the angle thresholdθ,DNN query can search the nearest neighbor in all directions around the query pointq, which can be applied to search the nearest object, and also can be used to search for photos of geographical objects according to the location of the photos taken. The proposed algorithms can answer point-DNN queries and range-DNN queries effectively and efficiently. Ref.[26]proposed a new type of query and devised a new index structure for efficiently indexing spatio directional objects. The index structure utilizes multiple R-trees with different directional ranges to minimize the distance search space. Two efficient query processing algorithms including single matching algorithm and adaptive matching algorithm are also proposed. Ref.[27] presented a novel algorithm of direction-aware continuous moving K-nearest neighbor (DACKNN) queries in road networks. In this method, the azimuth information of objects is adopted to determine the moving direction, ensuring the moving objects in the result set towards the query object.

2 Definitions and property

Definition 1 (Voronoi diagram[28]) Given a set of data point setsP={p1,p2,…,pn}⊂R2, of which 2＜n ＜∞,pi≠pjwheni≠j.The Voronoi region is defined asVH(pi)= {q|D(q,pi) ≤D(q,pj)},D(q,pi) is the minimum distance betweenqandpi,andpiis called Voronoi generation point. The Voronoi regionVH(pi) determined bypiis called a Voronoi polygon,the rib of the Voronoi polygon isVL(pi),and the Voronoi polygon that shares edges withVH(pi) is calledVH(pi) adjacent polygon, and its corresponding generating point is called the adjacency generation point ofpi. The graph defined byV(H) ={VH(p1),VH(p2),…,VH(pn)} is called a Voronoi diagram.

Property 1 The distance from any pointq(q∉Q) topin Voronoi polygonVH(p) must be less than the distance fromqto other Voronoi generating points[28].

Definition 2 (the minimum external rectangle of Voronoi polygon) The rectangle with the smallest area around Voronoi polygonVH(P) constructed by one or more vertices of Voronoi polygon is called the smallest circumscribed rectangle of Voronoi polygon, whose edges are parallel to the coordinate axis, and is denoted asVR(P).

Definition 3 (nearest neighbor query[1]) Given a set of data objectsPand a query pointq, the nearest neighbor query finds a subset of data objects in the setP, satisfying the following conditions:

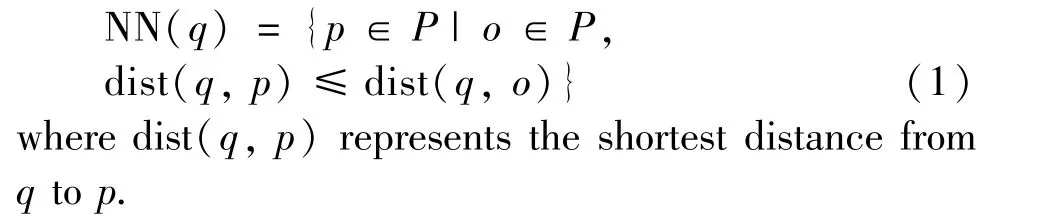
Definition 4 (the directional nearest neighbor query) Let the query point beq, the data object set beP, and the nearest neighbor query direction be DR,DR={East-North-West-South}. There is a data point setK⊂Pin the DR direction,and the nearest neighbor query aims to find the nearest neighbor of the query pointqin the setK, that is, DNN(q) ={pd∈K|∀pi∈P, dist(q,pd)≤dist(q,pi),K⊂P},pdrepresents the data object in the query direction.

3 Directional nearest neighbor query under static query points

In the process of the directional nearest neighbor query when the query point is static, since the nearest neighbor in a specified direction is queried, it is unnecessary to consider the data set points in the other directions. Therefore, the directional nearest neighbor query under the static query point proposed in this section includes two steps, the data preprocessing and the directional nearest neighbor query processing.

3.1 Data preprocessing

Due to the large number of data points and the long time consumed in the query, it is necessary to preprocess the data before query, that is, to prune the data points in other irrelevant directions.

First, the direction of geographical location is set to east, west, south and north. The east, west, south,and north directions are four directions, and the plane rectangular coordinate system with the same structure also has four quadrants. Therefore, in order to determine the nearest neighbor of the concrete direction,the plane rectangular coordinate system is combined with the east, west, north and south directions, and the nature of the plane rectangular coordinate system is used to reduce the scope of the query.

Second, a plane rectangular coordinate system is established.

(1) When the query direction is in any direction of northeast, southeast, northwest and southwest, a plane rectangular coordinate system is established with the query pointqas the origin, the east-west direction as the horizontal axis, and the north-south direction as the vertical axis. Let the horizontal axis bex-axis and the vertical axis bey-axis. The northeast direction is located in the first quadrant, and its abscissa and ordinate are positive; the northwest direction is in the second quadrant, and the abscissa is negative and the ordinate is positive; the southwest direction is in the third quadrant, the abscissa and ordinate are negative;the southeast direction is in the fourth quadrant, and the abscissa is positive and the ordinate is negative.

(2) When the query direction is in a single direction, such as east, west, south, and north, a plane rectangular coordinate system is established with the query pointqas the origin, the east-south direction as the horizontal axis, and the west-north direction as the vertical axis. Let the horizontal axis bex-axis and the vertical axis bey-axis. The east direction is located in the first quadrant, and its abscissa and ordinate are positive; the north direction is in the second quadrant,and the abscissa is negative and the ordinate is positive; the west direction is in the third quadrant, the abscissa and ordinate are negative; the south direction is in the fourth quadrant, and the abscissa is positive and the ordinate is negative.

Finally, because the points in the data setPare scattered in each quadrant and the nearest neighbor in a concrete direction is needed, the data points outside the required direction area are pruned by using the difference of positive and negative coordinates in each quadrant. To reduce the amount of calculation, Theorem 1 is proposed.

Pruning method 1 can be further obtained from Theorem 1.

Pruning method 1 Arbitrarily take the coordinates (denoted aspi(xpi,ypi)) in the desired direction area, and respectively make vertical lines from all the points in the data setPto thex-axis and they-axis. Then the symbols of the horizontal and vertical coordinates will be obtained. The abscissa or ordinate of the obtained point in the data setPis pruned inconsistent with the symbol of the coordinatespi(xpi,ypi).

The query range is reduced by judging the coordinates, and the pruning algorithm of the specified direction nearest neighbor (Pruning SDNN algorithm) is further given, as shown in Algorithm 1.

Algorithm 1 Pruning

SDNN

Input: dataset P, query direction.P(q).Begin:Output: dataset CDT 1. According to the direction of the query, establish the plane right angle coordinate system;2. Set any point in the area where the query direction is located with a coordinate of pi(xpi, ypi);3. Let the coordinate of the point in the data set P be denoted as pj(xpj, ypj);4. for j=1 to P. length do 5. if xpi ＞0 and ypi ＞0/ /The query direction is northeast 6. if xpj ＞0 and ypj ＞0 7. CDT P(q)←pj; / /Pruning method 1 8. else pruning;9. if xpi ＜0 and ypi ＞0/ /The query direction is northwest 10. if xpj ＜0 and ypj ＞0 11. CDT P(q)←pj; / /Pruning method 1 12. else pruning;13. if xpi ＜0 and ypi ＜0/ /The query direction is southwest 14. if xpj ＜0 and ypj ＜0 15. CDT P(q)←pj; / /Pruning method 1 16. else pruning;17. if xpi ＞0 and ypi ＜0/ /The query direction is southeast 18. if xpj ＞0 and ypj ＜0 19. CDT P(q)←pj; / /Pruning method 1 20. else pruning;21. return CDT P(q);End

Algorithm 1 firstly establishes the plane rectangular coordinate system, and determines the quadrant positions of northeast direction, northwest direction,southwest direction and southeast direction according to the properties of the plane rectangular coordinate system. Then, by using the positive and negative quadrants, the data points which are not consistent with the sign of the quadrant in the required direction are pruned to reduce the data set.

3.2 Identifying neighbors

In subsection 3.1, the plane rectangular coordinate system is combined with the east, west, north and south directions, and the redundant data points are pruned by using its properties. This section will conduct the specific queries. Since the redundant data set points have been pruned, it only needs to construct Voronoi diagram in the specific query direction. In order to facilitate searching, a minimum circumscribed rectangle is constructed based on the Voronoi polygon,and the properties of the Voronoi polygon minimum circumscribed rectangles are used to determine the nearest neighbor.

A Voronoi diagram is constructed in the desired direction, and a rectangle of the smallest area is constructed surroundingVH(P) by one or more fixed points of Voronoi polygonVH(P), that is, the minimum circumscribed rectangles of Voronoi polygon is constructed, as shown in Fig.1.

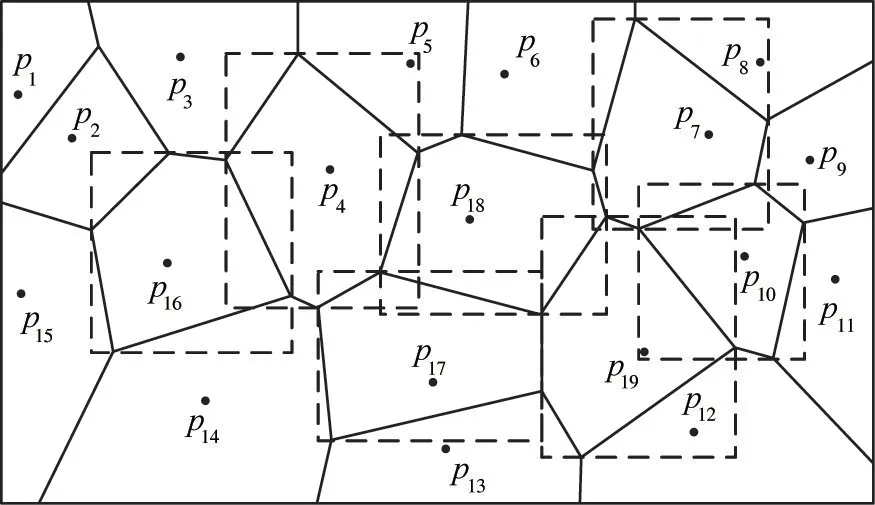
Fig.1 Minimum circumscribed rectangle of Voronoi polygon

The positional relationship between the query pointqand the minimum circumscribed rectangle generated by Voronoi polygon has the following two cases.

(1) When the number of the minimum circumscribed rectangle containing the query pointqis 1, the data pointpicorresponding to the minimum circumscribed rectangle is the nearest neighbor of the query pointqin the direction.

(2) When the number of the minimum circumscribed rectangle containing the query pointqism(m＞1), the query pointqis on the edge line of Voronoi polygons. According to the definition of Voronoi diagram, the distance from the query pointqtop1…pmis equal. At this time, all ofp1…pmare the nearest neighbor of the query pointqin this direction.

For example, let the query direction be northeast.As shown in Fig.2(a), the minimum circumscribed rectangle containing the query pointqisVR(p1), then the data pointp1corresponding toVR(p1) is the nearest neighbor of the query pointq. As shown in Fig.2(b), the minimum circumscribed rectangle containing the query pointqisVR(p1),VR(p2),VR(p3),VR(p4), then all of the data pointsp1,p2,p3,p4corresponding toVR(p1),VR(p2),VR(p3),VR(p4) are the nearest neighbor of the query pointq.

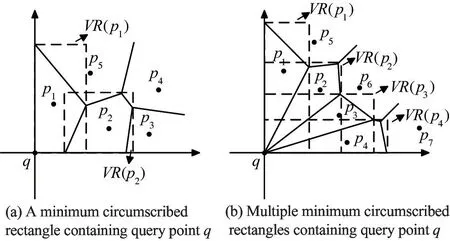
Fig.2 The relationship between query point q and VR(P)

In the query process, first, the Voronoi diagram of the data setP1is generated. Second, the minimum circumscribed rectangle of each Voronoi polygon is generated, and then the number of minimum circumscribed rectangles of Voronoi polygon determines where the query pointqis located. Finally, the Voronoi generation point is determined corresponding to the minimum circumscribed rectangle and the nearest neighbor ofqis found.Based on the above discussion, the direction nearest neighbor query based on Voronoi rectangle (VR DNN) algorithm for the nearest neighbor query based on the minimum circumscribed rectangle of the Voronoi diagram is given as Algorithm 2.

Algorithm 2 VR DNN Input: dataset CDT P(q), query point q.Output:directional nearest neighbor of q.Begin:1. Create P(q));2. Create Min Voronoi(CDT rectangle(pi, VH(pi));/ /Create minimum circumscribed rectangles of the Voronoi polygon 3. Judge the relationship between query point q and minimum circumscribed rectangular MR(P);4. Determine the number m of minimum circumscribed rectangles MR(P) containing q;5. if m=1 then / /q is only in one MR(P)6. DNN ←pi;/ /Add pi to directional nearest neighbor set

7. else ifm＞1 then/ /qis in the overlapping region of multiple MR(P)8. Determine the minimum distanced1…dmcorresponding to the data pointp1…pm;

9. DNN←p1…pm;/ /Addp1…pmto directional nearest neighbor set 10. return DNN;

End

In Algorithm 2, the minimum number of outer rectangles containing query pointqis determined by adding the minimum outer rectangle in Voronoi diagram, and then the data setpiorp1…pmis got corresponding to the minimum outer rectangle of Voronoi polygon. The data pointpiorp1…pmis the nearest neighbor of query pointqin this direction.

4 Directional nearest neighbor query under uniform motion of query points

When the query points move, the directional nearest neighbor of the query points will change accordingly. So, this section will mainly focus on the nearest neighbor query problem when dynamic query points are moving at a uniform speed. Prerequisites are that the motion trajectory of the query pointqis known, and the end point of the motion trajectory is recorded asz.

When the query pointQmoves uniformly, it mainly moves in the following situations: (1) uniform straight line; (2) uniform fold line; (3) uniform curve; (4) combination of uniform fold line and curve.

4.1 Data preprocessing

Firstly, the minimum circumscribed rectangle of the trajectory of the query pointqasR(t) is constructed, and then the plane rectangular coordinate system is constructed. The horizontal axis is the east-west direction, which is thex-axis; the vertical axis is the north-south direction, which is they-axis; and the intersection ofx-axis andy-axis is the origino, which is a vertex inR(t). When the query direction is northeast, the extension line of the lower boundary of the minimum circumscribed rectangle is the horizontal axis, and the extension line of the left boundary is the vertical axis; when the query direction is northwest,the extension line of the lower boundary of the minimum circumscribed rectangle is the horizontal axis,and the extension line of the right boundary is the vertical axis; when the query direction is the southwest direction, the extension line of the upper boundary of the minimum circumscribed rectangle is the horizontal axis, the extension line of the right boundary is the vertical axis; when the query direction is the southeast direction, the extension line of the upper edge of the minimum circumscribed rectangle is the horizontal axis, and the extension line of the left boundary is the vertical axis.

Secondly, the scope of the query is determined.Many data points which are not in the desired direction in the data set points do not need to be considered, so how to determine the query range is the key to prune the data set. The query range is determined by generating a decision circle and prune it.

Finally, since the query points are moving at a uniform speed in a certain direction,the points in other irrelevant directions are pruned to reduce the amount of calculation. So Pruning method 2 and Pruning method 3 are proposed.

Pruning method 3 In data setCDTPO(q),the data points which are not in the quadrant of the direction of motion in the judgment circle area are pruned, and the data set after pruning is recorded asCDTPI(q).

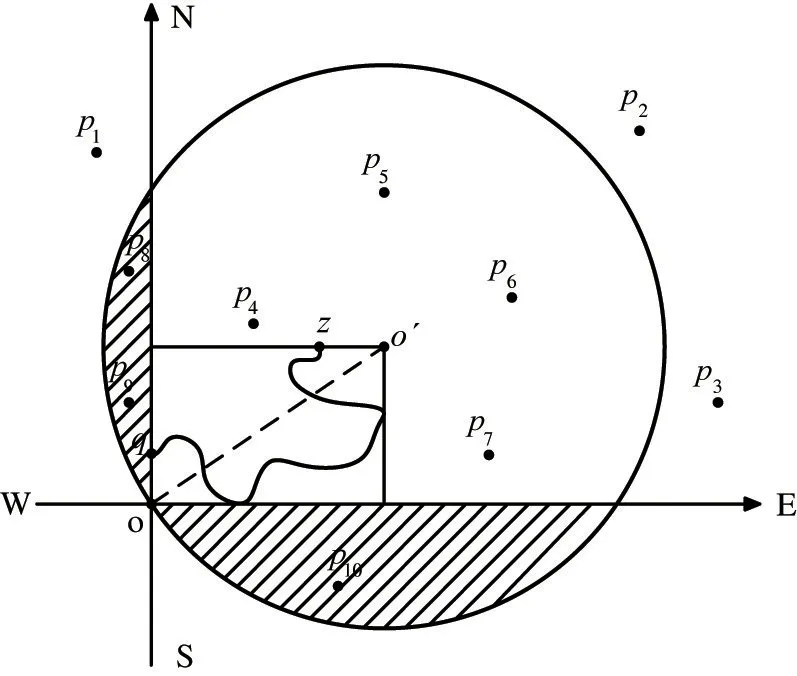
Fig.3 Pruning diagram when the query direction is northeast

Algorithm 3 Pruning DDNN Input: dataset P, query direction.PI(q).Begin:Output: dataset CDT 1. Establish a plane rectangular coordinates according to the query direction;2. Creat Circle (z, doo′);/ /Generate a decision circle Coo′ with the o′ as the center, the straight line distance between origin o and o′ denoted as the radius of the center, marked as doo.3. Let the coordinates of any point in the area where the query direction is located as pi(xpi, ypi);4. Let the coordinate of data set P as pj(xpj, ypj);5. for j=1 to P. length do 6. if pj is in Cqz 7. CDT PO(q)←pj; / /Pruning method 2 8. else pruning;9. Let the coordinate of data set CDT PO(q) as pk(xpk,ypk);

10. for k=1 to CDT PO(q). length do PO(q). length represents the number of data points in the data set CDT/ /CDT PO(q)11. if xpi ＞0 and ypi ＞0/ /The query direction is northeast 12. if xpk ＞0 and ypk ＞0 13. CDT PI(q)←pk; / /Pruning method 3 14. else pruning;15. if xpi ＜0 and ypi ＞0/ /The query direction is northwest 16. if xpk ＜0 and ypk ＞0 17. CDT PI(q)←pk; / /Pruning method 3 18. else pruning;19. if xpi ＜0 and ypi ＜0/ /The query direction is southwest 20. if xpk ＜0 and ypk ＜0 21. CDT PI(q)←pk; / /Pruning method 3 22. else pruning;23. if xpi ＞0 and ypi ＜0/ /The query direction is southeast 24. if xpk ＞0 and ypk ＜0 25. CDT PI(q)←pk; / /Pruning method 3 26. else pruning;27. return CDT PI(q);End

Algorithm 3 establishes a plane rectangular coordinate system, and determines the quadrant position of northeast, northwest, southwest, and southeast directions according to the properties of the plane rectangular coordinate system. A decision circleCoo′will be generated with theo′ as center and the straight line distancedoo′between originoando′ as radius. It prunes the data set points outside the decision circle,and prunes the area where the decision circle outside the quadrant of the motion direction.

4.2 Dircetional nearest neighbor query

In order to ensure the accuracy of the query results, this section will perform real-time search. A Voronoi diagram in the decision circle after pruning is established, and the nearest neighbor of the query pointqis found by using the properties of the Voronoi diagram. Theorem 3, Theorem 4 and Theorem 5 are given.

Theorem 3 There ispe∈CDTPI(q), and at a certain timeTiduring the motion,if the query pointqand data set pointpeare in the same location, then the data set pointpeis the nearest neighbor of the query pointqat the time ofTi.

Proof As shown in Fig.4(a), there ispe∈CDT_PI(q).At a certain timeTiin the process of uniform movement of the query pointq, the Euclidean formula between query pointqand data set pointpeis 0, that is

Theorem 4 There ispf,pg∈CDTPI(q).The data pointspfandpgshare a edgelof Voronoi polygon,and the edgelintersects with the trajectory of the query pointq. At a certain timeTjduring the movement, the query pointqmoves to the intersection pointm. At this time the Euclidean distanceDzpfandDzpgfrompf,pgto the end pointzare calculated. The corresponding data points ofDzpfandDzpgwith smaller values are the nearest neighbors of the query pointqat the time ofTj.

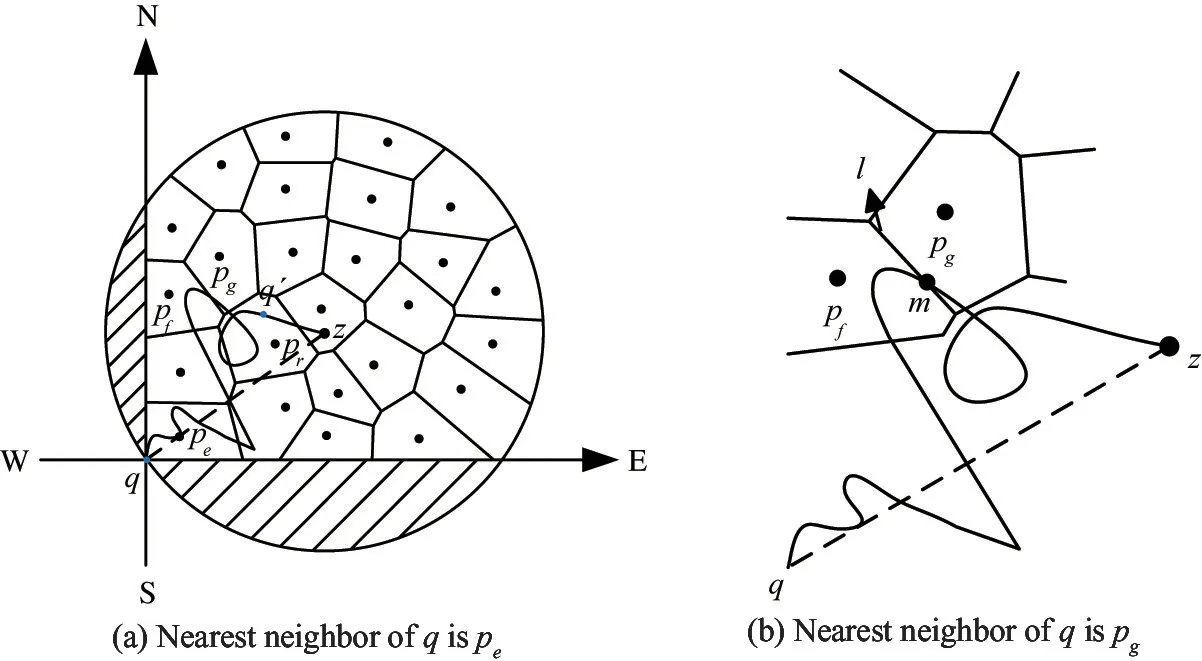
Fig.4 When the query direction is northeast

_Algorithm 4__V____M_DNN______________________________Input: dataset CDT_PI(q), query point q._Output: directional nearest neighbor of q_________________.Begin:P(q));2. Let the point pe be in the data set CDT_1. Create_Voronoi(CDT_PI(q);3. if query point q coincides with data set point pe 4. DNN←pe;/ /Add pe to the nearest neighbor set Theorem 3 5. Let the data set CDT_PI(q) contain points pf, pg, and the points pf and pg share a rib of a Voronoi polygon;6. else if the trajectory of the query point q intersects with l 7. Calculate the distance between pf and pg to the end point z, taking the minimum distance dmin;8. Determine the data point pf or pg corresponding to the minimum distance dmin;9. DNN←p;/ /Add p to the nearest neighbor set, Theorem 4 10. Let there be a point pj in the data set CDT_PI(q);11. else if query point q falls in the Voronoi polygon area of point pj 12. DNN ＜—pj;/ /Add pj to the nearest neighbor set, Theorem 5 13. return DNN;_En________________________________________________d

5 Experiments and analysis

This section analyzes the performance of the proposed algorithm through experiments. The experimental environment is 2.60 GHz CPU,8 GB memory,500 GB hard disk, programmed with Microsoft Visual Studio.NET2003, Windows 10 system. The experimental data are collected by using data sets generated by spatial data generation software and road network information in San Francisco and California, USA. The data have 1 965 206 nodes and 5 533 214 edges. During the experiment, the distribution of data and related information are appropriately adjusted. Some redundant information of the data is eliminated.

Two important comparison algorithms are used to compare with the method proposed in this paper. The experiment mainly tests the impact of data set size on runtime and I/O cost, the impact of dynamic query points on query time, and the impact of query time on the accuracy of the algorithm. Since the nearest neighbor query with the point as the query object cannot calculate the query in the specified geographic direction,the existing method cannot be directly compared with the method in this paper. In order to obtain the comparison algorithm, the existing algorithm is adjusted appropriately, and finally two comparison algorithms are obtained.

After adjusting the PointDNNBaseline algorithm based on direction perception proposed in Ref.[25],the comparison algorithm DNNBase + is got. Firstly,this paper mainly queries the nearest neighbors in the specific direction. Based on the results of the PointDNNBaseline algorithm given in Ref.[25], the direction constraint is added, that is, the polar angle range of the neighboring result is set according to the geographic direction of the east,west,south and north. Secondly,the nearest neighbor result in the query direction is determined according to the Euclidean distance. After the adjustment,the DNNBase+algorithm is finally formed.

The second comparison algorithm is the R_MULTI algorithm which is appropriately adjusted based on the UpperEvenLevel algorithm proposed in Ref.[26]. Firstly, since the Ref.[26] studied the Knearest neighbor query based on the direction constraint, and this paper studies the nearest neighbor based on the Voronoi diagram, theKof Ref.[26] is adjusted to 1; secondly, all the angle of the data point defaulted leads to the query pointq; finally, since the plane rectangular coordinate system established in this paper is divided into four quadrants, each of which is 90 °, the angle constraint in Ref.[26] is set to 90 °,the angle of the range is fixed to 90 °, and the R_MULTI algorithm can be formed after the adjustment.First, the impact of the data set size on the VR_DNN algorithm is tested when query pointqis static.Then the length of the query time is tested under the data sets of different scales when the query pointqis static. When the data sets scale is 20 000, 40 000,60 000,80 000, and 100 000, the test results of time consumed to execute queries are shown in Fig.5.

In Fig.5, the running time of the three algorithms is gradually increasing as the number of data points increases. The VR_DNN algorithm in this paper consumes relatively less time during the query process.This is because Dist_jDNN algorithm is used to prune the data point set before the query, and some non-candidate points are removed. In addition, in the query process, the nearest neighbor candidate set is filtered again according to the minimum circumscribed rectangle of Voronoi polygon and the query time is reduced.

The query I/O is tested under the data sets of different scales when the query pointqis static. The test results of the I/O cost of executing queries are shown in Fig.6 when the data sets scale is 20 000, 40 000,60 000,80 000, and 100 000. In Fig.6, the I/O cost of the three algorithms are gradually increasing as the number of query points increases. The query I/O cost of VR_DNN algorithm in this paper is relatively low.

Furthermore, the influence of data set size on VM_DNN algorithm is tested when query pointqmoves at a uniform speed. Since Ref.[25] and Ref.[26] do not mention the movement of the query points, DNNBase+algorithm and R_MULTI algorithm are called repeatedly.

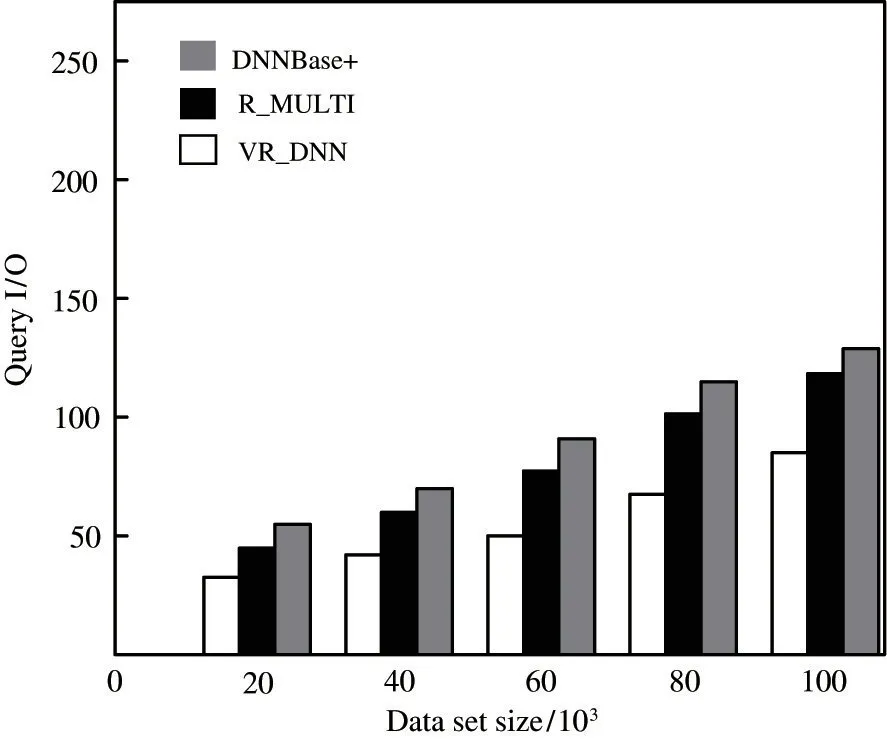
Fig.6 Comparison of query I/O under different scale data sets when query point q is static

The query time is tested under the data sets of different scales when the query pointqis moving at a uniform speed. When the data sets scale is 20 000,40 000, 60 000,80 000, and 100 000, the test results of time consumed are shown in Fig.7. In Fig.7, the running time of the three algorithms is gradually increasing as the number of data points increases. VM_DNN algorithm in this paper consumes relatively less time in the query process. This is because the data setPis pruned before query. In the pruning process, the query range is narrowed by means of coordinate judgment and generation of the decision circle, and finally the real-time search is carried out quickly by using the properties of Voronoi diagram.

Then, the query I/O is tested under the data sets of different scales when the query pointqis moving at a uniform speed. When the data sets scale is 20 000,40 000, 60 000,80 000, and 100 000, the test results of the I/O cost of executing queries are shown in Fig.8.

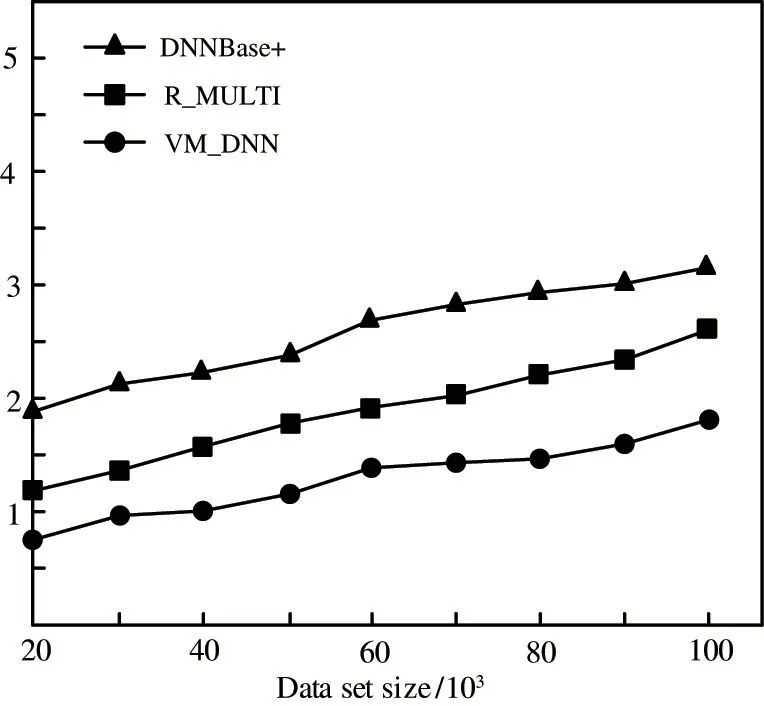
Fig.7 Comparison of query time under different scale data sets when query point q is used for uniform motion

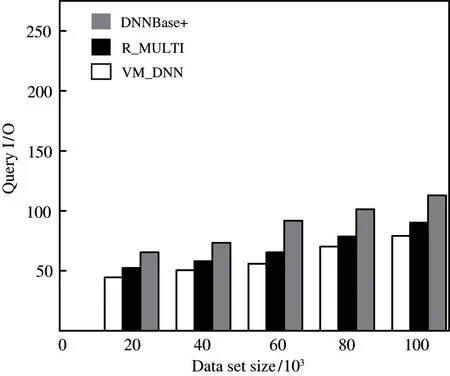
Fig.8 Comparison of query I/O under different scale data sets when query point q is used for uniform motion

In Fig.8, the I/O cost of the three algorithms are gradually increasing as the number of data points increases. The query I/O cost of VR_DNN algorithm in this paper is relatively low. This is because DNNBase+algorithm and R_MULTI algorithm can not calculate the nearest data points at a certain time from the query point in real time. After modifying and calling the original algorithm repeatedly, the amount of calculation increases.

The pruning efficiency will be tested in the data set with different density. From Fig.9, it can be seen that the number of the candidates gradually increase as the density of the data points outside the query target grows. The pruning algorithm proposed in this paper receives relatively low affect from the density of data set.

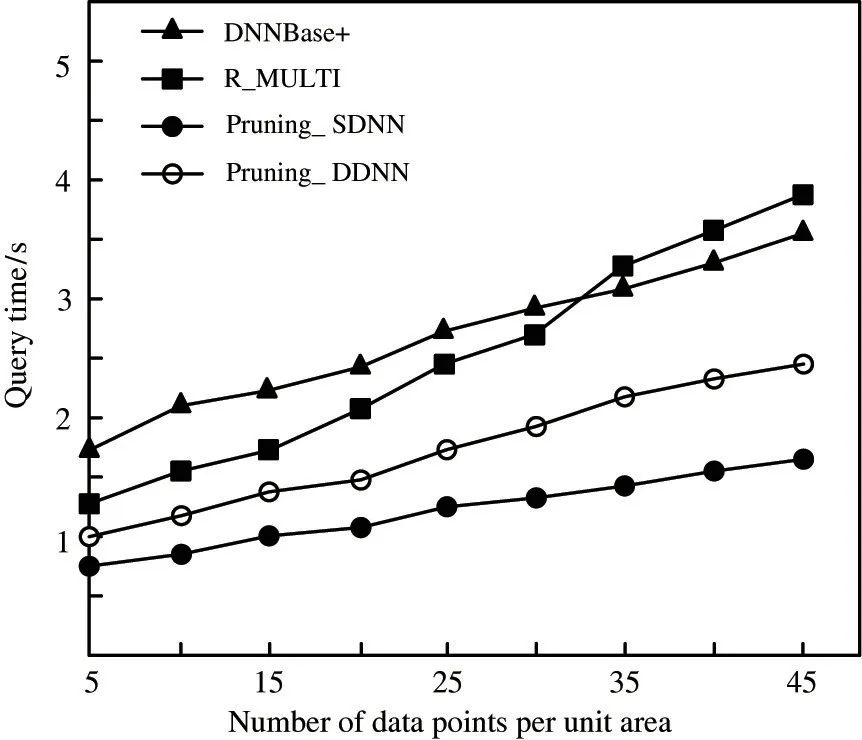
Fig.9 The impact of data set density on query time

Then the performance of VRDNN algorithm is tested when the number of dynamic query points changes. Table 1 shows the performance comparison of VR DNN algorithm, DNNBase +algorithm and RMULTI algorithm when query points increase dynamically. In order to observe easily, five query points are added to the test. When the number of query points changes from 15 to 20, the running time of DNNBase + algorithm and RMULTI algorithm are longer than that of VR DNN.

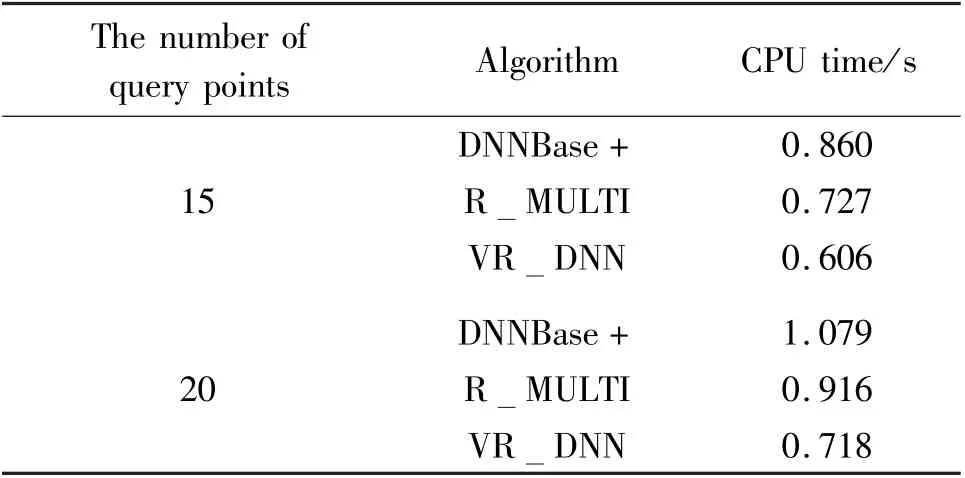
Table 1 Performance comparison of VR DNN,DNNBase+and R MULTI

Finally, the accuracy of the algorithm is tested.

When the data volume is 50 000 and other conditions remain unchanged, the accuracy of the three algorithms is tested in static and dynamic data sets respectively. As shown in Fig.10, the accuracy of the three algorithms increases with the number of queries,VR DNN algorithm proposed in this paper can achieve a higher accuracy than DNNBase + algorithm and R MULTI algorithm.

6 Conclusions

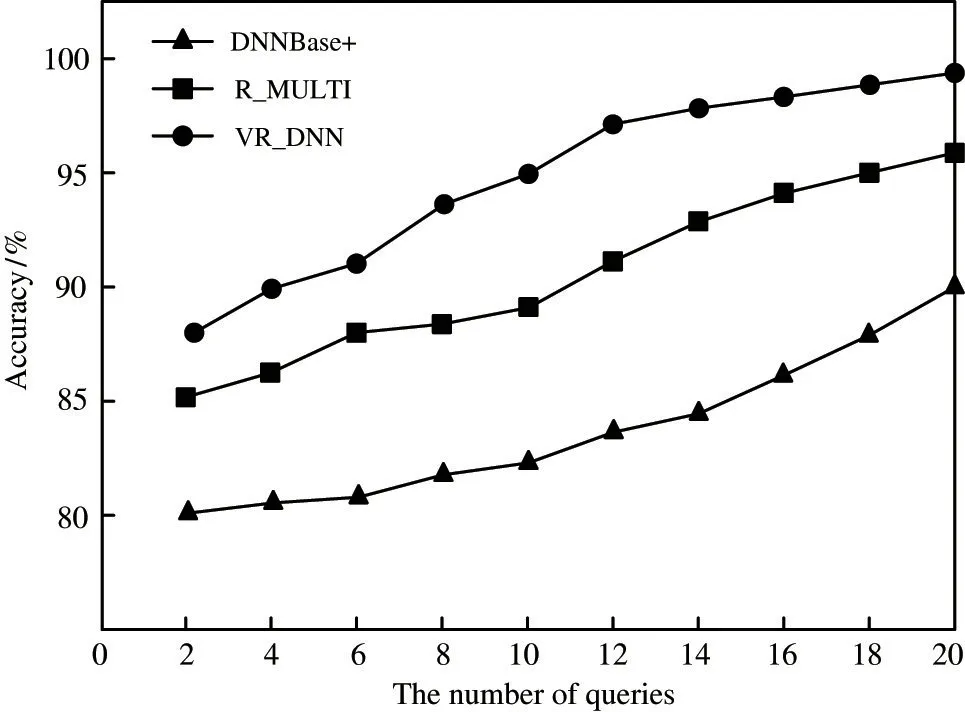
Fig.10 Effect of queries number on accuracy

A directional nearest neighbor query method is proposed based on Voronoi diagram for the nearest neighbor query problem in a specific geographic direction. This work studies two case, i.e. the query point is static and it does uniform motion. When the query point is static, the plane rectangular coordinate system is first combined with the east, south, west and north of the geographical position,and the positive and negative properties of the four quadrant symbols are used in the plane rectangular coordinate system for pruning.Then the directional nearest neighbor is determined by the minimum circumscribed rectangle of Voronoi polygon. When a query point moves at a uniform speed, at first, a plane rectangular coordinate system is established, after that a decision circle for pruning is generated. Finally the positional relationship is got between the query pointq, the data points, and the Voronoi polygon region, so as to determine the directional nearest neighbor. The theoretical research and experiments show that the algorithm proposed in this paper has good performances.