考虑装配变形的精密机床床身优化设计
2022-07-05孙光明王奕苗汪文津
孙光明,王奕苗,万 仟,弓 堃,汪文津,赵 坚
(天津城建大学控制与机械工程学院,天津 300384)
机床由多个零件装配而成。在机床装配过程中产生装配误差的来源有3个:一是由制造精度引起的零件的制造误差;二是由装配位置不准确引起的装配姿态误差;三是由零件之间的装配应力等引起的装配变形。前2种误差可以在机床装配之前进行测量[1-4],并通过提高加工质量和装配位置准确度来减小误差;而对于装配变形,由于变形的机理尚不甚清楚,其变形量难以预测。通常,操作人员进行预装配后检测装配精度,通过反复拆卸并调整的方法来完成装配。采用这种装配方法会增大装配的时间和成本,同时也会对装配零件造成损坏。因此,研究装配变形的机理及其影响因素,并在设计过程中予以考虑,对提高装配效率、保证装配精度具有十分重要的指导意义。
床身是精密机床的重要部件,是安装和固定导轨的基础[5-7]。导轨安装后,受螺钉拧紧力的影响,床身会产生弹性变形,且变形呈中间大、两边小的中凸形[8]。因此,工程上通常将装配基面刮研成凹形面,以达到减小或消除装配变形的目的。这种基于经验的装配方法大大降低了装配效率,因此有必要通过优化设计来减小或消除装配变形。目前,机床基础大件的设计方法涉及刚度设计[9]、动态性能设计[10]、热平衡设计[11]和轻量化设计[12-13]等,主要是针对外形结构和内部筋板的设计[14]。常采用不同的优化设计方法对筋板结构进行尺寸优化以获得较好的床身性能,常用的设计方法有基于响应面模型的多目标优化方法[15-18]、元结构法[19-20]和仿生结构法[21]等,其中基于响应面模型的多目标优化方法是目前使用较多的。在多目标优化过程中,床身的质量、静刚度和动态性能通常是被优化的目标,而床身的装配变形却未被顾及。
本文以某精密机床床身为研究对象,从理论上分析其装配变形产生的机理及其影响因素,并运用有限元分析软件ANSYS对导轨与床身的装配进行仿真,并通过导轨与床身的装配实验来验证装配变形理论分析和仿真结果的正确性;提出考虑装配变形的机床床身优化设计方法,采用响应面模型与多目标遗传算法相结合的方法对床身进行优化,以减小其装配变形,同时使床身的质量更小、刚度更大和动态性能更优。
1 机床床身的装配变形
1.1 机床装配变形部位
机床的装配流程如图1所示。首先将待装配零件装配成组件,然后将组件进行组装。在此过程中,根据被装配零件的不同,有些装配变形会引起被装配件的整体变形,进而对机床最终的装配精度产生影响,如导轨与床身的装配、导轨与立柱的装配、导轨与溜板的装配。这些装配变形部位如图2所示。其接触面积小,螺钉受到的拧紧力矩大,易造成导轨变形。有些装配只会引起局部变形,不会对机床最终的装配精度产生影响,如立柱与床身的装配,因装配部位的接触面积较大,不会引起整个立柱变形。
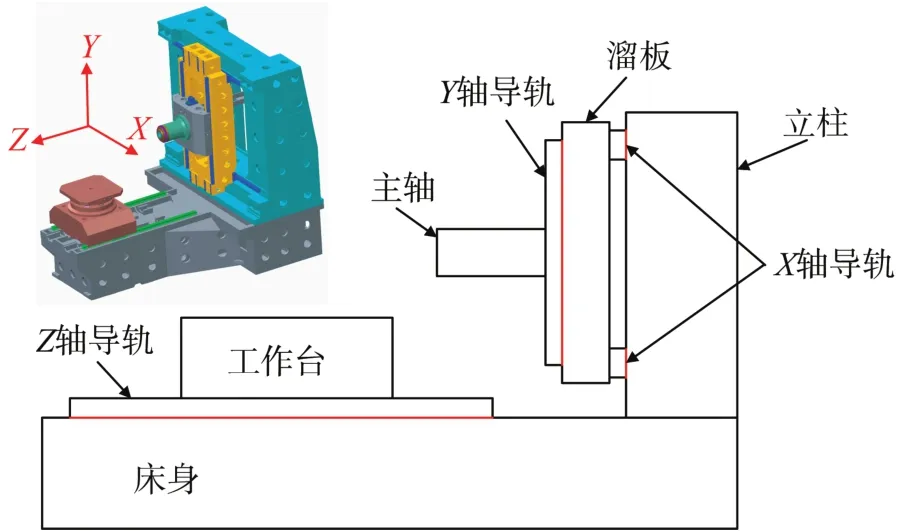
图2 机床装配变形部位Fig.2 Deformed parts of machine tool assembly
1.2 床身装配变形机理
为了研究床身装配变形的机理,以床身为研究对象,提取导轨与床身的配合部位,如图3所示。床身内部有筋板,导轨通过螺钉安装在床身上。螺钉受到的拧紧力矩为T,在螺钉孔处床身受到的向上的拉力为F,安装基面受到的向下的均布压力为Pd,则:

图3 导轨与床身的装配部位Fig.3 Assembly position of guide rail and bed

1.3 导轨与床身装配仿真
运用有限元仿真软件ANSYS分析导轨与床身的装配变形。导轨与床身装配部位的有限元模型如图4所示。在仿真中,在螺钉孔处施加向上的集中力F,在安装基面施加向下的均布力Pd,导轨与床身结合部位的刚度采用弹簧单元Combin14建立[22],在床身底部施加约束。取T=180 N·m,D=18 mm,k=1.2,筋板数量为4条,筋板厚度为25 mm。
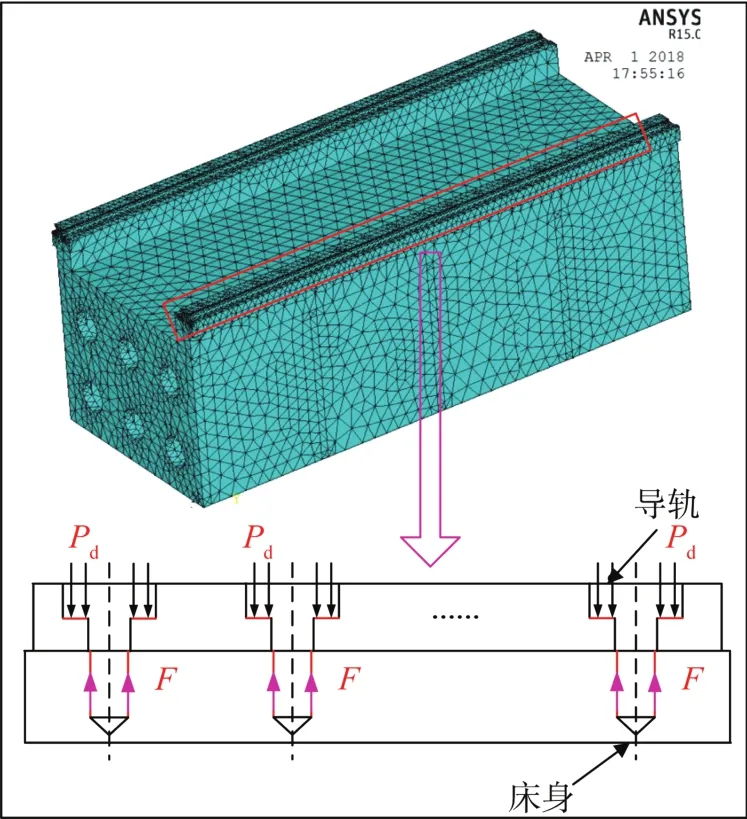
图4 导轨与床身装配部位的有限元模型Fig.4 Finite element model of assembly position of guide rail and bed
导轨与床身装配变形的仿真结果结果如图5所示。由图5(b)可知,导轨安装到床身后,受到装配应力的影响,装配变形δ呈中间大、两边小的中凸形。
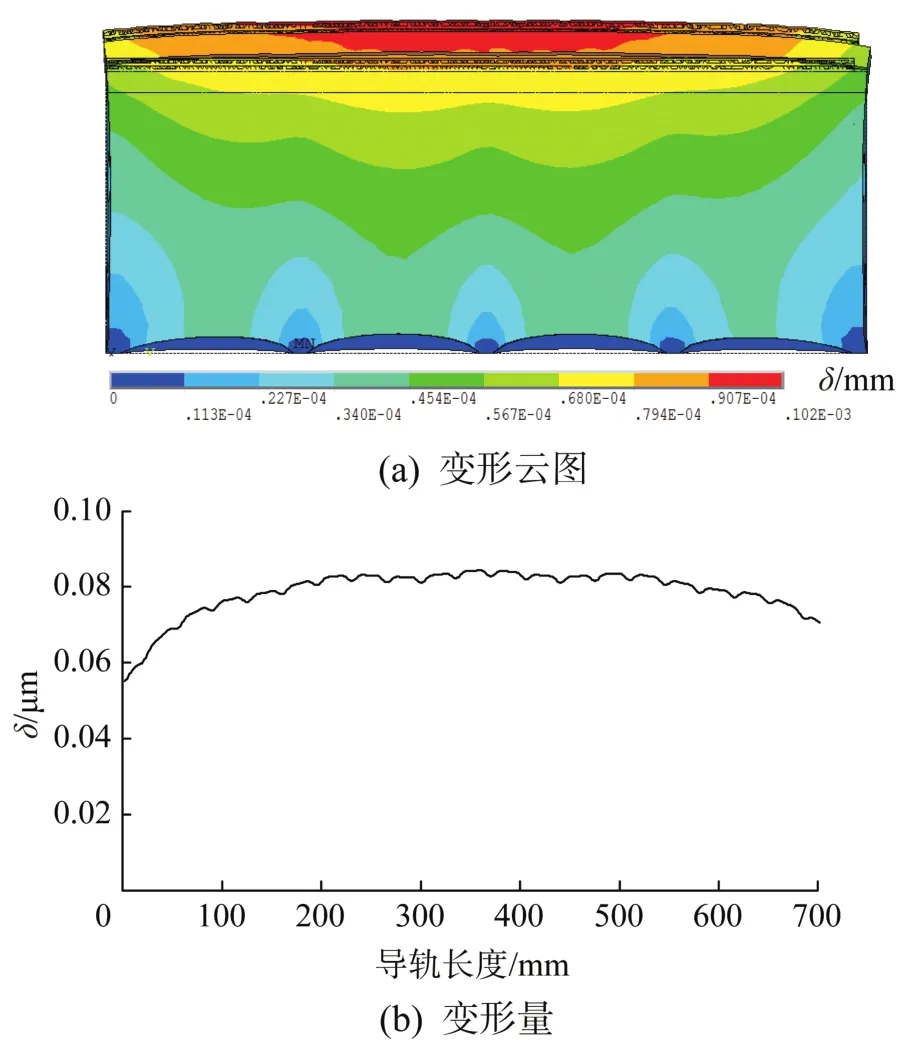
图5 导轨与床身装配变形的仿真结果Fig.5 Simulation results of assembly deformation of guide rail and bed
床身内部筋板数量和筋板厚度对装配变形有重要影响,因此有必要进行分析。当筋板厚度为25 mm,分别计算4,5,6条筋板时导轨与床身的装配变形,并以4条筋板时的装配变形幅值为基准,计算5,6条筋板时的装配变形幅值与它的比值ρ,结果如图6所示。同理,当筋板数量为4条,计算不同筋板厚度时的装配变形幅值之比,结果如图7所示。可知,装配变形均随着筋板数量和筋板厚度的增大而减小。
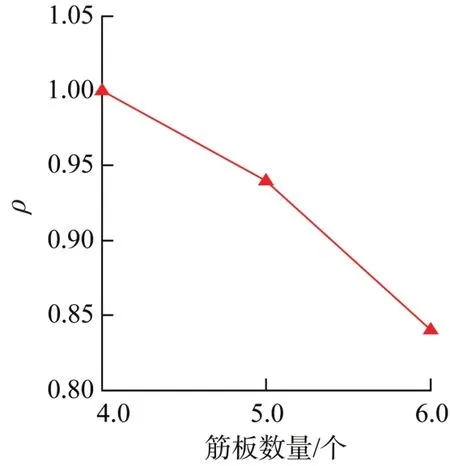
图6 床身筋板数量对装配变形的影响Fig.6 Influence of the number of the bed stiffener plat on assembly deformation
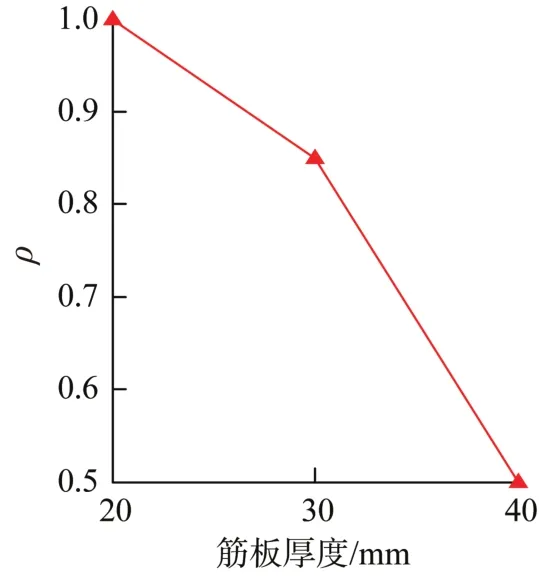
图7 床身筋板厚度对装配变形的影响Fig.7 Influence of the thickness of the bed stiffener plate on assembly deformation
1.4 导轨与床身装配实验
为了验证导轨与床身装配变形理论分析和仿真结果的正确性,在一台数控机床上进行导轨与床身装配实验,如图8所示。为了减小安装基面的制造误差对实验结果的影响,须对安装基面进行刮研。

图8 导轨与床身装配实验Fig.8 Guide rail and bed assembly experiment
实验主要包括以下几个步骤:
1)在装配导轨之前,对床身安装基面进行刮研处理,使装配前安装基面的制造误差在-2~2 μm范围以内,并用光电准直仪测量其直线度。
2)装配导轨。采用定力矩扳手从安装基面中间向两端拧紧紧固螺钉。
3)测量导轨的直线度误差。采用准直仪测量导轨在垂直方向的直线度,并记录结果。
实验结果如图9所示。由图可知,安装基面的制造误差为-2~2 μm,装配后导轨的直线度误差为13.2 μm,且基本呈中间大、两端小的中凸形,验证了仿真结果的正确性。

图9 导轨与床身装配实验结果Fig.9 Experimental results of guide rail and bed assembly
2 机床床身多目标优化设计
由以上分析可知,装配变形与机床床身的结构如筋板数量和筋板厚度等有关。如果能够在设计阶段考虑到装配变形,合理设置筋板数量和筋板厚度,则能大大提高装配精度和效率。因此,基于响应面模型和遗传算法对机床床身进行多目标优化设计,其优化设计流程如图10所示。优化过程主要包括参数设置、试验设计、响应面拟合和多目标优化等几个阶段,其主要步骤为:
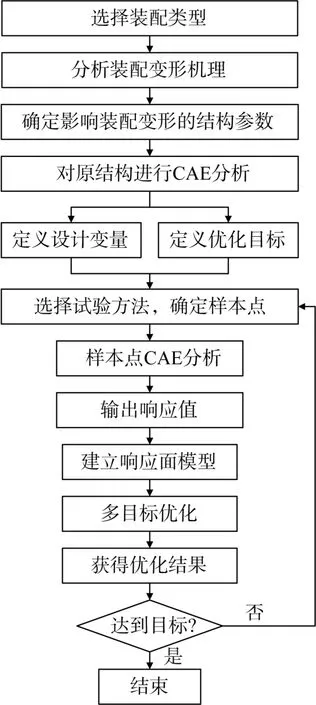
图10 机床床身多目标优化设计流程Fig.10 Multi-objective optimization design flow of machine tool bed
1)利用CAD(computer aided design,计算机辅助设计)软件建立设计对象的简化模型;
2)根据理论分析结果,确定设计变量,如筋板数量、筋板厚度和螺钉孔位置等;
3)采用合理的试验方法,如拉丁超立方体抽样技术、中心组合试验方法和正交试验方法等,选取合适的试验样本点;
4)利用CAE(computer aided engineering,计算机辅助工程)软件对所选取的试验样本点进行静力学分析、装配变形分析和模态分析,提取响应值;
5)根据响应值建立反映结构设计输入与输出关系的响应面模型;
6)运用多目标遗传算法获取响应面模型最优解集合,获取最优值;
7)对优化后的机床床身性能进行有限元分析,验证优化结果的可靠性。如果满足要求,则优化结束并输出优化结果;如果不满足要求,则重新拟合响应面,继续优化。


3 实例分析
以经典的机床床身为实例进行优化设计。机床床身的初始模型如图11所示。装配变形受到床身长度方向筋板数量x1和筋板厚度x2的影响,床身的刚度和固有频率受到床身宽度方向筋板数量x3和筋板厚度x4的影响,而这4个变量都会影响床身质量。根据经验,螺钉孔位置x5对装配变形也有重要影响,在设计中应加以考虑。因此,以x1、x2、x3、x4、x5为设计变量,以床身质量m、装配变形幅值δmax、最大静变形量Had和一阶固有频率f1为优化目标。优化原则是:m、δmax和Had尽可能小,f1尽可能高。设计变量的初始值为:x1=3条,x2=25 mm,x3=2条,x4=35 mm,x5=-45 mm(以床身侧面筋板的中心线为基准,负值表示螺钉孔位于床身外侧)。采用有限元分析方法分析床身初始的静动态特性,可得:m=1.56 t,δmax=17.2 μm,Had=0.030 2 μm,f1=559.1 Hz。
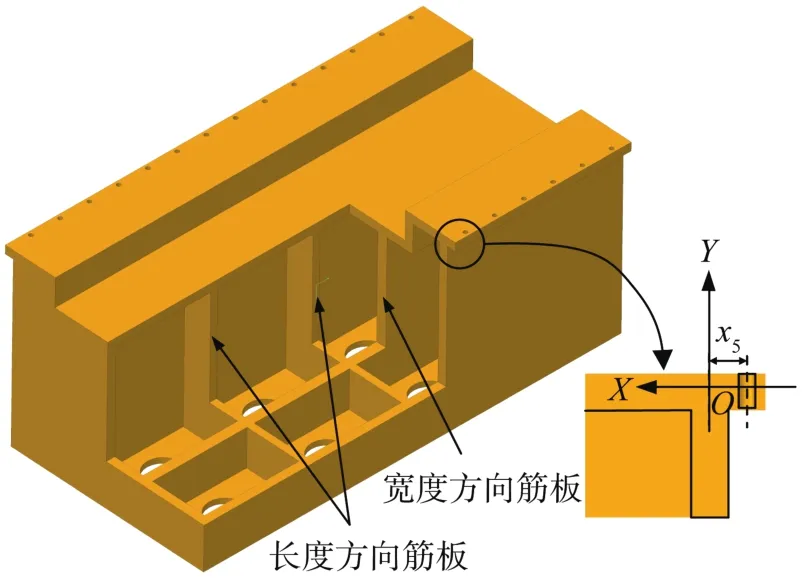
图11 机床床身的初始模型Fig.11 Initial model of machine tool bed
3.1 正交试验设计
正交试验设计是一种多因素、多层次的设计方法。该方法是根据正交性从全面试验中选取具有代表性的试验点,具有均匀性、整齐可比性等特点。根据床身的实际结构参数,设计了五水平五因素正交试验。正交试验的因素和水平如表2所示。利用有限元软件ANSYS进行了L25(55)正交试验,结果如表2所示。
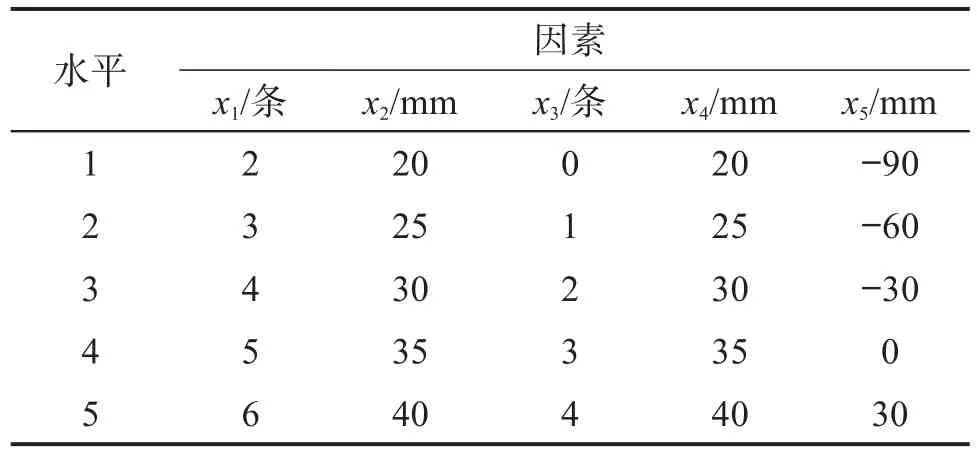
表1 机床床身优化正交试验的因素和水平Table 1 Factors and levels of orthogonal test of machine tool bed optimization
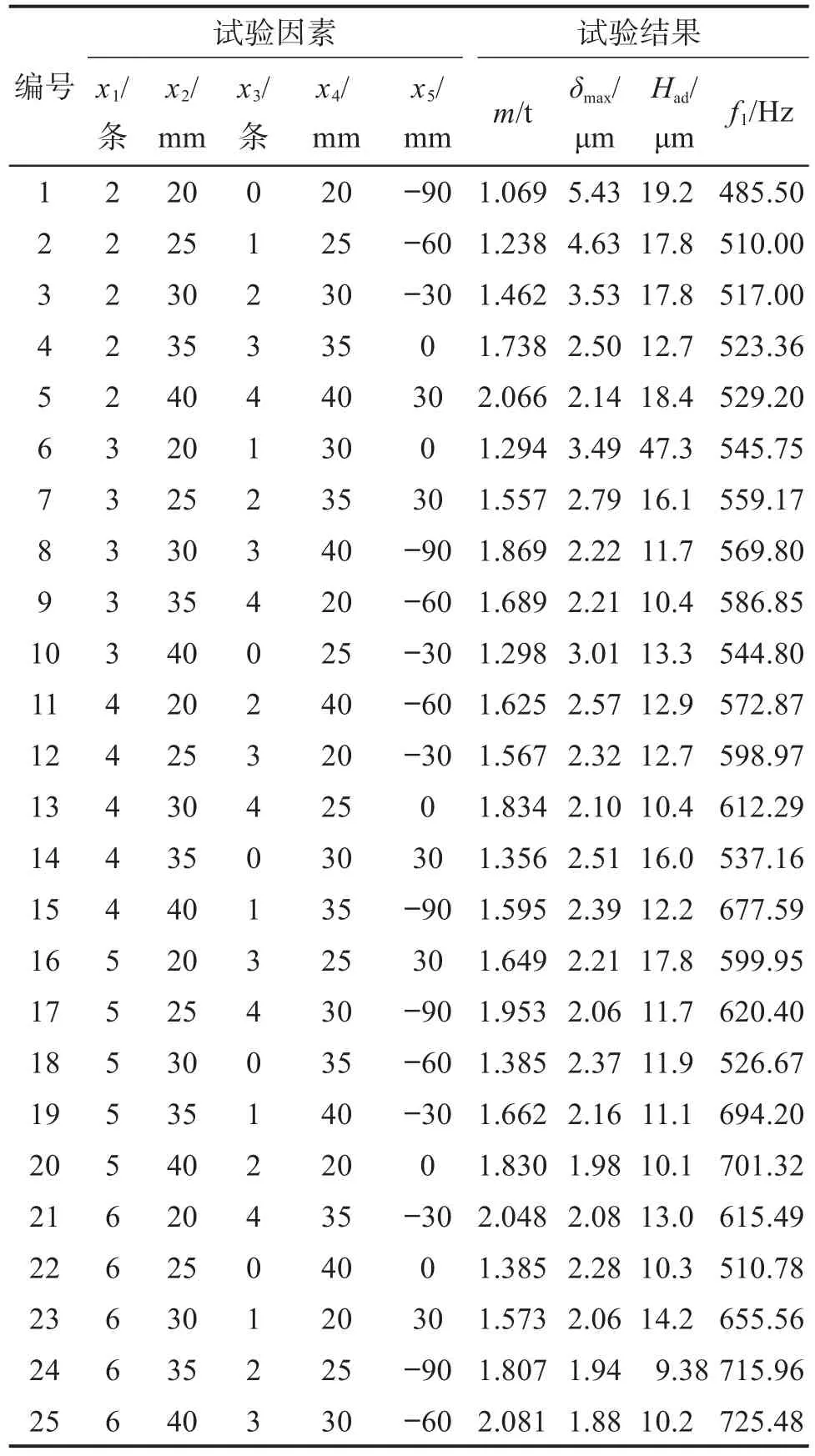
表2 机床床身优化正交试验结果Table 2 Result of orthogonal test of machine tool bed optimization
3.2 构建响应面模型
根据表2中的数据,利用MATLAB软件建立响应面模型,并对数据进行标准化处理,得到响应面函数Fm(x1,x2,x3,x4,x5)、Fδmax(x1,x2,x3,x4,x5)、FHad(x1,x2,x3,x4,x5)和Ff1(x1,x2,x3,x4,x5)。


响应面模型的拟合精度如表3所示。由表可知,模型具有较高的预测能力,为床身的优化奠定了基础。
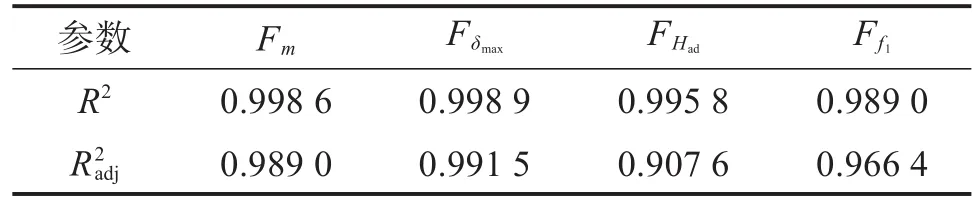
表3 响应面模型的拟合精度Table 3 Fitting accuracy of response surface model
3.3 基于遗传算法的多目标优化
根据机床床身的设计原则,内部筋板的间距不小于150 mm,筋板的厚度为30~50 mm。以m、δmax和Had最小,f1最大为优化目标,则多目标优化函数为:
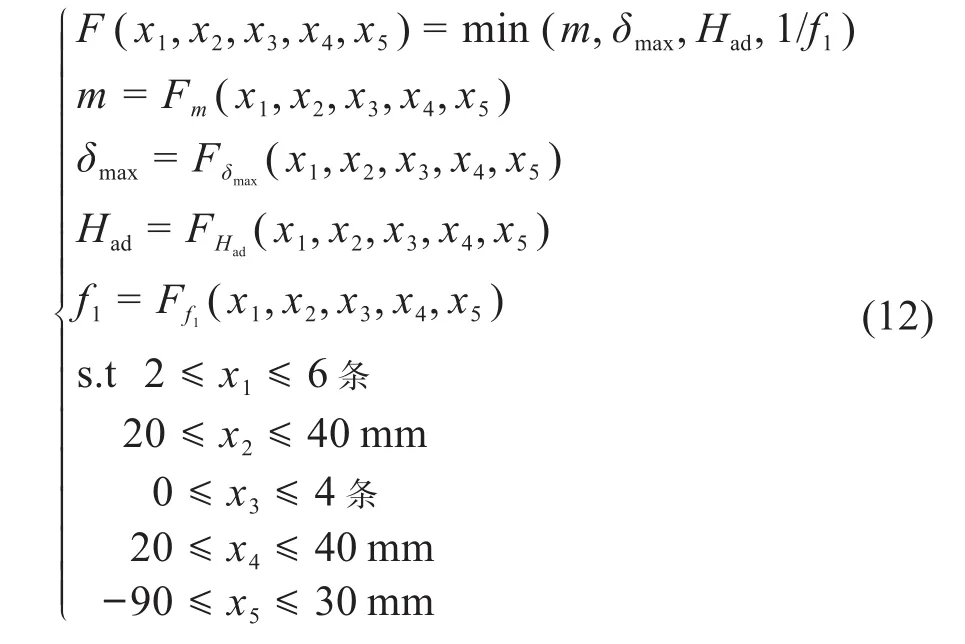
采用遗传算法求解响应面模型,并选取最优方案。优化前后机床床身的设计变量如表4所示。

表4 优化前后机床床身的设计变量Table 4 Design variables of machine tool bed before and after optimization
3.4 优化结果分析及对比
采用有限元分析软件ANSYS对优化后机床床身的结构进行仿真分析,并将优化结果与优化前作对比,结果图12和表5所示。结果表明,m减小了25.4% ,δmax减小了38.37% ,Had减小了14.90% ,f1提高了18.54% 。将螺钉孔设置在床身侧面筋板的正上方,可以减小装配变形。
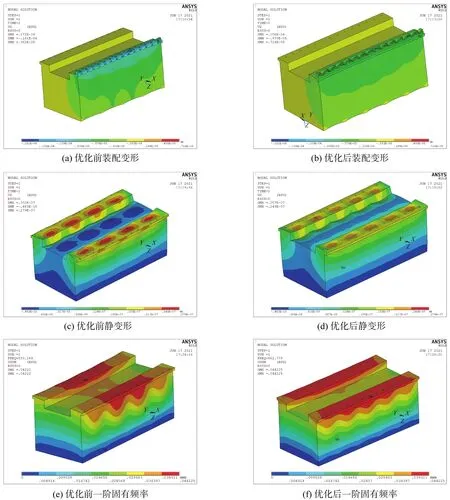
图12 优化前后机床床身有限元仿真分析结果的对比Fig.12 Comparison of finite element simulation analysis results of machine tool bed before and after optimization
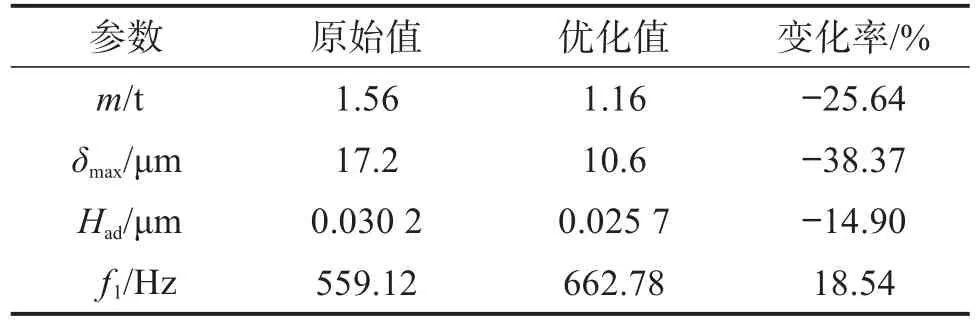
表5 优化前后机床床身动静态特性参数的对比Table 5 Comparison of dynamic and static characteristic parameters of machine tool bed before and after optimization
4 结论
装配变形是装配过程中的常见问题,经常发生在导轨与床身的装配、导轨与立柱的装配以及导轨与溜板的装配等环节。
以机床床身的结构参数为设计变量,以m、δmax和Had最小,f1最大为优化目标函数,基于响应面模型和遗传算法对床身进行多目标优化设计,得出如下结论:
1)装配变形受机床结构参数如筋板数量、筋板厚度等的影响,在设计过程中应予以考虑。
2)螺钉孔的位置是影响装配变形的重要因素之一。为有效减小导轨装配变形,螺钉孔位置应设置在床身侧面筋板的正上方。
3)考虑装配变形的机床床身优化设计方法不但为机床的优化设计提供了新的思路,也为其他类似设备的多目标优化提供了依据和参考。
