径向环形编织机机电一体化系统建模及控制策略研究

2022-07-05庄培灿李麒阳郗欣甫孙以泽

工程设计学报 2022年3期

庄培灿，李麒阳，郗欣甫，孙以泽

（东华大学机械工程学院，上海 201620）

三维编织技术发展于20世纪70年代。采用该技术编织的预制件具有纤维多向取向、整体连续分布的特点，使得三维编织复合材料的机械性能优异[1-2]，成为航空、航天领域的重要结构材料[3]，在汽车、船舶、建筑和医疗等领域也得到广泛应用[4]。编织机由编织环和牵引滑台组成，牵引滑台主要由永磁同步电机和滚珠丝杠组成。径向环形编织机的工作原理为：牵引滑台上的电机通过滚珠丝杠牵引滑台，使夹于三爪卡盘上的待编织芯轴朝编织环轴向进给运动；与此同时，编织环上的一组电机同步驱动相互啮合的齿轮转动，使与齿轮相连的拨盘相互转动，从而通过接触带动径向的携纱器按规定的8字形轨道运动，使得携纱器上的纱线对着轴向进给的芯轴缠绕编织[5]。大型径向编织机编织环上的齿轮、拨盘和携纱器数量较多，驱动功率要求大，须多个电机同步驱动才能满足其不间断运动的需求。编织环上的多个电机通过齿轮硬轴连接，从而达到转速强制同步的目的。然而，齿轮传动中齿轮啮合刚度的不同及其制造误差和齿侧间隙等的存在，易导致各电机所受负载力矩不同，从而可能引起个别电机过早出现超载甚至被烧毁[6]，因此有必要研究编织环上多个电机的转矩均衡控制方法。在预制件编织过程中，为了达到某个编织指标的要求，如使编织角达到期望值，编织环上电机组的转速与滑台电机的转速须满足比例关系[7-8]。编织环各电机之间的连接为齿轮硬轴连接，而编织环电机组与滑台电机之间并无物理连接，是相互独立的，只能通过交叉耦合控制使编织环电机组的转速与滑台电机的转速达到协同要求。在电机启动与加减速阶段，既要求编织环电机组和滑台电机快速达到各自给定的目标转速，又要求两者的速度满足协同关系，因此跟踪性能与协同性能的兼顾是研究的难点。当采用传统的交叉耦合控制方法时，在电机启动与加减速阶段，跟踪误差的补偿量较大，在输出限幅作用下，协同误差的补偿效果不明显。然而，相比于编织环电机组，滑台电机的负载明显较小，在快速达到给定转速的过程中，易出现滑台电机转速追踪过快而使达到协同要求的时间变长。因此，研究在电机启动与加减速阶段的新型控制策略以缩短达到协同要求的时间是很有必要的。

目前有关环形编织机的研究主要针对其机械传动部分。齿轮传动系统既受到时变刚度、传递误差和齿侧间隙等内部激励的影响，还受到来自电机端和负载端动态外部激励的影响，其振动现象较为复杂，并产生了极大的噪声和动载荷，因此许多学者对编织环的齿轮传动系统进行了研究。如：建立了编织环多级闭环齿轮传动模型[9]；分析了齿轮时变刚度、传递误差、齿侧间隙[10]及接触温度、时变摩擦[11]对编织环齿轮传动系统非线性动态特性的影响。目前对编织机的电气驱动部分及其控制策略研究较少。因此，笔者以某大型编织机为研究对象，分别建立编织环和牵引滑台的模型：针对编织环，建立了由88个齿轮组成的含齿侧间隙的闭环齿轮组的传动与4个永磁同步电机的驱动相耦合的机电耦合系统；针对牵引滑台，建立了电机驱动与滚珠丝杠运动相耦合的机电耦合系统。然后，根据速度协同要求对编织环和牵引滑台模型进行耦合，建立编织机机电一体化系统模型。在此基础上，针对编织环上4个电机转矩不均衡的问题，提出了转矩均衡控制方法。该方法对主电机采用速度环和电流环双环闭合控制，其他3个从电机只受电流环控制，主电机的速度环输出同时作为其他3个从电机电流环中的q轴电流给定量，以实现转矩均衡控制，既避免个别电机因过载而烧毁，又保证4个电机转速同步。针对在传统的交叉耦合控制下，在电机启动与加减速阶段编织环电机组与滑台电机达到协同要求所需时间较长的问题，提出了跟踪性能与协同性能解耦控制的交叉耦合解耦控制方法，将跟踪误差补偿量按一定的比例缩小至幅值以下，从而在速度环输出限幅的作用下保证协同误差补偿量不被大幅削弱，缩短达到协同要求的时间。最后进行现场实验，来验证上述所提方法的有效性和可靠性。

1 编织环齿轮闭环传动数学模型

以某大型径向编织机为研究对象。该编织机编织环上的4个电机等间隔分布于88个齿轮之间，驱动88个齿轮形成闭环传动。将编织环上的4个电机设为主机1、从机2、从机3和从机4，将88个齿轮按顺时针方向依次设为齿轮1、齿轮2、……、齿轮88，其中主机1通过减速器与齿轮1连接，从机2通过减速器与齿轮23连接，从机3通过减速器与齿轮45连接，从机4通过减速器与齿轮67连接。编织环上齿轮与电机的位置关系如图1所示。

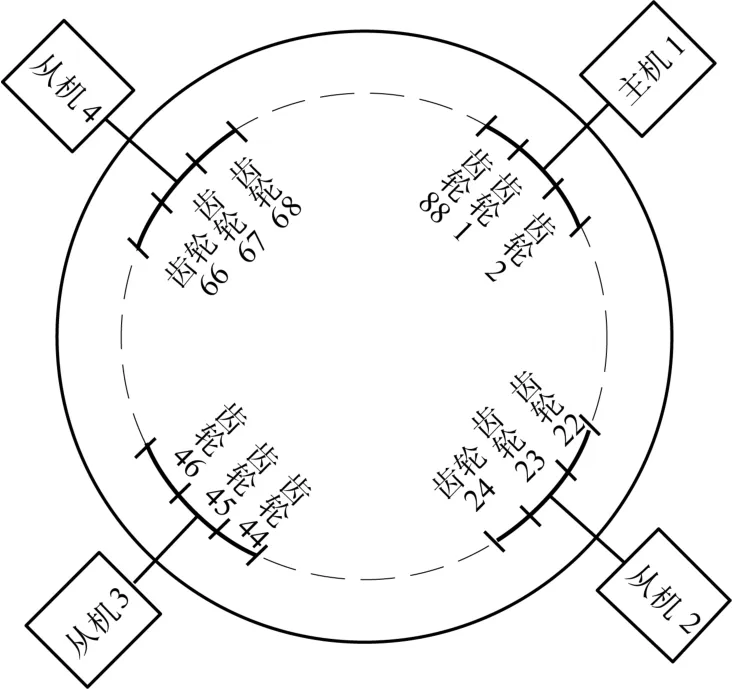
图1 编织环上齿轮与电机的位置关系Fig.1 Position relationship between gear and motor on braided ring

考虑齿轮时变刚度、静态传递误差和齿侧间隙，采用集中质量法建立齿轮闭环传动数学模型。齿轮闭环传动满足：

式中：Tg(i-1)，i为齿轮i-1 对齿轮i的力矩；Tg(i+1)，i为齿轮i+1对齿轮i的力矩；Tgri为携纱器对齿轮i的作用力矩；Jgi为齿轮i的转动惯量；θgi为齿轮i的转角。

式（1）中齿轮89即为齿轮1，且满足如下的动力学公式：

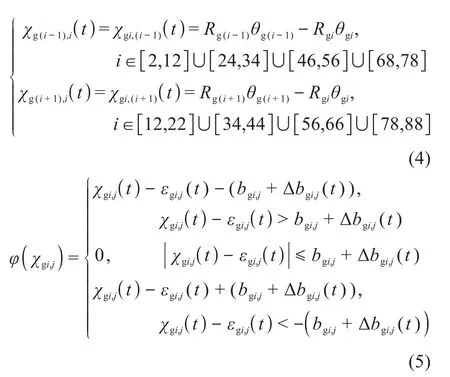
式中：j=i-1或j=i+1；Rgj为齿轮j的基圆半径；Wgi，j为齿轮i与齿轮j的动啮合力；Cgi，j为齿轮i与齿轮j的啮合阻尼系数；Kgi，j为齿轮i与齿轮j的啮合刚度系数；ΔKgi，j为齿轮i与齿轮j的啮合刚度系数的随机扰动量；χgi，j为齿轮i与齿轮j的动态传递误差；εgi，j为齿轮i与齿轮j的静态传递误差；bgi，j为齿轮i与齿轮j的齿半侧间隙；Δbgi，j为齿轮i与齿轮j的齿半侧间隙的随机扰动量；φ(χgi，j)为间隙满足一级刚度间隙模型时所对应的间隙函数。

2 编织环机电一体化数学模型

2.1 永磁同步电机有限控制集模型预测电流控制

永磁同步电机（permanent magnet synchronous motor，PMSM）具有功率密度高、可靠性好、结构简单等优越性能[12-14]。模型预测电流控制（model predictive current control，MPCC）是一种根据受控对象的当前状态及其数学模型预测受控系统未来状态，再通过价值函数在线寻优的控制方法[15]，具有较好的动态响应性能，得到了越来越多学者的青睐[16]。MPCC通常包含广义模型预测电流控制和有限控制集模型预测电流控制（finite control set model predictive current control，FCS-MPCC）两大类[17-18]。FCS-MPCC的主要优点是控制概念简单、实时性强及易于处理多目标和非线性约束问题[19-20]。

表贴式永磁同步电机在两相旋转坐标系（dq坐标系）下的定子电流状态方程为：

式中：Ls为定子电感；Rs为定子电阻；Ud、Uq分别为d、q轴电压；id、iq分别为d、q轴电流；ωe为转子电角速度；ψf为永磁体磁链。

对式（6）和式（7）离散化，可得预测的d、q轴电流为：

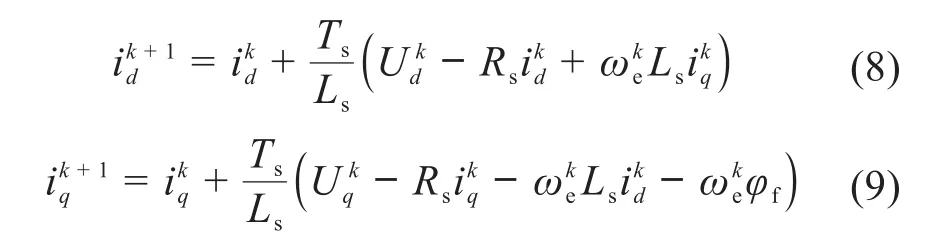
式中：k为当前时刻采样序号；k+1为下一时刻采样序号；Ts为采样周期分别为当前时刻的d、q轴电流值分别为下一时刻的d、q轴电流预测值；分别为当前时刻的d、q轴电压为当前时刻的转子电角速度。

该模型采用两电平电压源逆变器作为PMSM的驱动电源。该逆变器共有8种开关序列，能够产生8个基本电压矢量U（ii=0，1，…，7）。各基本电压矢量与对应的开关[sa，sb，sc]及其在两相静止坐标系（αβ坐标系）下α、β轴分量[Uα，Uβ]的关系如表1所示。其中：Udc为直流母线电压；sa、sb、sc表示上半桥臂的开关状态，其值等于0或1，0表示开关断开，1表示开关导通。

表1 基本电压矢量与开关序列的对应关系Table 1 Correspondence between basic voltage vector and switching sequence

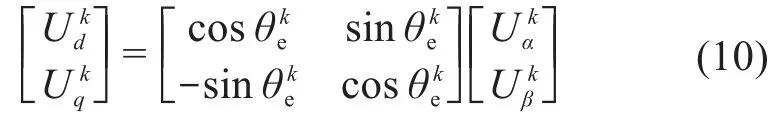
FCS-MPCC的价值函数gk选为：

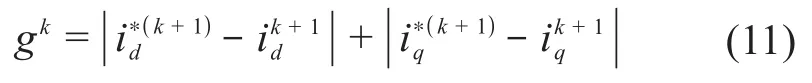
FCS-MPCC的工作原理为：首先，在每个采样时刻分别遍历8种开关序列所产生的8个基本电压矢量，根据表1及式（10）计算出8种开关序列下的；其次，将代入式（8）、式（9）即电流预测公式，预测出8种开关序列作用下各；最后，通过式（11）确定使价值函数最小的基本电压矢量及其对应的开关序列，并将该开关序列作用于逆变器。

2.2 编织环机电一体化与转矩均衡控制

编织机连续转动所需的驱动功率较大，一般采用多个电机共同驱动。

模型中编织环上的4个永磁同步电机通过齿轮硬轴连接使其转速强制同步。然而，由于编织机负载大，且负载跨距大，再加上齿轮时变刚度和齿侧间隙的存在，即使每个电机的型号完全相同，也难免会造成各电机载荷分配不均衡。为了解决该问题，本文采用转矩均衡控制策略，即：主机1受速度环和电流环双环闭合控制，其他3个从机只受电流环控制。主机采用的控制策略，速度环采用比例积分（proportional integral，PI）控制。PI控制器的输出量即为主机q轴电流的给定量，同时也作为其他3个从机的电流环给定量，电流环控制采用上文所提的FCSMPCC。编织环机电一体化与转矩均衡控制系统框图如图2所示。

图2 编织环机电一体化与转矩均衡控制系统框图Fig.2 Block diagram of mechatronics of braided ring and its torque balance control system

图2中，PMSM3、PMSM4的控制结构与PMSM2相同，故没有具体展开。KP1、KI1分别为主电机PI控制器的比例系数和积分系数；r为编织环电机减速器的减速比为相应齿轮通过减速器传动后对编织环4个电机的负载力矩为编织环电机的驱动力矩；kτ为电机转矩系数；Je为电机的转动惯量；Be为电机的黏性阻尼系数；p为极对数为电机转子机械转角为电机转子机械角速度为电机转子的三相电流为电机转子的α、β轴电流；nk为电机实际转速；n*k为转速给定量。

表贴式永磁同步电机在dq坐标系下的电磁力矩方程为：

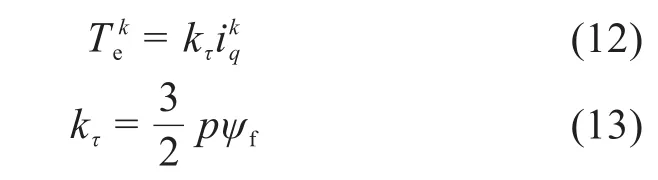
dq坐标系下永磁同步电机的运动方程为：

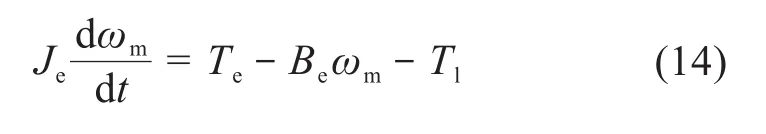
3 编织机机电一体化与解耦控制

3.1 编织机机电一体化与传统交叉耦合控制

编织环电机转速与滑台电机转速须满足比例关系，因此将编织环4个电机视为一个整体，编织环主电机与滑台电机采用交叉耦合控制。其传统交叉耦合控制系统框图如图3所示。

图3 编织环主电机与滑台电机传统交叉耦合控制系统框图Fig.3 Block diagram of traditional cross coupling control system for braided ring main motor and sliding table motor

在编织环主电机与滑台电机的传统交叉耦合控制中，ek由ek1和ek5组成，作为PI控制器的输入量，其中：

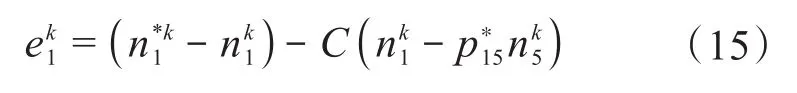
3.2 编织机机电一体化与交叉耦合解耦控制

基于传统交叉耦合控制策略，笔者提出一种跟踪误差补偿量与协同误差补偿量解耦控制策略，即将跟踪误差和协同误差解耦出来，分别作为PI控制器的给定量，控制器输出的跟踪误差补偿量与协同误差补偿量不直接耦合，而是通过跟踪误差补偿量限幅修正器将跟踪误差补偿量按一定比例缩小至限幅值iqmax以下再耦合。交叉耦合解耦控制系统框图如图4所示。

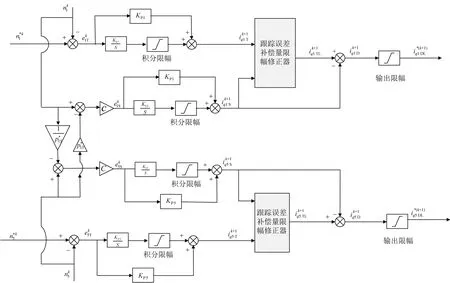
图4 编织环主电机与滑台电机交叉耦合解耦控制系统框图Fig.4 Block diagram of cross coupling decoupling control system for braided ring main motor and sliding table motor

跟踪误差补偿量限幅修正器修正如下：

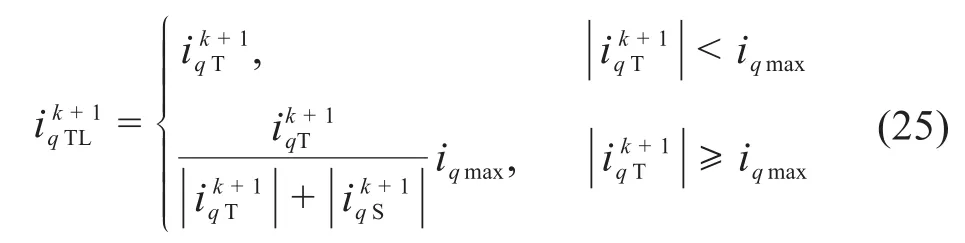
相比编织环主电机，滑台电机所受负载较小，加速度较大，转速大于相应的协同转速，须在协同误差补偿量的作用下使最终FCS-MPCC的q轴电流给定量小于跟踪误差补偿量。在电机启动阶段，由于实际转速与给定转速相差很大，跟踪误差补偿量会超出限幅值。传统交叉耦合控制中直接将跟踪误差补偿量与协同误差补偿量相减作为q轴电流给定量，该给定量仍大于限幅值，此时在输出限幅的作用下，协同误差补偿失效，系统协同性能较差。采用所提出的交叉耦合解耦控制，能够有效解决该问题，缩短系统达到协同要求的时间。电机启动阶段在传统交叉耦合控制和交叉耦合解耦控制下电流输出量的对比如图5所示。

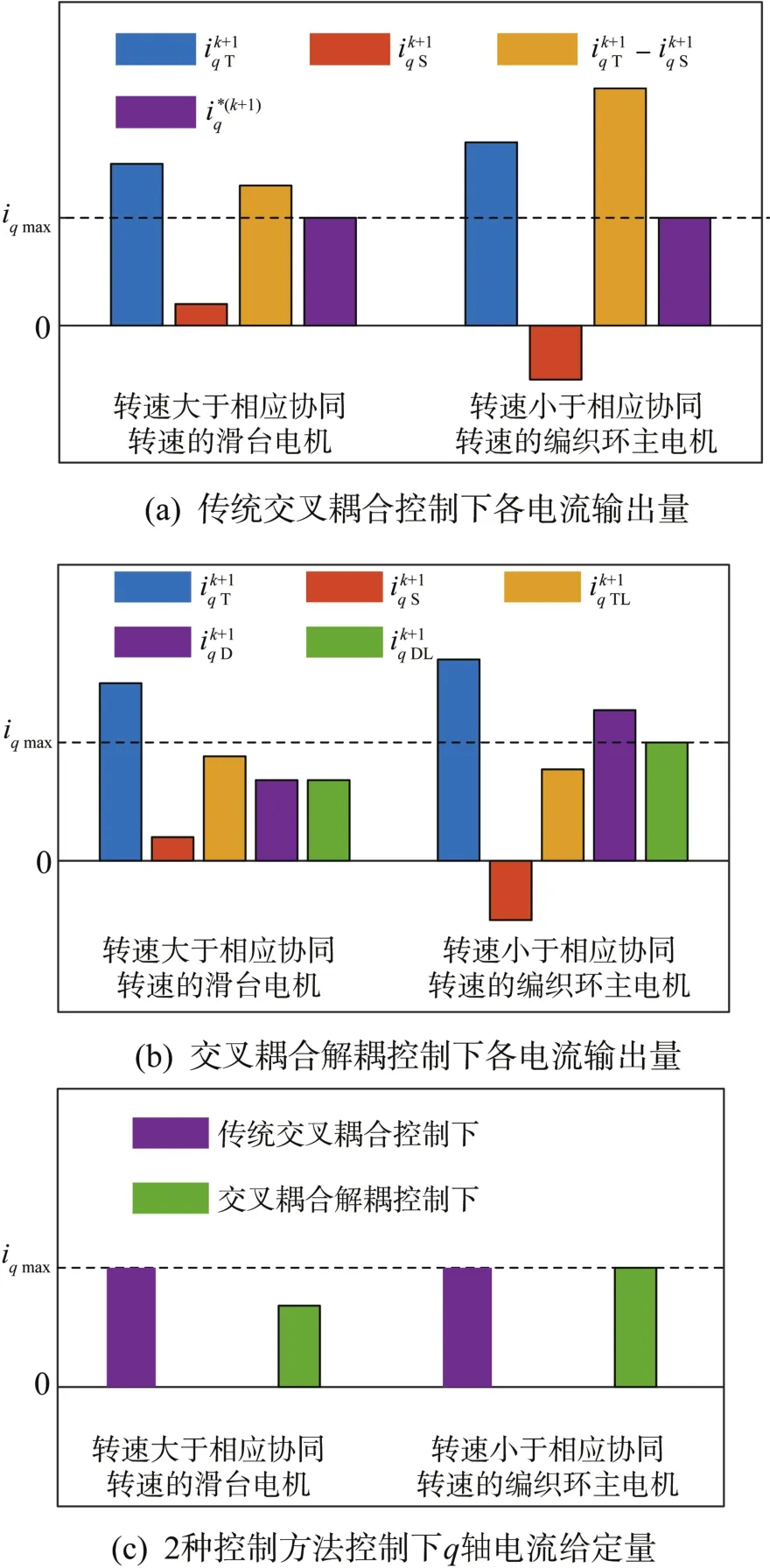
图5 电机启动阶段在传统交叉耦合控制与交叉耦合解耦控制下电流输出量的对比Fig.5 Comparison of current output under traditional cross coupling control and cross coupling decoupling control during motor starting

由图5可知：在电机启动阶段，对于转速大于相应协同转速的滑台电机，在传统交叉耦合控制下最终以作为FCS-MPCC的q轴电流给定量，协同误差补偿失效；在交叉耦合解耦控制下最终以作为FCS-MPCC的q轴电流给定量，确保协同误差补偿不失效。对于转速小于相应协同转速的编织环主电机，2种控制方法的作用相同。

4 实验验证

为了验证所提出控制方法的有效性和可靠性，进行了现场实验。实验中编织环电机与滑台电机的型号相同，其具体参数为：Udc=220 V，Ls=5.235 mH，Rs=0.958 Ω，Je=0.001 2kg⋅m2，p=4 对，ψf=0.192 Wb。径向环形编织机如图6所示，其伺服控制系统如图7所示。

图6 径向环形编织机Fig.6 Radial ring braiding machine

图7 径向环形编织机的伺服控制系统Fig.7 Servo control system of radial ring braiding machine

4.1 编织环电机并行控制与转矩均衡控制的对比

在并行控制和转矩均衡控制两种控制方式下控制器参数设置相同，速度环采样频率为1 kHz，电流环采样频率为 10 kHz，KP=0.586，KI=23，积分限幅值设置为6 A，输出限幅值设置为10 A，给定转速n*=1 000 r/min。在2种控制方式下编织机电机启动后第60秒至第61秒内电机转速和转矩如图8和图9所示。

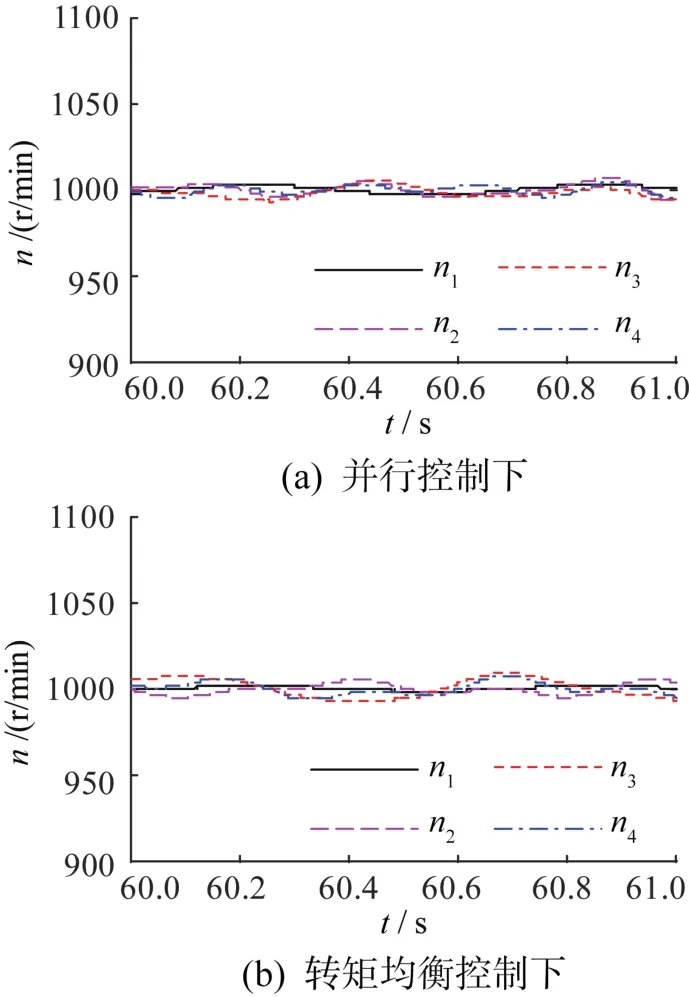
图8 编织机电机的转速Fig.8 Speed of braiding machine motor

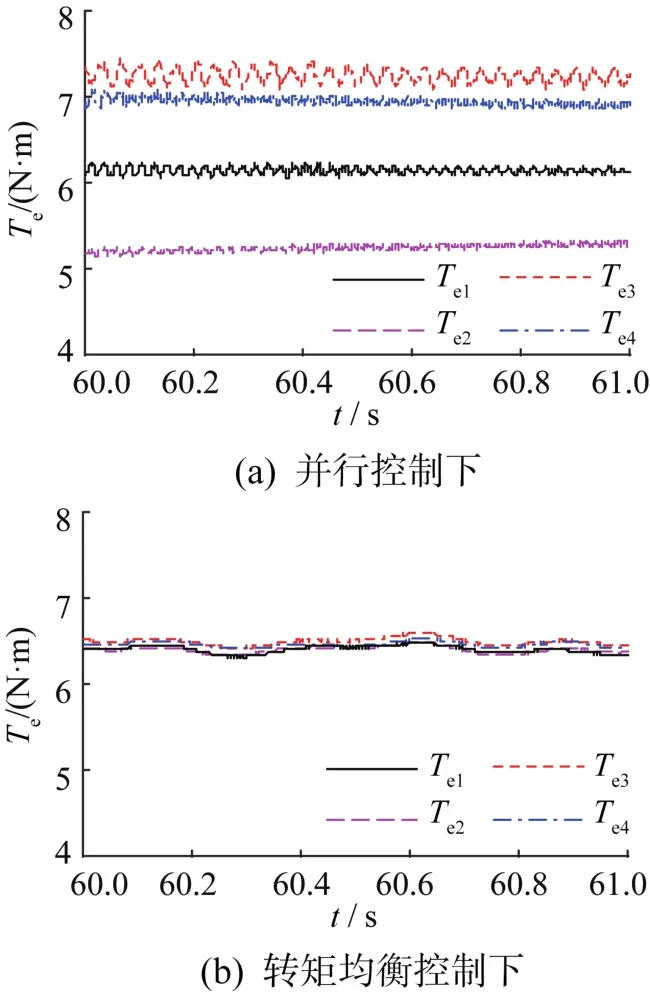
图9 编织机电机的转矩Fig.9 Torque of braiding machine motor

由图8可知，在2种控制方法下编织环4个电机的转速均达到了协同要求，差别不明显。由图9可知，与转矩均衡控制方法相比，在并行控制下编织环4个电机的输出转矩差别较大，最大输出转矩与最小输出转矩相差达2N⋅m，因此在重载下容易导致输出转矩较大的电机过载甚至被烧毁。

4.2 传统交叉耦合控制与交叉耦合解耦控制的对比

设置编制环主电机与滑台电机同时启动，编制环主电机给定转速为1 000 r/min，滑台电机给定转速为500 r/min；经过0.5 s后，主电机给定转速为200 r/min，滑台电机给定转速为100 r/min；速度协同关系为比例关系。在传统交叉耦合控制和交叉耦合解耦控制两种控制方式下控制器参数设置均相同，C=15，其他参数设置与上个实验相同。在2种控制方法下编织环主电机及滑台电机的转速和实际转速比p15如图10和图11所示。

图10 编织环主电机及滑台电机的转速Fig.10 Speed of braiding machine main motor and sliding table motor

图11 编织环主电机及滑台电机的实际转速比Fig.11 Actual speed ratio of braiding machine main motor and sliding table motor

由图10和图11可知：在电机启动阶段，在传统交叉耦合控制下，刚开始时滑台电机转速过大，与编织环主电机的转速基本相同，实际转速比p15与实验设置的比例系数偏差较大，在2个电机均达到给定转速后p15才满足协同要求，其达到协同要求的时间为0.125 s；在交叉耦合解耦控制下，2个电机的转速比一开始已接近，其达到协同要求的时间为0.02 s，相比传统交叉耦合控制缩短了84% 的时间。在减速阶段，在传统交叉耦合控制下p15会发生突变，最后趋于给定比例；而在交叉耦合解耦控制下p15无突变。证明了在交叉耦合解耦控制下在电机启动与加减速阶段编织环主电机与滑台电机的转速达到协同要求的时间可以大幅度缩短。