连续体结构的变密度拓扑优化方法研究
2022-07-05王景良朱天成朱龙彪许飞云
王景良,朱天成,朱龙彪,许飞云
(1.江苏海事职业技术学院轮机电气与智能工程学院,江苏 南京 211100;2.中国联合网络通信集团有限公司江苏省分公司,江苏 南京 211100;3.南通大学机械工程学院,江苏 南通 226019;4.东南大学机械工程学院,江苏 南京 211100)
拓扑优化是实现结构轻量化的一种有效的设计方法,蕴含如现代力学、现代数学、计算机科学等多学科知识。通过拓扑优化可产生材料分布合理、性能各异、质量最小的结构设计方案,故其已成为结构优化设计的热点研究方向[1]。于20世纪90年代提出的备受关注的变密度法作为连续体结构拓扑优化设计的一种主流方法,因自身所具备的技术优势而在航空航天、建筑、机械等领域的结构优化设计中得到广泛应用[2-5]。如:为了实现高速列车底架的轻量化设计,陈秉智等[6]采用基于OptiStruct软件的变密度法对高速列车的底架进行拓扑优化设计,获得了可同时满足强度、刚度及模态频率等设计要求且应力分布得到改善的优质轻质底架;为了得到轻质和性能完善的汽车用挡位互换机构,王铭昭等[7]也采用基于OptiStruct软件的变密度法对挡位互换机构的壳体进行了拓扑优化设计;周围等[8]借助基于ANSYS Workbench软件的变密度法研究了岩心钻机送杆机构运送支架的拓扑优化设计问题,得到了新型轻质运送支架。
尽管变密度法有诸多优点,但所得优化结构普遍存在如棋盘格、网格依赖及灰度单元等数值不稳定问题[9]。为了解决此类问题,学者们提出了如密度过滤法、敏度过滤法、灰度单元抑制算子等多种方法[10-13]。Biyikli等[14]采用一种简单有效的改进密度过滤法解决了采用变密度法引起的结构棋盘格问题。张国锋等[15]为了消除采用变密度法引起的棋盘格、网格依赖和边界扩散等问题,在保留原卷积因子的基础上,通过引入新卷积因子,提出了一种改进敏度过滤方法。高翔等[16]为了解决采用变密度法引起的灰度单元和现有Heaviside函数须频繁调用密度矩阵的问题,结合优化准则法和Heaviside函数,设计了基于改进Heaviside函数的拓扑优化方法。廉睿超等[17]从变密度法的材料插值方案出发,提出了一种灰度单元分层双重惩罚方法,在有效抑制灰度单元产生的同时提高了拓扑优化的收敛速度。但是,目前所提出的策略或方法尚不能很好地兼顾解决多类型的数值不稳定问题与改进拓扑优化方法。
为了解决体积约束和柔顺度最小的结构拓扑优化问题及采用变密度法引起的数值不稳定问题,以兼顾改进拓扑优化方法为前提,引入改进的固体各向同性材料惩罚(solid isotropic material with penalization,SIMP)法和基于高斯权重函数的敏度过滤法,并设计新的灰度单元抑制算子,对由变密度法和优化准则法形成的经典拓扑优化方法进行改进,提出了一种新的拓扑优化方法。
1 连续体结构拓扑优化
采用新的拓扑优方法研究连续体结构的优化设计问题,需要确定材料插值方案、建立结构拓扑优化模型、设计灵敏度、确定敏度过滤法、确定更新准则及给出评价指标等几个步骤。
1.1 基于改进SIMP法的材料插值方案
采用能在0与1之间连续取值的基于SIMP法的材料插值方案可以有效降低结构优化设计的难度。参考Andreassen等[18]的研究成果,目前应用较为普遍的材料插值方案为:
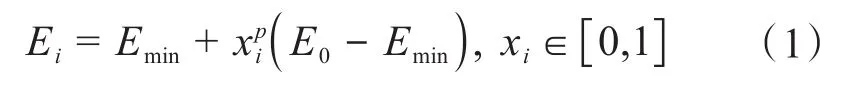
式中:E0为实体材料的弹性模量;Emin为无效材料的弹性模量;p为无效材料的惩罚系数;xi为拓扑设计变量,i=1,2,…,n;Ei为当量弹性模量。
通过进一步研究发现,式(1)所示的插值方案对改进拓扑优化方法的效果有限。为了进一步改进拓扑优化方法,采用Zhu等[19]提出的改进SIMP法构建材料插值方案,具体如下:
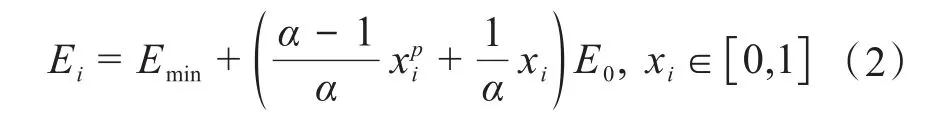
式中:α为调整系数。
须说明的是,文献[19]提出的材料插值方案中并没有Emin,此处加入Emin的目的是规避奇异刚度矩阵的产生和确保xi的下限值可取0。
1.2 结构拓扑优化模型
建立优化模型是开展结构拓扑优化设计的前提。在式(2)的基础上,参考文献[9,18],则使结构柔顺度最小的拓扑优化模型为:
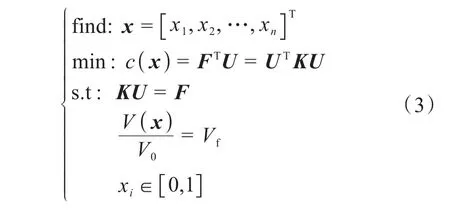
式中:x为结构拓扑设计变量的矢量;c为结构柔顺度;K为结构的刚度矩阵;U为载荷矢量F作用在结构上而产生的位移矢量;V0和V分别为结构设计域的材料体积和结构优化设计后的材料体积;Vf为优化结构的许用材料体积分数。
1.3 灵敏度
采用经典优化准则法求解式(3)所示的优化模型时,须设计目标函数和约束关于拓扑设计变量xi的灵敏度。根据文献[18],基于式(2)和式(3),求解c和V关于xi的灵敏度:
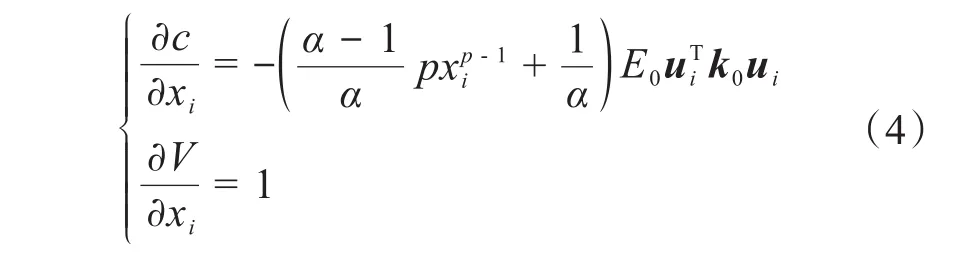
式中:ui为单元的位移矩阵;k0为具有单位弹性模量的刚度矩阵。
1.4 基于高斯权重函数的敏度过滤法
为了有效解决采用变密度法引起的数值不稳定问题及改进拓扑优化方法,选用合适的敏度过滤法极为重要。Cheng等[20]发现,采用基于高斯权重函数的敏度过滤法可以得到轻质且拓扑构型好的优化结构。本文采用基于高斯权重函数的敏度过滤法对c关于xi的灵敏度进行过滤处理,具体为:

式中:γ为为了规避当xi取为0时式中分母为0而引入的一个较小正值参数;Ni为与单元i相邻的单元j所组成的集合;Hi,j为敏度过滤的权重系数。
根据文献[10,20],得到:
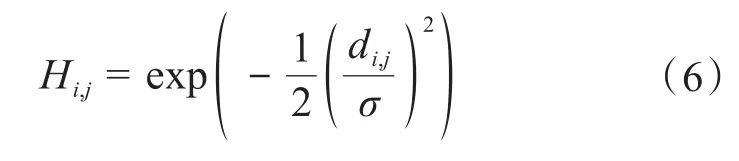
式中:di,j为单元i、j之间的距离;σ为高斯参数,与过滤半径R有关。
1.5 基于新灰度单元抑制算子的更新准则
基于优化准则法求解式(3)时,需要一种启发式更新准则。根据文献[18],常用的更新准则为:
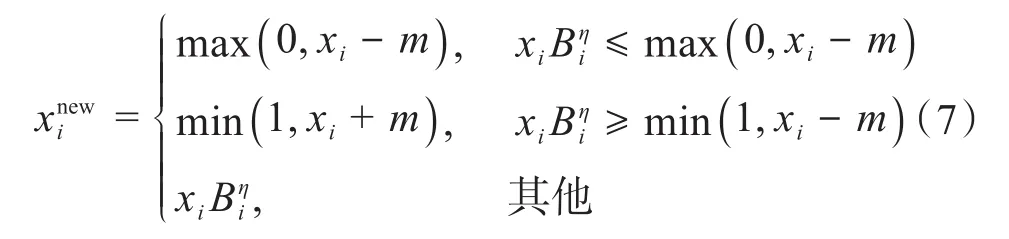
式中:m和η分别为正值移动步长和阻尼系数;xi与的结合物可以视为简单的灰度单元抑制算子,用于更新xi。
中间变量Bi为:

式中:λ为拉格朗日乘子,可通过二分法计算得到。
为了有效抑制灰度单元的产生,受Groenwold等[21]提出的灰度单元抑制算子的启发,在原灰度单元抑制算子的基础上,引入正值比例参数β,设计了一种新的灰度单元抑制算子,为:
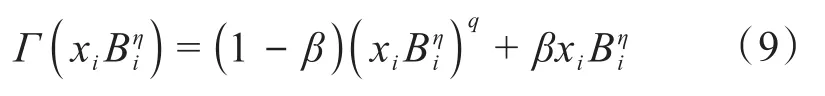
式中:q为灰度抑制参数。
为了提高拓扑优化方法的收敛速度,在综合考虑每次迭代计算所得的结构柔顺度的基础上,设计了新的参数q的更新方案,具体为:
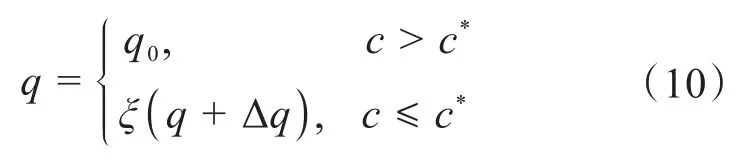
式中:q0和Δq分别为q的初值和增量;ξ和c*分别为强度因子和结构柔顺度的临界值。
须说明的是,通过测试发现,c*值设置合理与否会对优化结构的柔顺度、拓扑构型及拓扑优化方法的收敛速度产生较大影响。
根据式(7)和式(9),基于新灰度单元抑制算子的更新准则为:

1.6 评价指标
选择结构的柔顺度c、程序循环执行次数I和灰度单元比例指数G作为评价拓扑优化方法的指标。其中:c用于反比表征获取柔顺度小的优化结构的能力;I用于反比表征收敛速度或收敛性能;G用于反比表征抑制灰度单元产生的能力。
参考文献[9],可得:
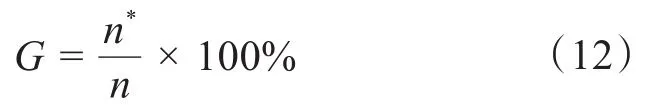
式中:n*为满足约束条件(xi< 0.01或xi> 0.99)的单元数量。
2 算例分析与讨论
采用2个经典的数值算例,分别测试改进SIMP法、基于高斯权重函数的敏度过滤法、新灰度单元抑制算子和新拓扑优化方法对其的优化效果,并与采用文献[14,8]提出的拓扑优化方法的优化结果进行对比。设置与文献[14,18]相同的基本参数:E0=1 MPa,Emin=1×10-9MPa,材料泊松比υ=0.3,p=3,m=0.2,η=1×10-3。采用双线性矩形单元对结构进行网格划分。另外,须特别说明的是,本文设计的拓扑优化方法的程序是在文献[18]所提出方法代码的基础上编写的,本文方法与文献[18]方法的区别在于材料插值方案、敏度过滤法和灰度单元抑制算子这几点上。
2.1 算例1
MBB(Messerschmitt-Bolkow-Blohm)梁结构如图1所示。其几何尺寸为280 mm×50 mm,顶端中部承受大小为2 N的外载荷F。对MBB梁结构进行拓扑优化,来测试采用改进SIMP法、基于高斯权重函数的敏度过滤法、新灰度单元抑制算子和新拓扑优化方法的优化效果。根据对称性,采用具有1/2设计域的MBB梁为优化对象。对梁结构进行网格划分,可以得到单元总数量为140×50个的有限元模型。设置R=3.1,Vf=0.4。
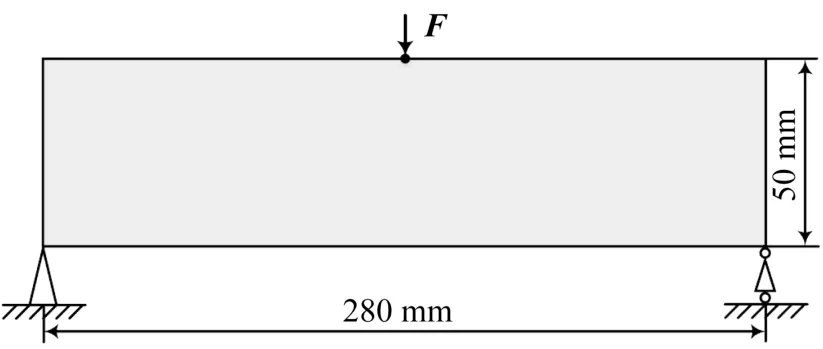
图1 MBB梁结构Fig.1 MBB beam structure
不同SIMP法下MBB梁结构的拓扑构型和优化结果分别如图2和表1所示;在本文SIMP法下,采用不同敏度过滤法得到的结构拓扑构型和优化结果分别如图3和表2所示;在本文SIMP法和敏度过滤法下,采用不同灰度单元抑制算子得到的结构拓扑构型和优化结果分别如图4和表3所示;在不同拓扑优化方法下结构拓扑构型和优化结果分别如图5和表4所示。

图2 不同SIMP法下MBB梁结构的拓扑构型Fig.2 Topological configuration of MBB beam structure under different SIMP methods
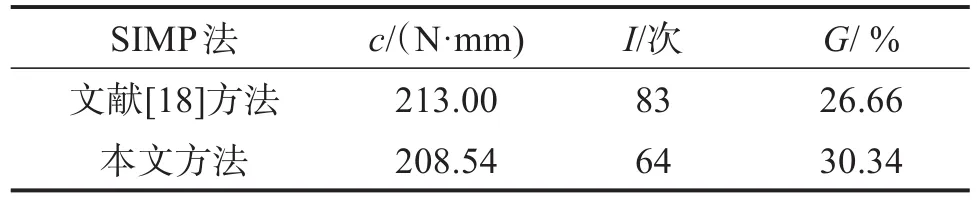
表1 不同SIMP法下MBB梁结构优化结果Table 1 Optimization results of MBB beam structure under different SIMP methods

图3 不同敏度过滤法下MBB梁结构的拓扑构型Fig.3 Topological configuration of MBB beam structure under different sensitivity filtration methods
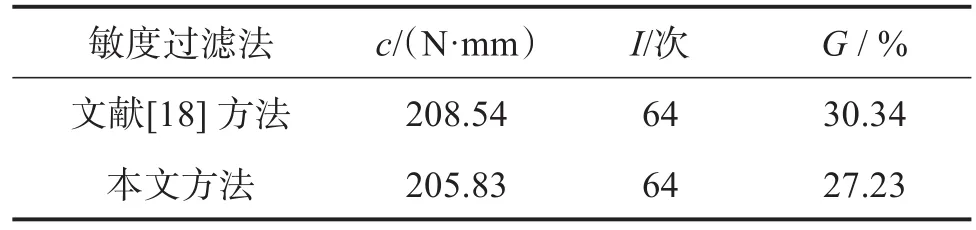
表2 不同敏度过滤法下MBB梁结构优化结果Table 2 Optimization results of MBB beam structure under different sensitivity filtration methods

图4 不同灰度单元抑制算子下MBB梁结构的拓扑构型Fig.4 Topological configuration of MBB beam structure under different gray-scale unit suppression operators
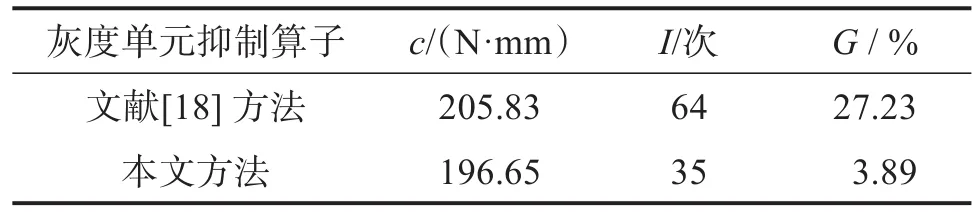
表3 不同灰度单元抑制算子下MBB梁结构优化结果Table 3 Optimization results of MBB beam structure under different gray-scale suppression operators
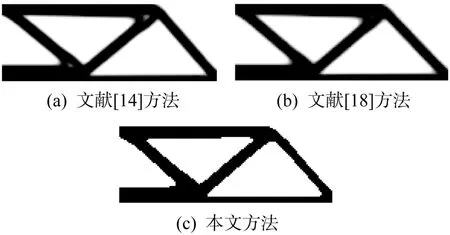
图5 不同拓扑优化方法下MBB梁结构的拓扑构型Fig.5 Topology configuration of MBB beam structure under different topology optimization methods
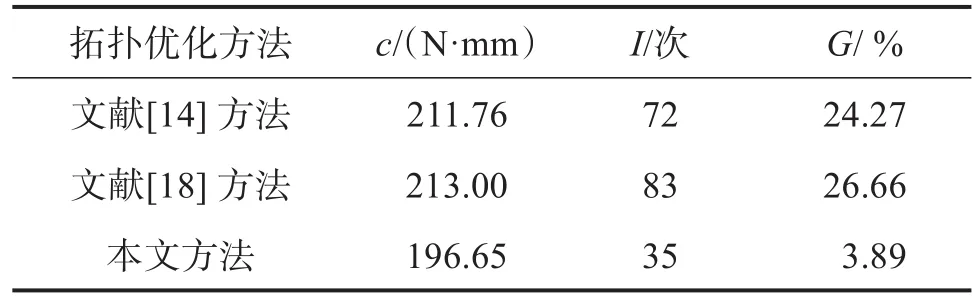
表4 不同拓扑优化方法下MBB梁结构优化结果Table 4 Optimization results of MBB beam structure under different topology optimization methods
由图2可知,采用不同SIMP法得到的MBB梁结构的拓扑构型存在一定差别:采用本文SIMP法所得优化结构在“区域A”和“区域B”处的颜色比较浅。意味着采用文献[18]的SIMP法所得结构在这些区域的xi值比较大。
由表1可知,相比于文献[18]的SIMP法,采用本文SIMP法所得结构的c和I分别减少了2.09% 和22.89% ,G增加了13.80% 。说明采用本文SIMP法可以使拓扑优化方法的收敛速度变得更快,而且可以增强获取柔顺度小的优化结构的能力,但也会削弱抑制灰度单元产生的能力。
由图3可知,图3(a)中“区域A”和“区域B”处的形状不同于图3(b),且在“区域A”处的区别更为明显,说明使用不同的敏度过滤法会得到不同的结构拓扑构型。
由表2可知,相比于文献[18]的敏度过滤法,采用本文敏度过滤法所得的c和G分别减少了1.30% 和10.25% ,I则相同。说明采用本文的敏度过滤法可以增强获取柔顺度小的优化结构和抑制灰度单元产生的能力。
由图4可知,采用本文灰度单元抑制算子所得优化结构的拓扑构型更为清晰。
由表3可知,相比于文献[18]的灰度单元抑制算子,采用本文灰度单元抑制算子所得的c、G和I分别减少了4.46% 、85.71% 和45.31% 。说明采用本文灰度单元抑制算子不仅可以增强获取柔顺度小的优化结构和抑制灰度单元产生的能力,而且可以提高收敛速度。
由图5可知,采用文献[14,18]方法所得结构的拓扑构型存在更多的灰度单元,而采用本文方法所得结构的轮廓非常清晰,且从宏观上看不到灰度单元,所得结构比较好。
由表4可知,相比于文献[14,18],采用本文拓扑优化方法所得的c分别减少了7.14% 和7.68% ,G分别减少了83.97% 和85.41% ,I分别减少了51.39% 和57.83% 。说明本文方法在收敛速度、获取柔顺度小和拓扑构型好的优化结构及抑制灰度单元产生等方面具有明显优势。
2.2 算例2
悬臂梁结构如图6所示。其几何尺寸为160mm×70 mm,梁的左端被固定,右端中部承受大小为1 N的竖直向下的外载荷F。网格划分后结构的单元总数量为160×70个。设置R=3.5,Vf=0.4。采用3种拓扑优化方法所得悬臂梁结构的拓扑构型和优化结果分别如图7和表5所示。

图6 悬臂梁结构Fig.6 Cantilever beam structure
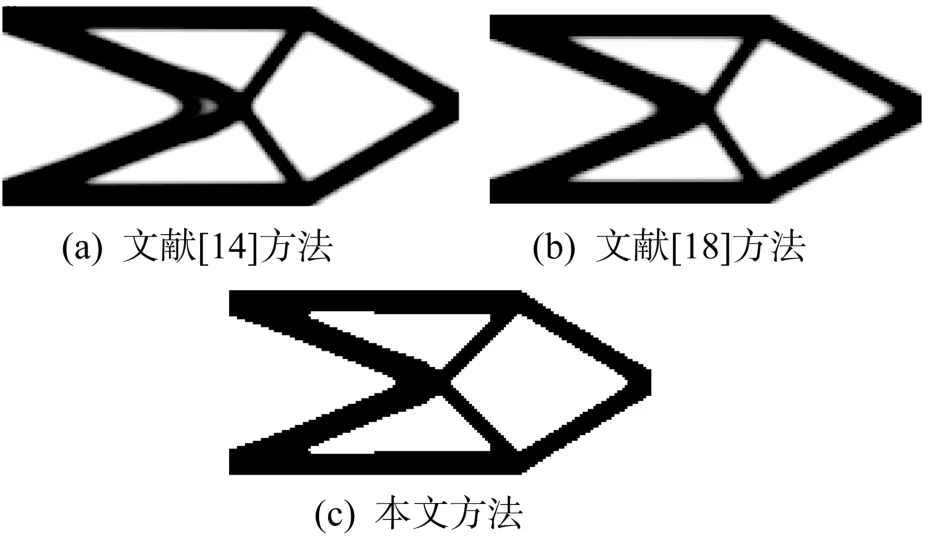
图7 不同拓扑优化方法下悬臂梁结构的拓扑构型Fig.7 Topological configuration of cantilever beam structure under different topology optimization methods
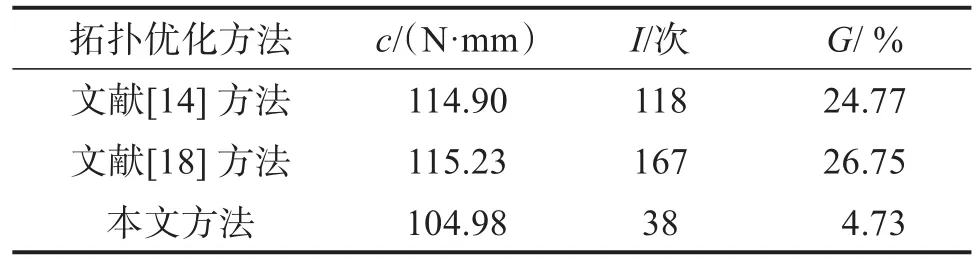
表5 不同拓扑优化方法下悬臂梁结构优化结果Table 5 Optimization results of cantilever beam structure under different topology optimization methods
由图7可知,采用不同拓扑优化方法所得结构的拓扑构型存在较明显差异。相比于文献[14,18],采用本文方法所得结构的轮廓更为清晰。由表5可知,采用本文方法所得的c、I和G分别为104.98 N·mm、38次和4.73% ,较文献[14]方法分别减少了8.63% 、67.80% 和80.90% ,较文献[18]方法分别减少了8.90% 、77.25% 和82.32% 。说明本文方法在获取柔顺度小且拓扑构型好的优化结构和抑制灰度单元产生等方面均明显优于文献[14,18]的方法,此外,收敛速度也明显加快。
3 结 论
为了实现使连续体结构的体积约束和柔顺度最小的拓扑优化及解决采用经典变密度法引起的数值不稳定问题,在兼顾改进拓扑优化方法的前提下,通过引入改进的SIMP法、基于高斯权重函数的敏度过滤法和新灰度单元抑制算子,并结合优化准则法,提出了新的拓扑优化方法。通过优化算例可知,新的拓扑优化方法能够有效解决连续体结构的拓扑优化问题,具有收敛速度较快、可更好地获取柔顺度小且拓扑构型好的优化结构和抑制灰度单元产生等优势。
