计算机模拟取样确定标准物质的最小取样量

江 泓

(福建省地质测试研究中心，福州350001)

在化验室内，检测的样品必须是均匀的。也就是说无论用什么方法从该样品中取任何一部分子样，对于被检测的项目它都能代表原来的样品。然而样品的不均匀性是样品的特性之一，它不能被消除，只能减小。因此绝对均匀的样品是不存在的，只有均匀程度不同的样品。因此，确定标准物质均匀程度，是标准物质认证的基本步骤之一。标准样品工作导则[1]中要求在标准样品定值过程中，同时要求进行均匀性试验。并建议[2]标准物质证书给使用者提供使用该标准物质的最小取样量，并要提醒使用者“只有满足该最小样本量要求，特性值及其不确定度才有保证。”早期的地质标准物质证书上没有最小取样量的信息，用户都默认0.1 g或0.2 g为最小取样量。进入21世纪后研制的地质标准物质以及从GS系列转到GBW系列的早期地质标准物质基本上都提供最小取样量的信息。但是考察这些标准物质研制报告发现，基本上都采用认证样品均匀性时所用的样品量为最小取样量。实际上这是将取样量与最小取样量混淆了。设想一下，有一个样品，从中取出一定量子样做样品均匀性检验，检测结果的方差满足标准物质定值的要求，证明样品是均匀的；然后逐步减小子样重量。当子样重量减小到一定程度，检测结果的方差不能满足标准物质定值的要求，说明样品不均匀。之所以会有这种现象，是因为样品不均匀的本质造成的。无论样品加工的粒度多么细，混匀操作多么完备，总会有少数被测物含量较高的颗粒存在。尽管这些颗粒数量很少，一旦被取到就会使结果异常偏高，检测结果的离散程度变大。当子样量比较大时，这个现象不太明显。而当子样量小时，这种现象就突出了。所以用认证均匀性时用的样品量来代替最小取样量是不合理的，它存在三个缺陷：第一，取样量偏大掩盖了样品的不均匀性；第二，过高估计了样品的不均匀性；第三，限制了该标准物质在微分析技术中的应用。最后一点越来越显出它的重要性。随着分析技术的进步的，微分析技术在实际应用中不断普及，这些技术常只要几十毫克、几毫克甚至更低质量的样品，若标准物质的最小取样量大到几百毫克，就不能用于监控这些技术的质量。王毅民等[3-4]在2009年就注意到这种问题，并指出“在过去标准物质研制中比较重视样品的分析定值，而对样品自身的特性(粒度分析、均匀性检验，特别是最小取样量的确定)研究较少，相关的文献少。”呼吁“地质分析者、标准物质研制者和实验管理部门共同关注和解决这个问题。”建议“鼓励支持分析方法研究者对74 μm地质标准物质的取样量进行系统研究，进一步实验证明最小取样量(小于100 mg)的可行性，并公示(发表)，以使最小取样量分析的做法具有更可靠的实验依据。”“提醒标准物质研制者……，有责任重新考察给出的最小取样量对现代主流分析技术的适应性和确定最小取样量方法的合理性，如与原来不符，应重新确定并发布。”然而，十几年过去了，这些声音并没有得到反应。查阅最近几年发表的标准物质研制的文献，地质部门以外研制的标准物质仍然少有最小取样量信息。地质部门研制的标准物质都公布了最小取样量，但大多仍然以均匀性研究或定值时用的样品量，通常为100 mg为最小取样量。虽有个别低到25 mg，也不是经严格研究样品的微不均匀性得来的。同时，登陆“中华标准物质网”(w.w.w.GBW365.com)，GBW系列中原来GSR、GSD或GSS系列的最小取样量没有修订过的迹象。另一方面，在中子活化(NAA)法或固体直接进样塞曼石墨炉原子吸收光谱(SS-ZAAS)法用于标准物质研制和日常检测工作中，用几十毫克的GSS、GSD或GSR系列标准物质作质量监控的报道文献不在少数。显然不符合标准物质制作规范和化验室质量管理规定。

我国标准样品的最小取样量确定多采用X-射线荧光光谱(XRF)法、电感耦合等离子体发射光谱(ICP-OES)法和电感耦合等离子体质谱(ICP-MS)法在均匀性检验时确定。PAUWELS J等[5]推荐用固体进样塞曼石墨炉原子吸收光谱(SS-ZAAS)法和中子活化分析(NAA)法进行最小取样量测定。这两种方法是取样量可小于1 mg，且不用化学预处理的分析技术之一。因为从质量小的样品结果外推到质量大的样品能保持样品的分布特征。因此，用大于由此而得的最小取样量的子样量，能保证子样的代表性。为了满足统计要求，往往要求重复测定100次以上，因此配备有自动称样和进样装置的SS-ZAAS仪，分析速度快更适用。他们以二元且粒度均匀体系为基础，推导出最小取样量M为：

(1)

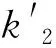
(2)

其中m为实验取样量，mg；cn为异常高含量颗粒对样品含量的贡献，%/颗；z为实验时取到异常高含量颗粒的平均颗粒数颗；c为样品含量值，%；HE为相对均匀常数。

(3)

则最小取样量M：

(4)

式中，RSE为定值时的相对取样标准偏差，%。

本文提出用计算机模拟取样过程，对不同的取样量重复进行测试多次，统计其检测结果的标准偏差，作出标准偏差s对取样量m的拟合曲线，再计算最小取样量。计算机运算速度快，参数转换方便，也可以取毫克甚至小于毫克数量级的样进行实验。设计的模式是一颗一颗地取样，这样不存在取样操作及测试过程带来的误差。只要有足够的岩矿鉴定的资料，可以模拟不同状态下的样品取样过程。

1 实验部分

1.1 软件

实验程序用Visual Basic软件编写和运行。

1.2 样品

没有标准样品，只能采用模拟的样品。模拟黄铜矿样品，主要成分为黄铜矿，其余矿物都归到脉石中去的二元体系。ω(Cu)=0.230%±0.005%，黄铜矿中ω(Cu)=34.56%，脉石中ω(Cu)=0.03%，铜样品的粒度分布如表1所示。

表1 模拟标准物质粒度分布[7]

黄铜矿密度为4.45 g/cm3，脉石的密度为2.75 g/cm3。黄铜矿与脉石完全解离。颗粒形状均为立方体。根据这些参数同时考虑到颗粒小于1 μm时，单颗粒对检测结果影响极小，而且比例不大，将它们的重量归并到1.04 μm粒级中。由此计算出200 g样品中各粒级的颗粒数和总颗粒数(表2)。

表2 200 g模拟样品各粒级的颗粒数

黄铜矿和脉石各分成7个不同粒径段，共14个样段。每一段内颗粒粒径、形状和铜含量等参数都一样。

1.3 模拟取样

1)将200 g样的13734306964585粒样品，按黄铜矿7个段，再按脉石7个段，由粗到细逐个编号，每粒一号，不重复。

2)将各段的颗粒数相加即200 g样的总颗粒数，构成一个随机数池。计算机用Visual Basic软件的随机函数从随机池中取一个数，代表取一粒样品。

3)每取一粒样品都检查它是哪一段的。则该段的被取颗粒数加1；被取的颗粒数乘以该段的单颗粒重，即为该段被取的样重；同时该段的颗粒数减1。

4)每取一粒样品后都要将各段被取的样重加和求得此时被取的子样重量。

5)将此时被取的子样重与预设的子样重比较。若被取的子样重小于预设的子样重，则重复2)到5)步骤，直到被取子样重比预设子样重。

6)计算被取子样中铜的含量：

(5)

其中，mineral是子样中黄铜矿重，是黄铜矿颗粒数与单颗黄铜矿重之积，g；gangue是子样中脉石重；是单颗脉石重与脉石颗粒数之积，g；W为被取子样重，g。

7)重复1)-6)步骤30次。计算30次铜含量结果的标准偏差，程序见图1。

图1 模拟取样程序框图Figure 1 The flow chart of simulating program.

2 结果与讨论

模拟30次取不同子样实验结果如表3所示，其中m为子样重；c为平均含量；s为标准偏差；n为子样中最大粒径(40.74 μm)黄铜矿的平均值颗粒数。

表3 模拟取样实验结果

2.1 取样量与误差的关系

根据表3作出取样量与误差的关系见图2。图2中m-s的拟合曲线，横坐标为取样量m(g)，左边纵坐标为标准偏差s(%)，右边纵坐标为子样中平均mineral颗粒数(颗)。拟合结果为幂函数，相关系数为0.963 9。

图2 m-s及m-n关系图Figure 2 The reltions of m-s and m-n.

s=0.000007296m-0.9573

(6)

2.2 取样量m与取得含量铜量异常高颗粒数n的关系

本实验用的样品最大的颗粒径为40.74 μm，表3第4行为子样中粒径为40.74 μm黄铜矿30次实验的平均值。子样量与铜量异常高颗粒数关系见图2。拟合结果为直线，相关系数为r=1，解析式为：

n=4082.6m+0.0223

(7)

数理统计认为当异常高颗粒平均颗粒数n≥9时，体系就从泊松分布转变成正态分布。因此将9代入(7)式：

两种方法得到结果比较接近，应当取4.1 mg为该黄铜矿样的最小取样量。

INGAMELLS[8-10]推导出的取样常数方程为：

s=Ksm-1

(8)

在前阶段[11]的计算机模拟取样确定取样常数研究中，也证实对于粒度均匀体系，这个公式是成立的。但从式(6)可见m-s的关系式与(8)式形式一样都是幂函数，指数却不同。原因可能是由于INGAMELLS推导时用的颗粒均匀的二元体系，而本模拟实验用的是有一定粒度分布的二元体系所致。式(6)与PIERRE M GY的取样理论也不同。KRATOCHVIL等[12-13]认为粒度分布不影响子样量m的指数，只影响不均匀常数Ks中的粒度分布指数，粒度分布指数随着粒度分布变宽从1逐渐变小。从实验过程观察推测s-m关系式推测应当是：

s=Ksm-n

(9)

n为0.5～1，从均匀粒度随粒度分布越来越广而增大，同时Ks也会变化。这一点以后还要设计实验来考察。

3 结论

1)计算机模拟黄铜矿样品取样，取xmg甚至0.xmg的子样研究样品的不均匀性，它不受取样操作和检测过程误差的干扰，误差只来自样品本身的不均匀性，操作是可行的。通过s-m拟合曲线和定值时的样品不均匀误差计算最小取样量，结果是可靠的。计算机还具有运算速度快，参数变换方便等优点。SS-ZAAS法和NAA法虽然设备比较贵，保养条件要求高，现在不少单位也开始配备，标准物质研制单位也应当充分利用它开展标准物质的最小取样量研究。

2)模拟的黄铜矿样品最小取样量为4.1 mg，假设它是标准样品并用它来监控SS-ZAAS法等微分析技术检测，进样量要大于4.1 mg才可使检测结果受控。若要进样0.xmg检测必须改用最小取样量更小的标准样品。从标准样品的研制实践看，现在例行的粉碎混匀设备与流程大部分能保证-0.074 mm粒度达99%以上，最大粒径大都在0.040～0.060 mm。最小取样量基本上都在xmg水平。若要制得最小取样量达0.xmg级，气流粉碎是可值得研究的方向。

3)对于s-m的拟合结果函数关系式，还要进一步设计实验研究。