一种基于离轴椭球面的小光程差波面整形系统

王泽宇，陈 洁，杨 磊，谢洪波

（天津大学 精密仪器与光电子工程学院，光电信息技术教育部重点实验室，天津 300072）

引言

反射式光学系统由于其无色差、传输损耗小、光路易折叠、系统空间尺寸小、反射镜易于制成大口径等诸多优点[1-3]被广泛应用于科学研究和工程应用领域。反射式光学系统可分为共轴反射式和离轴反射式。共轴反射式光学系统普遍在中心处存在较大的遮拦，导致光学系统的能量利用率降低[4]，不能对物体完全成像。为了消除这个不利影响，一般将其中一片或多片反射镜的光轴进行偏心和旋转，通过离轴放置来实现消除遮拦的目的。通常而言，离轴反射镜的数目越多，系统的像差校正及平衡能力越强，但是镜片数量的增加也会导致系统自由度增加，给实际系统装调带来更大的困难[5]。

为了进行高精度的电子束长测量，将脉冲电子束转换为光信号是目前常用的方法。电子束与物质进行相互作用产生的辐射光在进入条纹相机前，通常需要经过传输系统进行光路折叠。为了实现皮秒量级的时间精度，除了对条纹相机的测量精度有要求外，对传输系统也提出了一定的要求，即光场波前从光源面到达条纹相机入口处时应具有高度的一致性。真空中光速 c0≈3×108m/s，若想将传输系统引入的时间测量误差控制在1 ps以内，则各视场光瞳之间的波前差应小于0.3 mm。因为波前是由波源发出的具有相同振动状态的光子在相同时间到达相面的各点所构成的等相位面，所以波前的一致性可以通过控制光从物面传输到像面的各视场光瞳之间的光程差实现。光束传播的光程差主要来源于2个方面：一是光束在自由空间的传输路径；二是光路中的非理想光学器件。前者通常由光源的几何体积和发光特性决定，不同光源位置处发出的不同角度的光，在自由空间中传输到像面的光程不同。后者由非理想光学器件的像差决定，不同视场、不同孔径角的像差不同，所引入的光程差也不同。因此，分析光路的光程差时,应综合考虑不同视场的不同光瞳位置，特别是在离轴系统中对称性被破坏，使光程差与视场和光瞳的关系更为复杂，分析起来更加困难。

本文根据椭球面反射镜2个焦点之间的等光程传输特性以及离轴反射结构的优点，提出了2种基于离轴椭球面的小光程差波面整形结构，分别为平面-椭球面反射结构和双椭球面反射结构。通过分析光源面和探测面之间的物像关系，得到了椭球面反射镜圆锥系数和文中定义的离轴位置对光程差的影响，基于分析结果对上述2种结构进行优化设计。设计结果表明：2种结构均能实现空间中1 m距离的近似等光程传输，物面到像面以及各视场光瞳之间最大光程差分别为0.14 mm和0.04 mm。

1 椭球面反射镜整形原理

在空间直角坐标系下，椭球面的方程表达式为

式中a、b、c为任意正常数。旋转椭球面是一种特殊的椭球面，它由平面内的椭圆绕其长轴（或短轴）旋转一周得到，a、b、c这3个参数中有2个参数相等，从旋转轴的方向看，其截面为不同半径的圆面。

对于一般光学系统，视场往往是对称的，所以通常采用旋转椭球面反射镜，且默认在子午面内椭圆的长轴与光轴重合，椭圆绕长轴旋转，此时旋转椭球面的焦点位于其长轴上。旋转椭球面的特性由旋转的椭圆决定。

椭圆是平面内到定点A、B的距离之和等于常数（大于AB）的动点的轨迹，定点A、B称为椭圆的2个焦点，如图1所示。从A点发出的光经椭球面反射到达B点，在椭球面上的交点分别为C和D（均为任意点），由椭圆的性质可知：

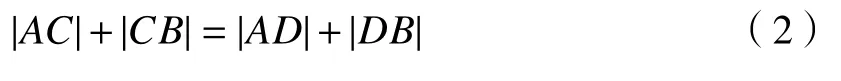
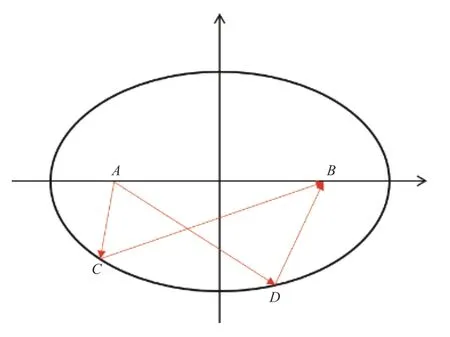
图1 椭球面反射光路示意图Fig.1 Schematic diagram of reflective optical path of ellipsoidal surface

当理想点光源位于椭圆的焦点处时，其发出的任意孔径的光经过椭球面反射镜反射后，都会汇聚到B点，光在这个传播过程中光程相等，旋转椭球内反射面对焦点A、B来说是等光程面。利用椭球面反射镜的这一特性，可以将光源和探测器分别放置在椭圆的2个焦点上，以达到波面整形的效果。

2 椭球面反射镜像差分析

光学设计中通常将z轴设为光轴，设坐标原点与非球面顶点重合，则二次曲面的一般方程可表示为[6]

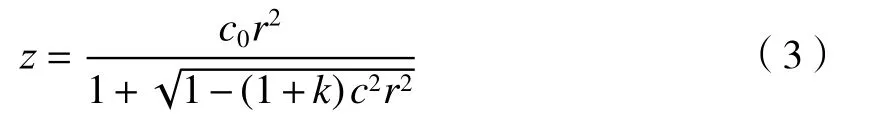
式中：c0为辅助基准球面的曲率；k为圆锥系数。当二次曲面为椭球面时，k的取值范围为

设椭圆半长轴为a，半短轴为b，则有如下转换关系：

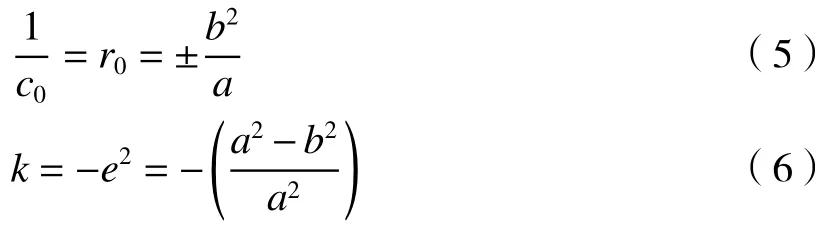
式中：r0为辅助基准球面的半径；e为椭圆的离心率。

由初级像差理论可知，对于二次曲面反射镜，当孔径光阑与z轴垂直时初级像差系数表达式为[7]

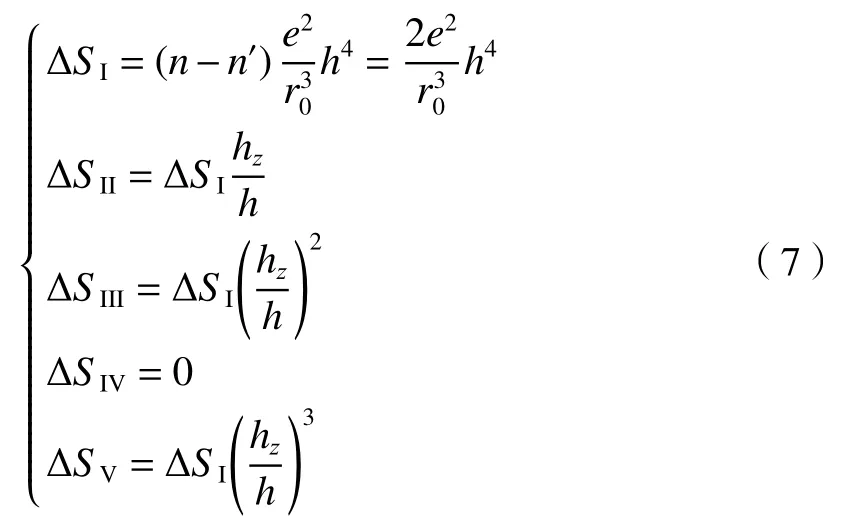
式中：h为近轴光线在椭球面上的入射高度； hz为主光线在椭球面上的入射高度。由上述公式可知，决定系统像差的参数主要为二次曲面圆锥系数k和主光线在椭球面上的入射高度 hz。

对于离轴反射光学系统，元件的倾斜和偏心并不会产生新类型的像差，也不会影响初级像差系数，只会影响与视场相关的像差[8-9]。由于离轴椭球面不存在旋转对称轴，中心视场主光线不再重合于共轴椭球面时的对称轴，此时，相同视场大小但方向不同的光线，其像差不再具有对称性。像差对视场的依赖关系十分复杂，定量描述较为困难[10-14]，并且对需要校正光程的实际需求帮助不大，因此不考虑单独的像差类型，直接分析所有像差的和即波前差与椭球面反射镜特性参数的关系。

为了对单个椭球面反射镜不同离轴位置处的波前差进行分析，建立如下模型：设旋转椭球面长轴a=500 mm，短轴b=300 mm，由（5）式和（6）式可得 r0=180 mm，k=-0.64；为了模拟实际情况，将理想点光源近似为半径为2 mm的均匀面光源；在初始结构中，设面光源的中心置于椭球面焦点A处，中心视场主光线垂直于面光源出射，出射光的孔径角为6°。当光源实际尺寸偏离椭球面焦点距离较小时，可以认为面光源上出射光只经过一次椭球面反射后就到达像面处。将像面初始位置设置在过椭圆另一焦点，且与面光源中心视场主光线垂直的位置。为了保证模拟过程中光阑的一致性，将孔径光阑放置在距离光源50 mm位置处。对上述模型在Zemax光学设计软件中进行建模并执行光路追迹，如图2所示。

图2 基于椭球面的波面整形模拟光路图Fig.2 Simulated optical path diagram of wavefront shaping based on ellipsoidal surface

由于面光源中心视场出射光满足完全等光程传输，以此定义波前差零位。以面光源中心视场主光线到达椭球面反射镜时的光程定义光束实际传输到椭球面时的离轴位置d，此距离即椭圆的焦半径，如图3所示。设光线在子午面内与椭圆的任意交点M的坐标为（m, n）,则由焦半径性质可知：

图3 椭球面离轴位置示意图Fig.3 Schematic diagram of off-axis position of ellipsoidal surface

对于上述模型，d的取值范围为100 mm～900 mm。根据光路追迹结果，可得到面光源子午方向归一化+1视场和-1视场光瞳的波前差P-V值与离轴位置d的关系，如图4所示。

图4 不同离轴位置处波前差P-V值Fig.4 Wavefront aberration P-V values at different off-axis positions

由图4可以看出，随着面光源中心视场主光线到达椭球面反射镜距离的增加，-1视场光瞳的波前差P-V值单调增大，+1视场光瞳的波前差P-V值先增大后减小。

由椭圆的几何特性可知，当逐渐增大中心视场主光线与光轴的夹角θ时，中心视场边缘光线在椭球面反射镜上的投影轨迹长度s先增大后减小，如图5所示。由于视场并不对称，以中心视场光线为界，负视场光线“慢于”中心视场光线在椭球面上的投影，正视场光线“快于”中心视场光线在椭球面上的投影，因此，图4所示的波前差P-V值曲线正负视场的变化趋势不同。

图5 投影轨迹s与中心视场主光线角度θ关系图Fig.5 Relationship between projection trajectory s and principal light angle θ of center field of view

基于上述所建模型，对椭球面反射镜的圆锥系数k与波前差P-V值的关系进行分析。默认椭圆长轴为500 mm不变，并假设面光源中心视场主光线到达椭球面反射镜时的光程为500 mm不变。由椭圆性质可知，此时该光线从反射镜到像面的光程也为500 mm，全视场在椭球面上的投影近似关于短轴对称。此时，面光源子午面方向归一化+1视场光瞳的波前差P-V值与圆锥系数k的关系如图6所示。

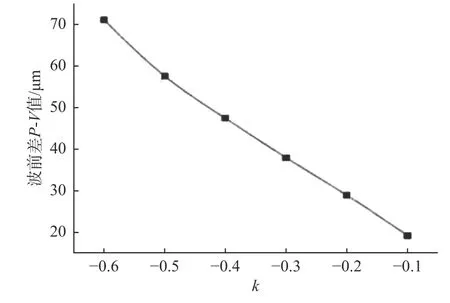
图6 波前差P-V值与圆锥系数k关系图Fig.6 Relationship between wavefront aberration of P-V value and conic coefficient of k

由图6可知，圆锥系数越大，椭球面越接近基准球面，其波前差P-V值越小。离轴情况下圆锥系数对像差的影响与共轴情况时相同。

3 系统设计与分析

3.1 系统结构设计

除了各视场光瞳之间光程差尽可能小之外，系统设计参数指标要求如表1所示。

表1 设计参数要求Table 1 Requirements of design parameters

考虑到实际应用场景空间的限制，采用离轴双反射镜结构将光路折叠，使空间更为紧凑。由上述分析可知，椭球面反射镜具有等光程传输的特性，同时平面反射镜是最简单的理想光学元件，因此，将平面-椭球面反射镜和双椭球面反射镜2种结构作为初始选型。

3.1.1 平面-椭球面反射镜结构

由于平面反射镜只起到折叠光路的作用，只有一个椭球面反射镜参与波前整形，因此系统结构可以等效于上述第2节所建立的模型。此时总光程L等于椭圆长轴2a（a=500 mm）。将没有平面反射镜时的等效光源中心设置在椭球面的一个焦点上，假设初始结构中面光源中心视场主光线到椭球面反射镜的光程为500 mm，光束孔径角为6°。设光轴和z轴重合，YZ平面为子午面，XZ平面为弧矢面。以物高表示视场，分别设置中心视场（0,0），+Y视场（0,3），-Y视场（0，-3），+X视场（3,0）和-X视场（-3,0）共5个视场位置。将平面-椭球面反射镜结构在Zemax光学设计软件中进行建模，结合上述第2节分析的圆锥系数和离轴位置的影响，综合考虑光程差和空间结构进行优化，最终优化后的3D结构图如图7所示。

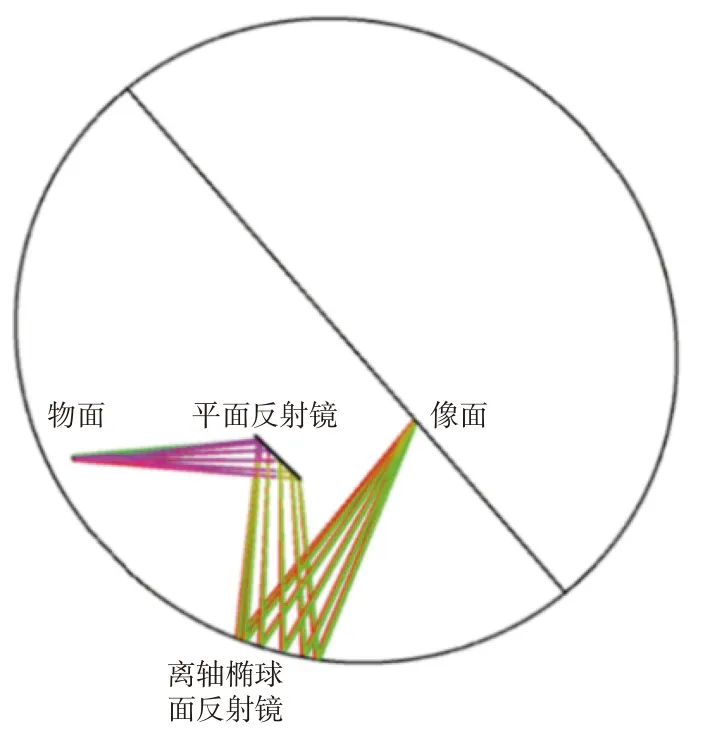
图7 平面-椭球面反射镜结构光路图Fig.7 Optical path diagram of planar-ellipsoidal reflector structure

3.1.2 双椭球面反射镜结构

由于物点和像点分别位于椭球面的2个焦点时才能等光程传输，所以采用存在中间像面的离轴双反初始结构，并且使2个椭球面各自的一个焦点重合。此时，对于物面、离轴椭球面反射镜1、中间像面，以及中间像面、离轴椭球面反射镜2、像面，可以分别等效成上述第2节所建立的模型。设2片椭球面反射镜的半长轴分别为 a1和 a2，则总光程L等于2个椭圆的长轴之和，即：

显然，当 a1=a2=250 mm时，整个系统成对称结构，光源经第1片椭球面反射镜后所成的像为第2片椭球面反射镜的物，此时的等效视场与原始视场方向正负相反，通过2次反射成像的弥补，可以有效消除单片椭球面反射镜视场不对称带来的光程差。将面光源中心设置在第1片椭球面的一个焦点上，假设初始结构中面光源中心视场主光线到椭球面反射镜的光程为250 mm，重复优化上述过程，最终优化后的3D结构图如图8所示。

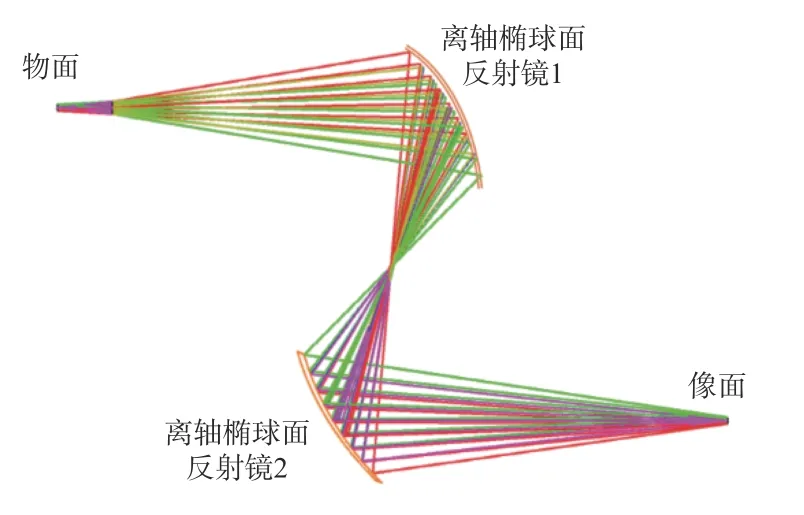
图8 双椭球面反射结构光路图Fig.8 Optical path diagram of double ellipsoidal reflector structure

3.2 系统成像分析

3.2.1 平面-椭球面反射镜结构

下面从系统所成像的点列图、光迹图、光程差和波前图4个方面对平面-椭球面反射镜结构进行分析。

1）点列图

如图9所示，由于面光源中心放置在椭圆焦点处，所以中心视场点列图很小，接近艾里斑半径。X视场和Y视场点列图近似对称，形状接近圆形，说明各视场光瞳内光线按孔径分布较为均匀；+X和-X视场的点列图大小相等，形状关于子午面对称；+Y和-Y视场的点列图大小近似相等，形状关于弧矢面近似对称，说明弧矢方向视场正负与光程差大小无关，子午方向视场正负对光程差大小有较小的影响。

2）光迹图

如图10所示，中心视场成像位置位于像面中心，+X视场和-X视场成像位置关于Y轴对称，+Y视场和-Y视场成像位置关于X轴近似对称，像面直径D=4.6 mm，满足设计要求。

3）光程差曲线图

图11和图12分别为各视场子午面和弧矢面的光程差曲线图。设子午面孔径以y表示，弧矢面孔径以x表示。其中+X和-X这2个视场在弧矢面内的光程差曲线大小相等，符号相反；在子午面内光程差曲线大小相等，符号相同。+Y和-Y这2个视场在弧矢面内光程差曲线分别关于子午面对称，2个视场之间光程差曲线差值极小。此外，2个视场在子午面内除了y=0时的一个光程差零点外，还分别存在另一光程差零点。不同Y视场对应的另一个零点位置各不相同，无法完全消除各视场之间的光程差。

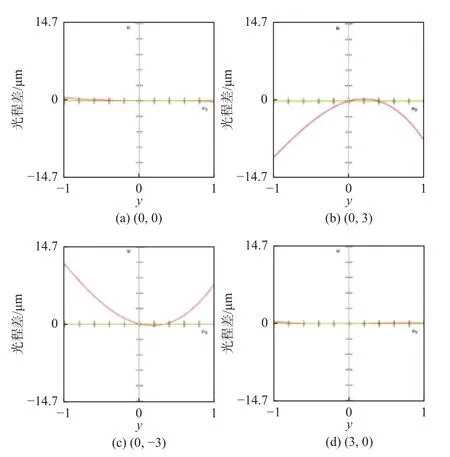
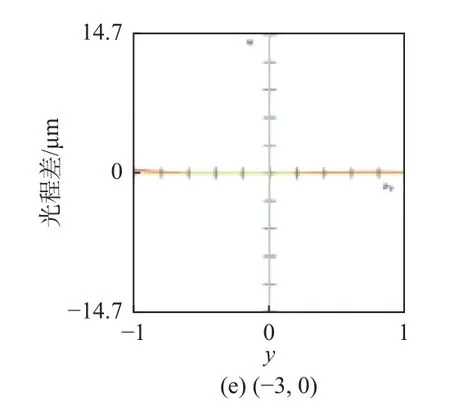
图11 平面-椭球面反射结构子午面光程差曲线图Fig.11 Curves of optical path difference in meridian plane of planar-ellipsoidal reflector structure

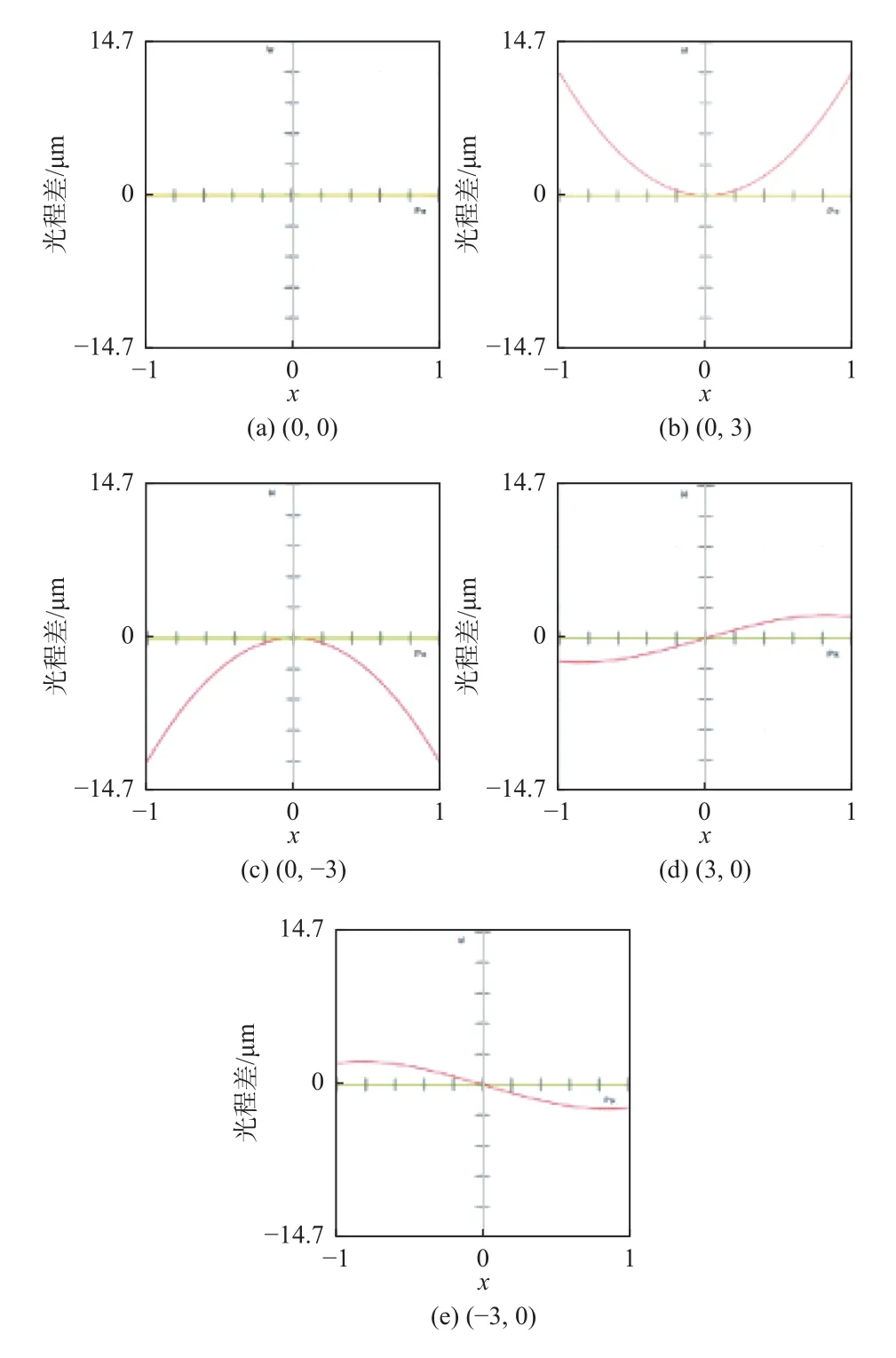
图12 平面-椭球面反射结构弧矢面光程差曲线图Fig.12 Curves of optical path difference in sagittal plane of planar-ellipsoidal reflector structure

4）波前图

图13为像面上不同视场光瞳的波前图。图13（a）为像面处中心视场的波前图，波前差P-V值为0.853 μm。根据上述分析可知，如果将光源中心放置在椭球面焦点上，则波前差P-V值理论上为0，优化后存在0.853 μm的波前差是因为优化过程中系统将光源位置偏离了椭球面焦点，以此平衡+Y视场和-Y视场之间的光程差。图13（b）～13（e）所示结果与之前光程差曲线分析结果相符合。

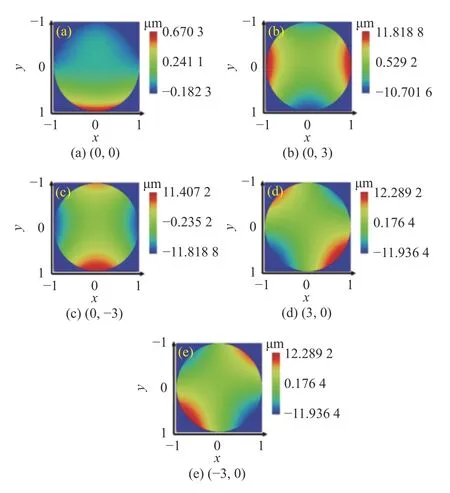
图13 平面-椭球面反射结构波前图Fig.13 Wavefront diagrams of planar-ellipsoidal reflector structure

3.2.2 双椭球面反射镜结构

下面从系统所成像的点列图、光迹图、光程差和波前图4个方面对双椭球面反射镜结构进行分析。

1）点列图

如图14所示，双椭球面反射镜结构各视场点列图大小均远小于平面-椭球面反射结构。此时X视场和Y视场点列图形状不再近似对称，系统存在一定的像散；+X视场和-X视场之间与+Y视场和-Y视场之间的关系与平面-椭球面反射结构相同。

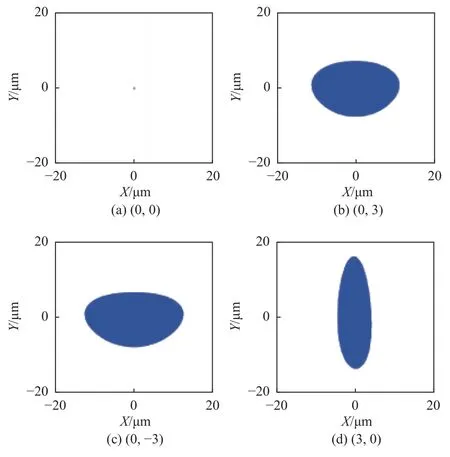
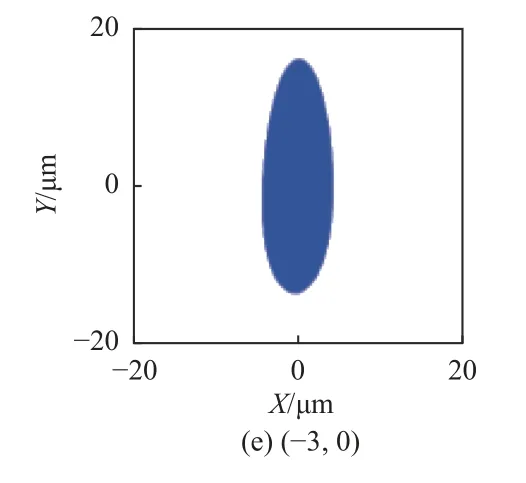
图14 双椭球面反射结构点列图Fig.14 Spot diagrams of double ellipsoidal reflector structure

2）光迹图

如图15所示，中心视场成像位置位于像面中心，+X视场和-X视场成像位置关于Y轴对称，+Y视场和-Y视场成像位置关于X轴近似对称，像面直径D=6.2 mm，满足设计要求。

图15 双椭球面反射结构光迹图Fig.15 Light trace diagram of double ellipsoidal reflector structure

3）光程差曲线图

图16和图17分别为双椭球面反射结构各视场子午面和弧矢面的光程差曲线图。+X视场和-X视场之间与+Y视场和-Y视场之间的关系与平面-椭球面反射结构相同，不同的是，双椭球面反射结构+X和-X视场在子午面内的光程差曲线关于弧矢面更接近对称，整体光程差更小。

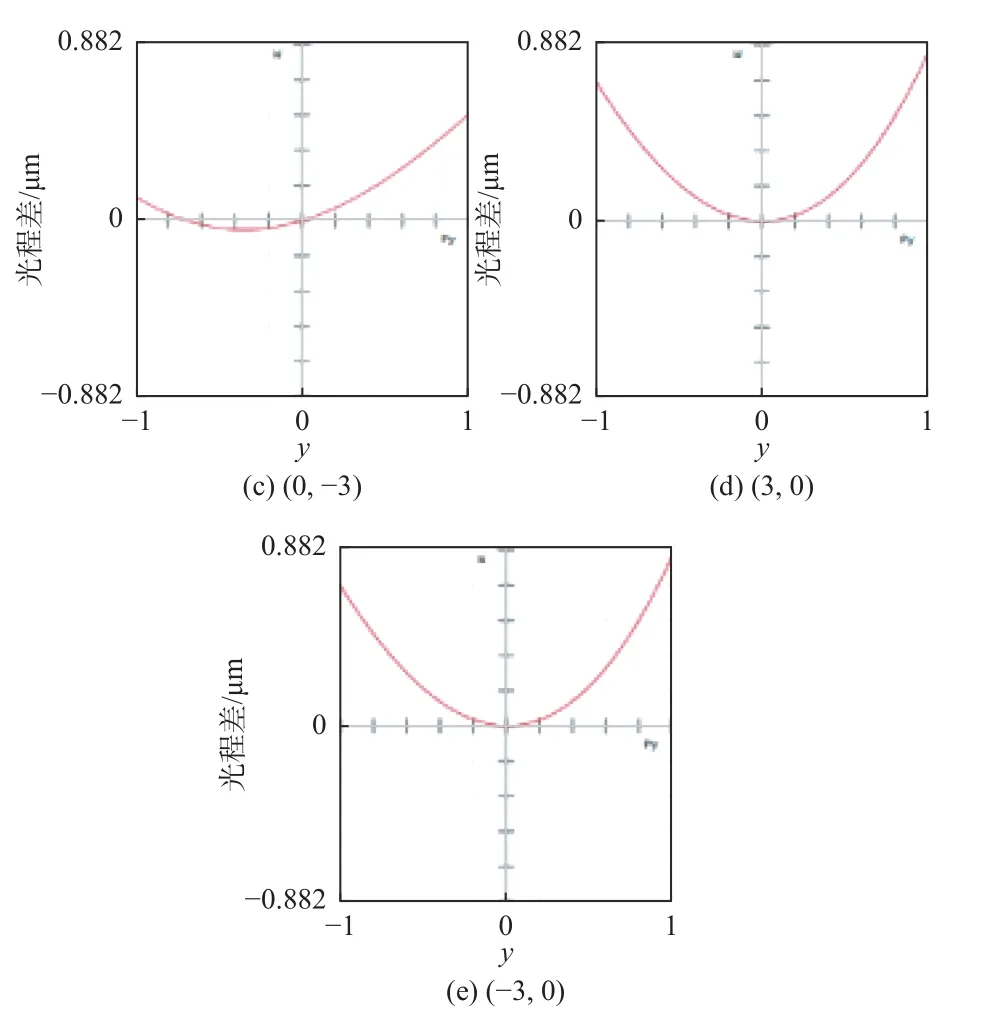
图16 双椭球面反射结构子午面光程差曲线图Fig.16 Curves of optical path difference in meridian plane of double ellipsoidal reflector structure

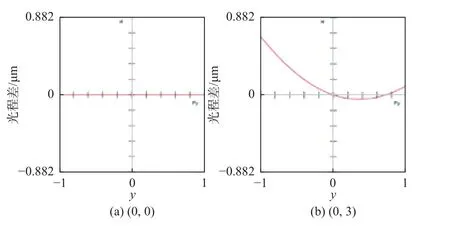
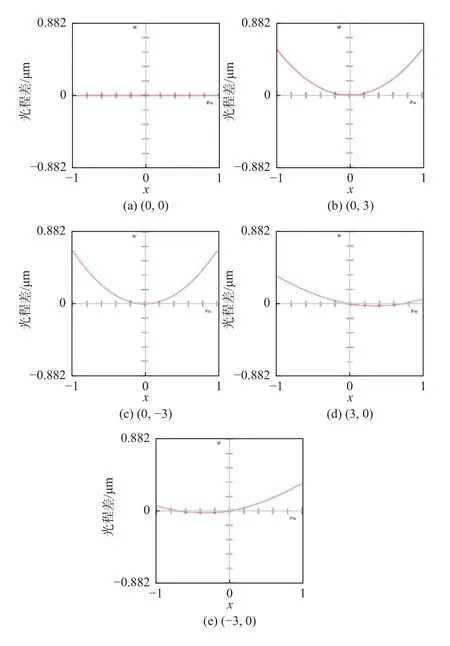
图17 双椭球面反射结构弧矢面光程差曲线图Fig.17 Curves of optical path difference in sagittal plane of double ellipsoidal reflector structure

4）波前图

图18为双椭球面反射结构像面上不同视场光瞳的波前图。如图18（a）所示，像面处中心视场的波前差P-V值近似为0，说明此时面光源中心在第一片椭球面反射镜的焦点处。不同视场的光程差由结构本身特性弥补，需要的光源补偿偏移量较小。图18（b）～18（e）所示结果与上述光程差曲线分析结果相符，Y视场的波前图关于弧矢面对称，X视场的波前图关于子午面对称。

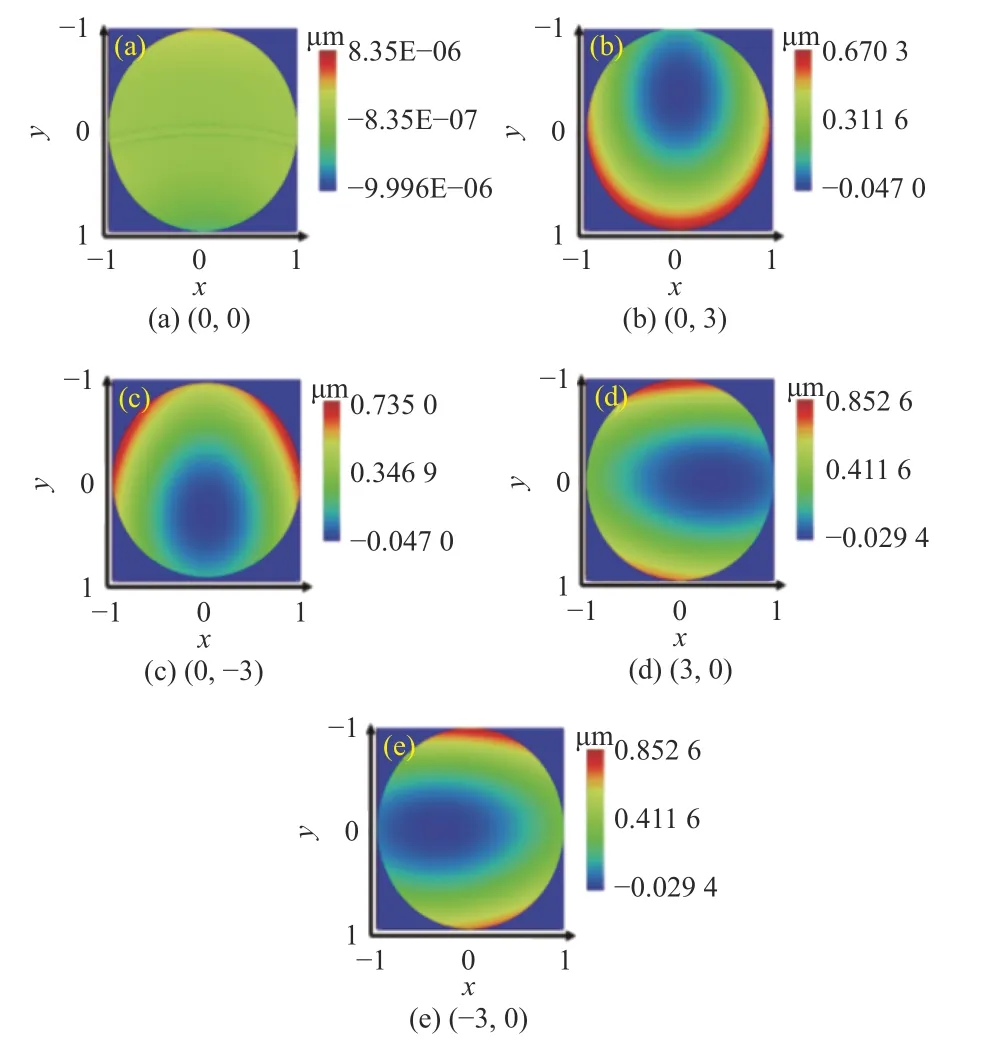
图18 双椭球面反射结构波前图Fig.18 Wavefront diagrams of double ellipsoidal reflector structure

3.3 公差分析

对本文设计的2种小光程差波面整形系统结构的公差类型进行分析。由于光学元件均为反射镜，所以不存在材料折射率和色散系数这些公差问题。系统的公差可分为平面反射镜和椭球面反射镜的加工公差以及装调时引入的装调公差。加工公差主要包括平面反射镜的面形精度，椭球面反射镜的曲率半径和圆锥系数；装调公差主要包括各元件的偏心和倾斜，以及它们之间的相对位置关系。根据上述公差类型，结合实际加工和装调的精度，在保证可行性的基础上，确定的各公差范围如表2所示。

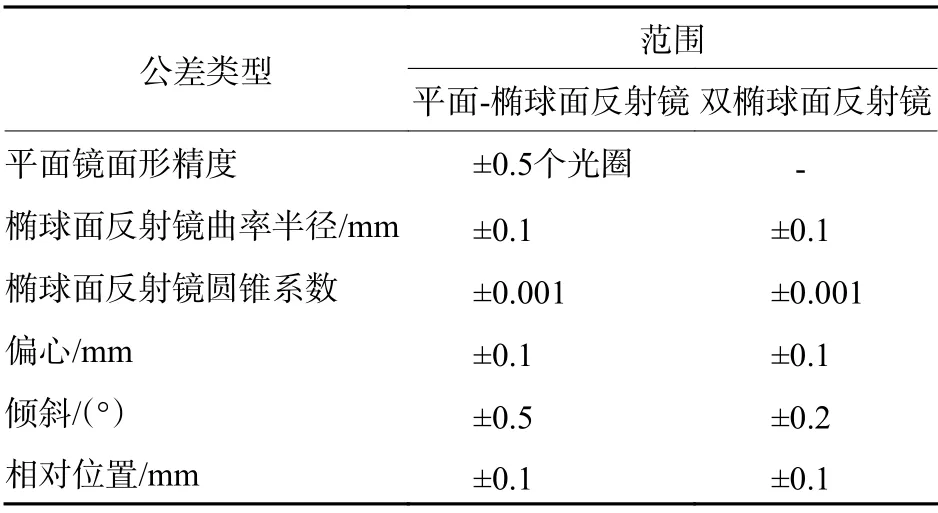
表2 公差类型及范围Table 2 Tolerance types and ranges

在Zemax软件中对表2中的公差范围进行公差分析，并以各视场光瞳之间的光程差作为评价标准。经过1 000次蒙特卡洛分析后，结果显示，平面-椭球面反射结构有80%的概率光程差大于0.19 mm，双椭球面反射结构有80%的概率光程差大于0.20 mm。虽然2种结构的公差分析结果均能满足实际使用需求，但是在反射镜倾斜偏差限制更严格情况下，双椭球面反射结构的公差分析结果比平面-椭球面反射结构稍差，说明前者的公差敏感度远高于后者。在加工装调过程中，平面-椭球面反射结构更有可能达到理论设计性能。

3.4 2种结构对比

从光程差角度考虑，双椭球面反射结构由于其对称性，2次反射能使视场引入的光程差互相抵消，整形效果优于平面-椭球面反射系统。从公差角度考虑，双椭球面反射结构的公差敏感度更高，在实际装调时很难同时保证2片离轴椭球面反射镜按设计位置和角度摆放到位。此外，离轴椭球面反射镜的加工成本比平面反射镜高。平面-椭球面反射镜结构较为简单，平面反射镜的位置比较容易保证，但是其消除不了视场引入的非对称光程差。另外，由于总光程等于椭圆长轴2a，如光程较大时，椭圆的长轴会很长，若仍想使离心率较小，短轴也会随之变长。实际加工时，刀具绕长轴旋转，短轴的长度直接影响离轴量的大小，离轴量过大会给实际加工带来困难[15]。在满足设计要求且实际加工可行的条件下，应优先考虑平面-椭球面反射镜结构。

4 结论

为了实现空间中一定距离的近似等光程传输，本文基于几何光学与初级像差理论，分析了椭球面反射镜的成像原理，基于光源面和探测面之间的物像关系，分析了椭球面反射镜圆锥系数和离轴位置对像面上各视场光瞳光程差的影响。设计了平面-椭球面反射镜和双椭球面反射镜,2种小光程差波面整形系统的初始结构，并在Zemax光学设计软件中进行了优化。最终设计结果表明，2种结构均实现了空间中光程1 m距离的光束传输，在3 mm物高视场和孔径角为6°条件下，平面-椭球面反射镜结构系统和双椭球面反射镜结构系统中各视场光瞳之间的光程差分别为0.14 mm和0.04 mm。