一种针对激光诱导击穿光谱技术的基线校正方法

潘高威，史晋芳，邱 荣，王慧丽，万 情，张志威，王 凯

（1.西南科技大学 极端条件物质特性联合实验室，四川 绵阳 621010；2.西南科技大学 制造科学与工程学院，四川 绵阳621010；3.陆军勤务学院 教研保障中心，重庆 401331）

引言

激光诱导击穿光谱（LIBS）技术是上世纪六十年代发展起来的一种原子发射光谱检测技术。LIBS技术同时具有无需专门制样、对样品破坏小、灵敏度高、检测限低等特点，在工业现场监测、环境污染检测、深空深海探测、文物鉴定等领域的研究热度不断上升[1]。中阶梯光栅光谱仪相较于传统光谱仪，具有分辨率高、衍射效率高的特点[2]，是LIBS检测技术的重要组成部分。但是，在利用中阶梯光栅光谱仪作为激光诱导击穿光谱分析的数据采集仪器时，为了增强弱峰信号，原始光谱数据中会存在周期性拱形基线，这种具有明显区域分布的拱形基线主要来源于激光等离子体的连续白光背景辐射和中阶梯光谱仪的周期性衍射效率差异，这不仅增加了光谱数据预处理的难度，也减少了定量分析的精度和准确性。因此为了减少这些特殊的基线对光谱数据的影响，基线校正成了LIBS数据处理中的一个重要环节。

常用的基线校正方法主要有多项式拟合[3-4]、小波变换[5-7]、惩罚最小二乘法[8-11]等。在多项式拟合中，利用最小二乘法对人为主观选择的拟合点进行多项式拟合，易导致过拟合或者欠拟合。小波变换通过将光谱信号分解成高频和低频2种信号。在低频信号中删去基线，针对不同种类的基线时，需要重新对小波函数和分解层数进行选择，该方法也会产生无意义的负值，在处理复杂基线时效果并不理想。2003年，Eilser提出了一种基于whittaker平滑器原理的非对称权重惩罚最小二乘法基线拟合算法（AsLS）[12]，并将其成功运用于飞行时间质谱分析的基线校正。赵恒等人将“局部对称加权”与“非对称加权”结合，提出了一种基于局部对称权重加权惩罚最小二乘法（LSRPLS）[13]，解决了非对称惩罚最小二乘法在噪声情况下拟合拉曼光谱基线时产生的局部抬升问题。但是由于LISB数据量大且光谱数据复杂，在将其他光谱基线校正方法运用在LIBS数据上时，会同时存在局部的欠拟合和过拟合现象。因此本文针对该周期性拱形基线的校正问题，提出了一种改进的惩罚最小二乘方法，在保留光谱数据有效信息的基础上，进行了LIBS光谱数据的基线校正。

1 改进算法原理

1.1 算法原理

LIBS光谱数据的基线主要由2部分组成，一部分是由等离子在激发后所带来的连续背景导致的光谱数据强度的整体抬升；另一部分就是中阶梯光栅光谱仪特有的周期性拱形突起所带来的局部变化。因此，要求基线拟合算法能在拟合连续背景的同时，不会忽视掉这一系列拱形突起。

LIBS光谱数据的基线主要来源于激光等离子体的连续白光背景辐射，由于中阶梯光谱仪的多级衍射和波长间的衍射效率差异，导致连续白光背景辐射基线被多级衍射调制从而形成周期性拱形基线。这种周期性拱形基线的存在，会增加光谱数据预处理的难度，影响LIBS定量分析的精度。因此，进行基线拟合时必须考虑该因素。

假设有一个数据长度为 N的经min-max标准化后的光谱数据y，设其拟合基线为z，利用 z的二阶差分来定义拟合基线的粗糙度：

式中：R表示粗糙度； Δ2zi表示二阶差分，Δ2zi=zi-2zi-1+zi-2，i∈[3,N] 。利用光谱强度 y 与拟合基线 z的差值来定义拟合线对于原始数据的保真度S （即拟合线对于原始数据的偏离程度）：

式中：ωi为权重系数。ωi会随着迭代的进行而发生改变，迭代的本质是将谱峰视为突变信号而基线视作连续信号，突变信号会在一次次迭代中逐渐减少，其对应的权重系数也会减小，即权重的“非对称性”。ωi的取值方式为

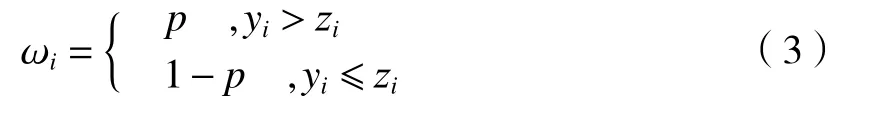
式中：p 为一个极小值，通常使 0.001≤p≤0.1。当yi高 于基线 zi时，则说明这部分数据为谱峰，将其权值设置为p；反之则认为这部分数据属于基线部分，权值设置为1 -p，保留这部分数据。但是由于LIBS光谱数据量大，使用原始方法对 ωi进行赋值会导致在无谱峰位置处产生欠拟合，因此引入新的权值系数赋值方式：

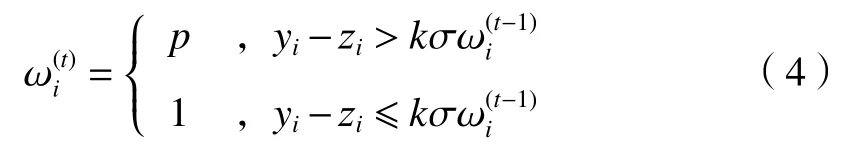
然而拟合基线 z越光滑，则对理想基线的保真度就越低。为了同时满足这2个方面的要求，令R作为惩罚项，引入代价函数Q =S+λR。λ为惩罚项系数，取值在1 02～109之间。代价函数的矩阵形式为

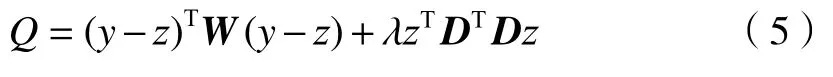
式中：W 是主对角线为ω 的稀疏矩阵； D为二阶差分矩阵 Dz=Δ2zi。因此求基线问题就转变成了寻找一个能够使Q达到最小值的z。为了使代价函数Q 最小化，令其对 z求偏导后等于零，得到：

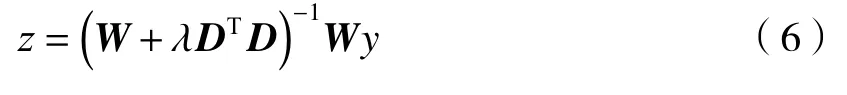
此外，在用非对称惩罚最小二乘法拟合LIBS光谱数据时，基线会在谱峰处有所抬升，且谱峰峰值越大，此处的基线受影响越大。因此引入惩罚系数数组α，在峰值处施加一个较大的惩罚系数，对基线则施加一个较小的惩罚系数，使拟合基线在谱峰位置处更加平滑，从而减小谱峰峰值对基线的影响。惩罚系数数组 α的取值方式如（7）式：

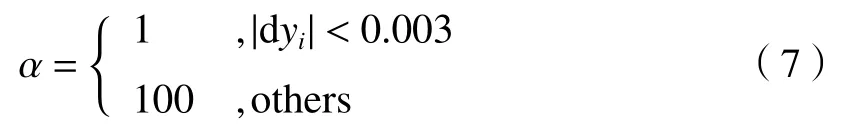
式中：dyi=yi+1-yi。α的数值根据标准化后光谱数据的一阶导数确定，在谱峰数据变化率大的位置施加更大的惩罚系数。

在引入了α和新的ω的取值方式后，（6）式变为（8）式：

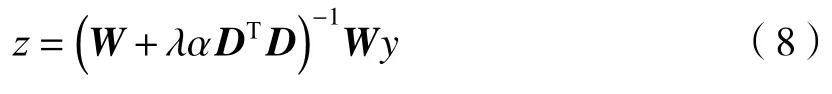
1.2 算法实现

本文算法流程如图1所示，步骤如下：

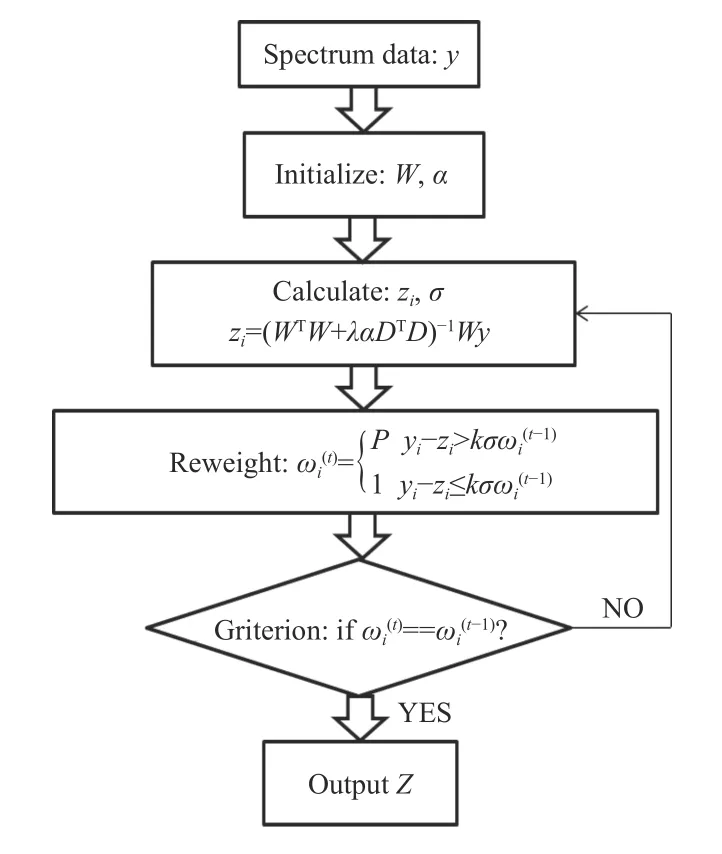
图1 改进后的算法流程图Fig.1 Flow chart of improved algorithm

1）输入预先经过min-max标准化后光谱强度部分数据y；

2）初始化权重数组 ω 和惩罚数组α；

3）计算标准差 σ ，根据（8）式，计算拟合基线z；

4）根据光谱数据 y与拟合基线 z的差值，对权重数组 ω和惩罚系数数组 α中的元素进行重新赋值；重复步骤3和步骤4，直至 ω 中的元素不再发生明显变化；

5）迭代终止，将光谱数据 y与拟合基线z相减得到去基线后的光谱数据。

2 仿真与实验

2.1 仿真

在实际的光谱检测中无法准确地得知其理论基线，因此需要通过仿真数据来模拟基线校正的过程，将改进后的基线校正方法与改进的非对称惩罚最小二乘法（IAsLS）[14]、惩罚最小二乘法（PLS）、非对称加权惩罚最小二乘法（asPLS）[8]和自适应迭代重加权惩罚最小二乘法（airPLS）[9]4种基线校正方法在仿真光谱数据上进行比较。LIBS光谱数据包含众多重叠峰与强弱不一的峰，为了尽可能还原真实光谱数据，模拟光谱数据由120个位置、半峰宽各不相同的洛伦兹峰、理论基线和信噪比为40的噪声组成。洛伦兹峰计算公式如（9）式：

式中：N为谱峰个数；Ai为光谱谱峰面积；hi为谱峰半高宽；ri为谱峰中心位置；x为光谱数据波长范围 [200,711.5] （nm）。

图2为不同基线拟合方法对模拟光谱进行拟合的结果，结合图2（b）和图2（c）可以看到，改进后的算法在短波段和长波段对模拟光谱均有良好的拟合效果，并在峰值处的基线抬升问题也得到了缓解。为验证拟合基线的效果，计算去基线后谱峰峰值与无基线时谱峰峰值之间的均方根误差Rpeak[15]以及拟合基线和理论基线之间的均方根误差Rbase[16]，计算结果见表1。从表1可知，在处理模拟光谱时，本文算法所估计的基线与理论基线更为接近，且能在一定程度上保留原始谱峰信息。

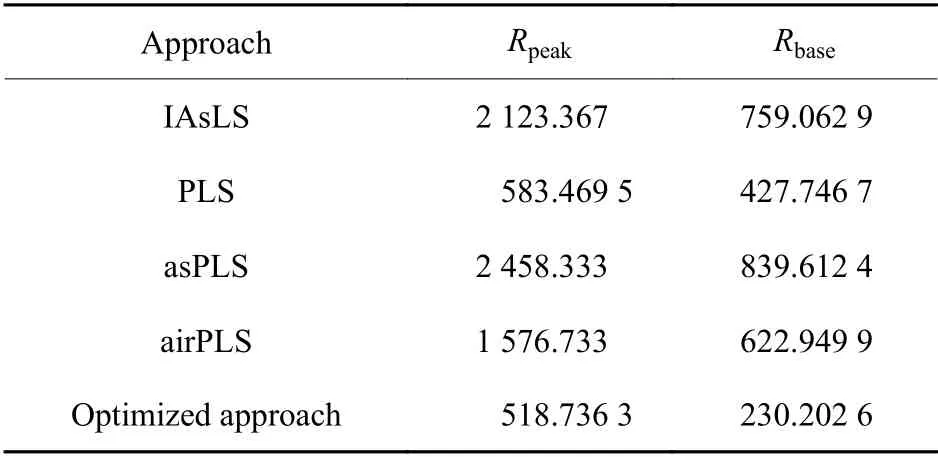
表1 基线校正前后谱峰峰值的均方根误差Rpeak以及拟合基线和理论基线之间的均方根误差RbaseTable 1 Rpeak of peak intensity before and after baseline correction and Rbase between fitting baseline and theoretical baseline

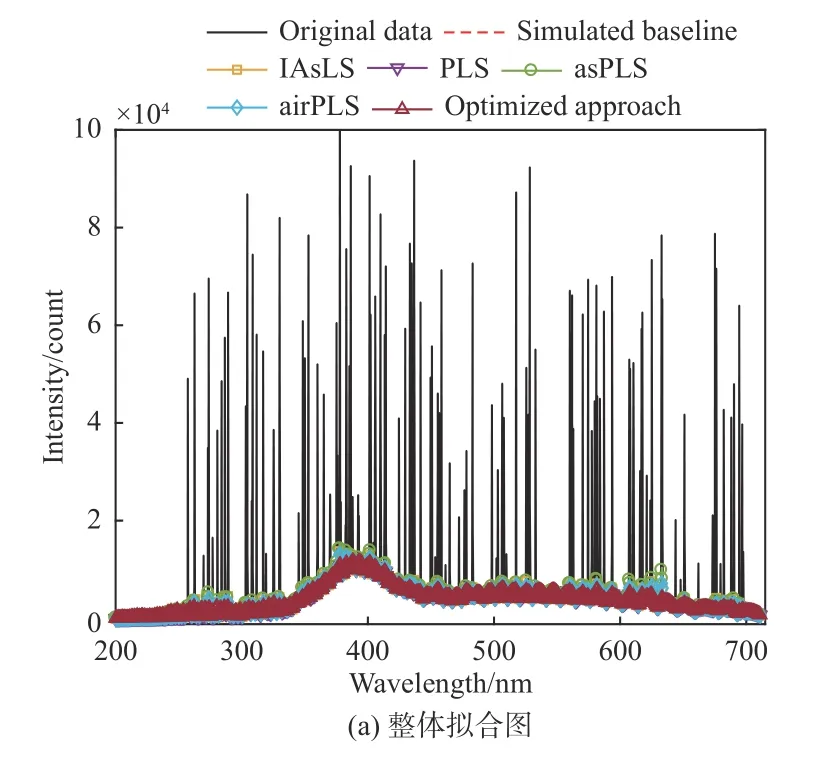
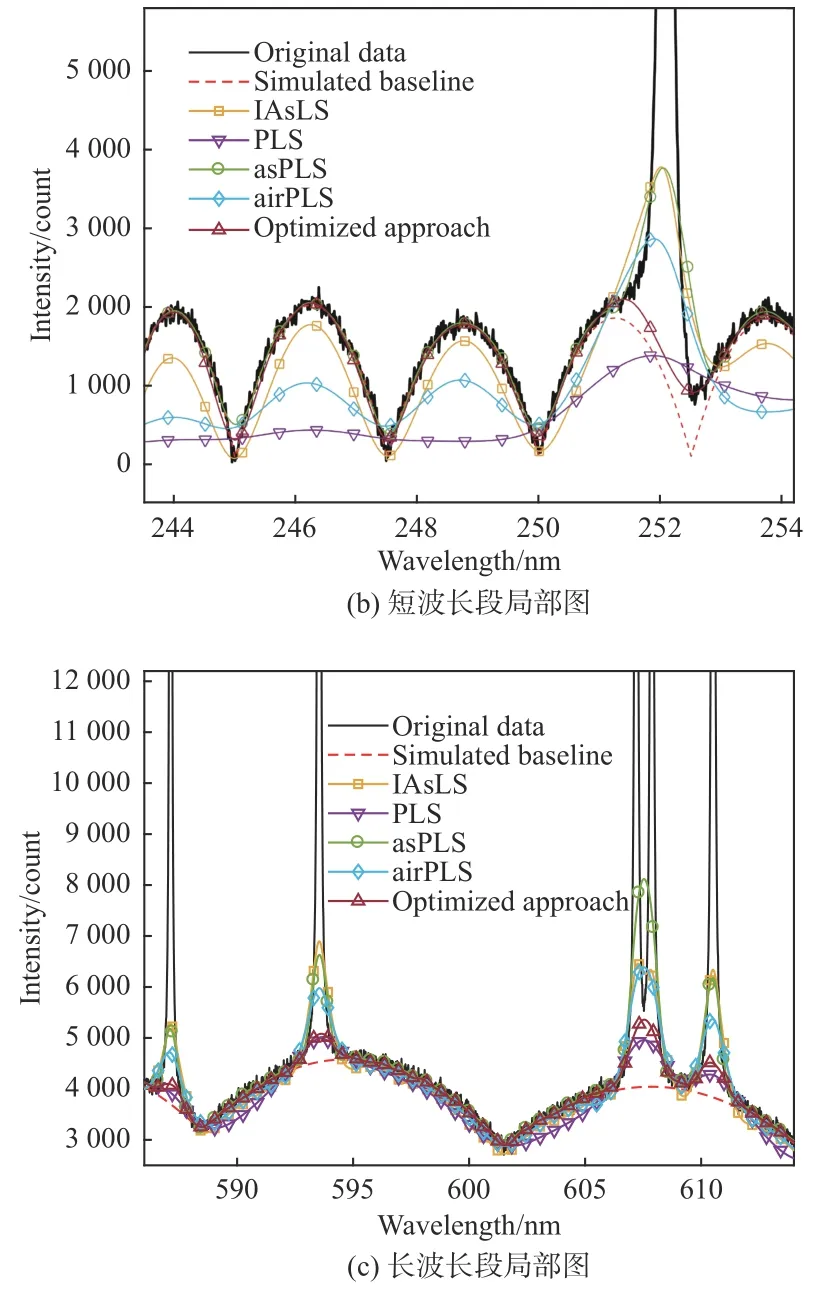
图2 模拟光谱基线拟合结果Fig.2 Baseline fitting results of simulated spectrum

2.2 实验

2.2.1 实验装置与样品配置

实验中采用的是共线双脉冲激发方式，其示意图如图3所示，利用DG645控制激光出光的先后顺序，第1束激光击打在样品表面产生等离子体，第2束激光则是对等离子体进行再加热，利用光谱仪采集等离子体在冷却时发出的光谱。使用的光谱仪为LTB公司的ARYELLE200型中阶梯光谱仪，曝光时间设置为4 500 ms，延迟时间设置为3 μs，。制备样品时，将标准土壤(GBW07386，GSS-32)或二氧化硅粉末(S5631-500)、PE微粉(HDPE，18180)和分析纯化合物硝酸铀酰，在玛瑙研钵中研磨均匀并烘干，土壤和PE微粉的比例为3:1，共配置6个浓度的标准样品。2束激光分别为波长1 064 nm、能量90 mJ与波长355 nm、能量50 mJ的激光。

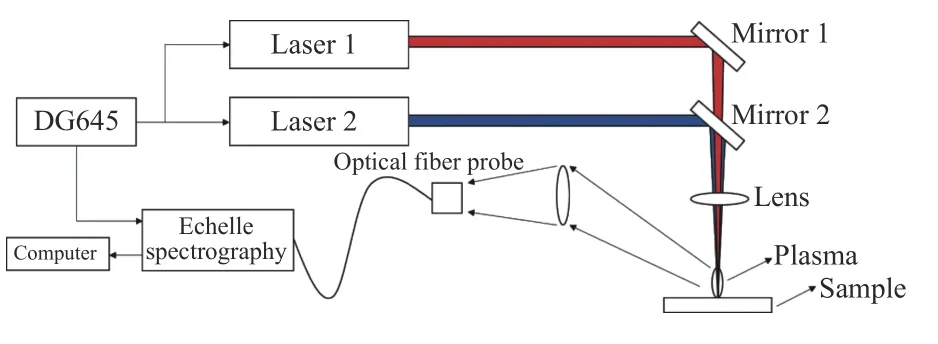
图3 LIBS实验示意图Fig.3 Schematic diagram of LIBS experiment

2.2.2 绘制定标曲线

为验证本文算法实际应用的可行性，将其与4种不同基线校正方法进行比较。图4是对整体光谱数据去基线后，选取UII 454.36 nm特征谱线作为分析对象绘制的定标曲线，可以看出，5种去基线方法下的定标曲线模型均有良好的性能。再结合表2可知，本文算法得到的定标曲线模型相关系数R2为0.997 2，且均方根误差只有347.128 6，小于其他4种去基线方法得到的模型，即改进后的基线校正方法处理后的样本数据偏离定标曲线的程度更小，说明在实际使用定标曲线进行定量分析时，本文方法能使去基线后的定标曲线模型依然有足够的可靠性，更适合处理LIBS光谱数据的基线。

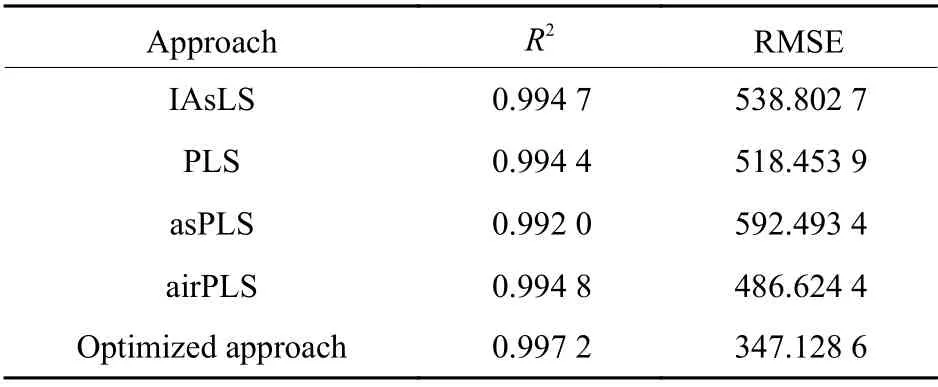
表2 定标曲线模型的相关系数和均方根误差Table 2 Correlation coefficients and RMSE of calibration curve model

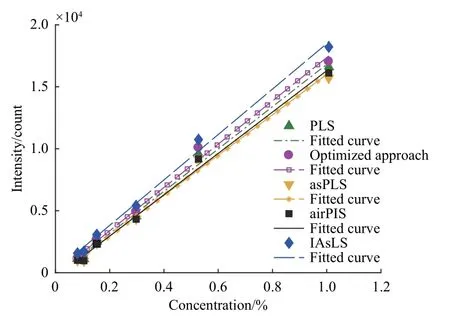
图4 采用不同基线校正方法后的定标曲线Fig.4 Calibration curves with different baseline correction methods

3 结论

本文针对激光诱导击穿光谱检测技术中中阶梯光栅光谱仪所引起的基线局部拱形突起问题，提出一种改进的惩罚最小二乘基线拟合方法。该方法通过在谱峰区局部增大惩罚函数来减小基线拟合方法在谱峰区域中的局部突起现象，同时还优化了权值数组的判别标准，避免了基线拟合方法在基线区域出现“欠拟合”现象，并在与其他四种去基线方法的仿真实验中得到了验证。通过对实际数据进行基线校正和绘制定标曲线，也证明了本文算法在实际应用中能提升定标曲线的回归效果，有助于后续对元素进行定量分析。