基于改进粒子群算法的LED光源阵列优化

明振兴，吕清花，明 月，曾 炜，吕 辉，张 杰

（1.湖北工业大学 理学院，湖北 武汉 430068；2.湖北工业大学 经济与管理学院，湖北 武汉 430068；3.湖北工业大学 电气与电子工程学院，湖北 武汉 430068）

引言

近年来，随着工业自动化、机器学习以及植物工厂的迅速发展，LED被广泛用于机器视觉照明[1]和植物照明[2-3]中。由于单个LED的输出功率有限，在大多数情况下需要使用LED阵列作为光源[4]。在机器视觉检测系统中，光源对其性能起着重要作用，光照均匀的光源系统能够获取高质量的图像，而光照不均匀的光源系统会使获得的图像无法满足需求。在植物工厂中，均匀的光源照明能够让所有的植物生长状态保持一致，不均匀的光源照明会导致植物的生长质量参差不齐，从而给后续植物光谱以及营养液的选取带来很大困难[5]。

国内外许多学者对LED光源的均匀性进行了研究，研究范围主要包括LED透镜的设计、LED阵列的算法设计等。其中Moreno等人[6]最早通过推导出简单的近似方程及公式得到LED间的最佳间距，在LED阵列个数较少时，推出的公式能够有效优化光照均匀度。Hidetoshi Takahashi[7]等人通过设计一种微透镜阵列结构来提高UV-LED光源的均匀度。秦宗等人研究了大视角LED阵列光照均匀分布的条件[8]。王凯等人优化了光强分布曲线并设计了相应的光学元件，在给定距离高度比的情况下实现了均匀照明[9]。王晓丽设计了一种环形LED阵列光源并分析了在不同大小的照射面积和照射高度下的光照均匀度[10]。苏宙平等人第一次提出使用数值优化方法来设计最佳LED阵列的排列来实现均匀照明[11]。何果等人使用果蝇算法并在三维空间上对LED光源阵列均匀度进行优化设计[12]。目前国内外在提高LED光源的照明均匀度上研究出了许多不同方法，考虑到实际设计中的成本以及算法的实用性，本文选择合适的算法并进行改进，对提出的一种新型等差LED阵列进行优化。

粒子群算法(PSO)是由Kennedy和Eberhart博士在1995年提出的一种智能优化算法，它源于对鸟类捕食行为的研究[13]，通过群体中的信息共享和比较来寻找最优解[14]。其优势在于容易实现并且无过多参数，目前已被广泛应用于函数优化、神经网络训练、模糊系统控制及其他领域[15-16]。缺点在于在全局寻优时收敛速度快，但是容易陷入局部最小值；在局部寻优时能够避开局部最小值，但是搜索速度较慢。

本文在粒子群算法中引入线性变化的惯性权重，并使用余弦函数来改善学习因子[17]，使其在优化过程中能够兼顾全局与局部寻优。此外，还提出一种等差LED阵列排布方式，并使用改进的粒子群算法对LED阵列的光照均匀度进行优化。对数据进行分析和对比可知，改进的粒子群算法在一定程度上提高了算法精度，并且能够大幅度优化LED阵列的光照均匀度。相比于传统的矩形和圆形LED阵列，本文提出的新型等差LED阵列的光照均匀度更高。

1 LED阵列光照分布模型

如图1(a)所示，在LED阵列平面中，有n个LED，坐标为O(Xi，Yi，0)(i=1,2,…,n)，照射面与LED阵列面的垂直距离为z。假设每个LED芯片均为理想的朗伯光源，则光源阵列中所有LED芯片在照射面上一点P(xp，yq，z)产生的光照强度可以表示为[18-20]

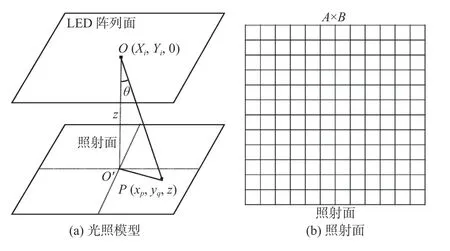
图1 LED阵列光照模型图Fig.1 Illumination model diagram of LED array

式中：I0是光线与光轴夹角θ为0°时的光强；m表示光源的朗伯辐射指数，和半光强角 θ1/2（光强下降为1/2 I0时光线与光轴的夹角）有关，m的计算公式为

如图1(b)所示，将照射面划分为A×B份。当A×B足够大时，把照射面上的每一小份看成一个点，因此照射面的光照强度平均值以及标准差可由(3)式和(4)式表示：

对于LED阵列的光照均匀度，在不同的研究中有着不同的评价方式。本文利用变异系数作为照射面的均匀度评价函数，变异系数越小，均匀度越高。将光照均匀度优化问题转化为求取评价函数的最小值问题，从而使用改进的粒子群算法来优化计算得到评价函数最小值，评价函数由（5）式给出:

2 粒子群算法及其改进

2.1 粒子群算法模型

粒子群算法源于对鸟类捕食行为的研究，基本原理是通过种群中个体的信息共享以及协作筛选来寻求最优解。系统首先初始化一组粒子种群，每个粒子都具有一个初始位置和速度，根据评价函数计算得到初始最优解，将其标记成当前个体极值，然后各个粒子之间通过协作共享信息得到群体极值并不断进行迭代，在每一次迭代得到新的个体极值和群体极值后，粒子通过(6)式和(7)式来更新自己的速度和位置[15]:

式中：t为迭代次数；xi和vi表示种群中第i个粒子的位置和速度；pbest表示个体极值，gbest表示群体极值；r1和r2是介于0到1之间的随机数；w为惯性权重，一般取常数，其值大小决定了全局以及局部的搜索能力；c1是个体认知因子；c2是群体认知因子，c1和c2通常为常数，其值大小也会影响全局以及局部的搜索能力。

粒子群算法流程图如图2所示。

图2 粒子群算法流程图Fig.2 Flow chart of particle swarm algorithm

2.2 粒子群算法的改进

当目标函数比较复杂时，普通的粒子群算法容易陷入局部最优，而且后期的收敛速度较慢，这会导致整个算法的精度下降。影响粒子群算法的效率和精度的参数主要有惯性权重w、个体认知因子c1、群体认知因子c2。当w较大时，算法有着更好的全局搜索能力；c1较小、 c2较大时，有着更好的局部搜索能力。因此在本文中使用线性递减策略对w进行改进，使其在初始迭代阶段有着很好的全局搜索能力，随着迭代进行，粒子的速度逐渐减小，有着更好的局部搜索能力。为了在初始阶段控制c1取较大值、c2取较小值，加强全局搜索能力，并且在最后迭代阶段加强局部搜索能力，使用正余弦函数来控制c1、c2，让c1的值能够非线性地减小，c2的值非线性地增加，具体改进公式如（8）式～（10）式所示：

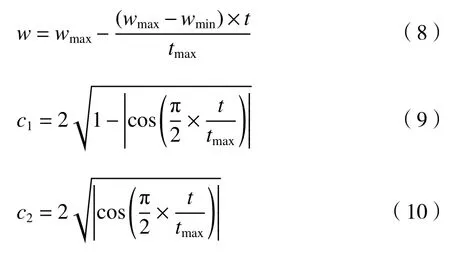
式中：wmax、wmin分别为惯性权重的最大、最小值；t和tmax分别为当前迭代次数和最大迭代次数。

通过对粒子群算法进行改进，不断地调整优化光源阵列中LED的坐标值，使得评价函数达到最小值，具体算法步骤如下：

1）根据（5）式构建评价函数；

2）初始化粒子群规模大小、迭代次数、惯性权重最大值和最小值，以及粒子的初始位置和速度等参数；

3）根据（5）式计算粒子的评价函数值，比较所有粒子的函数值并找到最佳评价函数值gbest，记录此时粒子的位置为最佳位置pbest；

4）根据（6）式和（7）式更新粒子的速度和位置，再次计算所有粒子的函数值，并更新最佳评价函数值gbest，更新粒子的最佳位置pbest；

5）当达到迭代次数时，输出评价函数值gbest以及粒子的最佳位置pbest，否则回到步骤4。

为了验证改进粒子群算法的有效性，选择4种不同的函数对其进行算法测试，其表达式如(11)式～(14)式所示，图3为这4个函数在三维空间中的图像。

图3 测试函数的三维函数图像Fig.3 Three-dimensional function images of test functions

1）Sphere函数(n=5,-5.12≤xi≤5.12,i=1,···,n)

当x*=(0,···,0)时 ，F1(x)取得全局最小值，F1(x*)=1。

2）Trigonometric函数(n=5,-10≤xi≤10,i=1,···,n)

当x*=(0.9,···,0.9)时 ，F2(x)取得全局最小值，F2(x*)=1。

3）Rastrigin函 数(n=5,-5.12≤xi≤5.12,i=1,···,n)

当x*=(0,···,0)时 ，F3(x)取得全局最小值，F3(x*)=1。

4）Schwefel函 数(n=5,-500≤xi≤500,i=1,···,n)

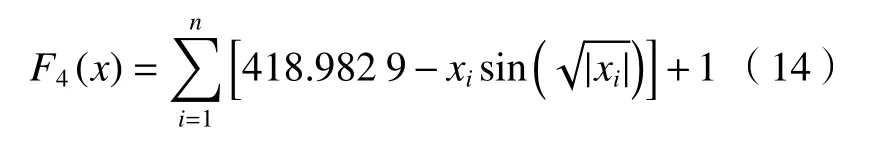
当x*=(420.9687,···,420.9687)时 ，F4(x)取得全局最小值，F4(x*)=1。

分别采用改进前后的粒子群算法(PSO)对这4个测试函数进行优化，把粒子群中的粒子个数设为20，迭代次数设为100。4个测试函数的优化迭代收敛图如图4所示，优化结果如表1所示。

表1 测试函数的优化结果Table 1 Optimized results of test functions

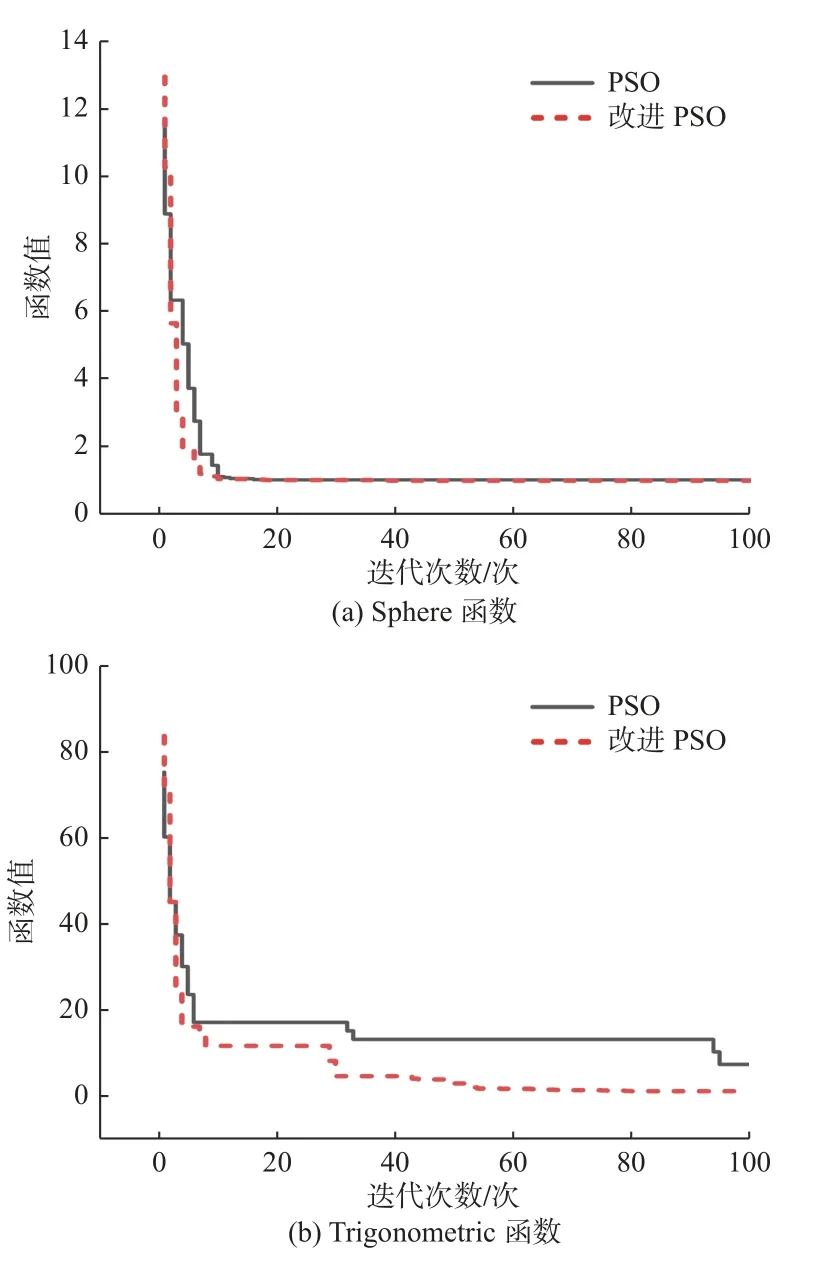
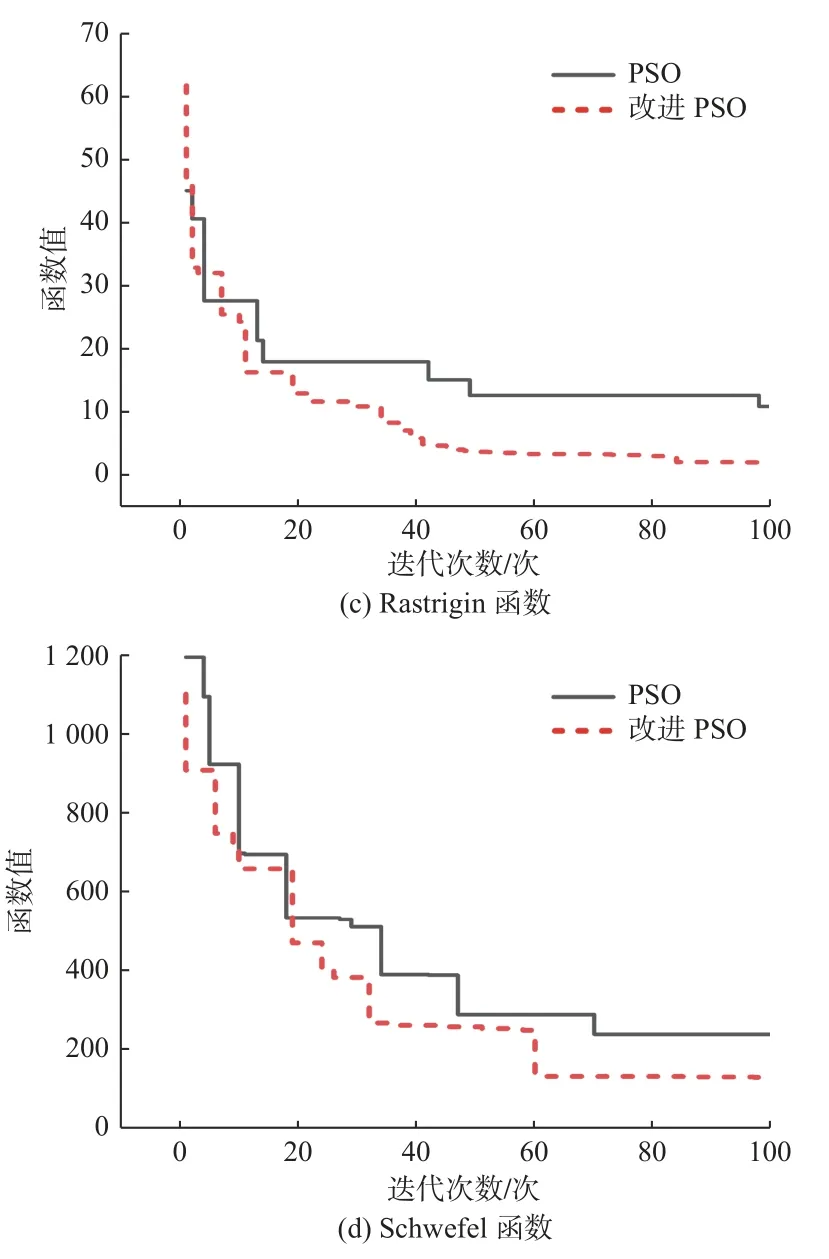
图4 测试函数的迭代收敛图像Fig.4 Convergence curves of optimization iterations for test functions

从图4和表1可以看出，对于这4种测试函数，改进粒子群算法的寻优速度及精度均有所提升，且算法运行时间无明显差异，表明改进粒子群算法的复杂度与原算法基本一致。

3 仿真结果与分析

3.1 LED阵列设计及算法对比

由于理想的LED光源为朗伯光源，发光强度为法线上的光强与方向角余弦的乘积，即光强由中心向周围逐渐减弱，因此我们提出了一种等差LED阵列排布方式，如图5所示，LED的间距由四周到中间逐渐增加。假设在等差LED阵列中，横轴方向上LED的首项间距为L1，间距公差为d1；纵轴方向上LED的首项间距为L2，间距公差为d2，那么所有LED的坐标都可以由L1、d1和L2、d2来表示。如图6(a)和图6(b)所示：在圆形阵列中，LED的坐标可由半径r和夹角θ表示；在矩形阵列中，LED的坐标可由横向间距a和纵向间距b来表示。

图5 等差LED阵列示意图Fig.5 Schematic diagram of arithmetic LED array

图6 圆形和矩形LED阵列示意图Fig.6 Schematic of circular and rectangular LED arrays

改进粒子群算法的初始化参数如表2所示。设定好算法的初始参数后，用LED坐标的表达式来表示评价函数，使用改进的粒子群算法对数据进行寻优处理，最终输出最佳光照均匀度的光源阵列中LED的坐标。

表2 改进粒子群算法的初始参数Table 2 Initial parameters of improved particle swarm algorithm

在优化等差LED阵列过程中，对未改进的粒子群算法和改进粒子群算法的评价函数值变化过程进行对比，如图7所示，由于改进粒子群算法中加入了线性惯性权重和非线性认知因子，因此在迭代前期的收敛速度较快，且在迭代中后期能够跳出局部最优值，收敛精度更高。

图7 PSO算法改进前后的评价函数值对比Fig.7 Comparison of evaluation function values before and after improvement of particle swarm algorithm

3.2 LED阵列仿真结果讨论

得到优化后的3种不同阵列的LED坐标后，为了检验优化后的阵列光照均匀度效果，使用光学仿真软件TracePro，将优化后的LED坐标输入到TracePro中进行模拟仿真。设定单个LED芯片的大小为 1 mm×1 mm×0.1 mm，LED阵列面与照射面的垂直距离为300 mm，单个LED的光强分布为朗伯分布，每个LED的光线出射数设为 50 000条。等差、矩形、圆形LED阵列光照度分布图和轮廓图如图8、图9、图10所示。其中，轮廓曲线图是在照射面上取一点，以该点为中心，取X轴与Y轴向2个方向上的垂线，根据垂线上面的照度变化生成的曲线。

图8 等差LED阵列的照度分布与轮廓曲线图Fig.8 Illumination distribution and contour curve of arithmetic LED array

图9 矩形LED阵列的照度分布与轮廓曲线图Fig.9 Illumination distribution and contour curve of rectangular LED array

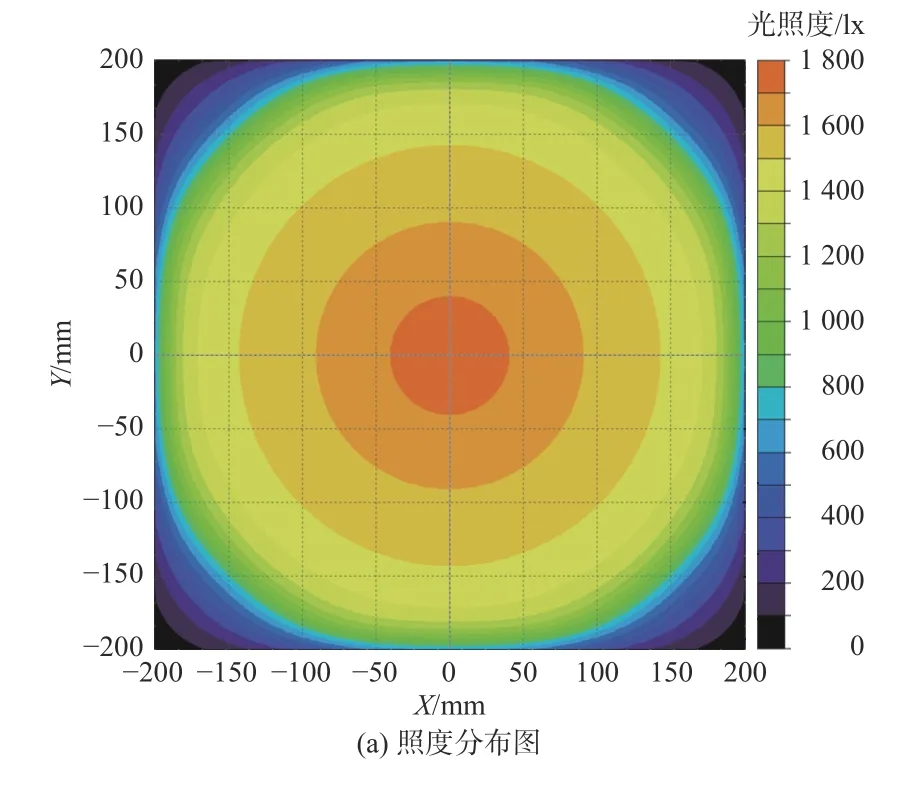
图10 圆形LED阵列的照度分布与轮廓曲线图Fig.10 Illumination distribution and contour curve of circular LED array

使用TracePro仿真完成后，得到3种LED阵列的光照度数据，根据数据分别计算出其光照均匀度，并与优化前的阵列进行对比分析，分析结果如图11所示。

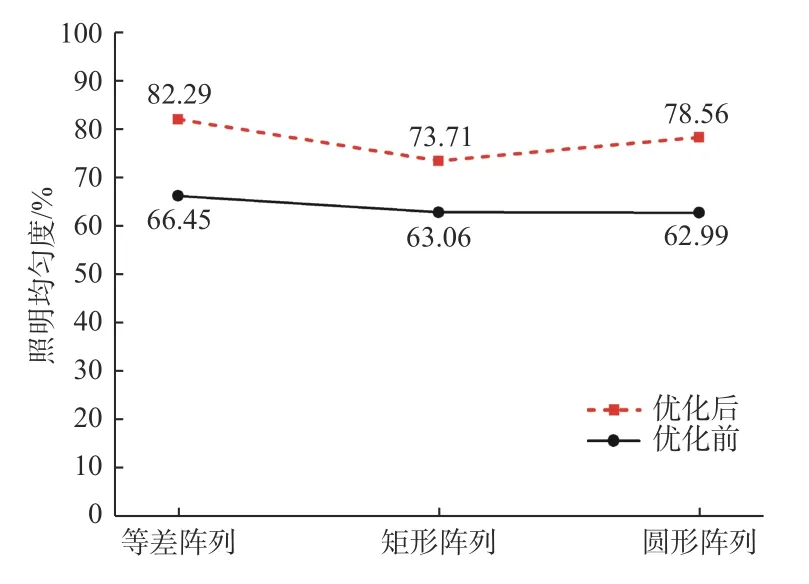
图11 3种LED阵列优化前后均匀度对比Fig.11 Comparison of uniformity of three LED arrays before and after optimization

通过对LED阵列的光照均匀度数据计算对比，得到优化后的等差阵列、矩形阵列、圆形LED阵列光照均匀度分别为82.29%、73.71%、78.56%，比未优化的LED阵列光照均匀度分别提高了15.84%、10.65%、15.57%。根据LED照度分布图和轮廓图可知，矩形LED阵列的光照强度由中间向四周的下降幅度较大；其次是圆形LED阵列；而等差LED阵列中心光照强度与周围相差不大，并且边缘光照强度大幅度下降的范围较小。这是因为矩形LED阵列中心的混光面积比较大，因此容易造成照射面中间光照强度大、周围光照强度弱，所以优化后的矩形LED阵列光照均匀度也不够高。圆形LED阵列则减少了照射面中间的混光面积，整体光照均匀度有所提高，但是边缘仍有一定区域的光照强度大幅度下降。而等差LED阵列则结合了矩形阵列和圆形阵列的优点：一方面，由于LED距离中间位置较远，所以照射面中心光照强度与四周差别不大；另一方面，LED在四周排布较为紧密，增强了照射面边缘处的光照强度，使其光照强度大幅度下降的区域变得更小，从而增加了整个平面的光照均匀度，与前面两种阵列相比光照均匀度有较大提升。

4 结论

本文提出了一种改进的粒子群算法与新型等差LED阵列，能够有效优化LED光源阵列的照明均匀度。基于普通的粒子群算法容易早熟收敛等缺点，引入了线性变化的惯性权重和非线性变化的认知因子，从而有效地解决了这一问题；同时，设计了一种新型等差LED阵列排布方式，使用改进的粒子群算法对等差LED阵列以及矩形和圆形LED阵列进行优化。最后使用光学软件TracePro对优化结果进行仿真，得到矩形阵列和圆形阵列的光照均匀度分别为73.31%和78.56%，而等差LED阵列光照均匀度达到了82.89%，证明提出的等差LED阵列有着更好的光照均匀度。随着植物工厂、机器视觉等光源阵列对光照均匀度的要求越来越高，本文中的改进算法以及新的LED排布方式能够指导LED光源阵列设计，具有广泛的应用价值。