几种新型异形椭球面方程、几何特征及其应用前景
2023-12-28武周虎
武周虎
(青岛理工大学环境与市政工程学院,青岛 266033)
引言
椭球面是一种3 参数二次闭曲面[1],蛋形曲线[2,3]绕其对称轴旋转180°形成的旋转面称为蛋形曲面。由于蛋形曲面建筑良好的抗风能力、抗震特性和优美的外观特征备受欣赏。
国际上有代表性的曲面建筑如[4]:中国国家大剧院、日本东京的巨蛋、英国埃克斯伯里的蛋形和印度孟买的赛博蛋形等造型。张群力等[5]建立了椭球面的斜驶线微分方程和等距曲面方程,给出了建筑造型的三维网格效果图。程健等[6]认为数字建筑具有数学韵律,当建筑和结构完美融合在一起时,往往能创造出与传统迥异、令人叹为观止的奇妙建筑形态。施永安[7]在数字化建筑背景下采用计算机辅助设计,提出了超椭球大跨空间网壳结构的参数优化方法,方便了建筑师与结构工程师的设计交融。基于武周虎[8-10]创建的Wu’s 单对称轴二参数平面闭曲线——异形椭圆,武周虎[11]在三维空间上首先创建了Ⅰ和Ⅱ型异形椭球面方程,分析了它们的几何特征和应用前景。
本文以异形椭圆和椭圆为基本图形,在三维空间上再分别构建Ⅲ~Ⅶ型异形椭球面(Wu’s 系列曲面)——5 种类型的3 参数闭曲面方程,分析它们的几何特性,为其推广应用提供理论支持。
1 构建条件与分类
以异形椭圆和椭圆的不同组合方式及定义区间为条件,对已有[11]和拟构建的异形椭球面一并进行分类。
在直角坐标系(O-xyz)中,Ox、Oy、Oz轴旋转的正方向遵循右手定则。定义异形椭球面的3 个独立参数分别为x坐标方向的半长度(a)、y坐标方向的半宽度(b)和z坐标方向的半高度(c)。其中:y的定义区间为(-b≤y≤b),x和z的定义区间见表1。按照在平行于yOz上的剖面线均为异形椭圆、xOy俯视轮廓投影线为椭圆和异形椭圆以及xOz剖面线为椭圆、半异形椭圆和半椭圆来构建新型异形椭球面的原则要求,在三维空间上分别构建Ⅲ~Ⅶ型异形椭球面的条件和几何特征列于表1。

表1 几种异形椭球面的构建条件和几何特征
如表1 所示,Ⅲ型异形椭球面在xOy坐标面以上部分与以下部分的高度相同,Ⅳ和Ⅴ型异形椭球面全部位于xOy坐标面以上,Ⅵ和Ⅶ型异形椭球面在xOy坐标面以上部分与以下部分的高度比值为(e-1),自然常数e≈2.718。
按照表1 所列Ⅲ~Ⅶ型异形椭球面的构建条件和几何特征,相应异形椭球面方程的构建如下。
2 方程构建
分类构建Ⅲ~Ⅶ型异形椭球面方程,分别绘制相应的三维空间建模曲面体图。
2.1 Ⅲ型异形椭球面
(1)在xOz坐标面上,Ⅲ型异形椭球面的垂直剖面椭圆方程为:
或
式中:z1为xOz垂直剖面椭圆的垂向坐标,其它符合同前(下同)。取值范围( -a≤x≤a, -c≤z1≤c);
(2)在yOz平行面上,Ⅲ型异形椭球面的横截面是异形椭圆(以下简称为“横截面异形椭圆”)。横截面异形椭圆的对称轴通过Ox轴上的相应点且平行于Oz轴,其上顶点和下顶点坐标为(y=0,z=±|z1|),垂向高度为2|z1|。设横截面异形椭圆非对称轴横向半宽度为|yb|。
按照标准形式的异形椭圆方程[8-10],则有横截面异形椭圆方程为:
式中:当z=|z1|时,为“未定式”,采用洛必达法则计算(下同)。取值范围( -|yb|≤y≤|yb|,-|z1|≤z≤|z1|);
(3)在xOy坐标面上,Ⅲ型异形椭球面的俯视轮廓投影线(也就是横截面异形椭圆的半宽度变化曲线,下同)为关于Ox轴两侧对称的椭圆,其数学方程为:
式中:yb为俯视轮廓投影椭圆的横向坐标,下同。取值范围( -a≤x≤a,-b≤yb≤b);
(4)将式(2)和式(4)代入式(3),化简整理得到Ⅲ型异形椭球面方程为:
由式(5)绘制的三维空间建模曲面体,如图1(a)~(b)所示。

图1 Ⅲ型异形椭球面的三维建模曲面体
2.2 Ⅳ型异形椭球面
(1)在xOz坐标面上,并在z≥0 时,Ⅳ型异形椭球面的垂直剖面半异形椭圆方程为:
式中:z1为xOz坐标面上的半异形椭圆的垂坐标。取值范围(0≤x≤2a,0≤z1≤2c);
(2)在yOz平行面上剖面线的上顶点和下顶点坐标分别为(y=0,z=z1)和(y=0,z=0),则有垂向高度为z1的异形椭圆方程为:
式中:取值范围( -|yb|≤y≤|yb|,0≤z≤z1);
(3)在xOy坐标面上的俯视轮廓投射线方程为:
式中:取值范围(0≤x≤2a, -b≤yb≤b);
(4)将式(6)和式(8)代入式(7),化简整理得到Ⅳ型异形椭球面方程为:
由式(9)绘制的空间三维建模曲面体,如图2(a)~(b)所示。

图2 Ⅳ型异形椭球面的三维建模曲面体
2.3 Ⅴ型异形椭球面
(1)在xOz坐标面上,并在z≥0 时,Ⅴ型异形椭球面的垂直剖面半椭圆方程为:
式中:z1为xOz垂直剖面半椭圆的垂向坐标。取值范围(a≤x≤a,0≤z1≤2c);
(2)在yOz平行面上,Ⅴ型异形椭球面的横截面异形椭圆方程与式(7)相同。
(3)在xOy坐标面上,Ⅴ型异形椭球面的俯视轮廓投影线为关于Ox轴两侧对称的椭圆,其数学方程与式(4)相同;
(4)将式(10)和式(4)代入式(7),化简整理得到Ⅴ型异形椭球面方程为:
由式(11)绘制的三维建模曲面体,如图3(a)~(b)所示。

图3 Ⅴ型异形椭球面的三维建模曲面体
2.4 Ⅵ型异形椭球面
(1)在xOz坐标面上,并在z<0 时,Ⅵ型异形椭球面的垂直剖面下半异形椭圆方程为:
式中:取值范围(0≤x≤2a, 2c/e≤z1≤0)。
在xOz坐标面上,并在z≥0 时,Ⅵ型异形椭球面的垂直剖面上半异形椭圆方程为:
式中:z1和z2分别为xOz坐标面的下半部和上半部剖面线的垂坐标。取值范围(0≤x≤2a,0≤z2≤2c(1-1/e));
(2)在yOz平行面上剖面线的上顶点和下顶点坐标分别为(y=0,z=z2)和(y=0,z=z1),则有垂向高度为(z2—z1)的异形椭圆方程为:
式中:取值范围(-|yb|≤y≤|yb|,z1≤z≤z2);
(3)在xOy坐标面上的俯视轮廓投射线方程与式(8)相同;
(4)将式(12)、式(13)和式(8)代入式(14),化简整理得到Ⅵ型异形椭球面方程为:
由式(15)绘制的空间建模曲面体,如图4(a)~(b)所示。
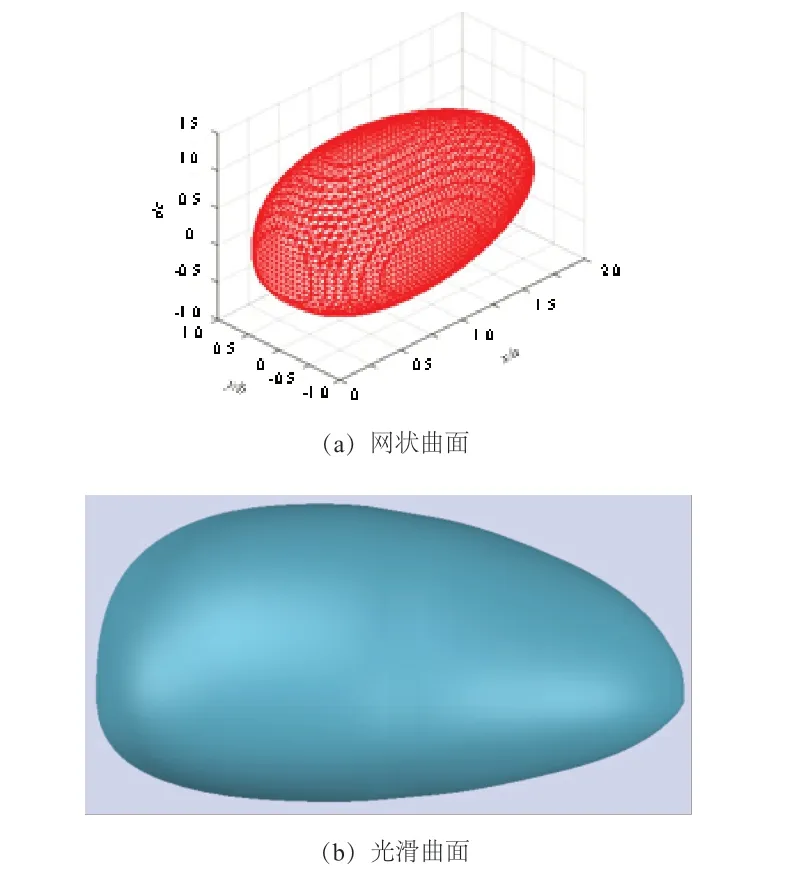
图4 Ⅵ型异形椭球面的三维建模曲面体
2.5 Ⅶ型异形椭球面
(1)在xOz坐标面上,并在z<0 时,Ⅶ型异形椭球面的垂直剖面下半椭圆方程为:
式中:取值范围(-a≤x≤a, 2c/e≤z1≤0)。
在xOz坐标面上,并在z≥0 时,Ⅶ型异形椭球面的垂直剖面上半椭圆方程为:
式中:z1和z2分别表示xOz垂直剖面下半和上半椭圆的垂向坐标。取值范围(-a≤x≤a,0≤z2≤2c(1-1/e));
(2)在yOz平行面上,Ⅶ型异形椭球面的横截面异形椭圆方程与式(14)相同;
(3)在xOy坐标面上,Ⅶ型异形椭球面的俯视轮廓投影线为关于Ox轴两侧对称的椭圆,其数学方程与式(4)相同;
(4)将式(16)、式(17)和式(4)代入式(14),化简整理得到Ⅶ型异形椭球面方程为:
由式(18)绘制的三维立体建模曲面体,如图5(a)~(b)所示。

图5 Ⅶ型异形椭球面的三维建模曲面体
3 几何特性
对Ⅲ~Ⅶ型异形椭球面,按一般性质和六至坐标、xOz剖面线、俯视轮廓线、横截面最大异形椭圆以及其它特性进行分析。
3.1 一般性质和六至坐标
一般性质包括凸面性和对称性等,“六至坐标”包括前、后、左、右、下和上的顶点坐标。
(1)一般性质
a.在表1 中所列的任何一种异形椭球面内部任何两点所连的线段都在相应异形椭球面的内部,则有异形椭球面为凸球面,对应的空间几何体为凸球体或凸面体。
b.除Ⅳ和Ⅴ型以外的5 种异形椭球面与任意一条直线最多只有两个交点,而Ⅳ和Ⅴ型异形椭球面与除Ox 轴以外的任意一条直线最多也只有两个交点。
c.根据Ⅲ~Ⅶ型异形椭球面的构建条件、方程和三维建模图不难得到:Ⅲ型、Ⅴ型和Ⅶ型异形椭球面关于xOz和yOz坐标面具有双对称性,Ⅳ型和Ⅵ型异形椭球面关于xOz坐标面具有单对称性。
(2)六至坐标
Ⅲ~Ⅶ型异形椭球面前、后、左、右、下和上的顶点坐标,如表2 所示。

表2 Ⅲ~Ⅶ型异形椭球面的顶点坐标
3.2 xOz 剖面线
在xOz坐标面上的垂直剖面线依次为:Ⅲ型异形椭球面为由式(2)表示的椭圆,如图6 所示; Ⅳ型异形椭球面为由式(6)表示的上半异形椭圆,如图7 所示; Ⅴ型异形椭球面为由式(10)表示的上半椭圆,如图8 所示;Ⅵ型异形椭球面为由式(12)和式(13)分别表示的下半和上半异形椭圆组合曲线,如图9 所示;Ⅶ型异形椭球面为由式(16)和式(17)分别表示的下半和上半椭圆组合曲线,如图10 所示。
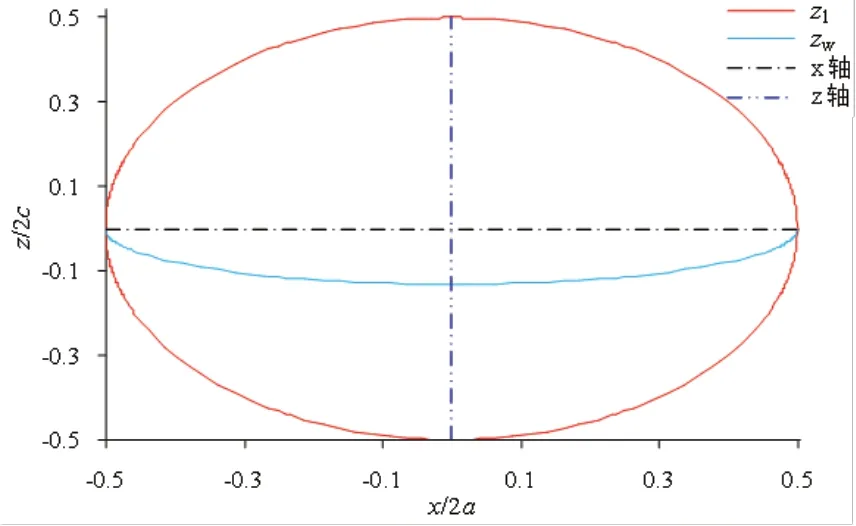
图6 Ⅲ型异形椭球面在对称面xOz 上的椭圆和最大宽度位置的垂坐标(zw)

图7 Ⅳ型异形椭球面在xOz 对称面上的半异形椭圆和最大宽度位置的垂坐标(zw)
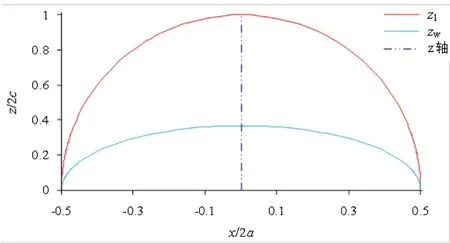
图8 Ⅴ型异形椭球面在对称面xOz 上的半椭圆和最大宽度位置的垂坐标(zw)
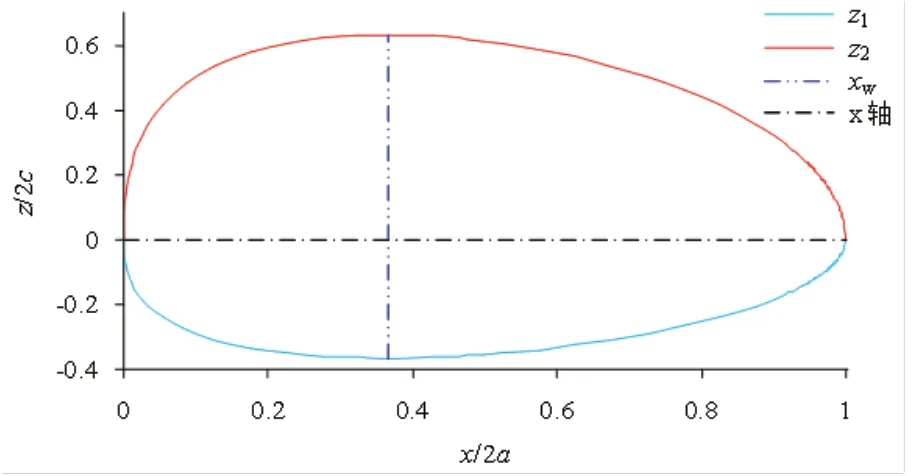
图9 Ⅵ型异形椭球面在xOz 对称面上2 个半异形椭圆的组合曲线
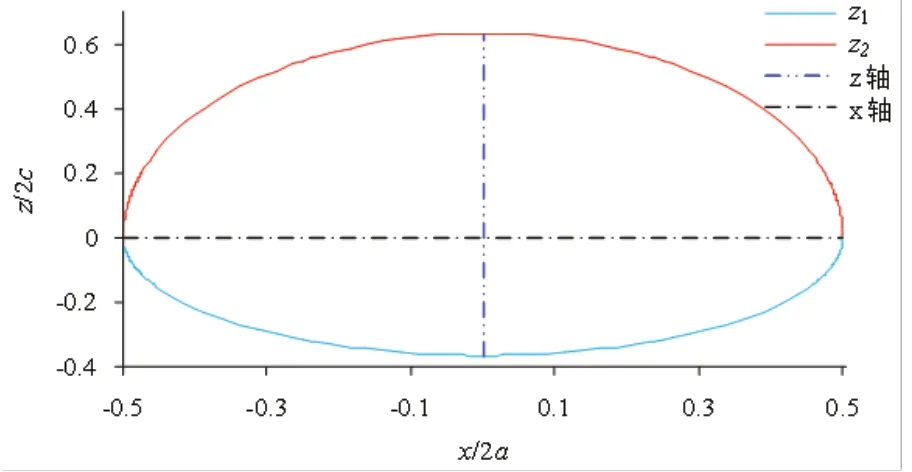
图10 Ⅶ型异形椭球面在对称面xOz 上2 个半椭圆的组合曲线
3.3 俯视轮廓线
(1)俯视轮廓投影线
Ⅲ型、Ⅴ型和Ⅶ型异形椭球面的俯视轮廓投影线为椭圆,其数学方程均由式(4)表示;Ⅳ型和Ⅵ型异形椭球面的俯视轮廓投影线为异形椭圆,其数学方程均由式(8)表示。Ⅵ和Ⅶ型异形椭球面的水平投影线与xOy剖面线重合。
(2)最大宽度位置的垂向坐标
根据Ⅲ~Ⅶ型异形椭球面的最大宽度位置坐标等于最大高度/e的条件[8],当x=定值时,可以得到对应的垂向坐标zw等于最大高度/e减去最小垂向坐标的绝对值|zmin|。据此,推导出最大宽度位置的垂向坐标计算公式,如表3 所示。

表3 Ⅲ~Ⅶ型异形椭球面最大宽度位置的垂向坐标
由表3 和图6 可知,Ⅲ型异形椭球面最大宽度位置位于z<0 处,zw的变化曲线为下半椭圆(半高度≈0.264c);再由图7 和图8 可知,Ⅳ型和Ⅴ型异形椭球面最大宽度位置位于z>0 处,zw 的变化曲线为半高度(=2c/e)的上半异形椭圆或上半椭圆;而Ⅵ型和Ⅶ型异形椭球面最大宽度位置均在xOy坐标面上。
3.4 横截面最大异形椭圆
Ⅲ~Ⅶ型异形椭球面在yOz平行面上均为异形椭圆。Ⅲ型、Ⅴ型和Ⅶ型异形椭球面均在x=0 处出现横截面最大异形椭圆,Ⅳ型和Ⅵ型异形椭球面均在xw=2a/e处出现横截面最大异形椭圆。
将x=0 代入(5)可以推导出Ⅲ型异形椭球面的横截面最大异形椭圆方程为:
将xw=2a/e代入式(9)或将x=0 代入式(11)可以推导出Ⅳ型和Ⅴ型异形椭球面的横截面最大异形椭圆方程均为:
将xw=2a/e代入式(15)或将x=0 代入式(18)可以推导出Ⅵ型和Ⅶ型异形椭球面的横截面最大异形椭圆方程均为:
3.5 其它特性
Ⅲ型异形椭球面在xOy坐标面以上和以下部分的高度相等;Ⅳ和Ⅴ型异形椭球面全部在xOy坐标面以上;Ⅵ型和Ⅶ型异形椭球面在xOy坐标面以上部分与以下部分的高度比值均为(e-1),即在xOy坐标面以上部分、以下部分的高度分别占最大高度的63.21%、36.79%。
由文献[10]给出的异形椭圆面积系数曲线图可知,异形椭圆最大宽度相应的位置高度以上和以下部分的面积系数分别为0.6 083 和0.3 917。根据Ⅲ~Ⅶ型异形椭球面最大宽度位置的垂向坐标,则有Ⅲ~Ⅶ型异形椭球体在最大宽度位置以上部分和以下部分的体积占各自总体积60.83%和39.17%。而Ⅵ和Ⅶ型异形椭球面最大宽度位置的垂向坐标为z=0,即在xOy坐标面以上部分和以下部分的体积占各自总体积比例也是如此。
4 应用前景
异形椭球面的连续性、光滑性和整体性好,具备G3 曲率相切连续。下面对几种新型异形椭球面的应用前景进行分析探讨。
Ⅲ、Ⅴ和Ⅶ型异形椭球面的俯视轮廓投影均为椭圆,即两端、前后均对称,调整垂向高度,剔除曲面的z 坐标较小部分,由相应的异形椭球面方程可得到形状各异的建筑造型,比如蛋形建筑、塔楼等。选择几何尺寸2a=212.20 m[4]、2b=1.354a和2c=0.746a,由式(18)可得到Ⅶ型异形椭球面,在xOy坐标面以上部分的蛋形曲面与中国国家大剧院的外形十分相似,建筑物高度偏高7.2%。如果将z 轴向下倒置的Ⅲ、Ⅴ和Ⅶ型异形椭球面(体),剔除曲面的z坐标较小(即上部)部分,可作为造船的基本形状,船体下水后浮体的浮心较高,有利于船舶稳定。
Ⅳ和Ⅵ型异形椭球面在三个坐标面上的轮廓线均为异形椭圆,合理调整3 个独立参数,剔除曲面的z坐标较小部分,由相应的异形椭球面方程可得到具有大小头的独特蛋形建筑造型,可建造成歌剧院、艺术馆、展览中心和体育馆等曲面穹顶以及景观雕塑造型的形状设计。
在实践中,可根据设计对象的功能需求、环境协调和主题,按照各种异形椭球面方程的构建特征和形状特征,进行方案比选与融合,取其所长,最终获得一种理想的优化设计方案。
基于武周虎[12]创建的一种新的异形超椭圆方程,采用类似于异形椭球面方程的构建方法,可以构建出多种型式的异形超椭球面方程及其更多风格独特的建筑物造型,具有更加广阔的应用前景。
5 结论
异形椭球是异形椭圆和椭圆在三维空间的推广。以异形椭圆和椭圆为基本图形,定义了异形椭球面的3个独立参数包含半长度、半宽度和半高度,在三维空间上分别构建了5 种类型的异形椭球面。
(1)Ⅲ~Ⅶ型异形椭球面是:xOy俯视轮廓投影线为椭圆或异形椭圆,在平行于yOz上的剖面线均为异形椭圆,xOz剖面线为椭圆或半异形椭圆或半椭圆;
(2)Ⅲ、Ⅴ和Ⅶ型异形椭球面关于xOz和yOz坐标面具有双对称性,Ⅳ和Ⅵ型异形椭球面关于xOz坐标面具有单对称性。Ⅲ、Ⅳ和Ⅴ型异形椭球面的俯视轮廓线不在同一平面上,Ⅵ和Ⅶ型异形椭球面的俯视轮廓线与xOy剖面线重合;
(3)Ⅵ和Ⅶ型异形椭球面在xOy坐标面(俯视轮廓线)以上部分的高度占各自最大高度63.21%,Ⅲ~Ⅶ型异形椭球体在俯视轮廓线以上部分的体积占各自总体积60.83%;
(4)Ⅲ~Ⅶ型异形椭球面在特殊建设工程、浮体和景观造型等设计中,具有广阔的应用前景。
