基于福岛核事故监测数据的辐射剂量场重构方法研究

徐 瑶，陈晓雷，黄广伟，吴涢晖，陈 林

(军事科学院防化研究院，北京 102205)

准确评定核事故后危险区等级是维护国家核安全和国防安全的重要课题，有助于缓解和遏制污染源，同时预测污染物时空传输和扩散情况，为防护、洗消和行动提供决策基础。当前对于核扩散的预测主要依靠放射性烟羽在大气中的扩散原理和数学扩散模型[1]，在掌握源项信息的基础上建立物理模型，计算辐射剂量场的分布，从而对核危害的发展态势做出评估，常用的模拟计算方法有蒙特卡罗方法[2]、点核积分方法[3]等。实际上，基于大气扩散模式的模型具有一定偏差，事故点地形、气象等条件复杂多变，且在核事故发生早期源项信息往往很难准确获得，导致计算结果往往会有较大误差。随着信息技术快速发展，核辐射传感器信息化能力得到大幅提升，将核辐射传感器广泛布设于监测区域内，可以实现剂量数据的实时采集和动态监测，为基于实测数据进行辐射剂量场重构奠定了技术基础。然而由于核事故后污染范围极大，很难获取整个污染区的精细数据，只能利用有限采样数据对辐射剂量场进行重构，在这种情况下，通过少量实测数据重构核辐射剂量分布的研究变得尤为重要。空间插值方法可以有效地基于少量样本实现大范围辐射剂量场重构：Thevenaz等人[4]研究表明插值计算在辐射剂量场重建中具有重要作用；李廷等人[5]利用反距离权重方法估算三维空间辐射剂量率场，实现真实场景下的光子剂量场与核素活度场耦合；张敏等人[6]基于MCNP程序模拟特定空间内存在中子源时，获取了辐射场内网格节点的浓度值，通过立方样条插值恢复网格线的浓度值，建立了一个基于网格节点的反演模型；赛雪等人[7]将径向基函数散乱数据插值方法应用于γ辐射场，对具有不同分布对称性的γ辐射场进行了数据重构；陈雷等人[8]采用克里金插值模型进行沉降量内插，获得可靠的估算数据，但选取的样本点的数量较少，影响克里金插值模型整体精度。可以看出，没有一种算法适用于所有的场景，不同的插值方法对计算结果影响不同。为比较不同插值方法重构辐射剂量场的精度，本文利用反距离权重插值法、克里格插值法、线性三角网插值法以及径向基函数插值法研究散乱节点的二维辐射剂量场的重构问题，探讨不同插值方法对辐射剂量值的插值效果，进一步通过交叉验证对比分析各种方法插值结果的精度。

1 问题和算法描述

在大量的应用领域中，通常面临利用某一个函数来描述测量值的任务。对于这个问题一般有插值和回归两种解决办法，插值法更适用于假定数据正确的环境。对于需要寻找多元解析函数来描述高维空间中多维数据的任务，如天气预报风云高压图、山川河流等高线测量等，二维插值是最常用的方法，辐射剂量场的重构也属于这类问题，其基本理论假设是空间位置上越靠近的点越可能具有相似的特征值，距离越远的点其特征值相似的可能性越小。实际问题中节点数据网格往往是散乱无规律的，为插值增加了难度。散乱节点网格插值的数学过程描述如下:

已知n个节点(xi,yi,zi),i=1,2,…,n，其中(xi,yi)互不相同。需要构造一个二元函数z=f(x,y)，通过全部已知节点，即f(xi,yi)=zi，再用f(x,y)计算插值，即z*=f(x*,y*)。

通过上述方法可以对不足或缺失数据进行补充插值，实现数据网格化，并且可以进一步获得等值线以显示数据的空间分布特征。

1.1 反距离权重插值法

反距离权重插值法(inverse distance weighted，IDW)是由 Shepard[9]提出的一种全局插值算法，其利用插值点周围样本点值的信息来计算插值点的值，以插值点与样本点间的距离为权重进行加权平均，离插值点越近的样本点赋予的权重越大，即[10]：

(1)

式中，n为样本点个数；Z*(x*,y*)为点(x*,y*)处的插值计算值；λi为插值点对于样本点的权重，与插值点与样本点之间的距离相关，Zi(xi,yi)为在样本点(xi,yi)处的测量值。

权重λi的表达式为：

(2)

式中，di为插值点(x*,y*)与各样本点(xi,yi)之间的欧氏距离；α为指数项，反映样本点之间的权重，通常取值1～3，α值影响插值图像的光滑度，α值越大，插值的光滑性越差。通过选取不同α值进行网格化分析，当α取3时得到一个较满意的结果，误差最小，因此本文中α取3。

1.2 克里金插值法

克里金插值(kriging)法又称空间自协方差最佳插值法[11]，综合考虑了监测点和被估计点的之间的相对位置关系和各监测点之间的相对位置关系，是一种基于变异函数理论对变量值进行无偏、最优估计的空间数据插值方法[12]。克里金插值法包括普通克里金法、简单克里金法、指示克里金法、协同克里金法、泛克里金法等。

设Z*(x*,y*)是区域化变量，满足二阶平稳或本征的，其数学期望为常数，Zi(xi,yi)是定义在样本点(xi,yi)上的一组离散的信息样品数据，在任一非样本点(x*,y*)处的克里金估计值为[13]：

(3)

克里金插值法的原则需要保证估计值无偏且估计方差最小，根据拉格朗日原理，求解得出n个权值系数应满足以下条件[13]：

(4)

式中，μ是拉格朗日乘子；c是协方差函数。通过求解方程组(4)得到权重系数λi，再根据式(3)可得出最终的插值结果。求解上述过程的关键一步是选择合适的变异函数模型，克里金提供了不同的理论变异函数模型，常用的有球体模型、高斯模型、指数模型、线性模型等[14]。本文通过实验对比验证，选择普通克里金模型以及线性变异函数模型使函数曲线与监测点进行最优匹配。

1.3 线性三角网插值

线性三角网插值(linear triangulation interpolation)又叫线性插值，线性三角网法采用最佳Delaunay三角化方法，将离散数据点直接相连构成三角形，区域内所有三角形的边互不相交构成一张三角形网[15]。

线性三角网插值的原理是根据区域内任意待插值点P(x,y)与其所在三角形的三个顶点之间的线性关系形成权系数，利用此权系数计算出待插值点的函数值，其插值函数为[16]：

(5)

式中，λi为点Zi(xi,yi)的权系数；Zi(xi,yi)，i=1,2,3为三角形顶点的函数值；Z*(x*,y*)为插值点P(x,y)的函数值，权系数λi须在待插值点位于三角形内的情况下进行插值。线性三角网插值方法充分利用了已知点的信息，反映数据点与其邻近点间的拓扑连接关系。

1.4 径向基函数插值

径向基函数(radial basis function，RBF)是一种基于距离的函数，具有结构简单、各向同性、尺寸无关和无网格等特点，适用于对大量离散数据的表面插值和拟合[17]。RBF插值的基本理论基础是未知函数在高维空间中，任一点的函数值Z*(x*,y*)可以用径向基函数的线性组合来逼近，计算公式为[18]：

(6)

式中，n为插值点个数；αi为第i个插值节点的权重；φ为径向基函数，函数值取决于n维空间的欧式距离；di为插值点(x*,y*)与各采样点(xi,yi)之间的欧氏距离。

径向基函数包括五种基本核函数：多重二次曲面函数(MQF)、多重对数函数(MLF)、反多重二次曲面函数(IMQF)、薄板样条曲面函数(TPSF)和自然三次样条曲面函数(NCSF)[19]。核函数是影响插值精度的重要因素，选用五种核函数对样本进行插值分析，采用标准偏差来分析不同核函数的插值效果。五种核函数插值精度从高到低排序依次为：多重二次曲面函数>自然三次样条函数>薄板样条函数>多重对数函数>反多重二次曲面函数，因此本文选择的核函数为多重二次曲面函数。

2 算例计算

2.1 数据来源

本文选用的数据来自日本原子能研究开发机构(Japan Atomic Energy Agency，JAEA)[20]在日本福岛第一核电站事故后发布的监测数据，事故发生地点地理位置为北纬37°25′17″，东经141° 01′57″，选用距福岛第一核电站约80 km区域内的空气剂量率数据，该数据根据空中监测调查的测量结果创建，通过转换在每个监测点上方空气中测得的计数率，计算得到地面上1 m处空气剂量率数据。数据库包括监测点的经纬度、剂量率数据、监测起止时间等信息。

2.2 辐射剂量插值实现

本次研究共选取2 000个样本点作为已知点进行计算，这些监测点的地理位置及对应位置的剂量率值如图1所示，随机分布于监测范围内。

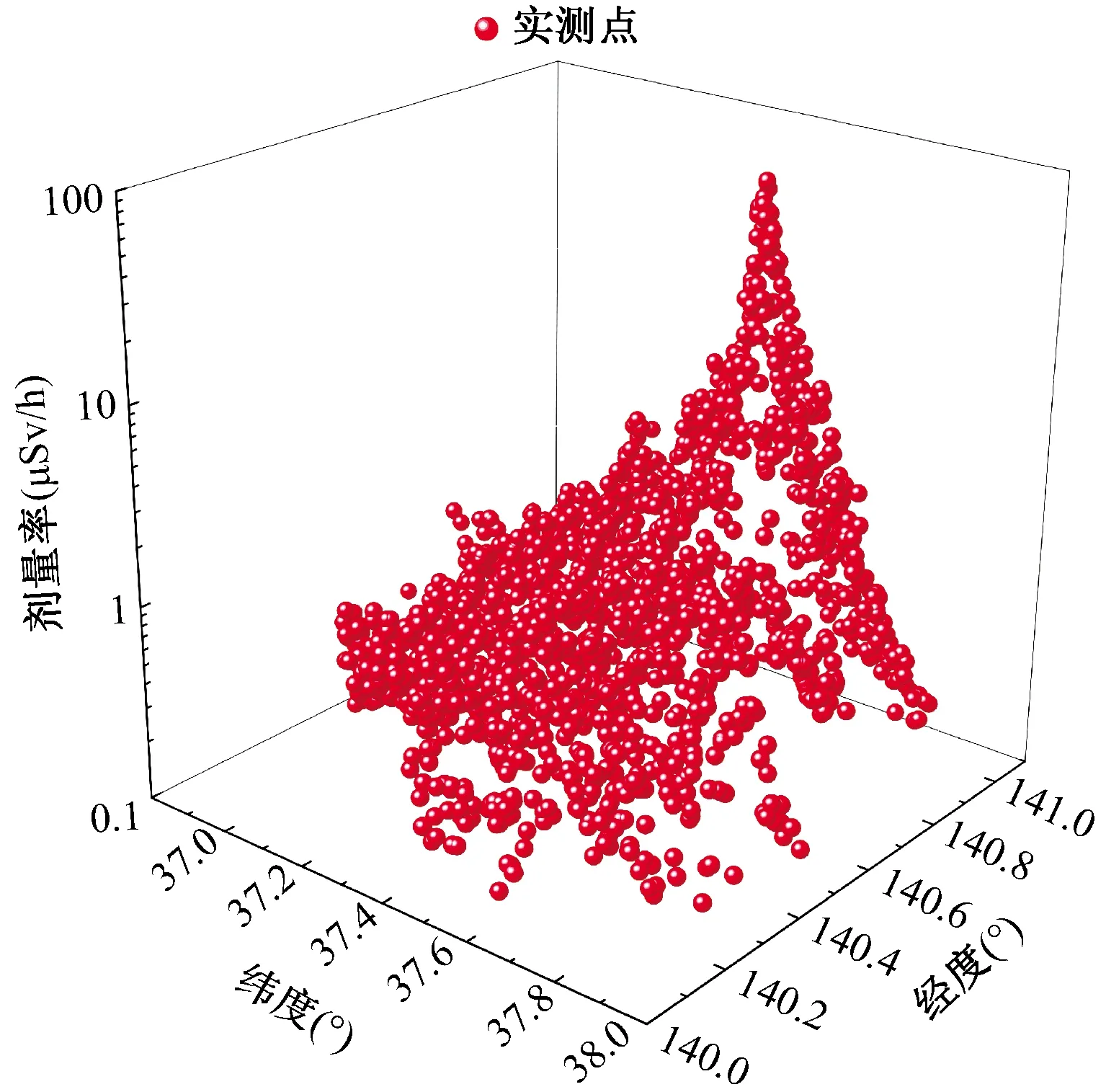
图1 监测点地理位置及对应剂量率值Fig.1 The geographic location of the monitoring pointand the corresponding dose rate value

该算例的计算过程通过美国Golden Software公司Surfer软件实现，该软件可用于制作基面图、数据点位图、等值线图等，并提供多种数据网格化和数据计算方法[21]。计算过程首先需要对数据进行网格化处理，网格间距往往对结果的准确性有影响：网格间距过大导致结果不准确，网格间距过小会导致计算时间长。本文分别选取不同大小的网格间距对辐射剂量数据进行网格化，计算插值数值与测量数值之间的标准偏差，同时综合考虑准确性以及计算机的容量和运行时间，最终选择行列节点数为200×200进行网格化，该间距下准确度较高且耗时较小。

将非均匀分布的原始剂量数据，通过反距离权重插值法、克里金插值法、线性三角网插值法以及径向基函数插值法计算得出200×200的网格节点数据。

依据得到的细网格数据，使用surfer软件进行辐射剂量场的显示。图2是利用2 000个样本点分别采用上述4种方法绘制生成的辐射剂量趋势面，从图2中可以看出，4种插值方法均能很好地呈现出辐射剂量场的空间分布状态，呈现效果相似。在监测区域内部，相比较于克里金插值法和径向基函数插值法，反距离权重插值法与线性三角网插值法得到的曲面峰值区域图形更加尖锐，更易受到临近点剂量值的影响。

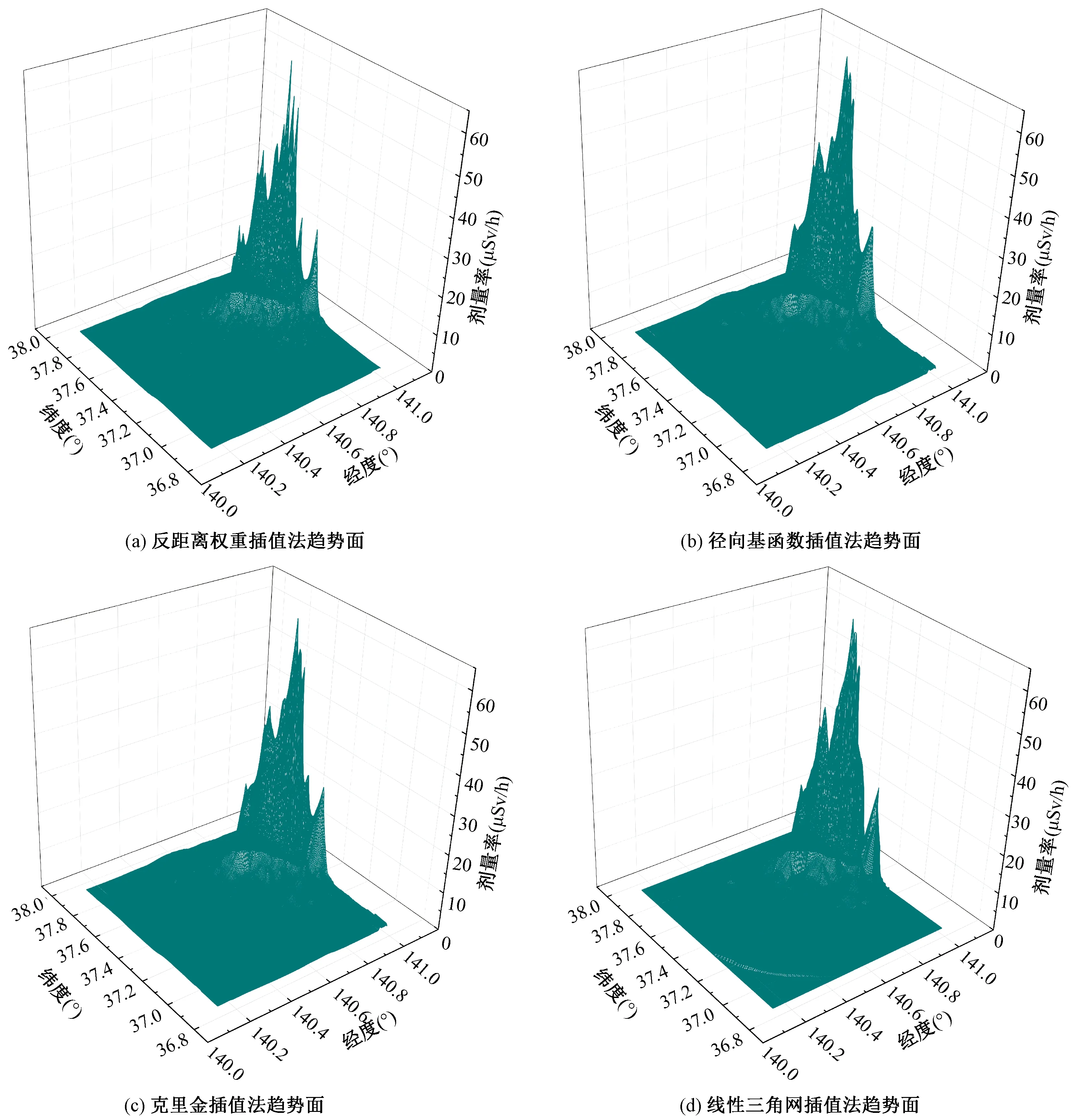
图2 基于四种方法生成的辐射剂量率趋势面Fig.2 Radiation dose rate trend surface generated based on four methods

为了更直观的比较网格化的结果，将四种插值方法生成的细网格数据在二维平面拟合生成辐射剂量率等值线分布，如图3所示。从图3中可以看出，4种方法都能较好地插值拟合出辐射剂量率的大致分布情况，且等值线趋势相近。但是，克里金插值法和径向基函数插值法得到的等值线分布图较另外两种方法在局部更加精细，比较右上角区域(经度140.7°以东，纬度37.6°以北区域)，可以看出克里金插值法和径向基函数插值法在剂量率0.13～0.25 μSv/h区间，层次仍然比较分明。线性三角网插值法得到的等值线分布图在整个区域内线条清晰，但其严格控制了实测数据的边界，插值范围有限，空白区域较大。而反距离权重插值法等值线比较粗糙，在局部监测区域更易出现“牛眼状”分布，插值结果会与真实值有较大偏差，无法真实地反映出这些点位的剂量变化。

图3 四种方法生成的辐射剂量率等值线分布图Fig.3 Distribution map of radiation dose rate contour generated by four methods

2.3 误差分析

为了进一步对比4种插值方法的准确性，采用交叉验证对插值方法进行比较。将采用计算的2 000个样本点划分为两部分，一部分为参与插值计算的训练集，一部分为未参与插值计算的测试集。对于测试集的选取，划分不同数量的样本作为测试集对结果进行评价，测试集的样本数量分别随机选取1, 10, 20, 50, 100, 200, 300, 400, 500, 600, 700, 800, 900, 1 000个，即假设这些测试集点位的数据未知，用训练集的数据使用不同的插值方法计算出测试集所在位置处的模拟值，然后再与测试集中实际的测量值进行对比，计算模拟值与测量值之间的误差。此步骤重复进行20次，最终计算误差的平均值。误差评价指标主要选择常用的标准偏差(σ)、平均绝对误差(MAE)和均方根误差(RMSE)[22]。标准偏差用来衡量数据自身的离散程度，平均绝对误差用来衡量模拟值的误差范围，均方根误差用来衡量模拟值与真值之间的偏差程度。这3个指标的计算方法如式(7)～(9)[22]，误差计算结果如图4所示。

图4 误差分析结果Fig.4 Error analysis result

(7)

(8)

(9)

式中，μ表示样本总体xi的均值；fi表示模拟值；yi表示测量值；n为样本数目。

从图4计算结果可以看出，不同插值方法之间的标准偏差、平均绝对误差以及均方根误差并不相同。测试集样本数逐渐增多，意味着训练集样本数减少，各插值方法精度均有所下降，σ、MAE和RMSE均随着训练样本数减少而波动提升。在相同的测试集样本数下，径向基函数插值法的预测误差最小，反距离权重插值法预测误差范围最大，线性三角网插值法和克里金插值法介于两者之间。径向基函数插值法的RMSE和σ均保持在1.7以下，MAE保持在0.41以下，在插值精度上优于其他3种方法，说明径向基函数插值法的插值精度更高，预测效果更好。对插值点与测量点对比分析，4种方法产生偏差主要分布在极值附近和剂量变化明显的地方，四周边缘区域由于缺乏测量数据作参考，插值填充后该区域失真较严重，也是偏差主要分布位置。但径向基函数插值法和克里金插值法能很好地表现出细节处的剂量变化情况，偏差相对较小，说明该两种插值算法的误差比较稳定。造成以上结果的原因是因为反距离权重插值法仅考虑了距离的影响，根据周围测量点的距离权重进行赋值，忽略了各样本点之间的空间关联性，导致计算值容易受数据点集群的影响，易出现孤立数据点现象，反映在辐射剂量等值线分布图上即“牛眼状”分布。线性三角网插值法构造三角形的速率会导致计算速度慢，且无法保证曲面的光滑性要求，采样数据点个数较少且分布不均匀的情况下重构精度不高，易出现明显的边界。克里金插值法不仅考虑了距离权重，还考虑了各监测点之间的相对位置关系，使得求取权系数更合理，利用变异函数所揭示的测量值的内在联系来估计插值点数值，插值精度高。径向基函数插值法具有很强的拟合数据点、产生光滑曲面的能力，能够突出辐射剂量的变化，在剂量数据变化较大时插值精度较高，模拟曲面能较好地保持剂量局部变化细节与趋势。这也解释了为什么图3中径向基函数插值方法得到的等值线分布图更精细且误差最小。

3 结论

本文基于有限数量的辐射监测数据，利用4种插值算法实现了辐射剂量场的重构，探索不同插值算法在辐射剂量场重构的可行性，并比较不同方法的精度。通过对插值结果与预测误差的分析，得到的结论如下：本文所涉及到的插值方法均能表达出辐射剂量场的空间分布特征，根据不同插值方法的误差统计和效果显示比较可以发现，径向基函数插值法无论是插值效果上还是插值精度上都优于其余插值方法，能更好地呈现出辐射剂量明显的变化趋势。同时，为提高插值精度，可以适当增加采样点数量和划分网格数量。

本研究为核事故早期源项信息不明的情况下基于实测数据构建辐射剂量分布提供一种有效的预测方法，对辐射剂量场的空间插值应用具有一定参考意义。下一步，可以考虑改进完善径向基函数插值法，尝试将该方法应用于其他辐射剂量场重构与分析中，同时将地形、气候等不同因素加入到插值模型，结合以上提出辐射剂量场分布特点的基函数，以此构造出更精确且符合真实场景的插值计算结果。