分层流中潜艇加减速对尾迹特征特性的影响
2022-07-05于祥胡开业
于祥,胡开业
哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001
0 引 言
潜艇潜航状态下产生的水动力尾迹主要有伯努利水丘(Benoulli hump)、开尔文尾迹、湍流尾迹、内波尾迹和涡尾迹等。在潜艇非声学探测领域,该类水动力信号可被遥感与雷达影像侦测[1-4]。其中开尔文尾迹与艇体上方伯努利水丘在遥感影像上识别度较高,潜艇通过增加潜深或降低航速等手段可有效抑制该类信号,从而显著降低被探测的概率。
常规方法不易控制分层海洋中潜艇航行产生的内波,因其存在时间久且传播范围广,即使在恶劣天气、雨、夜中,仍可通过星载或机载合成孔径雷达(SAR)全天候广泛地侦测潜艇位置,并通过散射影像推算出潜艇的运动状态、潜深及所处的位置。Voropayev[5-6]早在1999 年就发现,当潜艇在连续分层流体中进行操纵机动航行时可产生大尺度的漩涡,该类由潜艇非定常机动航行诱发的水动力兴波与海表波相互作用,在未来的潜艇非声学探测领域有重要的学术与工程研究意义。目前关于潜艇尾迹特性的理论、数值模拟及试验研究,几乎均假设潜艇作匀速定深航行运动,对非定常与潜艇机动运动方面的研究极少。
本文将运用CFD 技术,对强分层海洋环境下潜艇非定常机动模式对海表及内部流场的影响进行定量分析,研究潜艇运动状态及加速度大小对其隐身性能的影响,为潜艇非声学探测技术以及潜艇运动状态推演提供相关理论依据。
1 理论模型
针对不同时刻、不同空间上的各物理量,CFD 数值模拟是通过计算域内离散点变量来表示,以一定原则、方式为基础,建立并近似求解相关方程组来获取各离散点场变量关系[7-8],密度分层流中流动过程遵循质量守恒、动量守恒定律,基于温度分层的密度跃层时,还需遵循能量守恒定律。在水动力CFD 数值模拟领域,对流体黏性的处理通常采用求解雷诺平均纳维−斯托克斯(RANS)方程。
1.1 数值模拟控制方程
通过相关控制方程,来表示流体遵循的三大守恒定律。本节主要运用能量守恒、质量守恒和动量守恒方程实现潜艇在不同海洋分层环境中航行尾迹及流场的数值模拟。
1) 质量守恒方程。
任意流体微粒在单位时间内,其质量不随时间变化,且流入、流出微元体中的质量相同。也可认为相同时间内微元体中增加的流体质量等于流入该微元体的流体质量。其表达式为
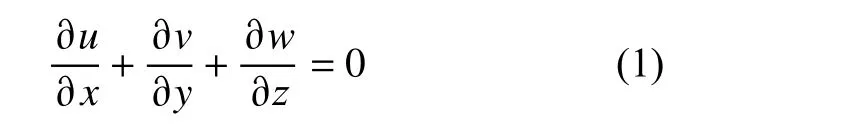
式中,u,v,w为速度矢量u在x,y,z这3 个轴方向上的分量。
2) 动量守恒方程。
流体所受合外力等于其单位时间内的动能增加量。不可压缩流体动量守恒方程为:
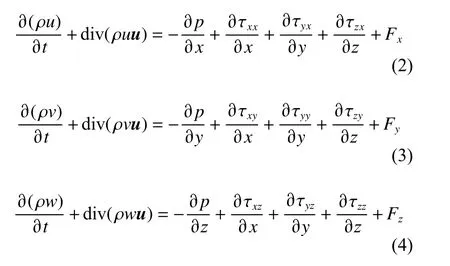
式中: ρ为流体密度;p为流体微团上的压力; τxx为流体微团上不同位置不同切向的黏性应力;Fx为流体微团所受到的各方向的体积力。
3) 流体域体积(VOF)多相流模型。
不可压缩流体,通过连续性方程∇·u=0的VOF 方程为:
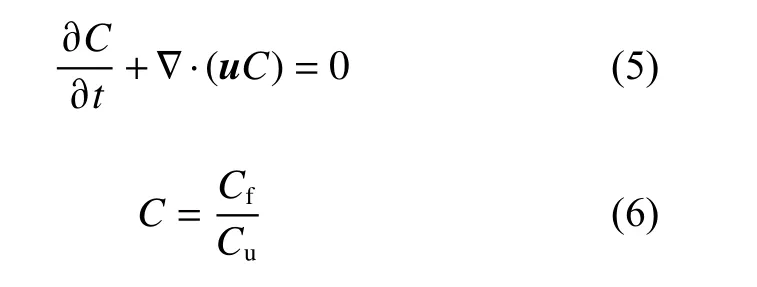
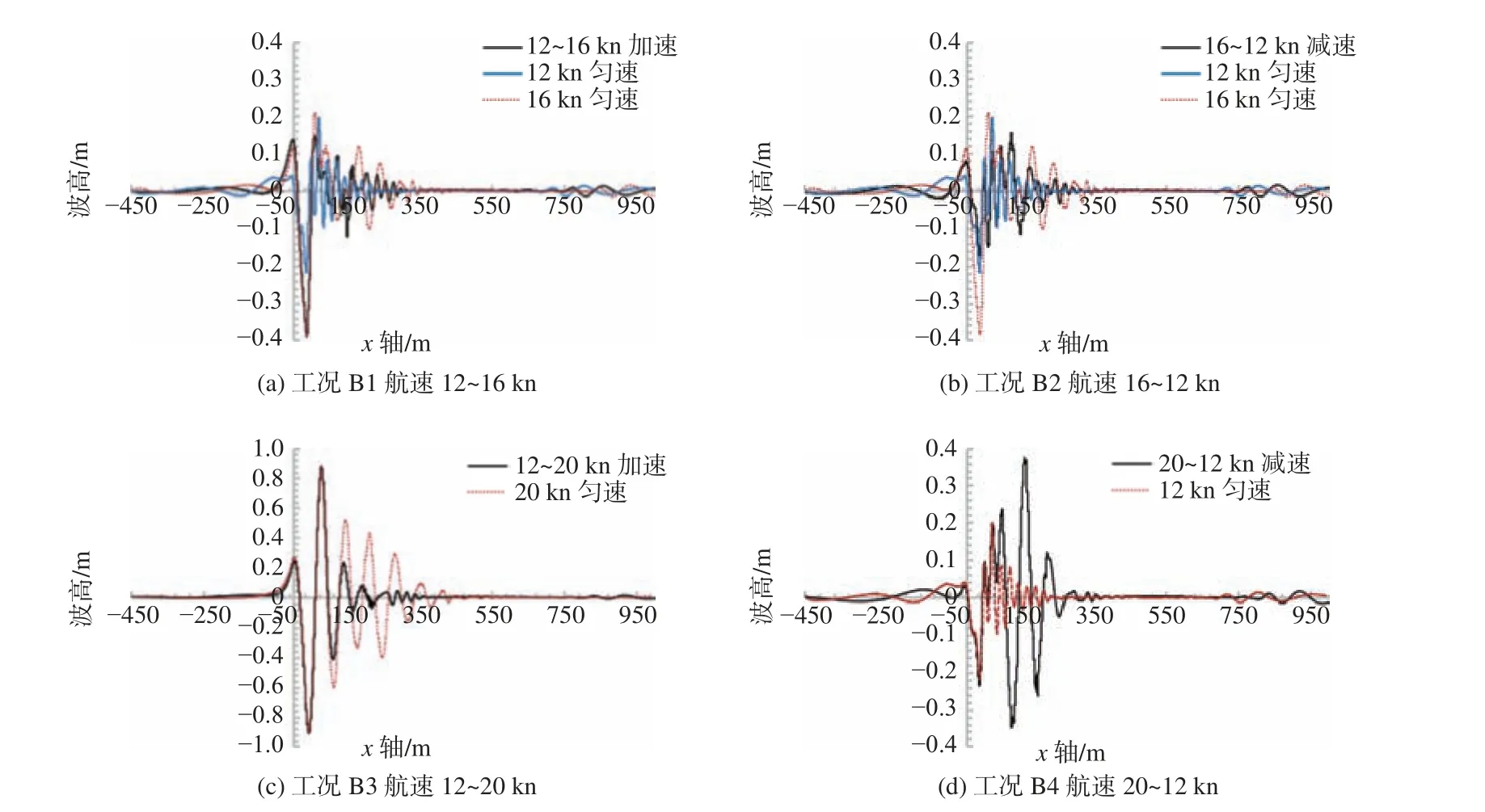
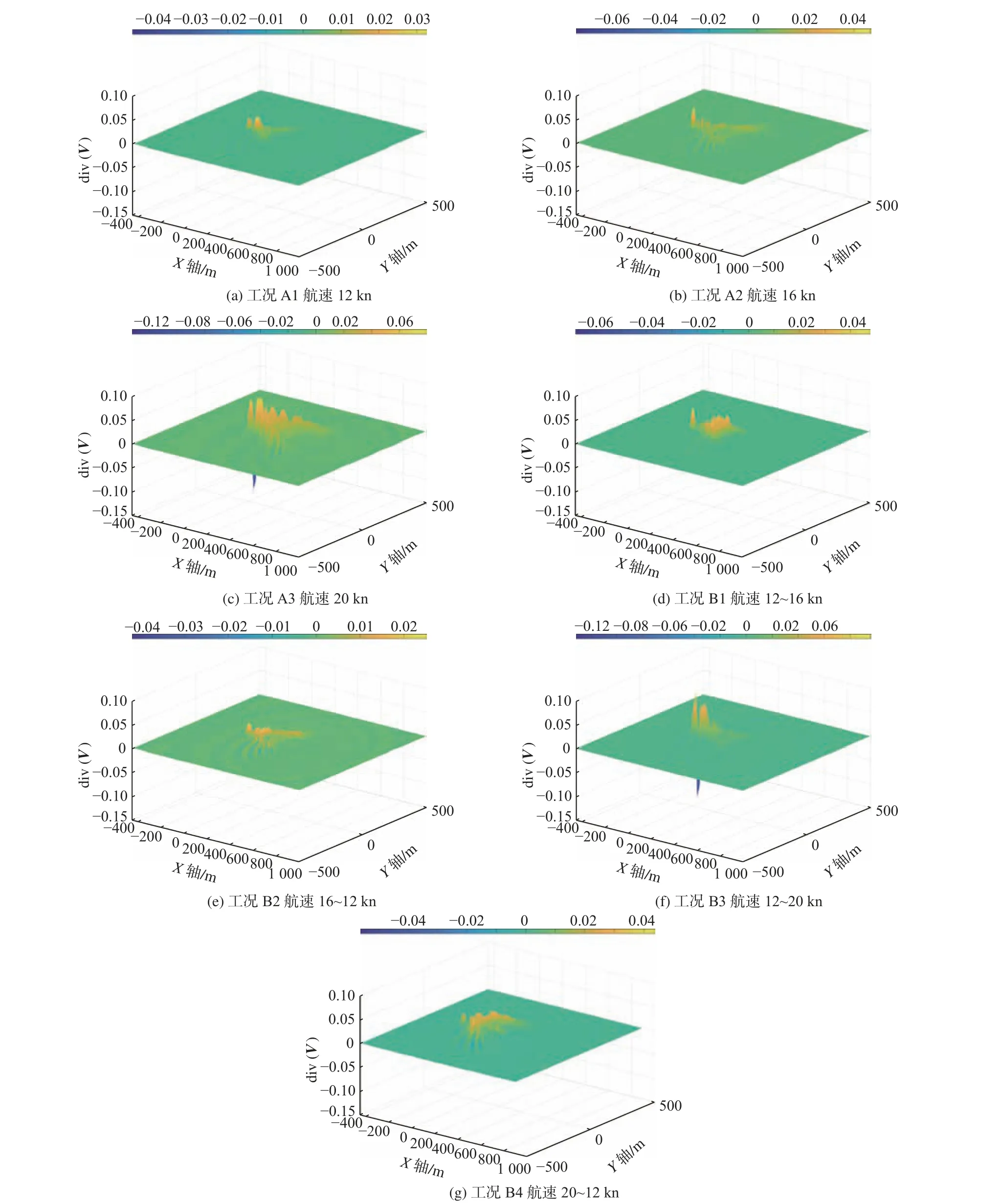
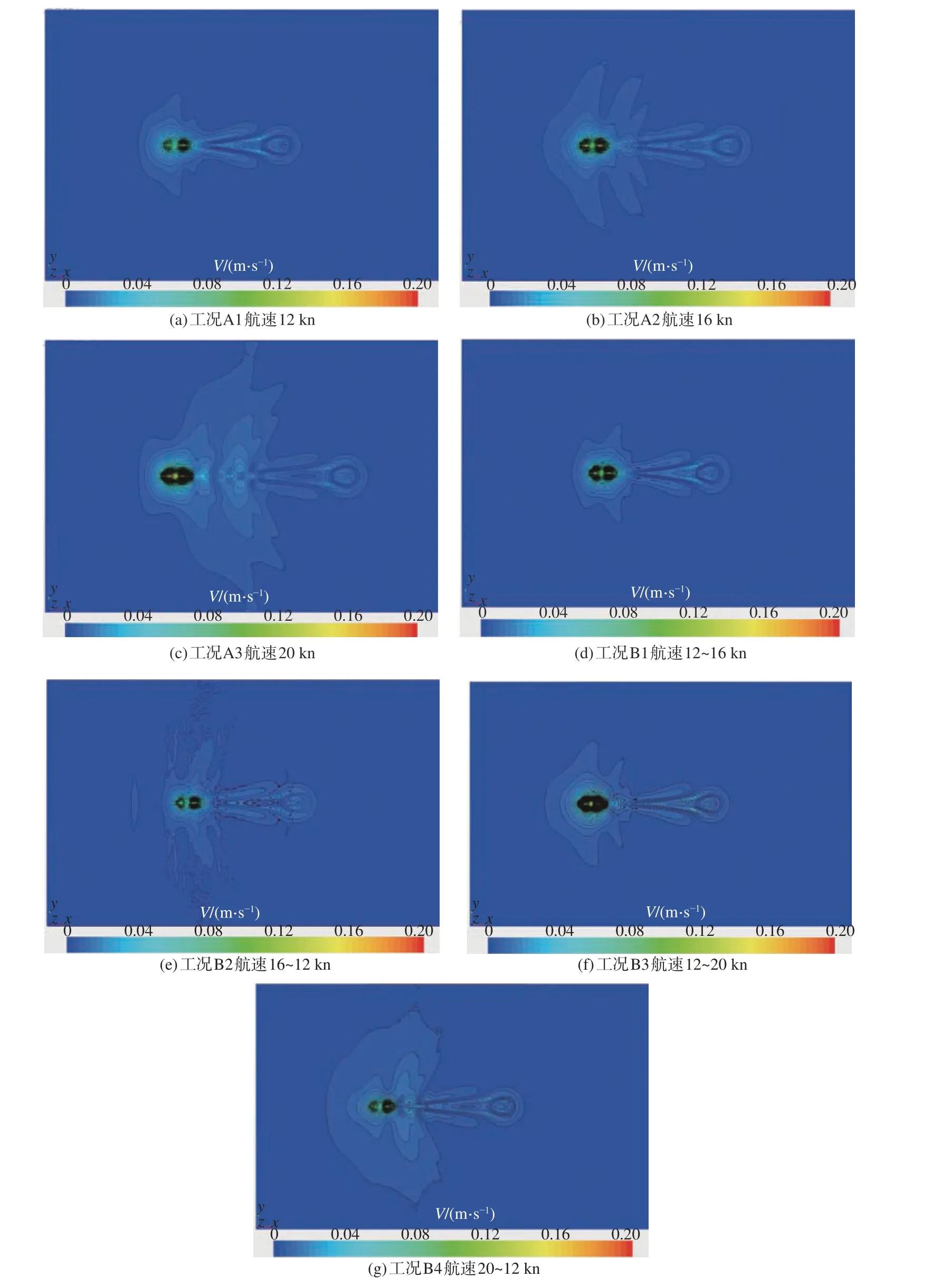
式中:u为 流体速度;Cf为单元中流体体积;Cu为单元体积。当计算的网格单元内充满该流体时,C=1;网格内无该流体时,C=0;0 1.2.1 潜艇加减速模型 潜艇变速机动过程的加速度通常为变加速,此过程中潜艇螺旋桨有效推力、水动力参数等诸多因素决定加速度瞬态值,数值计算中对其求解极为复杂[9-10],且许多参数在求解时无法获取,所以本文潜艇加减速不考虑螺旋桨。按式a=(vj−vi)/tij求解潜艇在该过程中的平均加速度,tij为变速时间,vi为变速前速度,vj为变速后速度。变速过程中速度瞬态值为aT+v(i−1),其中,v(i−1)为前一数据周期的速度,T为计算时间步长。直到潜艇速度加速或减速到vj时稳定,加(减)速过程通过编程对潜艇运动状态场函数进行自定义。 1.2.2 尾流场分析法 SAR 灵敏度由雷达波频决定,将波频设置低风速档时可消除海表阵风对内波影像的影响,即可从复杂海边信号中侦测到潜艇航行生成的内波。美国曾通过该方法有效侦测到前苏联潜艇在300 m 潜深航行时产生的内波信号。结合理论研究与实验观测,Alpers 等[11-12]得到SAR 可侦测识别潜艇潜航产生的内波与海表流场经过波流调制后的辐聚辐散信号强度区间为10−3~10−4s−1(s 为时间单位秒,下文均采用此单位计量)。潜艇运动产生的内波诱发海表流场的空间分布特征同内波水面映波类似,在波峰前与波谷后出现辐聚流,波谷前与波峰后出现辐散流,即水面映波的波节处出现明显的分散、聚集流动。 CFD 中流场辐聚辐散强度为对自由面水平速度场V求其散度,其表达式为: 本文首先验证RANS 方程、SSTk-ω 湍流模型、VOF 法对潜艇潜航状态尾流场模拟的可靠性及自由面捕捉的准确性。通过数值模拟Rankine ovoid model 在水下匀速潜航时的自由面兴波特性,将结果与1966 年David Taylor 水池试验[13]的兴波纵剖面波高数据进行对比,验证数值模拟潜艇航行的可行性与精度。 根据Rankine 卵形体几何参数[13],通过CATIA软件对Rankine 卵形体进行三维建模(图1)。本文参照泰勒水池潜艇拖曳航行试验数据进行参数设置,将模型潜深设置为0.457 m,以匀速方式进行拖曳。选取航速3.048 m/s 工况进行相关数值模拟,计算域取去流段长度30.48 m,进流段长度1.219 m。 图1 Rankine 卵形体三维模型Fig. 1 Three-dimensional model of Rankine ovoid 对该卵形体潜航流场运用STAR-CCM+软件进行数值模拟方案验证,计算域网格划分选取软件自带的切割体网格模型,针对黏性底层对卵形体表面划分边界层网格,对海表波高、波长方向网格进行精细加密,使单个波长与波高有充足的网格数,网格划分如图2 所示。 图2 卵形体计算域网格划分Fig. 2 Meshing of computational domain for ovoid 当潜艇潜深1.5 ft,航速V=10.0 ft/s,流场趋于稳定且结果收敛时,取海表纵剖面波高数据与泰勒水池浮标试验数据进行对比。如图3(右图波高以英尺为单位)所示,本文数值模拟方法的海表纵剖面波高、波形、波长数据与泰勒水池试验结果近乎一致,说明本文所采用的CFD 方法在模拟潜艇运动时对于捕捉海表“兴波”特性是有效且精准的,该方法对于实际海洋中潜艇运动尾迹特性的预报可行。 图3 数值模拟验证Fig. 3 Numerical simulation verification 以国外某常规潜艇为计算模型(图4),该艇长73.8 m,宽9.9 m,艇体为水滴线型,在艇艏导流罩下方设有艏舵,艇艉设有2 片水平艉舵与1 片垂直艉舵。 图4 潜艇计算模型Fig. 4 Submarine computational model 潜艇定深变速运动数值模拟采用重叠网格技术,流场取顶层为15 m 厚度的空气(海表空气为海平面条件),中层淡水厚度取40 m,密度为997.56 kg/m3,自由面以下40 m 处为强分层内界面。内界面下方取厚度110 m、密度1 024.2 kg/m3的盐水。计算域取来流段450 m 为入口,去流段1 000 m 处为压力出口,流场宽度为侧方500 m。网格采用切割体网格,对各界面网格进行垂向加密,确保波高范围内垂向网格30 个以上。同时为准确刻画海表开尔文波波长与波形,对自由面网格进行V 形双层加密,在潜艇近场波长方向设置网格数70 以上。网格总数约为2 500万,各角度网格划分视图如图5 所示。 图5 潜艇计算域网格划分Fig. 5 Meshing of computational domain for submarine 本文海洋密度分层环境数值模拟参数的选取根据中国近海相关水文数据[14-15]设置,将其合理简化为强分层海洋模型。设置航速分别为12,16 和20 kn。本文各加减速工况在0~10 s 内匀速直航,待流场稳定后,在10~50 s 内匀变速,50~60 s内以第50 s 速度匀速直航,各工况具体航行参数的选取如表1 所示。 表1 计算工况Table 1 Calculation cases 针对12 kn 匀速航行潜艇,划分了3 套粗细程度不同的网格,并针对相关物理量,用于验证数值模拟过程中的网格无关性。3 套网格数量分别为885 万(粗),2 500 万(中)和4 500 万(细),计算得到的兴波如图6 所示(下图所有工况波高与速度场均以m 为单位)。通过分析发现,中网格和细网格兴波差距最大值在5%内,综合考虑精度与计算耗时,最终选取中等网格方案。 图6 不同网格数自由面兴波Fig. 6 Free surface wave-making with different grid numbers 图7 为t=60 s 时潜艇在不同航速与非定常航行工况下内界面兴波波形图。匀速工况下,内界面兴波距离随航速增加而显著增加;当航速提升至20 kn 时,内界面横波逐渐清晰,波峰呈拖曳式传播,衰减较慢且幅值随航速增加显著降低,波谷随航速增加略微增加,其尺度同艇体尺度,状态稳定。加速工况B1 和B3 在t=60 s 时兴波波谷幅值已略高于工况A3 时的情况,波峰幅值也高于工况A2。相比匀速工况,加速工况在内界面波形与传播规律均较为相近,均呈窄V 型传播。在波峰尾端均存在漩涡,该漩涡尺度随航速增加而增加,但加速时,内界面波峰范围内幅值明显强于匀速航行工况A2 和A3,且向后方衰减更慢。而减速时,工况B2 和B4 显示艇体下方波谷幅值略小于匀速工况A2,后方波谷幅值仅在艇体近场略大,向后方衰减相比匀速、加速工况更快。其波峰幅值强于匀速16 kn 工况,波峰后方漩涡尺度也弱于匀速与加速工况。 图7 内界面兴波Fig. 7 Wave-making of the internal interface 图8 为t=60 s 时潜艇在不同匀速与非定常航行工况下自由面兴波波形图。潜艇开始运动时,潜艇周围流体由于潜艇自身的体积排挤效应产生“伯努利水丘”,在艇艏与艇艉分别对应首波峰与尾波谷。随着潜艇不断运动,“伯努利水丘”不断向后方及艇体两侧发展。低航速时(工况A1),艇体后方兴波以横波为主;随着航速增加至16 kn,该工况下自由面横波散波均较明显;当潜艇航速增加至最高20 kn 时,自由面兴波逐渐以散波为主。所有工况自由面兴波均呈V 型,波谷值位置除工况B4 外,均位于潜艇指挥台上方,匀速工况下兴波波长、波高、传播速度随航速增加显著增加,其兴波散波包络角随航速增加缓慢增加。工况B1 显示,当航速匀速增加4 kn,波谷值约为−0.392 m,较匀速16 kn 增加约2%,但波峰值降低约28%,该工况下艇体后方散波较16 kn 航速的情况尤为明显。当航速由12 kn 加速至20 kn 时,自由面兴波夹角小于工况A3,自由面兴波以艇体近场“伯努利水丘”为主,艇体后方兴波明显较弱,其兴波波高较工况A3 增加约2%,波峰波谷幅值均略有增加。当潜艇从16 kn 减速至12 kn时,自由面兴波波高较工况A1 降低约21%;当从20 kn 减速至12 kn 时,其兴波波高较工况A3 降低约55%。综上,减速可在短时间内将波高显著降低。本文加速工况下,兴波波长随航速增加呈逐渐增加趋势;减速工况下,随航速减小而减小,波长及艇艏兴波随航速变化极为敏感。自由面兴波夹角在加速时略微减小,但减速时却明显增加为宽V 型向艇体后方传播,且减速工况下,兴波由于前后期兴波波速差距而叠加,显得更加杂乱无章。 图8 自由面兴波Fig. 8 Free surface wave-making 为定量分析自由面兴波特征,取y=0 处兴波切面(图9)。t=60 s 时,工况B1 潜艇近场自由面兴波波形与航速16 kn 相似,最大波峰与航速16 kn一样均位于第2 波峰处。波长较航速16 kn 时短,且后方兴波波长不断变化。潜艇最大波峰波谷所在位置相差较小,第3 波谷后较航速16 kn 波长减小较明显,后方波形与航速12 kn 相似,且兴波衰减同12 kn 航速相似;其余工况艇体近场自由面兴波波高、波长与最终航速的匀速状态较为接近,工况B1 和B2 显示加速状态下兴波波长及波高随潜艇航速的增加逐渐增加;工况B2 和B4 显示减速工况兴波波长逐渐减小,由于末端航速较低,初始高航速兴波传播速度快于末端低航速兴波,从而产生兴波叠加的现象,使兴波波形无规律。综上所述,定潜深状态下进行潜艇变速机动航行时,艇体近场流体受到潜艇排开水的体积效应影响,而体积效应又受到潜艇航速、潜深影响,使得近场自由面兴波波长、波高对航速变化较敏感,可从该角度判断潜艇的运动状态。 图9 自由面兴波截面Fig. 9 The cross-section of free surface wave-making 为体现自由面粗糙度,采用自由面三维辐聚辐散强度来表示。如图10 所示,工况A1~A3,B1~B4 对应自由面辐聚辐散强度范围分别为−0.045 4~0.032 s−1,−0.066~0.043 s−1,−0.128~0.083 s−1,−0.068~0.047 7 s−1, −0.042 4~0.025 3 s−1,−0.126~0.088 s−1,−0.058 2~0.045 4 s−1。上述数据表明,无论匀速或加速、减速工况,其自由面辐聚流峰值均高于辐散流峰值,两峰值差距随航速增加而增加,且加速时差距明显增加,减速时差距减小,其峰值均位于最大波谷两侧。工况B1 航速由12 kn加速至16 kn 时,其自由面粗糙度较匀速16 kn 工况略有增加,加速工况B3 的粗糙度也略高于匀速20 kn 的工况。相比减速工况B2,在第60 s 时其自由面粗糙度甚至小于匀速12 kn 的工况,且减速工况B4 由20 kn 高航速减速至12 kn 时,较匀速20 kn 工况,其自由面辐聚流强度降低约55%,辐散流强度降低约45%。综上所述,在潜深不变的条件下,加速时会显著提升潜艇被探测到的概率,减速可明显降低潜艇被探测到的概率,潜艇在16 kn 航速以内进行减速时,其隐身效果明显较好。 图10 自由面辐聚辐散强度Fig. 10 Free surface convergence-divergence intensity 为分析潜艇运动状态改变对其尾流场的影响,在y=0 m 处取y方向为法向的纵截面,统一速度场区间为0~16 m/s,如图11 所示。图11(a)~图11(c)显示当潜艇航速逐渐增加时,潜艇指挥台处对自由面流场速度扰动较大,且随航速扰动逐渐增加,航速20 kn 时扰动尤为明显,此时指挥台对艇体后方数百米扰动均较大,衰减也较为缓慢。当工况B1 潜艇从12 kn 加速至16 kn 时,艇尾流场扰动甚至强于匀速16 kn 工况,且指挥台对自由面速度场扰动也明显强于工况A2。工况B2 从16 kn 减速至12 kn 时,指挥台对潜艇近场自由面速度场扰动弱于匀速12 kn 工况,但远场(艇身200 m 后)扰动略高,艇尾速度扰动略高于匀速12 kn,但明显小于工况A2。工况B3 和B4的艇尾流场扰动距离相当,但工况B3 在近场扰动与工况A3 相当,末端由于初始低航速扰动明显较小。而工况B4 与其相反,近场扰动略低于匀速12 kn 工况,远场扰动明显强于匀速12 kn。图中明显可见,相同加速减速区间内,加减速状态艇尾流场漩涡垂向尺度明显高于加速状态。 图11 垂向速度场分布Fig. 11 Distribution of vertical velocity field 为研究潜艇运动状态对内波速度场的扰动,取内界面速度场分布(图12)。所有工况速度场扰动均在潜艇艏艉近场扰动极为剧烈。匀速状态时,内波水平方向传播距离随航速增加逐渐增加,航速为16 kn 时,艇体后方横波逐渐明显,且横波随航速的增加越发明显。加速状态时,潜艇艇身附近水平传播的范围略微增加,远场传播距离均较小。减速时,潜艇近场内波水平方向的传播范围明显高于其匀速最高航速工况,相比加速工况,减速时内界面横波呈前方弱、后方强的趋势,该特征与加速时相反。可见非定常机动航行对近场内波水平方向传播较大,结合图11 可见减速状态尾流塌陷非常明显。综上所述,减速状态虽然可显著降低波高及海表粗糙度,但对于海洋内部的扰动较为剧烈,且存在的范围较广。 图12 内界面速度场分布Fig. 12 Distribution of internal interface velocity field 本文通过CFD 方法,采用RANS 方程、SSTk−ω湍流模型验证了数值模拟潜艇潜航状态兴波的准确性,在此基础上通过欧拉多相流对强分层海洋模型进行两层流分层,对潜艇在强分层海洋环境下进行匀速直航、变速机动的数值模拟。以潜艇非声学探测与隐身为目的,研究3 种不同航速区间内潜艇不同运动状态下自由面、内界面兴波尾流场特征,并从遥感(辐聚辐散强度)角度对潜艇的隐身效果进行评估。相比常规速度场分析,本文从多个角度及层面对机动航行的潜艇展开较为全面的分析研究。具体结果如下: 1) 数值模拟的Rankine 卵形体潜行状态兴波结果与试验相比误差较小,本文各物理模型及网格划分方法满足潜艇潜行状态自由面兴波的精度要求,为求解不可压缩密度分层流动提供了重要的方法。同时本文对实尺度潜艇数值计算网格无关性做出验证,可为进一步数值模拟潜航体机动航行分层流动提供必要的数值计算验证。 2) 强分层海洋环境中潜艇进行加速机动时,随着航速的增加,首波峰、波谷随之迅速增加,对应兴波波长逐渐增加,但相对波高增加速度较慢,可见艇体的体积效应激发的内波在自由面首波峰、波谷处响应较快,其体积效应受航速影响较大。无论加速还是减速工况,内界面兴波波峰幅值均有所降低,其内界面兴波波峰相比匀速状态衰减较慢,减速时衰减较快。当加速度增加一倍时,辐散流强度增加约1 倍,与匀速20 kn 相比,航速从12 kn 加速至20 kn 高航速时更容易被发现,因此加速状态可显著增加潜艇被探测到的概率。加速状态对整个尾流速度场扰动甚至强于其匀速最高速度航行工况。 3) 当潜艇以较低航速(16 kn)减速可显著降低自由面兴波幅值及其海表粗糙度,加速与减速时其波峰峰值相对潜艇位置不同,减速时位于散波波峰首部,加速时位于散波波峰尾部。以较高航速减速时,虽然相比最高航速(20 kn)时其兴波波高、自由面粗糙度会显著降低,但相比末端匀速12 kn 航速,其被探测的可能性仍较高。因此,当潜艇以较低航速(16 kn)减速可有效降低海表粗糙度。减速时对整个尾流速度场扰动有显著降低。无论加速或减速工况,艇体近场内波传播距离均有所增加,减速状态最明显,且对应近场尾流塌陷最为剧烈。1.2 计算模型及分析方法
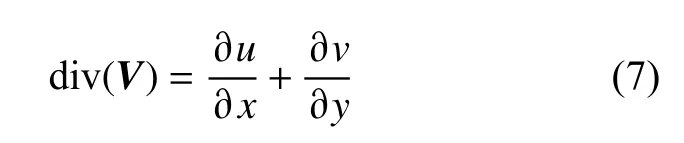
2 算例分析
2.1 数值模拟验证



2.2 计算模型及计算工况


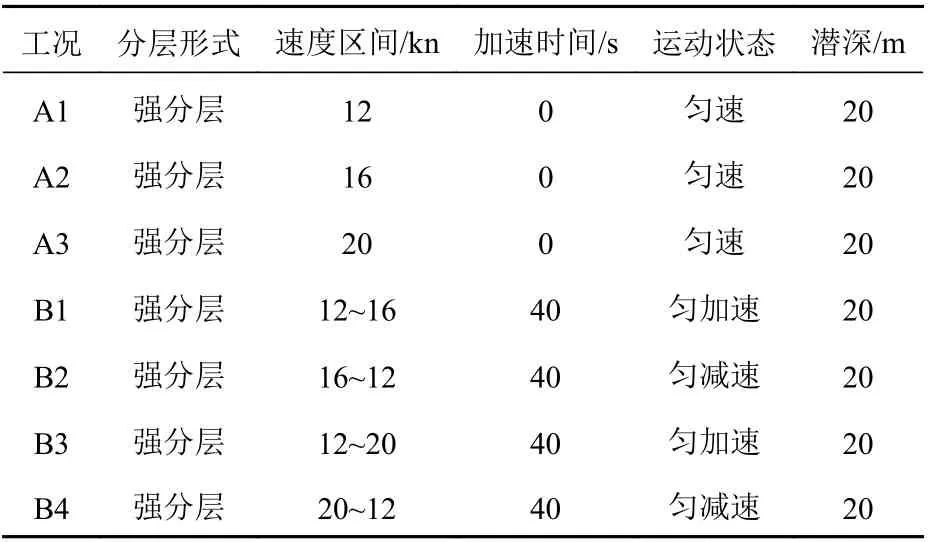
2.3 计算结果及分析




3 结 论
