艉斜浪下船舶倾覆特性直接CFD 数值模拟

刘李为，余嘉威，冯大奎*，张志国，陈美霞

1 华中科技大学 船舶与海洋工程学院，湖北 武汉 430074

2 华中科技大学 船舶和海洋水动力湖北省重点实验室，湖北 武汉 430074

0 引 言

水面舰船在随浪或艉斜浪中航行时，由于遭遇周期的增大，会使船舯位于波浪波峰处的时间变长，致使其稳性力臂显著降低，进而导致稳性失效模式的发生。这一失稳模式被定义为纯稳性丧失，是船舶在波浪中典型的3 种倾覆模式（参数横摇、纯稳性丧失和骑浪横甩）之一[1]，涉及非线性横摇运动、非线性复原力矩、非线性波浪力矩及其与船体的相互作用等强非线性动力学问题[2]。因此，由纯稳性丧失引发的船舶倾覆现象成为国际海事组织（IMO）针对船舶第二代完整稳性的研究问题之一。

在IMO 船舶与设计建造分委会（SDC）第四次会议中，完整船舶典型非线性失稳模式的直接稳性评估方法成为关注的重点。直接稳性评估方法的建立能够以更加精确的方式考虑所有相关因素，可以有效实现不同船舶的安全隐患评估，这在船舶设计阶段是较为重要的。目前，国内外有部分学者针对纯稳性丧失的预报方法以及运动特性进行了较为深入的研究。朱军等[3]针对船舶在波浪中的大倾角稳性问题，计算得到了规则波浪中船舶的稳性变化规律，结果显示船舶在正横浪与斜浪条件下稳性大幅度丧失的主要原因是波面相对船体横剖面的不对称性。鲁江等[4]构建了一种纵荡−垂荡−横摇−纵摇四自由度的耦合运动模型，其运用该模型对随浪规则波中的船舶稳性丧失进行直接评估，分析了纵荡运动对纯稳性丧失预报的影响。Umeda 等[5]基于一种纵荡−横荡−横摇−艏摇四自由度的耦合运动模型，对艉斜浪中船舶的纯稳性丧失以及倾覆现象进行了模拟。Lu 等[6]针对艉斜浪中船舶的纯稳性丧失问题分别进行了模型试验与六自由度数学模型预报研究，并进一步阐明了艉斜浪中船舶艏摇与横摇之间耦合作用的重要性。

以上研究主要是以基于势流理论的数学模型为预报方法，通过模型试验，将船舶操纵运动水动力导数、线性以及非线性横摇阻尼的测量作为参数输入来对船舶在波浪中的失稳运动进行直接评估。由IMO 对船舶典型失稳模式直接评估方法的建议与要求可知，稳性直接评估方法需要能对波浪中船舶稳性变化、横摇周期特性、主参数共振特性、骑浪平衡、波浪中的转艏特性、多自由度耦合运动以及艉斜浪中的直航特性等水动力性能实现可靠的模拟。基于全时域黏性流的数值模拟（CFD）方法正好能够满足上述要求，且无需依据试验测量或是经验公式估计的数据作为参数输入，因此可以考虑将其应用至船舶非线性失稳模式的直接评估中。

随着高性能计算技术的飞速发展，直接CFD预报方法已能应用到舰船复杂水动力性能研究中。目前，CFD 方法已被用于船舶的回转运动[7]、停船操纵[8]、骑浪运动[9]以及参数横摇现象[10]的直接模拟，说明直接模拟纯稳性丧失这类集船舶操纵性与耐波性于一体的强非线性问题已成为可能。因此，本文将基于CFD 方法对带螺旋桨、带舵的自航船舶在艉斜浪下保持航向操纵运动进行直接模拟，预报典型失稳模式下船舶的六自由度耦合运动，并对船舶的失稳运动及倾覆特性进行直接评估。

1 数值方法

1.1 流场求解方法

使用课题组自主开发的舰船水动力CFD 求解器HUST-Ship 进行数值仿真计算，通过对非定常RANS 方程的求解来获取流场特征，然后采用有限差分法进行数值离散，并基于结构网格模型在每个网格点上对差分方程进行求解。控制方程如下：

1.2 重叠网格方法

CFD 求解器在对流场压力速度特性进行求解的同时，也会耦合刚体六自由度运动方程来进行力和力矩以及运动的实时预报。考虑到船舶在波浪中的大幅度运动、船后螺旋桨旋转以及艉舵操纵运动特性，在CFD 求解器中应用了重叠网格技术（HUST-Overset），用以实现船体网格模型与计算域之间的大幅相对运动，以及自航船舶船、桨、舵多级耦合运动的数值仿真。另一方面，重叠网格模块的应用允许在前处理网格生成过程中单独对不同的对象（计算域、船体、各附体以及推进器）进行网格划分，并通过重叠区域的构建实现网格之间的组装和数值计算模型的生成，这大大降低了全附体船舶结构化网格的生成难度，提高了结构化网格的质量。

重叠网格模块的重点是生成不同网格块之间的物面重叠以及体重叠区域。在HUST-Overset中，首先通过洞映射方法进行洞点的处理以及附近插值点的识别，包括洞边界点与外边界点；然后，基于交替数字树算法（ADT）为插值点搜寻相对应的贡献点，其中插值点与贡献点之间通过三线性插值方法进行流场数据的传递；最后，基于插值点与贡献点之间的体积匹配及点距离进行重叠区域的优化，在保证网格单元体积匹配且至少2 层网格互相重叠的前提下尽可能缩小重叠区域的面积。

1.3 操纵控制模块

基于动态重叠网格方法，自航船舶在波浪中进行操纵运动过程中的船、桨、舵多级耦合运动得以实现。在CFD 求解器中集成了操纵运动控制模块，可以实现自航船舶在波浪条件下的航向保持操纵运动，然后通过使用PID 控制技术对螺旋桨转速进行控制来使船舶达到目标航速，并以船舶艏向角为输入对艉舵操纵角度进行反馈控制，从而保证船舶不偏离目标航向。基于PID 的控制形式如下：

式中：P，I，D分别为比例项、积分项和微分项的控制常数；e为实测值与目标值之间的差值。对于自航船舶在波浪条件下的航向保持运动，在计算过程中可通过不断调整舵角角度来使船舶在航行过程中保持目标航向。

1.4 移动数值试验水池

在船舶大尺度操纵运动（例如，自由自航运动、回转运动和Z 形操纵运动）的数值模拟过程中，如果类似于物理试验水池一样采用静止的数值水池进行仿真，会大大增加数值计算的网格量，从而降低计算速率。因此，可在CFD 求解器中采用随船一起运动的移动数值试验水池模型，以便节省数值水池网格量，提高数值计算的效率。

在移动数值试验水池模型的实现过程中，将船舶主体网格和数值水池网格分别予以处理：通过计算得到船舶受力和力矩，结合船舶六自由度运动方程的求解得到船舶在大地坐标系下的姿态和位置变化，提取船舶的纵荡和横荡速度以及位移信息，并赋值于数值试验水池上，从而保证在数值模拟过程中数值水池与船舶主体网格之间的纵向和横向相对位移足够小，具体实现流程图如图1 所示。在此过程中，可将速度入口造波方式与移动数值水池模型进行耦合处理，并将数值试验水池的速度入口边界与入射波浪的浪向设置为始终保持垂直，用以保证数值试验水池在移动过程中水池内的数值波浪模拟精度不受影响。图2直观地示出了船舶在不同类型操纵运动过程中数值波浪水池的移动方式。

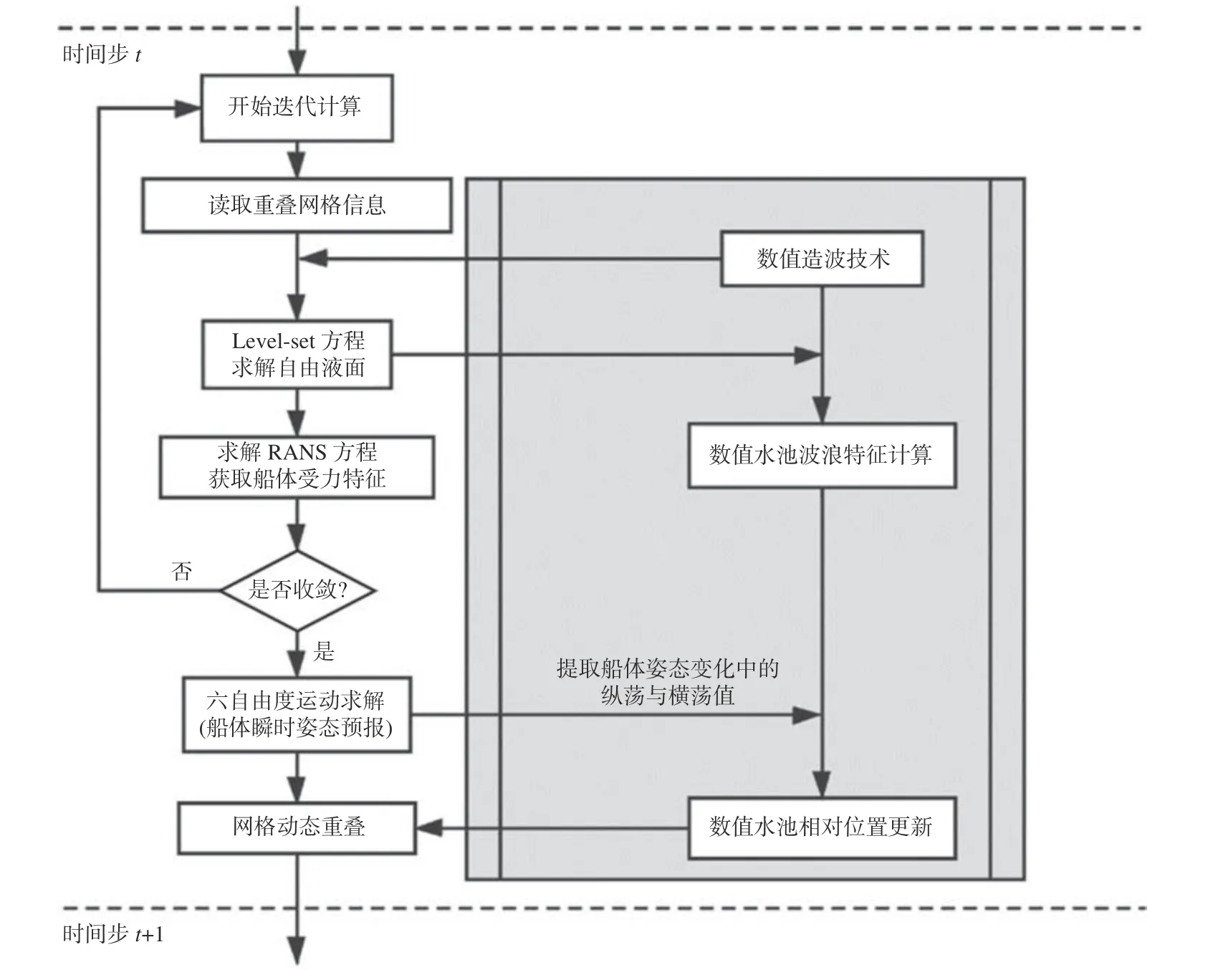
图1 移动数值波浪水池模型与船舶运动耦合求解流程图Fig. 1 Flowchart of the coupling solution between the moving numerical wave tank and ship motions

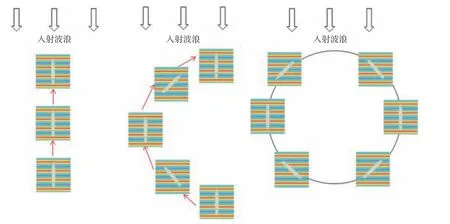
图2 船舶不同操纵运动过程中数值波浪水池的移动方式Fig. 2 The movement mode of the moving numerical wave tank during different ship maneuvering motions

2 计算对象与工况

选取全附体双桨、双舵的ONRT 船模为研究对象，该船模为被广泛应用于数值仿真算法验证的标准模型。文献[6]以ONRT 自航船模为对象对其进行了纯稳性丧失模型试验，相关的试验数据可用于验证本文CFD 方法的可靠性。模型的缩尺比为40.526，其几何形状如图3 所示，主尺度如表1 所示。根据文献[6]中的自航模试验工况，对自航船舶在30°艉斜浪规则波中的航向保持操纵运动进行数值模拟，其中规则波波长λ =1.25LWL，波高H= 0.05λ，波速C= 2.722 m/s，波浪频率f= 0.573 Hz。船模航速为1.831 m/s，对应的弗劳德数Fr= 0.30。在数值模拟过程中考虑船舶的六自由度运动，并通过航向角反馈控制器不断操控艉舵舵角来使船舶保持航向航行。

表1 ONRT 模型主尺度参数Table 1 Main parameters of ONRT model

图3 ONRT 模型几何图Fig. 3 Geometry of ONRT model

在数值模拟的前处理过程中，分别对计算域、船体以及各附体（呆木、艉舵、舭龙骨、轴系及螺旋桨）进行结构化网格划分，计算域网格与数值模拟边界条件的设置如图4 所示。全附体模型网格如图5 所示。运用重叠程序HUST-Overset 实现网格组装与重叠区域的生成，所建立的数值计算网格模型如图6 所示。在进行数值模拟之前，对螺旋桨网格进行网格收敛性分析，具体的结果参见文献[14]，从中可知中等数量网格与密网格方案下的螺旋桨敞水特性预报结果差别较小，且与试验结果间的误差均小于2.5%，而稀疏网格方案下螺旋桨敞水特性预报结果与试验结果间的误差则为6%。由于全附体模型网格收敛性分析结果与螺旋桨网格收敛性分析结果的现象一致，因此选用中等数量网格方案进行数值模拟。根据网格收敛性结果选取了最终适用的计算网格模型，网格节点总数量为978 万。

图4 计算域网格Fig. 4 Grid of the computational domain

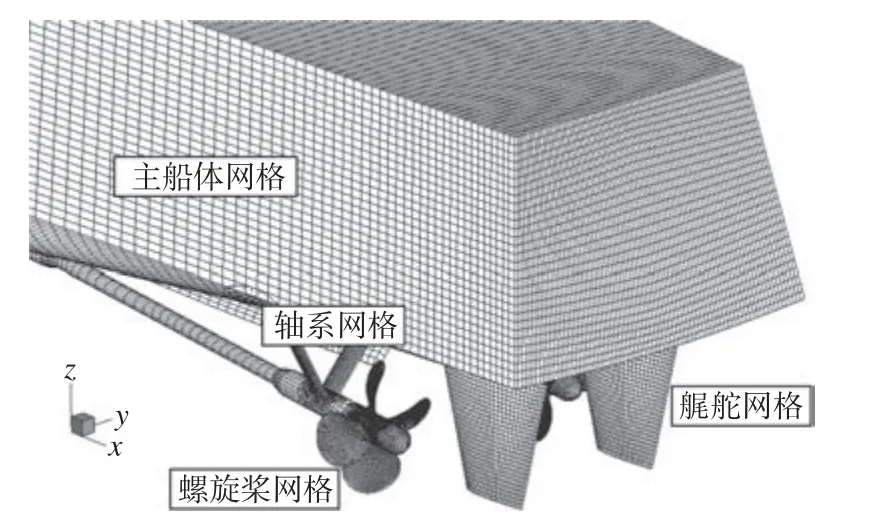
图5 全附体模型网格Fig. 5 Grid of the fully appended ship model

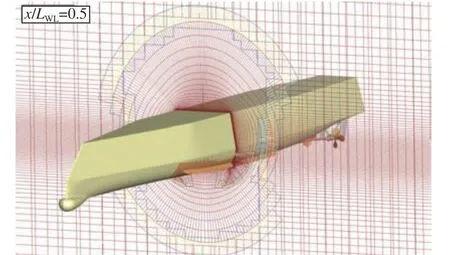
图6 数值计算网格模型Fig. 6 Numerical grid model

3 数值模拟结果分析

基于CFD 求解器HUST-Ship，耦合动态重叠网格方法，对ONRT 模型在30°艉斜浪规则波（λ = 1.25LWL，H= 0.05λ）中的典型失稳模式纯稳性丧失进行数值模拟。在数值模拟过程中放开了船舶的六自由度运动，并通过航向角反馈控制器不断操控艉舵舵角来使船舶保持航向航行。在文献[15]中，IIHR 水池运用PID 控制技术中的比例控制器（P= 1，I=D= 0）对ONRT 模型在不同浪向下的航向保持进行了试验，并取得了良好的效果。因此，本文进行数值模拟的控制设定将与该试验中的控制方法一致。

由文献[6] 中的自航模试验结果可知，模型在Fr达到0.30 时发生了强烈的稳性丧失现象，并导致船舶出现了倾覆。因此，在数值模拟过程中将参考该工况，固定螺旋桨转速以使模型航速与试验保持一致。数值计算工作在国家超级计算广州中心高性能计算机集群上进行，共采用120 个计算核心进行了并行计算，所花费的总计算时间约208 h，对应的CPU 计算时间为2.5 万计算机核时。图7 所示为纯稳性丧失过程中船后周围的涡结构。模型在波浪中自由自航时航速的时历曲线如图8 所示（图中，U为船舶航速）。由图可知，在该工况下船舶的瞬时航速接近于波速在船长方向的分量，这就意味着船舶与波浪之间的相对速度较小，即船舶在航行过程中，在波峰处的停留时间非常长，导致船舶在艉斜浪中的稳性长时间降低。由于缺乏足够的复原力，在持续的外部横倾力矩作用下，船舶会发生纯稳性丧失现象，从而导致大幅度的非线性横摇运动。

图7 纯稳性丧失发生时船后周围涡结构Fig. 7 Vorticity structure around the ship stern when the pure loss of stability occurs

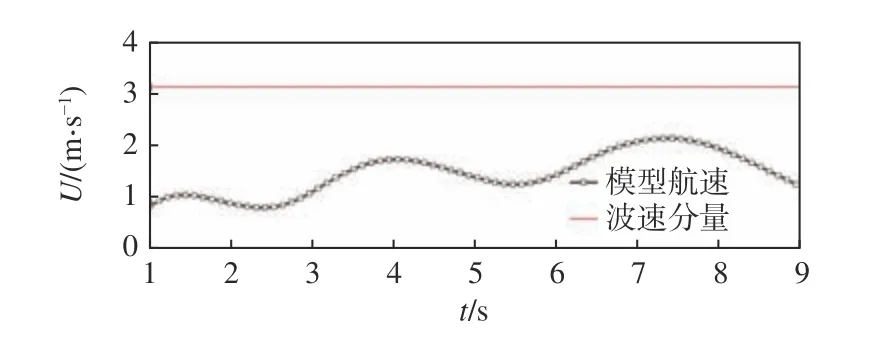
图8 船舶航速时历曲线Fig. 8 Time histories of the ship speed

图9 所示为自航船舶在艉斜浪规则波中的纵荡、横荡以及垂荡运动时历曲线（图中，x，y，z分别代表纵荡、横荡与垂荡），船舶在螺旋桨的推进作用下始终保持向前航行。图10 所示为自航船舶在艉斜浪规则波中的横摇、纵摇以及艏摇运动时历曲线（图中， ϕ，ψ，θ 分别为横摇角、艏摇角和纵摇角）。由图10 可知，船舶在持续的稳性丧失情况下发生了大幅度的横摇运动，最终，由于横摇角过大而导致了倾覆现象的发生。与此同时，船舶的艏摇角也显著增大，并与船舶横摇运动发生了耦合作用。当船舶横摇角达90°时，其艏摇角达到了16°，这说明船舶在稳性丧失状态下依靠操舵已无法有效控制船舶航向，从而导致了较为明显的横甩现象的发生。最终，纯稳性丧失、大幅度横摇、剧烈的横甩以及外部载荷的耦合作用导致了自航船舶的倾覆。

图9 船舶纵荡、横荡与垂荡运动的时历曲线Fig. 9 Time histories of the ship surge, sway, and heave motion

图10 船舶横摇、纵摇与艏摇运动的时历曲线Fig. 10 Time histories of the ship roll, pitch, and yaw motion

为了进行数值模拟可靠性的验证，将船舶横摇、纵摇以及艏摇角时域信号的数值模拟结果（CFD）与文献[6]中的模型试验数据（EFD）进行了对比，结果如图10 所示。由图可知，CFD 与EFD结果之间吻合较好，且这2 种方法对船舶运动随时间变化趋势的预报非常一致，说明采用CFD 方法模拟船舶失稳运动与倾覆现象准确性较高。

在CFD 数值模拟过程中，不同时刻下船舶姿态的实时变化及其周围自由面的波形如图11 所示，图中，Te为波浪遭遇周期。由图可以看出，艉斜浪的不对称性会造成船舶左右舷所受的外部载荷不同，从而导致船舶发生不对称的横摇运动，船艏处的涡结构同样也表现出了不对称性。同时，由图还可以发现，采用CFD 方法能准确模拟出船舶因稳性丧失而导致实时横摇直至最终倾覆的过程，以及在横摇过程中耦合发生的横甩现象。这表明运用CFD 方法能够直接模拟船舶的失稳运动与倾覆现象，且模拟结果已较为接近真实场景，有利于船舶典型失稳模式直接评估工作的开展。

图11 不同时刻下船舶姿态的实时变化及其周围自由面波形Fig. 11 The real-time change of ship attitude and the free surface wave around the ship at different time instances

4 结 语

本文基于黏性流理论建立了CFD 数值模拟方法，然后结合动态重叠网格技术与操纵运动反馈控制模块，对带螺旋桨和带舵的自航船舶ONRT在艉斜浪下保持航向操纵运动进行了直接模拟，预报了纯稳性丧失失稳模式下船舶的六自由度运动，并对船舶的倾覆特性进行了直接评估。结果表明，运用CFD 方法模拟船舶失稳运动与倾覆现象可靠性和准确性较高。

此外，CFD 数值模拟结果表明，船舶在持续的稳性丧失情况下会发生大幅度的横摇运动，最终会因横摇角过大而导致倾覆现象的发生。同时，船舶的艏摇角也将显著增大，说明船舶在稳性丧失状态下依靠操舵已无法有效控制船舶航向，从而发生了较为明显的横甩现象，这也是船舶发生倾覆的关键因素之一。

未来，将借助直接CFD 数值模拟方法对不同航速下自航船舶在艉斜浪中的失稳运动特性进行分析与比较，并对船舶由纯稳性丧失引发的大幅度非线性失稳运动的发生机理进行研究。