基于动力学模态分解的大跨度平屋盖风压场研究

冯 帅，谢壮宁

(华南理工大学亚热带建筑科学国家重点实验室，广东，广州 510641)

多次风灾调查[1]结果显示，大跨度屋盖结构[2−3]通常具有质量较轻、柔性较大、自振频率较低的特点，对风荷载十分敏感，其围护结构在风荷载作用下频频发生破坏。大跨屋盖结构形式多样，风压特性受其影响显著，屋盖表面脉动风压分布可以反映建筑物在湍流边界层下的风荷载特性[4]。一般来说，压力场是一个随机的、复杂的高维动态系统，很难直接理解其本质特征。而脉动风压中隐藏的时空模式与相干结构和气动机制密切相关，这些压力模式对识别随机变量场的基本物理机制和动态演化性质具有重要意义[5−6]。

为了提高流场动力学的分析效率，研究者提出了基于特征提取技术的模态分解方法—流场降阶模型(ROM)，其本质是寻找一组低维的子空间(即流动模态或相干结构)，将高维、复杂非定常流场表示为子空间在低维坐标系上的叠加，从而在低维空间中描述流场演化。这种技术需要高维、大规模的流场数据作为样本，可以直观地展示出流场流动随时间和空间的演化规律，对于流场的机理分析有重要意义。当前普遍采用的方法包括本征正交分解(POD)和动力学模态分解(DMD)2类。

POD技术将流场分解成若干空间正交模态，按照各个模态的能量(即特征值)大小进行排序，从而选择出随机场主要模态。这种方法作为一种数据压缩和特征值萃取工具被广泛应用于低矮建筑[7]、高层建筑[8]、大跨度建筑[9]的脉动风荷载及风致响应的研究中。尽管POD技术的应用范围很广，但由于协方差矩阵的存在，POD分析仅局限于变量的二阶特征，并且其无法直接识别单频动态相干结构解释随机系统的时间演化特征[10]。

DMD方法是一种从实验测量或数值模拟流场中提取动力学信息的数据驱动算法，能够用于分析流场的主要特征，或建立低阶的流场动力学模型，该方法由Schmid基于动态系统Koopman分析提出[11]。其本质是将流动演化看做线性动力学过程，通过对整个过程的流场快照进行特征分析，得到表征流场信息的低阶模态及其对应的特征值。DMD方法的最大特点在于分解得到的模态具有单一的频率和增长率。另外，DMD可以直接通过各个模态的特征值表征流动演化过程，因此不需要额外建立控制方程。这种同时得到模态特征和动力学信息的特点，使DMD方法相比于POD而言，可以更好地说明模态在时间和空间上的物理意义。研究人员已经证明了DMD在解释流场相干结构和动力学特性方面的有效性。例如，寇家庆等[12]针对DMD在流体力学研究的应用问题，综述了DMD算法自提出以来的一系列改进以及对不同流动现象的应用，并通过典型测试算例说明DMD的应用过程，讨论了DMD的研究现状及未来发展方向。张弛等[13]利用DMD方法研究其主导脉动模态，提取出了相关模态的空间形态和脉动幅值，证明燃烧组织方式的改变会对火焰脉动的形态和规律产生影响。Luo等[6]探讨了钝体上随机压力场的动力特性，并将其应用于湍流边界层中的棱柱体上的压力场，并介绍了一种利用有限的风洞试验数据进行气动特性分析的算子理论方法[14]。Li等[15]通过数值模拟将DMD技术应用于雷诺数为22 000的方形棱柱绕流的原型风工程问题，以考察DMD在压力流场分析中的准确性和实用价值。DMD方法对于模态排序没有一个明确的规定，许多准则已经被提出用于选择主导的DMD模态，包括α-准则[11]、I-准则[16]等。虽然DMD技术发展迅速且已被广泛应用于许多领域[17−19]，但是在结构抗风领域的应用仍然较为少见。

本文应用POD和DMD方法对大跨度平度屋结构的随机风压场进行模态提取和机理分析。首先，简述了两种模态分解方法的理论及其不同特性；然后，通过风洞试验获取大跨度平屋盖模型的随机风压场；最后，将两种方法应用于风压场中提取模态进行对比分析，并通过选取两种方法的不同模态数对脉动风压场进行重构比较，总结DMD和POD的独特特征，对比两种方法在研究屋盖表面的随机压力场的内在差异。

1 POD方法和DMD方法

1.1 POD方法

任意时刻的流场xi(如速度、压力、密度等)可以表示成平均值x¯和脉动值x′i的叠加。POD是从一组二阶统计意义上的空间数据中寻找最优正交基。要得到POD基，应求解脉动量的协方差矩阵C的特征值和特征向量。

式中，λj和uj分别为第j阶模态的特征值和特征向量(也称为POD基)。各阶模态对应的模态系数aj为：

通过POD基与模态系数乘积的叠加可以表示脉动分量：

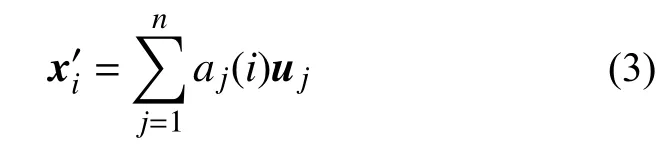
1.2 标准DMD方法及改进

通过试验或数值模拟得到N个时刻快照，即[x1,x2,···,xN]，其中第i个时刻的快照表示为列向量xi，任意两个快照之间的时间间隔均为Δt。基于Koopman算子理论假设[20]，流场xi+1与xi存在线性映射A，即：

式中，A为高维流场的系统矩阵，能够反映系统的动态特征。构建快照矩阵X=[x1,x2,···,xN−1]和Y=[x2,x3,···,xN]，代入式(4)可得：

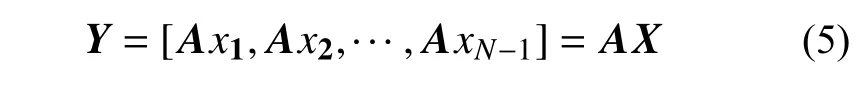
对于矩阵X，可提供一个矩阵A˜ 代替高维矩阵A，且这两个矩阵相似。为寻求相似变换的正交子空间，可通过对X做奇异值分解得到。

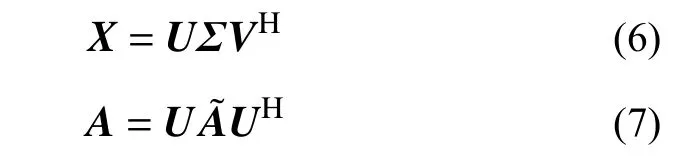
式中：Σ为对角矩阵；U和V为酉矩阵，满足UHU=I和VHV=I。矩阵的计算过程可视作Frobenius范数的最小化问题，结合式(5)～式(7)，可将A近似为：

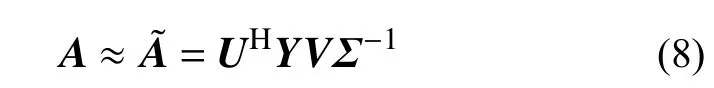
为了方便分析DMD模态，定义特征值的对数映射定义为特征谱：

则第j个DMD模态对应的增长率gj和频率fj分别为实部Re(λj)和虚部Im(λj)/2π。上述过程称为“标准DMD方法”。

然而，只有当特征值的个数与系统的维数相符时，用标准DMD方法得到的动态系统的线性近似才是合理的。此外，标准DMD不适用于高度非线性的系统，特别是对于时间维度往往大于空间维度的试验工况(例如风压测点布置有限而采样时间较长的大跨度屋盖风洞试验)。针对该不足之处，Le Clainche等[21]提出的高阶动力学模态分解(HODMD)和Williams等[14]提出的精确动力学模态分解(EDMD)，二者的相似之处是通过引入嵌入维数(Taken's延迟嵌入定理[22])改进标准DMD方法(后文称DMD方法)。

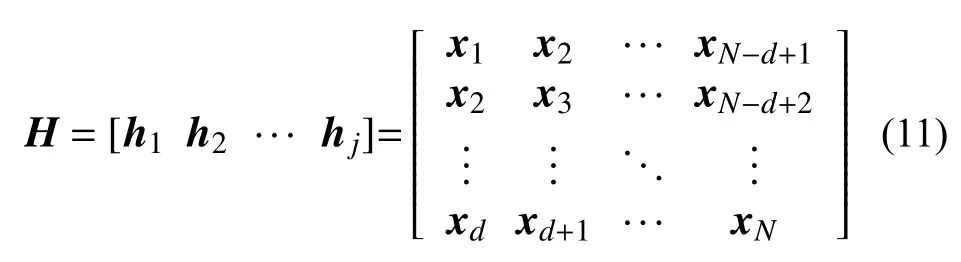
本文引入嵌入维数增广大跨度平度屋随机风压场的试验数据。将原始数据[x1,x2,···,xN]通过嵌入维数d进行扩展，即将延时坐标数据元素进行平移作为新的数据从而形成Hankel矩阵H：式中，hj为第j个时刻的Hankel矩阵列向量。嵌入维数d可以通过DMD模态特征谱的模是否等于或接近1确定(即DMD模态特征谱在复平面中是否位于或接近单位圆)。则时移矩阵对H1和H2分别为H1=[h1h2··· hj−1]，H2=[h2h3··· hj]。

数据以Hankel矩阵类型排列，通过将随机风压序列的延迟嵌入与DMD技术相结合，增强了隐藏在原始时间序列数据中的主导动力模态。最后将H1和H2代入标准DMD方法进行流场的动力分析。

对于DMD模态，本文采用Kou等[16]提出的模态排序准则，排序的模态不仅考虑了振幅大小，还包含模态的时间演变因素，综合考虑模态对整个流场的贡献，表示如下：

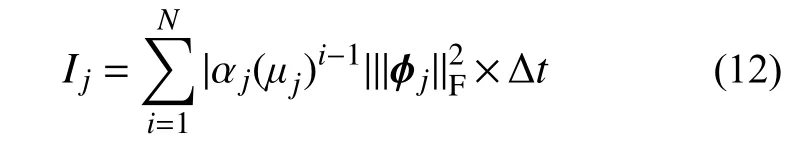
式中：Ij为第j阶模态排序的参数；i为第i时刻；|| ||F为Frobenius范数；αj为第j个模态的振幅，代表了该模态对初始快照x1的贡献，表示为：

原始快照可以近似地由DMD模态的线性组合表示：

式中：k为时间序号；xk为kΔt时刻的快照；j为第j阶模态；αj−1为第j阶DMD模态k时刻的模态系数，由于，特征值可以反映模态频率是单频，因此，模态系数的曲线是单频衰减或增长曲线。根据流场的主导模态，通过式(14)可进行原脉动流场的重构。

1.3 POD与DMD的不同特性

DMD和POD都是具有无方程的数据驱动方法。POD根据能量从动力系统中捕捉到占优势的空间特征，流场中的大部分能量可以用少数高阶的模态来表示。由于协方差的关系，POD提取模式仅仅基于二阶统计量。因此，POD缺乏捕捉精细流动结构和高阶统计特征的能力。此外，POD的模态通常对应于多个频率的耦合，而没有实际的物理意义。并且由于不存在相邻矩之间变量的动态关系的假设，所以POD方法不能确定所提取的模式的时间演化和稳定性。相反，DMD可以弥补POD的上述不足，对不同的流动现象具有更广泛的适用性。DMD基于Koopman分析提供了复杂非线性动力学的线性近似，因此它可以捕捉时空相干结构特征，而不需要理解控制系统的物理方程。同时，DMD方法可以有效地提取相应频率的相干结构模态，与POD侧重于能量的方法不同，DMD提供了一种提取模式的时空演化和稳定性特征的新方法。因此，DMD在复杂动态系统的稳定性分析中具有优势。

2 风洞试验及数据

2.1 风洞试验

试验在华南理工大学5 m量级气边界层风洞(SCUT-1)中进行。流场地貌按照《建筑结构荷载规范》(GB 5009−2012)[23]中规定的B类地貌模拟，图1(a)、图1(b)分别表示风洞试验的平均风速剖面V/Vref(Vref表示参考高度处平均风速)、湍流度剖面Iu和参考高度处的脉动风速功率谱，风洞试验中屋盖参考高度26.7 cm(即图1(a)中zref)处的平均风速和湍流强度分别为9.1 m/s和0.12。采集的风压以模型屋盖高度处风压作为无量纲化的参考风压。风压系数的表达式如下：

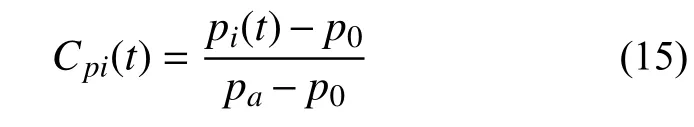
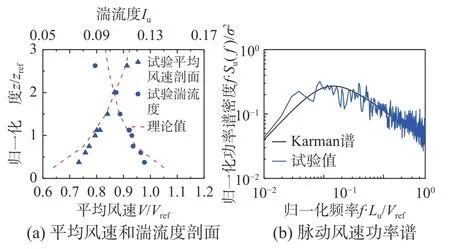
图1 风洞试验的流场参数Fig. 1 Flow field parameters of wind tunnel test

式中：Cpi(t)和pi(t)分别为测点i处的风压系数序列和风压序列；pa和p0分别为参考高度处的总压和静压。平面屋盖刚性测压模型尺寸为200 cm×133.3 cm×26.7 cm(长×宽×高)，屋面共布置467个测点，试验的几何、风速、时间缩尺比分别为1/150、1/5、1/30。模型测点的布置原则为边角区域加密，中间区域布置较疏，图2为试验模型和测点布置图。试验采样频率为300 Hz。

图2 平屋面试验模型和测点布置Fig. 2 Test model of flat roof and layout of tapping location

2.2 数据充分性分析

由于湍流结构和屋盖结构之间的相互作用是非线性、混沌性的，因此在实际分析随机风压信号时，无法将信号中的动力特征信息充分提取。故本文通过引入嵌入维数进行动力系统的相空间重构，其基本思想是根据系统中任意分量的演化都是由与之相互作用的其他分量所决定的，相关分量的信息隐含在已知分量的发展过程中，为了重构一个等价的状态空间，只需将已知分量在固定的时间延迟点上的测量数据作为新维处理，则可将原系统的许多性质保存，初步确定原系统的真实信息。图3表示不同嵌入维数的DMD模态特征值分布，横纵坐标分别表示复模态特征值的实部和虚部，颜色条表示模态排序参数Ij的数值大小。当特征点位于单位圆上或接近与单位圆周围，则特征值是稳定或中性稳定的[24]。从图3可以看出，特征值的数量随着所取嵌入维数的增加而增加，因为较大的嵌入本质上扩展了动态系统的自由度和模态。由图3(a)所示，当嵌入维数为1(即不考虑增广数据)时，DMD特征值分散在单位圆内，表明标准DMD算法在获取带有噪声的高维非线性数据的动力学方面需要更多的信息，因为理想情况下特征值应该位于或接近单位圆。从图3(b)、图3(c)、图3(d)可得，随着嵌入维数逐渐增大，特征值逐渐向单位圆靠近。当嵌入维数为8时，增广数据矩阵维数为3736×3500，空间维度(467×8=3736)大于时间维度，绝大多数特征值落在单位圆上，嵌入过程挖掘了数据集中隐藏的模糊动态特征，满足充分性要求。

图3 不同嵌入维数的DMD模态特征值分布Fig. 3 Eigenvalue distribution of DMD modes with different embedding dimensions

3 试验结果分析

3.1 风压分布

大跨度平度屋表面的风压可分为平均风压和脉动风压，图4为0°和45°工况下的平均风压系数pe和均方差风压系数(反映风压脉动特性)pe分布，从图中发现，屋盖表面主要以风吸力为主，每个工况的pe和pe分布轮廓相似。从图4(a)、图4(b)可以看出，当风垂直(0°)吹向屋盖迎风前缘时，剪切层在迎风前缘处分离，形成破坏性的柱状涡，故在分离区平均风吸力较大且脉动风压波动较剧烈，pe和pe最大值出现在屋盖角部，分别为−1.45和0.46。在柱状涡的诱导下，随着距离屋面迎风位置的增大，屋面风吸力先增大后逐渐减小并趋于平稳。由图4(c)、图4(d)所示，当来流与建筑迎风前缘成一定角度(45°)时会在屋盖边角区域产生锥形涡，锥形涡除具有旋涡截面的径向和切向流速外，还具有一个沿迎风前缘的速度分量，在此作用下，旋涡内耗散的涡量得以不断平衡和补充。因此，相比于柱状涡，锥形涡更加稳定、持续，其作用下的风吸力也更强劲，pe和pe最大值同样出现在屋盖角部，分别为−3.48和0.70。

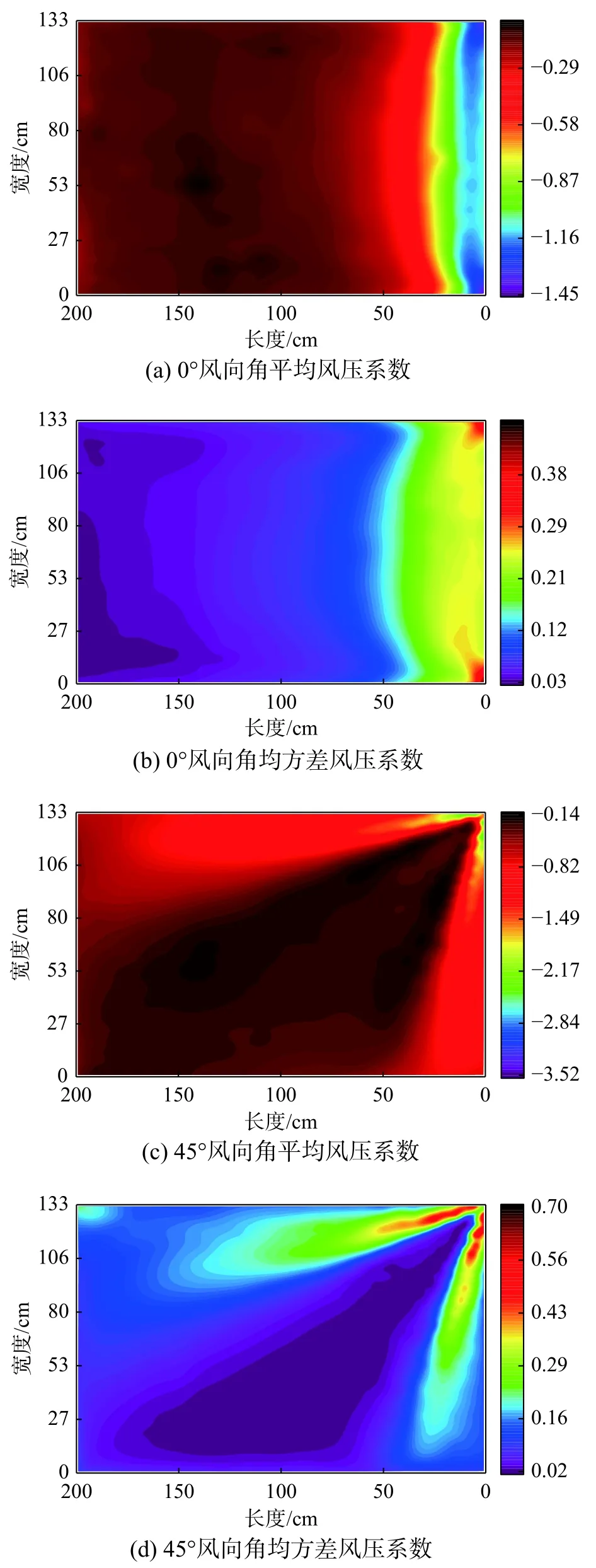
图4 平面屋盖风压系数分布Fig. 4 Distribution of wind pressure coefficient on flat roof

3.2 模态分析

图5给出了0°和45°风向角下大跨度平屋盖脉动风压场POD分解的前3阶空间模态。POD(或DMD)模态仅表示屋盖表面各点的相对压力值，符号(正负号)意义不大。由图5(a)～图5(c)可以看出，0°风向角下POD分解的第1阶模态在迎风角部区域脉动风压较大，与图4(b)中均方差风压系数在角部区域分布相似，并且第2阶、3阶模态的极大值区域也出现在迎风前缘的角部区域，说明当0°风向角下POD分解模态的大部分脉动风压能量包含在屋盖的边角区域，这与屋盖的迎风前缘由于分离泡的分离和再附运动出现强劲风吸力的现象相吻合。从图5(d)～图5(f)可以得出，45°风向角下第1阶和2阶POD模态关于对角线互为一对反对称模态，第3阶模态关于对角线对称，其模态分布在屋盖对角线两侧形成两个瓣状，与图4(d)中均方差风压系数分布形状相似，表现出明显的锥形涡特征。

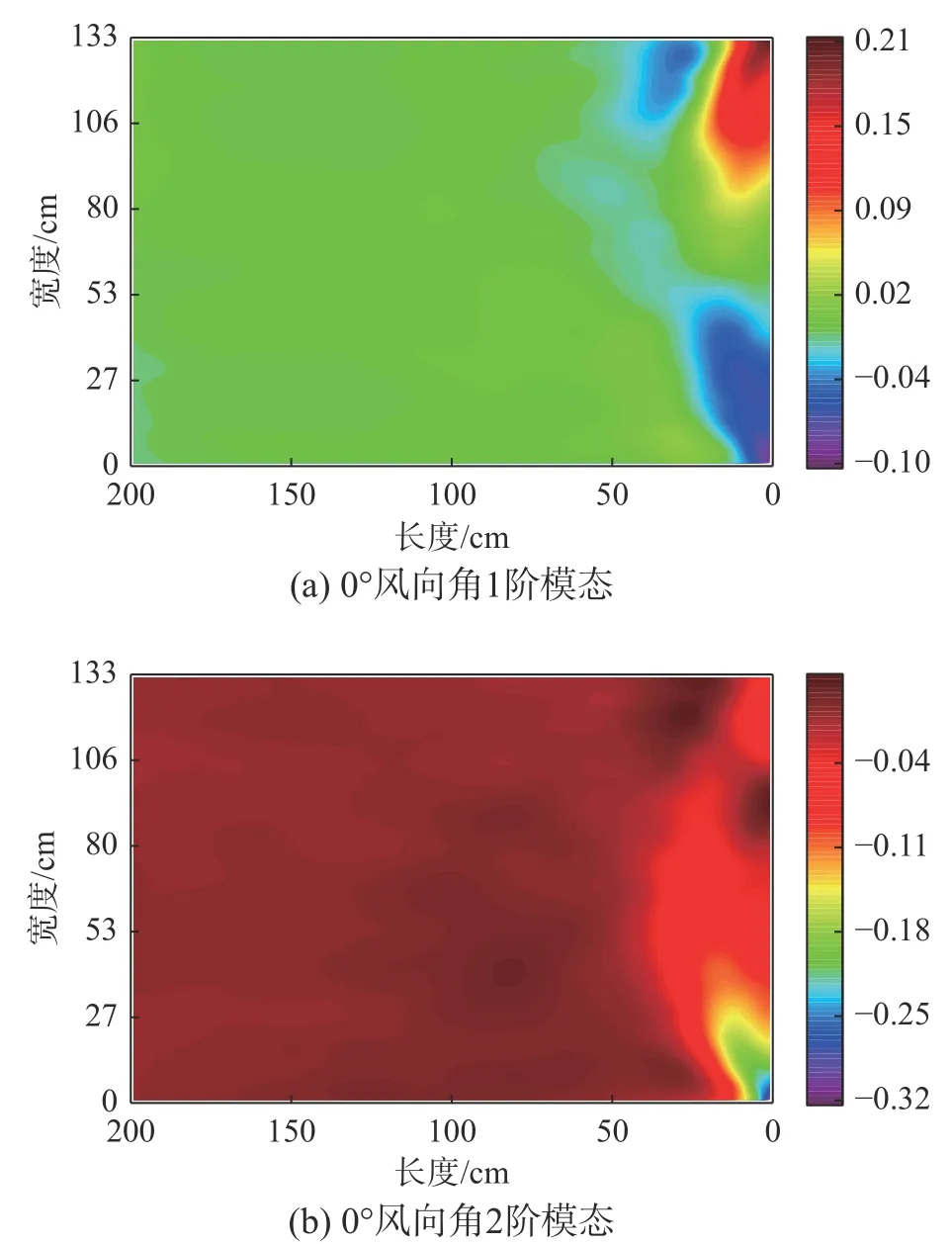
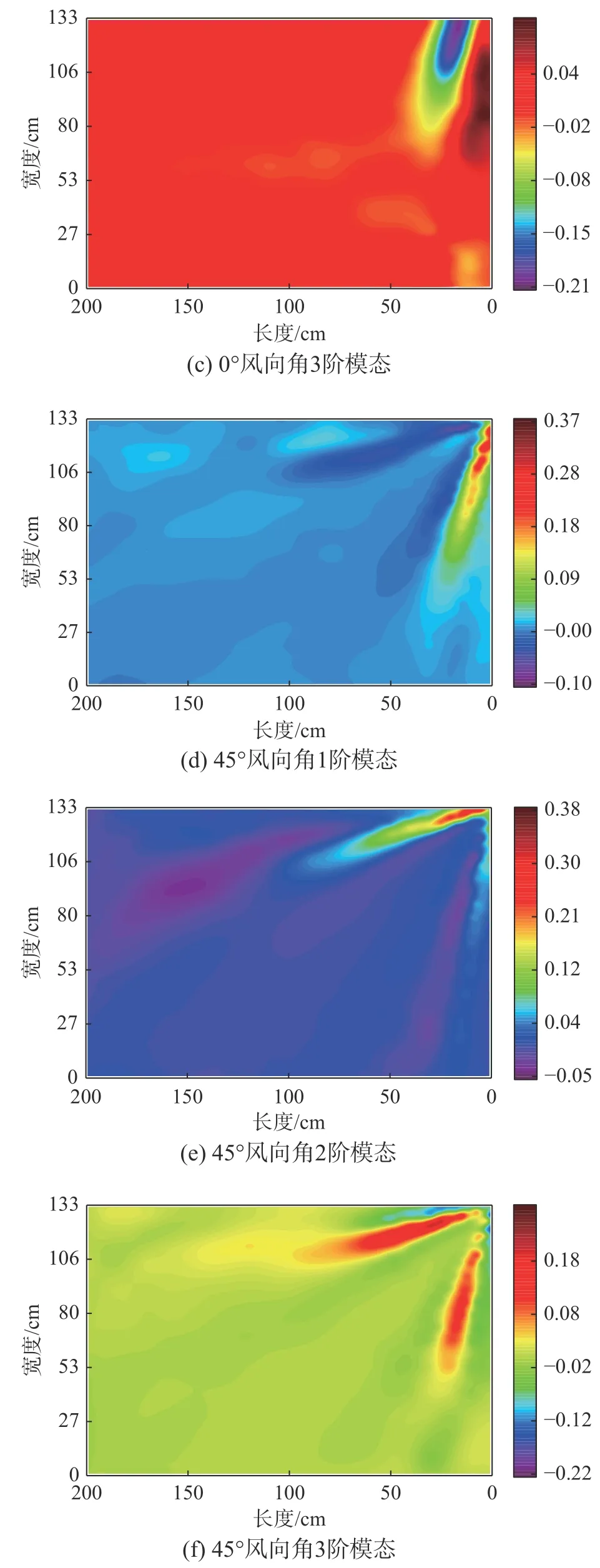
图5 前3阶POD模态Fig. 5 The first three-order POD modes

图6为0°和45°风向角下大跨度平屋盖脉动风压场DMD分解的第1阶～3阶空间模态。本研究中DMD分解的第0阶模态为频率为0的静态模态，反映了均匀流场特性的模态分布。为方便与POD模态进行对比，本文中取反映脉动风压特性的前三阶DMD模态进行分析。由图6(a)～图6(c)可以看出，在柱状涡的作用下，0°风向角下DMD分解的3阶模态能很好的捕捉到屋盖边角区域风压的脉动特点，模态频率分别为2.12 Hz、2.16 Hz和5.52 Hz，表明柱状涡内部存在低频运动，这将引起剪切层的拍打运动，进而形成屋盖表面的风压脉动[25]。增长率分别为−0.14、−0.16和−0.04，反映线性发展过程中各阶模态的增长趋势，如图7(a)所示。前两阶模态在迎风前缘的模态分布相似，说明第2阶模态是第1阶模态的漂移模态，体现了在动力学发展过程中脉动风压场随时间的演化。由图6(d)～图6(f)可见，45°风向角下前三阶模态均反映了锥形涡的特征，模态分布形状与POD模态相似，模态频率分别为0.08 Hz、0.32 Hz和0.94 Hz，第2阶模态分布是由于涡轴的低频摇摆运动使得屋盖表面关于对角线对称的两点出现反相位吸力脉动。增长率分别为−1.12、−0.14和0.16，第3阶模态的增长率大于0表示该模态能量在逐渐增大，这是由于锥形涡中沿迎风前缘的速度分量，在不断平衡和补充旋涡内耗散的涡量，如图7(b)所示。

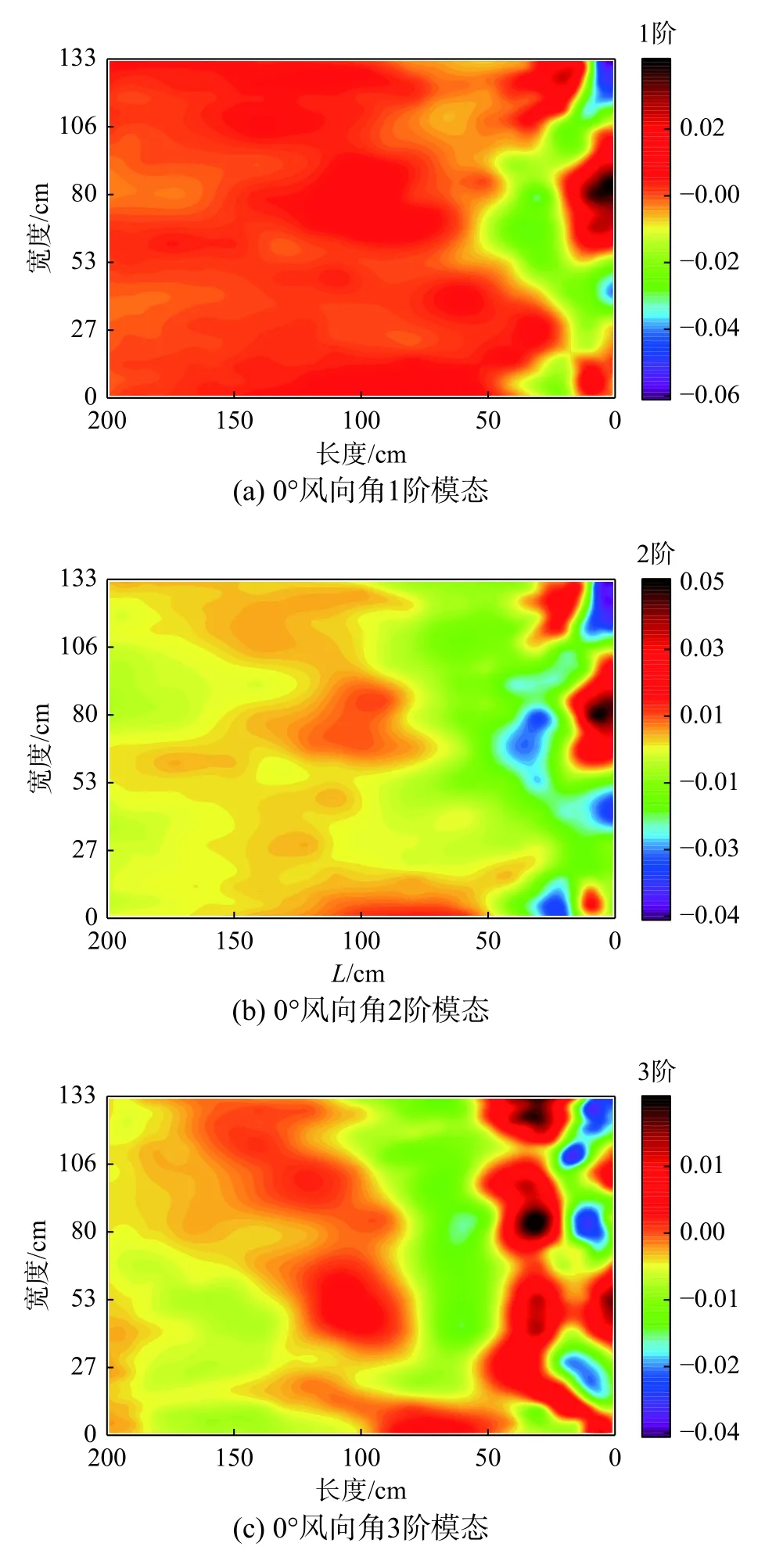
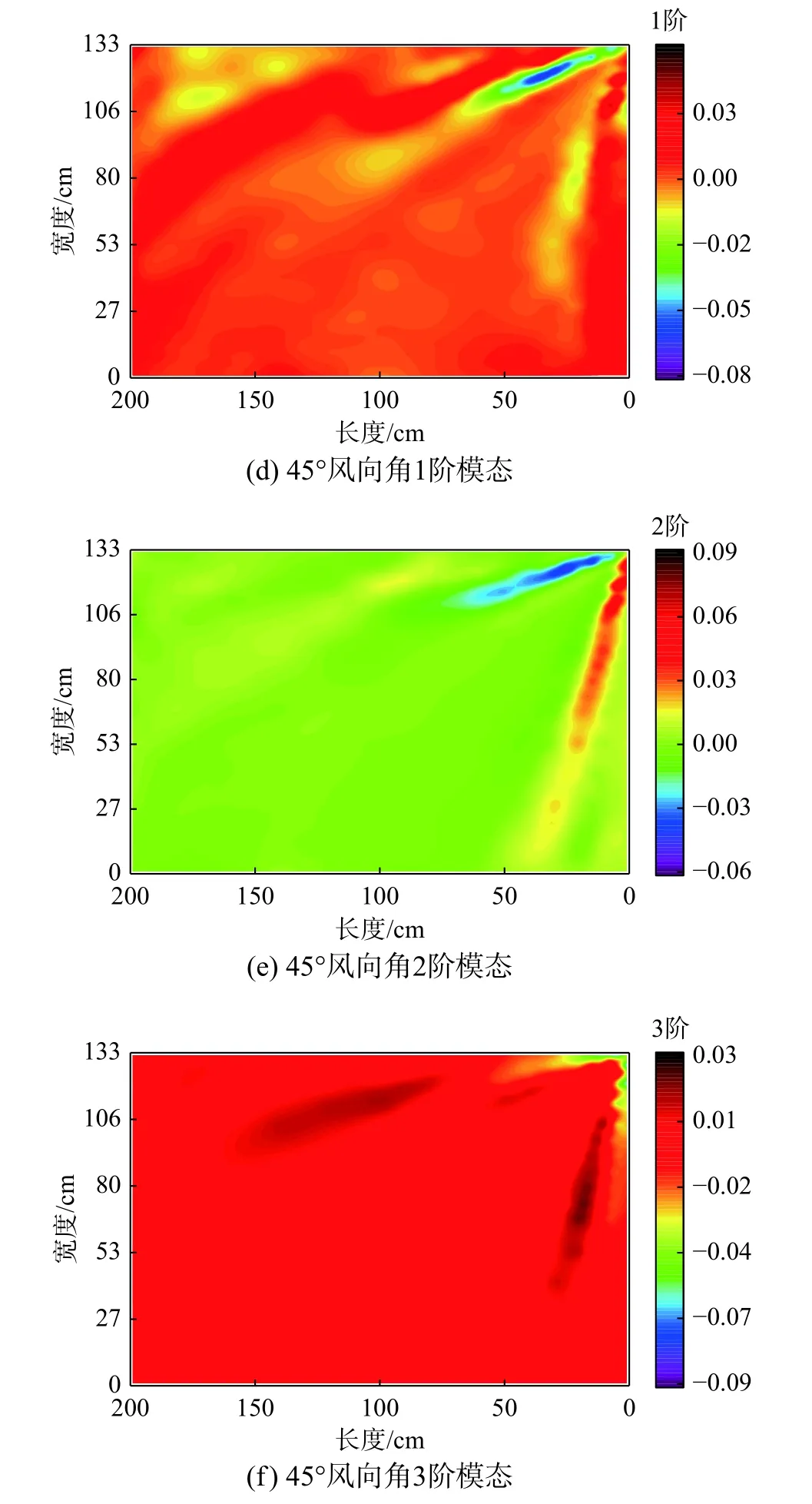
图6 前3阶DMD模态Fig. 6 The first three-order DMD modes

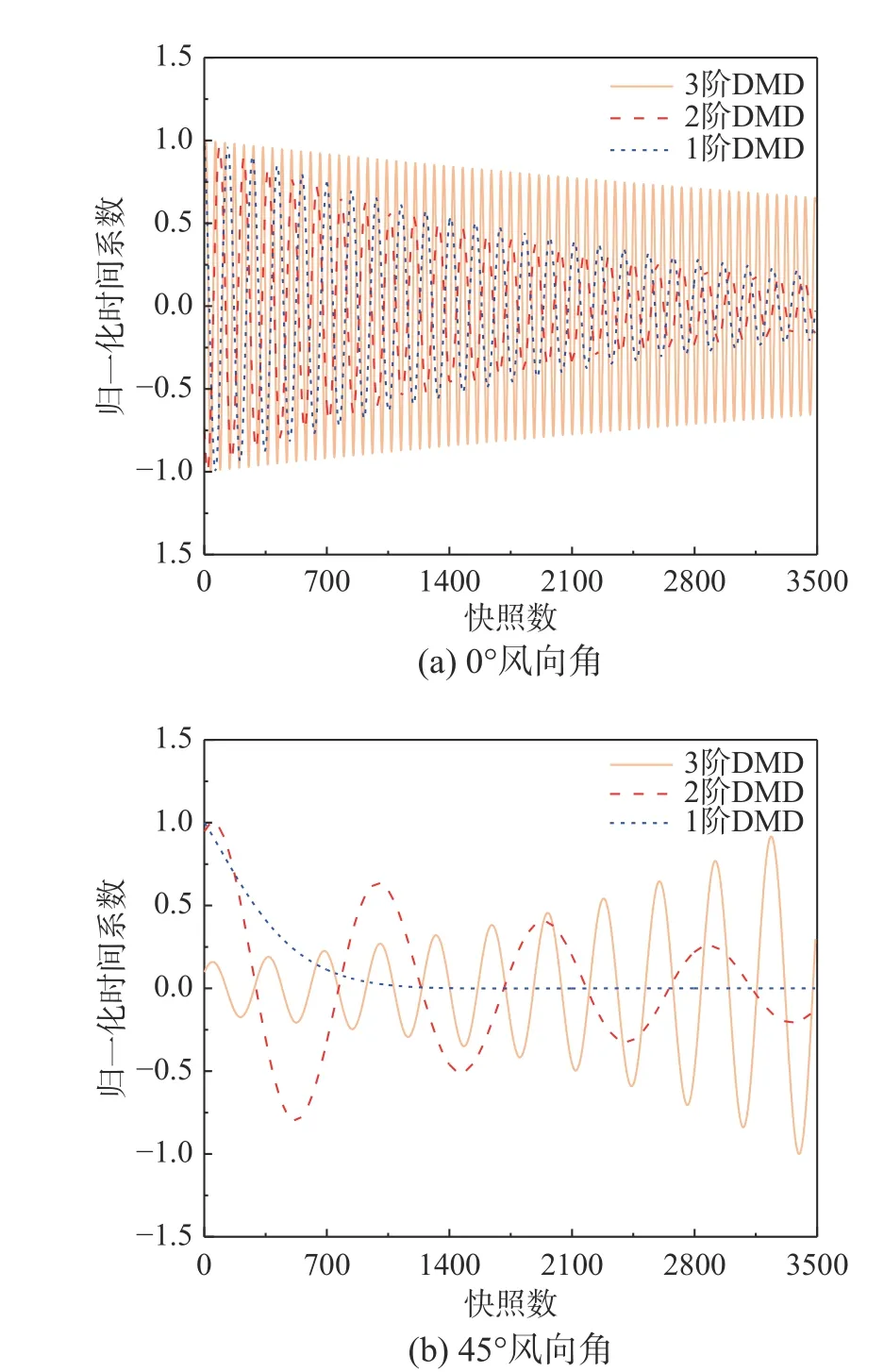
图7 前3阶DMD模态系数随时间快照的演化Fig. 7 The evolution of the first three-order DMD mode coefficients with time snapshot

通过比较发现，POD模态和DMD模态均能捕捉到屋盖迎风前缘处破坏性旋涡的脉动特征。但从模态分布的数值结果对比可得，POD模态结果大于DMD模态结果一个数量级。这是由于两种方法的模态时间演化机理不相同。如图7和图8所示，DMD方法提取的模态系数在固定频率下具有稳定振幅或衰减的简谐振荡行为，能够反映流场的时间特征，而POD的每个模态包含多个频率的信息[26]，时间演化表现为随机信号，这在一定程度上让POD的脉动模态成为多个频率段脉动的耦合。

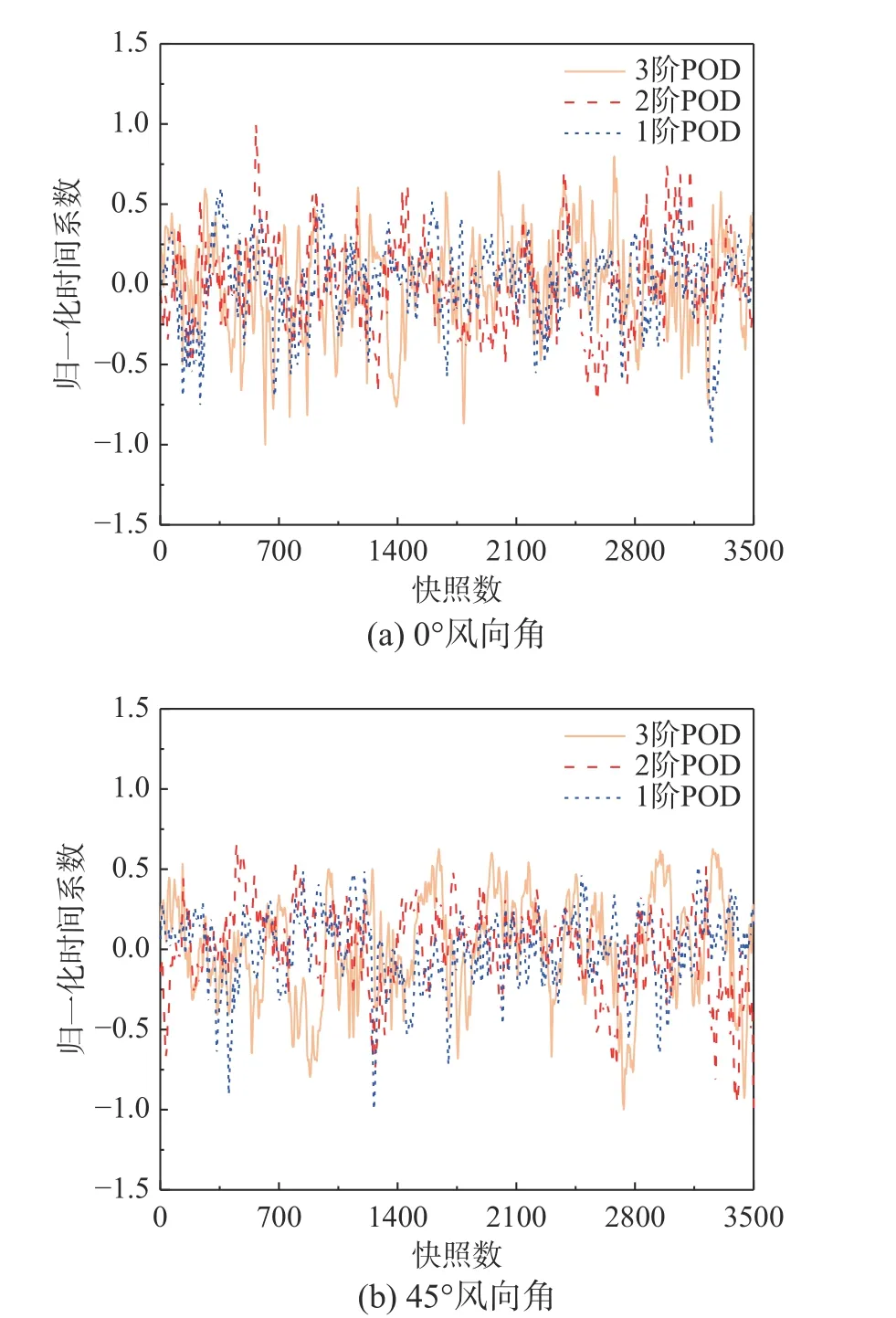
图8 前3阶POD模态系数随时间快照的演化Fig. 8 The evolution of the first three-order POD mode coefficients with time snapshot

3.3 脉动风压场的重构

目前，风压场重构的研究方法有POD方法[7]、径向基[27]等。本文基于DMD方法对大跨度平屋盖屋面风压场进行重构，并与POD重构结果进行比较。

图9所示POD和DMD模态归一化累积能量随模态数的变化示意图。x轴为模态数的累积比，由累积模态与总模态的比值来定义，y轴为模态能量的累积比。由图可得，两种模态分解方法在45°工况达到累积模态能量的80%均比0°工况速率快，说明相比于柱状涡，锥形涡作用下的脉动风压波动更剧烈；而两种方法的差别是，POD方法在0°和45°的累积模态能量达到80%所对应的模态比例分别为7.5%和5.6%，而DMD方法在0°和45°的累积模态能量达到80%所对应的模态比例分别为15.7%和13.6%。这可能与两种模态分解方法的数据构造和模态选取方法不同，由于DMD方法引入嵌入维数构造维数更大的数据矩阵和在挑选主要模态上除了考虑振幅还考虑了时间演变的影响。直观上在选取相同模态比例进行风压场的重构时POD方法的表现应该优于DMD方法，但在下面的脉动风压场重构中不尽其然，如图10和图11所示。

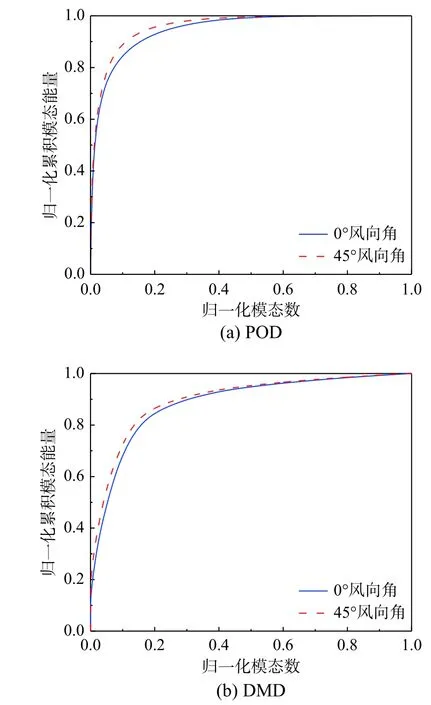
图9 模态累积能量随模态数的变化Fig. 9 The variation of mode cumulative energy with the number of modes

图10和图11分别表示0°和45°风向角下两种模态分解方法在第600个快照(即时刻t=2 s)的脉动风压场的重构。这里需要注意的是，DMD方法重构选取的模态数比例与POD方法相同(分别为7.5%、5.6%)，并且在重构脉动风压场时将不包含零频率的静态模态。由图可见，两种方法的重构结果在描述原始脉动风压场的迎风区域局部表现均较好，但DMD结果在整体轮廓上与原始风压场更为契合，特别是在风压场的再附和尾流区域。如前文所述，由于协方差的关系，POD提取模式仅仅基于二阶统计量，造成POD缺乏捕捉精细流动结构和高阶统计特征的能力。0°和45°风向角下DMD方法重构风压场的模态频率分别在0 Hz～22.8 Hz和0 Hz～18.9 Hz，说明低频模态包含大部分脉动风压能量。对比DMD和POD方法，DMD方法不仅可以从随机风压场中提取出脉动风压场的主要结构，直接得到模态及对应的频率，且可以判断其稳定性，因此DMD方法可以同时得到流场在空间和时间上的主要特征，在揭示随机风压场流动机理时，DMD方法更具优势。

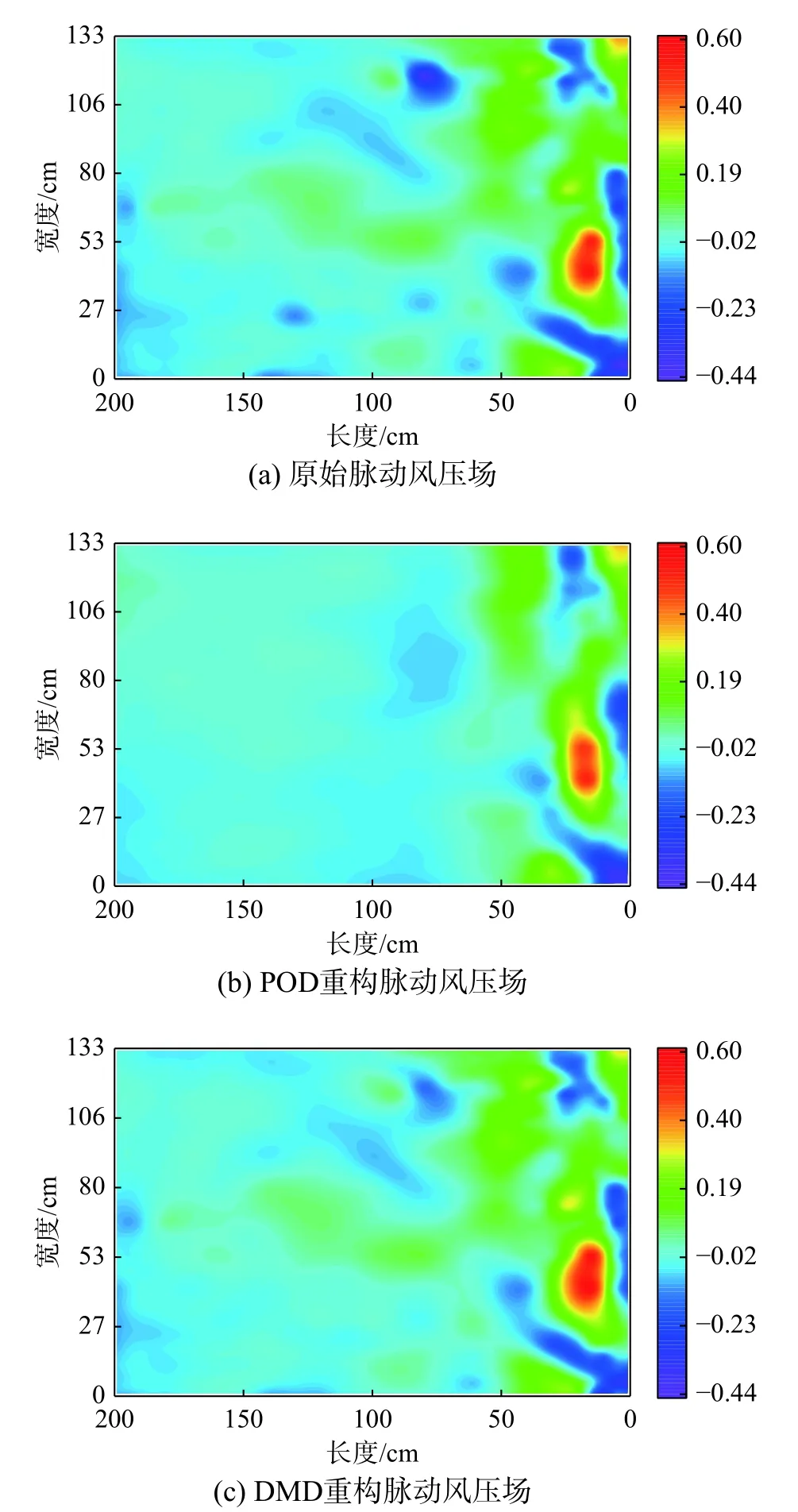
图10 0°风向角下脉动风压场的重构Fig. 10 Reconstruction of fluctuating wind pressure field at 0°

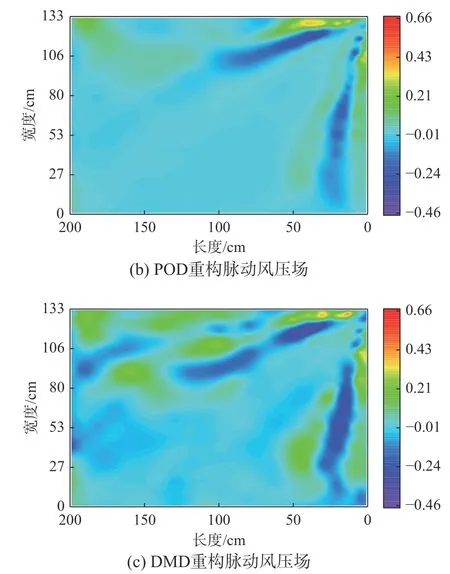
图11 45°风向角下脉动风压场的重构Fig. 11 Reconstruction of fluctuating wind pressure field at 45°

4 结论

综上所述，通过将POD和DMD模态分解方法应用在大跨度平屋盖模型的随机风压场的分析中，对比两种方法各自特征，得到如下结论：

(1) 通过将嵌入维数与DMD方法结合进行随机风压场动力系统的相空间重构，能够挖掘数据集中隐藏的模糊动态特征，使分解得到的DMD模态更加中性稳定。

(2) 虽然POD与DMD算法迥异，但两种方法分解的模态都能够捕捉到大跨度平度屋迎风前缘处的破坏性旋涡的脉动特征。POD模态分布数值大于DMD模态的结果。这是由于DMD方法分解的是单频模态，而POD的每个模态包含多个频率的信息，这在一定程度上让POD的脉动模态成为多个频率段脉动的耦合，造成POD模态数值大于DMD模态数值。

(3) 相同比例的POD模态包含能量大于DMD模态，但当使用相同比例的模态进行脉动风压场重构时，DMD结果比POD结果更能描述和契合原始脉动压力场的局部特征，这是由于DMD是直接对压力场进行重建，而POD主要是重建能量场。DMD方法分解的低频模态包含大部分脉动风压能量，解释了脉动风压场的主导频率。因此在揭示随机风压场流动机理和特征，DMD方法更具优势。