非均质材料与位错交互能的数值等效夹杂算法

2022-07-04侯佳卉谢东东钱厚鹏金晓清

工程力学 2022年7期

李璞，朱凯，侯佳卉，谢东东，钱厚鹏，金晓清,

(1. 重庆大学机械传动国家重点实验室，重庆 400030；2. 重庆大学航空航天学院，重庆 400044)

非均质材料因其优异的力学性能，被广泛地应用于航空航天、轨道交通、新能源汽车等领域中，如新能源汽车储氢载体普遍使用碳纤维增强环氧树脂[1]，飞机起落架、机翼通常选择钛基复合材料[2]。然而，随着机械零部件在高温、重载、高速等极端环境中的运行，由位错或裂纹引起的表界面失效越来越成为影响机械零部件服役寿命的关键因素[3−4]。位错作为工程结构中的重要缺陷，其在微观层面上的迁移变化，会极大地改变材料的宏观力学性能[5]，在非均质机械零部件中，位错在基体内的运动还会受到周围夹杂物如微孔洞、微裂纹、析出相、晶界等因素的极大影响，研究位错与周围介质的这种相互作用是工程领域和力学领域的热点问题之一[6−8]。

美国西北大学的Dundurs教授和Mura教授[9]首次推导出了平面问题下圆形杂质和刃型位错相互作用能(也称交互能)和位错受力的解析解。随后，Stagni和Lizzio[10]进一步考虑了自由表面对圆形杂质和刃型位错的影响，并给出了椭圆杂质与刃型位错之间的相互作用解[11]。他们的解[10−11]是以Laurent多项式给出的，但无穷级数的解在实际应用上则显得较为不便[12]。Santare和Keer[12]的表达式中规避了无穷级数带来的不便，他们利用Muskhelishvili的复变函数法[13]，对刃型位错与椭圆形刚体杂质的相互作用问题进行了解析研究。应用该方法[13]，Chen等[14]进一步给出了刃型位错与三层椭圆形杂质的弹性解。当杂质所在区域变成圆形孔洞时，Dai[15]进一步研究了半平面对刃型位错的影响，他们的研究是对Dundurs和Mura[9]全平面问题下位错与圆形孔洞相互作用解的有益补充。

需要指出的是，单个位错与杂质的相互作用问题是理解材料形变和微结构演化机制的基础问题，在众多方面有着重要的应用。如借助离散位错方法[16]，可以进一步将杂质与单个位错的相互作用关系扩展到杂质与裂纹的相互作用问题[17−19]中去，这里的杂质-位错解被作为了求解杂质-裂纹相互作用问题的格林函数[20−21]。另外，当考虑杂质的尺度效应时，可以分析纳米夹杂物对位错的影响[19−22]，相关的研究技术通常需要引入原子模拟[23 − 24]。

从上述研究[9−12,14−15,19,22,25−27]中可以看出，即使是圆形(或椭圆形)杂质与刃型位错的相互作用问题，其解析解的获得都显得颇为不易，而相关的表达式在数学上也显得较为复杂。但是，在实际的工程材料中，夹杂物不仅具有很强的分布离散性[28]。而且其大小、形态往往都不一样，这造成了夹杂物对周围介质不同的应力扰动状态[29−30]。Ehselby[31]所提出的等效夹杂理论为求解任意形状夹杂物对弹性场的扰动效应提供了可能。等效夹杂法(Equivalent inclusion method，EIM)通过将非均质材料问题转为均质材料叠加一个待定的“本征应变”问题，可以有效地统一解决塑性应变、残余应力、材料相变等问题[32]。虽然Eshelby的等效夹杂法最初是用于求解三维椭球杂质问题的，但是正如Jin等[33]在其研究中所指出的那样：Eshelby等效夹杂法同样是求解平面应变或平面应力杂质问题的一种有效方法。

对Eshelby上述理论的数值实现称为“数值等效夹杂法(NEIM)[34]”，即通过对杂质所在区域进行数值离散，相应单元上的等效本征应变通过迭代法来进行确定。Zhou等[34]应用数值等效夹杂法对远端受载的平面杂质问题进行了研究并指出：对于任意Dundurs参数的材料组合，数值等效夹杂法均具有很好的数值稳定性和鲁棒性。应该指出，著名力学家Hutchinson[35]提出了一种近似法，用于研究裂纹尖端大量微裂纹的影响，尤其是微裂纹区域内应力强度的降低或屏蔽效应。由于Hutchinson的方法只考虑零阶的局部扰动效应[35]而没有进行迭代逼近，因而在文献中[34]称为零阶迭代近似解。Hutchinson方法的这种思想也被Li等[36−37]应用于解决杂质和位错的相互作用问题。但是，和精确解[9]相比。这种近似法具有较大的数值误差，尤其是当计算点位于杂质附近区域时[34−38]。

位错和夹杂物的交互能及位错受力对于理解位错运动及其引起的材料微结构变化具有相当重要的作用。现有文献[9 − 12, 14 − 15, 19, 22, 25 − 27,36 − 37]对杂质-位错交互能和位错受力的解析解研究，主要探讨特定的夹杂形状，如圆形或椭圆形。而当用数值方法求解交互能时，需有效处理无穷域上积分，及位错奇异性问题。近年来，Li等[38]在螺旋位错与夹杂物的交互能研究上，取得了理论分析和数值算法的重要突破。在这项工作中，基于反平面剪切问题力学模型，他们[38]提出相应的等效夹杂算法并对圆形异质夹杂与螺型位错的相互作用能进行了解析求解，获得了交互能和弹性能的显式单元解，在此基础上，进一步提出了反平面剪切问题中求解任意形状杂质和螺型位错的数值计算方案。需要指出的是，这项研究首次报道了一种非多项式非指数形式的等效本征应变，并论证了等效夹杂法可以有效地用于解析求解非均匀本征应变。

然而，应用等效夹杂原理求解刃型位错问题的有效性尚未得到验证。一方面，刃型位错的数学表达式相对螺型位错而言更加复杂，加之周围杂质对其产生的扰动效应，这使得对该问题交互能的解析求解变得异常困难；另一方面，由于控制方程中待求解的未知量陡然增多，即使是构建数值算法进行计算，也将不得不考量由位错奇异性和材料错配性所造成的数值波动和计算失稳。本文所述及的夹杂物与刃型位错的交互能研究，进一步将反平面计算模型[38]扩展到了平面问题中，通过引入Dundurs参数，推导了平面问题下的理论模型，并论证了等效夹杂法在求解刃型位错问题中的有效性；同时，由于Dundurs参数的引入，本文数值算法相对前述论文[38]所提出的计算方法得到了较大改善，因本文算法极大地削减了迭代计算中的变量数目，这进一步提高了本文算法的鲁棒性和稳定性；此外，通过引入相对误差的范数形式，本文定量分析了计算结果的相对误差，并对本算法的有效性进行了评估。需要指出的是，三维问题下夹杂物与位错的耦合计算往往较难获得解析解，通常需要借助分子动力学模拟或者ab-initio理论。本文二维分析的计算，基于连续介质力学的理论框架，相应模型的计算结果在一定的宏观尺度上可以揭示具体工程实际的物理本质。

本文借助等效夹杂法，建立了非均质材料中杂质与刃型位错的应力控制方程，结合边界条件、平衡方程和高斯定理，推导了交互能的计算公式。同时，本文结合快速傅里叶变换算法，给出了基于面单元离散的数值化计算方案，通过和相应的精确解对比，验证了本文计算方案的有效性；并对本文计算方案和零次迭代解的无穷范数和2-范数进行了相对误差分析，证明了本文计算方案在求解任意形状杂质与位错问题上的数值稳定性和有效性。此外，本文还示例分析了任意杂质的形状参数对交互能的影响。

1 任意形状夹杂物与位错交互能的数值计算方法

在无限大的平面D中，在(ξ,η)处放置有一个刃型位错，在位错附近分布有一个任意形状的杂质Ω(图1)。在本研究中，假定杂质和其周围的基体是完美固结的，并且基体和杂质的弹性模量分别为Cijkl和kl。

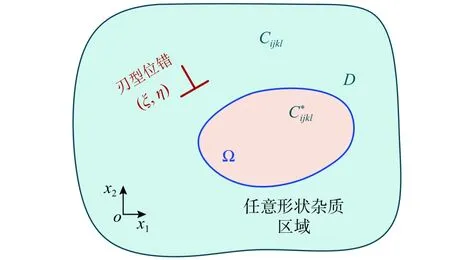
图1 任意形状杂质与刃型位错的相互作用示意图Fig. 1 Schematic of an arbitrarily shaped inhomogeneity interacting with an edge dislocation

1.1 夹杂物-位错问题中的等效夹杂法

根据Eshelby等效夹杂法的基本原理[29]，在刃型位错作用下，由于杂质Ω存在所产生的应力扰动，可以通过一个分布有合适本征应变ε∗ij的夹杂问题来模拟(图2)。因此，图1中杂质与位错的相互作用应力解可以通过叠加一个均质材料解(即位错解)和相应的夹杂解来得到(图2)。

图2 杂质-位错问题中的Eshelby等效夹杂法Fig. 2 Schematic of Eshelby's equivalent inclusion method for the interaction between an edge dislocation and an inhomogeneity

式中，α和β为Dundurs参数，其具体表达式为：

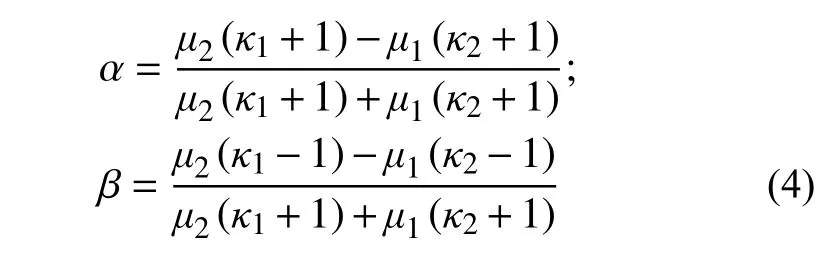
本文以平面应力情况为例，相应解可以用来解释平面应变的情况。上述式(4)中的κ为Kolosov常数，在平面应力问题中，κ=(3−ν)/(1+ν)；μ和ν分别表示材料的剪切模量和泊松比。需要指出的是，下标1和2分别表示基体和杂质。

1.2 夹杂物与位错的交互能及位错受力

在图1所示的任意形状杂质-位错问题中，在x3方向上单位长度内的弹性能W可以看作是杂质对刃型位错做功[38]：

式中：σij为单独由杂质产生扰动场；为由位错造成的位移梯度。

单独由位错在均质材料中引起的弹性能W0为：

因此，杂质与位错之间的交互能ΔW 为：

为了进一步简化上述式(7)，注意到有下列关系式：

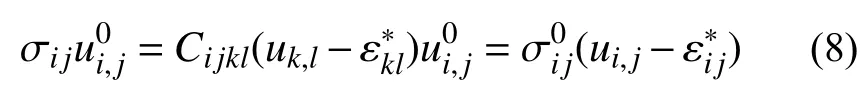
式中，uk,l为杂质产生的位移梯度。

考虑自由边界条件和平衡方程，并应用散度定理，式(7)还可以进一步推导成下述形式：

由于本征应变只作用在夹杂内部，而在夹杂外部为零。因此，式(9)将积分运算仅仅限定在了一个有限且确定的作用区域上，从而避免了如式(7)所示的在一个无穷大区域上的积分计算，这样使得在数值计算过程中，大大降低了计算机存储空间和不必要的时间浪费。

一旦获得了位错与杂质之间的交互能，可以进一步得到作用在位错上的力[39]：

式中，i 和j为笛卡尔坐标系下的单位基矢量。需要指出的是，正向的位错受力表示杂质和位错之间是排斥关系，相反，位错则受到杂质的吸引。

1.3 交互能的数值计算方法

从交互能的式(9)可以看出，求解的关键在于确定杂质-位错问题中的等效本征应变以及相应的应力扰动场σij。图3显示了基于数值等效夹杂法求解交互能和位错受力的计算流程图。参数N为位错的位置编号，K为迭代次数。当位错的位置确定时，在整个循环流程中，位错应力场σi保持不变，其具体表达式可由Hills等[16]专著得到。需要说明的是，在等效夹杂法的数值实现中，初始的应力扰动场输入均为零，即K=1时，σ=0。在不断迭代过程中，当迭代次数大于最大迭代次数Kmax，或者迭代精度小于程序设置误差δ时，输出最终的等效本征应变ε和相应的应力扰动场σ。

图3 杂质-位错问题中的交互能和位错受力的计算流程图Fig. 3 Flow-chart of the present computational scheme for solving the interaction energy and force on dislocation due to an edge dislocation interacting with an inhomogeneity

在上述计算过程中，夹杂应力场的耗时占据了整个流程的大部分时间。根据叠加法的基本原理，夹杂应力场可以表示为如下公式：

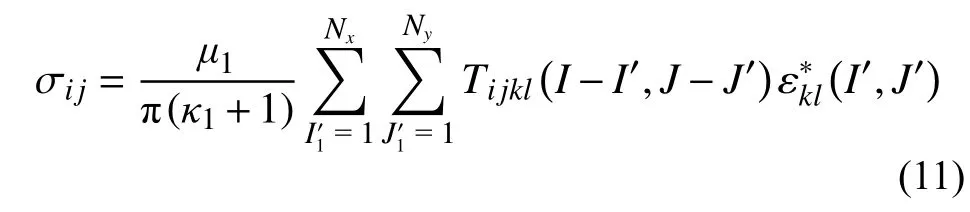
式中：Nx、Ny分别为夹杂区域Ω上沿x和y方向的离散单元数；(I,J)和(I′,J′)分别表示目标场和激励场的单元编号。这里的Tijkl为影响系数 (其矩阵形式见式(3))，相关的具体解析表达式见文献[40]。

式(11)展示了一类卷积型叠加，利用快速傅里叶变换算法的加速性质，可以显著地提高其运算速度，具体操作过程简述如下[41−43]：首先，将影响系数矩阵和本征应变所代表的激励矩阵扩展到(2Nx×2Ny)的区域上；接着分别对上述两个矩阵完成包卷循环填充(wrap-around order padding)和补零(zero-padding)操作；经过离散傅里叶变换后，将上述两个序列在傅里叶频域内进行点对点相乘；通过对上述乘积进行傅里叶逆变换，抛去扩展区域上的无效数值，即得到傅里叶时域内的夹杂扰动应力解。对比直接叠加法和离散傅里叶变换算法可知，式(11)所需的时间复杂度为O(9Nx2Ny2)，其中，O(·)表示乘法运算的阶数，相应地，经过傅里叶变换算法加速后，所需的时间复杂度为O(108NxNylog2(4NxNy))。由此可知，当网格数取32 ×32时，直接叠加法所消耗的时间将是傅里叶变换算法所消耗时间的近24倍。随着网格数的增多，傅里叶变换算法所取得的时间加速将更加明显。需要指出的是，快速傅里叶变换算法是对离散卷积的精确求和[41−43]，可以显著地提高计算速度；由于，本文采用了单元离散-叠加的方法，因此，可以用于求解任意形状杂质，包括边界为平滑或者非平滑截面的夹杂物[34,44]。

为了进一步获得交互能的数值解，对等效夹杂所在的区域进行矩形单元离散，式(9)可以进一步：

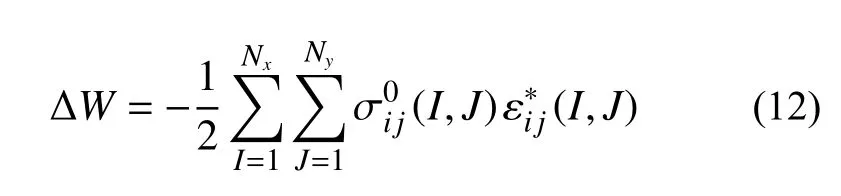
在获得交互能的基础上，通过中心差分法即可得到作用在位错上的力。

2 算例分析

2.1 数值化计算方法的验证

为了验证本文计算方法的有效性，考虑在无限大的平面介质中分布有一个半径为a的圆形夹杂物(图4)，其剪切模量和泊松比分别为μ2和ν2。在杂质外(2a, 0)处作用有一刃型位错，相应的基体弹性模量和泊松比分别为μ1和ν1。表1列出了相关计算参数的数值大小，其中刃型位错的Burgers矢量bi取值大小为(1, 0)，其符号的方向定义为：沿着位错轨迹从位错核走向无穷远处，轨迹的右侧为bi的正向，左侧为bi的负向。

图4 圆形杂质与刃型位错的相互作用示意图Fig. 4 Schematic of a circular inhomogeneity interacting with an edge dislocation

表1 夹杂物和相应基体的计算参数Table 1 Computational parameters of an inhomogeneity and the corresponding matrix

本文算法采用了迭代次数K=5的数值计算方案，其中，在面单元所离散的夹杂区域上，单元数取Nx=32,Ny=32。图5、图6中的零次迭代解表示在计算过程中忽略夹杂扰动场所得到的数值结果。本文的解析解来自于Dundurs和Mura教授[9]的计算结果，其中的交互能可以从总能量中除去位错自身能量得到。

图5 无量纲交互能的变化图，其中位错位置ξ/a在x1轴上从1.1移动到1.6Fig. 5 Variation of the normalized interaction energy with dislocation position varying along x1-axis from 1.1 to 1.6

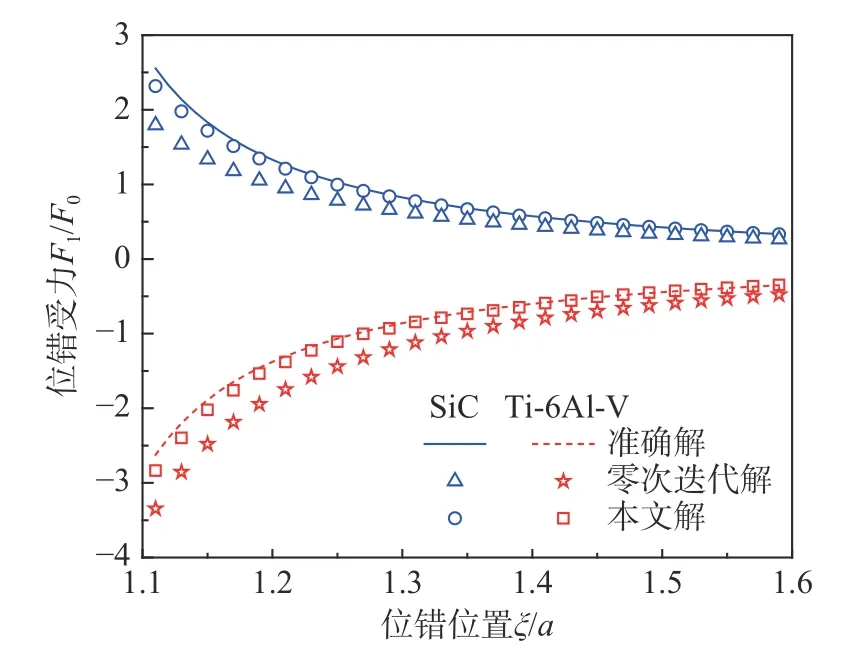
图6 无量纲位错受力的变化图，其中位错位置ξ/a在x1轴上从1.1移动到1.6Fig. 6 Variation of the normalized force with dislocation position varying along x1-axis from 1.1 to 1.6

在图5和图6中，分别对夹杂物(SiC和Ti-6Al-V)和位错之间的交互能和位错受力进行了无量纲化研究，其中，ΔW0=μ1/[2π(k1+1)]，F0=μ1/[πa(k1+1)]。随着刃型位错位置不断地靠近杂质，二者之间的交互能绝对值越来越大，相应地，位错受到杂质的排斥效应也越来越剧烈。从上述两幅图中还可以明显看出，相对于零次迭代解，本文计算方案与准确解具有更好的数值吻合度。

在文献[45]中，给出了在刃型位错(位置在(3.0×10−3mm, 0))周边存在一个圆形的非金属氧化物Al2O3(如图4所示)，其剪切模量为152 GPa，泊松比为0.22，半径为2.0×10−3mm，伯格斯矢量的大小为(1.0×10−7mm, 0)。通过本文的计算，此时非金属夹杂物与刃型位错的交互能和位错受力如图7和图8所示。

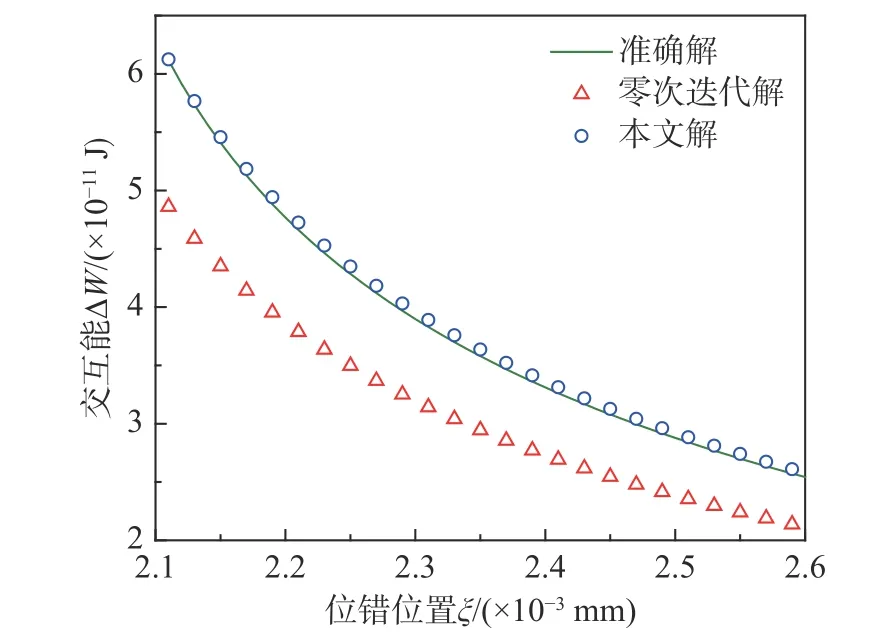
图7 刃型位错与Al2O3交互能的变化图，其中位错位置ξ/a在x1轴上从2.1移动到2.6Fig. 7 Variation of the interaction energy between edge dislocation and Al2O3 where dislocation position varies along x1-axis from 2.1 to 2.6

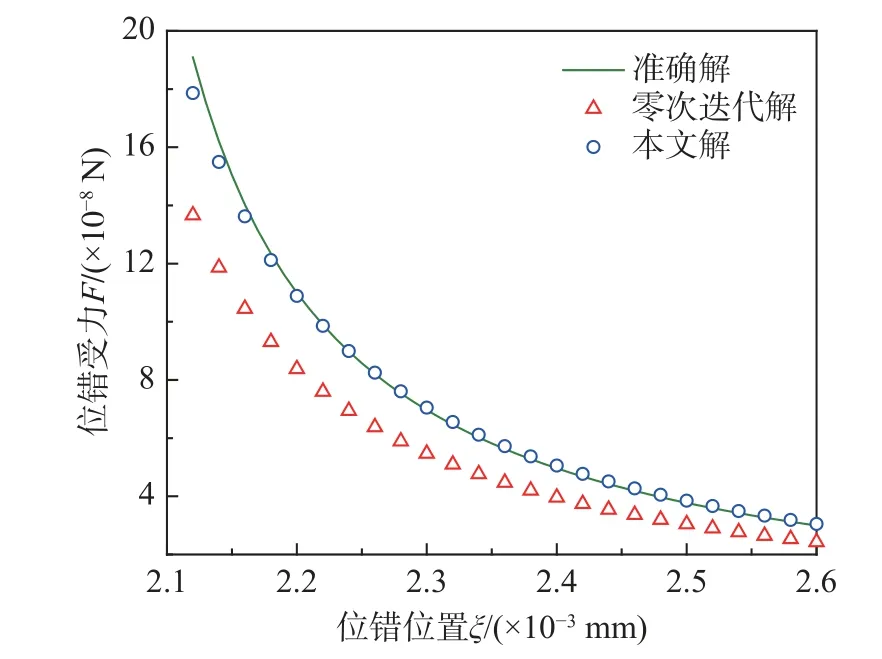
图8 位错受力的变化图，其中位错位置ξ/a在x1轴上从2.1移动到2.6Fig. 8 Variation of the force on edge dislocation with dislocation position ξ/a varying along x1-axis from 2.1 to 2.6

2.2 本文计算方法的可靠性分析

为了更加准确地分析本文计算方案与准确解之间的相对误差，引入无穷范数和2-范数，对零次迭代解和本文数值方法所得到的交互能和位错受力进行误差分析，相关的对比结果见表2。需要说明的是，计算中选取了位错位置ξ/a从1.1到1.5上均匀分布的50个点进行了计算。从表格中可以看出，零次迭代解在无穷范数和2-范数上均具有较大的相对误差，而采用本文计算方案后，相对误差的范数均得到极大地减小，说明本文计算方案在求解过程中具有很好的数值收敛性和稳定性。结合图5、图6及表2可以进一步看出，对于只考虑材料解的零次迭代法，当计算点位于杂质附近区域时，所得到的计算误差尤为明显。

表2 本文数值计算方案和零次迭代解之间的相对误差结果对比Table 2 Comparisons on relative error of results between the present numerical scheme and 0th solution

2.3 SiC或Ti-6Al-V杂质对位错能量及受力的影响

在航空结构中，通常添加碳化硅或钛合金颗粒来增强重要部件的机械强度，但是相关研究也表明，微裂纹的萌生通常会出现在夹杂物的周边。为了进一步说明本文计算方法对于求解任意形状杂质与刃型位错交互能的适用性，对图9所示的不同形状的椭圆SiC杂质进行了分析，其中椭圆的两个短半轴比a2/a1分别取0.25、0.5、1.0、2.0、4.0，其中，a1和a2的方向分别沿x1和x2。椭圆形SiC杂质和基体的材料常数采用如表1所示的计算参数。从图9可以看出，随着刃型位错沿x1轴移动并不断靠近杂质，二者之间的交互能逐渐增大，且曲线的斜率在靠近杂质处渐渐变陡；当位错位置固定时，随着a2/a1的比值变大，交互能则逐步增加，但增加趋势则逐渐变小。

图9 椭圆形SiC杂质与刃型位错的交互能Fig. 9 Schematic of an elliptical SiC inhomogeneity interacting with an edge dislocation

已有的解析解研究通常只能针对特定的夹杂物形状展开分析，如标准的椭圆形或圆形，但是实际工程中的夹杂物更多是以任意形状方式进行分布的，此时的解析解在工程应用中则受到了极大地限制。在图10和图11中，本文选择了由杂质形状函数r(m)(ψ)=1+2ancos(mψ)控制的参数方程，其中，an为形状系数，m为粗糙度系数。在本算例中，形状系数取0.03，粗糙度系数分别取5和8。本文图10和图11则对这种形状的SiC杂质和Ti-6Al-V杂质与刃型位错之间的交互能和位错受力进行了研究。

图10 复杂形状杂质与刃型位错的交互能Fig. 10 Schematic of the interaction energy between an inhomogeneity with complex boundary and an edge dislocation

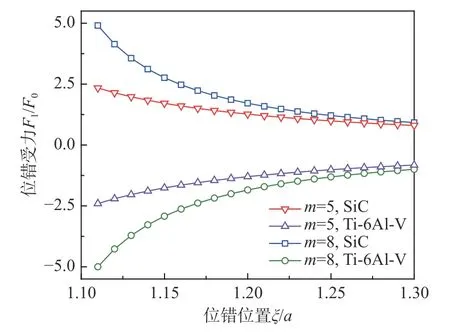
图11 复杂形状杂质与刃型位错作用下的位错受力Fig. 11 Schematic of the force due to an inhomogeneity with complex boundary and an edge dislocation

从图中可以看出，比基体较硬的SiC杂质对刃型位错产生的是排斥力，而较软的钛铝合金Ti-6Al-V则会吸引刃型位错。更为一般的，当夹杂物区域变为孔洞时，即弹性模量为零，此时孔洞对其周边位错产生的吸引力会进一步导致位错在材料中的湮灭，这种理论所预测的现象已在实验中被证实[46]。此外，对于同一杂质与刃型位错而言，不同形状杂质下产生的交互能和位错受力大为不同，且这种影响在杂质附近处表现尤为明显。