切向流作用下单层声衬噪声阻尼性能的数值研究
2022-07-04赵鹏瑜杨兴林吴维维
赵鹏瑜,杨兴林,马 恒,吴维维
(江苏科技大学 能源与动力学院,江苏 镇江 212100)
声衬是民航涡扇客机消声短舱的核心单元,作为降低和控制噪声的一种有效、简单的结构,在航空稳定推进系统方面受到普遍关注[1-2]。过去已经有很多基础的实验和数值模拟来研究无流情况下声衬中流体和声学之间的相互作用,以此探明声衬的吸声机理[3-5]。为了完善和丰富声衬的阻尼机理以及吸声特性,研究者在切向流对声衬的阻尼性能方面的影响也进行了实验和数值研究[6-8]。Tam等[8]的实验和数值模拟结果表明,在切向流存在的情况下,声衬会产生自噪声,这似乎是一种反馈声学共振现象,产生这种现象的原因是谐振器空腔开口的自由剪切层的Kelvin-Helmholtz不稳定波驱动的。最近,Zhao等[9-10]实验研究了在切向流和偏置流共同存在的情况下,具有不同穿孔率的单双层穿孔管的吸声性能。结果表明,增加穿孔管的穿孔率可以增加其在较高频率下的噪声阻尼效应,且增加偏置流速也会增加穿孔管的吸声特性。杨嘉丰等[11]使用声学流管实验台对单/双自由度声衬在切向流条件下进行了实验研究。但是需要注意的是,大部分先前的研究都是在较小的切向流速下进行的,并且所进行的实验和数值研究只与一种切向流速或者孔隙率有关,所以这也在一定程度上推动了目前本文的工作。
在实际应用中,声衬通常安装在管道一侧的壁面上,以抑制噪声在管道中的传播。由于声衬对声能的吸收和反射,声压级沿衬垫表面逐渐降低[12]。因此,对于不同的入射声波频率,声衬不同部分的声阻和声抗可能不同,所以声衬的声阻抗会逐渐变化,而声阻抗在空间的变化量最终会影响声衬的声学性能。近年来研究人员主要集中研究了声阻抗在内衬管道中的变化。Chen等[13]用二维数值模拟方法研究了由狭缝赫姆霍兹谐振器组成的声衬的声阻抗变化,以此判断每个谐振器对声能吸收的影响。通过对管道中特定位置的声能量进行分析,发现声阻抗变化是由于在共振频率下,衬垫长度上的声压级快速减小引起的,所以每个谐振器表现出不同的声学特性。随后Chen 等[12]进一步进行了直接数值模拟和实验分析,研究了在无流情况下,不同频率和声压级的入射声波在均匀分布的多狭缝声衬上的声阻抗变化。结果表明,当激发共振频率附近的高强度声波时,上游的狭缝谐振器工作在非线性区域,而下游狭缝谐振器工作在线性区域,这直接证明,由于不同的局部入射声压级,声阻抗在衬垫长度上是不均匀变化的。
声阻抗作为评估声衬性能最主要的参数之一,是模拟管道中声传播和管道声场变化不可或缺的边界条件[14-15]。对于常规的声衬而言,其穿孔板表面上的孔径非常小,且数量很多,所以很难通过计算每个小谐振器来确定声衬的声学性能。因此,对于工业应用来说,这种声衬在建模过程中被视为在每个特定频率下具有平均阻抗的阻抗边界[12]。但国内外现有的声衬实验研究只能得到声衬的声阻抗,无法直观地反应出声衬的吸声性能[11]。所以本文通过COMSOL Multiphysic 5.5软件求解频域线性Navier-Stokes方程,来建立由8个狭缝谐振器组成的声衬的二维数值模型,使用传输损失具体分析不同孔隙率的声衬在切向流条件下的吸声性能,更加直观地给出声衬的主要吸声频带和共振频率。首先描述二维数值模型,并与现有文献进行验证比较,然后研究在有无切向流条件下,声衬在不同孔隙率下的声学衰减性能,最后对孔隙率、切向流、层数的这些影响进行比较和讨论。
1 模型描述及其验证
1.1 单层声衬几何模型
模型的整个计算域和边界条件如图1所示。声衬安装在矩形管道的下壁面,由一系列8 个几何参数相同的狭缝赫姆霍兹谐振器组成,相邻两个谐振器之间的厚度为wt=1.3mm。图2 为1 个狭缝赫姆霍兹谐振器的结构示意图,其中h为共振腔的高度,w为共振腔的宽度,ws为狭缝的宽度,t为狭缝的厚度,因此孔隙率定义为:σ= 8ws(8w+7wt)。整个模型几何参数由Tam等[8]之前的实验研究确定,如表1所示。该模型用来研究切向流作用下声衬的声学特性。切向流也被称为平均流[16]。
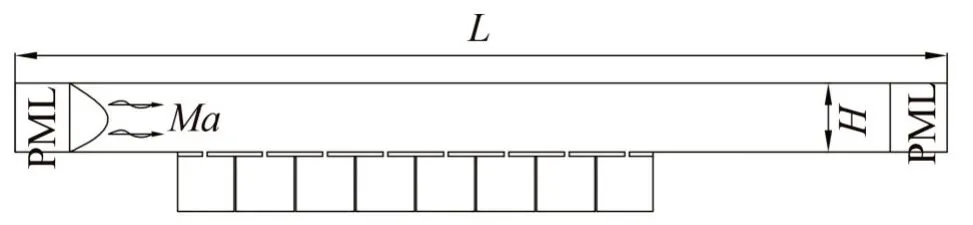
图1 整个模型计算域

图2 狭缝赫姆霍兹谐振器

表1 声衬的几何尺寸
1.2 控制方程、边界条件和网格剖分
本文中,建立的是二维模型,使用雷诺平均Navier-Stokes 方程(RANS)作为系统控制方程[8,16-17],包括:
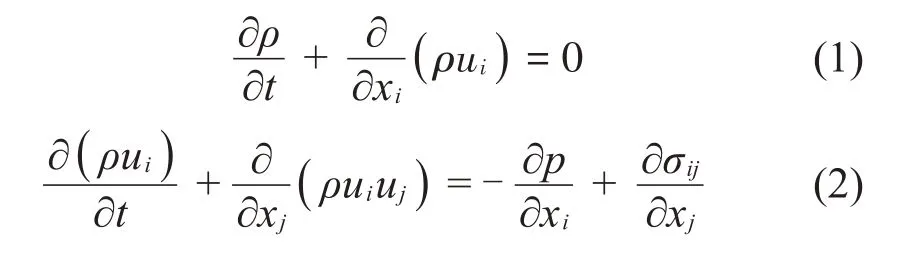

其中:σij定义为黏性应力张量,sij定义为应变率张量,κ表示空气比热容比,μ表示动力黏性系数,c表示声速,ρ、ui、p指的是瞬时密度、速度矢量和压力变量。
理想气体状态方程p=ρRgT在此也成立。可压缩的Navier-Stokes方程通过线性化可以得到声学控制方程,假设瞬时变量由平均值和波动值叠加组成,表示为:

本模型建立的是二维矩形管道流动和平面波传播,流体流动扰动可以被认为是与时间相关的简谐波,因此空气密度、流速和压力的波动部分经过傅里叶变换转化为频域表示为:
将方程(5)代入到系统控制方程式(1)至式(3)并进行线性化,线性化的Navier-Stokes方程表示为:

为了简化模型,节约计算成本和时间,选择COMSOL Multiphysics 5.5 软件中的SST 湍流模型来计算流体,SST 湍流模型组合了自由流体的k-ε模型和近壁的k-ω模型,趋向于更精确地求解壁面,之后使用线性Navier-Stokes 频域声场模型确定本模型的声学特性。通过映射将CFD中的压力,速度,动力黏度作为线性Navier-Stokes 频域声场的背景平均流。因为平面波能够满足管道壁面边界条件,所以从管道入口引入声压级为140 dB的平面波作为背景声场激励此模型。管道两端通过添加完美匹配层(Perfect Matched Layer,PML)[18]完全吸收边界条件,以防止管道两端驻波的形成。在PML处使用滑移和绝热边界条件来避免壁面的数值噪声,而在其他壁面上使用默认的无滑移和等温条件来模拟边界层中发生的声学衰减行为[16]。以上边界条件的设置与COMSOL 中相关实施例的边界条件设置基本相同,对于类似问题的建模过程,边界条件的设置都大同小异。传输损失作为描述声学衰减行为的参数,在这里被定义为[17]:

式中:Wi和Wt分别表示为管道进口处的入射声功率和出口处的透射声功率,pi和pt表示管道上游入口处入射声波的声压和管道下游出口处透射声波的声压。在实际实验测量中,通常使用双麦克风技术测量TL。
声衬安装段流场和声场的非结构化网格分别如图3(a)和图3(b)所示。为了在狭缝和谐振器连接处观察到清晰的涡流和剪切层[19-20],此模型选择了更细化的网格,更加细化密集的网格有利于提高计算的精确度,得到更精确的解。其中,流场域单元包含96 015个单元数,声场域单元包含24 998个单元数,在边界条件方面,将流场网格计算得到的CFD解映射到声场网格上。
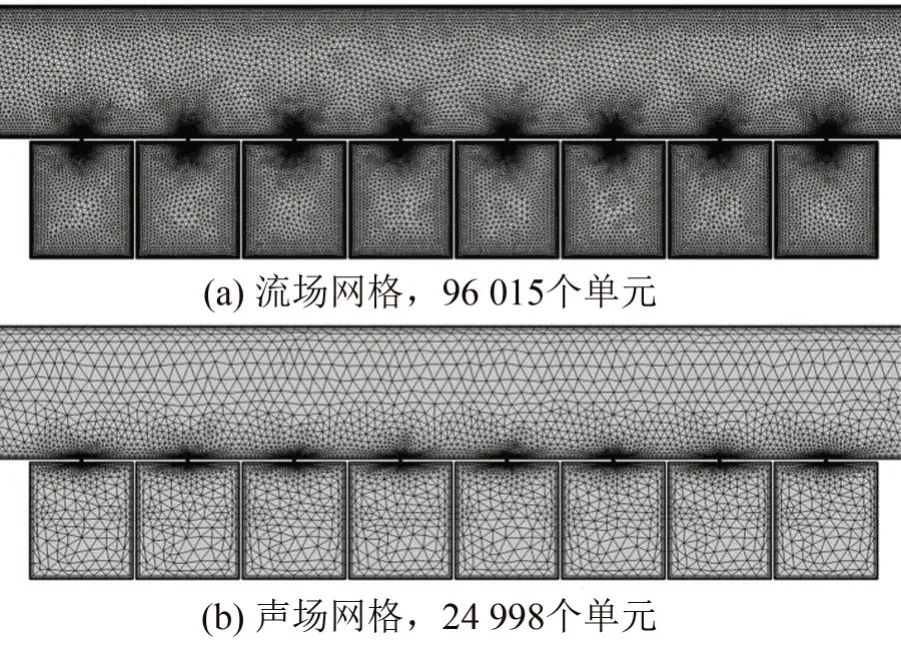
图3 单层声衬的非结构化网格
1.3 模型验证
为了验证此模型的准确性和可行性,我们将模拟结果与Tam 等[8]的实验结果进行比较。模型所选取的几何参数与文献实验研究的参数相同,其孔隙率均为2.57%,切向流马赫数设置为0.3。为了得到文献实验中2 000 Hz的入射声频率和148.6 dB的高入射声压级,模型验证过程中在管道入口引入声压级为148.6 dB 的平面波,在线性Navier-Stokes 频域声学接口中通过参数化扫描,选择切向流马赫数为0.3,频域计算范围设置为(1,2 000),频率步长设置为5 Hz,以便得到更精确的解。图4(a)、图4(b)分别为当前数值模拟与实验测量结果声压级和相位分布的比较,可发现两种结果存在良好的一致性。值得一提的是,为了与实验测试结果相同,所研究的是与声衬相对的壁面上声压级和相位的分布。模拟结果表明,声衬安装段的声压级分布和相位分布与实验测量结果存在高度一致,而在管道下游,两种结果发生明显偏差,如图中0.4 m~0.8 m所示,这是由于实验所使用的掠流阻抗管(Grazing Flow Impedance Tube,GFIT)下游终端的反射波引起的,相比之下,模拟通过在管道两端添加PML吸收边界条件,因此模拟结果显示的管道下游没有出现声波振荡。
第三阶段(1992年—1997年),稳步增长阶段。1992年,邓小平同志南巡讲话摆脱了姓“社”、姓“资”的困扰,党的十五大确立了以公有制为主体,多种所有制经济共同发展的基本经济制度,明确了非公有制经济是我国社会主义市场经济的重要组成部分。
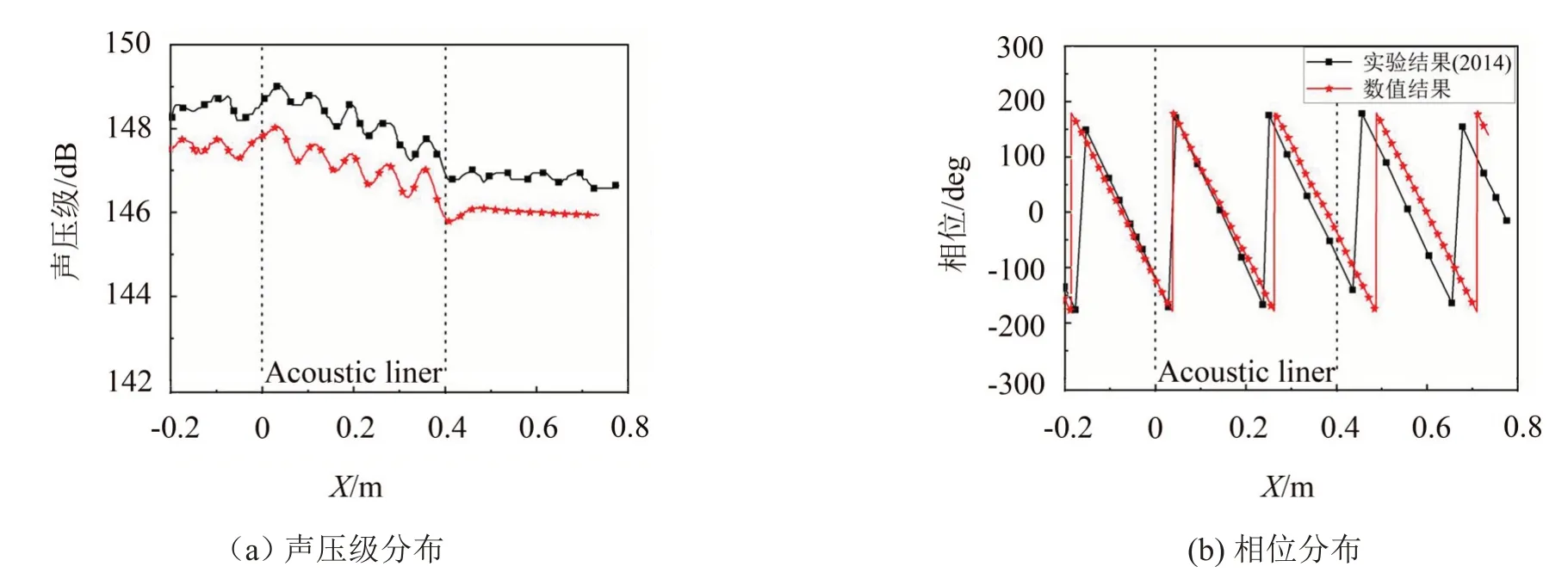
图4 Tam等实验结果与当前数值模拟结果的比较
2 结果与讨论
2.1 孔隙率和切向流的影响
孔隙率为2.57%的单层声衬在各切向流速下的传输损失如图5 所示。当无切向流,即Ma=0 时,其局部最大传输损失达到110 dB,有效吸声频率范围在450 Hz~700 Hz 之间。随着切向流速的增加,单层声衬的吸声性能越来越弱,当Ma=0.3 时,最大传输损失只有5 dB。相对于无流条件,有流情况下声衬在不同频段的吸声能力各有不同,如200 Hz~400 Hz 以及800 Hz~1 000 Hz,其吸声能力均比无流时较强。综合来看,传输损失在整个频段上的变化为先增加后减小,最大传输损失对应的最佳吸声频率随切向流速的增加向高频移动,即共振频率向高频漂移。随着切向流速的增大传输损失越来越小的主要原因是高流速条件下增加了声衬的声阻,导致其离壁面的最佳声阻越来越远,这时声场边界条件变为硬边界条件,声波更多地是被反射而不是被吸收[15]。

图5 当σ=2.57%时,单层声衬产生的传输损失
图6所示为无流情况下不同孔隙率的单层声衬产生的传输损失随频率的变化。当孔隙率从1.28%增加至2.57%时,局部最大传声损失由50 dB增加到110 dB,增幅较大。当孔隙率继续增加至6.42%时,局部最大传声损失在115 dB 上下波动,变化幅度很小。此时伴随着共振频率向高频移动的现象,这是由于孔隙率的增加,声衬表面上的总声阻和声抗反而降低,从而导致共振频率向高频移动[21]。这表现为声衬这种抗性消音器[17]在共振频率附近有较强的吸声能力。无流情况下单层声衬产生的局部最大传输损失随孔隙率的增加不再增大这一现象需要进一步进行实验研究确定,并分析其原因,这也为今后的工作提供了思路。

图6 当Ma=0时,单层声衬产生的传输损失
图7所示为当Ma=0.05时,6种不同孔隙率的单层声衬产生的传输损失随频率的变化。随着孔隙率的增加,声衬的噪声阻尼性能越来越强,孔隙率为6.42 %的单层声衬的局部最大传输损失达到110 db。且随着孔隙率的增加,其共振频率同样向高频移动,消声频带也越来越宽。但是在远离共振频率的频段,如900 Hz~1 000 Hz,孔隙率的增加削弱了声衬的吸声能力,传输损失出现了负值。与无流情况下不同的是,随着孔隙率的增加,单层声衬的局部最大传输损失逐渐增大,变化更为明显。
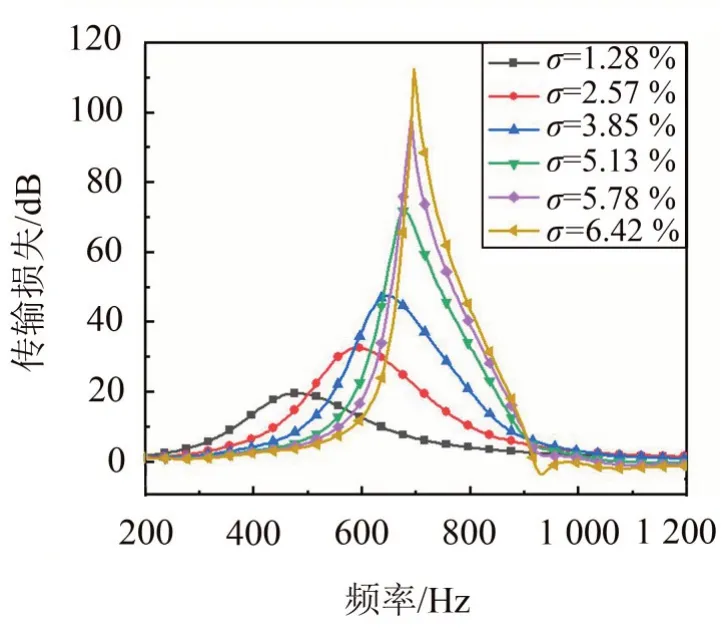
图7 当Ma=0.05时,单层声衬产生的传输损失
图8 进一步比较了单层声衬在各切向流速下,孔隙率的变化对其传输损失的影响。结果表明,随着切向流速的增加,单层声衬的局部最大传输损失不断减小,且在同一流速下孔隙率的增加增强了吸声能力,这也与图6、图7 的变化相同。值得注意的是当Ma≥0.15 时,σ≥3.85%的单层声衬产生了两阶传输损失,两阶峰值之间近似成2倍关系,且随着切向流速的增加,1阶传输损失占主导地位,其表现为在低频和高频均有较强的吸声能力。这种变化同时也说明孔隙率和切向流对声衬吸声性能的影响是显而易见的。
为了更进一步分析单层声衬能够产生两个传输损失峰值的原因,图9 给出了当Ma=0.2 时,组成单层声衬的第一个狭缝赫姆霍兹谐振器的速度云图。由图可知,当孔隙率较小,即σ=2.57%时,仅在狭缝中形成了较小的速度漩涡,这表明了在孔隙率较小时,噪声衰减主要发生在狭缝之间,从而也说明了单层声衬在孔隙率较小时吸声性能弱的原因。当孔隙率较大时,如图9(b)、图9(c)所示,在狭缝和空腔中都形成了较为强烈的速度漩涡,且随着孔隙率的增加形成的速度旋涡越强烈,噪声衰减主要通过狭缝和空腔的共同作用,此时声学和流体之间的相互作用也更加明显。并且从图8 进一步观察到产生的1 阶共振频率随着切向流速的增加仅在550 Hz~700 Hz之间变化,范围较小,而产生的2阶共振频率随着切向流速的增加有明显向高频移动的现象。由此结合速度云图也可预测1阶共振频率是由狭缝振动引起的,此频率也为狭缝的固有频率,2阶共振频率是狭缝振动和空腔共振共同作用引起,表现为向高频移动。图10 至图11 分别所示为σ=5.13%以及σ=6.42%的两种较大孔隙率的声衬在各自产生的两个共振频率下的总声压云图,以此观察在两个共振频率下,声衬中的声压力场变化,此时Ma=0.2。
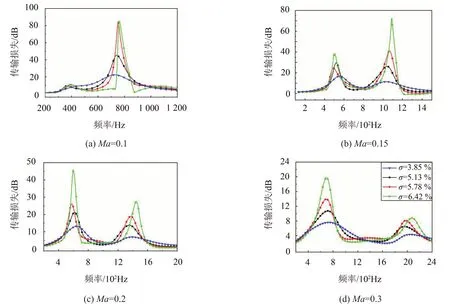
图8 不同切向流速情况下单层声衬产生的传输损失对比
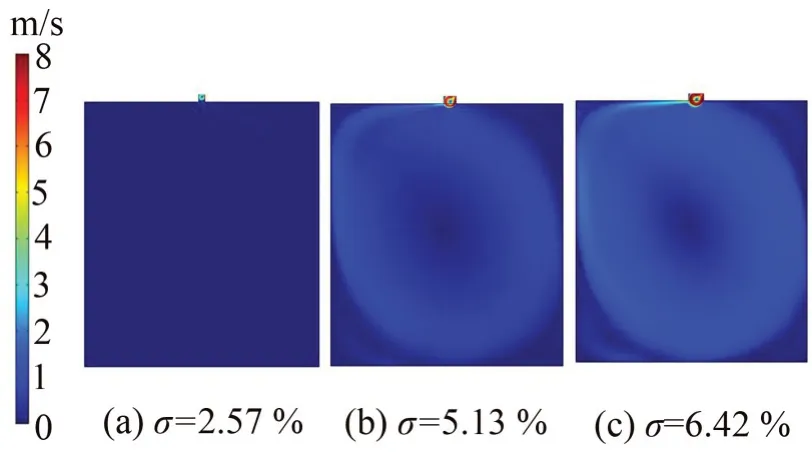
图9 当Ma=0.2时第一个狭缝赫姆霍兹谐振器的速度轮廓的比较
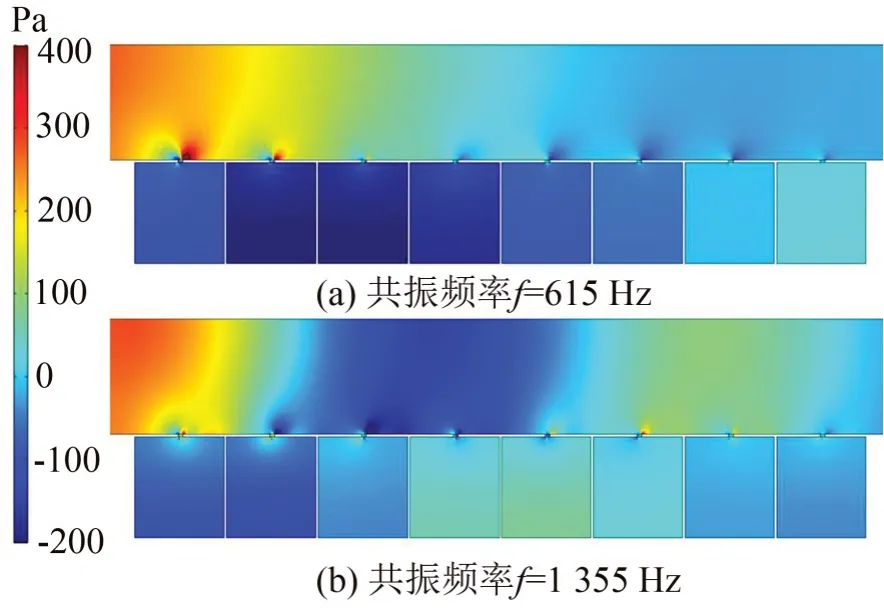
图10 当Ma=0.2时σ=5.13%的声衬在两个共振频率下的压力分布

图11 当Ma=0.2时σ=6.42%的声衬在两个共振频率下的压力分布
由图可知,声压在狭缝开口处的变化最为明显,且孔隙率越大,变化越剧烈。相较于2阶共振频率,狭缝开口处在1 阶共振频率下的压力变化更为剧烈,这也进一步说明1 阶共振频率是由于狭缝振动引起的。进一步观察主管道和空腔中压力场的变化,发现主管道在1阶共振频率下的声压连续衰减,但在2阶共振频率下出现负压,管道中形成驻波,这是因为2阶传输损失小于1阶传输损失的原因,声波更多是通过狭缝的振动在1阶共振频率下耗散。但对应主管道压力为负的空腔在2阶共振频率下的压力增大,这是由于空腔共振以及狭缝振动与主管道之间的强耦合行为引起的压力变化。总之,在这种情况下,声衬的声学特性主要由1阶共振频率处狭缝的振动决定,而2 阶共振频率处空腔共振对传输损失和拓宽消声频带贡献更大。结合速度变化和压力场的变化,可以看出由于声衬结构的改变和切向流作用导致其产生了两个传输损失峰值。
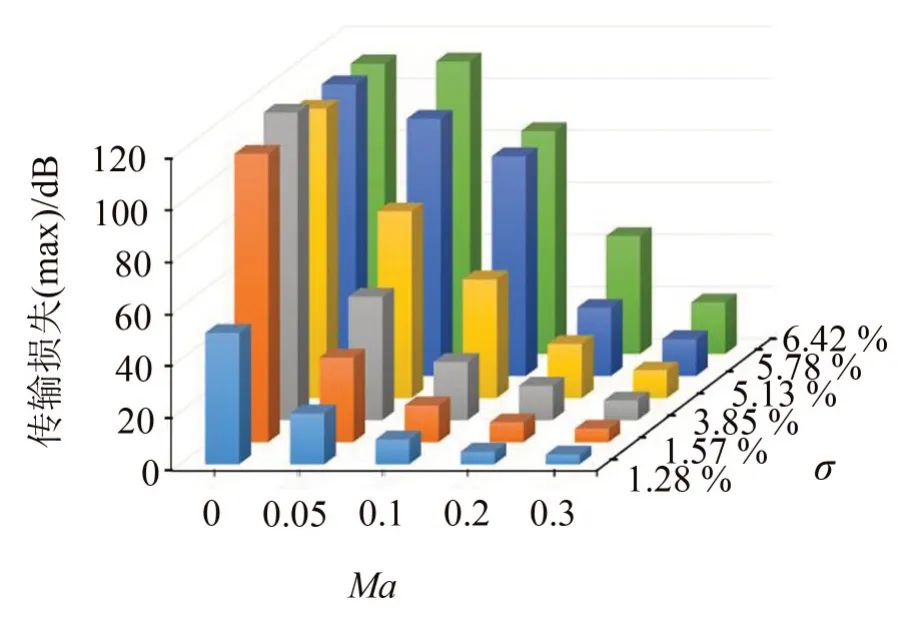
图12 单层声衬最大传输损失随切向流和孔隙率的变化
2.2 单/双层声衬的吸声性能对比
为了全面地了解声衬的声学特性,优化设计一种双层声衬,并对其进行模拟研究。双层声衬的上层(内衬)孔隙率为3.85 %,下层(外衬)孔隙率为2.57%,其余的几何尺寸均与单层声衬相同,如图13所示。这相当于两个不同孔隙率的单层声衬的叠加。模拟所设定的入射平面波声压级仍为140 dB,图14 为双层声衬的声学非结构化网格,包含40 090个单元数,其他边界条件和单层声衬的完全相同。

图13 双层声衬模型结构

图14 双层声衬声学非结构化网格
图15 给出了双层声衬在不同切向流速下的吸声性能。随着切向流速的增加,双层声衬的传输损失逐渐减小,这也和单层声衬的变化相同,传声损失在整个模拟的频带上总体变化表现为先增后减再增再减的趋势。与单层声衬不同的是,双层声衬在任一切向流速下都会产生两个传输损失峰值,但是,在两个峰之间,存在吸声低谷,传输损失很小,如图中的600 Hz~800 Hz,这种现象可能是由于双层声衬的反共振现象[11]引起的。值得注意的是,当Ma≥0.2时,双层声衬产生了三个传输损失峰值,在高频处的吸声能力较低流速时更强。一方面这也是因为随着流速和孔隙率的增加,在狭缝和谐振器中产生了更为强烈的涡流,进而加强了声学与流体之间的相互作用,另一方面是由于内衬和外衬之间形成的多腔体的共振效应引起的。
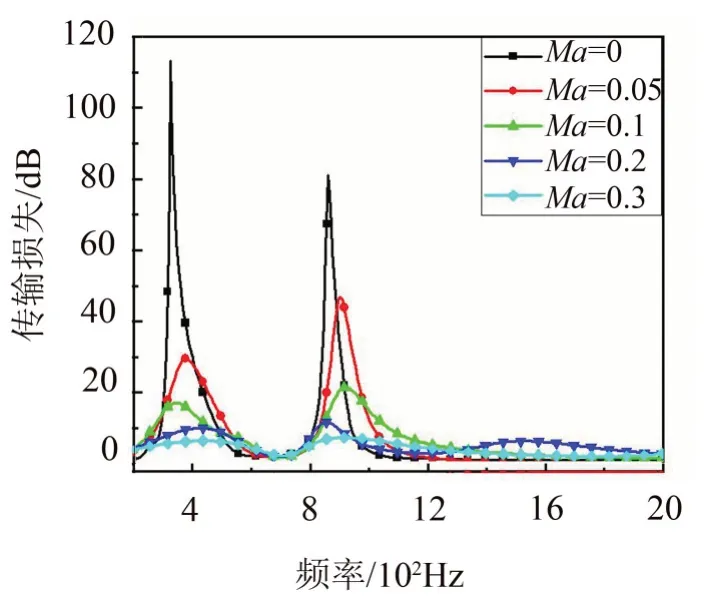
图15 双层声衬产生的传声损失
图16 比较了双层声衬与孔隙率为3.85 %的单层声衬在有无切向流条件下的吸声特性。在无切向流条件下,如图16(a)所示,双层声衬在频率为200 Hz~1 200 Hz之间,产生了两个传输损失峰值,单层声衬仅在500 Hz~800 Hz之间产生了一个传输损失峰值,但是单层声衬产生的局部最大传输损失大于双层声衬。当Ma=0.2时,如图16(b)所示,总体的变化趋势和在无流情况下基本相似。总体来讲,虽然单层声衬的局部最大传输损失大于双层声衬,但是双层声衬在有无切向流情况下均会产生多个传输损失峰值,并且拓宽了消声频带,在有效吸声频率范围内,双层声衬在噪声阻尼方面更加有效,这为宽频噪声的消音处理提供了可靠的方法。
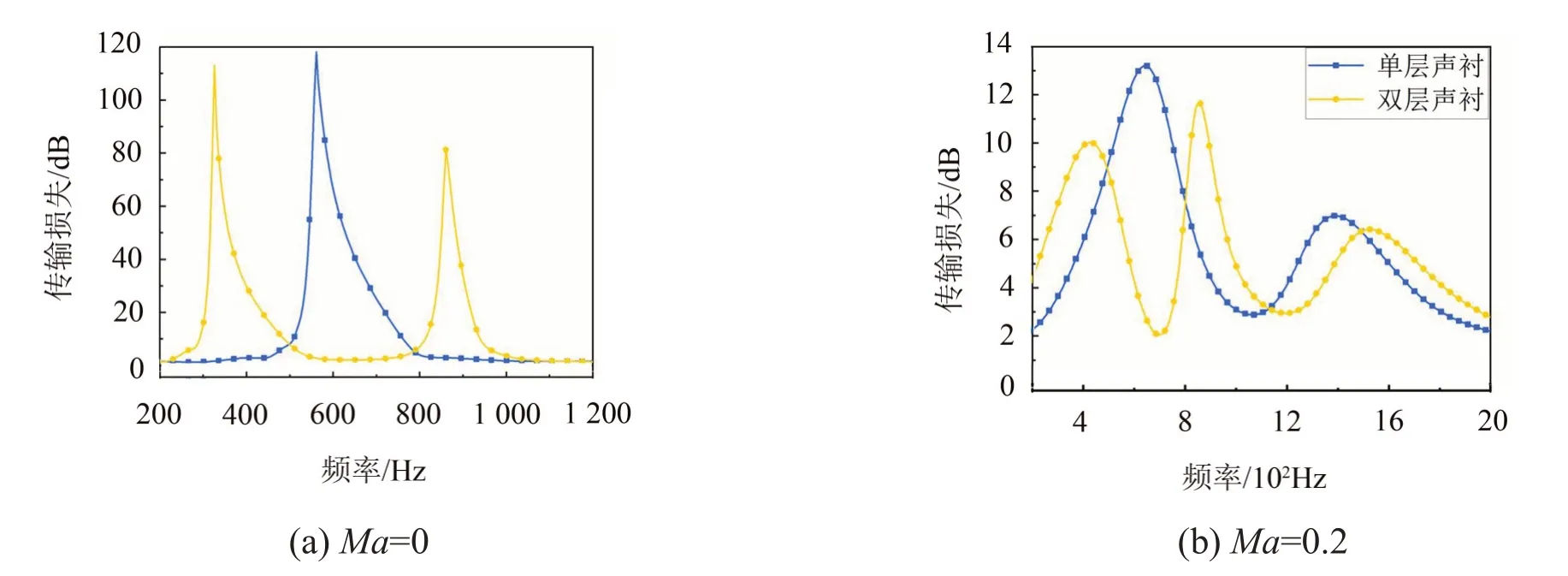
图16 不同切向流速下单/双层声衬产生的传声损失对比
3 结语
(1)在无流情况下,增加孔隙率不一定会增强单层声衬的吸声性能;当存在切向流时,随着孔隙率的增加单层声衬产生的传输损失逐渐增大。但无论是否存在切向流,共振频率均向高频移动,单层声衬表现为在共振频率附近具有较强的吸声能力,所以共振频率附近的声学行为无疑是声衬设计的关键特征。
(2)随着切向流速和孔隙率不断增加,单/双层声衬均会产生多个传输损失峰值,一方面与在狭缝和谐振器中形成的涡流强度有关,另一方面是由于双层声衬的内衬和外衬之间形成的多腔体的共振效应引起的。
(3)随着切向流速的增加,单/双层声衬的吸声性能逐渐降低,产生的最佳吸声频率的范围也随之改变,因此在声衬的优化设计中应该充分考虑切向流的作用。
(4)对于在有效吸声频率范围内而言,和单层声衬相比,双层声衬在噪声阻尼方面更加有效,但是由于反共振现象的存在,在某些频段的消声能力很弱。因此在实际的研究设计中,针对不同的工况,应该选择参数合适的声衬,以便达到最佳的吸声效果。
