新型血液防振荡储运装置隔振性能优化研究

2022-07-04张孝强骆星九

噪声与振动控制 2022年3期

杨猛，王猛，张孝强，骆星九

（中国人民解放军海军特色医学中心，200433 上海）

悬挂式减振系统以弹簧（含阻尼）作为减振缓冲元件将被隔振物悬吊于减振系统内部，如图1所示。这种减振系统特别适用于脆值较低的精密仪器设备的隔振，如大型电子管、制导装置等，它可以使被隔振物在多个方向上都能得到缓冲保护，而且实现起来比较容易，因此在运输过程中应用较多，尤其是在空投和军事领域[1-10]。

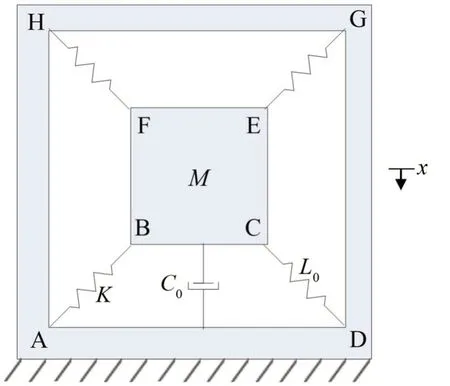
图1 悬挂式减振系统

而血液在运输过程中较易发生由振动引起的振荡性溶血（细胞膜破裂造成K+、FHb上升），进而引起血液失效[11]，造成极大的浪费。为解决这一问题，本文在悬挂式减振系统的基础之上设计一种新型血液防振荡储运装置，以期能够降低运输过程中的振动对血液保存质量的影响，进而延长血液的保存周期。

1 新型血液防振荡储运装置隔振性能验证计算

新型血液防振荡储运装置具有两级减振系统，主要由空气弹簧、外框架、钢丝绳隔振器、内框架、滑轨和储血框组成，该装置能够实现三向隔振，并满足集约化要求，具体结构如图2所示。

图2 新型血液防振荡储运装置

本文采用动力学分析软件ADAMS对新型血液防振荡储运装置进行研究，以验证装置的隔振效率，具体步骤如下：

（1）建立新型血液防振荡储运装置的三维实体模型（本文采用Solidworks建模）；

（2）将三维实体模型保存成Parasolid 格式，并导入ADAMS；

（3）在原有减振器的位置加入力模块（Force，以下简称力），转变成如图3所示的模型，其中，红色部分为弹簧和力，斜向力模拟钢丝绳隔振器，垂向力模拟空气弹簧，水平弹簧主要用来限定模型振动方向，质量块用来模拟地板，血液（用blood表示）简化为质量块，与储血框固连；

（4）限定模型下部的四个质量块沿垂直方向运动，对每个质量块施加位移激励，激励数据为某履带急救车在越野路上的车厢地板振动数据，时长176.124 s，采样频率250 Hz，其时域波形如图4所示；

图4 激励数据

（5）对模型进行验证计算。

针对图3模型，斜向力代表钢丝绳隔振器，其刚度和阻尼分别为50 N/mm和5 N·s/mm；垂向力代表空气弹簧，设空气弹簧非线性力的表达式为k1x+k2x2+k3x3+cx[12]，其中k1、k2、k3和c分别为40 N/mm、10 N/mm2、10 N/mm3和10 N·s/mm；水平弹簧主要用于限定模型运动方向，其刚度和阻尼分别为100 N/mm、10 N·s/mm；内框架、外框架和储血框设定为钢材料，密度为7 800 kg/m3；血液的密度设定为1 000 kg/m3；blood1～blood4代表血液。经过仿真计算，可以获得质量块和blood1～blood4 质心处的垂向振动加速度如图5所示。

图3 新型血液防振荡储运装置振动模型

由图5 可知，经过两级隔振系统的减振，blood1～blood4 的垂向振动加速度基本相同，这说明随着高度的增加，血液的垂向振动加速度并没有大幅度改变，即血液储存位置的高低对隔振效果影响不大。此外，blood1与质量块相比，垂向振动加速度大幅度减小，这说明该装置的隔振效果非常明显。为了进一步明确该装置的隔振效果，计算blood1～blood4以及质量块的垂向振动加速度功率谱密度和概率密度分布，如图6所示。

图5 振动加速度

图6 功率谱密度与概率密度分布

由功率谱密度曲线可以看出，经过该装置的减振，质量块在40 Hz～80 Hz 范围内的激振能量几乎被完全消减，减振效果明显，但对低于10 Hz的激振能量却反而有放大作用，由于血液对高频振动敏感，对低频振动的耐受力相对好一些[13]，所以该装置的减振对血液保存仍然具有明显益处。由概率密度分布曲线可以看出，经过该装置的减振，血液的垂向振动加速度更加集中于0 m/s2附近，振动环境得到明显改善。

以垂向振动加速度均方根值来代表振动能量，经过计算可得blood1～blood4和质量块的垂向振动加速度均方根值分别为2.454 5 m/s2、2.454 4 m/s2、2.454 4 m/s2、2.454 3 m/s2、11.176 3 m/s2。由以上计算结果可知，blood1～blood4 的垂向振动加速度均方根值基本没有变化，再次验证了储存高度对血液振动能量基本没有影响。blood1～blood4 相对于质量块，垂向振动加速度均方根值分别下降了78.04%、78.04%、78.04%、78.04%，减振效果非常明显。

根据概率密度分布计算blood1～blood4 和质量块的垂向振动加速度在-0.1 m/s2～0.1 m/s2范围内的概率，分别为0.072、0.072、0.072、0.072、0.008 6，blood1～blood4 垂向振动加速度在-0.1 m/s2～0.1 m/s2范围内的概率相比于质量块分别提高了737.3%、737.3%、737.3%、737.3%。由以上计算结果可知，经过该装置的减振，血液垂向振动加速度更加集中于0附近。

综合以上分析结果，经过本文所设计的血液防振荡储运装置的减振，血液所承受的振动能量在理论上可以下降78.04%，垂向振动加速度在-0.1 m/s2至0.1 m/s2范围内的概率在理论上可以提高737.3%，血液的振动环境得到明显改善，隔振效果满足使用要求。

2 新型血液防振荡储运装置抗冲击性能验证计算

对新型血液防振荡储运装置的抗冲击性能进行验证计算，装置各物理参数与第1节相同，改变激励数据，在ADAMS中以双STEP函数求和的方式来表示冲击激励。本次计算采用位移激励，激励幅值为30 mm，激励时间从2.5 s开始，至3 s结束，仿真时间为6 s，激励点数设置为1 000，具体形式为先逐渐增加，至最大值后再逐渐减小，表达式如下：STEP(time，2.5，0，2.75，30)+STEP(time，2.75，0，3，-30)。由第1 节分析可知，血液储存高度对血液所承受的振动能量基本没有影响，因此以blood1 处的冲击响应代表血液的冲击响应，具体如图7所示。

图7 冲击响应

由图7 可以看出，从激励结束开始（3 s），blood1的冲击响应经历大约1 s便衰减至0 mm。冲击激励的峰值为30 mm，而冲击响应的峰值仅为17.448 9 mm，下降41.84%，下降幅度明显，这充分证明了本文所设计的新型血液防振荡储运装置具有明显的抗冲击效果。

3 新型血液防振荡储运装置敏感度分析

针对新型血液防振荡储运装置进行敏感度分析，观察装置各参数对blood1 垂向振动加速度均方根值的影响程度。ADAMS可以计算出参数在不同值处的敏感度值，不同值所对应的敏感度一般是不同的。针对于本次分析，我们主要计算各个参数在初始值（第1 节中各个参数的值）处的敏感度值，激励数据与第1节相同，计算结果如表1所示，表中Kx、Cx分别代表钢丝绳隔振器的刚度和阻尼，k1、k2、k3和c为第1节中空气弹簧非线性力表达式中的参数。

表1 敏感度计算结果

由表1可以看出，在初始值处，敏感度大小的顺序为：k3＞Kx＞k1＞c＞k2＞Cx。敏感度越大，说明影响程度越大，即在初始值处，k3对blood1垂向振动加速度均方根值的影响程度最大，Cx的影响程度最小。

4 新型血液防振荡储运装置优化研究

本文采用MATLAB 与ADAMS 联合仿真的方法对新型血液防振荡储运装置进行优化研究。首先，在ADAMS 中建立7 个系统状态变量，分别代表钢丝绳隔振器的刚度和阻尼（Kx、Cx）、空气弹簧非线性力表达式中的参数（k1、k2、k3及c）、和blood1 垂向振动加速度均方根值。其次，将状态变量与模型关联并指定输入变量与输出变量，针对于本次计算，设钢丝绳隔振器的刚度和阻尼（Kx、Cx）、空气弹簧非线性力表达式中的参数（k1、k2、k3和c）为输入变量，blood1 垂向振动加速度均方根值为输出变量。然后，导出控制模型，控制软件设置为MATLAB，分析类型设置为nonlinear，求解器设置为Fortran。最后，在MATLAB 中导入ADAMS 生成的模型，建立包含ADAMS_sub 的simulink 模型，并设置MATLAB 与ADAMS的交互参数以及仿真运算的参数。完成以上设置之后，ADAMS 的模型就可以在MATLAB 中计算，采用遗传算法对以上模型进行优化计算，目标函数设定为blood1 垂向振动加速度均方根值，激励数据和各参数的初始值与第1 节相同，经过计算可以获得最优设计参数如表2所示。

表2 优化结果

将以上参数重新带入ADAMS 的模型进行计算，可得优化前后blood1 垂向振动加速度功率谱密度和概率密度分布对比如图8所示。

图8 优化前后对比

由功率谱密度对比可以看出，优化后在10 Hz～20 Hz 和40 Hz～80 Hz 范围内blood1 的振动能量明显下降。由概率密度分布对比可以看出，blood1 垂向振动加速度在-0.1 m/s2至0.1 m/s2范围内的概率明显上升。优化后，blood1 垂向振动加速度均方根值为1.475 6 m/s2（优化前为2.454 5 m/s2），比优化前下降39.88%，blood1 垂向振动加速度在-0.1 m/s2至0.1 m/s2范围内的概率为0.157 8（优化前为0.072），比优化前上升了119.1%。综合以上分析，优化后血液的振动能量明显下降，振动环境得到明显改善。