基于信号分离技术的波束形成算法研究

陈士斌，王 谛，吴 健，于 洋，贺 义

（1.中车长春轨道客车股份有限公司，长春 130062；2.西南交通大学 机械工程学院，成都 610031）

声源识别技术能够获取声源位置和声源强度信息，具有广泛的应用前景。常见的声源识别算法有波束形成、声全息以及反卷积等算法[1-3]。波束形成算法通常采用阵列各麦克风同步采集的信号进行延时求和运算，其结果在实际声源位置产生极大值，从而识别真正的声源位置[4]。波束形成算法由于定位精度高，计算速度快等优点被广泛用于汽车、轨道交通和航空等领域[5-7]，并且常作为其他优化算法的初始结果。但是，传统波束形成算法计算的声源云图结果很难与其激励源相关联，尤其是激励源与阵列之间被其他结构遮掩的情况[8]。

在过去的研究中，为了将响应信号中的成分与各个激励源进行关联，研究信号中不同成分产生的机理，多种信号分离技术被提出。将信号分离技术应用于波束形成算法的前处理，可以衍生出多种高级的波束形成算法，其结果有助于将声源云图与其激励源相关联。以下分别对特征值分解和相干输出谱分析两种信号分离技术进行介绍。

特征值分解可以将信号分离成多个相互正交的不相关分量。对信号的互谱矩阵采用特征值分解[9]，原始互谱矩阵可以表示为各个特征值对应分量的叠加，各个特征值分量之间是相互正交的。相比于相干分析技术，特征值分解技术不需要任何额外的参考信号作为输入条件。当激励源产生的信号互不相干时，采用特征值分解技术可以对信号进行有效、准确的分离[10]。

Halvorsen 和Bendat[11]提出的相干输出谱分析技术，通过同步测量的参考信号，计算参考信号与响应信号的相干输出谱，进而对信号进行分离。相干输出谱分析已经在各行业被广泛应用于信号分离，能够有效地研究信号产生的机理[12-13]。相干输出谱分析需要采用与被分析信号同步测量的参考传感器信号，如激励源的结构振动或近场声压信号。当参考传感器采集的信号与其他激励源信号不相关时，相干输出谱分析能够准确对信号进行分离。相干输出谱分析技术适用于单输入-多输出的系统。

为了研究各个激励源对传统波束形成结果的贡献量，分析声源云图产生的机理，特征值分解和相干输出谱分析可以用于波束形成算法的前处理。以下部分分别介绍传统的互谱矩阵和去自谱的互谱矩阵波束形成算法。在此基础上，提出基于特征值分解和相干输出谱分析的互谱矩阵和去自谱的互谱矩阵波束形成算法，并且通过试验验证算法的有效性和准确性。

1 传统波束形成理论

波束形成算法被广泛应用于基于麦克风阵列的声源识别。根据各个阵列麦克风和被识别网格点的位置坐标，基于声波传播理论，可以计算声波到达阵列各麦克风的相对时间差，进而通过延时求和算法对各个网格点进行聚焦，真正的声源位置将出现极大值。频域波束形成算法包括基于自谱、互谱矩阵和去对角线元素的互谱矩阵等计算方法。其中，基于互谱矩阵和去对角线元素的互谱矩阵波束形成算法由于结果稳定，能够有效消除各通道间和传声器的不相关本底噪声进而提高声源识别的空间分辨率和动态范围而被广泛采用[14-16]。以下为基于互谱矩阵的波束形成算法原理阐述。

基于互谱矩阵的传统波束形成算法的输出结果通常表示为如下形式：

其中：B(r,ω)为波束形成算法在r方向的聚焦网格点，圆频率为ω的声压平方的频谱输出结果，e(r)=[e1(r),e2(r),…,em(r),…,eM(r)]T称为转向列向量，其中w向量各个元素分别等于对应转向列向量元素的模的平方，G为阵列麦克风信号组成的M阶互谱方阵，I为M阶元素均为1 的方阵，M为阵列麦克风的数量，上标“T”和“*”分别代表转置和共轭。

波束形成若按照公式(1)的表达形式，转向列向量中的元素表达式如下：

其中：|r-rm|表示阵列上第m个麦克风到聚焦网格点r的向量的模，k表示波数。

根据不同的应用场景，转向列向量元素可以有多种不同的表达形式[17]。公式（2）所示的表达式能够表征无流动媒质，自由场中声波传播到阵列麦克风的幅值变化，延时和相移特征。

为了进一步消除信号间的不相关成分，如不相关的本底电噪声，可以将互谱矩阵G的对角线自功率谱元素进行剔除，将剔除对角线元素的互谱矩阵应用于波束形成的计算能够提高声源识别的动态范围，去自谱的互谱矩阵波束形成算法公式如下：

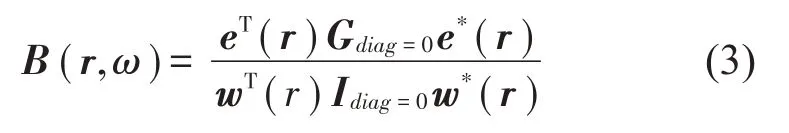
其中：Gdiag=0为阵列麦克风信号组成的M阶互谱方阵，并将对角线元素置为0，Idiag=0为M阶元素均为1的矩阵，并将对角线元素置为0。

当激励源与麦克风阵列之间被其他结构遮掩，或与麦克风阵列垂直的测试方向存在多个激励源时，传统波束形成获取的声源云图结果很难与其真正的激励源相关联。为了克服上述传统波束形成的缺点，以下第2部分和第3部分分别提出基于特征分解和相干输出谱的波束形成算法，两种算法均可对声源云图结果进行分离，提高声源识别的总体动态范围。第4部分通过实验验证这两种算法的适用场景和算法的有效性。

2 基于特征值分解的波束形成

阵列麦克风信号组成的互谱矩阵为Hermite 方阵，可以对其进行特征值分解。对阵列麦克风信号互谱矩阵进行特征值分解，公式如下：

其中：G为M阶阵列麦克风信号的平均互谱矩阵，Q为M阶方阵，每一列为矩阵G的特征向量，Λ为M阶特征值对角矩阵，对角线元素为由大到小依次排列的特征值，上标“-1”表示矩阵求逆运算。

矩阵的特征向量之间是相互正交的，可以利用该特性对原始的阵列麦克风信号的互谱矩阵进行正交分解。如果各个声源产生的信号互不相干，利用互谱矩阵对应的每个正交分量进行波束形成计算可以分别获取各个声源产生的云图位置。互谱矩阵第i个分量的表达式如下所示：

其中：ui为Q的第i列组成的向量为Q的逆矩阵的第i列组成的向量的转置，λi为矩阵G的第i个特征值。

另外，较小的特征值通常表示了系统的噪声干扰，将前若干个特征值对应的互谱矩阵分量进行叠加用于波束形成的计算，剔除较小的特征值分量，有利提高波束形成计算结果的动态范围。公式如下所示：

其中：N≤M，M为阵列麦克风的数量。

分别采用公式(5)和公式(6)对应的互谱矩阵分量Gi和Gsub进行波束形成的计算，能够对不相关声源产生的云图进行分离。由于较小的特征值通常表示外界噪声干扰和信号中能量较小的成分，对其剔除后采用较大的特征值分量叠加后的互谱矩阵进行波束形成的计算，能够提高波束形成声源云图结果的动态范围。

基于原始互谱矩阵的某个特征值分量的波束形成公式如下所示：

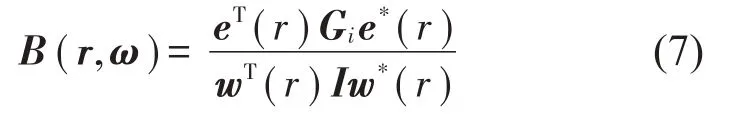
对应地剔除互谱矩阵Gi对角线自功率谱元素的波束形成公式如下所示：

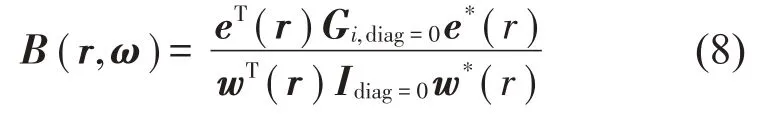
基于原始互谱矩阵的前若干个特征值分量叠加的波束形成公式如下所示：

对应地剔除互谱矩阵Gsub对角线自功率谱元素的波束形成公式如下所示：

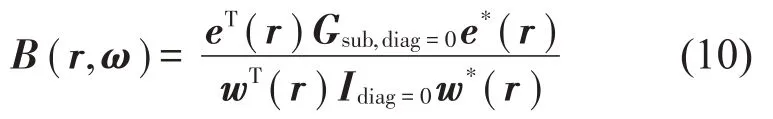
基于特征值分解的波束形成算法，能够对不相干声源产生的云图结果进行分离，有助于将声源云图结果与其激励源相关联。第4部分通过实验验证了基于特征值分解的波束形成算法的有效性。

3 基于相干输出谱的波束形成

相干输出谱常用于分析信号中与某一参考信号相干的成分，其表达式如下所示：

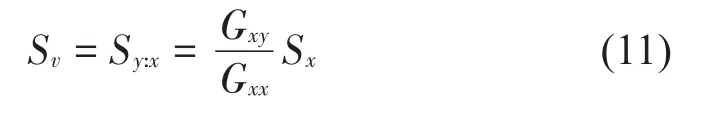
其中：Sv表示信号y中相对于参考信号x的相干输出谱，G表示信号间的平均互谱。

与相干输出谱对应的噪声输出谱或非相干输出谱表达式如下所示：

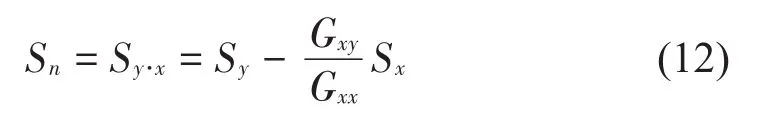
其中：Sn表示信号y中相对于参考信号x的非相干输出谱。

进行声源定位测试的同时，可以同步测量激励源的参考信号，如激励源的振动或近场声压信号，计算阵列麦克风信号相对于激励源参考信号的相干输出谱或非相干输出谱。分别采用相干输出谱或非相干输出谱代替原始的麦克风频谱进行基于（非）相干输出谱的波束形成的计算，公式如下所示：

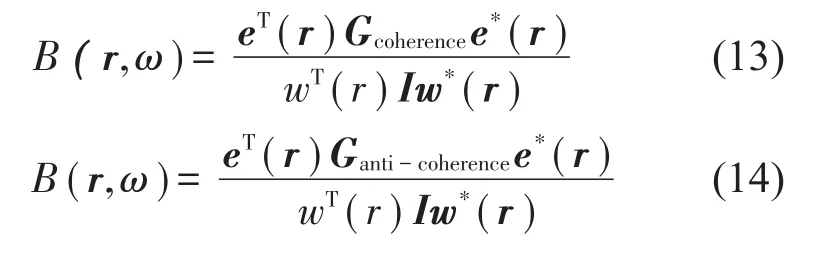
其中：Gcoherence表示采用阵列麦克风信号的相干输出谱计算的平均互谱矩阵，Ganti-coherence表示采用阵列麦克风信号的非相干输出谱计算的平均互谱矩阵，其余符号与公式(1)代表相同的物理意义。

对应地剔除互谱矩阵Gcoherence和Ganti-coherence对角线自功率谱元素的形式如下：

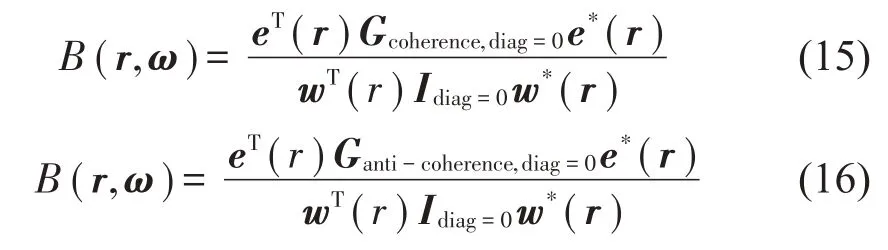
采用（非）相干输出谱分析对噪声源进行定位，能够通过参考信号对声源云图结果进行分离，有助于将声源云图结果与激励源相关联，进而研究声源云图产生的原因。文章的第4 部分，通过实验验证基于相干输出谱的波束形成算法的有效性。

4 实验验证

为了验证基于特征值分解和（非）相干输出谱的波束形成算法的有效性和适用场景，实验设置如下：

如图1 所示，采用36 通道的圆形二维平面麦克风阵列对3个人工声源进行定位。由于基于（非）相干输出谱的波束形成算法需要同步测量声源的参考信号，分别在3个声源背面粘贴了3个振动加速度传感器Acc1，Acc2和Acc3采集3个声源对应的振动参考信号。声源1 与声源2 的驱动电信号为部分相干的信号，声源3的驱动电信号与声源1和声源2的驱动电信号不相干，驱动电信号均为宽频白噪声信号。

图1 实验设置

各个声源的振动参考信号相互之间的相干函数如图2 所示。由图2(a)所示，由于声源1 与声源2 的驱动电信号为部分相干的信号，因此Acc1 与Acc2的相干系数较大；由图2(b)和图2(c)所示，声源3 的驱动电信号与声源1和声源2的驱动电信号不相干，因此Acc3与Acc1和Acc2的相干系数较小。由于声源3与声源2在安装结构上距离较近，两者由于安装结构较近发生部分耦合，因此Acc3 与Acc2 的相干系数在某些频率处高于Acc3与Acc1的相干系数。

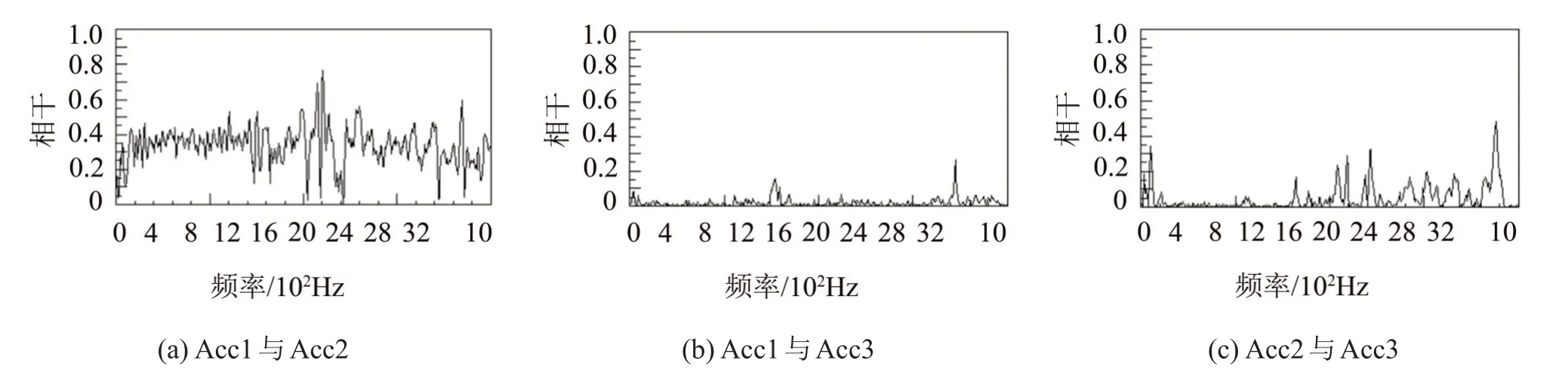
图2 相干函数

首先，采用基于互谱矩阵的波束形成算法对上述3 个声源进行定位，分析频率范围为2 500 Hz～4 500 Hz，显示动态范围为6 dB，声压云图幅值归一化到距离识别表面1 m远处。由图3所示，采用基于互谱矩阵波束形成算法能够对3个声源进行准确定位。以基于互谱矩阵波束形成算法结果作为基准，分别与基于特征值分解和（非）相干输出谱的波束形成算法进行对比分析。

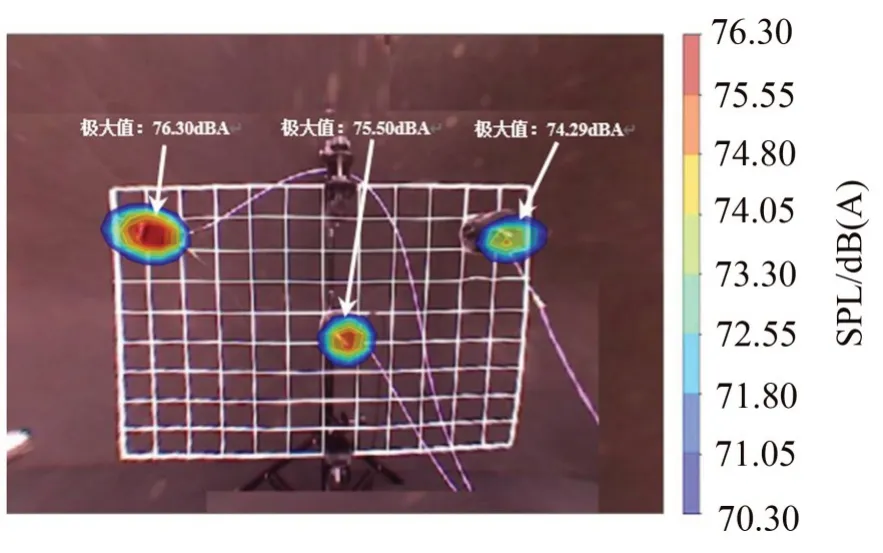
图3 互谱矩阵波束形成结果

为了验证基于特征值分解的波束形成算法的有效性与适用性，对相同的试验数据，采用基于特征值分解的波束形成算法进行计算，结果如图4 至图6所示。

由图4至图6结果可知，基于特征值分解的波束形成算法，采用各个特征值对应的相互正交的互谱矩阵分量进行波束形成计算能够对声源云图进行有效的分离，有助于将声源云图与其激励源相关联。由图2(b)和图2(c)中参考信号的相干函数可知，声源3的参考信号与声源1和声源2的参考信号不相干，图5结果表明采用第二大特征值对应的互谱矩阵分量进行波束形成计算能够将声源3产生的云图进行准确地分离，说明声源3 对互谱矩阵的贡献量可以独立地用第二大特征值对应的互谱矩阵分量表示；由图2(a)中参考信号的相干函数可知，声源1和声源2的参考信号部分相干，图4和6中最大的特征值和第三大的特征值对应的互谱矩阵分量并不能独立表示声源1 和声源2 的贡献，因此，并没有将声源1 和声源2产生的声源云图进行准确有效的分离。

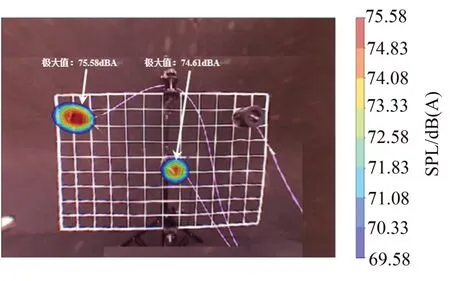
图4 基于特征值分解的波束形成：最大特征值分量

图5 基于特征值分解的波束形成：第二大特征值分量

图6 基于特征值分解的波束形成：第三大特征值分量

为了验证基于（非）相干输出谱的波束形成算法的有效性与适用性，对相同的试验数据，进一步采用基于非相干输出谱波束形成算法进行计算，结果如图7和8所示。

图7 基于非相干输出谱的波束形成：Acc1作为参考信号

图8 基于非相干输出谱的波束形成：Acc2作为参考信号

由图7和8可知，基于非相干输出谱的波束形成算法，能够剔除与参考信号线性相关的声源云图，对声源云图进行有效分离，有助于将声源云图与其激励源相关联。声源3与声源1和声源2不相关，基于非相干输出谱的波束形成算法分别对声源1和声源2产生的声源云图进行剔除后，声源3产生的声源云图的声压幅值几乎没有衰减。结果说明基于非相干输出谱的波束形成算法能够对不相关声源产生的云图进行准确有效的分离。声源1 与声源2 产生的参考信号部分相干，采用基于非相干输出谱的波束形成算法分别对声源1或声源2产生的云图剔除时，声源2 或声源1 对应的云图的幅值也相应地衰减了。结果说明基于非相干输出谱的波束形成算法对某个声源产生的云图进行剔除时，与之部分相关的声源产生的云图幅值也会随之衰减。

5 结语

提出了基于特征值分解和（非）相干输出谱的波束形成算法，分别与传统的互谱矩阵波束形成算法进行了实验对比，主要结论如下：

(1)本文研究了基于特征值分解的波束形成技术及其应用。实验结果表明，基于特征值分解的波束形成算法可以对不相关声源产生的云图进行有效分离，有助于将声源云图与其激励源相关联。对于部分相关的声源，不能用某个特征值对应的分量独立表示，因此对部分相关的声源云图分离效果不佳。

(2)本文研究了基于（非）相干输出谱的波束形成技术及其应用。实验结果表明，采用同步测量的激励源参考信号，基于非相干输出谱的波束形成算法可以剔除与参考信号相关的声源云图，能够将声源云图与其激励源相对应。

(3)基于（非）相干输出谱的波束形成技术，能够有效、准确地分离不相关声源产生的云图；对于部分相关的声源，基于非相干输出谱的波束形成技术对声源云图进行分离时，与之部分相关的声源所产生的云图声压幅值也会衰减。