多机器人协作的灵活性分析与仿真
2022-07-04陶平邹成文王天瑞
陶平 邹成文 王天瑞
(①武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉 430081;②武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉 430081)
现代工业中,多机器人协作系统具有更高的自由度、较大负载能力和灵活操作方式,可以完成更加复杂的任务。多机器人协作系统的运动灵活性反映了协作系统整体协调操作的运动能力,其机械臂的协调运动灵活性直接影响协作系统的整体运动性能[1]。
目前国内外学者对机械臂的灵活性进行了大量的研究,李宪华[2]采用基于雅克比SVD可操作度的指标,评估了单机械臂的操作能力。符晓[3]利用雅克比矩阵条件数,求出6R机器人在工作空间内各处的奇异度,并将其可视化。孙青[4]针对双臂6R服务机器人,进行了灵活性分析,研究了双臂在协调操作过程中的奇异性和灵活性。潘建龙[5]阐述了多机器人协作时可操作度的定义,对多机器人焊接系统进行了最优轨迹的规划。Paul R P等[6]针对非冗余度机器人的运动特点,采用雅可比矩阵的行列式分析出腕关节的位姿。Yang D C H等[7]对机器人条件数进行了定义,Angeles J等[8]将条件数作为机器人灵活性的评价指标,并将这一指标用来分析机器人动力学性能。当前,多机器人协作大多集中在双机器人协作的研究上,国内对多机器人协调操作的灵活性研究较少。
基于以上分析,本文针对多机器人系统在工业应用中的运动特征,选用可操作度为机器人灵活性评价指标,并根据该指标的定义分析得到多机器人系统整体可操作度的数学评价模型。同时提出了一种求取机器人在单位节点多姿态下的加权可操作度数值的算法,采用该算法计算多机器人系统在协作空间内的整体可操作度,并将多机器人系统的灵活性可视化表达出来,由此得到灵活性较高的区域,为以后的多机器人协调运动的轨迹规划打下基础。
1 多机器人系统模型
1.1 运动学分析
以3个六自由度的IRB1410机器人组成的多机器人焊接系统为研究对象。在该系统中,其中2个机器人1和2起搬运作用,将工件夹持到工作空间中,而焊接机器人3则对工件进行焊接操作,多机器人协作焊接系统图如图1所示。
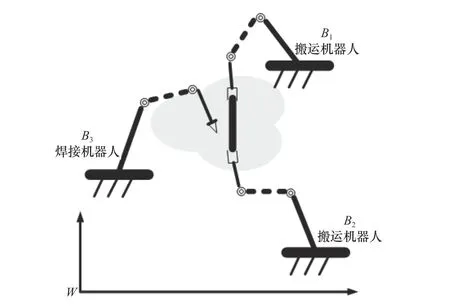
图1 多机器人协作系统示意图
多机器人协作系统进行作业时,各机器人的基座位置固定,其相对位置始终不变,即{B1}、{B2}、{B3}固定,机器人基坐标系到世界坐标系{W}的齐次变换矩阵是一个定值。作业中,2个搬运机器人1和2夹持工件,两搬运机器人之间的运动关系存在紧协调运动关系;焊接机器人3进行焊接时,它与搬运机器人之间的运动关系是松协调运动关系,其协调关系如下:
(1)紧协调:两搬运机器人搬运工件时存在,在该过程中,两机器人之间无相对运动,相对位姿保持不变,速度保持同步,满足关系

式中:x1、x2分别表示两搬运机器人的末端位姿向量;U表示两个搬运机器人之间的齐次变换矩阵。
(2)松协调:存在于焊接机器人与搬运机器人之间,满足关系

式中:x3表示焊接机器人的末端位姿向量;α(t)表示搬运机器人与焊接机器人还存在相对运动,为时变向量。
1.2 协作空间分析
对其中的焊接机器人建立D-H坐标系,如图2所示。由此得到D-H坐标参数,如表1所示。表1中,θi为第i个关节的角度值,di为相邻关键之间的杆件长度,ai为相邻关节之间的杆件偏移量,αi为相邻坐标系之间的扭转角。同理,2个搬运机器人的D-H坐标建立方法同上,在此不再赘述。

图2 焊接机械臂D-H坐标系

表1 焊接机器人连杆D-H参数
利用Robotics工具箱,搭建多机器人协作系统模型的仿真平台,如图3所示。图3中,两搬运机械臂和焊接机械臂的基座坐标分别为(−1,−1,0)、(1,−1,0)、(0,1,0)。

图3 多机器人协作系统模型
图2中,d1=475mm,d4=720mm,d6=85mm,a1=150mm,a2=600mm,a3=120mm。
相邻两连杆之间的齐次坐标变换矩阵为
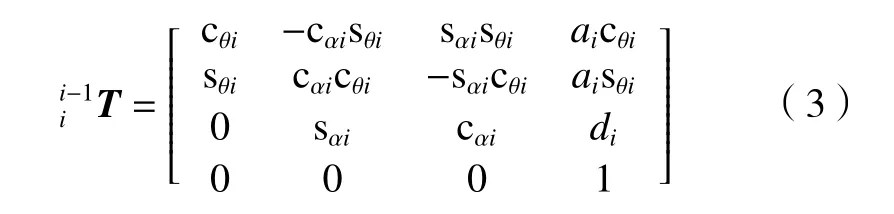
式中:cθi表示cosθi;cαi表示cosαi;sθi表示sinθi;sαi表示sinαi。
结合机械臂的正运动学方程、表1的参数和上面的公式,利用蒙特卡罗法,可以得到焊接机器人的工作空间,同理也可得到2个搬运机器人各自的工作空间,由3个机器人工作空间的交集得到协作空间的范围,如图4所示。
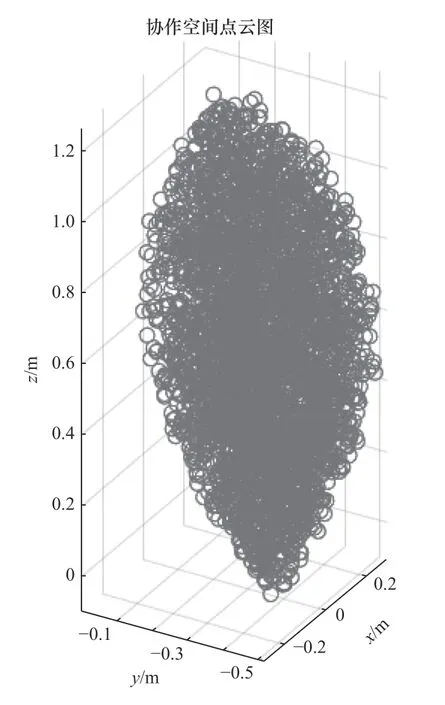
图4 协作空间点云图
2 多机器人灵活性评价
机器人运动灵活性评价指标,主要有条件数、可操作度及各向同性指标等,其中可操作度、条件数和最小奇异值是比较经典的3个灵活性评价指标[2]。可操作度作为衡量机器人灵活性的重要指标之一,被广泛运用机器人尺寸优化、运动性能优化等各个方面,用来改善机器人的传输性能,从而提高工作效率[9−10]。
本文选取可操作度作为机器人执行任务时的灵活性评价指标。
2.1 机器人可操作度定义
可操作度定义为机器人对任意改变末端执行器位置和方向的能力,是一个非常重要的评价指标。可操作度越大,机器人从关节空间到工作空间运动的转换能力就越强,灵活程度越好。
雅可比矩阵表示了机器人运动时自关节空间到操作空间的运动速度的传递关系,可得

式中:x为操作空间的坐标,x∈Rm,Rank(J(q))≤m,x˙为操作空间的速度;q为关节空间坐标,q∈Rn;q˙为关节空间的速度;J(q)为雅克比矩阵,J(q)∈Rm×n。
机器人可操作度的定义为

可操作度的大小表现了机器人在操作空间中各个方向传递速度的能力,根据可操作度的定义可知,当可操作度ω=0时,J(q)=0,机器人瞬时位于奇异位形。
2.2 多机器人可操作度
在多机器人协作工作时,协作系统灵活性反映了其整体的传力和传速性能。在协作系统中,存在紧协调和松协调两种不同的协作关系,在计算可操作度时,先分别计算各自的可操作度,再计算协作系统的可操作度。
两搬运机器人满足紧协调关系时,两机器人之间的运动可描述为

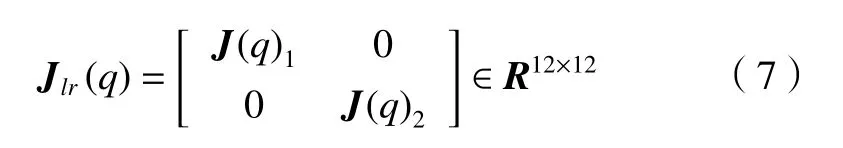
式中:J(q)1、J(q)2分别为两搬运机器人的雅克比矩阵。
由此,得到两搬运机器人的可操作度Mt的定义为
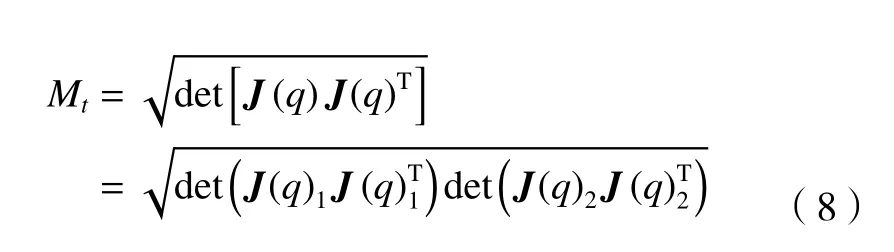
焊接机器人与搬运机器人之间的运动关系为松协调,需要单独计算它的可操作度。
综合上述考虑,得到多机器人协作时的可操作度MMR为
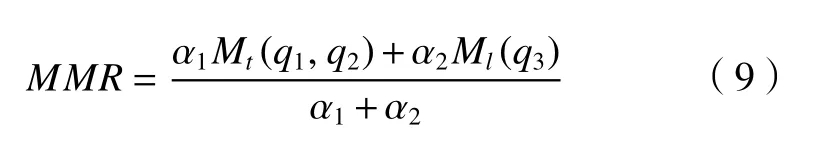
式中:α1为两搬运机器人的灵活性系数,α2为焊接机器人的灵活性系数,根据系统中所有机器人可操作度椭球的体积交集大小占各个椭球体积的比值,可确定出α1和α2;Mt为两搬运机器人的可操作度;Ml为焊接机器人可操作度。
3 多机器人协作空间灵活性分析
机器人的工作空间分为可达空间和灵巧空间。其中,可达空间即为机器人可以到达的所有点构成的空间;而灵巧空间为机器人以任意姿态能到达的点所构成的空间。机器人的奇异点指在工作空间中,由于机器人位于一些特殊位姿(如轴线相交或者平行等)关系时,机器人丧失1个或者多个自由度,导致机器人在某个方向上传递速度为0,即机器人在此时处于卡死状态。根据前文的分析,当机器人处于奇异位形时,可操作度ω=0,可以得到此时机器人的雅可比矩阵J(q)=0,由矩阵的定义可知,Rank(J(q)) 本文的研究中,将每个转角分为11份,步长为0.2π,可以得到对应的位姿矩阵,根据算法可以计算出对应点的可操作度。本文首先分析了焊接机器人在工作空间内的可操作度,考虑到在z=0.69m的平面上,其工作空间面积最大,给出该平面内焊接机器人的可操作度分布情况,如图5所示。图5中,对该平面的x轴和y轴等间距划分为21等份,所取得的样本工作点共441个。利用网格节点的颜色来表征可操作度ωi的值,由此得到焊接机械臂在工作空间内其可操作度分布情况,其中右侧的竖条表征了不同颜色所代表的可操作度值。 图5 z=0.69m 平面下焊接机器人可操作度分布 同样方法可以得出多机器人在协作空间内的可操作度分布情况,图6给出了z=0.69m的平面上3个机器人协作时的可操作度MMR的分布情况,其中右侧的竖条表征了不同颜色所代表的可操作度值,由图6中可以看出,在黑色区域可操作度趋近于0,此时由于某个机器人接近或处于奇异位形,导致协作系统灵活性最差,而灰白色区域可操作度较大,协作系统灵活性较好。 图6 z=0.69m 平面下多机器人可操作度分布 对多机器人系统的协作空间的整体可操作度进行计算并归一化处理,得到协作空间内系统的灵活性表达剖视图,在MATLAB中可视化表达出来,如图7所示。图7中,用多种颜色分别表示多机器人协作时的灵活性程度,系统的灵活性范围在[0,0.2)的区域用蓝色表示;系统的灵活性范围在[0.2,0.4)的区域用青色表示;系统的灵活性范围在[0.4,0.6)的区域用绿色表示;系统的灵活性范围在[0.6,0.8)的区域用黄色表示;系统的灵活性范围在[0.8,1]的区域用红色表示。从图中可以得到多机器人协作的系统灵活性的分布规律。 图7 协作空间灵活性剖视图 由多机器人协作系统在协作空间中的灵活性分布情况可知,工作范围在(x、y、z单位为m)x∈[−0.1,0.1],y∈[0.15,0.35],z∈[0.55,0.75]区域的多机器人协作灵活性较高,因此,在进行运动规划时,应当尽量保证工作区域在x∈[−0.1,0.1],y∈[0.15,0.35],z∈[0.55,0.75]的范围内。而靠近协作空间边界的部分无法实现多机器人协作,机器人运动灵活性最差。分析可知,点C0(0,0.25,0.6)位于灵活性较高区域的中心点,因此,将该点作为最优初始焊接位置点,搬运机器人搬运工件到协作空间内,并将工件坐标系原点与该点重合,然后配合焊接机器人进行焊接任务,如此可以保证工件上的焊缝点均处于灵活性较高的区域,从而确保多机器人协作系统在焊接过程中的运动灵活性。 本文以多机器人协作系统为研究对象,通过蒙特卡罗法得到多机器人协作空间,采用可操作度作为灵活性指标,建立了一种用于多机器人协作系统的灵活性评价模型,并使用MATLAB进行仿真将系统的灵活性可视化,从而选取机器人合适的操作空间。在本文选取的灵活性高的空间工作的基础下,为后续多机器人的轨迹规划做好铺垫。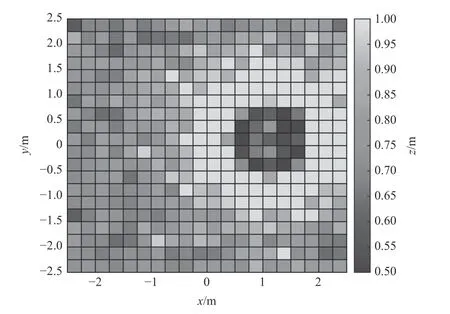


4 结语
