基于混合摩擦模型的机器人关节摩擦建模与仿真*

董雅文 王鸿飞 张宝锋 宋栓军

（①西安工程大学机电工程学院，陕西 西安 710048；②西安理工大学机械与精密仪器工程学院，陕西 西安 710048）

摩擦现象存在于生活中的方方面面，在不同情况下，摩擦发挥的作用不同。在某些情况下，摩擦是有利的，如在路上高速行驶的汽车，正是因为摩擦力车辆才能向前走，在紧急情况下才能刹车。但在多数情况下，没有摩擦，效果更好，如传动轴带动轴承高速转动时，滚珠和内外圈的摩擦，使整个系统产生稳态误差，降低了整个系统的运动精度，如果没有摩擦的影响，传动精度会更高并且系统寿命会更长。当今，工业机器人技术发展如火如荼，而摩擦是影响机器人关节运动精度的主要原因，尤其在一些对机器人工作精度有一定要求的场合更是如此。对机器人关节准确建模可以提高运动精度和平稳性，并且可以延长连续工作时间和寿命，因此，机器人关节摩擦引起了越来越多专家学者的关注。

为了研究关节摩擦对运动精度的影响，并对机器人进行有效控制，学者们对机器人关节摩擦问题进行了相关研究。Stribeck在1902年提出了Stribeck摩擦模型，LI C B等在1982提出了一个指数模型描述Stribeck现象[1]，该模型描述了低速时的摩擦情况，但缺乏对摩擦动态特性的描述。Dahl Philip R等在1976年提出Dahl摩擦模型[2]，Dahl是最简单的动态摩擦模型，该模型避免了在静态状况下两阶段间切换不连续的问题，但没有描述低速时的摩擦现象。Armstrong-Helouvry B等在1994年提出七参数模型[3]，该模型描述了摩擦力在不同阶段的摩擦，但该模型是一个离散的动态摩擦模型，而且涉及到两个阶段之间转换不合理的问题，故在具体应用中受到了限制。Canudas-de-Wit C等在1995年提出了LuGre模型[4]，该模型可以描述摩擦力在不同阶段的切换，更能符合实际摩擦现象，但由于其参数很难辨识，故在实际应用中受到限制。王毅等建立了一个基于Simulink的仿真摩擦模型，分析摩擦对伺服系统的影响，得到了与理论分析一致的结果[5]。王霞等建立了动态仿真摩擦模型，分析了摩擦力对高精度伺服控制系统的影响[6]。刘丽兰等系统地介绍了常见的6种静态摩擦模型和7种动态摩擦模型，并对每种模型进行了详细的说明[7]。许宏等对Stribeck摩擦模型进行了模糊PID控制，对无刷直流电机控制系统进行了仿真，解决了控制系统在实际运行中存在摩擦负载的问题[8]。徐智浩等建立了一种自适应模糊神经网络控制器，并建立了动态LuGre摩擦的机械臂模型，解决了由于摩擦非线性导致机械臂控制精度低的问题[9]。朱松青等建立了一个混合摩擦模型来描述关节摩擦问题，以提高机器人动力学建模精度和控制精度[10]。

考虑到单一的摩擦模型不足以解决复杂的关节摩擦问题，从而会影响动力学建模精度，导致控制精度降低。为了更加准确地描述机器人关节内部的摩擦特性，本文采用混合摩擦模型对机械臂关节进行建模，使用MATLAB/Simulink模块对该摩擦模型进行仿真分析。

1 机器人关节混合摩擦模型建立

机器人关节主要由伺服电机、减速器、力矩传感器和编码器组成，其模型如图1所示。机器人关节作为连接两机械臂和力矩传输的重要部件，相对于其他机械传动结构，机器人关节的输出端转速较低，在一些特殊作业中换向频繁，并且机器人关节内部结构复杂，摩擦副较多。摩擦对机器人的运动精度、稳定性和可靠性有重要的影响，高速时关节内部的摩擦不太明显，但在低速高精度的情况下，摩擦的非线性影响较为明显。可以通过改善机械结构或者对伺服系统进行控制来降低摩擦对系统的影响，但第一种方法由于技术工艺和材料的限制，不容易实现，第二种方法对控制器进行控制，相对第一种方法更经济有效，但第二种方法需要对关节摩擦进行建模，因此，包含摩擦的关节动力学建模尤为重要。

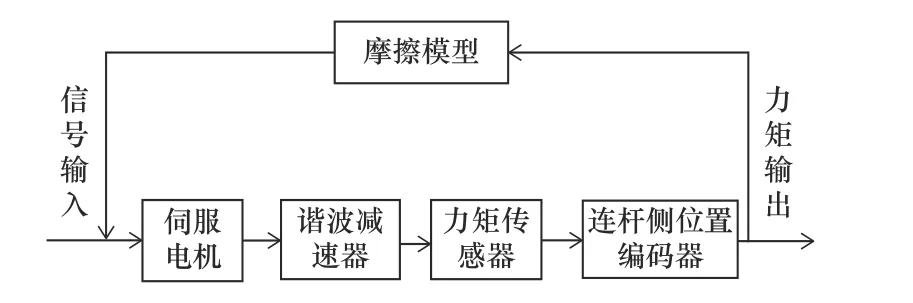
图1 机器人关节模型

对于机器人关节伺服系统，位置状态方程表达如下。

式中：Ff(t)为摩擦项；Ku为功率放大器放大系数；R为电枢电阻；Km为电机力矩系数；Ce为电压反馈系数；J为电机的转动惯量；θ˙(t)为转速；u(t)为控制输入。

1.1 机器人关节混合摩擦机理

针对机器人关节伺服系统动力学方程的摩擦项为Ff(t)，本文在朱松青等[10]研究成果的基础上，提出一种基于静摩擦、库伦摩擦和Lorentzian模型的机器人关节混合摩擦模型以准确描述关节内的摩擦特性，其中Lorentzian摩擦模型是对Stribeck摩擦模型的改进，包含了粘性摩擦，该模型可以较好地描述机器人关节低速时的摩擦特性，并且可以以90%的准确度来描述关节部位的实际摩擦现象[7]，其混合摩擦模型曲线如图2所示。

图2 混合摩擦模型曲线

1.2 机器人关节混合摩擦模型

当机器人关节间有相对转动趋势而未转动时，此时主要为静摩擦，函数关系式表示如下[7]。

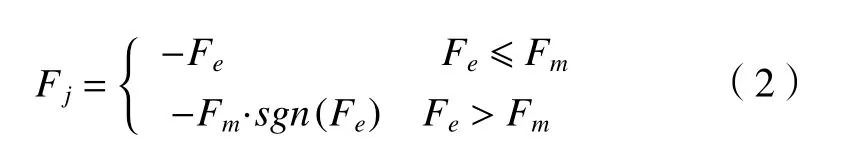
式中：Fj为关节静摩擦力矩；Fe为外力矩；Fm为最大静摩擦力矩；sign()为符号函数(Fe>0，sign(Fe)=1；Fe=0，sign(Fe)=0；Fe<0，sign(Fe)=−1)。

当机器人关节低速转动时，关节内的摩擦主要表现为滑动边界摩擦，函数关系式表示如下[7]。

式中：Fc为库伦摩擦力矩；µ为摩擦系数；Fn为法向力矩。

当机器人关节由静摩擦转换到滑动摩擦时，摩擦并非是非连续的。摩擦力克服静摩擦力后不断下降，在低速时克服摩擦力使其随着速度的增加而减小，此时摩擦为两接触面间相对速度的连续函数，这一现象称为负斜率摩擦现象。为了充分表达这一转换过程以及机械臂运行时的黏滞摩擦，可应用Lorentzian摩擦模型[7]。

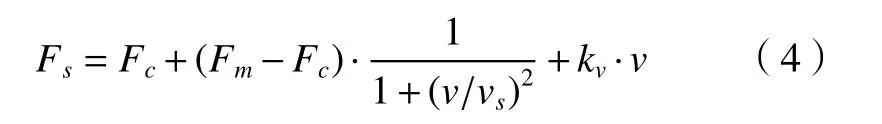
式中：Fs为Stribeck摩擦力矩；kv为黏性摩擦系数；vs为Stribeck速度；v是相对滑动速度。

由式（2）～（4），可得机器人关节的混合摩擦模型如式（5）所示。

从机器人关节摩擦模型关系式可以看出，混合摩擦模型为外力矩Fe、相对速度v和法向力Fn的函数。混合摩擦模型的摩擦曲线如图2所示，该曲线既表述了摩擦随速度的稳态运动特性，又体现了摩擦的静态特性，且通过Stribeck效应更真实地体现了关节在低速段的摩擦特性，提高了关节摩擦建模精度。将式（5）代入式（1）中，可得到含摩擦的关节动力学方程。

2 模型求解和仿真

为了验证本文建立的基于机器人关节混合摩擦模型的可靠性及准确性，使用MATLAB/Simulink对该混合摩擦模型进行动力学建模仿真[11]，其仿真框图如图3所示。

图3 MATLAB/Simulink仿真框图

设该仿真系统参数：R=7.77Ω，Km=6N·m/A，Ce=1.2V/(rad/s)，J=0.6kg·m2，Ku=11；摩擦模型参数：取Fc=15N·m，Fm=20N·m，a1=1.0，kv=2.0Nms/rad，Vs=0.05。

低速正弦跟踪指令信号为y(t)=0.1sin(2πt)，仿真运行时间为3 s，采用PD控制，取Kp=200，Kd=40，机器人关节角速度和摩擦力的仿真结果如图4所示。

图4 混合摩擦模型仿真结果

由图4可以看出，在输出关节角速度很小时，摩擦力为最大静摩擦力，此时摩擦力的大小主要与外力Fe大小有关。当角速度在0～0.05 rad/s时，摩擦力由静摩擦向动摩擦转换，在两接触面刚产生相对运动时，此时为边界润滑状态，由于速度很低，故在两接触面间润滑剂填充不完全，只能依靠边界部分润滑以减小磨损。此时为边界摩擦状态，并且在低速下随着速度的增大而减小，为速度的连续函数，这种现象称为Stribeck现象。随着速度的增加，部分润滑剂填充在两接触面间，此时为部分流体润滑阶段，由于润滑剂的黏性，这个阶段的摩擦力主要为黏性摩擦。由于该摩擦模型建模过程涉及到符号函数，根据式（5）可得速度变化时摩擦力的变化刚好相反，并且该仿真结果与图2的结果基本一致，达到了预期的结果。

图5为关节输出角位移跟踪仿真结果，从误差曲线可以看出误差随时间周期性变化，且最大误差为0.007 1 rad。虽然产生抖动，但无平顶现象，位置偏移小。

图5 关节输出角位移仿真结果

图6为关节输出角速度跟踪仿真结果，从误差曲线可以看出，在关节由由静态转变为动态的过程中，速度会有突变，随着速度的增加，误差变化趋于平稳，精度较高。

图6 关节输出角速度仿真结果

图7和图8为3种常用的工业机器人摩擦模型对比分析，各个模型伺服参数的选取与混合摩擦模型相同，选取仿真稳定状态时的结果进行对比分析。图7中混合摩擦模型输出角位移误差范围在−0.007 1～0.007 1 rad，LuGre摩擦模型输出角位移误差范围在−0.013 1～0.013 1 rad，Stribeck摩擦模型输出角位移误差范围在−0.012 9～0 rad。从数据结果可以看出，在参数设置相同的情况下，混合摩擦模型的精度要比其他两种常用模型的精度高一个数量级。

图7 三种摩擦模型位移误差比较

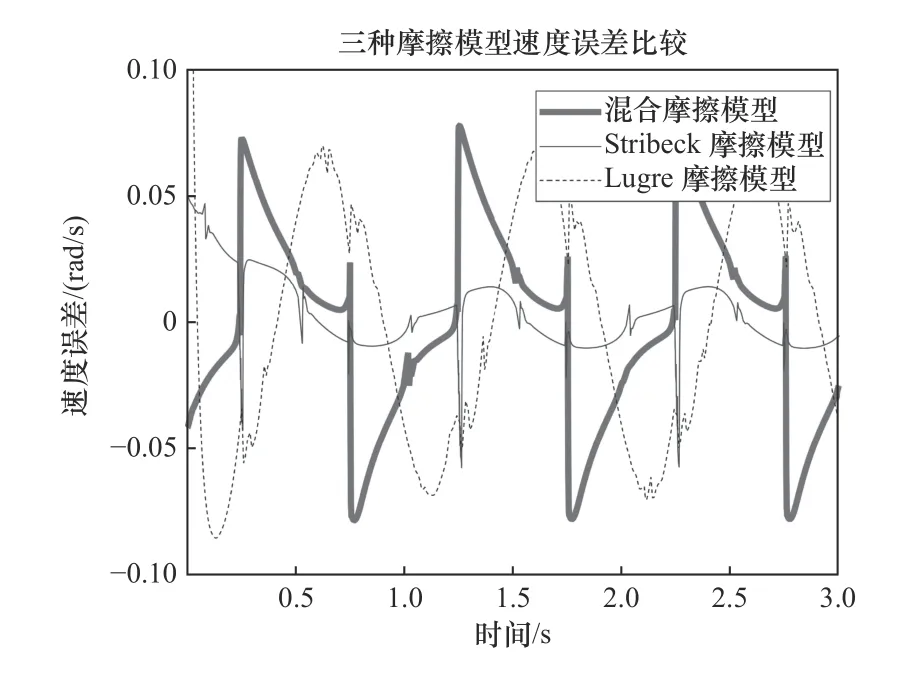
图8 三种摩擦模型速度误差比较

图8中混合摩擦模型角速度误差范围在−0.073 1～0.073 1 rad/s，LuGre摩擦模型角速度误差范围在−0.070 2～0.071 1 rad/s，Stribeck摩擦模型角速度误差范围在−0.070 2～0.071 0 rad/s。仿真结果表明，混合摩擦模型在加速减速切换时会有突变，其余时刻较为平稳，故不适用于需要经常切换速度的场合。

3 结语

本文提出一种基于静摩擦、库伦摩擦和Lorentzian摩擦混合表达的混合摩擦模型，建立了包含摩擦的关节动力学模型，使用MATLAB/Simulink进行仿真，并对仿真结果进行对比分析。结果表明，仿真系统参数及控制器参数不变的情况下，取仿真稳定运行的结果，机器人关节输出角位移误差为−0.007 1～0.007 1 rad，关节输出角速度误差相对比较稳定。由于混合摩擦模型能够较为准确地表达机器人关节内部实际的摩擦问题，并且，该混合摩擦模型中Lorentzian摩擦模型是对Stribeck摩擦模型的优化，因此，该模型精度比其他模型更高，仿真结果还表明该模型适用于不经常切换速度的场合。