热梯度环境下梁高频振动的能量流模型
2022-07-04刘知辉牛军川贾睿昊
刘知辉,牛军川,2,*,贾睿昊
1. 山东大学 机械工程学院,济南 250061
2. 山东大学高效洁净机械制造教育部重点实验室,济南 250061
航空领域中高速飞行器常工作于复杂、严苛的极端热环境中,并承受来自动力源、气动湍流、噪声等多种形式的外界激励。在这些外界振源的激励下,结构产生的振动会影响系统的平稳运行,同时也对精密仪器仪表、电子设备等造成危害。此外,结构振动引起的声辐射还会影响设备中操作人员的舒适性。因此在系统设计阶段针对结构动力学特性进行预测分析,从而实现结构声振特性的优化设计具有重要的理论与工程价值。
在高速飞行器等航空航天设备的声振特性分析中,往往需考虑极端热环境对结构动态特性的影响。极端热环境一方面可显著改变结构的材料属性,从而影响结构的刚度等关键动力学参数;另一方面,处于极端热环境中的结构热膨胀被约束时,结构内还将产生热应力。杨雄伟等以X43A超高速飞行器为例,研究了热效应对飞行器结构各部分材料的物性及声振耦合特性的影响规律。胡君逸等对热环境下正交各向异性板的动力学特性进行了理论和试验研究,结果表明热应力和热变形会显著影响结构的动力学特性。
在航空航天领域,梁单元被广泛用于高速飞行器中机翼、壁板、航空叶片等结构的动力学建模分析。在这些应用中,结构常处于极端热环境。Gu等建立了Timoshenko梁在热环境中的动力学理论分析模型。Avsec和Oblak对自由和简支边界条件下的梁在热环境下的振动进行了研究。Chen等在考虑参数不确定性的情况下,使用基于间接Trefftz方法的波函数法(Wave Based Method,WBM)分析了均匀热环境下梁的中低频动力学响应。在高速飞行器运行时,气动湍流、外界噪声等激励往往频率较高,且飞行器中结构一般较为轻薄,易表现为短波高频振动特性。上述以位移为基本变量的确定性分析方法由于计算量及参数敏感性等原因难以适用于高频动力学分析。
高频分析时一般采用以声振能量为基本变量的统计性分析方法。为考虑高速飞行器在极端温度场中的高频响应,陈强等建立了热环境下的统计能量分析(Statistical Energy Analysis,SEA)模型,并就L型折板的长宽比对SEA模型关键参数的影响规律进行了研究。胡婉璐等研究了轴向力对SEA模型中耦合梁耦合损耗因子的影响规律。
近年来,以能量密度为基本变量的能量流方法在结构高频分析领域得到了广泛应用。相比于SEA,该方法可得到振动能量的空间分布信息,从而可提供更为详细的高频动力学预测结果。代文强等使用能量有限元方法对高速列车车内的噪声进行了理论预测。王怀志等使用能量有限元法对卫星的整流罩和仪器舱的中频声振响应进行了分析。陈兆林等使用能量有限元法和虚拟模态综合法(EFEM-VMSS)分析了航天器分离等冲击状态下的瞬态响应。滕晓艳等通过采用大阻尼假设建立了分析自由阻尼梁高频响应的解析模型。为实现对热环境中梁的高频分析,Zhang等考虑轴向热应力和材料属性的变化,建立了均匀热环境下梁的能量流模型。Wang等基于板的平面波叠加假设研究了板在热环境中具有各向不同薄膜力时的能量流模型。
飞行器在超音速飞行时,气动加热等效应往往在壁板等结构内外表面产生较大的温差,壁板等结构的内外表面之间也因热传导而存在较大的温度梯度。此时结构内的材料参数以及热应力等将具有明显的空间变化。而在上述热环境高频分析模型中,结构被认为处于均匀的温度场中,此时建立的高频分析模型也因此无法准确反映温度场的空间变化对结构高频振动的影响。
二维壁板是飞行器结构振动问题研究中广泛采用的模型。当考虑此类结构的柱形弯曲(Cylindrical Bending)而忽略展向弯曲(Spanwise Bending)时,可采用梁单元进行建模分析。为分析飞行器中此类结构因气动加热等效应而处于非均匀热环境时的高频动力学特性,建立热梯度环境下梁的能量流解析模型。通过求解稳态热传导方程得到梁内温度的空间分布,考虑温度对材料属性的改变及热应力,引入物理中性层以消除轴向与横向弯曲变形之间的耦合。使用哈密顿原理导出梁在非均匀热梯度环境下的运动控制方程,得到波动的频散关系。基于微元体的功率平衡关系得到梁的能量流解析模型,并通过与基准解的对比验证其正确性。
1 热梯度环境下梁的模型
1.1 梁中的温度场
图1为处于热梯度环境中的梁,其长度为,截面宽度为,截面高度为。梁的上下表面温度分别为和。由于外界温度在梁的上下表面存在差异,热传导将使梁在厚度方向上的温度呈梯度分布。外界温度在梁轴向上的变化率一般较小,因此不考虑轴向的温度变化。
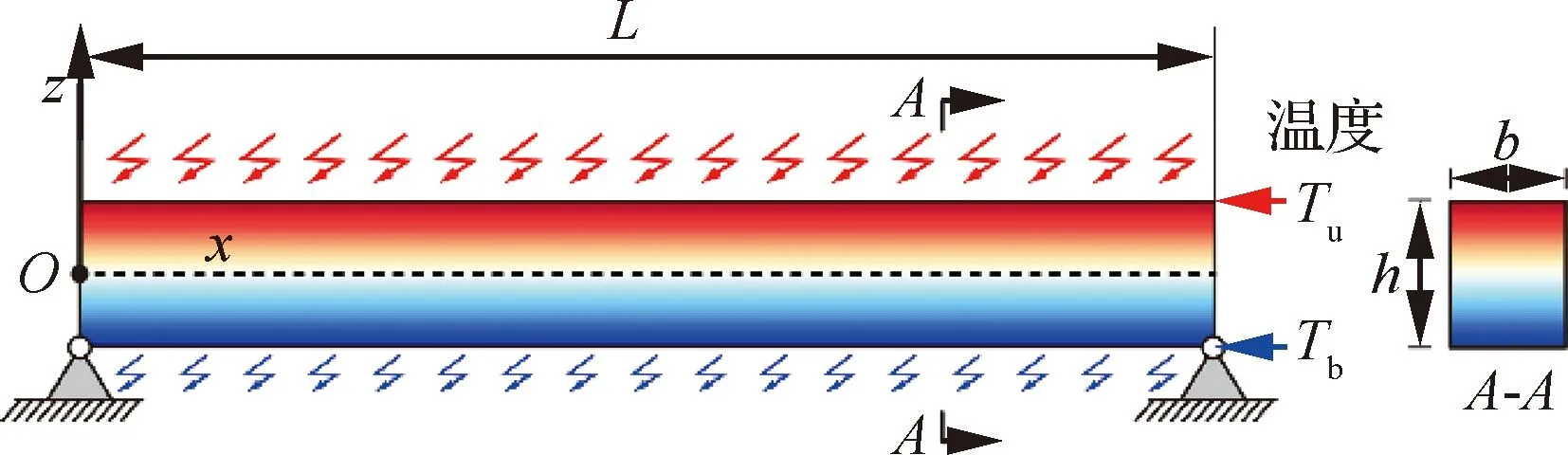
图1 处于热梯度环境中的梁Fig.1 Beam exposed in thermal gradient environment
首先对梁内的温度场进行建模。以梁的几何中性层为参考,坐标为处的温度满足一维稳态热传导方程
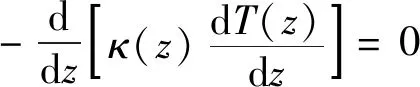
(1)
式中:()为坐标处的材料热传导系数,对于均质材料,()为常数;为温度,K。式(1)的边界条件可表示为
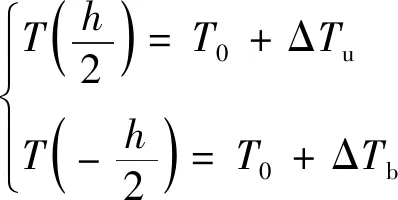
(2)
式中:为参考温度,取为室温300 K,此时材料不产生热膨胀;Δ和Δ分别为梁的上下表面处温度与参考温度的差值。将式(2)代入式(1),对于均匀材料可求解得到在厚度方向的温度为
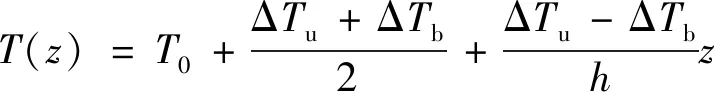
(3)
根据Touloukian提出的高阶多项式拟合材料属性-温度拟合关系,材料参数与温度的关系可表示为
=(+1+++)
(4)
式中:表示密度、弹性模量、泊松比、热膨胀系数等材料物性参数;(=-1,0,1,2,3)为材料参数的温度系数,需根据具体材料确定。在厚度方向的热传导导致温度在厚度方向连续变化,由式(4) 可知,此时梁的材料参数在厚度方向也将呈现连续性变化。
1.2 运动控制方程
厚度方向存在的热梯度使梁的材料属性在空间中具有非均匀的特点。同时,若轴向变形被约束,热膨胀还将产生轴向应力。这两方面因素使热梯度环境下梁的运动控制方程异于常温下梁的运动控制方程。
已有的一些研究表明,基于等效单层理论(Equivalent Single Layer,ESL)建立非均匀材料结构的位移场时,由于在厚度方向弹性模量等力学参数的空间变化,结构横向弯曲变形与轴向伸展之间将存在耦合。一些学者为此引入了物理中性层的概念以消除这一耦合。图2中热梯度环境下的梁由于在厚度方向的弹性模量也具有非均匀性,因此亦可使用物理中性层的概念建立热梯度环境中梁的运动控制方程。
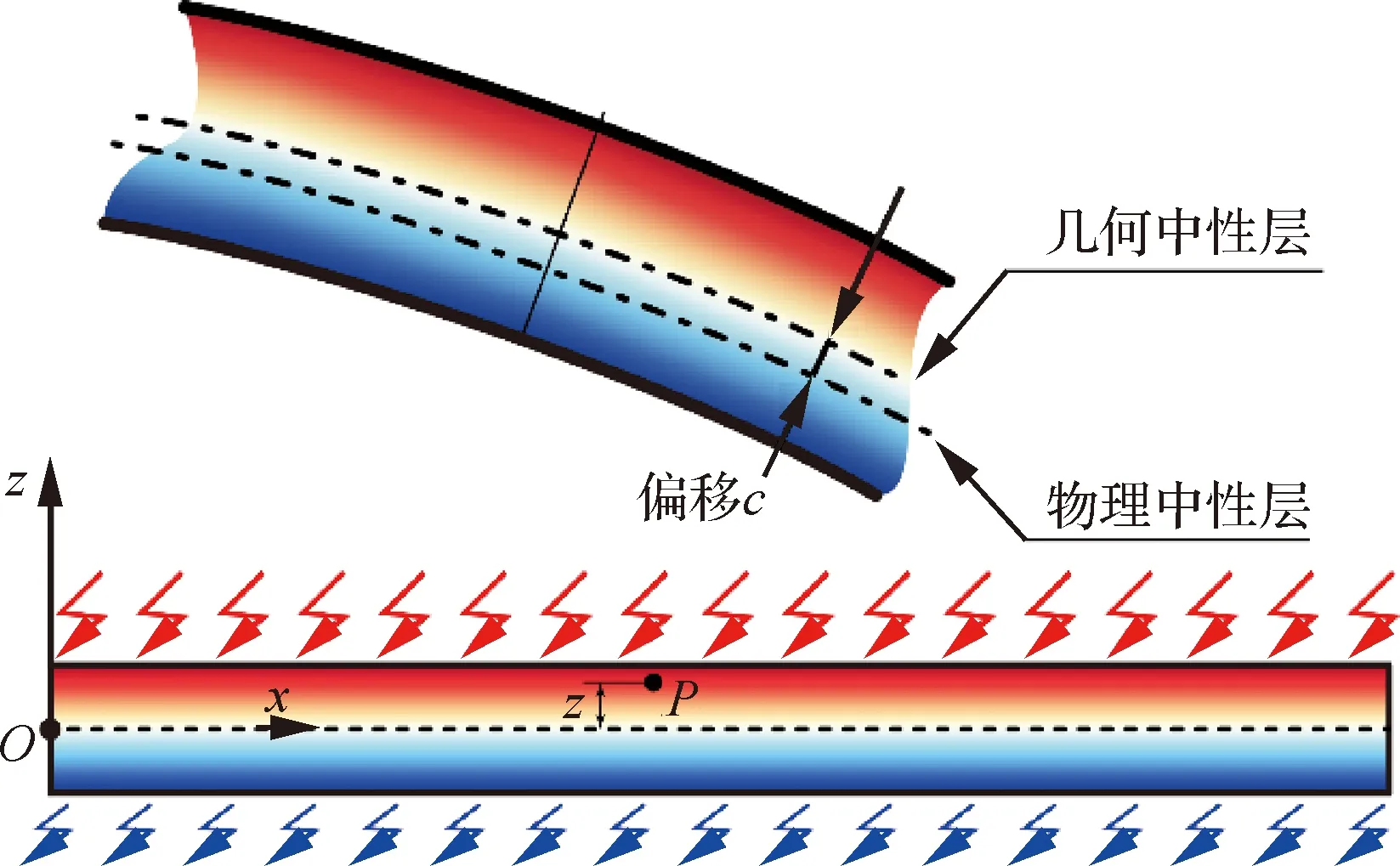
图2 梁在热梯度环境中的变形Fig.2 Deformation of beam in thermal gradient environment
当梁的轴向跨度远大于截面高度时,一般可忽略其截面转动惯量及剪切变形的影响而采用欧拉-伯努利梁对其进行分析。在飞行器中,薄壁类壁板等结构一般具有这一特性。基于欧拉-伯努利梁理论的位移场可表示为
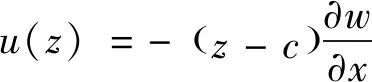
(5)
式中:为梁的轴向位移;为弯曲变形对应的横向位移;为物理中性层与几何中性层的距离,表示为
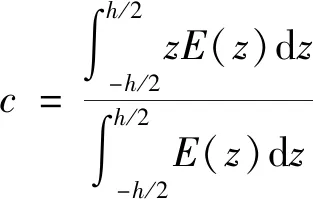
(6)
式中:()为几何中性层坐标下处的弹性模量,可通过式(3)和式(4)确定。一般情况下高温将减小材料的弹性模量,因此对于图2所示的热梯度环境下的梁,物理中性层相对于几何中性层将向温度较低的方向偏移。基于式(5)给定的位移场,梁的弹性变形势能可表示为
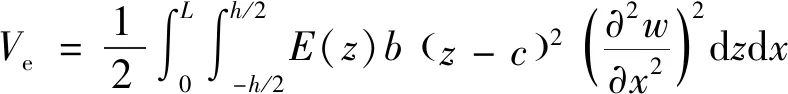
(7)
当梁处于超静定约束状态、热膨胀完全被约束时,由热梯度环境产生的轴向热应力可表示为
()=-()()Δ()
(8)
式中:()为梁的热膨胀系数;Δ()为温度差。
对于小变形情况,变形后梁的微弧段长度d与未变形状态长度d之间的差值可表示为
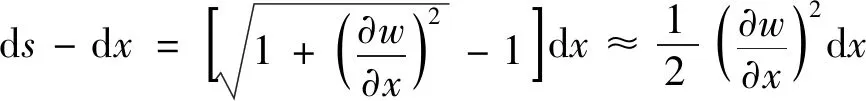
(9)
从而轴向上初始热应力对应的势能密度可表示为
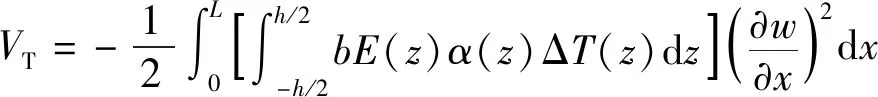
(10)
由于热应力在结构超静定状态下产生压缩轴向力,式(10)中的势能密度将是负的,这实质上将减小梁的固有频率。当热应力使一阶固有频率为0时,梁将失稳发生热屈曲,此时梁将产生非线性变形。能量流分析是基于线性小变形假设的,因此不讨论梁在热梯度环境中处于后屈曲状态时的能量流模型。
基于等效单层理论,热梯度环境下梁的动能可表示为
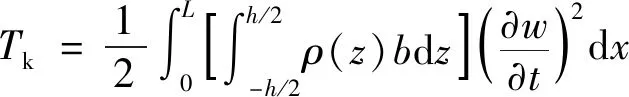
(11)
式中:()为梁的材料密度。
由外力对处于热梯度环境中的梁所做的功可表示为
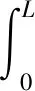
(12)
式中:(,)为外力;为时间变量。
当外力为集中力形式时,可采用δ函数进行描述。由式(7)、式(10)~式(12)可得热梯度环境下梁弯曲变形的能量泛函。对能量泛函使用哈密顿原理并收集变分项δ的系数,可得热梯度环境下梁的弯曲振动控制方程:
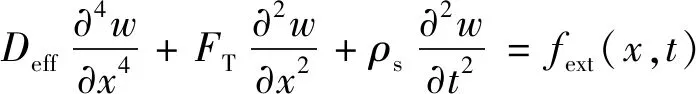
(13)
式中:为在热梯度环境下梁的截面有效弯曲刚度;为处于超静定状态的梁在热环境中产生的有效轴向力;为等效截面密度。它们可分别表示为
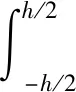
(14)
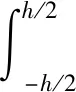
(15)
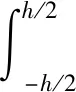
(16)
当梁处于均匀的温度场时,式(13)将转换为Zhang等使用的梁运动控制方程。进一步地,当不考虑梁的轴向热应力时,式(13)将退化为均匀梁的运动控制方程。
式(15)中由热应力产生的轴向力是在默认热膨胀被完全约束时得到的。在实际工程中,薄壁结构的屈服极限往往较小,为避免过大的温度应力引起结构的热屈曲,在实际工程中细长薄壁类结构的两端可能留有伸缩缝以削弱对热膨胀的约束。如图3所示,可使用端点的轴向弹簧模拟轴向伸缩缝的效应。当该轴向弹簧刚度系数为0时,将不存在针对轴向热变形的约束,此时梁中也将不存在热应力,温度将仅改变梁的材料属性。当弹簧刚度系数远大于轴向刚度时,热膨胀可视为被完全约束从而产生热应力。其他刚度值可类似设定。
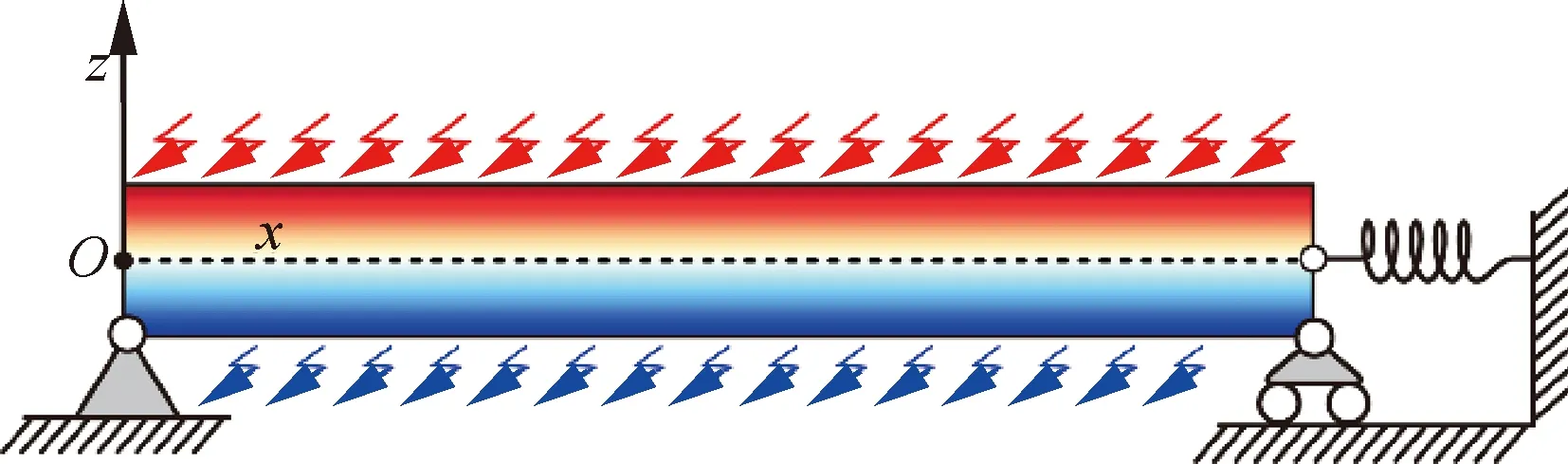
图3 轴向未完全约束的梁Fig.3 Beam without full axial constraint
对于图3中的梁,根据弹簧与梁的轴向力相等可得
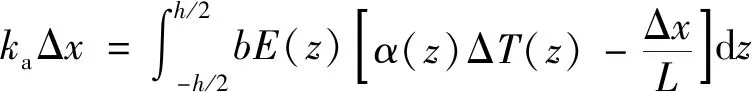
(17)
式中:为轴向弹簧的刚度系数;Δ为弹簧的伸缩量,Δ一般远小于梁的尺寸,因此不计这一微小变形对梁几何尺寸的影响。通过在式(17)中求解Δ便可得到梁的轴向力。将代入式(13) 便可得此时对应的运动控制方程。
2 热梯度环境下梁的能量流模型
2.1 波动频散关系
在结构的能量流研究中需建立能量密度控制方程,而能量密度控制方程基于振动的波动解。因此需要首先求解式(13)波动形式的解。
为考虑在高频时结构阻尼的影响,可在势能表达式中引入复刚度,此时导出的式(13)将被改写为
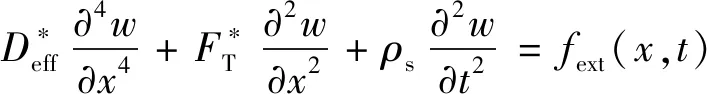
(18)
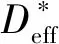
式(18)具有时间简谐和空间简谐形式的波动解可表示为
(,)=ejej
(19)
式中:为弹性波幅值;为波数,表征弹性波的空间振荡特性;为圆频率,表征弹性波的时间振荡特性。将式(19)代入运动控制方程式(18)对应的齐次方程,可得
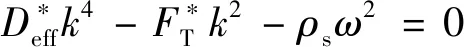
(20)
式(20)建立了波数与圆频率之间波动频散关系。通过求解式(20)便可得到热梯度环境下弹性波时间振荡与空间振荡之间的关系。数学形式上式(20)为关于波数的四次多项式方程,共有4个根:
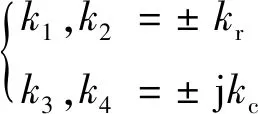
(21)
式中:为远场波波数的实部;为近场波波数的虚部。
式(21)中的根可根据多项式求根公式得到:

(22)
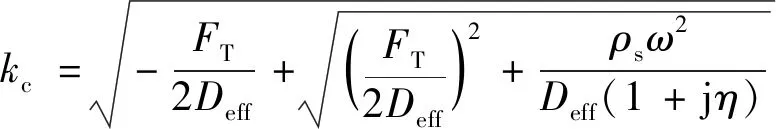
(23)
将式(21)中的前两项代入式(19)后,得到以波数为频率、在空间振荡的远场波,式(21)中的后两项对应于指数衰减的近场波。能量流中一般不考虑近场波的影响,从而式(19)可表示为
(,)=(ej+e-j)ej
(24)
式中:为第个波的幅值。
由于使用复刚度模拟结构迟滞阻尼效应,式(24) 中的波数也将变为复数,也即=+j。基于小阻尼假设(≪1),对式(22)以j为未知量、以0为原点进行一阶泰勒展开,可得
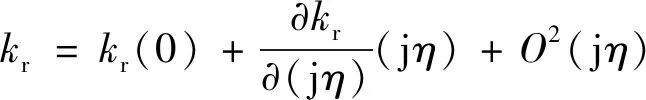
(25)
常见金属材料的阻尼系数一般是小量,此时≪1,因此式(25)中与同阶的项可忽略,从而可得
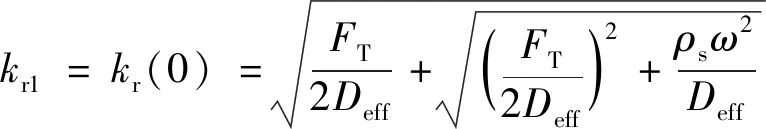
(26)
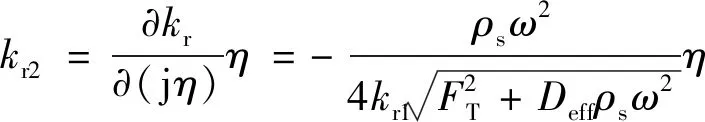
(27)
式中:和分别为复波数的实部和虚部。
由式(26)可得弹性波的波长
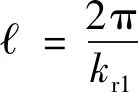
(28)
式(26)表明在小阻尼假设下导出的表征波动空间振荡特性的波数实部部分与无阻尼的波数一致,也即
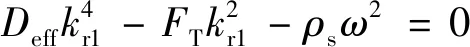
(29)
为得到表征远场弹性波能量传递速度的群速度,对式(26)两边应用隐函数求导法则,可得
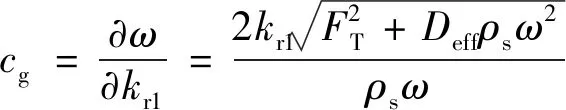
(30)
式中:为弯曲波的群速度。
类似的,由式(29)还可得
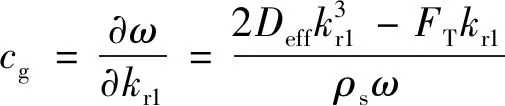
(31)
比较式(27)和式(30),表征波动随空间衰减的项可表示为
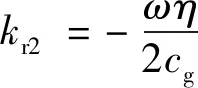
(32)
2.2 能量密度控制方程
时间周期平均后,热梯度环境下梁的动能密度可表示为
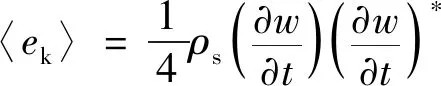
(33)
将式(24)代入式(33),可得动能密度为
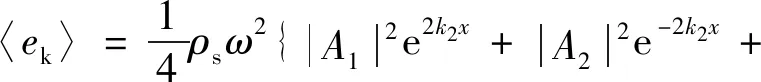
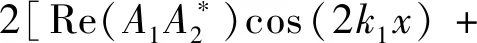
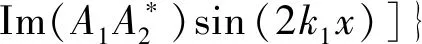
(34)
同理,由梁的轴向热应力以及弹性变形对应的势能密度表达式为
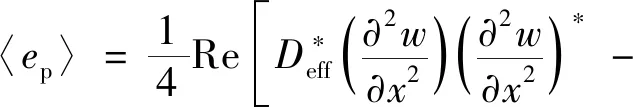
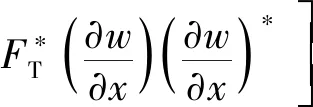
(35)
将式(24)代入式(35),忽略阻尼系数的高阶项,可得势能密度为
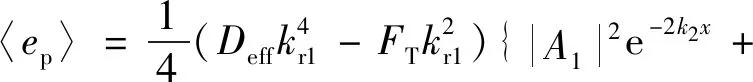
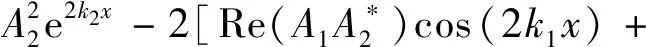
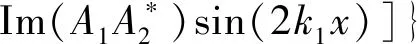
(36)
在式(34)和式(36)中,均包含指数衰减项和三角函数项。在物理意义上,前者对应于远场波的衰减,而后者对应于正负向远场波的干涉。在能量流分析中,基本变量为局部空间平均后的能量密度,因此式(34)和式(36)中的三角函数项在经过波长局部空间平均后可被消除。注意到式(26) 给出的频散关系,时间与空间平均后总的能量密度可表示为
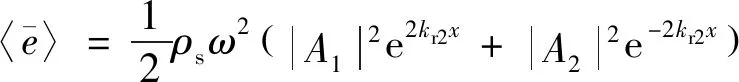
(37)
图4为热梯度环境下梁的受力示意图。振动功率流将同时由弯矩、剪力和热应力传递。时间周期平均意义下的振动能量流可表示为
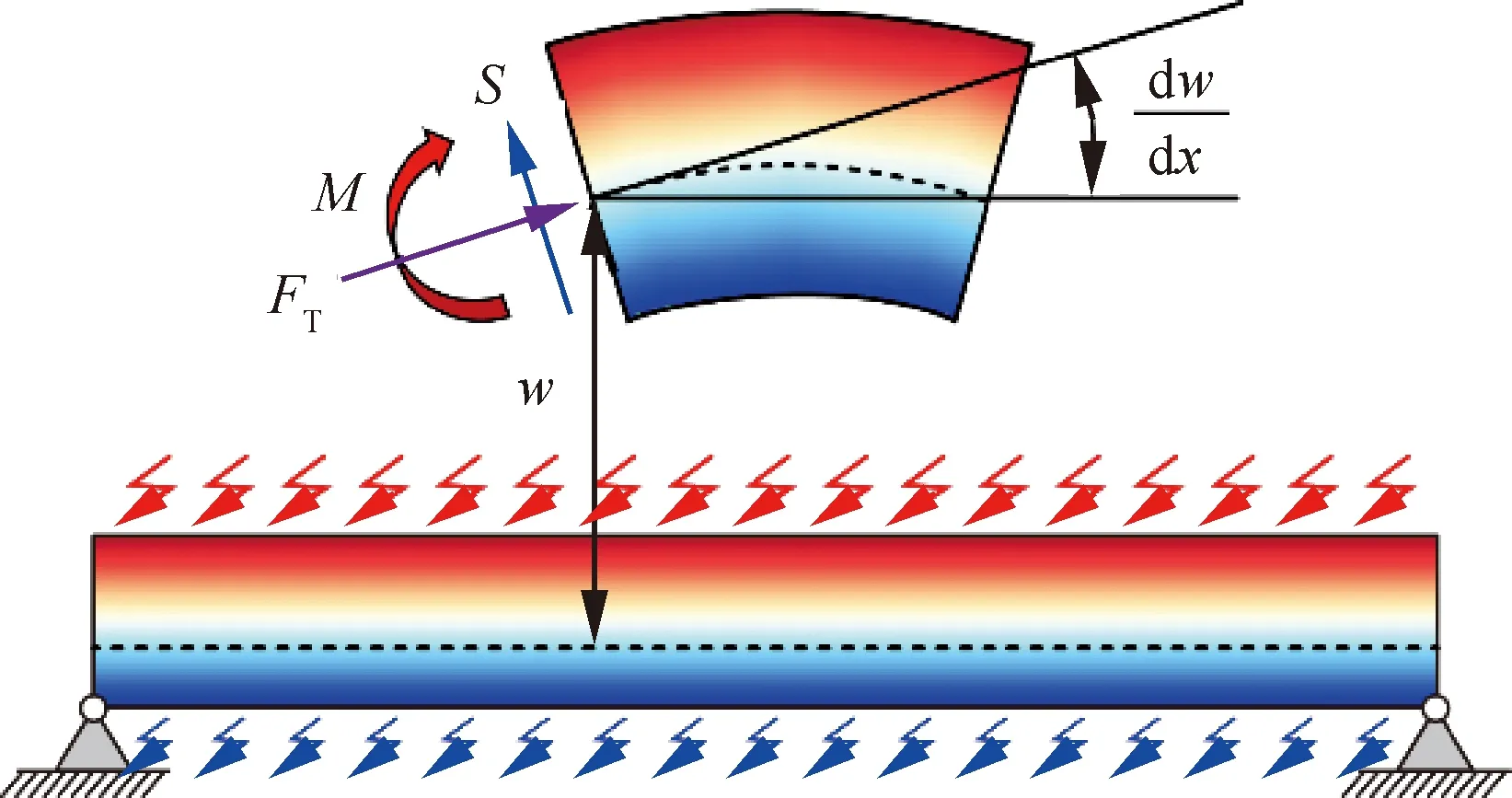
图4 热梯度环境下梁的受力示意图Fig.4 Schematic diagram of forces acting on beam in thermal gradient environment
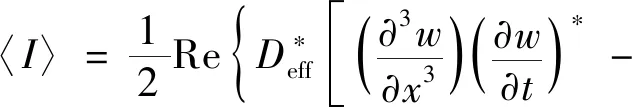
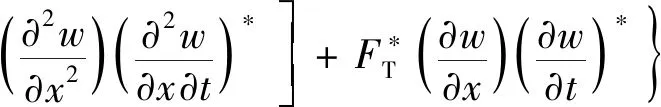
(38)
将式(24)给出的波动解代入式(38),进一步经局部空间平均以消除行波之间干涉项引起的功率流,可得时间与局部空间平均后的功率流表达式:
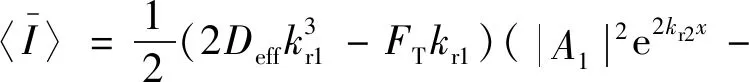
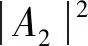
(39)
比较式(37)与式(39),可得
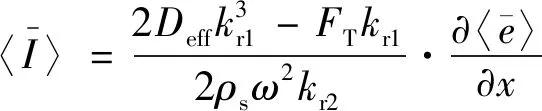
(40)
将式(31)和式(32)代入式(40),可得
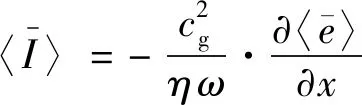
(41)
在能量流分析中,能量密度控制方程可根据微元体控制体积内的能量流平衡导出。如图5所示,图中为外部输入的功率,对于热梯度梁的任意微段d,在稳态下能量输入、能量耗散及能量传导三者间具有平衡关系。对于采用的迟滞阻尼模型,Cremer等的研究表明时间周期内对振动能量的平均耗散功率可表示为
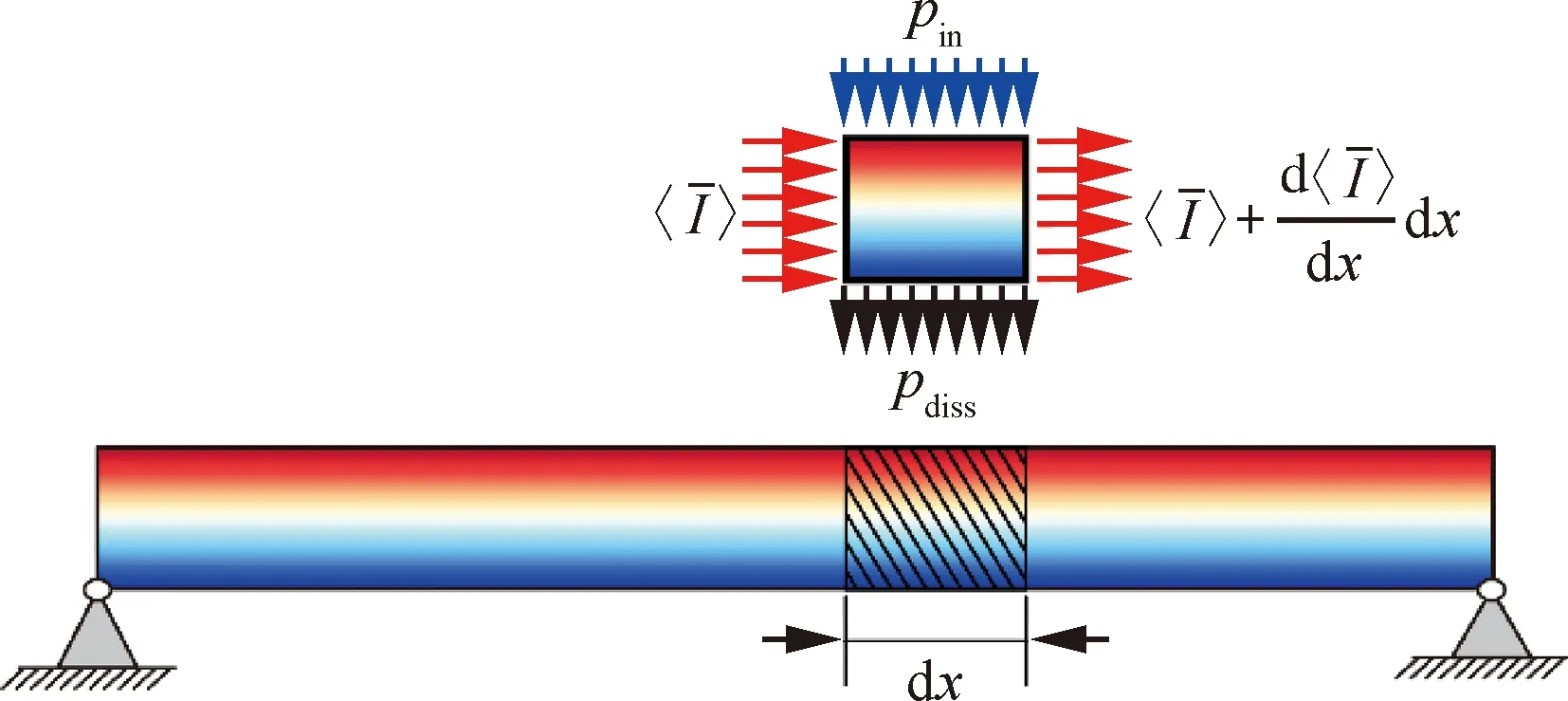
图5 微元体的能量流平衡Fig.5 Energy flow balance in a differential element
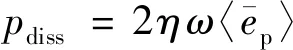
(42)
由式(29)、式(34)和式(36)可知,时间和局部空间平均后势能密度与动能密度相等。这一性质在Navazi等进行的试验中也得到过验证。基于此,式(42)可表示为
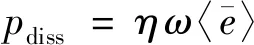
(43)
考虑图5所示的微元体的能量平衡关系,可得
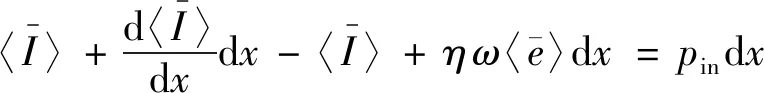
(44)
将式(41)代入式(44),可得
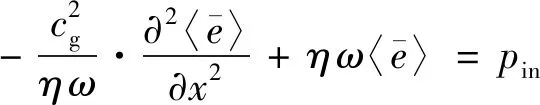
(45)
式(45)即为建立的能量密度控制方程。该方程与Wohlever和Bernhard建立的常温环境下梁的能量密度控制方程具有一致的形式。但式(45) 的导出同时考虑了热环境产生的热应力以及材料的温度相关性,因此式(45)中的关键参数群速度将与未考虑热环境影响的群速度不同。
2.3 能量密度控制方程的求解
在高频分析时,结构的输入点导纳一般可在忽略边界条件的情况下使用无限结构的输入导纳进行近似。Chen等使用波动法精确求解了预应力梁在两端简支条件下的输入导纳,结果表明考虑具体边界条件得到的输入导纳在无限结构导纳上下随频率振荡,且二者随激励频率的增加逐渐接近。高频分析一般在倍频程下以频率平均意义进行,因此在高频时使用无限结构的导纳可以较好地反映在频率平均时外界激励对结构统计意义下的输入功率。
图6所示为忽略边界时处于热梯度环境中的梁及梁中的弹性波,图中为外部集中形式的激振力,和分别为左侧半梁和右侧半梁的弯矩,和分别为左侧半梁和右侧半梁的剪力。由于忽略了边界的存在,以激励位置为分割点,两侧的梁均只有由外界力激起的远离激励点的弹性波。忽略时间简谐项,左侧半梁(梁1)和右侧半梁(梁2)中的弹性波位移可分别表示为
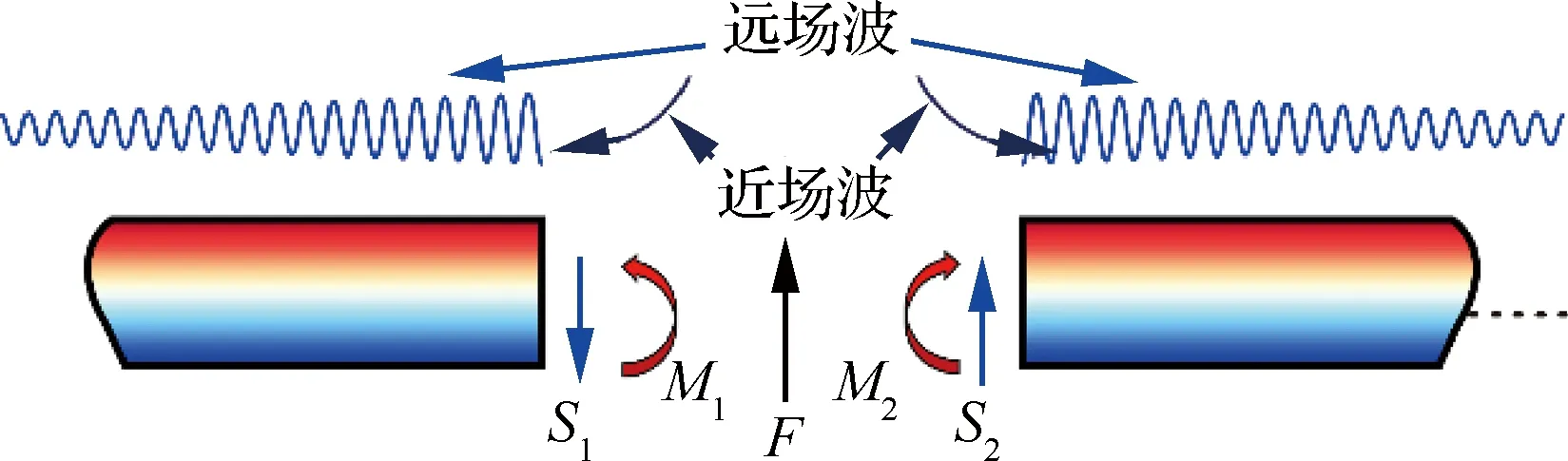
图6 无限尺寸热梯度梁中的弹性波Fig.6 Elastic waves in infinite beam in thermal gradient environment
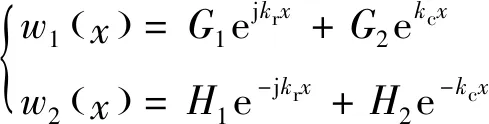
(46)
式中:和分别为左侧半梁和右侧半梁的横向位移;和分别为左侧半梁远场波和近场波的幅值;和分别为右侧半梁远场波和近场波的幅值。
式(46)共有4个未知数,由激励位置处的连续性条件可得到4个协调方程。
在计算得到式(46)中的4个参数后,使用输入导纳的定义可得处于热梯度环境下无限梁的输入导纳为
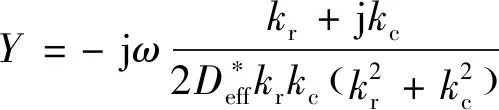
(47)
由式(47)给出的输入点导纳可得输入功率:
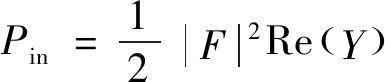
(48)
将式(48)确定的外界激励输入功率流代入式(45) 便可得梁上的能量密度的空间分布。式(45) 在数学形式上为定义在空间域上的二阶常微分方程,它的解可表示为
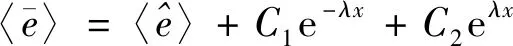
(49)
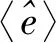
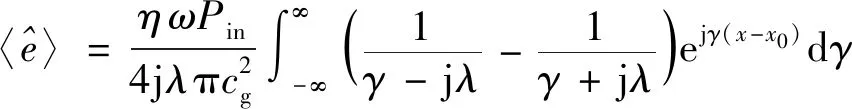
(50)
式中:为复平面内的积分变量。
由式(50)可见式(49)中的积分在复平面内有两个留数点。由留数定理可得式(45)的特解为
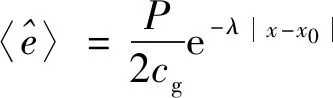
(51)
将式(51)代入式(49)便可得热梯度环境下梁上的能量密度分布。对于单梁,在梁的左右两端应不存在能量流的输入输出,因此在左右两端的边界条件可表示为
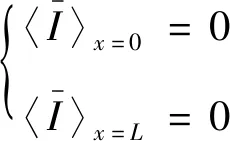
(52)
式(52)中的能量流可通过式(41)确定。由式(52) 中的两个边界条件便可确定两个未知系数和。基于式(19)~式(52)得到的是能量密度控制方程的解析解,当使用有限元方法进行数值求解时,该模型也被称为能量有限元方法。相比于数值解,解析形式的能量流模型在参数化分析和优化时将具有优势。
3 数值算例与讨论
对建立的能量流模型进行验证,并通过数值算例对处于非均匀热环境中梁的高频振动特性进行研究。算例中采用的梁材料为Ti-6Al-4V。Ti-6Al-4V具有良好的低温和高温性能,可稳定工作于400~500 ℃的环境下。温度对这种材料弹性模量和热膨胀系数的影响如表1所示,材料密度为4 439 kg/m,不随温度变化。
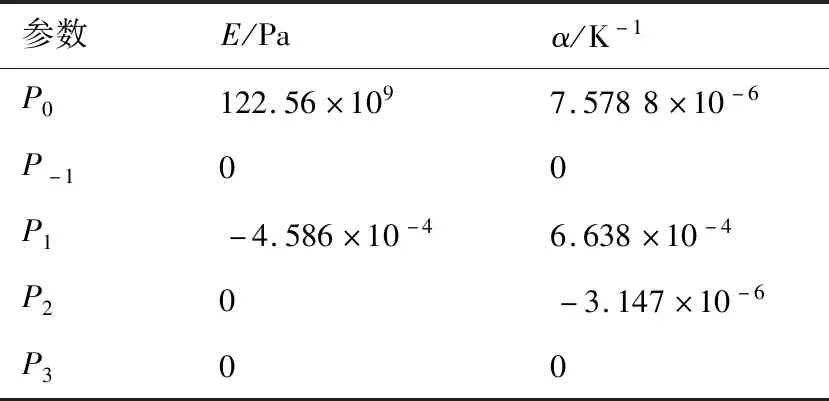
表1 Ti-6Al-4V随温度变化的参数Table 1 Temperature-dependent coefficients of Ti-6Al-4V
3.1 模型有效性验证
首先对建立的能量流模型的有效性进行验证。基于能量泛函和多项式形函数可得热梯度环境下梁的单元矩阵,通过组装可得有限元模型。在验证对比时使用有限元方法在稠密网格时得到的结果作为参考对比值。为确保有限元结果的收敛性,在有限元中设定网格长度小于1/10波长,因此有限元计算所需的自由度和计算量远远大于能量流模型。
能量流模型对结构高频振动响应的预测需要首先实现对外界激励功率输入的估计。在式(48)中使用无限结构的导纳求取外界激励的功率输入,图7使用有限元法并划分稠密网格精确求解了几种常见边界条件下单位幅值简谐力作用于梁中点时引起的功率流输入,梁的长度为3 m,截面宽度和高度分别为5×10m和1×10m,材料阻尼=0.05且不随温度变化。梁的上表面处于温度为500 K的热环境中,下表面温度为300 K,轴向热膨胀约束弹簧刚度为1 000 N/m。
由图7可见由无限结构导纳法得到的输入功率流在频率内较为平滑,且整体上随激励频率升高而下降。而考虑边界条件时得到的精确输入功率流则在前者上下振荡。这是由于无限结构导纳法不考虑边界,也因此不存在由驻波效应引起的共振和反共振现象。从图7中还可看出虽然考虑具体边界条件时输入功率流在频域内有一定振荡,但它们总体是在无限结构输入功率的上下波动。同时随频率升高考虑边界条件得到的输入功率逐渐接近无限结构的输入功率。这一现象可通过边界对波传递的影响解释。对于保守边界,无论其具体形式,波在传递至边界而反射时只产生相位的变化而不产生幅值的变化。随波长变小,相位变化的影响逐渐变小,且这一影响往往可经频率平均进一步进行消除。因此,式(48)可较为合理地预测各种边界条件下高频激励时外界的功率输入。
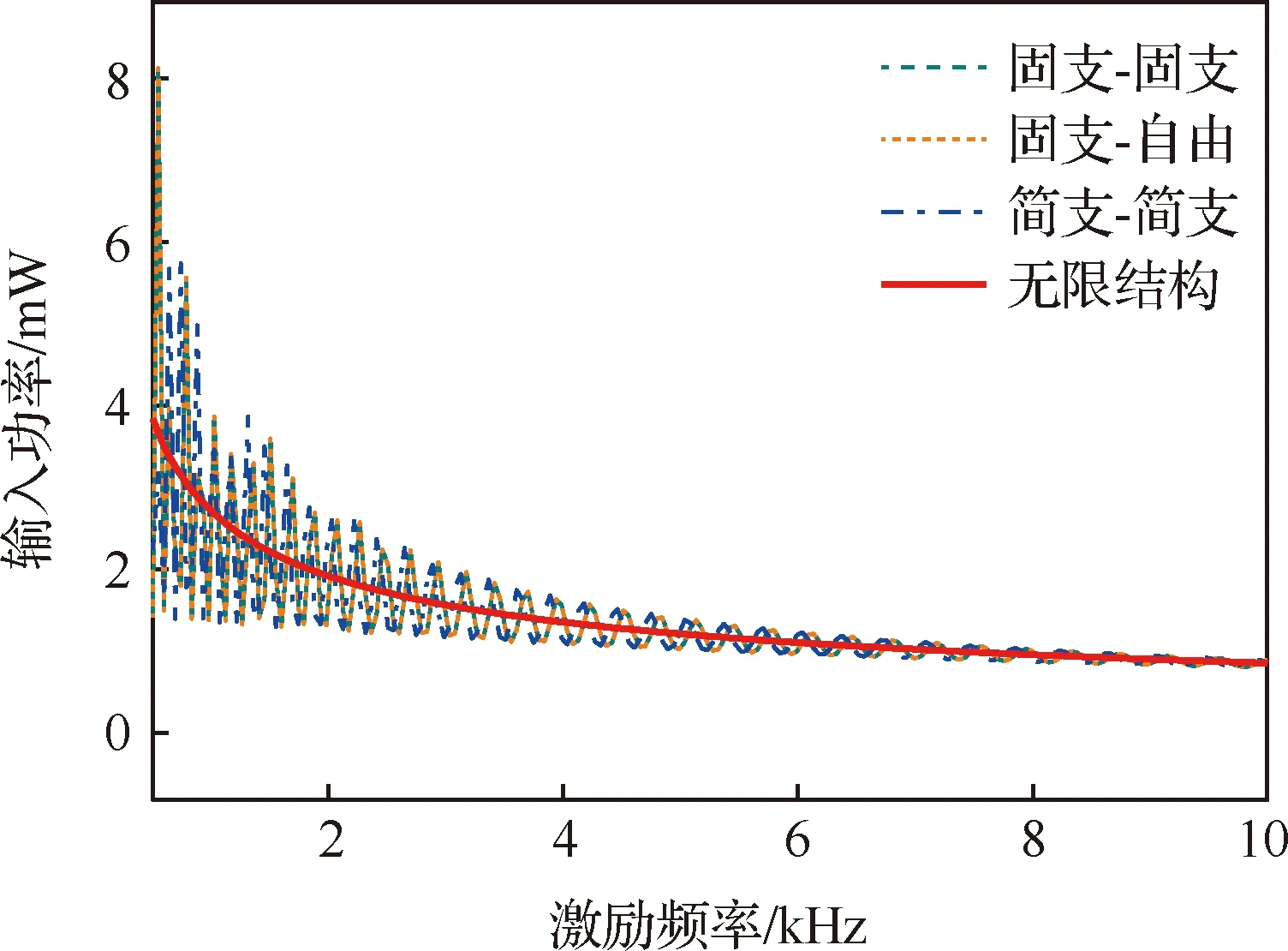
图7 外界功率流随激励频率的变化Fig.7 Variation of power input with excitation frequency
图8为波长与波数随激励频率的变化曲线,可见随激励频率增加,波长逐渐变短,而波数逐渐增大;随波长变短,近场波的影响范围将逐渐减小;随着波数的增加,波动在空间中的振荡频率将更快,此时进行局部空间平均以消除能量密度和能量流中与波数同频的振荡项也将是合理的。
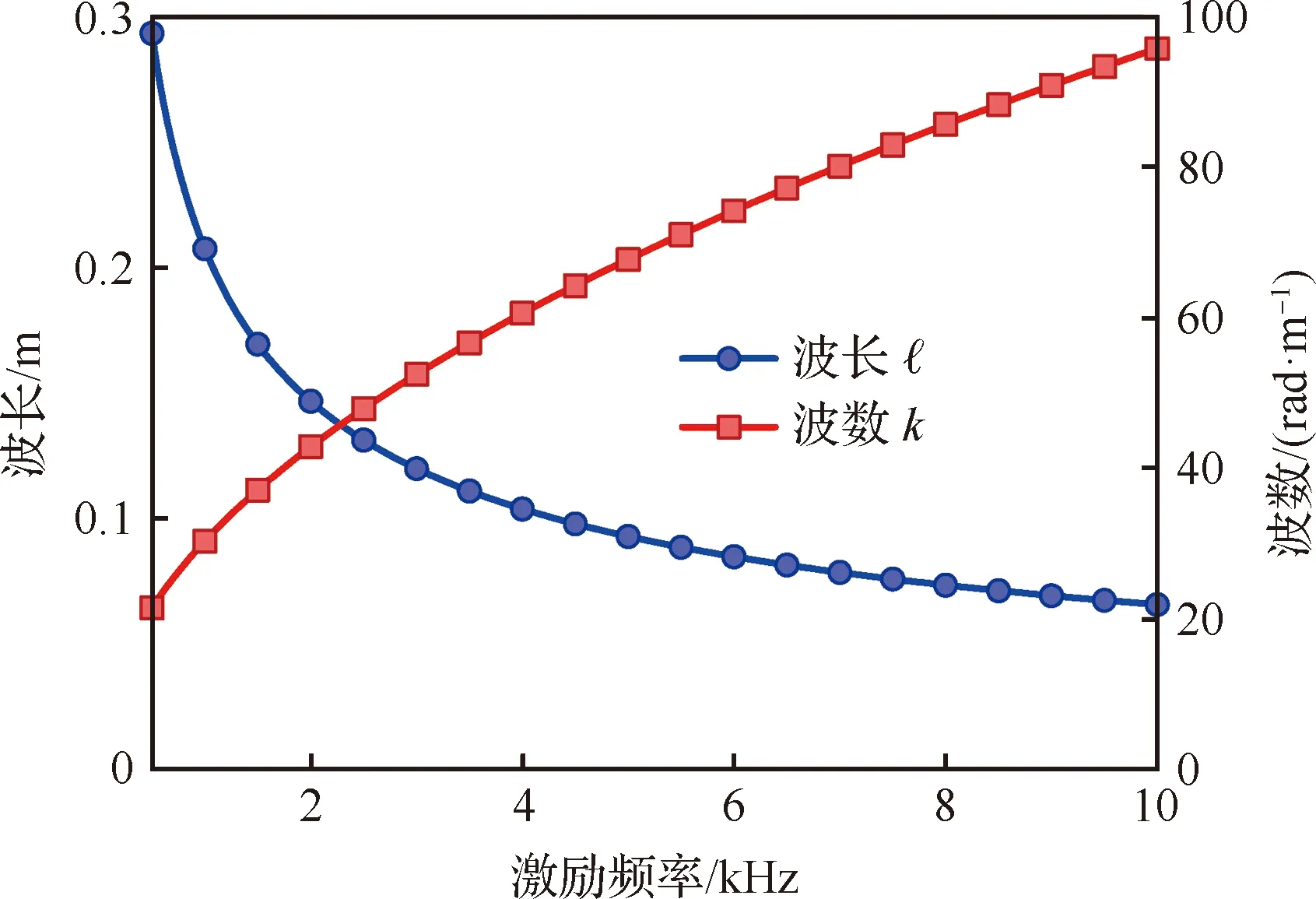
图8 波长与波数随激励频率变化Fig.8 Variations of wavenumber and wavelength with excitation frequency
图9为具有单位幅值的简谐力作用于梁中点时,在不同激励频率下能量密度的空间分布。在图9中,使用具有稠密网格的有限元结果作为对比参考值。有限元计算在以激励频率为中心频率的1/3倍频程内进行,并取1/3倍频程内100个频率对应结果的均值为基准值。由图9可见能量流模型预测的能量密度结果在空间内较为平滑,而基于确定性有限元方法所得的结果在空间中呈现振荡。能量流模型的结果可较为准确地反映1/3倍频程内响应的空间整体变化趋势,且与基准值具有较好的吻合性。能量流模型的预测结果在激励位置及边界处与有限元结果具有一定的差别,这一现象是由于激励位置和边界处存在近场波。由图8可知随激励频率增加波长逐渐减小,从而近场波存在的范围也越来越小,这一现象也可在图9中观察到。在图9中随激励频率增加,边界处振荡的范围与幅度都趋向减小。
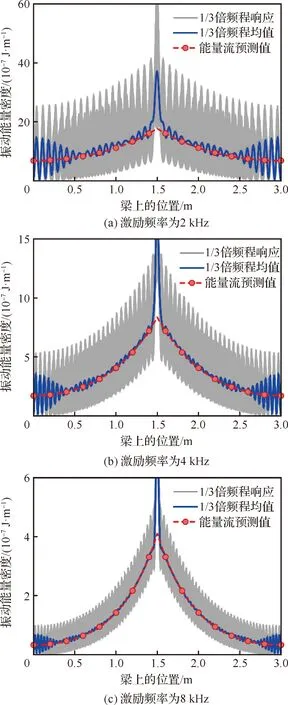
图9 不同激励频率下梁振动能量密度分布情况Fig.9 Energy density distributions of beam at different excitation frequencies
图10为不同激励频率下梁中的功率流。由图7可知随激励频率增加,由简谐激励力引起的功率输入逐渐减小。由于激励处于对称位置,因此梁上的功率流也呈对称性分布,从激励位置处向边界传播,并在传播过程中衰减。
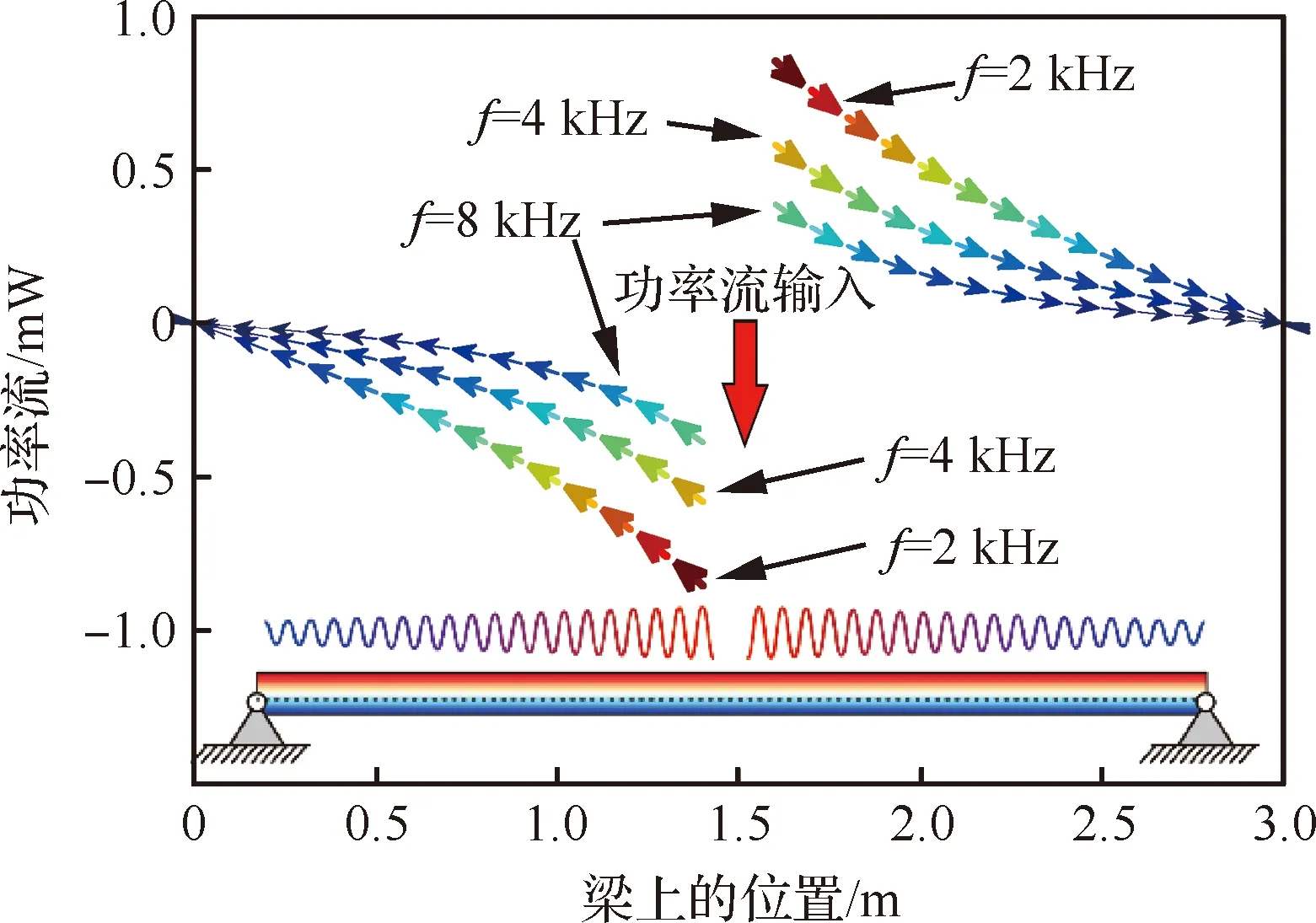
图10 不同激励频率f下梁中的功率流Fig.10 Power flow in beam at different excitation frequency f
由式(43)中迟滞阻尼模型可知,在相同的功率输入下,总体的振动能量密度将反比于激励频率。因此对比图9中3种激励频率下梁的能量密度响应可见,随着激励频率的增加梁的整体振动能量响应减小。同时由于波长减小,输入功率流向边界时将在空间内经历更多的波长周期衰减,因此在图9中随激励频率的增加能量密度在空间中的衰减趋势也更为明显。
图11为激励位置在1/3梁长度(激励点坐标=1,坐标系原点位于梁左端点处)、激励频率为4 kHz时梁上的能量密度分布。其他参数与图7中的算例相同。由图11可见对于非对称激励,能量流模型给出的结果仍能与参考值较好吻合。在靠近激励位置的左侧边界由于近场波效应明显,基准值具有较大的振荡性。但总体来说,能量流模型的结果较好地反映了振动能量的空间分布变化趋势。能量流模型的准确性依赖于对外界功率输入的准确估计。对于高频激励,式(48)基于无限结构导纳给出的功率输入计算公式在激励位置距离边界数个波长时便较为准确,而波长在高频时较短,因此对于梁上的绝大多数位置式(48)均能给出合理的输入功率流。对于图11 中的算例,虽然激励处在非对称位置,但其距离边界位置仍有若干波长,因此能量流模型也较准确地得到了梁上的振动能量分布特性。
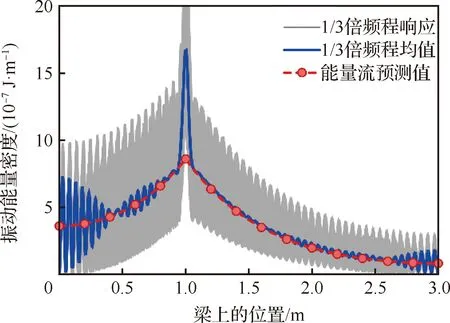
图11 非对称激励时梁中的能量密度Fig.11 Energy density in beam with asymmetrical excitation
由上述对比可见,能量流模型的结果较为准确地反映了处于热梯度环境下的梁在承受高频激励时的振动能量分布特性。
3.2 热环境的影响
高速飞行器等设备在运行中可能处于温度不断变化的热环境中。温度的变化将直接引起结构刚度及热应力的变化。图12为梁的上表面温度变化时,截面刚度与轴向热应力的变化趋势,其中下表面温度被设定为=0.6,激励频率为4 kHz。由图12可见随上表面温度增加,截面刚度逐渐减小而轴向热应力变大。本质上这两种变化趋势都将降低系统的固有频率,也即使得梁的振动更趋向于高频振动。
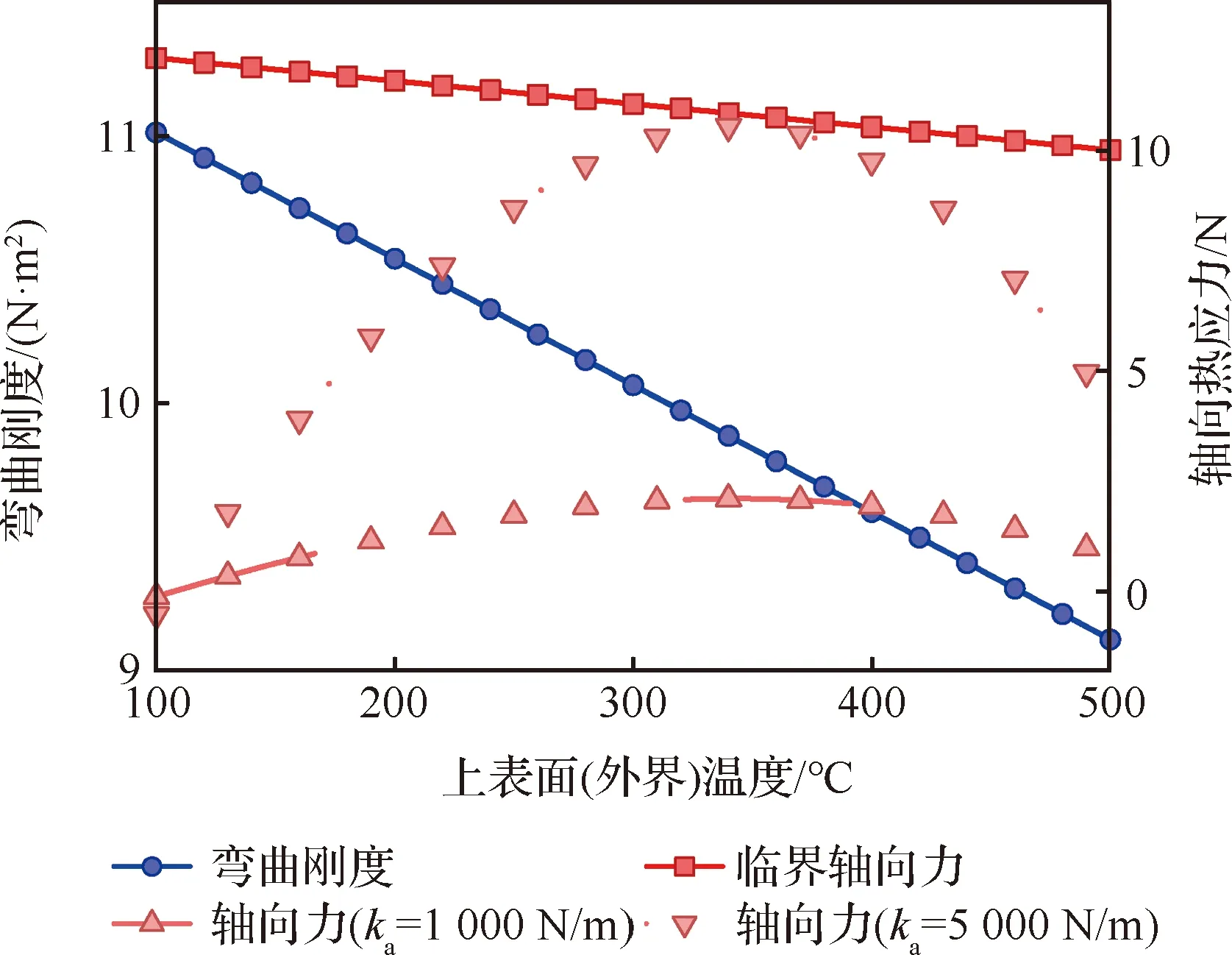
图12 温度对弯曲刚度和轴向力的影响Fig.12 Influences of temperature on bending stiffness and axial force
图13为上表面温度变化时波长和输入功率的变化曲线。由图13可见随温度增加,输入功率也增加,而波长将变短。由图13还可看出,对于不同的轴向约束弹簧刚度系数,波长与输入功率基本相同。这表明此时轴向力的大小对高频振动特性的影响较小。对于细长梁这类薄壁结构而言,其临界轴向压应力一般较小。Chen等的研究表明,较小的轴向力对高阶固有频率影响不明显,因此对高频响应的影响也较小。
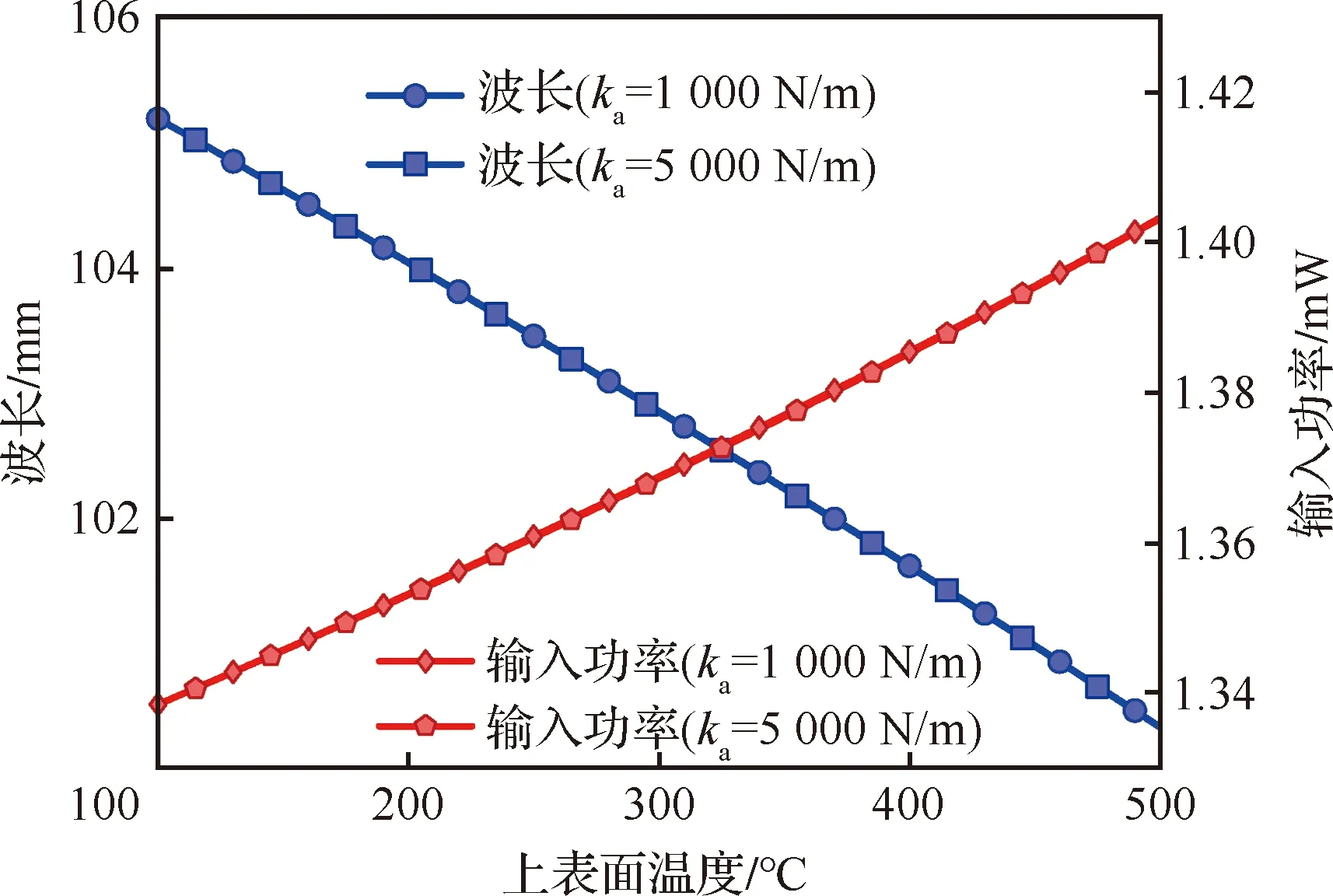
图13 温度对波长和输入功率的影响Fig.13 Influences of temperature on wavelength and power input
图14为简支梁在仅考虑轴向热应力和仅材料变化时时固有频率与常温下的梁的固有频率平方之比。固有频率使用经典的分离变量法由式(13) 得到。由图14可知,当仅考虑轴向力时,低频模态相比于常温下的梁具有明显的改变,热梯度环境引起的轴向力较大幅度地降低了低阶固有频率,但其对高频模态的影响并不显著。由于高频响应一般由激励频率倍频程内的若干高阶模态决定,因此轴向热应力的影响将不显著。而非均匀热环境造成的材料变化引起了刚度的降低,从整体上降低了固有频率,因此其对全频段的响应均将有明显影响。图14中的趋势虽是基于简支边界条件,但高频时结构响应对边界并不敏感,因此上述讨论对于任意边界具有一般性。
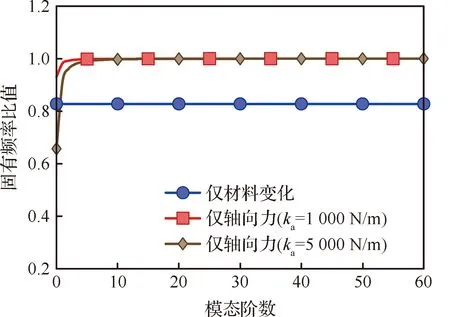
图14 材料变化与热应力对固有频率的影响Fig.14 Influences of material variation and thermal stress on natural frequencies
图15为不同上表面温度时梁的振动能量密度分布。分析频率为4 kHz,=1 000 N/m,上表面温度分别设置为30 ℃和500 ℃。
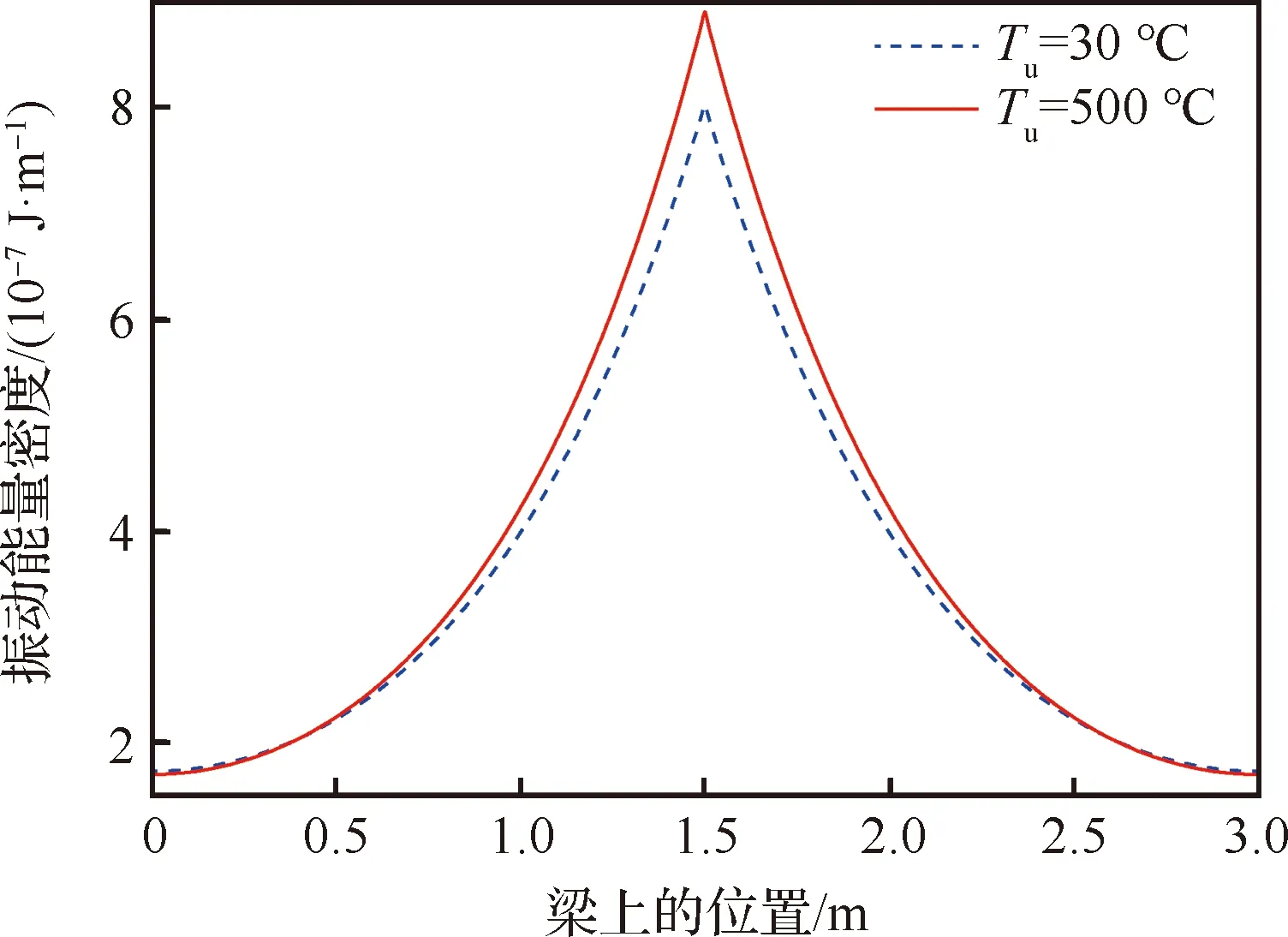
图15 温度对梁上能量密度的影响Fig.15 Influence of temperature on energy distribution of beam
由图15可见温度的增加总体上提高了梁上的振动能量,同时在温度较高时梁上的能量密度在空间中的衰减更为明显。这一现象对应于图13 所得结论。随温度升高外界激励力对梁的功率输入增大,因此梁上的总体振动能量水平增高,而较小的波长使振动能量在空间中的衰减更为明显。
4 结 论
通过求解稳态热传导方程得到了热梯度下梁的内部温度场,考虑温度场对材料物性参数的改变及产生的热应力,引入物理中性层概念消除轴向拉伸与横向弯曲变形之间的耦合,进而基于欧拉梁理论建立了运动控制方程,并详细推导了能量流模型及其解析解。通过数值算例将能量流模型与基准解进行对比,结果表明:
1) 基于无限结构导纳得到的功率输入能较好地评估外部高频激励对热梯度梁的功率流输入。
2) 与基准解的对比表明,建立的能量流模型能以较小的计算量准确预测热梯度环境中的梁在高频激励下的振动能量分布情况。
3) 热梯度环境对梁高频振动特性的改变主要是由于结构的材料属性在非均匀温度场中产生了变化,而热应力对高频振动产生的影响较小。
4) 随外界温度升高,非均匀热环境整体上使热梯度梁中弯曲波波长变短,外界激励力输入功率增加,从而振动能量具有更明显的空间衰减。
