基于BPNN的封严涂层孔隙分布均匀性超声表征

2022-07-04董珍一林莉雷明凯马志远

航空学报 2022年5期

董珍一，林莉，雷明凯，马志远,*

1.大连理工大学无损检测研究所，大连 116024

2.大连理工大学材料科学与工程学院，大连 116024

可磨耗封严涂层(简称“封严涂层”)常涂覆于航空发动机中压气机、涡轮机叶尖与机匣内壁，能提高航空发动机效率、保护叶片、降低油耗。封严涂层通常由金属相、非金属相和孔隙复合而成，其中孔隙能降低涂层硬度，提高可刮削性。但孔隙分布不均匀易引起应力集中，破坏涂层完整性。因此，发展定量表征封严涂层孔隙分布均匀性的无损检测技术对提高其综合性能、保证服役安全和使用寿命具有重要意义。

超声检测技术基于超声波场与异质界面、增强相和孔隙等散射体的相互作用，获得携带大量材料微观结构特征信息的超声回波信号，进而建立信号特征与目标材料属性之间的关系，近年来在非均质材料几何与物性参数表征方面得到应用。在对封严涂层孔隙分布均匀性进行超声定量表征时，需解决两个问题：① 寻求定量描述孔隙分布均匀性的参数；② 解析超声信号特征参量与孔隙分布均匀性参数间多因素耦合影响下的数学关系描述。对于问题①，已有学者提出了一些均匀性量化方法，其中面积分数多尺度分析(Multi-Scale Analysis of Area Fractions，MSAAF)技术能有效定量描述不连续增强金属基复合材料的微观结构均匀性。本课题组的李宗艺等将该技术应用于铝硅聚苯酯(AlSi-polyester，AlSi-PHB)封严涂层孔隙分布均匀性的定量表征，提取均匀性参数绝对斜率和均匀性长度，发现随集群系数增大，绝对斜率减小、均匀性长度增大，孔隙分布均匀性变差。对于问题②，超声波在封严涂层中传播时受到各相形貌、含量、分布等多种因素耦合影响，声学特征与均匀性参数间存在复杂非线性关系，使用数学解析方法对其进行描述存在一定困难。随着机器学习在模式识别、工业检测、数值预测等多个领域掀起热潮，参数间非线性关系复杂或物理机制不明确等问题都迎刃而解。以BP神经网络(Back Propagation Neural Network，BPNN)为代表的人工神经网络是经典机器学习模型之一，具有结构简单、可操作性强等优点，许多学者已将BPNN成功应用于超声检测。超声信号特征的提取是影响BPNN预测准确性的重要因素，而小波变换凭借其优异的时频局域化特性，在用于表征材料几何及物性参数的超声特征提取方面逐渐得到应用。如Acciani等提取反射超声导波的小波系数特征，使用BPNN预测管道腐蚀缺陷角度及尺寸，实验最大平均误差分别为15.23% 与12.48%。Lin等采用粒子群优化支持向量机算法，结合小波变换提取多尺度衰减系数预测封严涂层孔隙率，其结果决定系数和均方误差(MSE)分别为0.947和0.067。上述研究利用了小波变换的去噪声及多维分解能力，并未结合超声特征具体分析将小波变换应用于超声信号分解的本质原因；不同于宏微观缺陷自身的特性参数，孔隙分布均匀性耦合了涂层内部微细孔隙形貌、尺寸、位置等多种因素，基于机器学习的超声方法能否对其进行准确定量表征，这些问题还有待研究。

针对上述问题，本研究建立孔隙率相同、孔隙分布状态不同的AlSi-PHB封严涂层随机多相介质模型，利用MSAAF技术获取封严涂层孔隙分布均匀性参数绝对斜率和均匀性长度，提取涂层顺序界面超声回波的时域、频域及小波分解时频域衰减系数，结合BPNN分别预测绝对斜率与均匀性长度，实现封严涂层孔隙分布均匀性的超声定量表征，并对上述3种衰减系数及其预测结果进行对比分析。

1 原理

1.1 面积分数多尺度分析技术

对于在介质中随机分布的面积分数为、平均直径为的第二相颗粒，可将介质区域划分成若干边长为的子区域，使用每个子区域中颗粒含量的变化来表示其空间分布均匀性。如图1所示，MSAAF曲线反映的是式(1)中面积分数的变化系数CV()与标准化子区域尺寸/的关系。

图1 随机分布颗粒的MSAAF曲线(双对数坐标)[9]Fig.1 MSAAF curve of randomly distributed particles (lg-lg coordinates)[9]

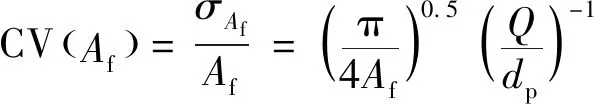
(1)

式中：为各子区域颗粒面积分数标准差。均匀性长度定义为面积分数局部变化不超过1%时对应的标准化子区域尺寸，与曲线斜率绝对值共同表示颗粒分布均匀性。越小、越大，表明介质第二相颗粒分布均匀性越差。

1.2 超声衰减与小波变换

超声波在封严涂层的异质界面处发生散射，这种散射导致的超声衰减携带了大量有关涂层组成相分布均匀性的信息。常用的超声衰减特征包括时域和频域衰减系数：

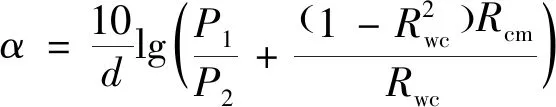
(2)

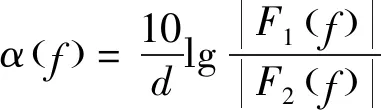
(3)

式中：为超声衰减系数；为涂层厚度；和分别为水/涂层、涂层/基体界面反射波峰值；为超声波从水中垂直入射到涂层中的声压反射系数；为超声波从涂层垂直入射到金属基体中的声压反射系数；为超声波频率；()、()为两界面波幅度谱。小波变换是一种时频局域化的多尺度信号分析方法，适用于处理非平稳超声宽带信号。连续小波变换为

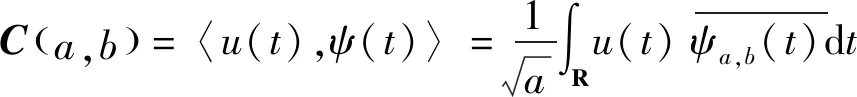
(4)

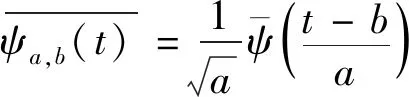
(5)

式中：(,)为超声信号()的小波系数矩阵；为时间；()为母小波函数；为尺度因子；为实数集；,()为任意小波族母函数；为平移因子。采用矩形窗截取脉冲信号顺序界面回波，经小波分解后在尺度(为分解层数，=1,2,…,)下对应的小波系数分别记为(,)和(,)，则尺度下的超声衰减系数可表示为

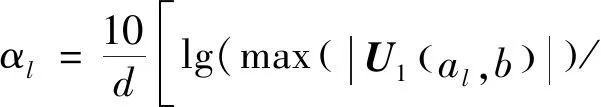
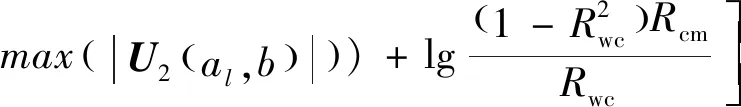
(6)

1.3 BP神经网络

BPNN由输入层、隐含层和输出层组成，常用3层BPNN如图2所示。通过并行分布的信息处理方式自适应训练，能够模拟任意非线性输入-输出关系，适用于非线性预测。

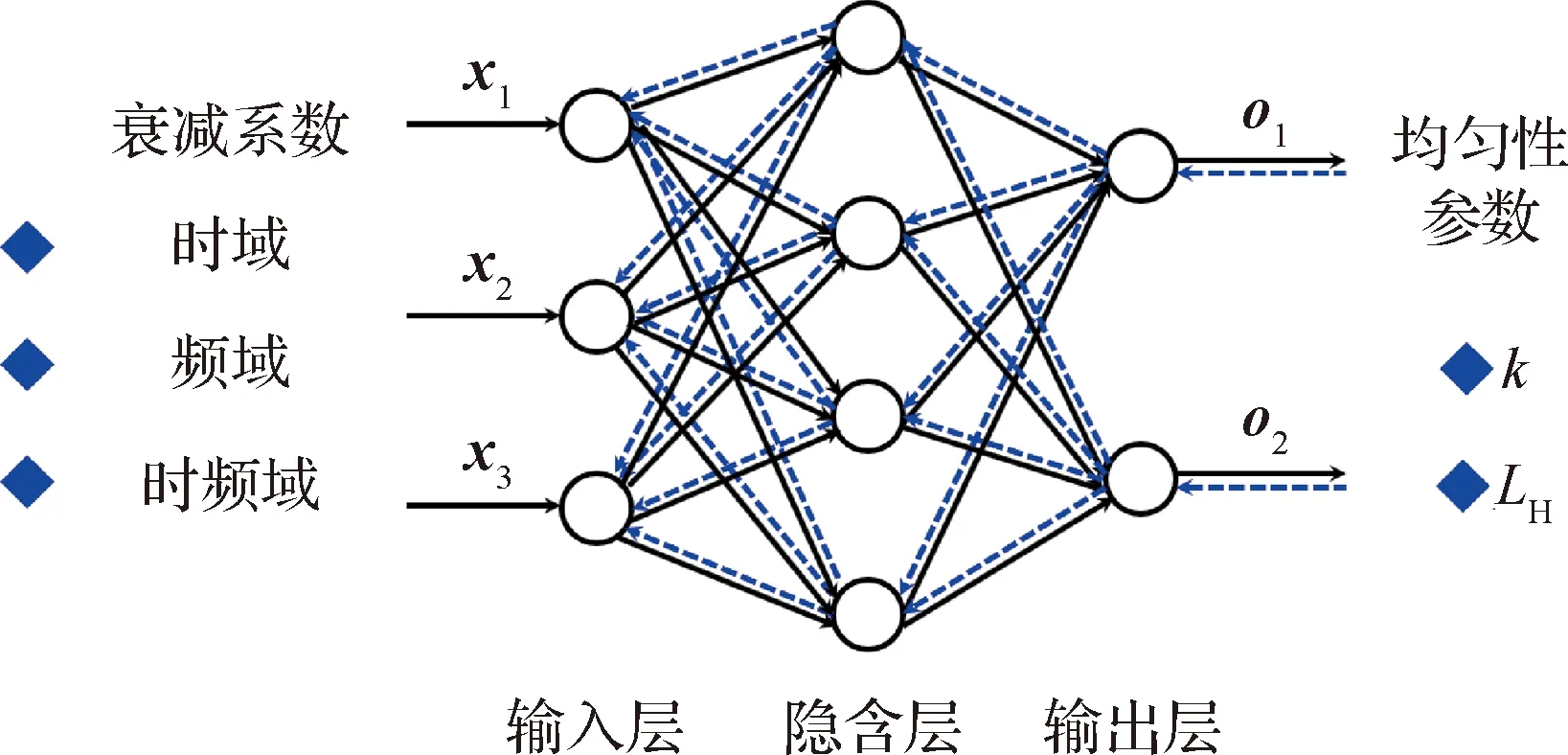
图2 经典3层BPNN架构Fig.2 Classical 3-layer BPNN architecture

设有个输入、输出训练样本向量，分别以、表示(=1,2,…,)，其中输入向量为=[1,2,…,]，=1,2,…,，网络输出向量为=[1,2,…,]，=1,2,…,，目标输出向量为=[1,2,…,]。记为输入向量的第个分量映射到输出向量的第个分量的权重，该权重在第一次计算时随机分配。BPNN通过输出结果的反馈，利用梯度最速下降法修改权重，使网络输出值与目标值的误差平方和最小，见式(7)。不断重复上述过程，直到误差小于设定阈值。

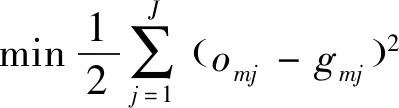
(7)

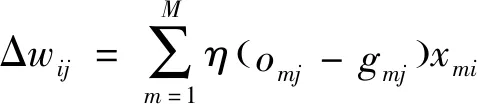
(8)

式中：为学习速率，表示每次更新权重的程度。

2 建模与数值仿真

2.1 封严涂层随机多相介质模型

基于随机介质理论和统计学方法建立的随机多相介质模型(Random Multi-phase Medium Model，RMMM)已被证实能够较为灵活地反映非均匀介质组成相形貌的多样性和随机性。使用高斯-指数混合型椭圆自相关函数(,)构建随机场，其表达式为

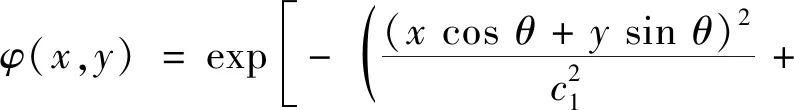
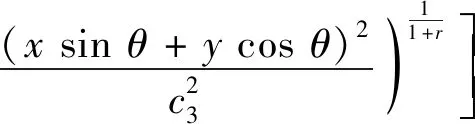
(9)

式中：和分别为二维平面中点的横、纵坐标；为孔隙取向角，即孔隙等效椭圆长轴与轴方向的夹角，如图3所示；和分别为随机介质在对应旋转坐标轴方向上的自相关长度，和越小则孔隙越细小弥散，和越大则孔隙越容易聚集长大；为粗糙度因子。这些孔隙分布参数可通过封严涂层显微图像的参数反演获取。

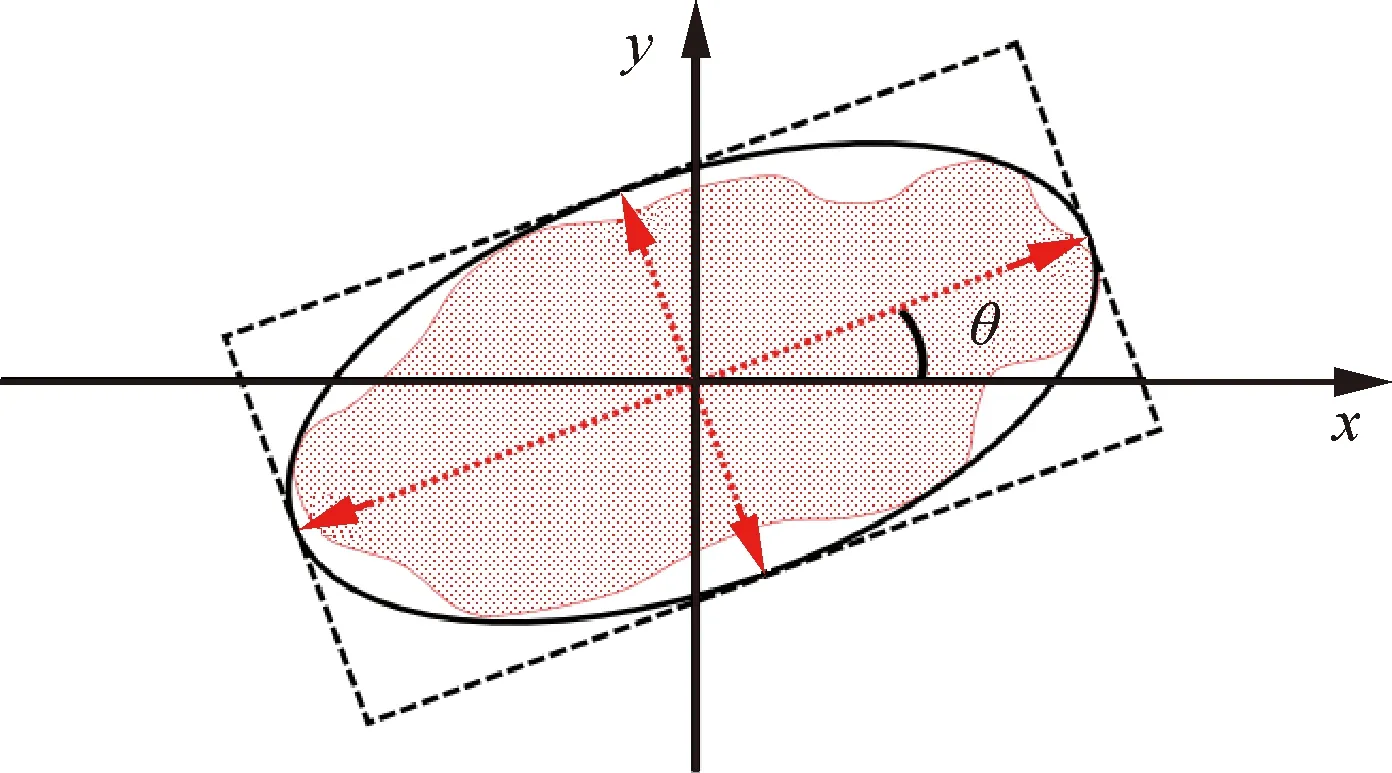
图3 孔隙取向角θFig.3 Orientation angle θ of pore

将封严涂层试样切割、镶嵌、研磨、抛光、超声清洗后，采用激光共聚焦显微镜进行观测。试样及其横截面显微图像如图4所示。使用Image-Pro Plus软件对显微图像进行预处理，并按各相灰度进行阈值分割，得到仅含孔隙的图像。由孔隙密度分布计算其功率谱，经傅里叶逆变换得到服从空间分布自相关函数的二维序列′(,)，将其与自相关函数进行最小二乘拟合，反求、、、等孔隙分布参数。图5给出了孔隙分布参数获取流程。选取不同位置的显微图像，对孔隙分布状态进行观测分析。图6为孔隙取向角的分布情况，可见封严涂层孔隙分布无明显取向。

图4 AlSi-PHB封严涂层试样与显微图像Fig.4 Sample and metallograph of AlSi-PHB seal coating

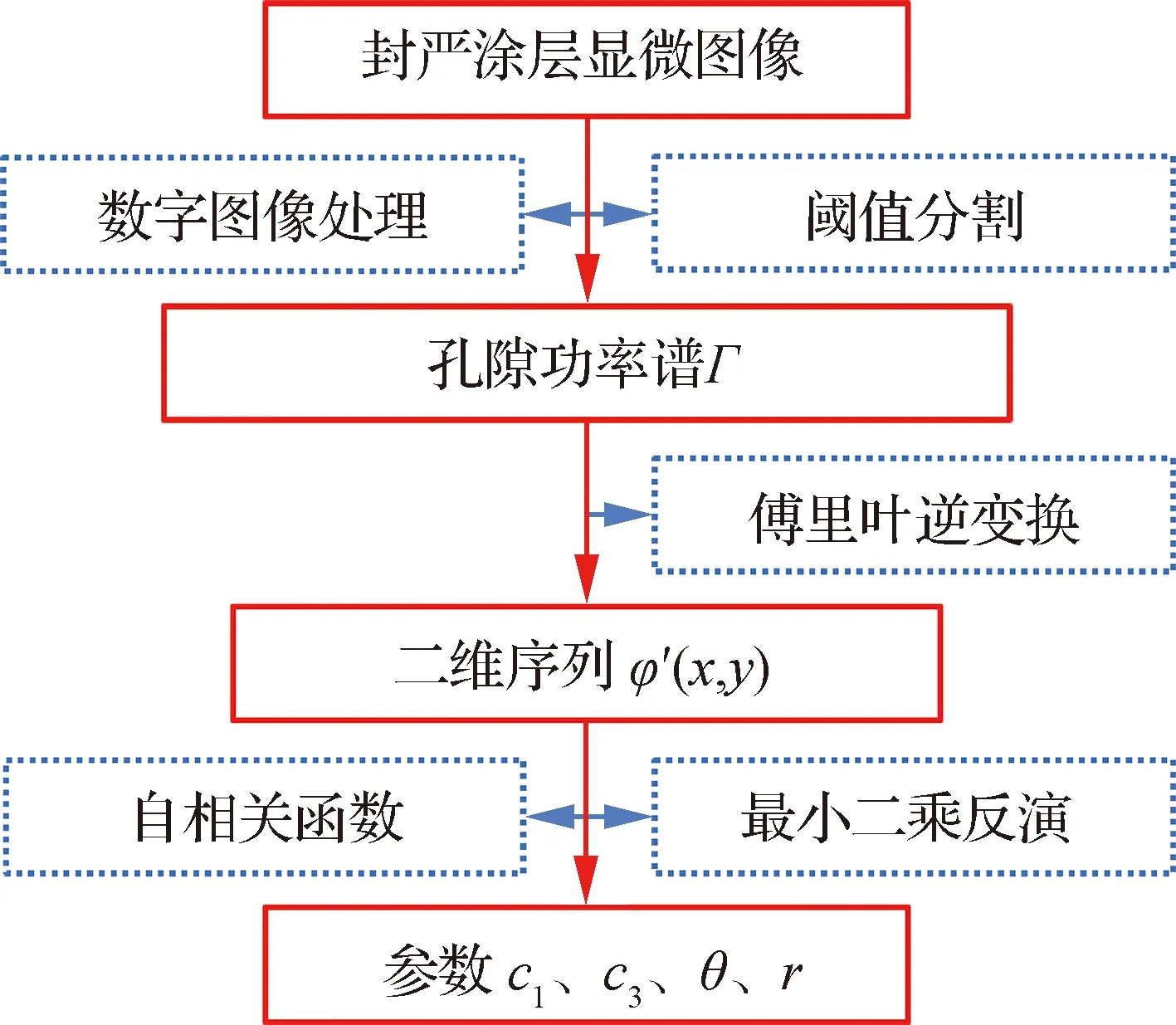
图5 封严涂层孔隙分布参数获取流程Fig.5 Flow for obtaining pore distribution parameters of seal coating

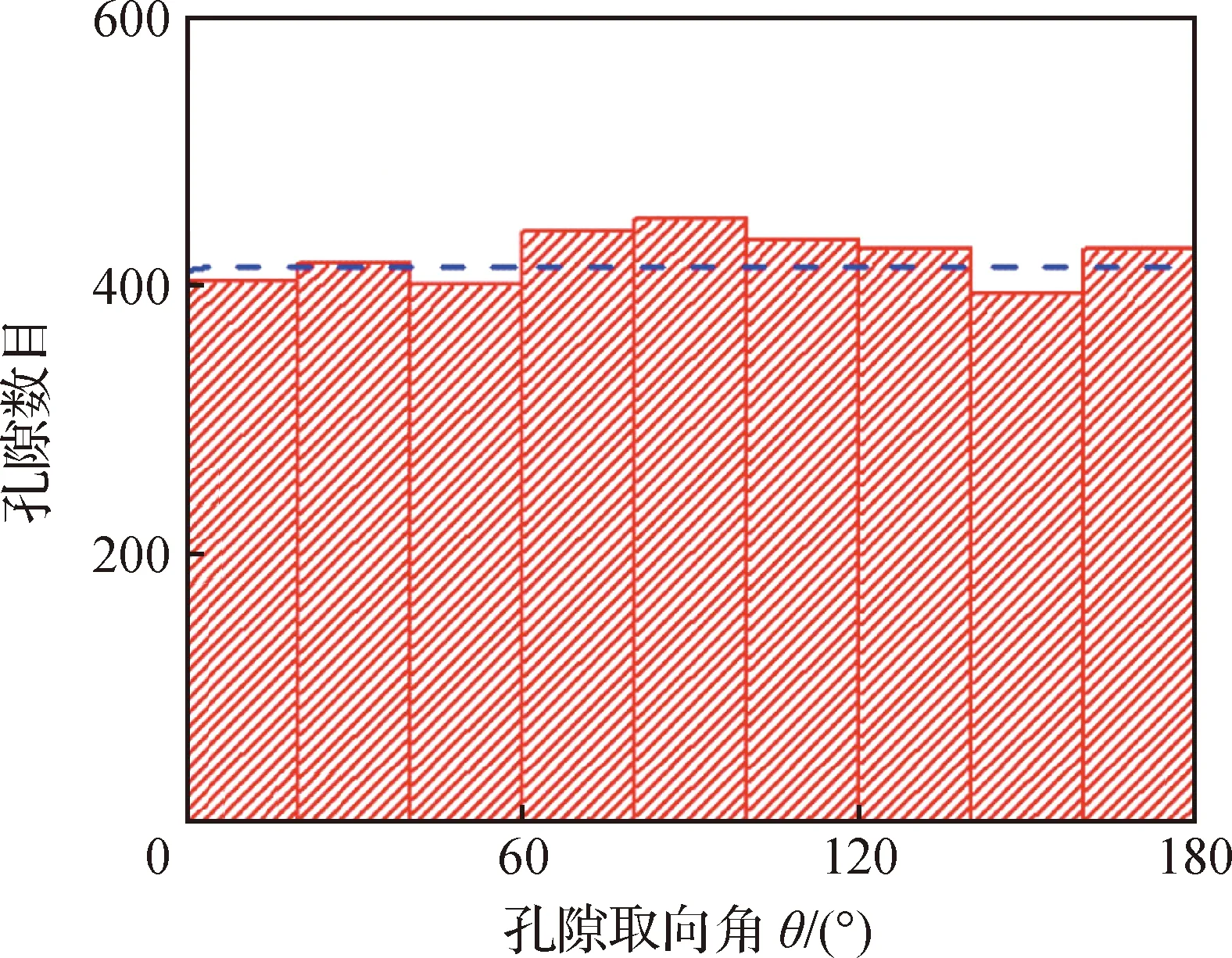
图6 AlSi-PHB封严涂层试样孔隙取向分布Fig.6 Pore orientation distribution of AlSi-PHB seal coating samples

理论上随机介质的自相关长度不同，表示在对应方向上随机介质扰动的平均尺度不同，非均质体随机分布状态也不同，因此先通过调节自相关长度参数和得到不同分布状态的随机多相介质模型，再用与对其均匀性进行准确定量描述。依据实验统计的孔隙分布参数构建5组共25个尺寸为2.0 mm×1.0 mm(1 mm=540 px)、孔隙率为5%的随机多相介质模型，设置每个模型自相关长度=，5组模型自相关长度分别设为6、8、10、12、14 px，对应平均尺寸为11～26 μm，每组包含5个随机状态，孔隙分布如图7所示。每组中4个模型的超声数值仿真结果用于BPNN的训练，剩余1个结果用于孔隙分布均匀性的预测。

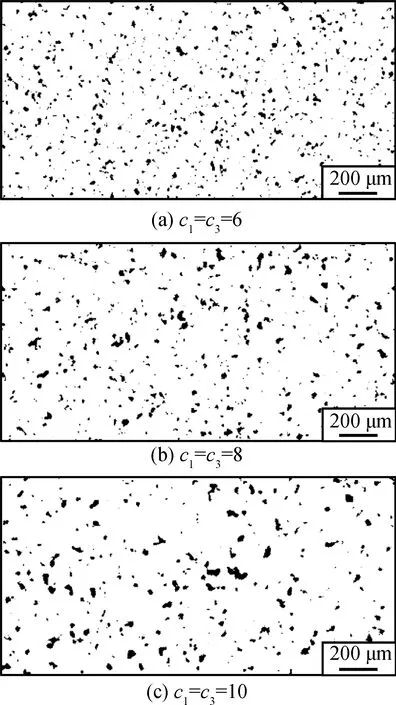
图7 AlSi-PHB封严涂层RMMM的孔隙分布Fig.7 Pore distributions of RMMMs for AlSi-PHB seal coating

2.2 孔隙分布均匀性参数

在进行图像子区域划分时，过大则子区域数目过少，不满足统计学要求，图像的MSAAF曲线末端易出现随机波动，影响参数计算。设的最大值为1/10模型短边长，计算得到的MSAAF曲线如图8(a)所示。所有模型的与分布如图8(b)和图8(c)所示，可见随自相关长度增大，从0.86减小至0.76，从550 μm增大至6 785 μm，即若要实现模型孔隙面积分数的局部变化小于1%，所需最小标准化子区域尺寸从550 μm增大至6 785 μm，表明模型孔隙分布均匀性降低。

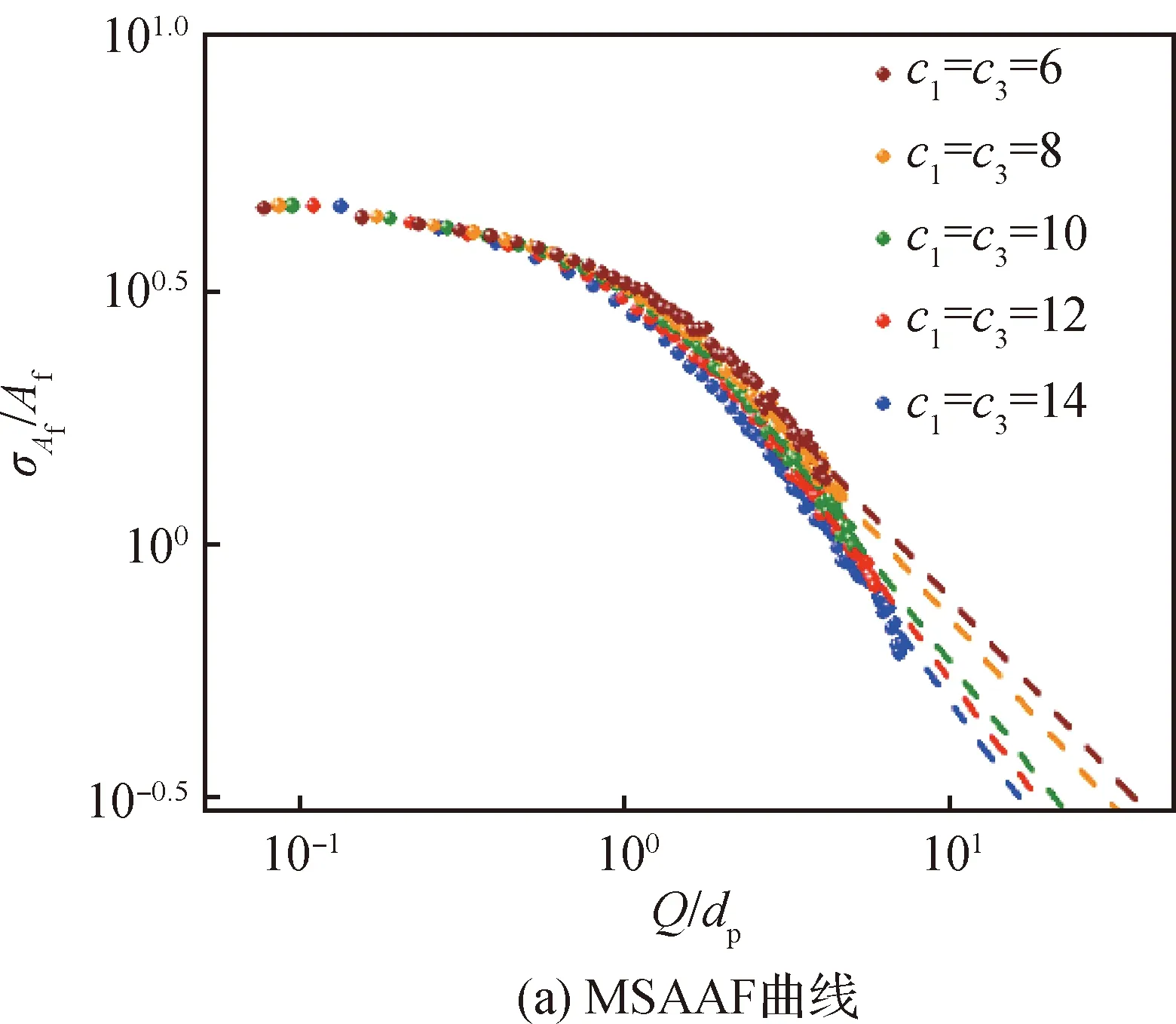
图8 均匀性参数计算Fig.8 Calculated uniformity parameters

2.3 超声检测建模与仿真

AlSi-PHB封严涂层超声检测数值仿真模型如图9所示，模型宽度为2.0 mm，水层厚度为1.5 mm，涂层和基体(GH4169)厚度分别为1.0 mm 和2.5 mm。激励源和接收探头设置在水层上表面，选用中心频率为5 MHz的高斯正弦型脉冲作为激励函数，其他材料参数见表1。

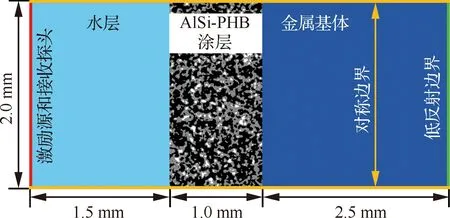
图9 AlSi-PHB封严涂层超声数值仿真模型Fig.9 AlSi-PHB seal coating model used for ultrasonic numerical simulation

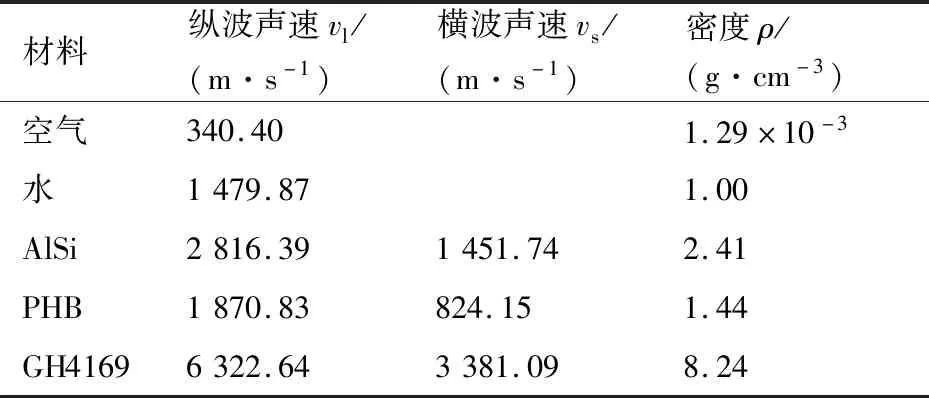
表1 超声数值仿真模型材料参数Table 1 Parameters of material used for ultrasonic numerical simulation

3 结果与讨论

3.1 衰减系数特征提取与分析

封严涂层随机多相介质模型超声仿真结果如图10(a)所示。采用矩形窗分别截取水/涂层、涂层/基体界面回波，对应幅度谱如图10(b)所示，计算得到探头的-6 dB有效频带宽度为2.88～7.11 MHz。由图10(b)可知，超声波在传播过程中的散射衰减造成了涂层顺序界面回波在一定程度上的主频偏移，当使用有效频带内的衰减系数表征材料结构时，这种偏移可能会产生影响。

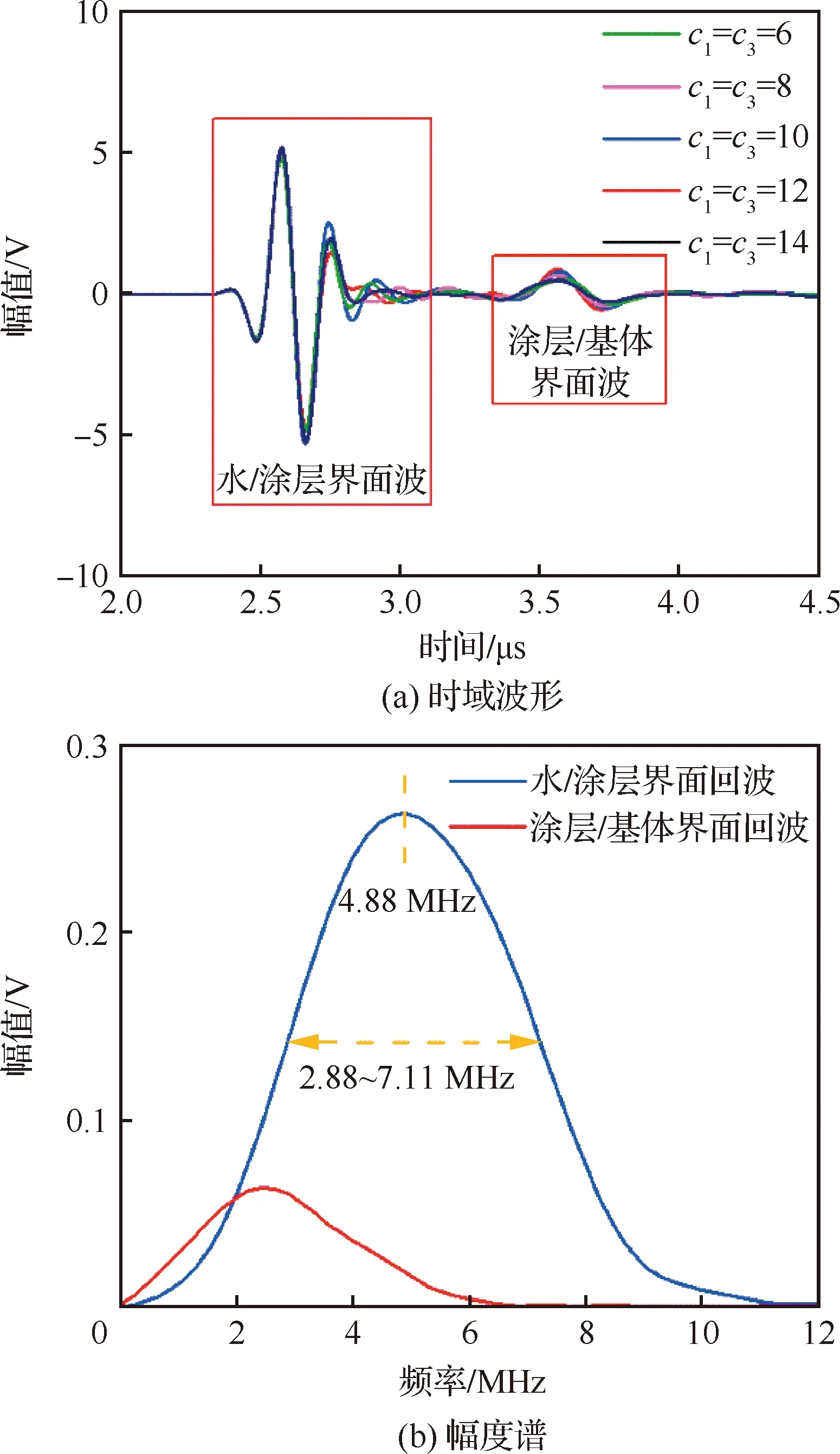
图10 AlSi-PHB封严涂层超声数值仿真结果Fig.10 Ultrasonic simulation results of AlSi-PHB seal coating

采用gaus3小波分解有效频带内的涂层顺序界面回波，考虑到计算效率，将每个超声信号分解为64个尺度下的信号分量。根据式(2)～式(5)计算仿真结果的3种衰减系数，如图11所示。由图11(a)可知，随着孔隙分布均匀性降低，时域衰减系数逐渐增大，但数据离散程度较大，线性关系不明显。图11(b)中，在频率低于5 MHz时，总体呈现出随孔隙分布均匀性降低衰减系数及其斜率均增大的趋势；但均匀性较差时，由于涂层内部散射、噪声严重，衰减系数存在局部突变点；当频率高于5 MHz时，这种线性规律不复存在，分析可能是由于频率已超出涂层/基体界面回波的有效频带范围，或涂层组成相尺寸不一导致涂层中存在着多种散射衰减机制。图11(c)显示小波分解时频域衰减系数随孔隙分布均匀性降低而增大，且与小波分解尺度(即对应频率)呈清晰的线性关系，通过该衰减系数能较为清晰地分辨不同均匀性的涂层，这或许有助于BPNN在训练过程中建立衰减系数与均匀性之间的关系。

图11 衰减系数随孔隙分布均匀性变化Fig.11 Variations of attenuation coefficients with pore distribution uniformity

3.2 预测结果与讨论

使用BPNN对时域、频域及小波分解时频域衰减系数进行训练并预测两均匀性参数和。引入均方根误差RMSE和决定系数对BPNN的预测性能进行评价：

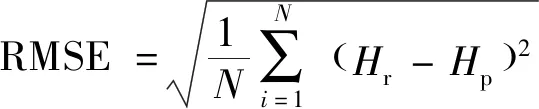
(10)

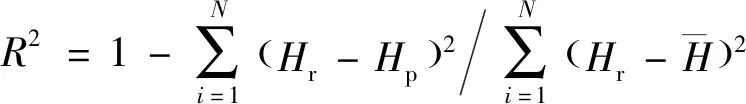
(11)

式中：为信号数量；为实际均匀性参数；为预测均匀性参数。决定系数体现预测值与实际值的偏离程度，均方根误差能反映BPNN的预测稳定性。

预测结果如图12所示。对于参数，时域、频域及小波分解时频域衰减系数预测结果的RMSE分别为0.03、0.02、0.01；分别为0.74、0.88和0.97；对于参数，3种衰减系数预测结果的RMSE分别为1 546.26、401.15、267.81；分别为0.41、0.96和0.98。由此可见使用小波分解时频域衰减系数训练的BPNN能较好地预测封严涂层孔隙分布均匀性参数和，相比时域和频域衰减系数的预测结果准确性更高。

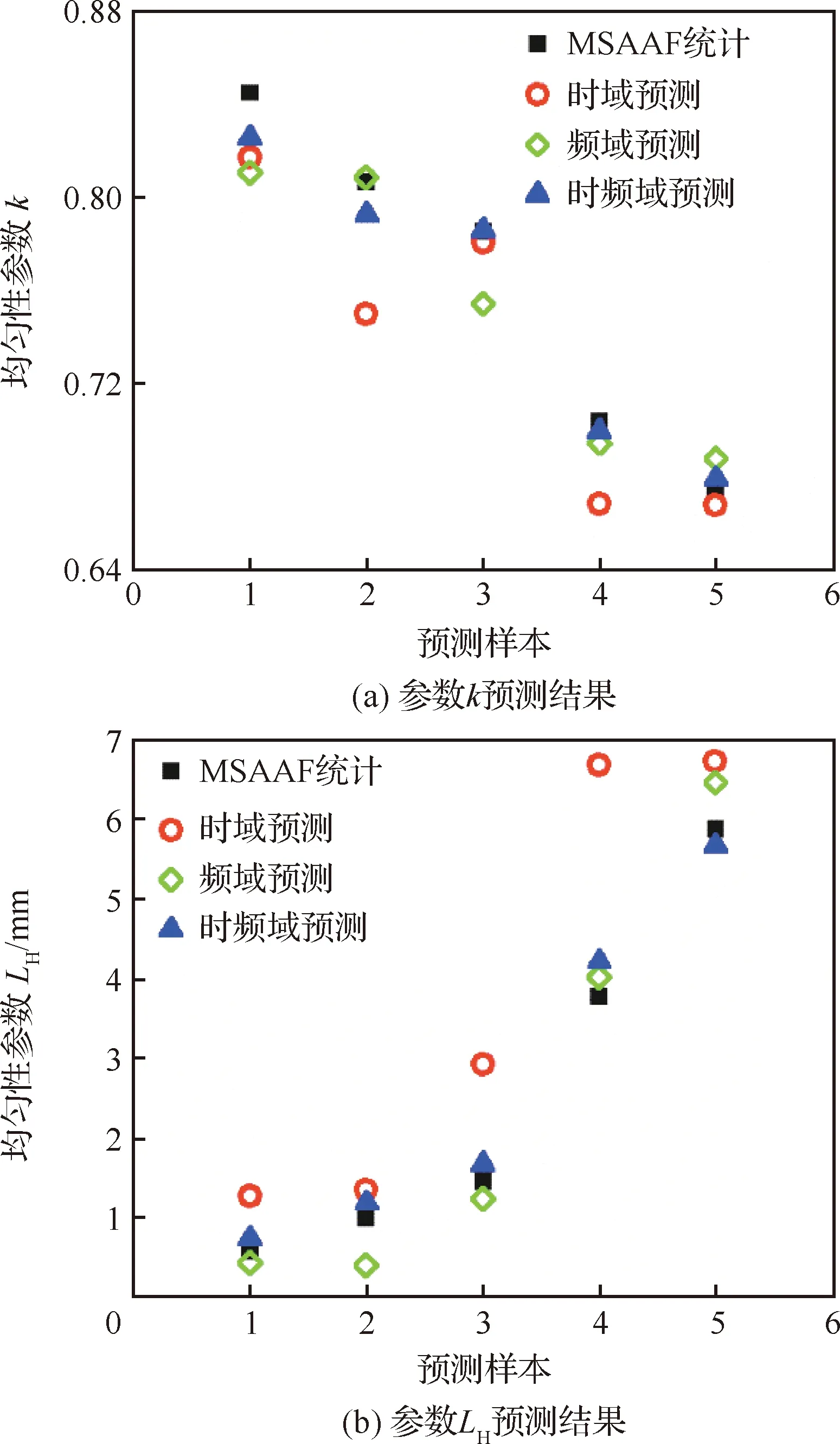
图12 基于超声时域、频域、时频域衰减系数的BPNN预测孔隙分布均匀性参数Fig.12 Pore uniformity parameters predicted by BPNN based on ultrasonic attenuation coefficients in time domain, frequency domain, and time-frequency domain