韧性无人机群多域协同方法建模与求解
2022-07-04孙沁李鸿旭王毓智周丽萍张英朝
孙沁,李鸿旭,王毓智,周丽萍,张英朝
中山大学 系统科学与工程学院,广州 510006
无人机(Unmanned Aerial Vehicle, UAV)因具有移动性强、部署灵活等特点被广泛应用于通信中继、搜索救援、军事对抗等领域。尤其是在军事对抗领域,无人机凭借其执行任务时间长、生产周期短、价格低廉等优势,被应用于情报侦察、电子干扰、火力打击等行动中。在军事智能化的背景下,战场环境更加复杂,单架无人机常常无法满足任务需求,无人机群(Unmanned Aerial Vehicle Swarm, UAVS)受到了国内外学者的广泛关注。无人机群是通过多架无人机相互协作实现整体效能的倍增,使其态势感知更灵敏、作战协同更高效、遂行作战更持久。
构成机群的无人机数量多、协作关系复杂,容易受环境干扰,使其安全、可靠运行是任务成功的关键。现研究分别从无人机群鲁棒性、可靠性及韧性等性质展开。由于韧性不仅包含了抗干扰能力,同时涵盖了恢复能力,能更加全面表征从抵抗到受损、再从受损到恢复的过程,成为近年来研究的热点。
韧性概念最初由生态学家Holling提出,用于衡量生态系统在扰动环境下的抵抗、恢复等能力。现研究大部分围绕韧性评估、韧性优化等内容展开。Tran等通过网络对干扰的吸收、恢复及适应时间,提出了具有波动因子的网络韧性定量评估方法。Bai等改进了上述方法,并提出了考虑无人机通信距离限制的无人机群韧性评估模型。Cheng等结合侦察无人机的使命特性,从对扰动的吸收和恢复两方面的能力,定量分析了面向任务的无人机群的韧性。韧性优化是以韧性评估结果为准则,通过优化方法,提高研究对象的韧性。崔琼等通过节点修复的方式,提高网络信息系统的韧性。该方法可适用于造价较高的单系统,并不适用于数量大、成本低的无人机群。Tran和Mavris提出了通过链路随机重连的方式重构受攻击的指控网络,从而提高网络的韧性,但该方法在重要节点遭受攻击后,性能提升效果受限。Chen等结合了博弈论的子博弈精炼均衡方法提高无人机通信网络的韧性。Ordoukhanian和Madni研究了受攻击时无人机之间策略的调整、协同,提高了多无人机系统的韧性。上述方法计算复杂性高,使得应用范围局限于数量较少的无人机群,无法扩展到大数量、多区域执行任务的无人机群上。
因此,为了有效克服节点修复方式成本代价高、链路重连方式性能恢复能力有限等问题,提高无人机群的韧性。本文针对无人机群在复杂战场环境下的韧性优化方法展开研究。首先,对韧性无人机群恢复因子进行改进,使其更准确表征无人机群面向任务基线的恢复过程;其次,提出一种韧性无人机群多域协同方法,通过多域无人机群之间的自组织接替协同以提高无人机群韧性;最后,对方法性能进行仿真验证。
1 基本概念
1.1 无人机群网络建模
针对无人机群的多区域侦察任务,根据任务需求,构建不同结构、不同数量的无人机群。如图1 所示,无人机群UAVS1、UAVS2、UAVS3分别对区域、、执行侦察任务。
通常将无人机群拓扑为复杂网络,从整体角度研究无人机群之间的协同性、涌现性。如图2 所示,将图1中每架UAV视为复杂网络模型中的节点,UAV之间的通信链路视为节点之间的边。机群间通信仅用于传递各机群状态,不在本文研究范围之内,故可忽略。从而构建基于复杂网络=(,)的无人机群模型。
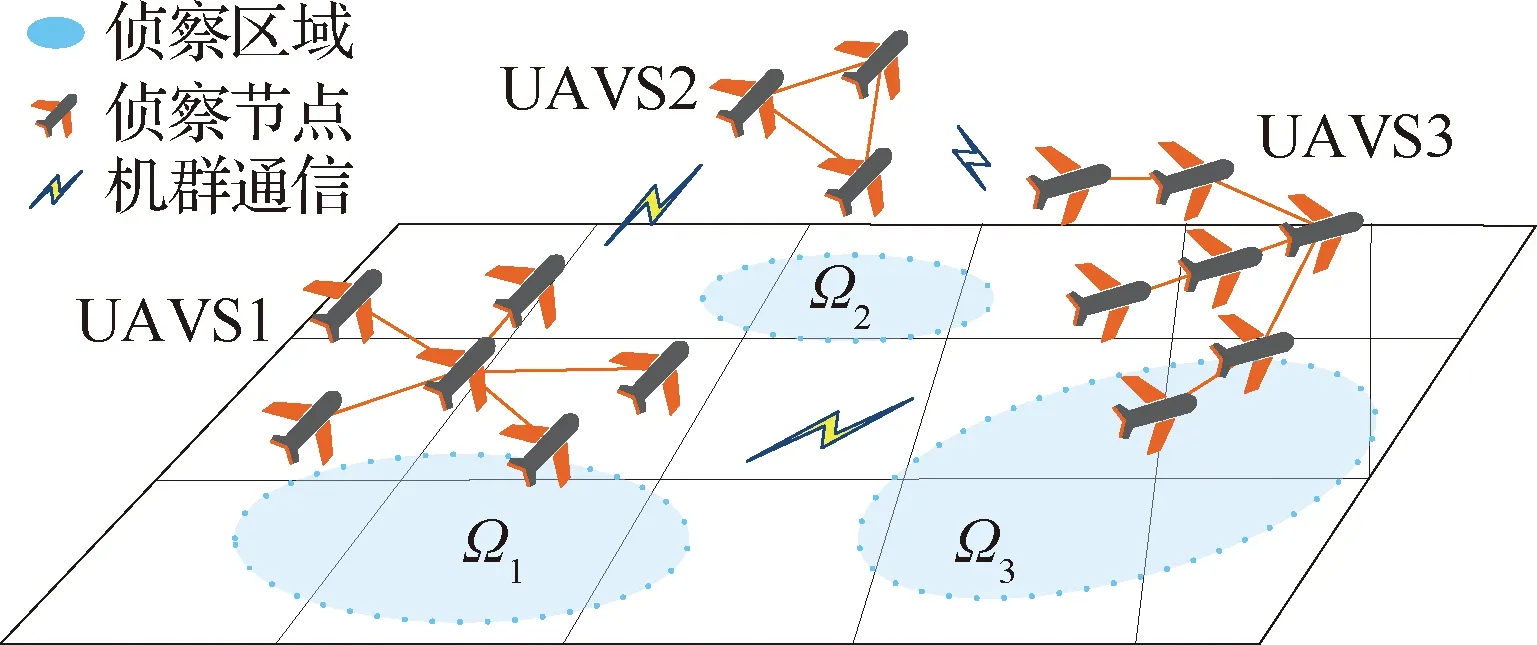
图1 侦察无人机群示意图Fig.1 Schematic diagram of reconnaissance UAV swarms
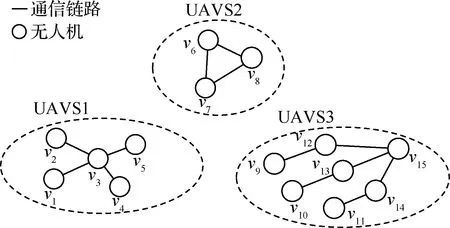
图2 无人机群的复杂网络拓扑模型Fig.2 Complex network topology model of UAV swarms
假设共有架无人机分为个机群,同时在个区域执行侦察任务,其中=,故可建立侦察网络模型
=∪∪…∪
(1)
式中:为架无人机组成的侦察网络;,,…,分别为第1,2,…,个无人机群子网络。
第个无人机群的网络模型为
=((),())=1,2,…,
(2)
式中:()为第个子网络中的无人机节点集合;()为第个子网络中无人机节点之间的连接关系集合。
无人机群网络模型中,节点之和为,且各子网络之间节点不相交,即
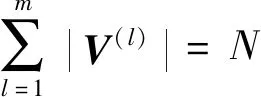
(3)
∩∩…∩()=∅
(4)
1.2 韧性无人机群
无人机群数量众多、分布广,易受到敌人的攻击。为更好反映节点受到攻击或发生自损时面向任务的执行情况,引入韧性的概念,用于描述无人机群在执行任务过程中,对外界扰动的抗压能力与恢复能力。结合文献[21]韧性概念,本文定义了韧性无人机群。
韧性无人机群是指在面对攻击或自损时,具备抵抗、恢复等韧性过程,以达到完成特定任务需求的无人机群。
韧性无人机群的韧性过程如图3所示。为任务基线,表征无人机群执行某特定任务时应达到的基本标准;为无人机群在初始时刻的性能值,具备一定的冗余配置,所以其值略高于任务基线;在时刻,遭受攻击或自损时,出现性能下降;在时刻,达到最低值;此时,无人机群执行恢复策略,使性能回升;在时刻,恢复至稳定值,直到时刻任务结束。
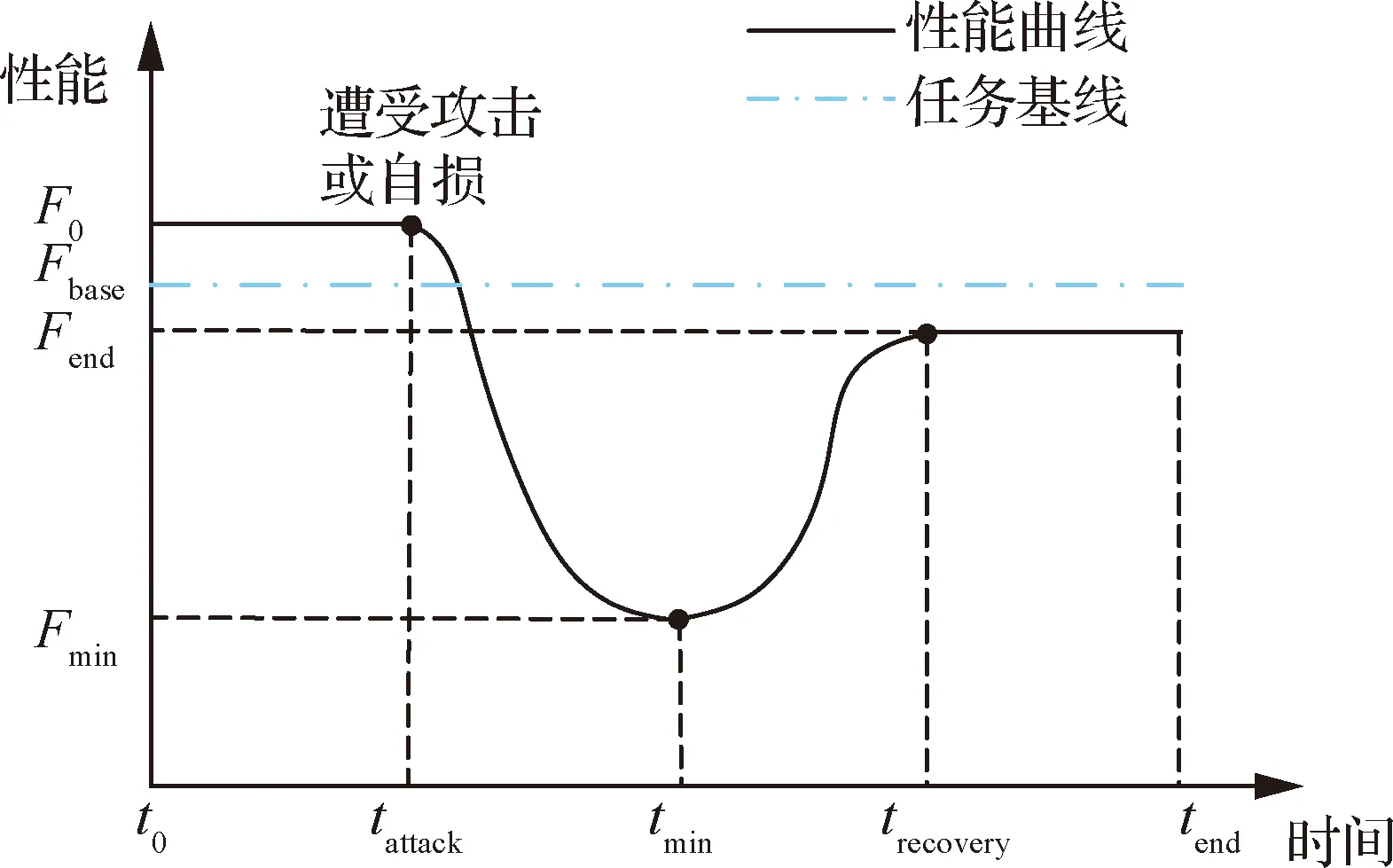
图3 无人机群的韧性过程Fig.3 Resilience process of UAV swarms
1.3 韧性无人机群恢复因子
文献[7]基于性能变化曲线,从总体性能变化、鲁棒性、快速性和恢复度描述了韧性度量指标。其中恢复度为
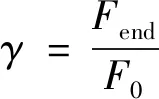
(5)
然而,在实际执行过程中,因为冗余配置的存在,并不需要完全恢复至初始性能,只需要达到任务基线即能确保任务的完成。在此基础上,提出韧性无人机群恢复因子′,表征韧性无人机群执行恢复策略后所能达到的性能相对于任务基线的恢复程度,能更准确表征无人机群面向任务基线的恢复过程,更贴近实际应用。′的计算公式为
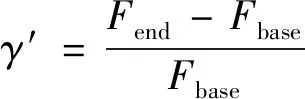
(6)
式中:′≥0时,表示无人机群通过恢复策略可确保完成任务;当′<0时,表示无人机群出现了功能降级,恢复策略只能恢复部分性能,影响了任务的完成。
2 韧性无人机群多域协同方法建模
2.1 多域协同过程
韧性无人机群多域协同方法是指在执行任务的多个无人机群遭受攻击后,部分无人机群无法满足任务要求。此时,无人机群自组织执行接替协同,即指派使目标函数最大化的无人机群执行多域协同方法,具体的多域协同过程为:按特定规则指派满足任务要求的无人机群中的非重要无人机,去接替受损无人机,使得各个无人机群均能满足任务要求。
方法示例如图4所示,假设无人机群UAVS1、UAVS2对区域、执行侦察任务过程中遭受攻击,UAVS2凭借自身恢复策略仍能确保任务完成,而UAVS1由于无人机的战损,导致无法满足任务要求。此时,通过组织协同UAVS2中的无人机接替UAVS1中受损无人机,并以一定的概率与受损链路进行重连,使UAVS1性能恢复至基线以上。UAVS2因的离开,性能出现一定的下降,但依旧能满足任务要求。该方法通过多域无人机群的协同,确保在遭受攻击时,UAVS1、UAVS2均能完成任务。
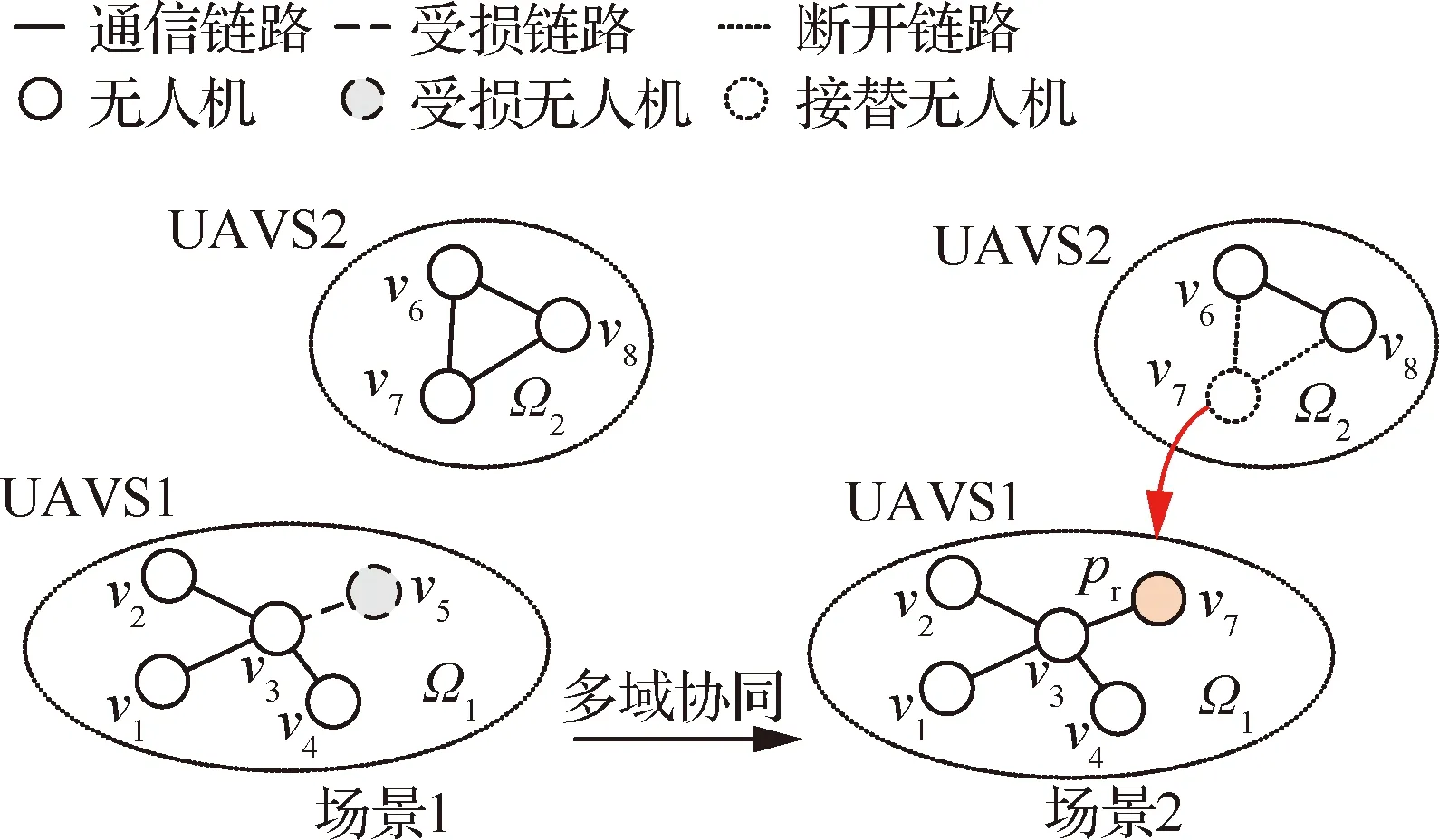
图4 无人机群多域协同示意图Fig.4 Schematic diagram of multi-domain collaboration of UAV swarms
2.2 模型构建
2.2.1 模型假设
针对上述内容,可建立多域协同模型。首先,对模型做以下假设:
1) 无人机节点受损或参与协同时,与该节点相连的边也同时断开。
2) 参与协同的无人机以节点最小度优先脱离原无人机群,若节点度相同,则随机断开。
3) 参与协同的无人机以受损节点最大度优先接替,若受损节点度相同,则随机接替。
4) 参与协同的无人机以一定重连概率(∈[0,1]),与原断开的边重新建立连接,用以反映接替的不确定性,从而更接近现实场景。
2.2.2 性能函数
假设架无人机在个区域执行侦察任务时,其总体性能可表示为各区域性能之和:
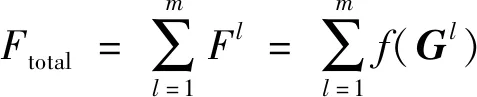
(7)
式中:为第块区域无人机群的性能;()为与无人机群构成的子网络之间的函数值;()可采用文献[11]中对无人机节点收发的信息数量来表示
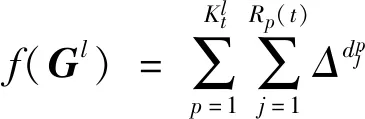
(8)
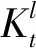
2.2.3 参数变量
设协同变量=[,,…,],且∈[1,],∈。当>0时,表示无人机子群中被接替节点的数量为||个;当<0时,表示脱离无人机子群的数量为||个;当=0时,表示无人机子群参与协同后数量保持不变。整个协同过程中,没有外界新节点的加入,故协同数量之和为0,即

(9)
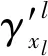
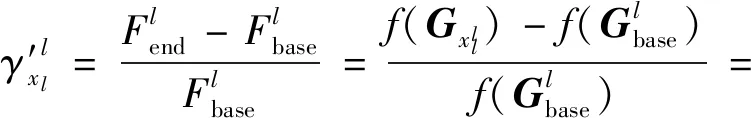

(10)
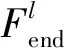
2.2.4 目标函数
无人机群在受到攻击后,部分区域不能满足任务要求,通过其他无人机群的协同,以确保任务的完成。所以,在协同过程中,应优先确保任务的完成。在任务完成的基础上,使得恢复因子越大越好,可建立目标函数

(11)

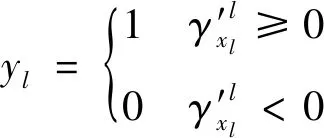
(12)
式中:=1时,表征无人机群已恢复到任务要求;=0时,表征无人机群未恢复到任务要求。∈为满足约束式(13) 的一个较大正实数
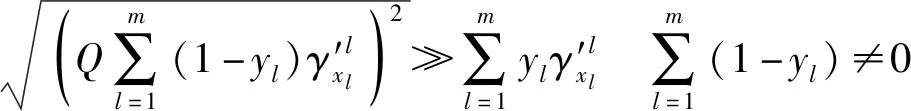
(13)
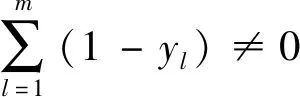
3 韧性无人机系统模型求解
根据韧性无人机群多域协同模型,设计了相应的协同算法,如算法1所示。该算法通过输入无人机群的模型={,,…,}、迭代次数,得到协同节点对集合。
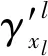
其次,在执行算法过程中,为使式(11)最大,则可等效为使参与协同的无人机群在协同前后性能变化最小,受接替无人机群在接替前后性能变化最大,证明过程如附件A所示。算法1第6~7行表示获取参与协同的机群和接替的机群。
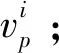
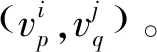
最后,输出相应的协同节点对集合,使得各无人机群满足任务要求,且目标函数最大。

算法1 多无人机群多域协同算法
4 应用案例分析
4.1 应用场景假设
为验证文中所提出的方法,构建了一种复杂战场环境下的侦察任务场景。假设根据任务需求,共派出150架无人机,组成5个Barabási-Albert网络结构的无人机群分别对5块区域同时开展侦察任务,构建了=∪∪∪∪的侦察网络,如图5所示。
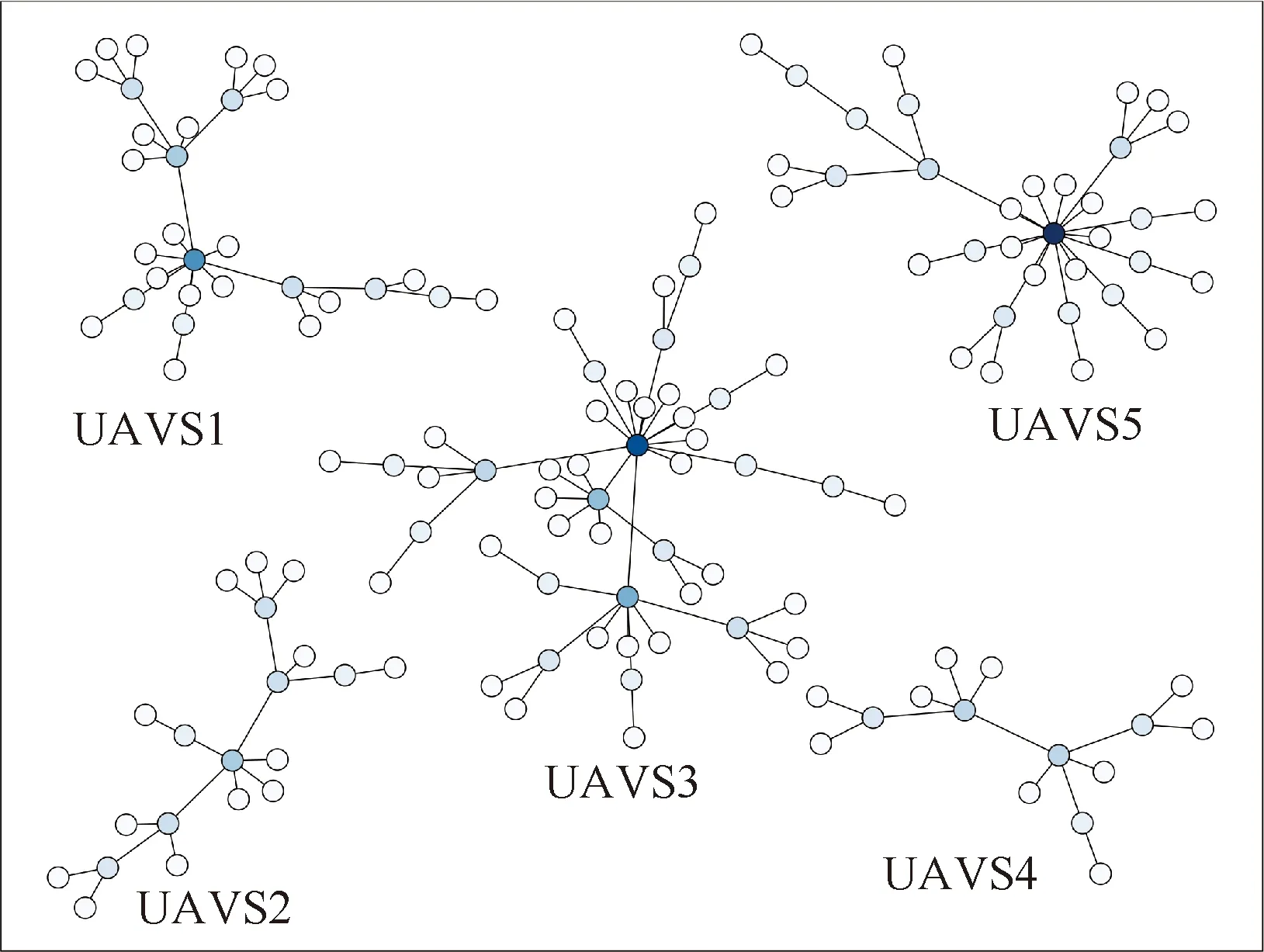
图5 无人机群侦察网络示意图Fig.5 Schematic diagram of UAV swarm reconnaissance network
在随机攻击策略下,无人机节点被随机的击毁,与该节点相连的边也被打断,致使无人机群出现不同程度的损毁。本文通过无人机被击毁的数量来表示损伤程度,并构建了具有不同损伤程度的2个场景。同时,各无人机群具有一定的自恢复能力,即通过增加无人机节点间的通信链路,来提高性能。仿真中设定时长为70 s,在=10~30 s 时,无人机群遭受随机攻击;在=30~50 s时,无人机群执行自恢复策略,即每时刻按重连概率=08随机增加一条边;在=50~60 s时,无人机群执行多域协同策略,令=1。具体参数如表1所示。

表1 无人机群仿真实验参数Table 1 Parameters of UAV swarms simulation
4.2 仿真结果分析
4.2.1 总体性能
根据4.1节设定的实验参数,分别针对场景1、场景2进行了30次独立仿真实验,并将30次实验结果的均值作为性能值输出,其中总体性能等于UAVS1~UAVS5性能之和。
1) 场景1
在随机攻击策略下,导致25架无人机被击毁,各无人机群的毁伤情况如表1所示,各机群的性能曲线如图6所示。在正常执行侦察任务时,无人机群总的性能均值为74.032。假设任务初始配置时具有20%的冗余,为确保完成该侦察任务,无人机群总的任务基线性能需达到59.23,UAVS1~UAVS5的任务基线性能分别为11.89、8.04、18.38、5.99和13.92,如图6(b)~图6(f)所示。
从图6(a)可知,在=10 s时,无人机群开始受到攻击,导致无人机群总体性能发生快速下降,直至在=30 s性能降到最低点47.02,相对于初始性能下降了36.16%。从图6(b)~图6(f) 可知,各无人机群性能均低于任务性能基线以下,从而导致无法完成任务。由于各无人机群中节点受损的数量不同,性能下降程度也不相同,UAVS1性能下降最大,低至5.77,下降了61.28%,其次是UAVS2,低至4.27,下降了57.47%。

图6 场景1无人机群性能曲线Fig.6 UAV swarm performance curves in Scenario 1
在=30 s时,无人机群开始执行自恢复策略,使性能得到了一定程度的恢复,且相对于初始性能恢复了12.3%。UAVS2恢复程度最大,恢复了24.97%。但由于损伤程度不同,经过自恢复策略后,UAVS1、UAVS2、UAVS5仍不能达到任务基线要求,UAVS3、UAVS4恢复到任务基线以上,可确保任务的完成,但冗余性不强。尤其是UAVS4恢复后其性能值与任务基线很接近,极易导致再次低于任务基线以下。这是因为自身恢复策略能力有限,不能使性能整体跃升。因此,需其他无人机群的协同配合,使性能快速提升。
=50 s时,无人机群执行多域协同策略。在执行该策略后,各无人机群的性能得到了快速提升,且在=50~55 s期间,性能恢复程度最大,总体性能恢复至73.96,相对于初始性能恢复了99.86%。各无人机群均恢复到任务基线以上,确保了任务的完成。
进一步比较无人机群自恢复策略与多域协同策略的恢复因子与恢复度。如图7所示。
从图7可知,多域协同策略下的恢复因子与恢复度曲线均高于自恢复策略下的恢复曲线,说明多域协同策略下恢复性能更好。其中,UAVS1~UAVS5自恢复策略下的恢复因子′分别为-0.29、-0.18、0.02、0.09、-0.01。恢复因子在[-0.29,0.02]之间波动,且波动较大,均值为-0.074,方差为1.95%。说明在自恢复策略下,不能确保所有无人机群均恢复至任务基线以上,尤其是针对受损比较严重的UAVS1、UAVS2,恢复因子很难恢复至任务基线以上,而针对损毁相对较小的UAVS3、UAVS4则较为容易。该恢复策略仅可用于局部、小规模的损伤后的修复。在多域协同恢复策略下,UAVS1~UAVS5的恢复因子分别为0.27、0.29、0.21、0.29、0.24,恢复因子均大于0,且相对均匀,均值为0.26,方差为0.1%。说明该策略不仅能够使得各无人机群快速恢复,而且还具有较好的协调性,使得恢复因子比较均匀,恢复后的各无人机群性能相对于任务基线都有较好的冗余性,更有能力抵抗多次打击。如图7中恢复度曲线所示,该曲线与恢复因子曲线相似。在自恢复策略下,UAVS1~UAVS5的恢复度分别为0.58、0.68、0.84、0.88、0.79,恢复度均小于1,说明该策略下,始终出现了功能降级的现象,并不能恢复至初始性能。而在多域协同策略下,UAVS1~UAVS5恢复度分别为1.01、1.03、0.97、1.03、0.99。这是因为在最大度的多域协同接替策略下,不仅接替节点能够很好地完成接替任务,同时未发生接替的节点大部分为影响较小节点或冗余节点,使得协同后性能出现略高于初始性能现象。

图7 场景1恢复因子与恢复度曲线Fig.7 Recovery factor and recovery degree curves in Scenario 1
2) 场景2
在加强攻击后,致使更多的无人机被击毁,数量达到了50架,各无人机群的毁伤情况如表1所示,无人机群性能仿真结果如图8所示。
场景2性能曲线与场景1相似,但在加强攻击后,性能下降更快,=30 s,总体性能下降至最低点32.67。相比于场景1,在攻击数量高出1倍的情况下,性能下降率从36.16%降至55.86%。由图8(b)~图8(f)可知,遭受大强度攻击后各无人机群性能均低于任务性能基线以下,都不能达到完成任务基线要求,且被击毁的无人机主要出现在UAVS3~UAVS5,使得该3个无人机群性能相比于场景1,出现了更大的下降。

图8 场景2无人机群性能曲线Fig.8 UAV swarm performance curves in Scenario 2
在=30 s,无人机群开始执行自恢复策略,使性能得到了一定程度的恢复。其中,UAVS4性能恢复最快,这是由于该无人机群中无人机数量较少,在自恢复策略资源有限,即节点边重新连接数量一定的情况下,性能恢复得更好。但相比于场景1,该场景下的无人机群性能都无法恢复到任务基线以上,仍无法确保完成任务。
在=50 s,无人机群开始执行多域协同策略。在该策略下,无人机群的性能得到了快速恢复,且使性能全部都恢复至任务基线以上,确保了任务的完成。但相比于场景1,各无人机群的性能恢复相对平缓,这是由于受毁节点较多,而接替节点数量有限,仍有部分重要节点没有得到接替。
场景2中无人机群的恢复因子与恢复度,如图9所示。该曲线与图7相似,但均值更小,这是因为攻击强度攻击较大,损毁的无人机较多。UAVS1~UAVS5在自恢复策略下恢复因子均小于0,说明了自恢复策略只能恢复部分性能,恢复后各无人机群仍无法满足任务要求。多域协同策略下的恢复因子均大于0,且相对均衡,说明即使在打击强度较大的场景下,多域协同策略仍具有较好的恢复能力。UAVS1~UAVS5在自恢复策略下的恢复度分别为0.49、0.72、0.58、0.74、0.543。多域协同恢复策略下的恢复度为0.97、0.99、0.87、0.98、0.93,均小于1,说明在较大强度攻击下,无人机群即使通过协同,仍无法恢复至初始性能。
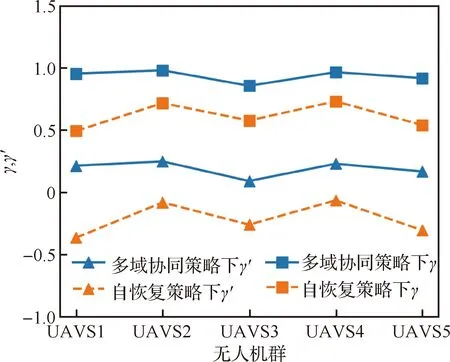
图9 场景2恢复因子与恢复度曲线Fig.9 Recovery factor and recovery degree curves in Scenario 2
通过仿真分析可得,多域协同方法在场景1、场景2下均能很好地恢复无人机群的性能。其不仅能够使性能得到较大的提升,而且在协同后使各无人机群的恢复因子更加均衡,能够更好地抵抗多次攻击,使无人机群具备更强的韧性。
4.2.2 单次协同仿真
选取场景1中无人机群在受攻击后所执行的一次协同策略,并截取=49~53 s各无人机群的性能变化参数,如表2所示。~的基线值分别为11.89、8.04、18.38、5.99、13.90。

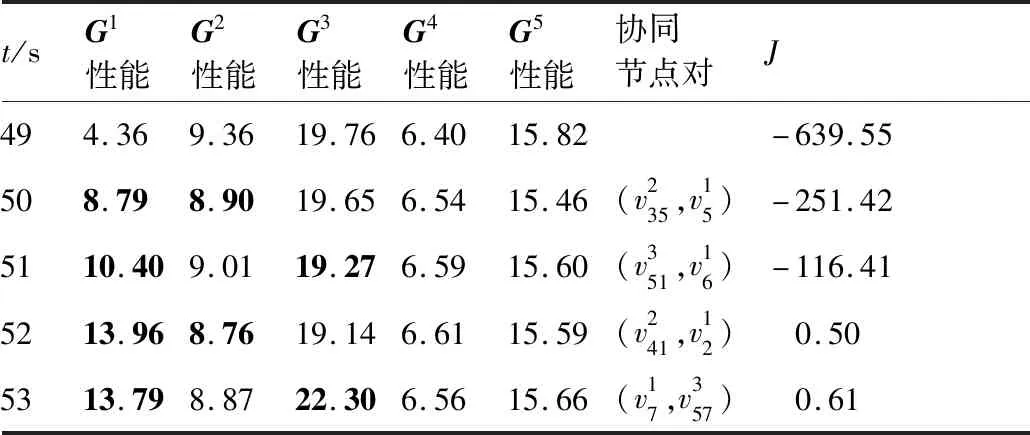
表2 无人机群协同性能变化参数Table 2 Parametric variation of collaborative UAV swarm
通过上述仿真分析可得,多域协同方法能快速恢复不满足任务需求的无人机群的性能,且均恢复至任务基线后通过协同使整体性能相对于任务基线更加均衡。
4.2.3 无人机群韧性
韧性能够度量无人机群在特定任务中对于扰动的响应能力。文献[11-13,15]都针对韧性过程提出了评估方法,本文采用文献[13]中韧性评估模型对场景1、场景2的无人机群进行韧性评估,记录了30次仿真实验的韧性值,如图10所示。
从图10可知,场景1、场景2在多域协同策略下的韧性曲线均高于在自恢复策略下的韧性曲线,在场景1中,多域协同策略和自恢复策略的韧性均值分别为1.26、0.85,韧性值提高了0.41。在场景2中,可得相似结果,多域协同策略和自恢复策略的韧性均值分别为0.95、0.56,韧性值提高了0.39。说明多域协同策略能有效提升无人机群的韧性,在遭受攻击后,更容易恢复性能,从而保持继续完成使命任务的能力。场景1的韧性均值高于场景2的韧性均值,这是因为场景1的攻击强度低于场景2的攻击强度,说明无人机群韧性值会随着攻击强度的不同而不同,且在较低的攻击强度下,韧性更强。

图10 无人机群韧性曲线Fig.10 UAV swarm resilience curves
4.2.4 韧性无人机群多域协同方法对比
针对场景1、场景2设定了3种不同韧性提升方法的对比实验,并从性能、韧性值2个方面对结果进行分析,对比方法如表3所示。

表3 无人机群韧性提升方法对比Table 3 Comparison of improvement methods of UAVS
1) 性能对比
场景1仿真结果如图11所示,本文所提方法1的性能明显优于其他方法,=10~30 s时,曲线大致相同,这是因为相同的无人机群在遭受相同强度的攻击下,所表现出的性能一致,而引起微小变化的原因是攻击的随机性导致的。在=30~70 s时,因为执行恢复策略不同,性能曲线发生不同变化。

图11 场景1无人机群性能对比曲线Fig.11 UAV swarm performance comparison curves in Scenario 1
由图11中方法3的性能曲线可知,在无人机群遭受攻击后,性能不再提升,仅依靠自身的鲁棒性抵抗外部攻击,且性能值小于任务基线,不能满足任务要求,因此需要通过恢复策略提升性能。
对比方法1、方法2可知,2种方法均能使性能得到恢复,并达到任务基线要求。在恢复效果上,方法1恢复效果更好,比方法2高出10.5%。方法1最终能恢复至99.2%,而方法2只能恢复至88.7%。在恢复时间上,方法1恢复速度更快,在=50~60 s内提升了26.5%,而方法2只提升了15.4%。
场景2仿真结果如图12所示,与图11相似。在加强攻击后,本文所提方法1相比于其他方法仍具有较好的恢复能力,最终能恢复至初始性能的93.2%,而方法2只能恢复至80.2%。相比于场景1,方法1、方法2性能分别下降了6.0%、8.5%。这是因为加强攻击后,场景2中损失了更多的节点,导致出现能力降级的现象,但方法1能更好地缓解降级程度。
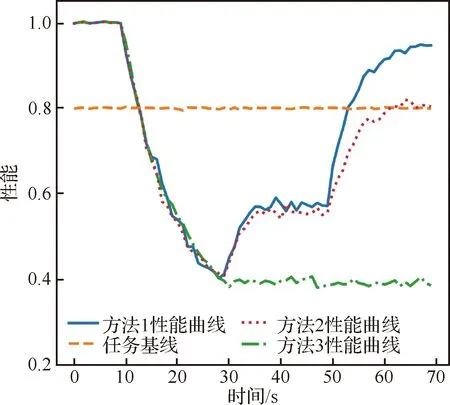
图12 场景2无人机群性能对比曲线Fig.12 UAV swarm performance comparison curves in Scenario 2
2) 韧性值对比
韧性值对比实验中,分别对场景1、场景2的无人机群进行了5次重复实验,并根据文献[13]韧性评估模型对性能曲线进行韧性评估,评估结果如表4所示。
由表4可知,本文所提方法能够获得更高的韧性值。场景1中,方法1比方法2、方法3分别高出0.20、0.51。场景2中,方法1比方法2、方法3分别高出0.20、0.56。

表4 无人机群韧性值对比Table 4 Comparison of UAV swarm resilience value
综合上述对比分析可得,本文所提方法相比于其他方法对无人机群的性能恢复效果更好、恢复时间更快,能有效提升无人机群的韧性。
4.2.5
多域协同方法中参与协同无人机节点的度值与受接替无人机节点的度值对无人机群的韧性过程有重要影响。本节从协同节点度、受接替节点度2个方面进行分析。
1) 协同节点度
仿真中保持2.2.1节模型假设条件3)不变,改变假设条件2),构建依次从最小度节点到第6小度节点优先脱离规则,分别在场景1、场景2中对整个韧性过程进行仿真。
场景1中参与协同节点在不同度优先脱离规则下的性能对比曲线如图13所示。随着参与协同节点的度值升高,性能恢复程度快速降低,由采用最小度节点协同时的1.00下降至0.89,并最终稳定在0.80。最小度节点协同与第2小度节点协同性能恢复差异较大,而其他规则性能恢复差异性小。这是因为度值越大的节点在无人机群中的重要性越大,脱离后使得原来所在机群性能下降大,从而导致总体性能恢复程度没有达到最优。其他规则性能恢复差异很小,并最终趋于稳定。因为受攻击节点的度值主要分布在1、2上,如图5所示,导致其他规则下参与协同节点的度值近似,所以性能恢复程度大致相同。在场景2中可得相似结果,如图14所示。
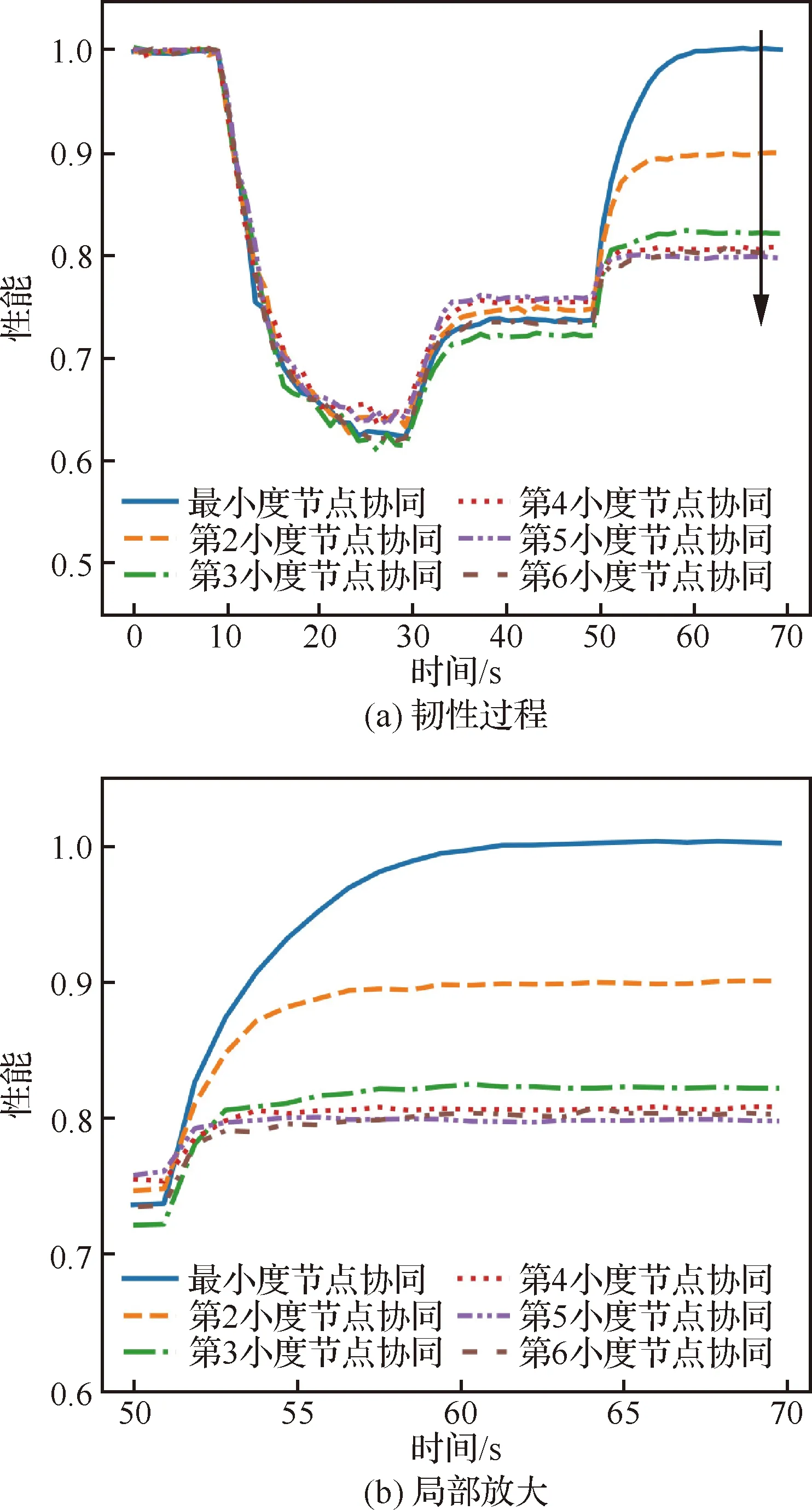
图13 场景1中不同度节点协同性能对比曲线Fig.13 Performance comparison curves of different collaborative node degree in Scenario 1
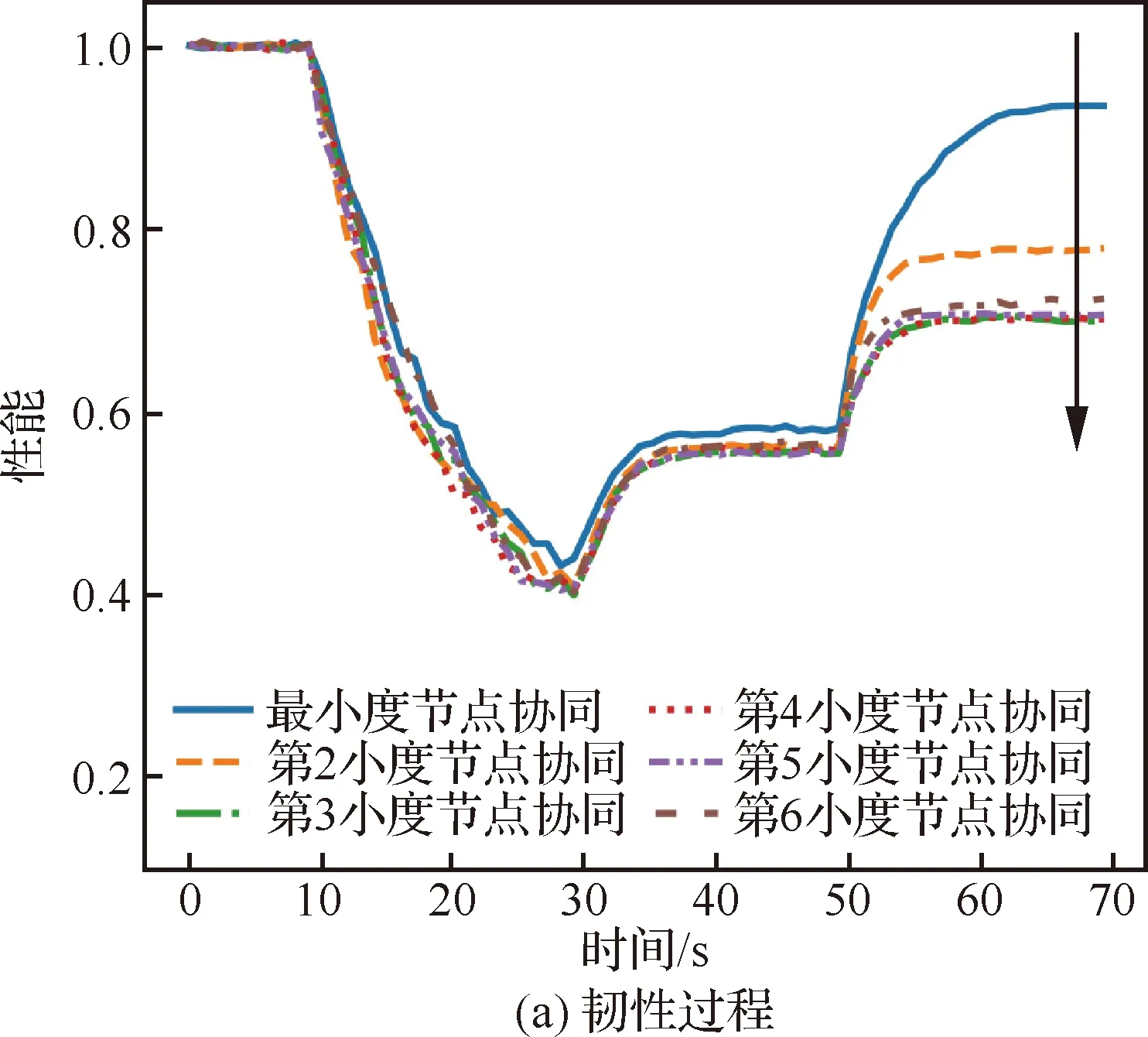
图14 场景2中不同度节点协同性能对比曲线Fig.14 Performance comparison curves of different collaborative node degree in Scenario 2
2) 受接替节点度
进一步分析受接替节点的度值不同对韧性过程的影响。保持2.2.1节模型假设条件2)不变,改变假设条件3),构建依次从最大度到第6大度优先接替受损节点规则,分别在场景1、场景2中进行分析。
场景1中不同度节点接替性能对比曲线如图15 所示。随受接替节点的度值降低,性能恢复程度依次从最大度接替时的1.00下降至0.76、0.69、0.71、0.71、0.70。这是因为度值越大节点的重要性越大,优先接替最大度节点越有利于性能的恢复。第3大度节点接替至第6大度节点接替性能曲线近似,这是因为受攻击节点的度值主要分布在1、2上,导致均优先接替度值为1的节点。同时,接替后性能曲线相比于未接替时略微下降了0.006、0.012、0.012、0.012,这是因为优先接替度值为1的节点,使无人机群网络直径增长,从而导致无人机群总体性能下降。
对比图13、图15韧性过程曲线可知,不同度节点协同均能使得性能得到恢复,且平均性能恢复至初始性能的85%,而不同度节点接替时,平均性能仅恢复至初始性能的77%。在场景2中可得相似结果,如图16所示。
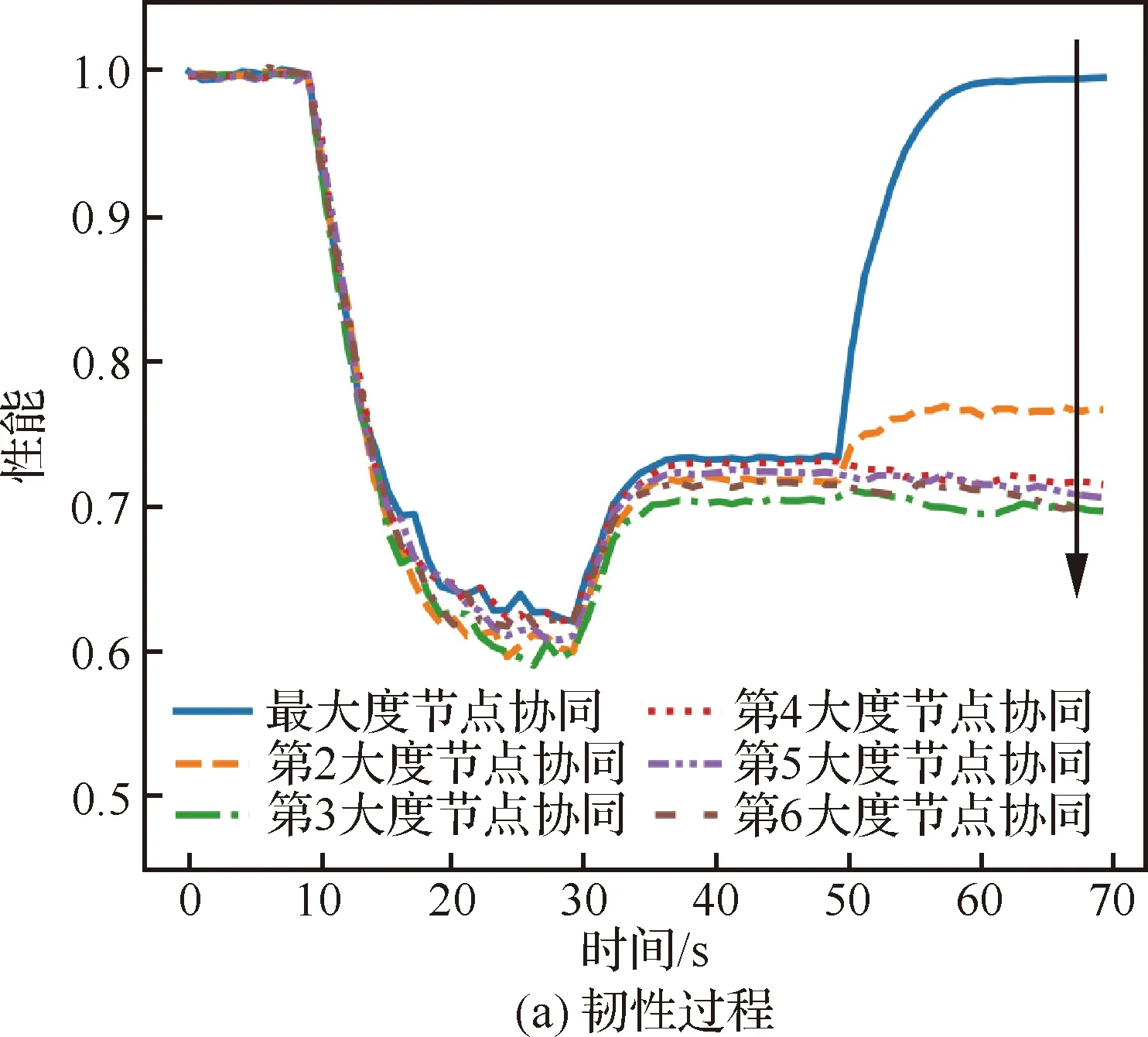
图15 场景1中不同度节点接替性能对比曲线Fig.15 Performance comparison curves of different replaced node degree in Scenario 1
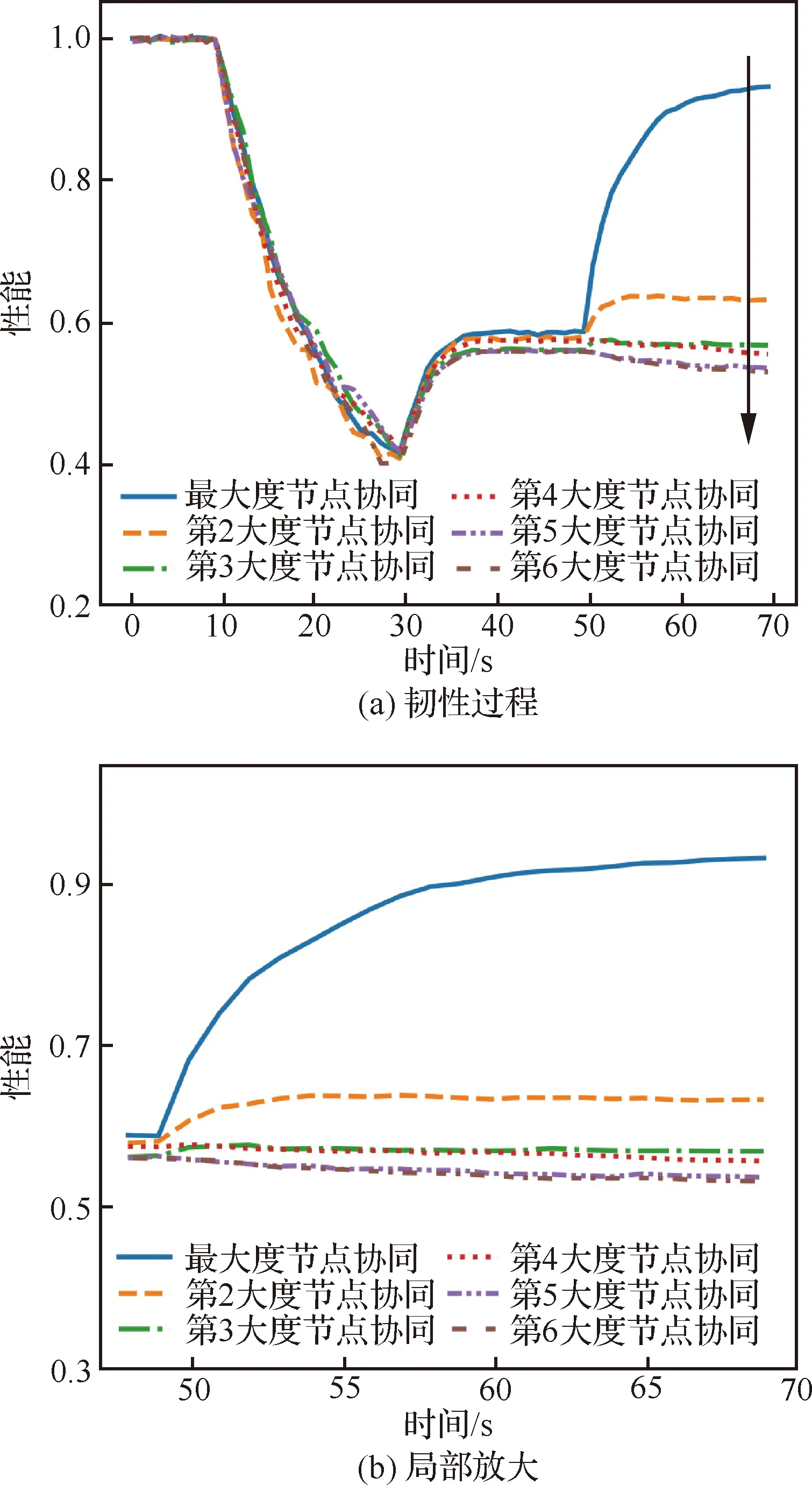
图16 场景2中不同度节点接替性能对比曲线Fig.16 Performance comparison curves of different replaced node degree in Scenario 2
综合分析可得,参与协同的节点度值越小,越有利于性能的恢复。受接替节点的度值越大,越有利于性能的恢复,且受接替节点度值相比于参与协同节点度值对性能恢复影响更大。
5 结 论
本文通过对无人机群多域协同方法建模与求解,可得以下结论:
1) 改进了韧性无人机群的恢复因子′,该因子不仅能有效表征无人机群的任务满足情况,还能更准确表征无人机群面向任务基线的恢复过程,更贴近实际应用。
2) 所提出的韧性无人机群多域协同方法能有效恢复受干扰无人机群的性能,使各无人机群快速恢复到任务基线以上,从而确保无人机群任务的完成。
3) 该方法能够使各无人机群的恢复效果更佳,且恢复因子更加均衡。相对于任务基线的冗余分配更平均,能够更好地抵抗多次攻击,使无人机群具备更强的韧性。
4) 模拟了不同节点损毁状态的战场环境并进行了韧性过程分析,验证了所提方法的有效性,为提高无人机群在执行中的韧性提供了有益参考。下一步将围绕多域博弈协同方面展开研究。
附录A:
为使得目标函数最大,则可等效为使参与协同的无人机群在协同前后性能变化最小,受接替的无人机群在接替前后性能变化最大。
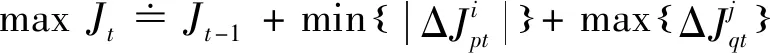
∈[0,]
(A1)
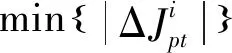

借鉴局部贪心思想,将整个过程缩小为每个时刻目标函数的变化,可表示为
≐-1+Δ∈[0,]
(A2)
式中:为当前时刻的目标函数值;-1为前一时刻-1的目标函数值;Δ为当前时刻协同过程引起的变化量。

所以,式(A2)可表示为
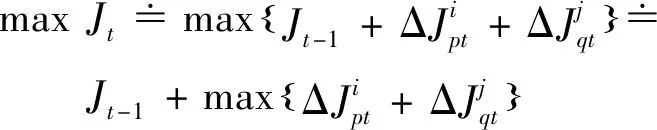
(A3)

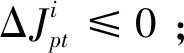
故式(A3)可等效为
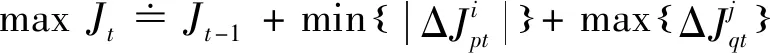
∈[0,]
(A4)
得证。
