循环热机载荷作用下航空涡轮盘蠕变疲劳寿命预测

陈克明，田若洲，郭素娟,*，王润梓，张成成，陈浩峰，张显程，涂善东

1. 华东理工大学 承压系统与安全教育部重点实验室，上海 200237

2. 中国航发商用发动机有限责任公司，上海 201100

作为典型的航空发动机热端部件，涡轮盘长期处在高温、高压、高载荷的服役条件下，承受复杂的热机载荷。飞机稳态巡航过程中，其将持续承受涡轮盘自身离心力和叶片接触载荷，伴随达到材料蠕变温度范围的温度场；而伴随飞机起/降过程，其又将承受交变机械载荷和热应力作用，引起蠕变-疲劳损伤。蠕变-疲劳失效是涡轮盘的主要失效模式之一。由于真实涡轮盘的蠕变-疲劳试验不仅非常昂贵也非常难以实现，因此选取和建立合理的蠕变-疲劳寿命模型，进行适用于结构的修正和拓展，结合合理本构模型，建立稳定的数值算法和流程，实现对涡轮盘蠕变-疲劳寿命的合理预测和设计，是目前国内外学术界和工程界亟待解决的难点和热点问题。

航空涡轮盘蠕变-疲劳载荷下准确的寿命预测，依赖于精准的蠕变-疲劳寿命模型。近年来，国内外的研究者们分别从宏观和微观的角度出发，发展了众多针对高温材料的蠕变-疲劳模型。微观模型虽然可以较好地反映材料在蠕变-疲劳载荷下的失效机理，但由于其涉及较多微观参数而不适用于大型热端部件。基于宏观损伤参量的宏观唯像寿命模型，由于其相关参数可以直接或间接地与材料的宏观应力、应变场关联，因而更加适用于对实际高温部件的蠕变-疲劳寿命预测。已有宏观唯像蠕变-疲劳寿命模型大都基于Manson-Coffin方程或线性累积(Linear Damage Summation,LDS)等准则建立。基于LDS方法建立的蠕变-疲劳寿命模型由于所需参数少，可操作性强，同时能更好地满足结构健康管理技术中对剩余寿命的评估而被很多现行标准广泛采纳。该类模型进行蠕变-疲劳寿命预测时，其疲劳损伤主要通过材料的纯疲劳曲线，根据循环分数的概念获得；蠕变损伤则可采用基于应力的时间分数法、基于应变的延性耗竭法或应变能密度耗竭法获得。其中，应变能密度耗竭法(Strain Energy Density Exhaustion)在应力和应变控制的蠕变-疲劳条件下显示了其寿命预测的准确性和稳健性。近期，Wang等在应变能密度耗竭模型的中考虑平均应力效应，纳入反映应力松弛的经验公式，提出MSEDE(Modified Strain Energy Density Exhaustion)模型，实现了对镍基合金GH4169蠕变-疲劳寿命的高精度预测。然而，该模型基于对材料的单轴蠕变-疲劳试验提出，虽然在文献[8]中基于逐周次的概念合理预测了缺口试样的蠕变疲劳寿命，但是其对处在不均匀、变化温度场下，承受热机蠕变-疲劳载荷的真实高温部件，如航空涡轮盘的适用性还需进一步拓展和验证。此外，已有蠕变-疲劳寿命预测模型，大都基于材料对称加载情况下的蠕变、疲劳行为建立，虽然有的模型在一定程度上考虑了平均应力效应和加载历史，但是对于真实结构的启-停循环载荷谱引起的平均应力效应和真实结构中特有的介于应力、应变之间的控制模式所引起的弹性跟随效应还未予以充分考虑。

针对上述研究背景和现状，本文以某型低压涡轮盘为研究对象，发展和建立了模拟涡轮盘稳态服役蠕变-疲劳行为的数值流程和算法，实现了对涡轮盘的蠕变疲劳寿命的合理预测。该数值流程基于涡轮盘稳态服役的温度场，考虑循环热-机载荷谱，选用了纳入Chaboche随动硬化演化方程的弹塑本构模型和应变强化蠕变本构模型。同时，选取基于临界平面法由SWT (Smith-Watson-Topper)模型修正的MGSA (Modified Generalized Strain Amplitude)损伤方程。MGSA损伤方程中显含最大应力和应变幅值等关键参量，因而实现了对基于应变能密度耗竭理论的MSEDE蠕变损伤模型的针对真实结构的扩展。最终，本文讨论了涡轮盘不同区域的蠕变损伤、疲劳损伤和蠕变+疲劳损伤的分布和主导情况，同时分析了单次巡航时间对涡轮盘蠕变-疲劳损伤的影响。研究成果将为航空发动机关键部件长寿命、高可靠设计提供重要参考。

1 蠕变-疲劳寿命预测的数值流程及模型

以对涡轮盘进行蠕变-疲劳寿命预测为目标，本文建立了图1所示数值流程。该数值流程基于对涡轮盘稳态周次的蠕变-疲劳行为进行相关的寿命预测。流程首要任务是确定涡轮盘三维实体模型及其对其不同服役温度的稳态应力-应变曲线和材料参数确定。第2项任务是对涡轮盘在蠕变疲劳载荷作用下稳态周次的服役情况进行数值模拟，获取整个周次涡轮盘的整体应力-应变场及其演化过程。第3项任务则是提取涡轮盘不同位置的基本信息(即等效应力，等效塑性应变等)，考虑应力三轴度影响因素，获得涡轮盘最终疲劳和蠕变损伤变量及其分布，进而获得其蠕变-疲劳寿命和分布特征。

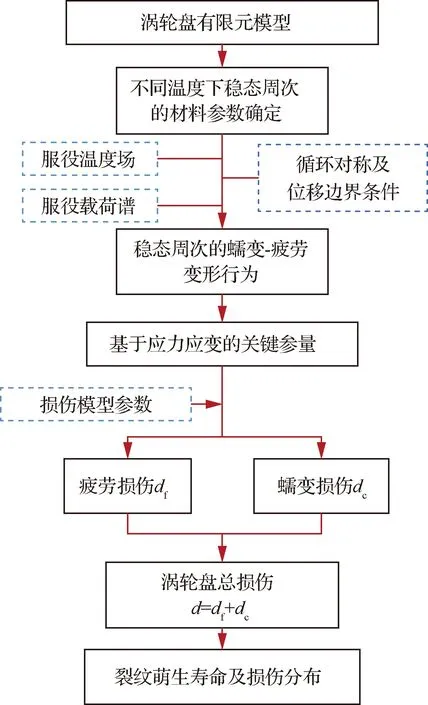
图1 涡轮盘蠕变疲劳寿命预测数值流程Fig.1 Numerical procedure for prediction of creep fatigue life of turbine disks

1.1 本构模型

本文在模拟涡轮盘在其稳定循环周次的蠕变-疲劳行为时，采用非统一的蠕变-疲劳本构模型进行结构的应力-应变描述。模型采用ABAQUS自带的基于Chaboche非线性随动强化演化律的循环弹塑性本构模型描述起飞和降落(加卸载)过程中涡轮盘的应力-应变行为，选用应变强化的蠕变本构模型描述飞机低空和高空巡航(保载时间)过程中涡轮盘的蠕变行为。循环弹塑性本构的主控方程如下：

=+

(1)

=:(-)

(2)

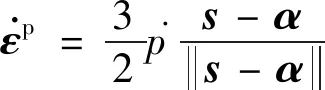
(3)

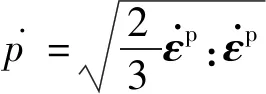
(4)

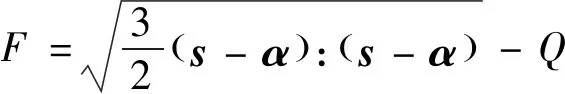
(5)

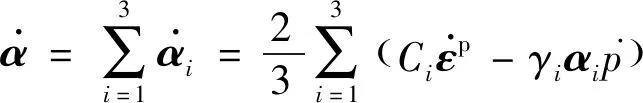
(6)

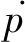
非统一的蠕变-疲劳本构模型中描述涡轮盘材料蠕变变形行为时选择基于应变强化的蠕变本构模型：

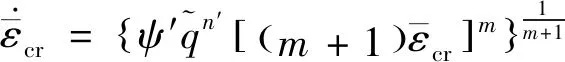
(7)

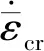
1.2 蠕变-疲劳损伤模型

本文对涡轮盘蠕变疲劳寿命进行分析预测时，考虑结构三维应力、应变状态，采用基于临界平面法的MGSA损伤方程确定积分点的疲劳损伤：

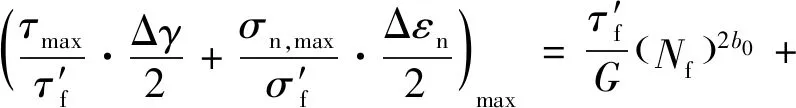
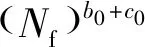
(8)

式中：和分别表示一个循环周次内的最大剪应力和最大正应力；Δ2和Δ2分别表示剪切应变幅和正应变幅；′和′分别表示剪切疲劳强度和剪切延性强度；′为疲劳强度常数；为疲劳寿命;为剪切模量；和表示2个关于疲劳强度和延性的指数，可通过对材料的疲劳试验获得。在具体的有限元计算过程中，将通过对有限元软件的二次开发，对涡轮盘上所有的积分点，选出MGSA损伤参量最大的平面，基于最大平面的损伤参量算出相应积分点的疲劳寿命。

计算低压涡轮盘的蠕变损伤时，选取MSEDE模型作为初始框架。对于处在复杂应力状态下的发动机涡轮盘，本文对MSEDE模型进行进一步的修改和扩展。一方面，考虑结构的多轴蠕变行为，论文在模型中引入材料发生多轴蠕变损伤的多轴蠕变延性因子(Multiaxial Ductility Factor，MDF)，以实现对真实结构中应力三轴度引起的多轴蠕变效应及其损伤的合理描述。针对三维涡轮盘结构，多轴蠕变因子最终作为修正系数添加到应变能密度的计算公式中。另一方面，考虑结构在蠕变-疲劳载荷下的弹性跟随效应，即在载荷保持阶段结构的特征位置表现出介于应力与应变控制之间的混合载荷状态，在应力发生松弛的同时，蠕变应变代替弹性应变增长，需要在模型中引入反映结构弹性跟随幅度的弹性跟随因子。弹性跟随因子反映弹性跟随过程中应力松弛和蠕变变形同时发生的相关比例，当应变控制即纯松弛发生时=1；当应力控制即纯蠕变发生时=∞；而当混合控制情况时介于1～∞之间，具体示意图如图2 所示。

图2 弹性跟随因子定义Fig.2 Definition of elastic follow-up factor

综上，本文最终选取Wen-Tu多轴延性因子和R5中定义的弹性跟随因子表达式，对MSEDE模型进行结构扩展和修正。多轴延性因子和弹性因子表达式如式(9)和式(10)所示：

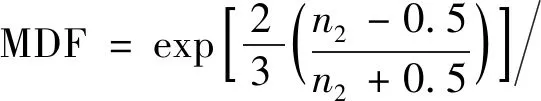
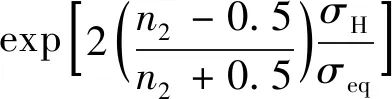
(9)

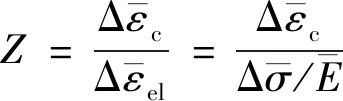
(10)

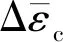
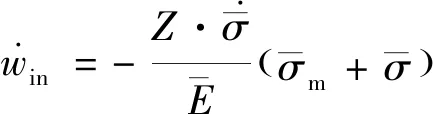
(11)

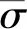
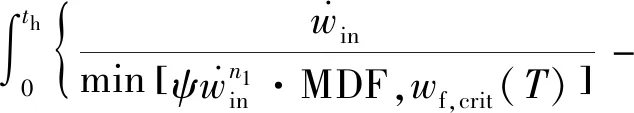
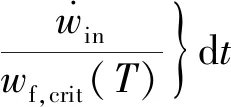
(12)

式中：()为应变能密度失效临界值,为温度；为蠕变保载时间;为材料常数，最终蠕变疲劳预测总寿命可表示为

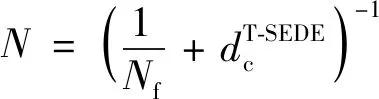
(13)

1.3 相关参数确定

本文模拟的低压涡轮盘材料选取镍基合金(GH4169)，该材料在高温下具有优良的综合机械性能。目前国内外已有不少研究者对该材料的单轴拉伸、疲劳和蠕变疲劳进行了实验研究。论文通过查阅相关文献和手册获取和确定不同温度下GH4169合金的杨氏模量、热膨胀系数、热传导率，密度，应变强化蠕变模型的参数′、′、和基于Chaboche非线性随动强化演化律的循环弹塑性本构模型相关参数等信息，最终参数分别如表1～表4所列。

表1 GH4169不同温度下的杨氏模量Table 1 Young’s modulus of GH4169 alloy at different temperature

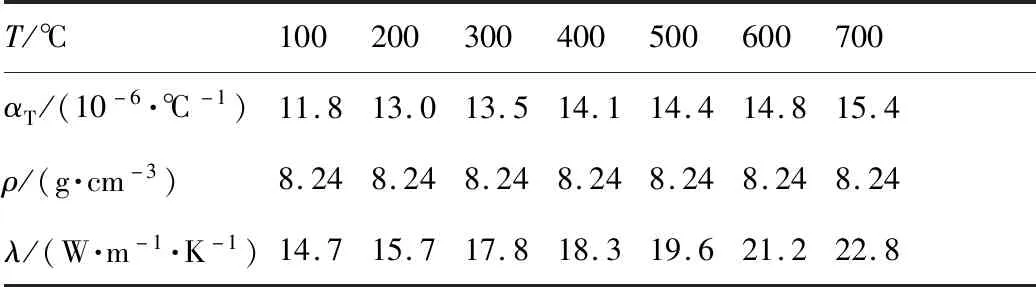
表2 GH4169在不同温度下的热性能参数Table 2 Thermal performance parameter of GH4169 alloy at different temperature

表3 GH4169在不同温度下的蠕变本构参数Table 3 Creep constitutive parameters of GH4169 alloy at different temperature

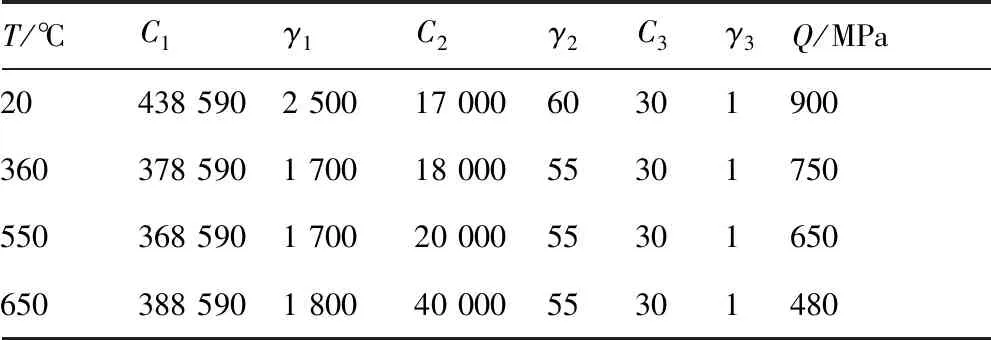
表4 不同温度下GH4169的循环塑性本构参数Table 4 Cyclic plastic constitutive parameters of GH4169 at different temperature

在650 ℃下，GH4169合金与式(8)～式(13)相匹配的参数，如表5所列。由于目前国内外缺乏对GH4169材料其他温度的蠕变-疲劳寿命模型相关的参数的试验和标定工作，为了保守起见，本文的多轴疲劳和蠕变损伤方程针对不同温度均采用650 ℃时合金的损伤参数。需要强调的是，本文的数值流程在本构模块和损伤评定模块都带有温度相关的接口，可以将不同温度的材料本构参数和损伤参数考虑进来。由于参数缺乏，同时考虑650 ℃接近涡轮盘的最高服役温度，可以涵盖涡轮盘中最危险点的损伤情况，因此选取这一个温度的参数。

表5 GH4169用于多轴疲劳和蠕变损伤模型的模型参数汇总Table 5 Summary of model parameters of GH4169 alloy used in multiaxial fatigue and creep damage models

为了验证本构模型和扩展后蠕变-疲劳损伤模型的合理性，本部分采用上述参数，结合有限元方法，对文献[8,19]中关于GH4169材料及单边缺口构件的蠕变-疲劳试验寿命进行了预测和对比，预测对比结果如图3所示。可见各种工况下预测结果几乎全部落在±2倍误差带中，本文的模型和参数合理可用。

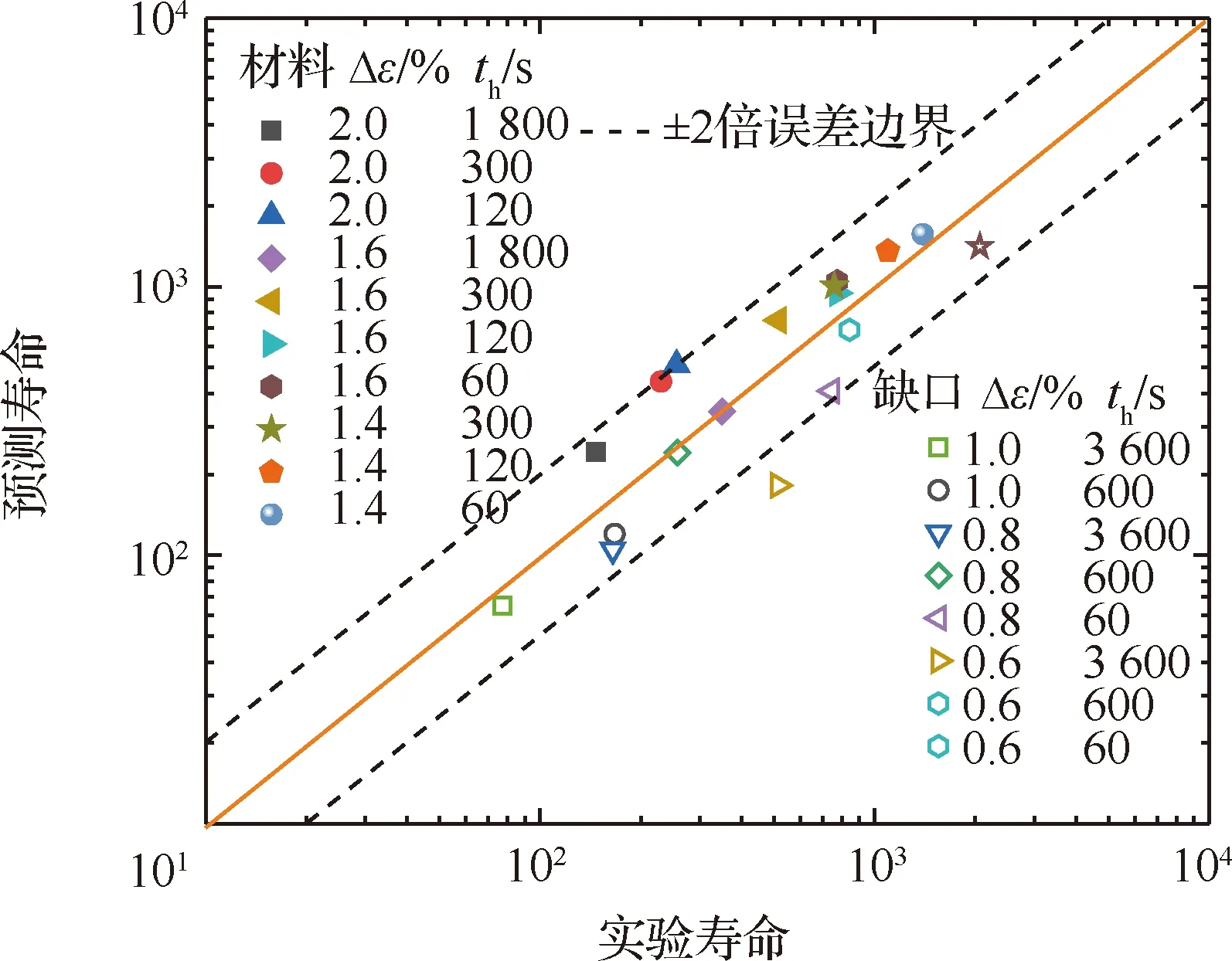
图3 蠕变-疲劳寿命模型验证Fig.3 Verification for creep-fatigue life model

2 有限元模型及载荷谱施加

基于第1节中介绍的材料性能参数、本构和寿命模型参数，本文采用有限元软件ABAQUS对某低压涡轮盘热机载荷作用下的蠕变-疲劳行为进行有限元模拟，预测其蠕变-疲劳损伤情况。模拟时根据涡轮盘叶片数量和结构、载荷对称情况，选取1/72扇区建立有限元模型，对其施加循环对称约束条件并在对应位置施加位移约束。考虑叶片和涡轮盘间为榫接接触，采用六面体C3D8R单元进行网格划分，最终划分16 275个单元，如图4所示。为了研究涡轮盘运行时发生蠕变-疲劳损伤的一般性规律，本文选用图5所示简化的蠕变疲劳载荷谱。载荷谱中涡轮盘结构承受的机械疲劳载荷考虑飞机启停过程中涡轮盘交变离心力和叶片离心力引起的榫槽交变接触载荷，热疲劳载荷则考虑启停过程中涡轮盘的交变温度场。与文献[23-24]相似，叶片离心力根据叶片质量计算，以压力的方式均匀分布在叶片与榫槽转动过程中的接触面。蠕变保载载荷为涡轮盘稳态运行时的机械载荷和稳态温度载荷，保载时间为,h。由于涡轮盘的重力、运行时气流等载荷相对很小，在计算中忽略不计。图5载荷谱采用归一化的表述方式，纵坐标分别为某个时刻涡轮盘的当前转速/稳态服役转速(/)和当前温度/稳态服役温度(/)。涡轮盘稳态服役时最大转速为12 936 r/min，温度场分布如图6所示。

图4 涡轮盘分网Fig.4 Turbine disk split network

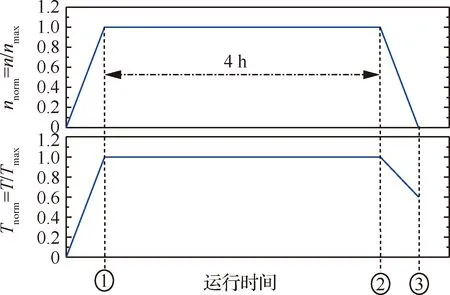
图5 涡轮盘服役热-机载荷谱Fig.5 Thermal-mechanical load spectrum of turbine disc in service

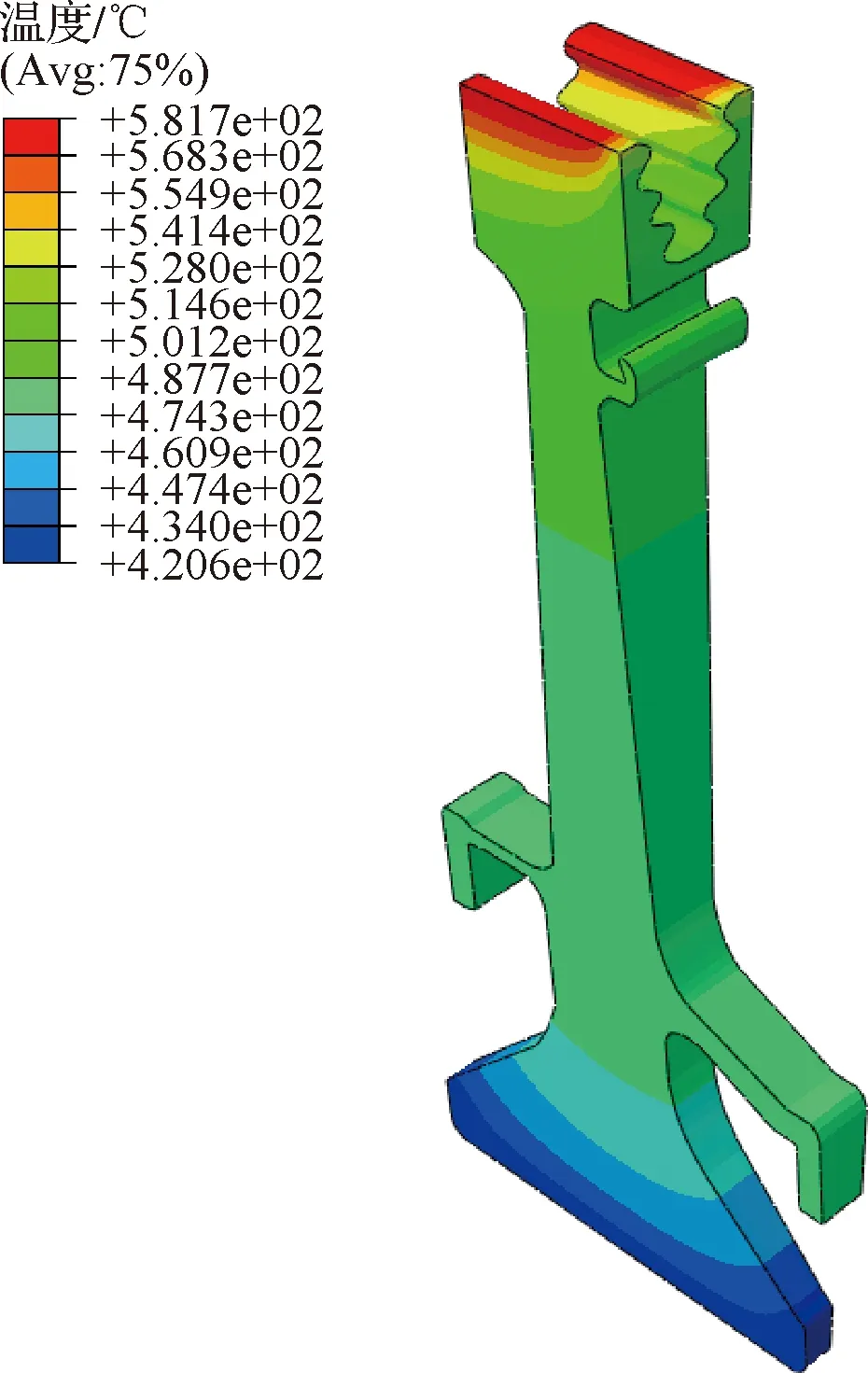
图6 巡航过程温度场Fig.6 Temperature field during cruise

3 结果和讨论

3.1 涡轮盘服役过程中等效应力和蠕变应变观察

对涡轮盘在图5载荷谱下的蠕变-疲劳行为进行模拟时，本文首先考虑稳态服役时间为=4 h 的飞行情况。为了讨论涡轮盘蠕变疲劳分析考虑叶片影响的必要性，图7先给出了对应载荷谱中时刻①(最大载荷、保载起始时刻)不考虑和考虑叶片接触载荷的涡轮盘等效应力分布云图，从图7(a)可以看出，当不考虑叶片离心力引起的接触载荷时，涡轮盘自身离心力引起的最大等效应力主要集中在涡轮盘盘心处，约为567.7 MPa。而在考虑了叶片离心力引起的接触载荷后，涡轮盘最大等效应力增加了榫槽区，且最大等效应力值达到852.7 MPa。可见，叶片离心力引起的接触载荷对整个涡轮盘的等效应力分布影响很大，故而在对涡轮盘进行蠕变疲劳分析时不可忽略。此外，从图7(b)还可以看出，最大应力主要集中在榫槽底部，涡轮盘盘心和涡轮盘的形状突变处也出现了较大的应力集中。图8给出了考虑叶片接触载荷情况下进行涡轮盘的服役蠕变-疲劳分析，继图7(b)中时刻 ① 之后，时刻 ② 的等效应力云图和等效蠕变应变云图。从图8(a)可以看出，在轮盘经历了4 h的保载巡航阶段后，最大应力仍出现在榫槽底部，值为848.5 MPa，相比时刻 ① 最大应力有所减小，产生了少量的应力松弛。而从图8(b)可以看出，经历一次4 h的保载巡航阶段后，涡轮盘也产生了蠕变变形，最大等效蠕变变形约为5.98×10%，涡轮盘发生了明显的蠕变损伤。

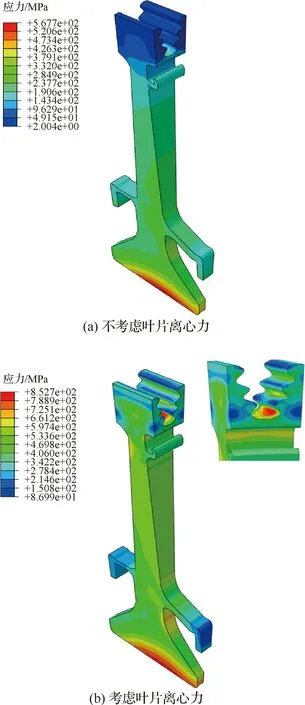
图7 时刻 ① 不考虑和考虑叶片接触载荷的涡轮盘等效应力分布云图Fig.7 Stress contours for turbine disk with or without blade contact loads at Moment ①

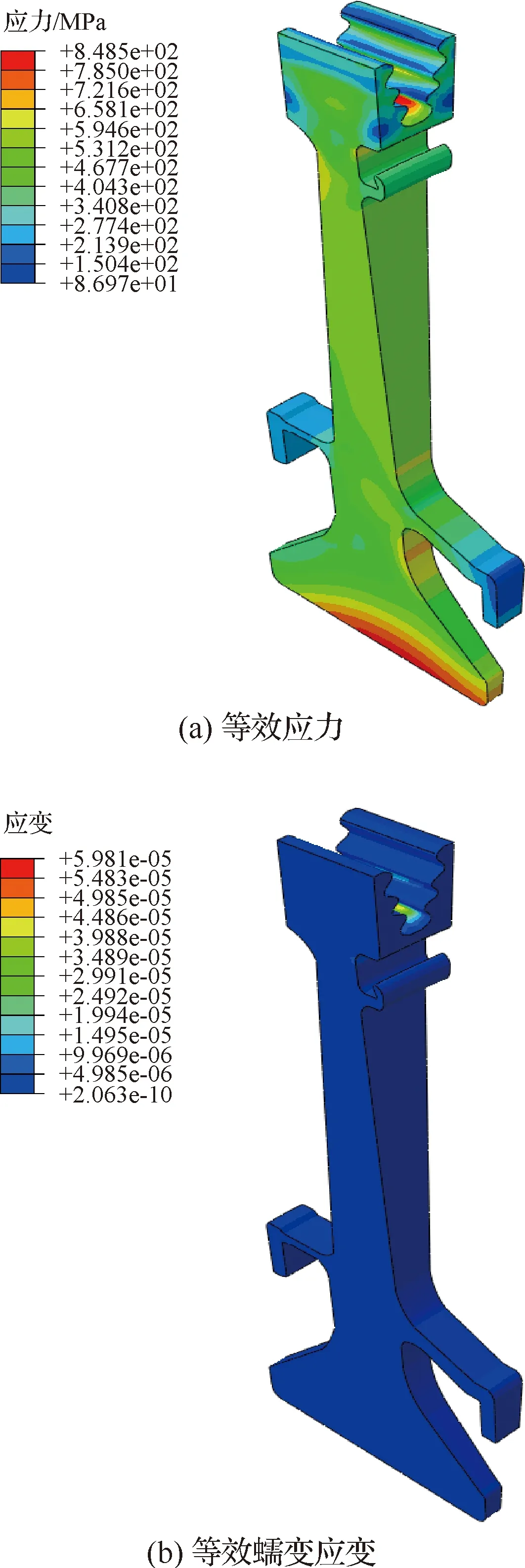
图8 时刻 ② 考虑叶片离心载荷的涡轮盘等效应力与等效蠕变应变云图Fig.8 Equivalent stress and creep strain contours for turbine disk considering blade centrifugal load at Moment ②

此外，为了探究危险点应力-应变的变化情况，本文采用不同转速(=，1.2, 1.3)进行涡轮盘蠕变-疲劳服役情况模拟，同时选取了循环过程中危险点处的应力-应变曲线，如图9所示。可以看出涡轮盘危险点是一种典型的蠕变-疲劳载荷下的变形情况。当转速为1.2和1.3时，涡轮盘危险点的塑性和蠕变损伤程度非常严重，转速时塑性和蠕变损伤相对较小，针对飞机的真实服役情况，在合理范围之内。

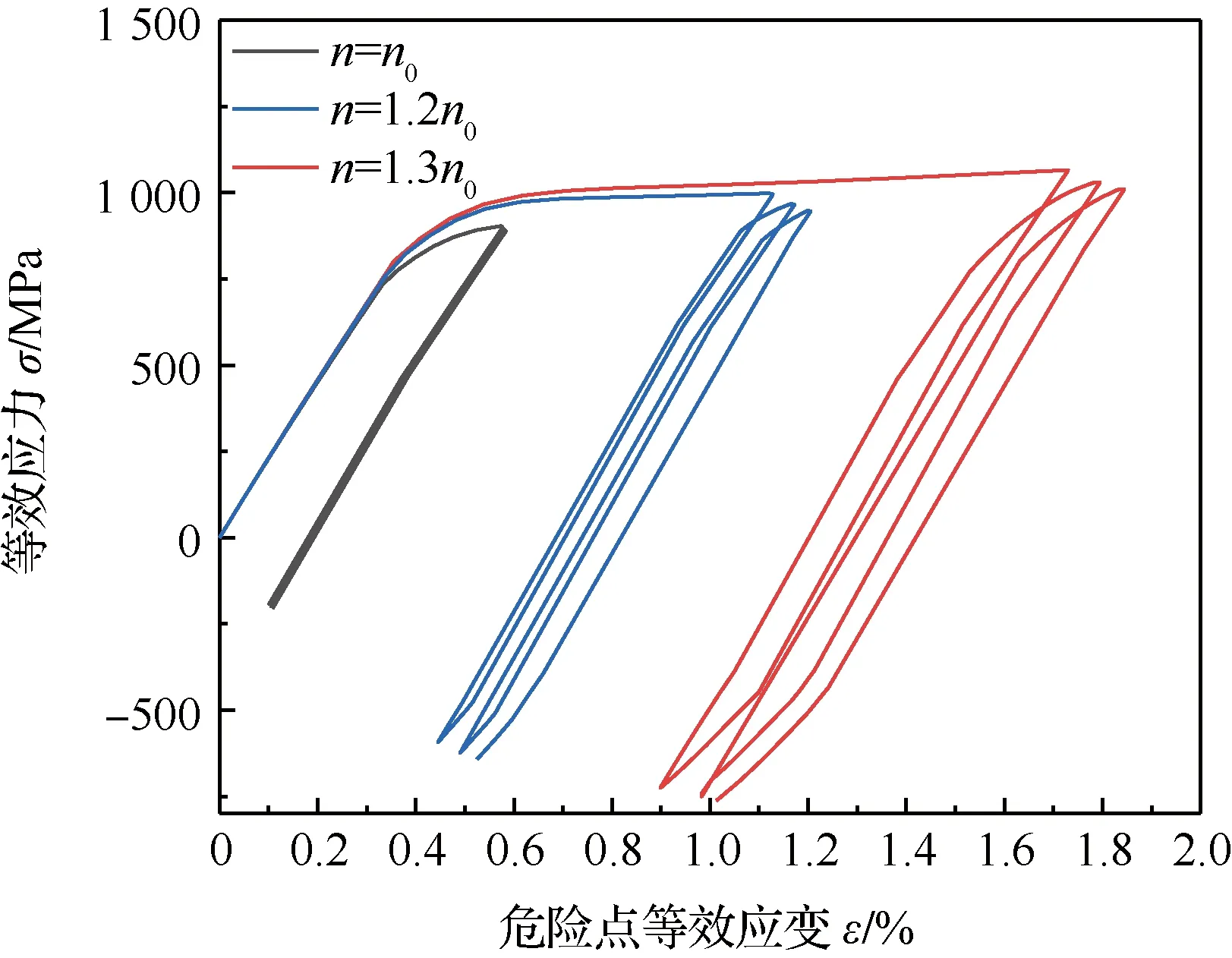
图9 危险点应力-应变滞回曲线Fig.9 Stress-strain hysteresis curves of dangerous point

3.2 涡轮盘的蠕变-疲劳损伤分析

基于3.1节中所获得的涡轮盘的应力、应变场及其分布特征，结合第1节中介绍的蠕变疲劳预测模型，并通过ABAQUS大型有限元软件的UVARM用户子程序进行二次开发，最终获得涡轮盘在图5所示载荷谱下每个服役周次产生的蠕变损伤、疲劳损伤和蠕变+疲劳损伤分别如图10所示。可见，涡轮盘的损伤分布情况与其等效应力分布情况几乎一致。最大蠕变、疲劳和蠕变+疲劳损伤均集中在榫槽右侧底部，其余涡轮盘的形状突变处也产生了较大的损伤值。这是由于这些区域一方面温度较高，另外一方面发生了严重的应力集中和应力三轴度效应。模拟所得涡轮盘的疲劳损伤分布情况与文献[22]中的结果几乎一致。整体涡轮盘的最大蠕变损伤约为2.833×10，对应服役周次约为3 529周，最大疲劳损伤值约为1.782×10，对应服役周次约为5 611周。总损伤为4.130×10，对应的服役周次约为2 421周，约为10 088.7 h。可见，在蠕变-疲劳的交互作用下，涡轮盘的整体损伤值明显增大。

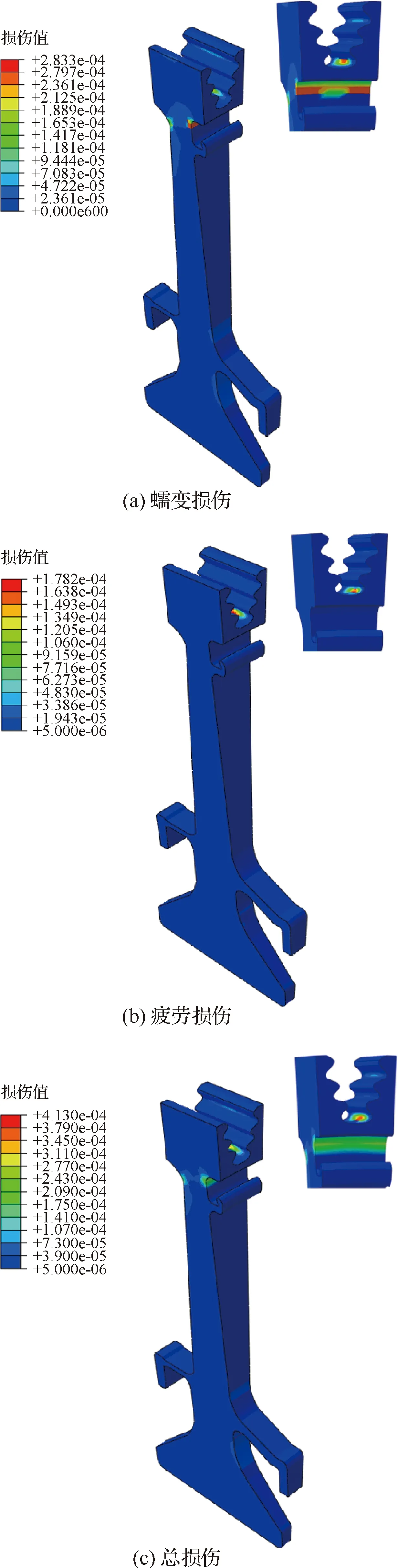
图10 涡轮盘稳态周次的损伤云图Fig.10 Damage contours of turbine disk at steady state cycle

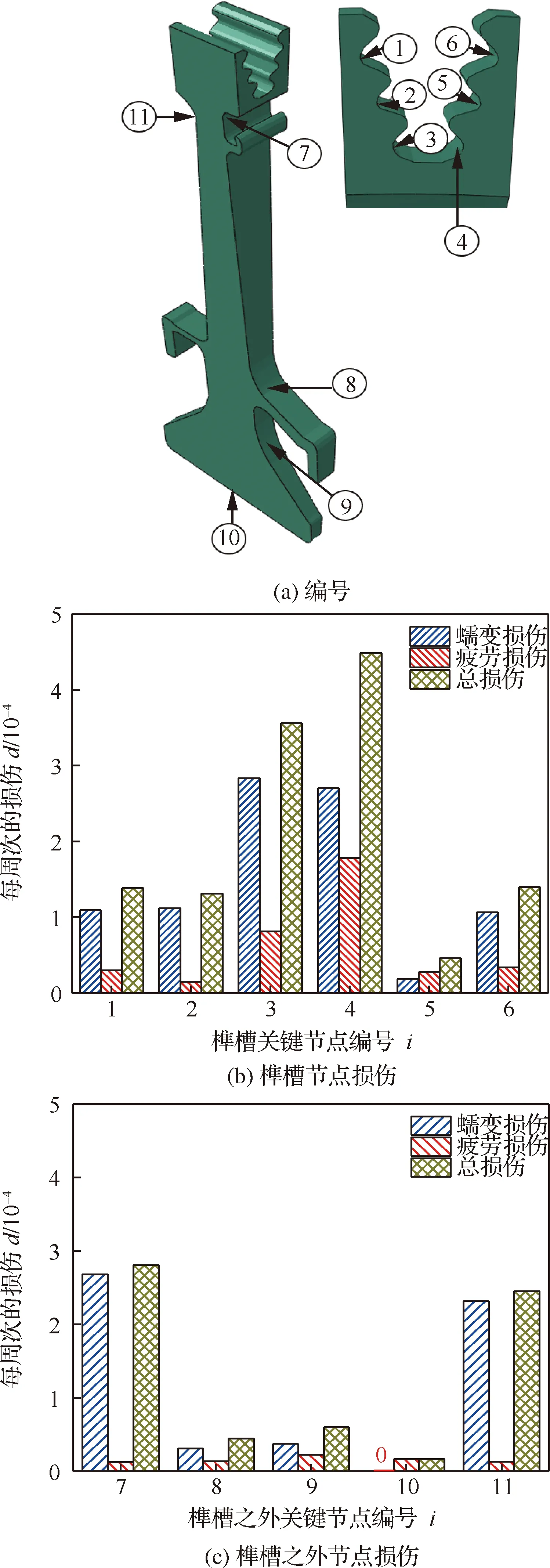
图11 榫槽关键位置编号及损伤情况Fig.11 Number and damage of key positions of tongue and groove

3.3 涡轮盘巡航时间的影响

为探究巡航时间对涡轮盘蠕变-疲劳损伤情况的影响，本节分别设定单次巡航时间为1～8 h，其余工况不变，计算涡轮盘的危险点处疲劳、蠕变及总损伤的变化。图12为涡轮盘危险点处一次服役过程中蠕变、疲劳和蠕变+疲劳损伤随巡航时间的变化曲线。可见单次巡航时间小于2 h时，疲劳损伤为主导，疲劳损伤大于蠕变损伤。随着巡航时长增大，蠕变损伤不断升高，并逐渐超过低周疲劳损伤，低周疲劳损伤几乎不受巡航时间影响。原因主要是由于疲劳损伤起源于循环载荷，其损伤值与飞机启停过程中引起涡轮盘承受的循环载荷次数和水平有关。而在飞机稳态服役过程中，疲劳损伤处于稳定状态。而蠕变损伤却是随时间发展、演化的变量，在飞机启/停和巡航的任何时刻，只要温度足够高，蠕变损伤一直在产生。随着飞机单次飞行任务时间的增加，疲劳损伤不会在单次循环中出现增加，蠕变损伤却会大幅度增加。从图12可以看出在巡航时长为2～3 h之间蠕变及疲劳存在损伤量相等的时刻，之后蠕变损伤全面超越疲劳损伤。蠕变损伤在保载1 h时约为9.60×10，在保载8 h时约为4.91×10。巡航时间从1 h增加到8 h的过程中，总损伤也随着蠕变损伤的增大而增大，由2.227×10增大至6.535×10。即随着单次服役时长的增加，涡轮盘最危险点处的损伤模式从疲劳损伤为主导的情况，逐步过渡到蠕变损伤为主导的情况。蠕变-疲劳损伤是涡轮盘服役过程中不可规避的影响因素，受转速、涡轮盘形状和巡航时间等多种因素影响。

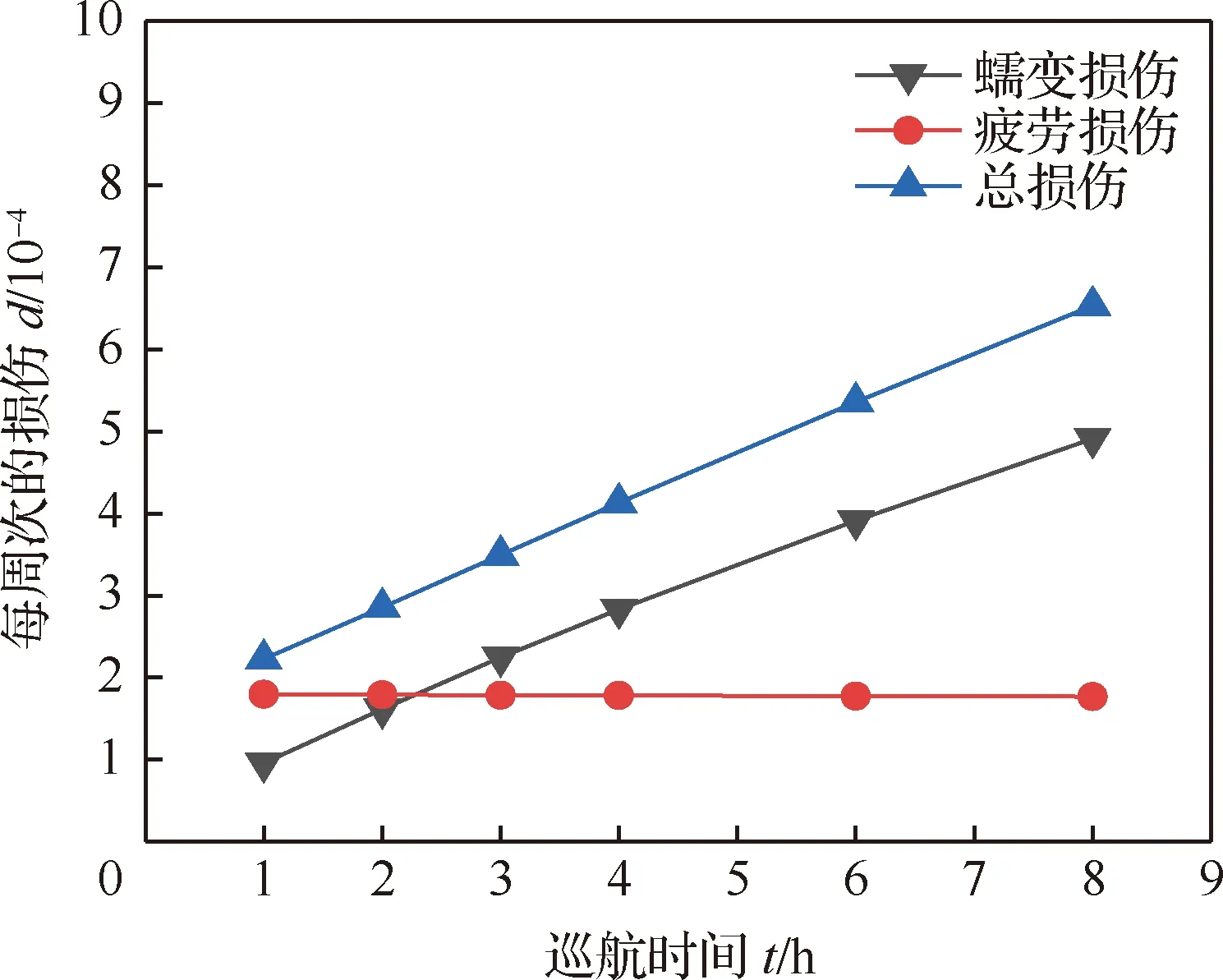
图12 损伤及循环周次随巡航时间的变化Fig.12 Changes of damage and cycle time with cruise time

4 结 论

本文采用基于Chaboche非线性随动强化演化律的循环弹塑性本构模型和应变强化蠕变本构模型，结合基于临界平面法的MGSA疲劳损伤方程和基于应变能密度耗竭理论的MSEDE蠕变损伤模型(考虑应力三轴度效应)，模拟和预测了航空涡轮盘在蠕变-疲劳载荷谱下的蠕变疲劳损伤情况，得出如下结论：

1) 本文所考虑的涡轮盘在简单热-机载荷谱作用下，其蠕变疲劳损伤分析需要考虑叶片接触载荷的影响，涡轮盘在稳态服役过程中榫槽底部、盘心处和形状突变区将出现较大的应力集中。

2) 涡轮盘在服役过程中，将伴随明显的蠕变损伤和疲劳损伤，最大损伤区集中在榫槽处，在盘体上较大的损伤区则集中在榫槽下面的轮缘处和涡轮盘其余形状突变处。在4 h的单次服役时间下，榫槽处温度较高以蠕变损伤为主，且由于轮盘和叶片的不对称性，榫槽左右相对应位置损伤值存在差别。在靠近盘心的有些区域则以疲劳损伤为主，其总损伤量相对较小。

3) 单次巡航时间在1～8 h之间变化，其余工况保持不变，随着巡航时长的增大，涡轮盘蠕变损伤不断升高，疲劳损伤基本不变，总损伤也不断升高。随着巡航时间的增加，其损伤模式逐渐从疲劳损伤为主导演化为蠕变损伤为主导的情况。