递进式路径转移姿态机动快速规划方法

2022-07-04王卓徐瑞李朝玉

航空学报 2022年5期

王卓，徐瑞,*，李朝玉

1. 北京理工大学宇航学院，北京 100081

2. 深空自主导航与控制工业和信息部重点实验室，北京 100081

随着空间探测技术的不断发展，当前空间探测任务迫切需要航天器具备大角度姿态机动能力，特别是用于遥感卫星对地观测和敏捷卫星快速机动等任务中。然而，在大角度姿态机动过程中，航天器由于内部因素或外部环境的影响，通常会面临多种复杂的姿态约束问题。比如光学敏感器件(例如红外敏感器件等)的可见视场不能指向太阳或其他的强光天体，而星载光学相机为了能够跟踪或观测则需要一直指向选定目标。这些姿态指向约束缩减了姿态机动的可行域，致使传统的大角度姿态机动规划难以满足当前的任务要求。同时，航天器的角速度以及控制力矩的限制也会影响其姿态机动能力。此外，面对复杂的空间环境和各种突发任务，当前的航天器也需要控制系统能够快速响应姿态指令。基于上述多种指标要求和姿态约束，实现姿态快速规划是一个极大的挑战。

针对多约束姿态机动规划方面的研究，Kjellberg将姿态空间离散化以便于约束处理，通过A*算法得到安全的姿态机动路径，并基于星载系统设计对应的反馈控制器，但是该算法并没有考虑到姿态有界约束。McInnes考虑航天器大角度机动过程中光学敏感器件视场对太阳的躲避，采用高斯距离函数描述姿态约束区域，构建欧拉角形式的人工势函数并设计基于Lyapunov函数的姿态控制器，但是只能处理单轴和少量的姿态指向约束。程等对姿态指向约束的约束形式和Hesse矩阵展开研究，将非凸约束进行凸化映射，并将目标能量消耗函数表示成系统状态的二次型，解决了非凸约束下能量优化收敛困难的问题，但是忽略了姿态路径节点之间的姿态约束。Spiller等通过粒子群优化算法处理单轴姿态约束并生成姿态路径的近似最优解，同时采用逆动力学方法求解姿态控制力矩，但程序运行时间过长。

针对快速姿态规划方面的研究，Hablani采用几何规划方法处理姿态指向约束，在初始姿态路径进入禁止指向区域时，通过求解对应姿态回转角获得切向路径，使航天器沿着切线方向进行姿态机动，给后面的几何规划提供了可行思路，但是考虑约束太少只能处理简单的路径规划。Frazzoli等将快速搜索随机树将应用到姿态规划中，在全局姿态路径节点扩展过程中，判断当前姿态路径节点是否进入姿态约束区域，能够快速得到安全的姿态机动路径，但是生成的姿态路径随机性大且占用过多资源空间。Xu等提出了一种基于旋转路径分解(Rotational-path Decomposition-based Recursive Planning，RDRP)的姿态递归规划方法，可以转化姿态指向约束并且快速得到安全的姿态路径，但是其需要多次判断和处理路径约束。

本文主要研究多种复杂姿态约束下的大角度姿态机动问题，提出一种基于路径转移策略的快速规划方法，使航天器在执行姿态机动之前能够快速规划出一条满足多种约束的安全姿态机动路径。该方法由参考路径规划、松弛路径规划和路径转移规划3部分组成，递进式处理姿态规划中的初始参考路径生成、姿态有界约束满足和姿态指向约束满足问题。本文的方法和以往快速姿态规划方法的区别和创新性主要在于提出了路径转移规划方法，通过设计约束评价函数和转移动作集合，确定性满足姿态约束。同时，本文设计的递进式姿态路径生成方案可以快速高效的得到满足多约束的姿态机动路径。在松弛路径规划中，建立姿态有界约束评价函数，在路径转移规划中，建立基于指向角的姿态指向约束评价函数，并设计对应的转移动作集合，得到满足多种约束条件的安全机动路径。最后，通过大角度姿态机动仿真，验证了该方法的快速性和有效性。

1 大角度姿态模型

航天器在执行任务时通常需要大角度姿态机动来完成各种空间探测或交会对接等航天任务，姿态系统需要建立姿态机动模型，且姿态路径需要满足由航天器内部特性和外部空间环境因素共同形成的多种姿态约束。

1.1 姿态动力学模型

对航天器姿态动力学以及相关约束的建模和分析是设计航天器姿态规划方法的前提，用以保证航天器从初始姿态到目标姿态的安全姿态机动。本文将航天器视为三轴运动的刚体，采用四元数形式描述姿态运动学和动力学方程:

(1)

(2)

式中：姿态四元数=[,,,]，并满足归一化约束=1，而且

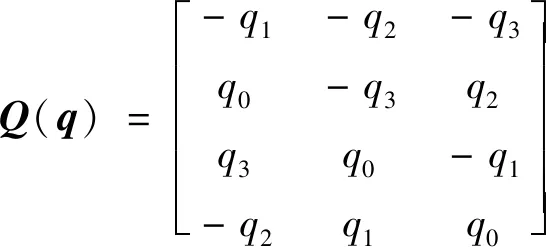
(3)

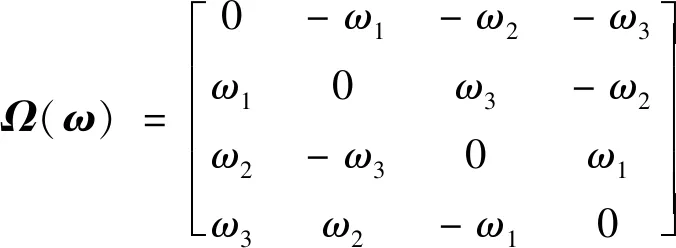
(4)

=[,,]为航天器相对惯性系的角速度在航天器本体系下的表示形式，为的叉乘矩阵形式,

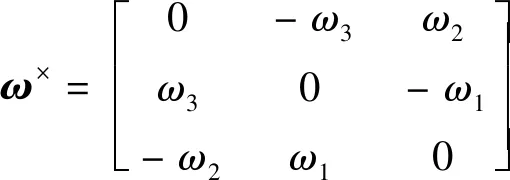
(5)

=diag(,,)为航天器相对本体系的惯性矩阵;=[,,]为控制力矩在航天器本体系下的分量。

角速度可以通过式(1)的逆运动学方程直接表示：

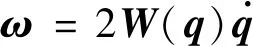
(6)

式中：

(7)

1.2 姿态指向约束

航天器在执行姿态机动任务过程中，时常会面临较为复杂的姿态指向约束，这些指向约束缩小航天器姿态机动的可行域空间。而且一旦违反该类指向约束，会对航天器携带的光学敏感器件造成严重的影响，因此对航天器的姿态指向约束进行建模和分析。

航天器需要避免敏感光学元件指向强光天体，图1为航天器姿态指向约束示意图，表示该敏感光学元件在本体系下的方向，表示强光天体在惯性系下的方向。

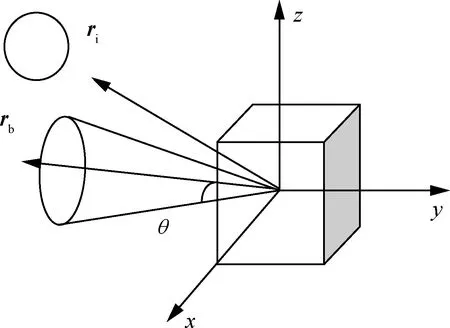
图1 航天器指向约束示意图Fig.1 Illustration of spacecraft pointing constraint

大角度姿态机动过程中要求强光天体的方向矢量和敏感光学元件的视线轴方向夹角不能低于视场角，约束表示形式为

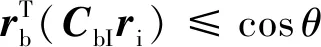
(8)

式中：表示光学元件的安全视场角;表示从本体坐标系到惯性坐标系的姿态余弦矩阵：

(9)

将上述指向约束形式的姿态余弦矩阵展开，表示为更加简洁的二次型形式：

≤0

(10)

式中：

(11)

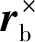
1.3 姿态有界约束

通常航天器处于全驱动工作状态，由其自身内部机械机构特性带来的相关姿态约束是航天器姿态有界约束。

在实际姿态机动任务中，航天器的姿态执行机构输出的姿态控制力矩有限，形成姿态控制输入有界约束：

||<=1,2,3

(12)

式中：表示航天器的控制力矩上限幅值。

同时，由于航天器的角速度敏感器的量程有限，航天器的角速度必须保持在限定范围内，形成航天器角速度有界约束：

||<=1,2,3

(13)

式中：表示航天器的角速度上限幅值。

1.4 姿态规划模型

大角度姿态机动过程中需要满足多种复杂约束条件，则姿态规划模型建立如下形式：

(14)

式中：表示初始姿态点；表示目标姿态点；表示初始机动时刻；表示最终机动时刻。

2 路径转移姿态机动规划

本节提出基于路径转移策略的姿态机动快速规划方法，该方法由参考路径规划、松弛路径规划和路径转移规划3部分组成。递进式处理姿态规划中的初始参考路径生成、姿态有界约束满足和姿态指向约束满足。

2.1 参考路径规划

本文递进式地生成姿态机动路径，本节首先通过参考路径规划生成初始路径，便于后续进行约束处理。

不同于随机或多次优化算法生成参考姿态路径，本节采用具有最短角度距离的欧拉旋转姿态机动路径作为初始路径，快速生成无约束条件下的初始姿态路径。则参考路径规划问题可以归纳为

(15)

式中：()(=1,2,…,)为初始路径集合；()为对应的角速度集合；()为对应的控制力矩集合。取当前路径段中的初始姿态为，目标姿态为，则连接整段初始路径的欧拉四元数为

(16)

根据欧拉定理，获得路径中的欧拉转轴矢量和欧拉转角：

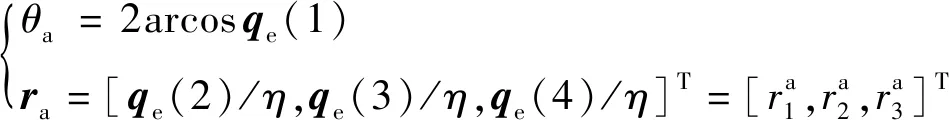
(17)

式中：=sin(2)。同时由于大角度姿态机动中转动角度可能大于，则会由于四元数的奇异性产生退绕，则将式(16)设计为

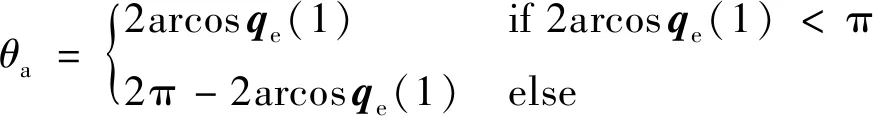
(18)

(19)

则通过欧拉转轴和欧拉转角得到初始路径的旋转四元数：

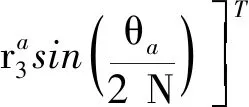
(20)

进一步地，根据姿态转动定理即可得到初始路径集合()

()=(-1)⊗=1,2,…,

(21)

式中：当=1时，()表示初始姿态节点；当=时，()表示初始姿态节点。

将式(21)代入式(15)中，即可实现参考路径规划，得到初始路径的路径集合、角速度集合以及控制力矩集合。当然，初始参考路径无法保证满足姿态有界约束和姿态指向约束，还需进一步进行约束判断和约束处理。

2.2 松弛路径规划

航天器姿态指向约束和航天器有界约束分别从三维空间指向和节点间空间距离2方面对路径进行空间限制。在规划过程中，根据两种姿态约束的特性进行分步处理，能够针对性地处理姿态约束并提高规划效率。

基于参考路径规划得到初始路径，本节进行松弛路径规划，以期快速获得满足有界约束的姿态路径，便于后续进行姿态指向约束处理。

在姿态路径中，姿态有界约束和路径步长负相关，通过限制路径的控制力矩和角速度压缩节点间空间距离，进而限制路径中的节点数量。

因此，本节将姿态有界约束满足问题转化为松弛路径节点数量的生成问题，通过姿态有界约束评价和生成松弛路径节点数量。

通过初始路径集合() (=1,2,…,)和规划模型式(14)，建立离散化的松弛路径规划模型：

(22)

式中：()(=1,2,…,)为松弛路径规划得到松弛路径集合，能够满足姿态有界约束；()为松弛路径角速度集合；()为松弛路径控制力矩集合；由对集合()(=1,2,…,)进行姿态有界约束评价得到；表示航天器的控制力矩上限矢量；表示航天器的角速度上限矢量。

设计姿态有界约束综合评价函数进行松弛路径节点判断。在姿态有界约束中，控制力矩和角速度对节点距离的影响规律一致，程度不同。基于初始路径集合中的控制力矩集合()和角速度集合()，分别建立控制力矩和角速度对初始路径集合中节点数的评价函数()和()：

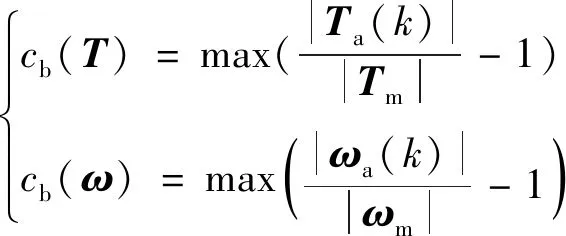
(23)

式中：当()>0时，表示初始路径集合()(=1,2,…,)违反了控制力矩有界约束，同理可以判断初始路径集合是否违反角速度有界约束。

根据式(23)的控制力矩和角速度评价函数()和()，建立初始路径集合的姿态有界约束综合评价函数()：

()=

(24)

通过()判断是否违反姿态有界约束和违反有界约束的程度，再基于欧拉机动路径的节点等分性质，综合评价得到松弛路径节点数量：

=ceil((()+1))

(25)

式中：ceil表示返回大于或者等于指定表达式的最小整数;表示权值系数。

根据松弛路径节点数和式(22)得到松弛路径的单步欧拉转角和旋转四元数，值得注意的是，欧拉转轴保持不变。

(26)

(27)

将式(27)代入式(21)中，得出松弛路径集合()：

()=(-1)⊗=1,2,…,

(28)

进一步地，将式(28)代入式(22)中，即可实现松弛路径规划，得到松弛路径集合、角速度集合以及控制力矩集合。虽然松弛路径满足姿态有界约束，但无法保证满足姿态指向约束，因此需要进行姿态指向约束判断和约束处理。

2.3 路径转移规划

航天器姿态指向约束通过限制限制航天器的三维空间指向来大幅度减小航天器的姿态可行域。因此对姿态指向约束的处理也是衡量姿态规划方法有效性的重要指标。

对于姿态指向约束的处理，快速搜索随机树方法可以在姿态约束段进行姿态路径节点随机扩展，扩展到约束区域之外得到安全的姿态机动路径，但是该方法随机性太强，生成路径节点质量较差，难以在轨应用。还可以通过RDRP方法进行约束区域的姿态路径修正，将陷入约束的姿态路径节点旋转到约束区域之外，通过多次递归分解判断旋转后的姿态路径节点是否满足约束，但是需要多次重复判断，存在资源浪费。

区别于上述方法，本节设计路径转移规划方法，通过转移动作集合和指向约束评价，快速获得满足姿态指向约束的安全姿态路径，同时该路径也需满足有界约束。

基于松弛路径集合()(=1,2,…,)进行路径转移规划。根据式(14)，建立离散化的路径转移规划模型：

(29)

式中：()(=1,2,…,)为路径转移规划得到的安全路径集合;为节点数目;()为安全路径角速度集合;()为安全路径控制力矩集合。

设计姿态指向约束评价函数进行安全路径节点判断。根据图1和式(8)可以看出，姿态指向约束区域呈现空间圆锥形式。为了得到有效的评价函数，基于图2天球坐标系下的姿态指向约束示意图，对约束区域内外的姿态节点性质进行分析。

图2 天球坐标系下姿态指向约束示意图Fig.2 Illustration of initial attitude maneuver path in celestial coordinate system

(30)

可以看出，通过计算指向角可以直观的进行姿态指向约束判断。因此，本节将姿态指向约束满足问题转换为姿态路径节点的指向角运动问题，同时建立基于指向角的姿态指向约束评价函数(())。

(())=exp(cos()-cos)-1

(31)

当(())<0时，表示当前路径节点满足姿态指向约束，相反，当(())>0时，表示当前路径节点违反姿态指向约束，且(())越大，表示违反约束程度越大。

基于姿态指向约束评价函数(())，设计路径转移规划中的转移动作集合()。

(32)

式中：动作()为空动作，当路径节点满足姿态指向约束时无需进行路径转移。动作()为环绕动作，当前路径节点到达姿态指向约束区域的邻域时，进行绕轴的姿态旋转机动。动作()为回退转移动作，当前路径节点进入姿态指向约束区域内时，回溯到路径中的上一节点，并转移到动作()。

通过基于指向角的姿态指向约束评价函数(())对松弛路径集合()(=1,2,…,)判断，可以得到动作()的起始点和目标点，然后进行环绕动作()的姿态旋转机动。姿态转动四元数为

(33)

旋转角为和旋转轴为

(34)

式中：h表示姿态节点处在本体系下的方向矢量：

(35)

式中：表示在惯性系下的方向矢量。

同时，在起始点和目标点之间进行松弛路径规划，得到节点数和单步旋转机动四元数(=1,2,…,)：

()=

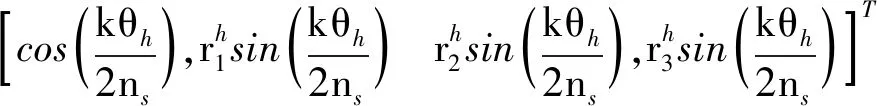
(36)

旋转机动即可得到转移段的姿态路径集合()(=1,2,…,)：

()=⊗

(37)

至此，通过环绕动作()实现约束段的转移机动。则将松弛路径集合()(=1,2,…,)基于指向角的姿态指向约束评价函数(())进行判断，通过转移动作集合()执行路径转移规划，得到安全路径集合()(=1,2,…,)。同时通过松弛路径前后连接转移路径()，实现转移段路径的平滑过渡。这样即可得到满足多约束的安全姿态机动路径。

3 仿真验证

本节进行了多约束条件下航天器大角度姿态机动仿真，以校验本文提出的路径转移姿态机动规划方法的有效性。

在大角度姿态机动仿真验证中，航天器在其轴方向安装了一个光学相机，方向矢量由表示，航天器在姿态机动中需要躲避的4个明亮天体在惯性系下的指向分别是、、和，视场角分别是、、和，初始角速度为，目标角速度是，仿真参数如表1所示。

表1 仿真参数Table 1 Simulation parameters

图3～图5分别给出了大角度姿态机动过程中的姿态四元数、控制力矩和角速度曲线。图3表示航天器能够实现从初始姿态点到目标姿态点的大角度姿态机动，验证了参考路径规划的有效性。图4和图5表示通过本文方法得到的路径满足姿态有界约束，整段路径中控制力矩以及角速度都没有超出上限值，验证了松弛路径规划的有效性。同时姿态四元数和角速度的前后转变相对平稳，方便实际工程应用。

图3 路径转移姿态四元数曲线Fig.3 Attitude maneuver quaternion curves of path transfer method

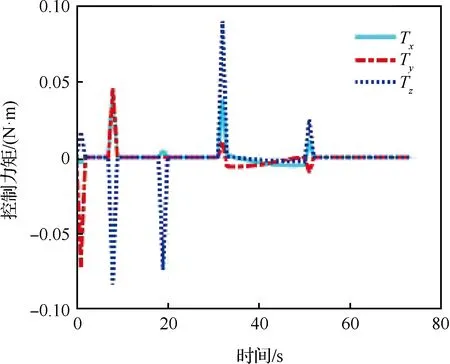
图4 路径转移控制力矩曲线Fig.4 Control torque curves of path transfer method

图5 路径转移角速度曲线Fig.5 Angular velocity curves of path transfer method

图6给出了航天器在天球坐标系下的平面投影姿态机动路径，图7给出了航天器在天球坐标系下的三维空间姿态机动路径。图6中的椭圆以及图7中的圆表示姿态指向约束区域，粗实线为路径转移方法得到的航天器姿态机动路径，细实线为RDRP方法得到的航天器姿态机动路径。可以看出，2种方法都可以满足姿态指向约束，但是路径转移曲线更加平滑稳定，且更快脱离姿态指向约束邻域。这是因为路径转移规划中的基于指向角的姿态指向约束评价函数可以提前捕获姿态约束区域，并通过环绕动作进行快速躲避和逃离。

图6 平面投影姿态机动路径Fig.6 Planar projective attitude maneuver path

图7 三维空间姿态机动路径Fig.7 Three-dimensional attitude maneuver path

同时将本文的路径转移方法与RDRP方法在相同约束要求和仿真条件下进行对比，计算机主频为 3.2 GHz，内存是4 G。RDRP方法作为各方面优于快速随机树的快速姿态规划方法，已经在高光谱卫星上面成功应用。对比姿态路径图如图6和图7所示，对比仿真结果如表2所示。

如表2所示，RDRP方法和本文的路径转移方法都能够有效处理姿态指向约束和姿态有界约束。同时，路径转移方法的姿态路径机动时间比RDRP方法减少了约85%，说明通过本文提出的路径转移方法得到的路径具有较短的姿态机动时间，具有一定的时间优化效果，能够实现快速姿态机动。这是因为通过松弛路径规划合理分配节点间的控制力矩和角速度，同时通过转移动作集合能够快速通过姿态指向约束区域，减少路径机动时间。