临近空间高超声速多目标检测前跟踪算法

2022-07-04薄钧天王国宏于洪波张翔宇

航空学报 2022年5期

薄钧天，王国宏，于洪波，张翔宇

海军航空大学信息融合研究所，烟台 264001

距离地面20～100 km的临近空间具有着丰富的资源和潜在开发价值，作为临近空间重要军事部署载体的高超声速飞行器也得到世界各国的高度重视。美国的“HTV-2”，俄罗斯的“匕首”以及中国的“DF-17”高超声速导弹均表明各国在该领域取得突破性进展。由于高超声速飞行器速度达到马赫数5以上，其表现出了飞行速度快，突防能力强，作战半径远的特点。同时，该类飞行器表面生成等离子体鞘套，使雷达反射截面积(Radar-Cross-Section，RCS)产生严重衰减，造成雷达对该类目标探测难的问题。因此，研究对临近空间高超声速飞行器的检测跟踪问题具有重要意义。

检测前跟踪(Track-Before-Detect，TBD)是在强杂波环境下有效检测微弱目标的技术，可以用于检测高超声速目标。TBD算法通过积累多帧数据，使航迹整体积累值高于虚假航迹，提高信杂比。目前TBD技术主要分为基于投影变换的TBD方法，基于动态规划的TBD方法和基于粒子滤波的TBD方法等。基于Hough变换(Hough-Transform，HT)的HT-TBD方法属于基于投影变换的TBD方法，具有对局部缺损不敏感，对杂波噪声鲁棒性强的特点，Carlson等于1994年首次提出应用到雷达目标检测中，并提出点数积累的方式同时检测不同回波能量的目标。之后，HT-TBD技术不断得到改进，Moyer等提出一种基于多维度Hough变换检测强杂波环境下微弱目标的方法，采用量测点的-、-和-坐标数据分别进行Hough变换，提高了目标的检测概率。王国宏等提出一种点集合并HT-TBD算法，使得参数平面上每个单元只包含基于雷达扫描帧数的有限个量测点，有效减小虚假航迹。

但是，检测多个高超声速目标时，由于多目标活动范围广易给雷达引入较多杂波量测点，且目标之间距离较远使它们的回波能量差异较大。采用传统的TBD算法将出现“维数灾难”问题，而传统的HT-TBD算法中点数积累空间将出现大量峰值，能量积累空间会存在峰值簇拥现象且多目标所在不同参数单元积累值相差较大，单纯设置门限的方法将导致强目标淹没弱目标或目标伴随大量虚假航迹被检测出。面对多目标检测问题，裴家正等提出一种基于序贯蒙特卡洛的势均衡多伯努利前向后向平滑TBD算法，加入多目标粒子群优化步骤，提升了目标数目和状态的估计精度；直方图概率多假设跟踪方法能够有效解决多目标检测时的“维数灾难”问题，张奕群等在此方法基础上将传感器噪声引入量测模型，提高了低信噪比条件下多目标的检测跟踪效率。但是上述方法均未考虑强目标对弱目标的影响问题，田瑞琦等提出通过估计、重构强目标回波信号，再在原信号中将其删除实现强弱目标同时检测的算法，具备较强的检测能力。但该方法属于相参积累，具有一定的复杂度。

针对上述问题，本文提出一种基于峰值聚优Hough变换的检测前跟踪(Peak Convergence Hough Transform，PCHT-TBD)方法。在完成双重积累后，以能量积累为参考，将每个量测点只存于其所在参数单元中能量积累最大的那个单元，得到新的点数积累和能量积累结果，再按照点数积累结果设置门限，提取目标航迹，进行航迹约束和合并之后得出最终结果。在不同总体信杂比环境下进行仿真验证，结果显示，与原积累方式相比，改进积累结果的方式不仅解决峰值簇拥现象，减少虚假航迹，同时也使多个目标能够同时被有效检测出。

1 模型建立

1.1 目标状态模型

假设二维平面以雷达作为坐标原点，临近空间高超声速目标作匀加速运动，目标在时刻的状态向量为

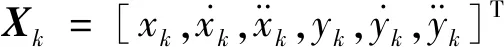
(1)

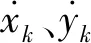
(2)

目标状态转移方程为

+1=,+1+

(3)

式中：=[,]表示过程噪声向量且和均服从高斯分布。表示过程噪声分布矩阵：

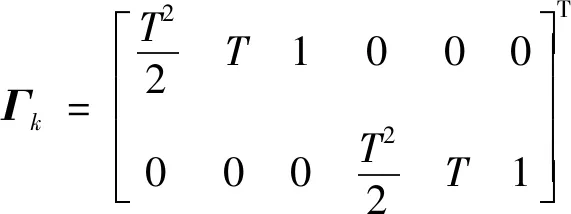
(4)

1.2 目标量测模型

考虑到雷达直接测量到的数据为目标的径向距离和方位角度，设目标量测方程为

=[]+

(5)

式中：=[,]表示时刻目标的量测向量，表示目标到雷达的径向距离，表示目标方位角；=[,]为量测噪声矩阵且和均服从高斯分布。

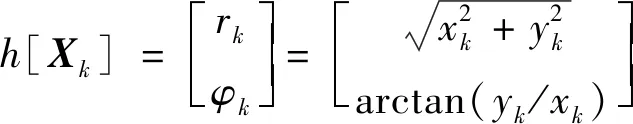
(6)

二维平面上每个量测点迹的回波能量为

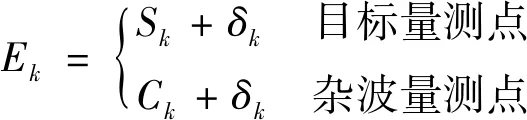
(7)

式中：表示高斯白噪声；表示杂波量测点能量；表示该点为目标量测点时的回波能量，由雷达方程得出

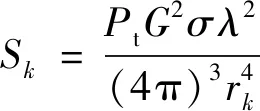
(8)

式中：表示雷达发射机发射功率；表示天线方向性增益；表示雷达散射截面积；表示发射信号波长；表示目标到雷达径向距离。TBD方法主要作用是在不同信杂比下积累航迹属性值，提高对于非航迹的相对峰值，不失一般性，设总体信杂比SCR为，杂波量测点的回波能量为

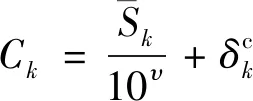
(9)

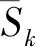
2 算法原理

算法总体上分为4个步骤，首先将回波量测点映射到径向距离-时间平面以减小量测误差影响；接着采用点集合并Hough变换进行初级积累；然后根据能量积累结果，通过峰值聚优的方式改进积累结果得到新点数积累结果，在点数积累空间中设置门限，提取峰值回溯航迹，峰值聚优也是算法的核心步骤；最后进行航迹修正得到最终检测结果。算法流程图如图1所示。

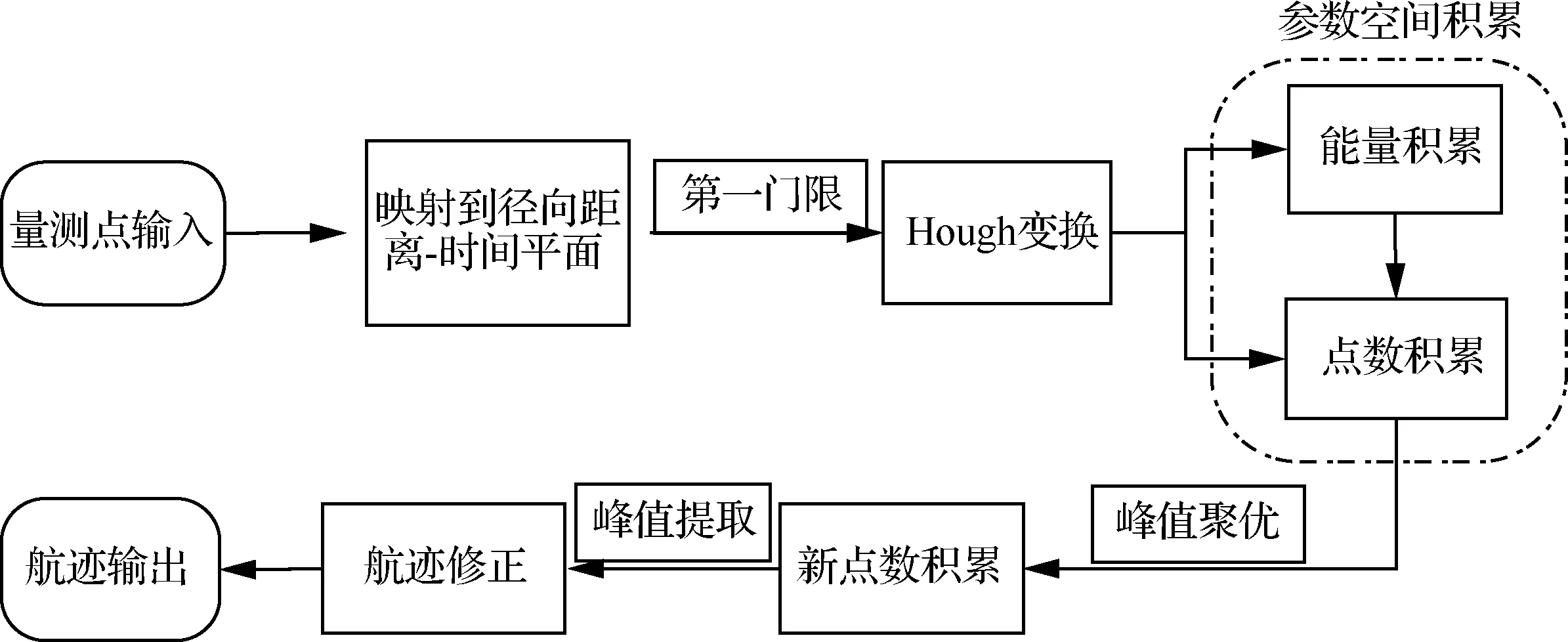
图1 PCHT-TBD算法流程图Fig.1 Flow chart of PCHT-TBD algorithm

2.1 数据平面映射

Hough变换的原理是，将数据平面上的量测点映射到参数平面进行带值积累，通过提取峰值进行航迹检测。然而，由于临近空间目标与雷达距离远，飞行速度快，使得雷达量测误差被放大。当数据平面的维度采用目标的-轴位置坐标时，两个维度均存在量测误差，使得航迹检测结果偏差较大。如果采用径向距离-时间坐标时，时间量测不存在误差，只存在径向距离一个维度的量测误差，因此，数据平面维度选择径向距离和以雷达接收到第一帧量测点为第一时刻的时刻信息。

2.2 基于Hough变换的非相参积累

目标运动模型采用匀加速运动模型，但要强调的是，匀加速运动并非直线运动，当加速度与速度不在一条直线上时，长时间目标将表现为不沿直线运动。但实际情况中，在短时间内，目标的加速度对航迹表现出的直线特性影响较小，可近似为直线，因此可采用基于Hough变换的非相参积累方法。Hough变换的计算量随着点迹的数目呈线性增长。因此，为减小计算量，可设置第一门限将部分能量较小杂波点进行滤除。考虑到部分目标量测点回波能量较小，门限根据较高的虚警概率获得

=-ln

(10)

然后保留通过第一门限的点迹进行后续变换，滤除没有通过第一门限的点迹。

通常情况下，点迹的时间量测值与径向距离量测值相比相差达几个量级，直接使用径向距离和时间量测进行Hough变换，时间信息将会丢失。文献[19]提出规格化维度的方法，将量测维度置于同一量级下，很好的解决了这个问题。设规格化系数为

=10[lg(||)]

(11)

式中：[·]表示向上取整;表示所有点迹中径向距离最大值。因为时间信息数量级小，因此对将所有量测点坐标进行变换：

(,)→(,·)

(12)

将规格化后的坐标进行Hough变换映射到参数空间中：

=·cos+··sin

(13)

式中：表示数据空间经过量测点直线到原点的距离；表示该量测点和原点连线与坐标轴正向之间的夹角；按照从0～π以π为公差的等差数列依次取值，表示的取值个数。

由于有量测误差的存在，目标在数据空间中的航迹并不是严格意义上的直线。为在参数空间中实现对量测误差的容错，本文对参数空间进行离散化处理，使来自同一航迹的点迹曲线能够落在同一个单元内进行有效积累。设-参数空间被分为×个单元，表示维度的分割数目，每个单元的边长为

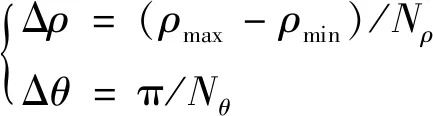
(14)

式中：和分别表示数据空间中所有点迹所在的全部直线到原点距离的最大值和最小值。

设置×的二值积累矩阵和能量积累矩阵，对于任意一个规格化后的量测点=[,·]，当满足：

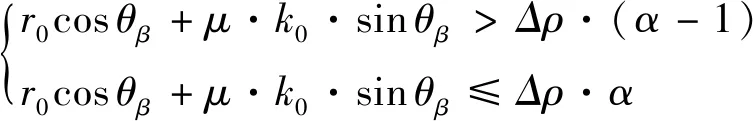
(15)

对2个积累矩阵进行积累，积累过程中，为充分利用时间信息，更有效地检测航迹，假设该单元时刻有个的曲线穿过，只取能量最大值进行积累:

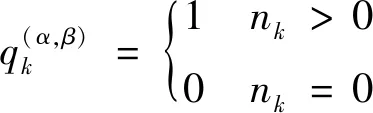
(16)

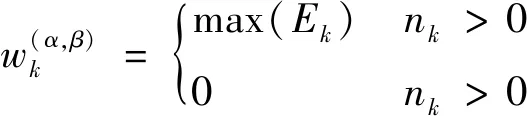
(17)

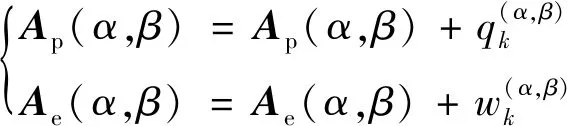
(18)

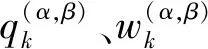
2.3 积累矩阵峰值聚优

Hough变换中，积累帧数的值与计算量成线性关系。在密集杂波情况下，较小的积累帧数使得点数积累中很多参数单元均可达到上限，失去积累意义。同时，与雷达径向距离不同的目标其能量积累值相差较大，能量积累矩阵也会出现包含少数近距离目标的参数单元能量积累值淹没远距离目标，此时如果只是通过简单设置门限的方式将会导致远距离目标漏检。

为将多个目标能够同时被检测的同时又保证较小的计算量，本文采用峰值聚优的方法，使每个目标只存放于其所在参数单元中能量最大的那个单元进行积累。

设数据空间经过第一门限后共有个量测点，设为经过上述积累后每个参数单元存储量测点元胞组：

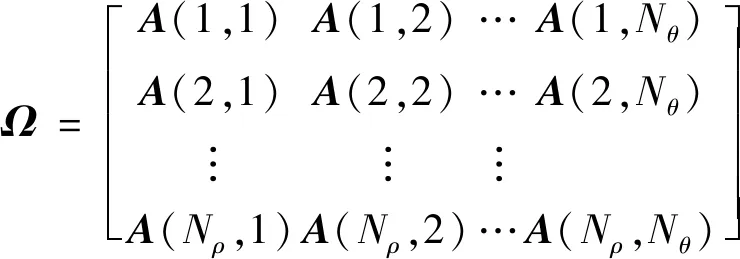
(19)

参数单元(,)内有个量测点时：

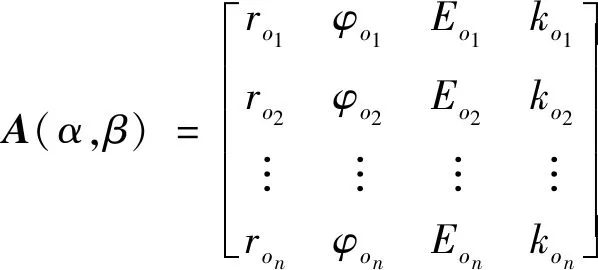
(20)

式中：(,)为参数单元(,)内存点矩阵，存储量测点的径向距离，方位角，能量和时间信息。

给所有量测点进行编号，设置标签矩阵和最终存放单元，用于给量测点标记所在的所有参数单元。设量测点共存在于个参数单元内，则

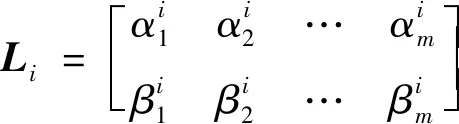
(21)

令量测点编号=1。

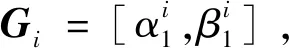
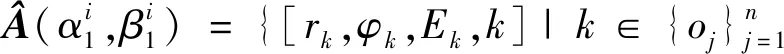
(22)

然后令编号=2。

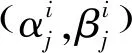
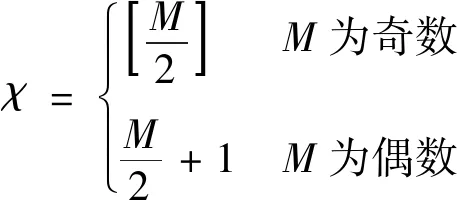
(23)

式中：[·]表示向上取整，这样做是为步骤5中能够找到相同时刻的量测点进行比较。

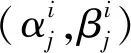
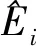
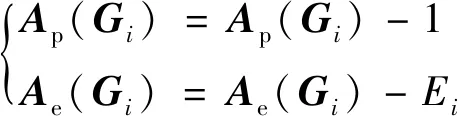
(24)

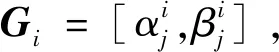
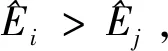
当<时，=+1，返回步骤4，否则执行步骤8。

当<时，=+1，返回步骤3，否则执行步骤9。

对点数积累结果设置门限，提取峰值输出航迹。

经过峰值聚优，航迹量测点集聚到同一个参数单元内，且每个量侧点只存在于一个单元，此时在能量积累空间中仍然存在近距离目标积累值高于远距离目标积累值，因此只在新点数积累空间中设置门限，提取积累值超过门限的参数单元内点迹。

为充分说明核心步骤，对步骤5和步骤6在网格化的参数平面和数据平面进行举例说明，如图2和图3所示。

图2中[,]为量测点在参数空间中的曲线通过所有单元中能量积累值最大的单元，且量测点在参数空间中的曲线穿过该单元。参数单元[,]存在量测点和量测点在参数空间中的曲线穿过，[,]存在量测点和量测点的在参数空间中的曲线穿过。遍历量测点在参数空间中的曲线穿过的所有单元，当满足式(25)时，删除内除[,]外所有单元的量测点：

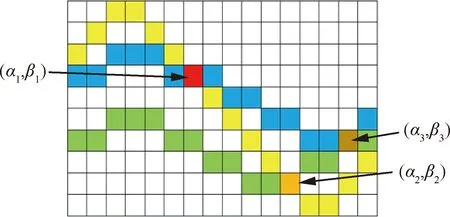
图2 峰值聚优网格示意图Fig.2 Schematic of peak convergence grid

(,)=max(())

(25)

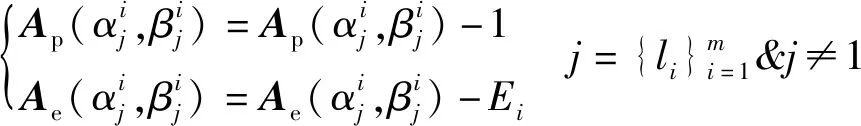
(26)

图3为数据平面峰值聚优过程，五角星代表当前量测点，为第4时刻量测。与圆形量测点构成1条航迹，包含从时刻1，时刻3～时刻7共6个量测点。与爆炸形量测点构成1条航迹，包含从时刻2～时刻4及时刻6～时刻7共5个量测点。2条航迹分别落在量测点在参数平面曲线穿过的2个单元内。除当前量测点外，两条航迹均包含时刻3，时刻6和时刻7的量测点。发现第1条航迹的时刻3，时刻6和时刻7量测点回波能量和大于第2条航迹的时刻3，时刻6和时刻7量测点回波能量和，因此将当前量测点保留在第1条航迹中并在第2条航迹中删除当前量测点。

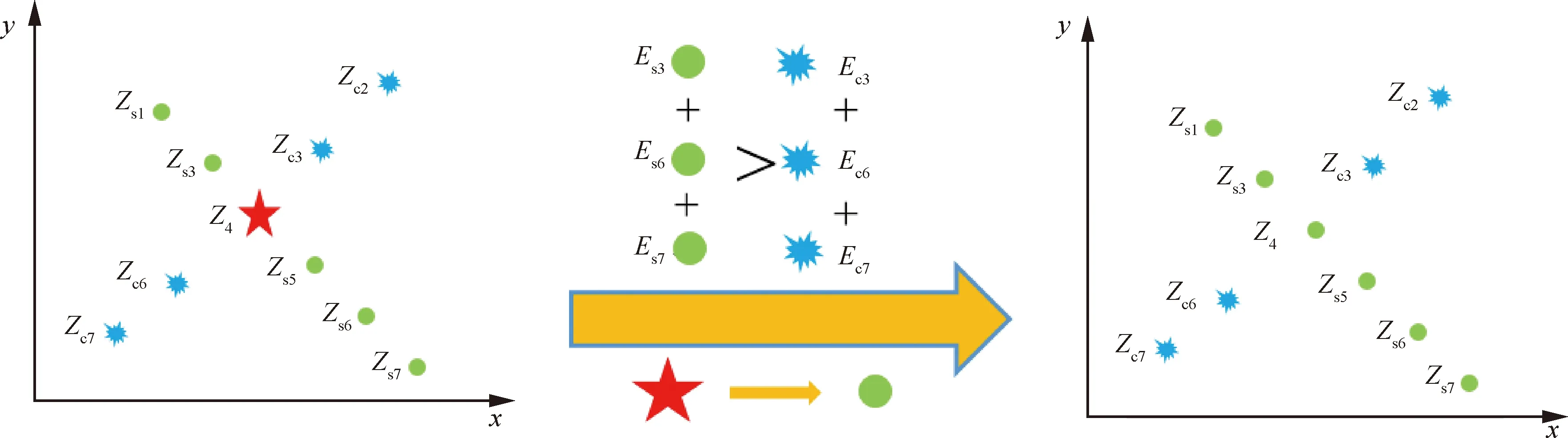
图3 峰值聚优数据平面示意图Fig.3 Schematic of peak convergence in data plane

2.4 航迹修正

经过上述过程之后，目标航迹被有效检测，但也存在由杂波点构成的虚假航迹，需要通过航迹修正进行删除。

2.4.1 航迹约束

受飞行环境、动力设备等条件限制，临近空间高超声速目标飞行时遵循一定的物理条件限制。设置速度、航向和加速度约束条件，删除虚假航迹。

在同一条航迹中任取3个时刻的量测点,,(<<)：

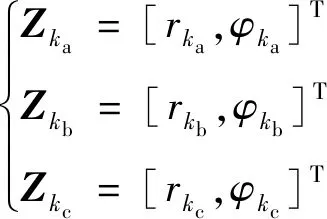
(27)

按时刻大小设置距离矢量

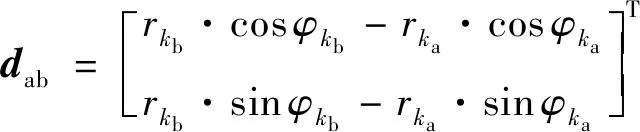
(28)

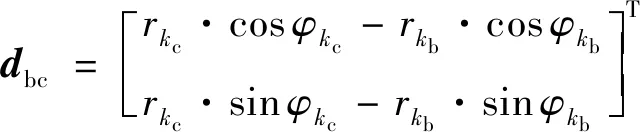
(29)

设目标飞行速度的上限和下限分别为和，目标飞行转向角最大值为，且与其他飞行器相比，高超声速飞行器加速度不可忽略，但其值也存在上限，设目标加速度最大值为，则目标航迹应当满足式(30)：

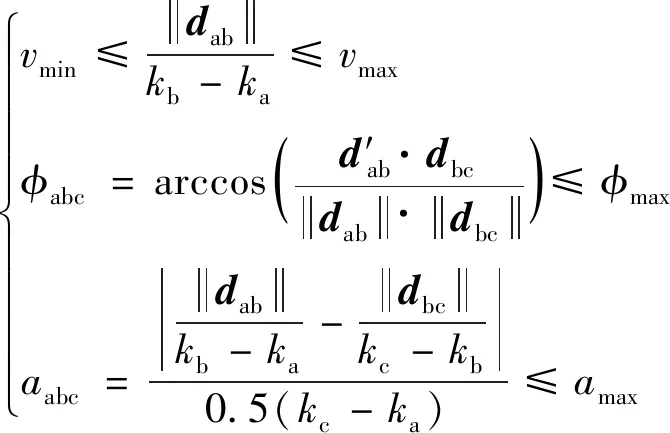
(30)

2.4.2 航迹融合

采用峰值聚优的方法，每个量测点最多存在于一个参数单元中进行积累，将不会使参数空间积累后出现峰值簇拥问题，因此检测出的航迹也不会在目标航迹量测周围出现冗余量测的现象。但是，因为量测点最多只存在于一个单元，目标航迹可能会由于参数单元的分割被截成两节。因此需要进行航迹融合，将原属于同一条航迹的短航迹相连。

设2条航迹与分别由和个量测点构成，假设航迹最后一个时刻量测点早于航迹第一个时刻的量测点：

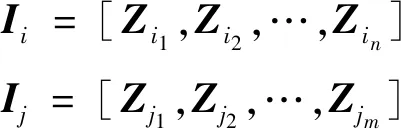
(31)

当满足2条航迹总量测点个数小于总帧数，且航迹最后一个时刻量测点与航迹第一个时刻的量测点满足速度约束条件时，连接两条航迹合并为新航迹：

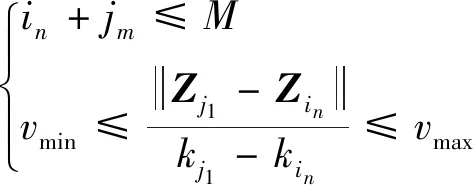
(32)

3 算法分析

3.1 峰值聚优可行性

峰值聚优是对每个量测点变换后曲线进行单元遍历，寻找能量最大单元进行存放。表现在笛卡尔平面上为，平均分割以量测点为中心的360°范围为个无界对顶扇形(以下简称为扇形)，如图4所示。找出该点放在不同扇形内能构成最大能量的扇形，在参数平面中即为最终存放单元。图4中，红色五角星代表当前量测点，红色圆点代表目标量测点，蓝色圆点代表杂波量测点。

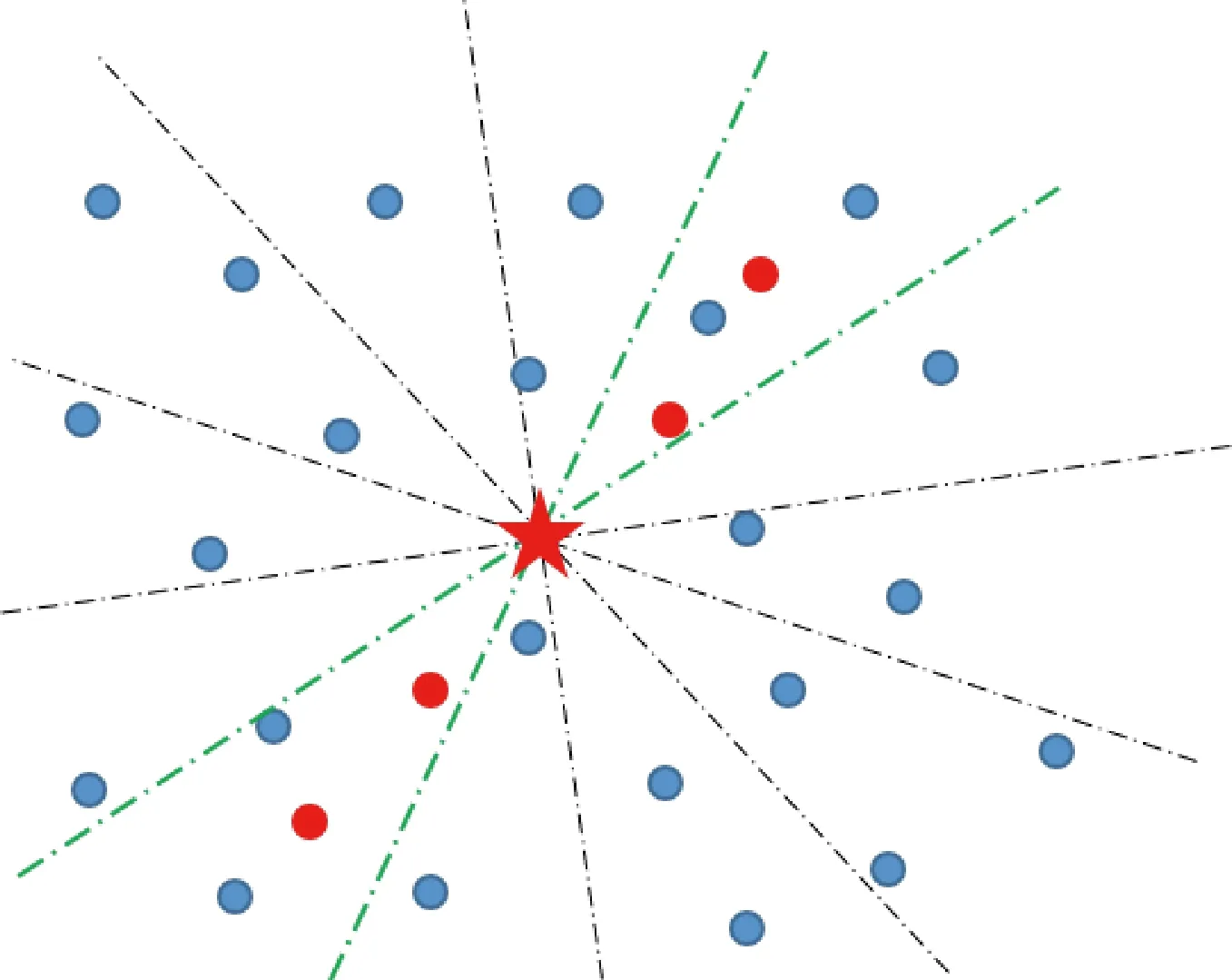
图4 对顶扇形分割图Fig.4 Segmentation map of opposite sectors

由于非相参积累本身是为提高航迹整体积累值，在信杂比达到某一程度时，真实航迹目标量测点的能量积累值高于杂波量测点构成的虚假航迹能量积累值。因此在峰值聚优过程中，会发现绿色边构成的扇形与其他所有的扇形相比，相同时刻量测点能量的合并积累值最大，所以将五角星量测点在参数平面中只保留在该扇形代表的参数单元中。

而当信杂比较低时，可能会出现虚假航迹能量积累值高于真实航迹。导致本方法不适用，但此时传统HT-TBD方法也将无法有效检测目标，因此峰值聚优方法具有可行性。

3.2 峰值聚优效果

峰值聚优的效果主要体现为能够使目标航迹所有量测点存储到一个参数单元内并保留此峰值，同时消除虚假航迹所在参数单元内的峰值，解决峰值簇拥现象。

能够聚集目标航迹量测点并保留峰值的原因是：目标航迹整体能量积累值大于虚假航迹积累值，因此经过比较后，目标量测点存放单元即为航迹所在单元。

能够解决峰值簇拥现象的原因是：峰值簇拥主要由于目标航迹所在单元的相邻单元内有目标量测点所变曲线通过，提高了这些单元的能量积累值。经过峰值聚优后，不仅删除了这些单元的目标量测点积累值，还在聚优过程中的同一时刻量测点能量比较过程中，将部分杂波量测点同时删除，因此峰值簇拥现象能够被很好的解决。

4 仿真验证与分析

4.1 基础参数设置

为验证算法能够对与雷达相距不同距离的多目标进行有效检测，在二维平面设置3个临近空间高超声速目标，以雷达位置作为2维平面坐标原点，目标参数如表1所示。

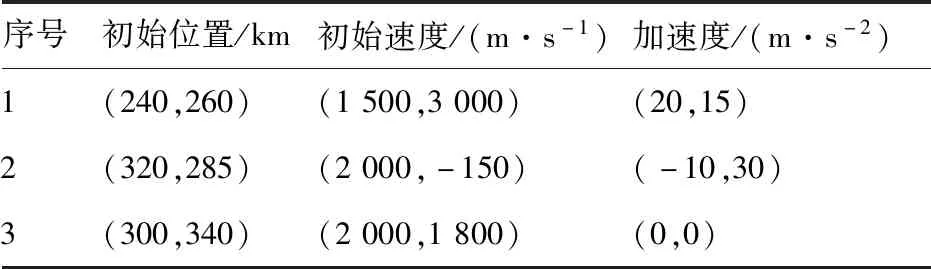
表1 目标参数Table 1 Target parameters

雷达目标参数通过文献[17,23]设置，此类文献均已证明HT-TBD算法适用于检测高超声速目标。此外，设雷达发射功率=2 000 W，天线增益=10，波长=0.1 m，扫描周期=1 s，测距误差设为200 m，方位角测角误差设为0.2°。速度约束条件取马赫数为5，取马赫数为20。由于量测误差存在，航向约束条件设为=150°。加速度约束条件设为=50 m/s。

4.2 仿真验证

以上述参数为基础，环境参数设置杂波数量服从每帧=100的泊松分布，位置服从均匀分布，总体信杂比为SCR=10 dB进行仿真验证。集中处理=10帧数据。得到雷达量测结果如图5所示。

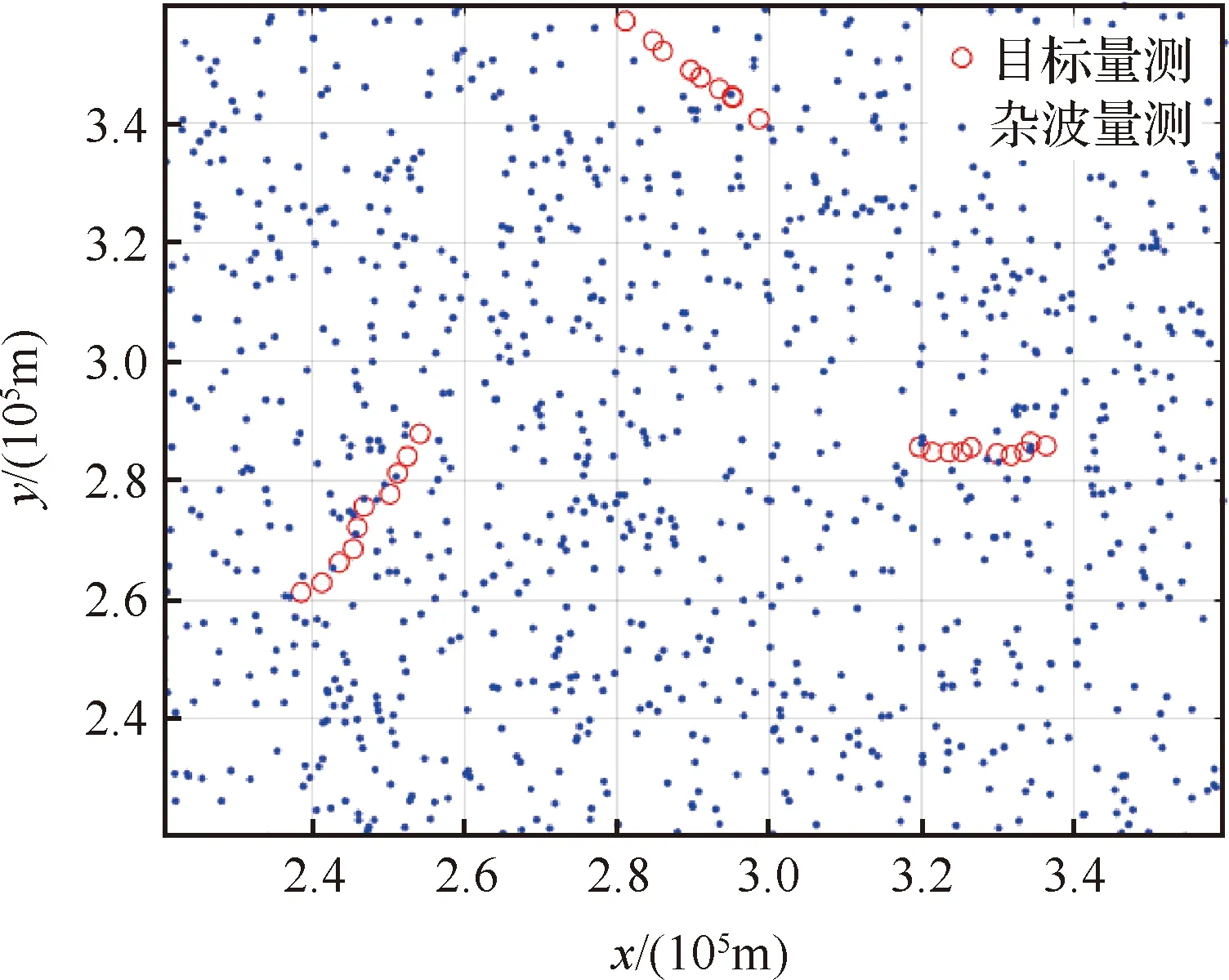
图5 x -y坐标下雷达量测图Fig.5 Radar measurements in x -y coordinates

以虚警概率为=10设置第一门限滤除部分杂波。计算规格化系数，得=5 079.4，将-二维平面数据转换为-平面数据，并将数据点规格化，得规格化后的平面图如图6所示。

由图6也可以看出3个目标到雷达径向距离距离不同。对-平面数据进行Hough变换，将参数空间分割为180×300个分辨单元，设立点数积累矩阵和能量积累矩阵进行点数积累和能量积累，如图7所示。

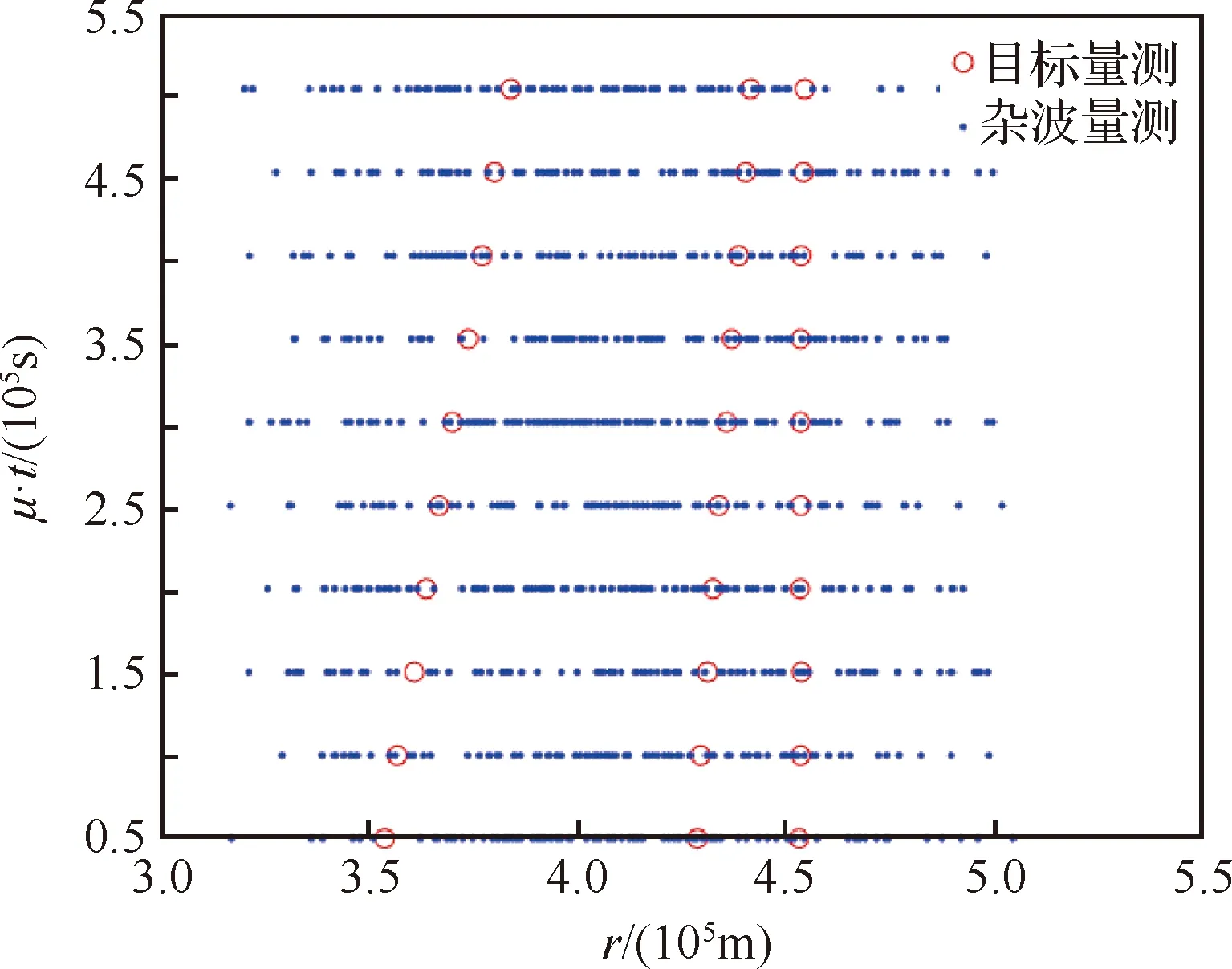
图6 r -μ·t坐标下雷达量测图Fig.6 Radar measurements in r -μ·t coordinates

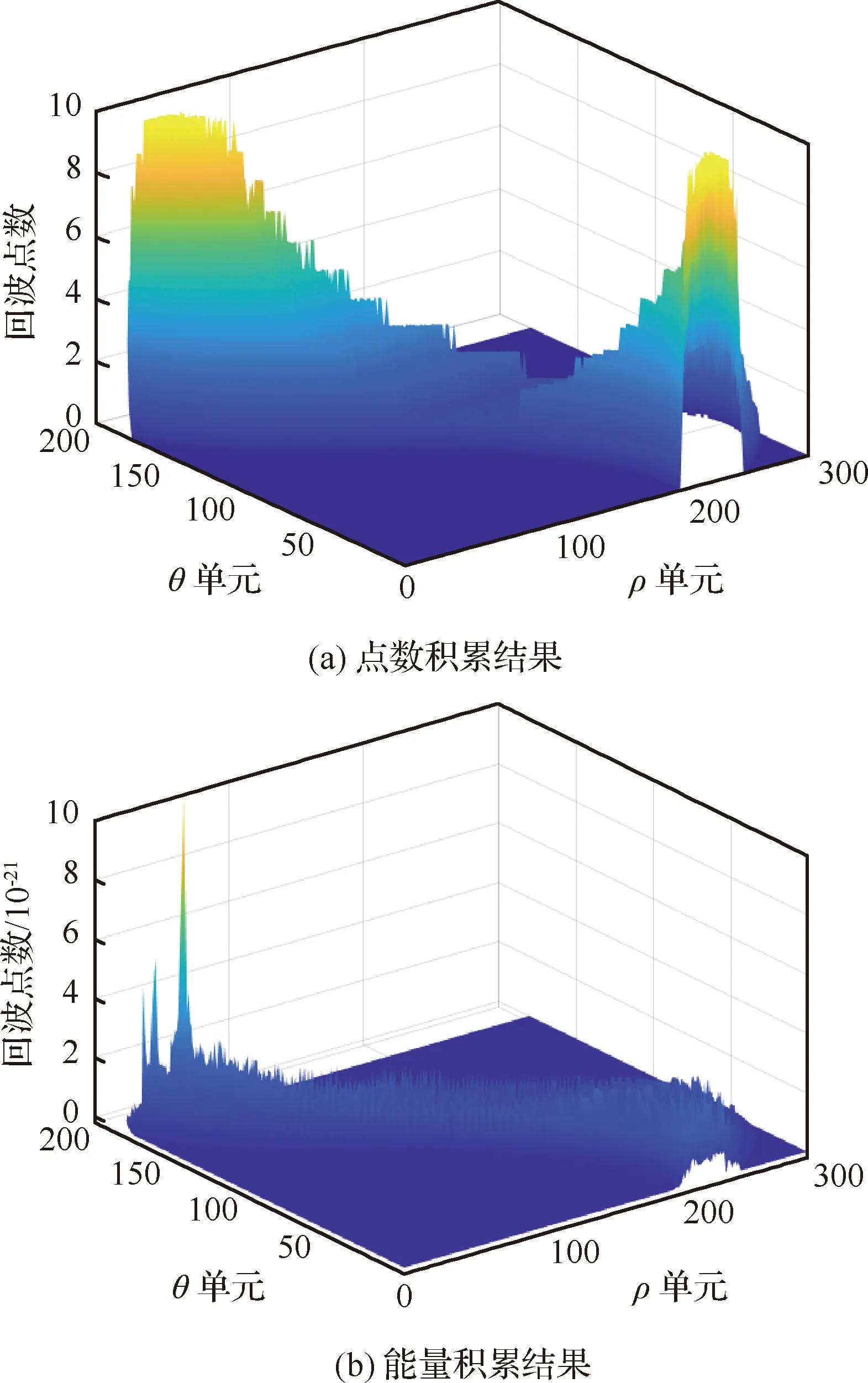
图7 传统积累方式积累直方图Fig.7 Traditional accumulation histogram

此时，无论是点数积累空间还是能量积累空间均存在峰值簇拥现象，且近距离目标功率积累值较大，将会淹没远距离能量积累值。但是可以发现，存在目标航迹的参数单元积累值高于其周围参数单元积累值，采用峰值聚优的方法，按照本文2.3节的方法，将每个量测点只存放于能达到其所在积累值最大的参数单元中去，得到新的点数积累空间和能量积累空间如图8所示。

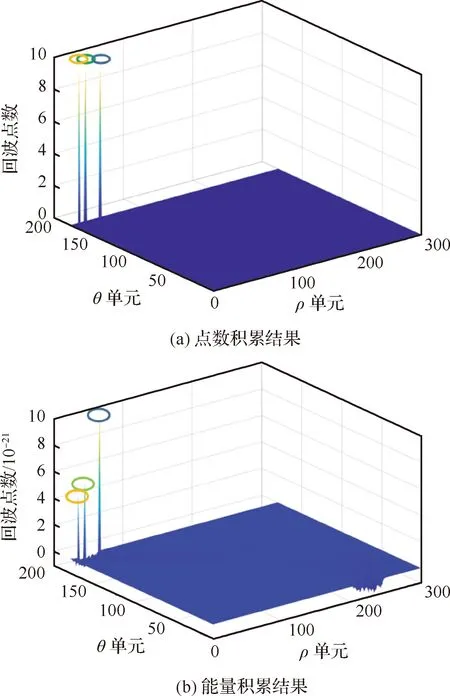
图8 改进积累方式积累直方图Fig.8 Improved accumulation histogram

此时参数空间峰值簇拥问题得到有效解决，虽然能量积累仍然存在近距目标淹没远距目标的现象，但是点数积累空间目标所在参数单元积累值相差不大，只需在点数积累空间中设置门限便可提取不同目标。对于=10帧积累，考虑到会出现航迹截断现象，设置新点数积累门限为

(33)

当点数积累矩阵积累值超过门限时，提取单元内航迹。计算约束后每条航迹长度，连接满足航迹连接条件航迹，当不再存在任意两条航迹之和小于总帧数时，输出包含量测点数大于7的航迹，最终检测结果如图9所示。

图9 检测结果图Fig.9 Detection results

4.3 对比分析

4.3.1 算法检测概率

采用峰值聚优方法的主要目标是实现同时检测出到雷达径向距离不同的多目标航迹，表征此算法性能的主要指标是全局检测概率，即将全部目标检测出来的概率。

算法进行=500次的Monte-Carlo仿真，假设第次仿真中，第个目标的航迹量测为，航迹中第个量测点被检测到系数为，则

(34)

设第个目标航迹检测成功系数为，采用7/10逻辑，认为当航迹中7个量测点被检测到时航迹检测成功：

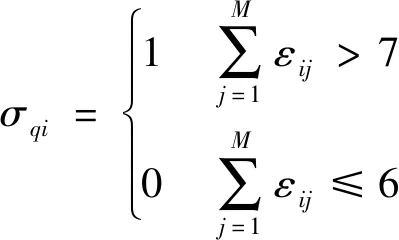
(35)

设第个目标航迹的检测概率为

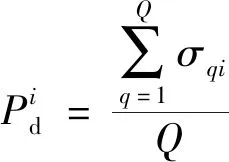
(36)

定义第次仿真中平面上所有目标至少有个目标均被检测到的系数

(37)

则仿真结束后，至少有个目标被检测到的概率为

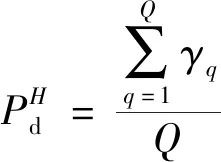
(38)

设每帧杂波数目服从=100的泊松分布，在不同总体信杂比下进行仿真，观察当按照3.1节设置空间中出现3个高超声速目标时，本文算法至少能检测出1个目标，至少能检测出2个目标和3个目标全部检测出来的检测概率变化曲线如图10所示。

再采用文献[9]算法和文献[10]算法在相同参数设置环境下进行仿真，观察2种算法对不同数目的目标检测概率变化，如图11和图12所示。

由图10～图12可以看出，文献[9]和文献[10]算法对单个目标检测性能较好，但当平面内目标数目增多且目标间距离较远时，全局检测概率较低。PCHT-TBD算法在总体信杂比3 dB以下时，几乎无法将全部目标检测出来，当总体信杂比大于3 dB时，检测概率快速提升，总体信杂比大于5 dB时，至少检测到2个目标的概率接近于1，全局检测概率维持在0.9附近。可见，PCHT-TBD算法相较于传统参数空间积累方式，在总体信杂比5 dB以上时，能够有效解决峰值簇拥和目标淹没的问题，更加适用于平面中多个目标存在的情况。但是在总体信杂比小于5 dB时，部分目标回波能量与杂波回波能量相差不大，依照能量积累结果进行峰值聚优失效，造成检测概率下降，因此本文算法具有一定局限性。

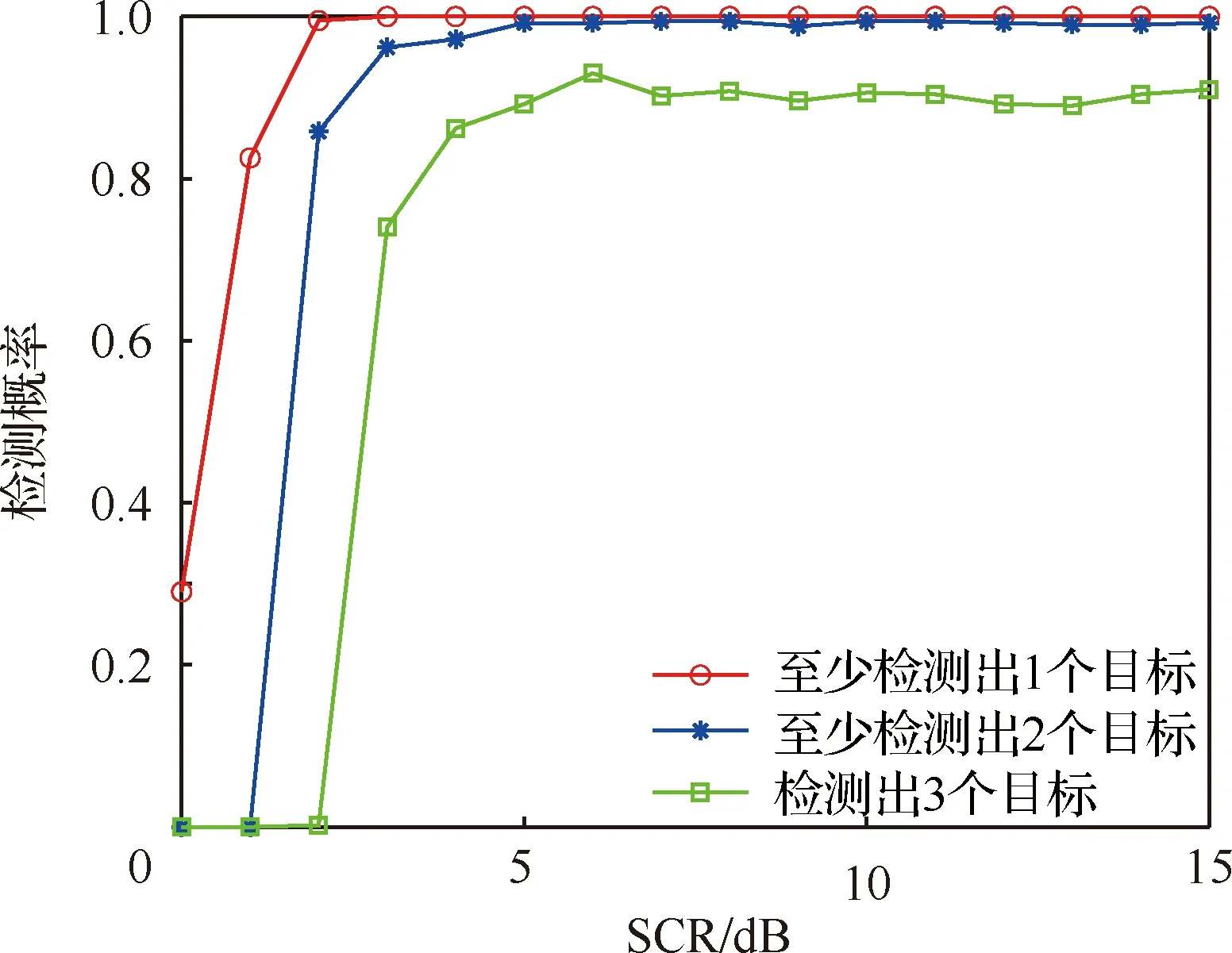
图10 PCHT-TBD算法对不同数量目标随信杂比变化检测概率Fig.10 Detection probability of PCHT-TBD algorithm with different number of targets changing with the ratio of SCR

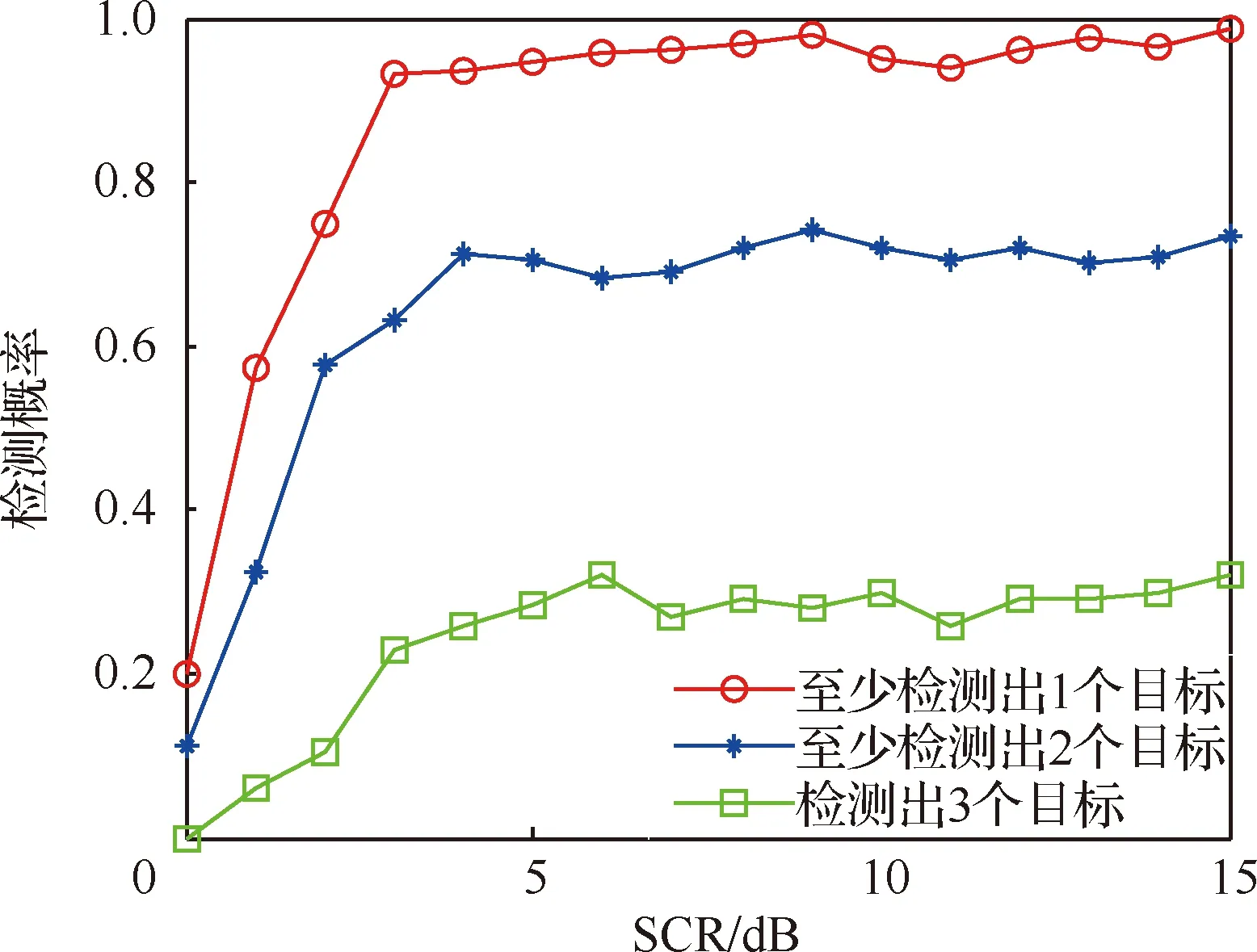
图11 文献[9]算法对不同数量目标随信杂比变化检测概率Fig.11 Detection probability of algorithm in Ref.[9] with different number of targets changing with the ratio of SCR

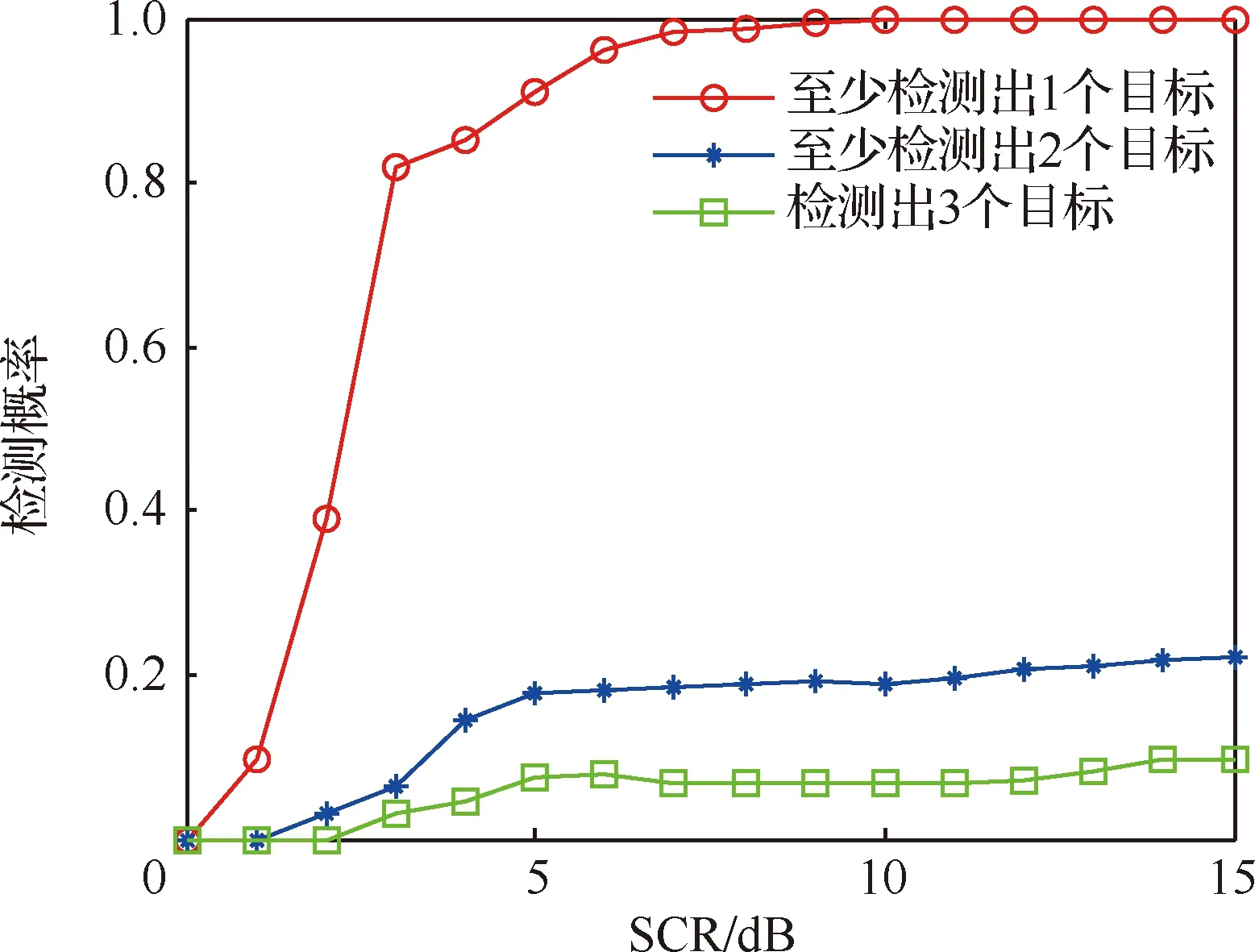
图12 文献[10]算法对不同数量目标随信杂比变化检测概率Fig.12 Detection probability of algorithm in Ref.[10] with different number of targets changing with the ratio of SCR

4.3.2 算法运行时间

衡量算法可行性的指标除检测概率外，算法处理数据的能力即运行速度也十分重要。按照3.1节设置基础参数，令总体信杂比SCR=10 dB，杂波数服从泊松分布，在每帧不同杂波密度条件下观察算法运行时间，结果如表2所示。

由表2得出文献[10]算法运行速度最快，PCHT-TBD算法比文献[10]算法平均运行时间多出0.304 9 s。文献[9]算法由于采用多个维度的Hough变换，运行时间最长。综合来看，在保证检测概率的前提下，PCHT-TBD算法拥有较高的运行效率，综合性能最佳。

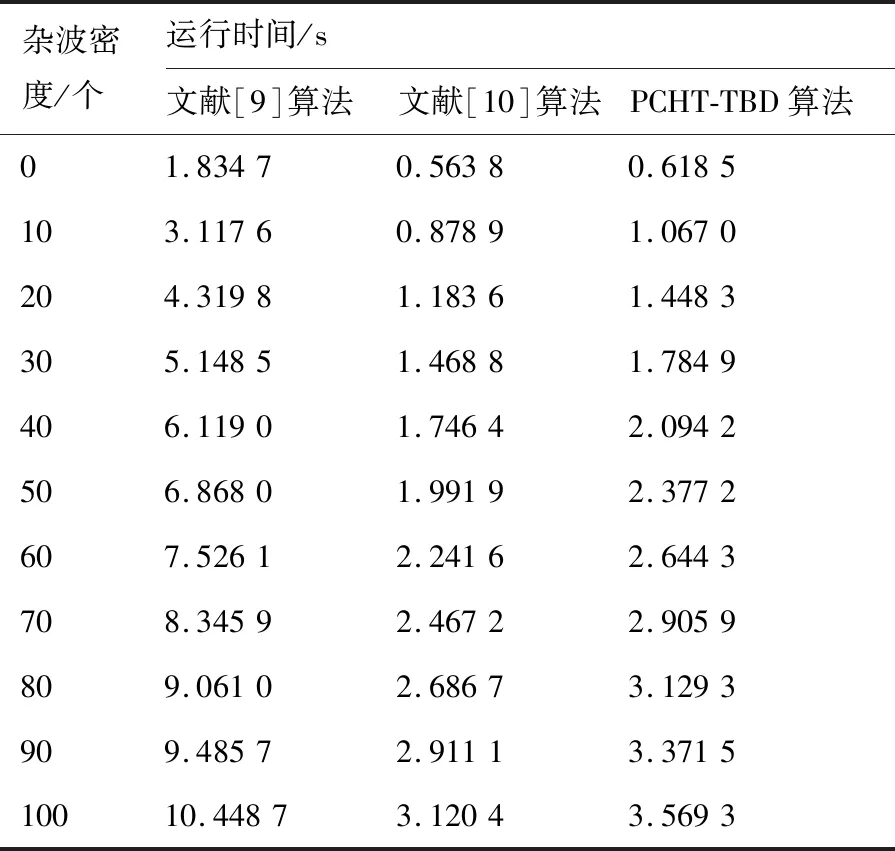
表2 不同杂波密度下算法运行时间Table 2 Running time of algorithm with different clutter density

4.3.3 新点数积累门限

算法进行峰值聚优后，只在新点数积累空间设立门限进行峰值提取，当门限设置不同，算法的检测概率和虚假航迹率也不相同。由于总积累帧数为10帧，在4.1节参数设置前提下，设新点数积累门限为从1～10的10个整数，进行=500次的Monte-Carlo仿真观察不同门限设置下全局检测概率和虚假航迹率的变化。其中，全局检测概率由4.3.1节说明，设虚假航迹率为，则有

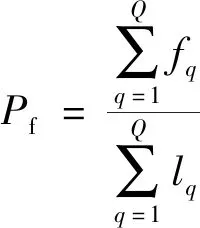
(39)

式中：表示第次仿真中输出的虚假航迹数；表示第次仿真中输出的航迹总数。

仿真结果如表3所示。由表3得，PCHT-TBD算法具备较高的全局检测概率和极低的虚假航迹率。当新点数积累门限设置不同时，全局检测概率和虚假航迹率不同。发现当新点数积累门限从7变到8时，全局检测概率和虚假航迹率均下降明显，考虑到虚假航迹率本身很低不影响后续观测，因此在4.1节仿真环境下，应设置新点数积累门限为7。