跑道侵入与冲突检测的共形几何代数描述
2022-07-04焦卫东王瑞冬姚军强庞艳丽
焦卫东,王瑞冬,姚军强,庞艳丽
中国民航大学 天津市智能信号与图像处理重点实验室,天津 300300
随着中国经济快速发展,民航飞行器数量越来越多,机场日渐繁忙,跑道侵入、冲突导致的危险事件发生的可能性增大,严重影响机场场面的安全运行。跑道侵入与冲突检测成为空中交通管理的重要环节。
目前,跑道侵入与冲突检测算法均基于欧氏空间研究。沈笑云等利用广播式自动相关监视(Automatic Dependent Surveillance-Broadcast, ADS-B)提供的实时位置数据和地理信息系统(Geographic Information System, GIS),采用射线法及计算欧氏距离判断的方式实现了实时跑道冲突检测与告警功能。该方法在用射线法判断飞行器和跑道保护区(Runway Protection Zone,RPZ)的位置关系时,需通过求解线性方程组确定射线和多面体的交点个数,且需要考虑边界、边界顶点及边界延长面等特殊情况,逻辑复杂;在冲突检测时需要分别判断水平和垂直方向的距离,向高维扩展较困难,基于复杂场景的算法结构较复杂。Cai等提出一种基于深度学习的跑道侵入检测方法,具有更好的可靠性和准确性。但该算法需要通过监控获取大量视频图像,经大量学习和训练获得可靠的网络及参数,工作量较大,且由于视频视角原因,很难检测遮蔽情况下的目标。Li等基于地面运动制导控制系统检测跑道侵入,通过及早发现和警告跑道侵入来提高跑道安全性。该方法将保护区分成进场区、排队区、跑道区和离去区,需要将航迹点和各个区进行比较,检测冲突场景众多。Wang等使用基于图形处理器的高效算法检测潜在的航路冲突,但由于航迹影响因素的不确定性,需要同时处理大量航迹,不适合用于跑道冲突检测。王献锋等针对航路与终端区的防撞安全问题,提出一种基于蒙特卡罗法的飞行冲突检测方法,能够得到较为准确的总体飞行冲突概率。Miao等提出一种基于多级网格时空索引的新型低空轨迹冲突检测算法,提高了轨迹规划和空域利用率。Yang等提出一种基于计算几何的概率冲突检测快速算法,取得了不错的准确率和效率。文献[6-8]中的方法都是基于计算冲突概率的方法,在具有大量航迹数据的情况下,准确率会有一定保证。但对于发生跑道侵入后的冲突检测,属于实时检测的情况,不会有足够数据用于冲突概率计算和比较,不利于已经发生跑道侵入后的实时冲突检测。
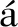
考虑到ADS-B已经成为民航飞机的标配,能够提供实时位置及速度等数据,本文利用ADS-B数据,基于共形几何代数优越的几何计算能力和统一维度的表达能力,对实时跑道侵入与冲突检测进行研究。首先,利用共形几何代数进行RPZ的模型描述,通过共形几何的外积运算判断飞行器与RPZ各面之间的位置关系,进而判断是否形成跑道侵入。然后,基于共形几何代数的球面表示方法建立飞行器安全保护区的模型描述,通过共形几何的内积运算判断飞行器的安全保护区是否相交,从而判断飞行器是否冲突。
1 共形几何代数
1.1 基本定义
共形几何代数是建立在欧氏几何模型之上的几何代数,它将三维欧氏空间扩展成五维共形空间,其一组正交矢量基为、、、、,满足

(1)
式中:,=1,2,…,。
引入矢量
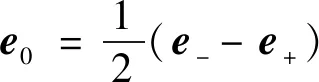
(2)
=+
(3)
分别表示坐标原点和无穷点,则
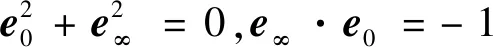
(4)
从而五维共形空间的基变为、、、、,定义单位伪标量为=。
1.2 基本运算
共形几何代数的核心运算包括内积、外积与几何积,即
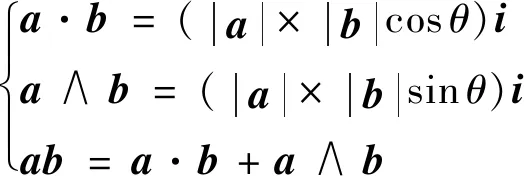
(5)
式中:和为矢量;为和的夹角;表示运算空间。
内积是一种降维操作,其结果多用来表示距离与角度的运算。外积是将一个向量延伸到另一个向量的运算,是一种升维操作,其结果为二维子空间,也称为二重向量(Bivector)。几何积同时包含内积和外积,类似于复数中的实部与虚部,符号“+”仅对不同维度的几何对象进行连接,并不进行任何其他操作。
在共形几何代数中,几何实体有2种表示形式,如表1所示。其中,在表示法1中:=++为五维欧氏空间的点;球的表示中:为该球球心;为该球半径;平面的表示中:为该面法向量,为坐标原点到该面的距离;圆和点对的表示法中等变量为球;线的表示法中等变量为平面。表示法2中:“*”表示对偶运算符;、、、分别为欧氏空间中的点对应的表示法1中的共形几何代数形式。通常情况下用表示法1可以解决共形几何代数中的问题,而当只知道欧氏空间几个点时,可以用表示法2快速表示共形几何代数中几何图元的描述问题。

表1 共形几何图元列表Table 1 List of conformal geometric primitives
2 方法介绍
2.1 跑道保护区
国际民航组织(International Civil Aviation Organization,ICAO)对跑道侵入的定义:在机场中任何飞行器、车辆或人员误入指定用于飞行器着陆和起飞的地面保护区。RPZ由《防止机场地面车辆和人员跑道侵入管理规定》定义,由地面保护区和空中保护区组成,如图1所示。其中,地面保护区由机场跑道、滑行道、升降带、跑道端安全区和电磁敏感区确定;空中保护区是从跑道升降带起始端两侧开始,以3°角向上扩张,15°角向两侧扩张,直至达到距离跑道入口4 km处。这些线面围成的区域及其地面部分共同组成RPZ。
以天津滨海国际机场为例,其经纬度分别为E117°20.7′和N39°07.4′,16R/34L跑道长3 600 m,宽60 m。以跑道中心点为原点、平行跑道的方向为轴、垂直跑道的方向为轴,建立直角坐标系,则RPZ的8个顶点坐标如表2所示。
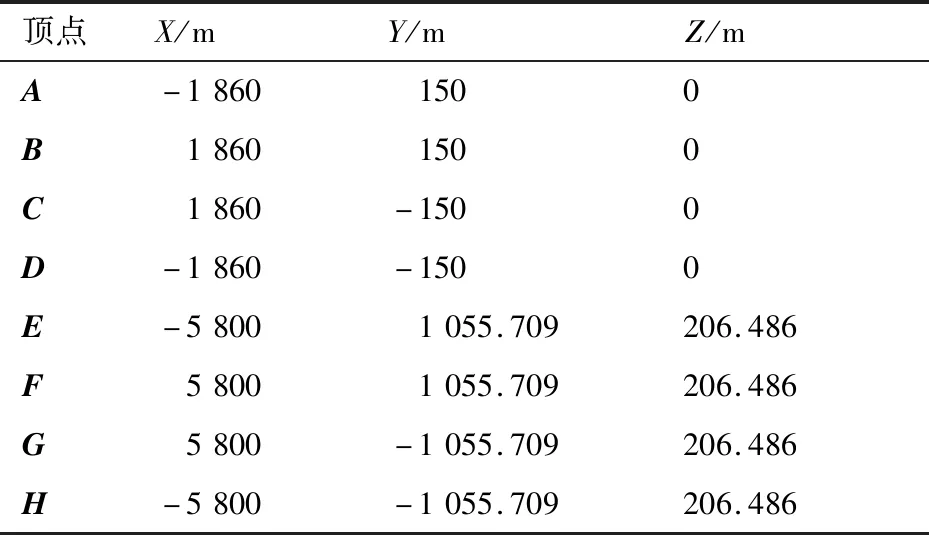
表2 RPZ的8个顶点坐标Table 2 8 vertex coordinates of RPZ
根据表1中点的表示法1和面的表示法2,共形几何代数中的平面可以由该面上3点和表示,如由点,,得到RPZ的一个面(如图1 所示)的共形几何代数表示为
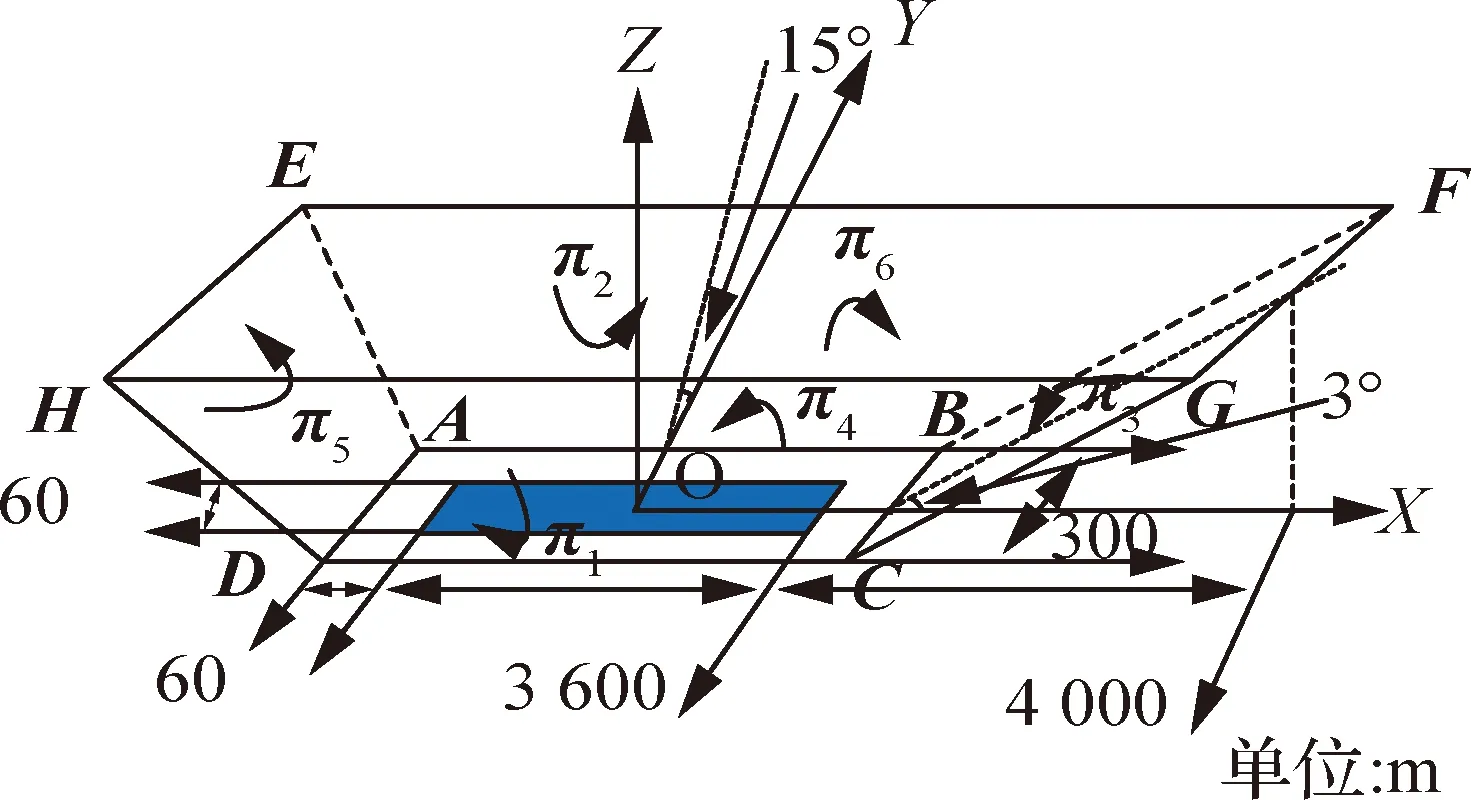
图1 跑道保护区Fig.1 Runway protection zone
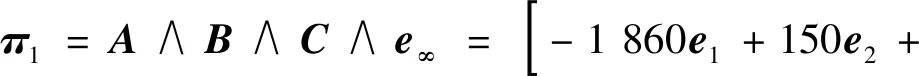
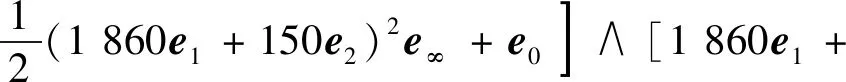
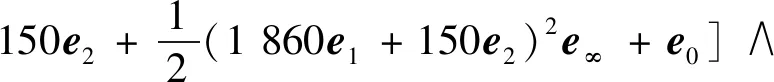
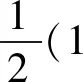
+]∧
(6)
此时,应注意共形几何代数中的面具有方向性,如图1中各平面上的箭头所示,3点的顺序不同,则生成面的方向也不同。同理可获得RPZ的其他5个面的共形几何代数表示的详细形式。
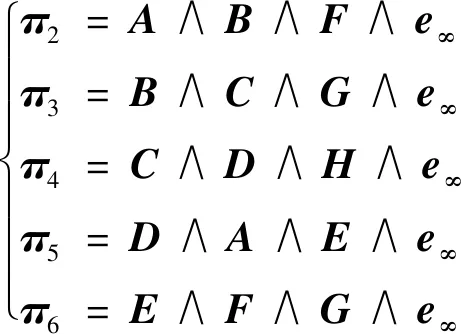
(7)
以上6个面围成RPZ,其内部均在各面的后方,如图1所示。
2.2 跑道侵入
飞行器大小远小于RPZ,其形状大小可忽略不计,近似看成一点,而RPZ可看成一多面体,从而飞行器与RPZ的位置关系可看作点与多面体的位置关系。虽然共形几何代数的Meet运算符可以以统一的方式确定不同尺寸的2个对象之间的相交关系,且可以直接处理无边界的基本几何对象,但只能进行基本元素(点、线、面)的运算,而不能对“体”直接运算。为判断点和多面体的位置关系,需要依次考虑点和形成该多面体边界的几个面的位置关系。
点面位置关系的问题,通常采用定性的方位描述方法,这类定性的空间描述在共形几何代数空间一般只需要利用外积运算的方向性,直接判断点面外积结果的正负号即可。本文引入共形几何代数中外积的性质来判断点是否在多面体内,从而判断飞行器是否在RPZ内。以图1跑道保护区中的面为例,其在共形几何代数空间的属性如图2所示。

图2 点面位置关系Fig.2 Position relationship of point and surface
令
=(∧)
(8)
在共形几何代数中,当>0时,点位于平面顺时针方向,即点位于平面前方;当<0时,点位于平面逆时针方向,点位于平面后方;当=0时,点位于平面上。
通过上述方法可以得到点与一个面的位置关系。RPZ是由6个面围成的多面体,实际情况中飞行器始终在跑道所在面的上方,对
始终有≤0。因此只需依次判断飞行器与其他5个面之间的位置关系:如果对某个面出现>0时,可以断定飞行器不在RPZ内;如果对这5个面都有≤0,则飞行器在RPZ内。
这样,通过共形几何代数将有界的RPZ用无界的平面组合进行表示,只需要通过外积运算考虑飞行器相对于RPZ各面的方向或点面位置关系,减少判定因素,而且不依赖坐标系建立。避免了欧氏空间中需要将点代入多面体的边界平面方程计算经过点的有向射线与多面体的交点个数来判断位置关系,以及处理RPZ边界延长面等各种特殊情况的处理,逻辑相对简单。
2.3 飞行器保护区
为防止飞行器与其他飞行器、障碍物相撞,确保飞行器安全运行,必须提供其在空间上的安全距离即最小安全间隔。对于RPZ中的飞行器,水平最小安全距离由飞行器的长宽决定,垂直最小安全距离为规定值:=60.96 m。因此以飞行器中心点为球心,=max{,}为半径的球即为飞行器保护区(保护球),其共形几何代数形式为
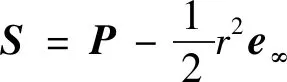
(9)
实际应用中,可根据应用要求适当调节半径大小。
2.4 跑道冲突检测
跑道冲突检测中,为保证有充分的安全冗余,分别以2架正在作业的飞行器中心位置、为球心,不妨以作为飞行器1保护区(球)的半径、作为飞行器2保护区(球)的半径做球、,用表1中球的共形几何代数表示法1表示为

(10)
几何代数中,为定义2点之间的度量性质,引入内积运算,计算式(10)中2球、的内积得
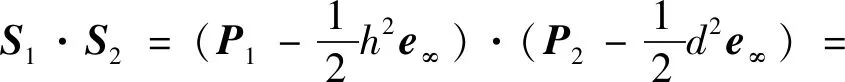
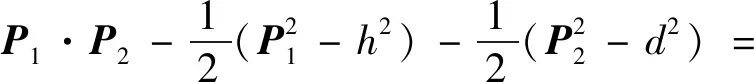
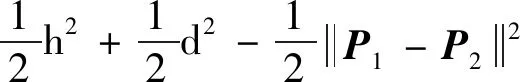
(11)
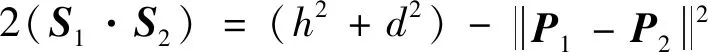
(12)
式(12)等号右边等于2球半径的平方和减去2球心之间距离的平方。考虑两球相切的充分必要条件为
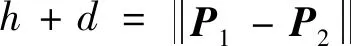
(13)
可以得到:
1) 若·<-,则2球不相交,此时认为2飞行器不发生冲突。
2) 若·≥-,则2球相交或相切,此时认为2飞行器发生冲突,其中等号成立时为相切。
这种判断方法利用共形几何代数的多维统一表示将水平和垂直方向维度的属性统一起来,只需要考虑2飞行器保护区(球)之间的内积运算即可确定是否冲突,避免了欧氏空间中需要分别判断水平和垂直方向的距离,实现了运算低维向高维的扩展,算法结构简单。
2.5 跑道侵入与冲突检测步骤
对机场跑道定义保护区后,设飞行器1为跑道上当前作业飞行器,飞行器2为后续作业飞行器,则基于共形几何代数的跑道侵入与冲突检测步骤为(流程图如3所示):

图3 跑道侵入与冲突检测流程图Fig.3 Flow chart of runway incursion and conflict detection
输入RPZ的各面的共形几何代数表示。
对RPZ内的当前作业飞行器1(点),计算及。
对飞行器2(点),依次计算
=(∧)=2,3,…,6
如果某一>0,则飞行器2不够成跑道侵入,继续判断下一时刻该飞行器或下一作业飞行器是否构成跑道侵入或算法终止;如果所有≤0,则飞行器2侵入RPZ,转步骤4进入冲突检测过程。
计算、、·。
如果·≥-,则飞行器2与飞行器1发生冲突,进行报警或冲突解脱。如果·<-,则2机不发生冲突,继续判断下一时刻该飞行器或下一飞行器是否构成跑道侵入或算法终止。
3 实验结果
准确的航迹预测是检测飞行器是否发生冲突的基础,由于Kalman滤波具有较强的鲁棒性和工程应用潜力,本文实验过程中利用卡尔曼滤波进行航迹预测。
利用2020年12月14日天津滨海国际机场的ADS-B航迹数据,在GIS中构造冲突场景进行实验分析,并同欧氏空间算法比较验证本文算法的有效性。实验环境为macOS Catalian、2.6 GHz双核处理器、8 GB内存计算机、Python3.8平台。共形几何代数运算使用Python中基于Gaigen系统的Clifford模块实现,该模块可以将欧氏空间的点转换为共形几何代数空间形式,并进行内积、外积和几何积等基本运算。
对图4所示2架航班,在10∶49∶27前,计划推入跑道的航班CCA8286(波音737机型,长度37.57 m)在RPZ内,从西北方向准备进场的航班CCA8284(波音737机型)不在RPZ内,此时经本文跑道侵入算法检测到CCA8284不发生跑道侵入,系统也不产生告警。

图4 未发生跑道侵入Fig.4 No runway incursions
随着飞行器继续运行,在10∶49∶27时检测出CCA8284和CCA8286同时处在RPZ内,即CCA8284对CCA8286产生了跑道侵入,系统产生跑道侵入告警提示,如图5和图6所示。此时利用本文冲突检测算法进行冲突检测,结果为CCA8284和CCA8286并不冲突,但此时仍然发出跑道侵入告警,随着飞行器的继续运行,需要继续进行冲突检测。

图5 未发生冲突的跑道侵入Fig.5 Runway incursion without conflict
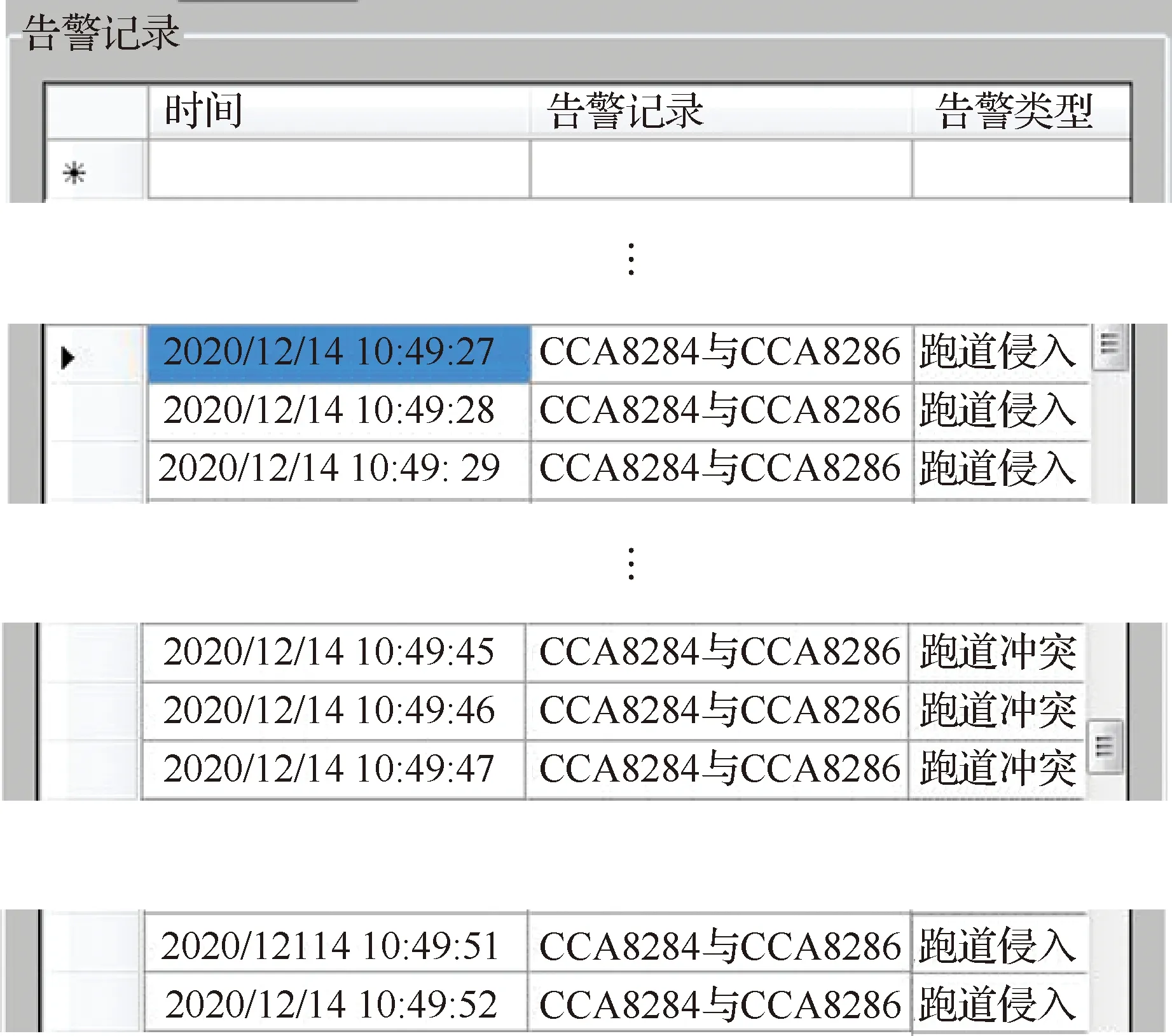
图6 告警记录Fig.6 Alarm record
在10∶49∶45时检测出2机发生冲突,如图7所示,此时系统产生跑道冲突提示告警,需立即进行冲突解脱。在10∶49∶51时,由于降落的飞行器操作优先级大于穿越跑道的飞行器,所以CCA8286减速至停止,CCA8284正常降落,变成跑道侵入状态,系统中产生跑道侵入提示告警,如图8所示。

图7 跑道侵入并发生冲突Fig.7 Runway incursion and conflict
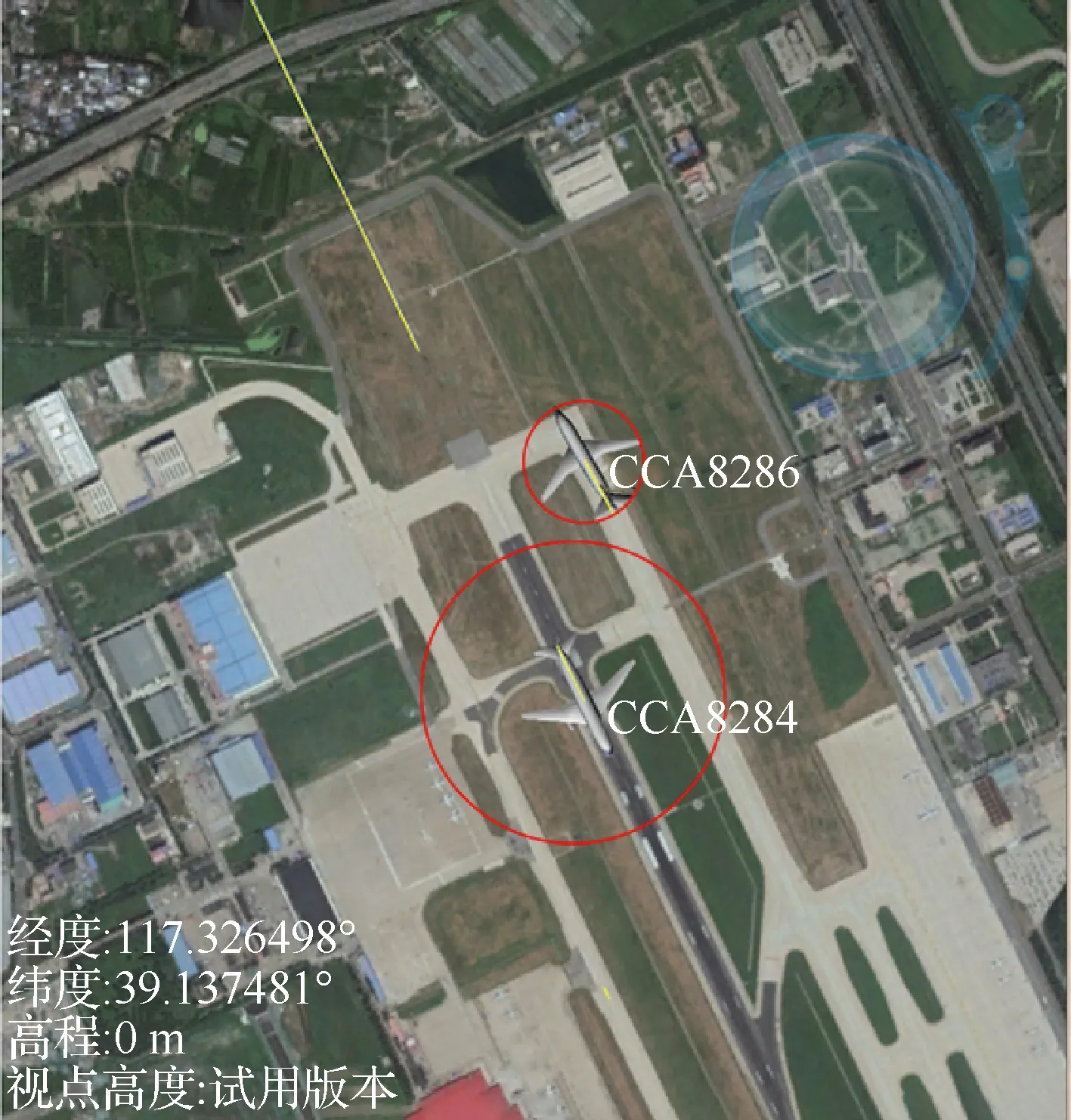
图8 冲突后解脱Fig.8 Liberation after conflict
本文方法本质上是共形几何代数空间中判断点面关系及计算距离的检测方法,因此,在相同条件及数据下通过实验复现了文献[1-2]中欧氏空间基于射线法和距离计算的跑道侵入和冲突检测算法,和本文算法检测结果一致。
实验中对各时刻对应的跑道侵入检测过程占用CPU时间进行了统计和对比。表3为在10∶49∶27 时刻发生跑道侵入以前,随机选取5个时刻的跑道侵入检测耗时结果。其中在10∶49∶27时刻,由于在该时刻发生了跑道侵入,需要完整判断航班CCA8284与围成跑道保护区的所有面之间的位置关系,故该时刻完成一次跑道侵入判断的用时最长。而其他时刻只需要判断航班与部分面之间的位置关系,耗时较短。结果表明:文献[1-2]中欧氏空间的跑道侵入算法平均用时63 ms,而本文跑道侵入算法平均用时21 ms。即使是在跑道保护区所有面都参与运算的情况下,本文方法的运算速度也比传统欧氏空间算法速度快近1.5倍。
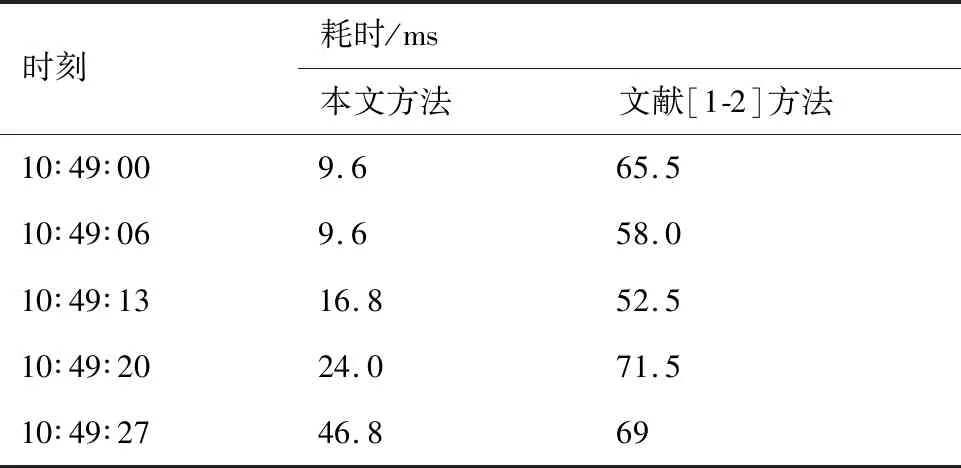
表3 跑道侵入耗时对比Table 3 Time-consumption of runway incursion conflict
这是因为:① 文献[1-2]中跑道侵入算法需建立坐标系,确定RPZ边界平面的方程,将点代入多面体的边界平面方程计算经过点的有向射线与多面体的交点个数来判断位置关系,需要解线性方程。实际计算中还需要考虑点在多面体(RPZ)的边界或所围面上、点在多面体所围面的延长面上、点的射线与多面体相交于多面体的顶点上等特殊情况,需要判断的因素过多,较为复杂,减少工作效率。② 本文算法在共形几何代数空间中将有界的保护区通过无界的平面组合进行表示,只需要通过外积运算考虑各个点相对于保护区各面的方向就可以确定位置关系,无需建立坐标系及求解线性方程组,减少了运算量。③ 本文实验使用Python中基于Gaigen系统的Clifford模块实现共形几何代数运算,通过布尔运算和预编译实现了高性能的计算,在内积等算子运算上效率高于欧氏空间的线性代数运算效率。因此相对于欧氏空间跑道侵入计算方法,本文用时较短。
对于RPZ中的冲突检测效率,实验中发生跑道侵入后对各时刻对应的冲突检测过程占用CPU时间进行了统计和对比。其中表4为在10∶49∶27发生跑道侵入以后,随机选取5个时刻的冲突检测耗时结果。可以看出本文算法对于RPZ中的冲突检测效率也优于文献[1-2]中冲突检测算法。这是因为本文算法利用共形几何代数的多维统一表示将水平和垂直方向维度的属性统一起来,只需要考虑2飞行器保护区(球)之间的内积运算即可确定是否冲突。而欧氏空间需要分别判断水平和垂直方向的距离,向高维扩展较困难,基于复杂场景的算法结构复杂,从而计算效率低。共形几何代数运算不需要建立坐标系,在冲突检测中减少计算量。
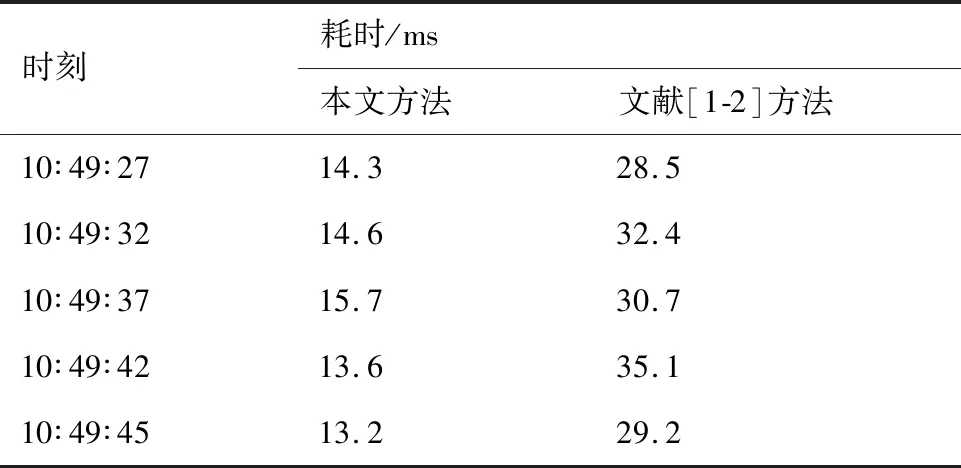
表4 冲突检测耗时对比Table 4 Comparison of time-consumption of conflict detection
4 结 论
建立了机场跑道保护区和飞行器保护区模型的共形几何代数描述方法,基于共形几何代数的外积和内积运算分别提出了共形几何代数空间的跑道侵入和跑道冲突检测算法。研究结果表明:
1) 基于共性几何代数的跑道侵入算法,由于将有界的保护区通过无界的平面组合进行表示,只需要通过外积运算考虑各个点相对于保护区各面的方向,减少了建立坐标系对算法效率的影响,避免了欧氏空间中各种特殊情况的处理,逻辑简单,用时较短。
2) 基于共形几何代数的跑道冲突检测算法,利用共形几何代数的多维统一表示将水平和垂直方向维度的属性统一起来,只需要考虑2飞行器保护区(球)之间的内积运算即可确定是否冲突。避免了欧氏空间中低维向高维扩展这一难点,算法结构简单,计算效率高。
3) 实验表明基于共形几何代数的跑道侵入与冲突检测方法能够快速、准确地判断跑道侵入及冲突的发生,相比于欧氏空间方法在运算效率上有显著提高。
4) 鉴于共性几何代数优越的空间表达能力和运算效率,民航中仍有许多应用可以基于共形几何代数方法进行描述,如飞行程序验证中的障碍物评估以及飞行器航迹预测等。
