航空发动机管路系统动力学特性综述

汪博，高培鑫，马辉,3,*，孙伟，林君哲，李晖，韩清凯，刘中华

1. 东北大学 机械工程与自动化学院，沈阳 110819

2. 烟台大学 机电汽车工程学院，烟台 264005

3. 东北大学 航空动力装备振动及控制教育部重点实验室，沈阳 110819

4. 空装驻沈阳地区第二军事代表室，沈阳 110043

航空发动机管路主要用于燃油、滑油和空气等介质的输送，除个别管路单独与机匣或附件相连外，大多数管路通过管接头和卡箍彼此相连，构成复杂的管路系统，如图1所示。如果将发动机比喻为飞机的心脏，那么管路则相当于发动机的心血管，其结构完整性对于发动机乃至飞机结构的安全可靠运行具有重要影响。

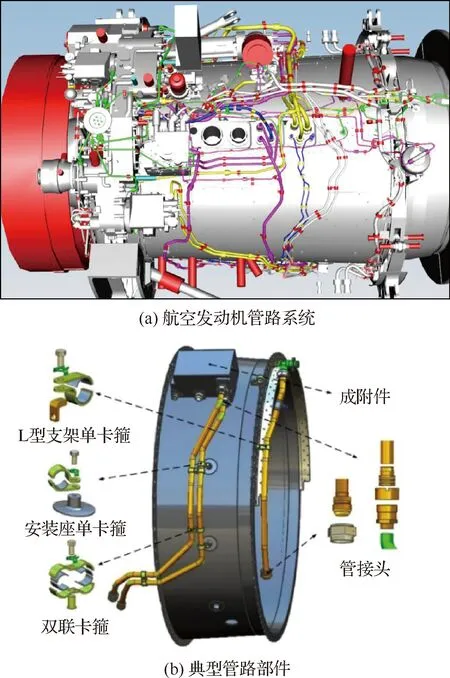
图1 发动机管路系统及典型部件示意图[1]Fig.1 Schematic of pipe system and typical components[1]

发动机管路系统具有以下特征：① 零部件数量众多、结构特征多样，难以形成统一的动力学建模方法；② 管路系统安装在机匣上，承受来自发动机不同区域的不同性质载荷激励，如发动机高低压转子不平衡激励、叶片气流扰动激励、燃烧脉冲激励、齿轮啮合激励、燃油泵/滑油泵输出流体脉动激励；③ 发动机管路通过卡箍、支架等结构件相连，存在大量结构耦合。

目前中国发动机管路系统的设计思路依旧采取先经验设计，再型号验证，出现问题进行改进的设计方法，如图2所示。但是由于发动机管路之间大量耦合的存在以及管路之间的相互影响，造成多根管路同步修改的现象。对于管路系统响应，以动应力为评判依据，如果测试动应力超过标准值，则修改卡箍数量、位置及管型参数，并重新进行经验设计，周而复始，延长设计研发周期。由于发动机管路系统结构的复杂性、激励的多源性、以及耦合的关联性，使得其在工作过程中极易出现由于设计不合理导致的管路系统共振，以及由于动应力过大诱发管路疲劳使得发动机系统提前失效。

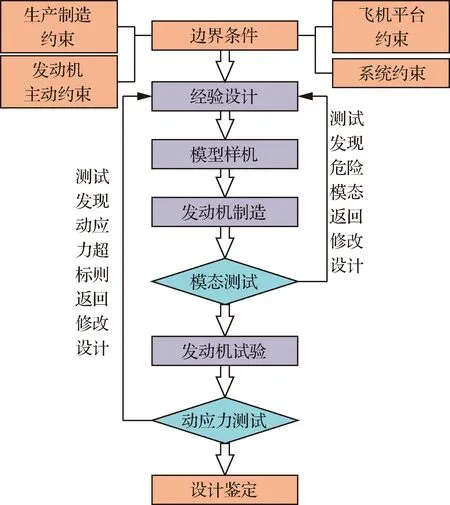
图2 航空发动机管路系统设计全流程Fig.2 Whole design process of aero engine pipeline system

早期世界航空大国对外部管路重视不够，导致发动机管路系统断裂、漏油、渗油故障频发。中国某型发动机在试车过程中，由管路系统共振及动应力过大等振动问题诱发故障也较多，直接影响试验进度，有时甚至影响发动机的整个研发周期。因此在设计过程中充分考虑管路系统的振动特性并进行动力学优化设计，以提高设计质量并缩短研发周期是十分必要的。

通过对国内外有关管路系统振动研究的检索可知，将统计数据列于表1。在主题/标题中包括 “pipe/pipeline vibration” 的文章中，中国所发表的文章与其他国家相比处于世界前列；但当主题中包含“pipe, vibration, aircraft/aero-engine”时，世界范围内所发表SCI文章仅18篇，其中中国8篇；EI文章229篇，中国63篇。可以看出，对于管路系统的振动问题，以“航空发动机管路系统”为研究对象的文章较少，大多是飞机液压管路、舰船以及其他输油管路等。

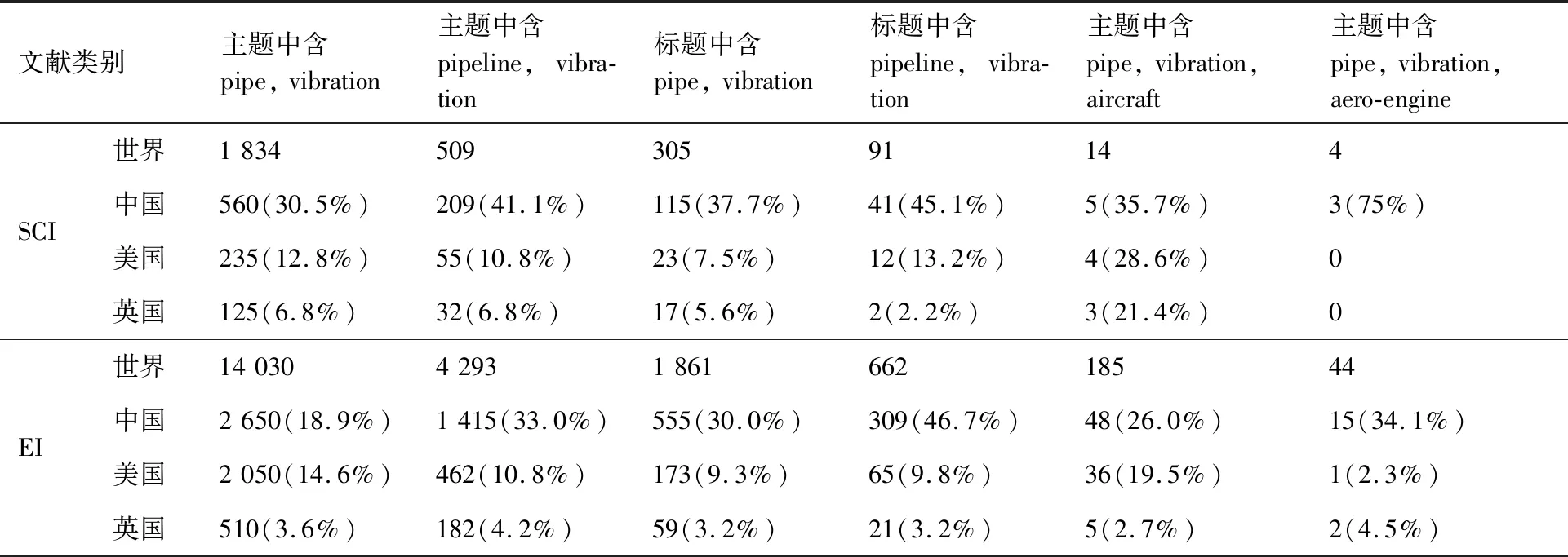
表1 管路振动相关文章中国文章数与世界其他国家对比Table 1 Comparison of number of published papers related to pipe vibration in China with those in other countries

因此，结合中国和世界范围的研究成果、设计单位对航空发动机管路系统设计及应用的迫切需求，航空发动机管路系统动力学特性及动力学优化仍存在较大研究及提升空间。

本文紧密围绕航空发动机管路系统的动力学特性展开，对管路系统的重要支撑部件卡箍的静力学特性及动力学特性表征，弹性支撑边界管路系统动力学特性，流固耦合管路系统动力学特性，以及管路系统动力学优化等方面研究工作进行综述，并对未来发动机管路系统动力学研究方向进行了展望。

1 卡箍力学特性表征

航空发动机管路是通过若干个管路支架和卡箍约束到机匣结构上，从而实现管路的支撑和固定(见图1)。管路支架和卡箍通常以组合形式构成一个支撑组件，其中，卡箍用以约束管路及吸收振动和冲击。

欧美国家的航空发动机卡箍包括钢制卡箍、带橡胶卡箍及其他材质卡箍(见图3)。目前中国航空发动机卡箍与俄罗斯发动机卡箍相似，多采用带金属橡胶衬垫卡箍，此类卡箍一般是金属箍带和金属橡胶衬垫的组合件，箍带起到支撑固定作用，金属橡胶衬垫起到减振的作用(见图4)。

图3 欧美航空发动机卡箍示意图Fig.3 Photos of aero-engine clamps in Europe and America

图4 单联及双联金属橡胶卡箍Fig.4 Single and double clamps with metal rubber

卡箍作为重要的支承部件，其力学特性对管路系统动力学特性有很大影响，为了准确预估管路系统的动力学特性，首先需要准确预估卡箍的刚度和阻尼特性。目前表征卡箍刚度和阻尼特性的方法主要包括静力学法和动力学法。

1.1 卡箍静力学特性表征

对于金属橡胶卡箍，国内早期研究成果发表于1999年，基于NASTRAN软件，尹泽勇和陈亚农建立了单联和双联卡箍的有限元模型(见图5)，通过力和变形之间的关系，计算了卡箍横向刚度和转角刚度，并建了模型试验台，通过悬挂砝码法来施加转矩和横向力，测试了双联卡箍的横向拉伸刚度和一个方向的转角刚度。仿真及实验表明双联卡箍横向刚度接近3×10N/m，角刚度接近45 N·m/rad。2011年，基于ANSYS软件朱昭君和陈志英建立了单联金属橡胶卡箍静接触有限元模型，不同直径卡箍横向刚度和角刚度，结果表明，单联卡箍横向刚度最大接近10×10N/m，角刚度最大210 N·m/rad，并分析了卡箍的长度和厚度等结构参数对卡箍刚度的影响规律。2019年，柴清东等搭建了单联金属橡胶卡箍横向刚度和转角刚度的试验台(见图6)，通过施加不同方向的力和转矩，测定了对应的横向变形和转角变形，通过力/力矩和变形之间的迟滞曲线，确定直径8 mm卡箍的横向和角向刚度，并通过模态实验对拧紧力矩为7 N·m和12 N·m的卡箍刚度进行优化，结果表明，在7 N·m 拧紧力矩下，卡箍方向线刚度2.73×10N/m，方向线刚度2.66×10N/m，方向角刚度34.99 N·m/rad，方向角刚度17.5 N·m/rad；并通过不同拧紧力矩下管路-卡箍系统固有频率的变化，得出拧紧力矩8 N·m是卡箍刚度趋于稳定的临界值。

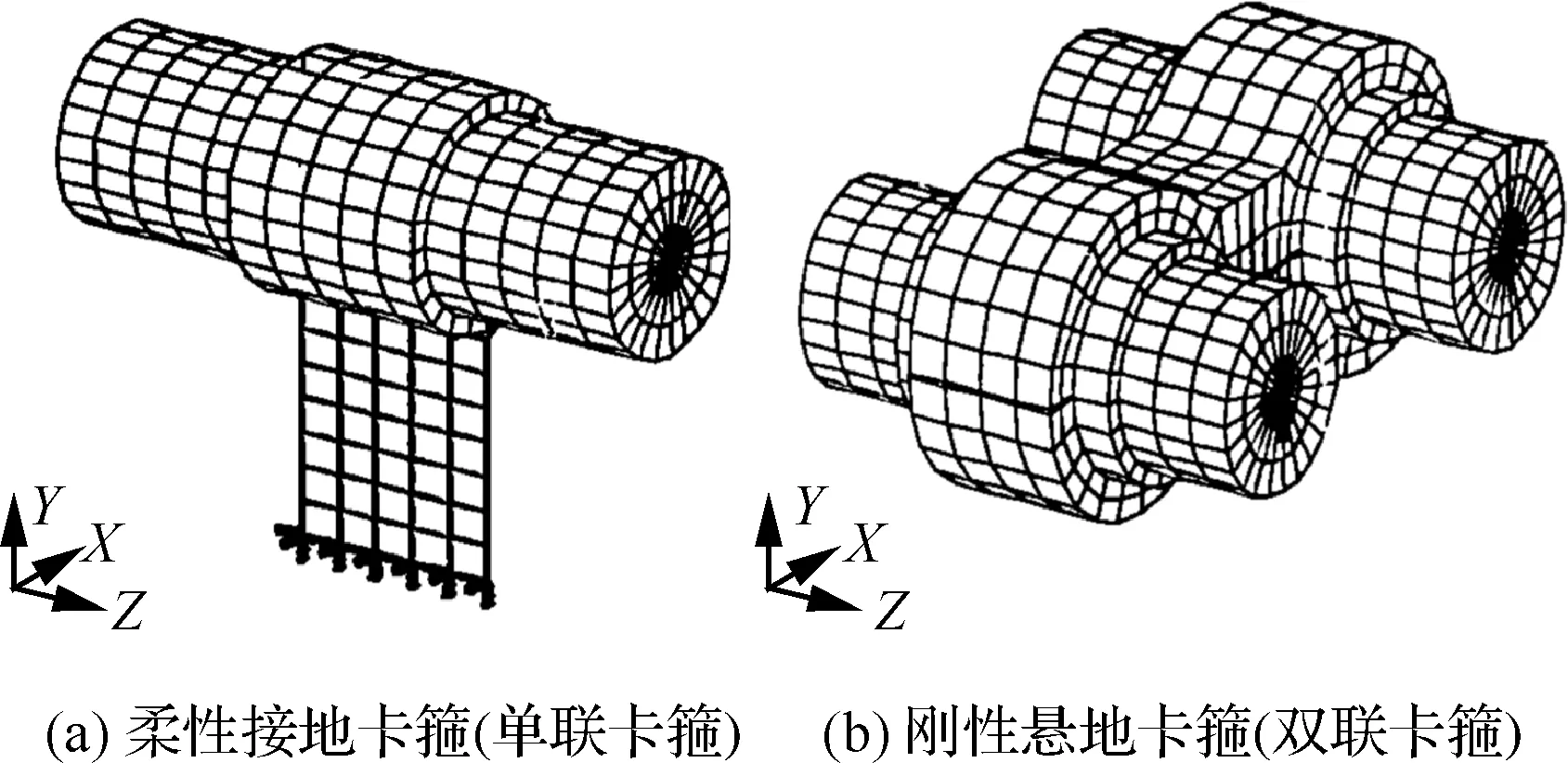
图5 单联及双联卡箍有限元模型[11]Fig.5 Finite element models of single and double clamps[11]

图6 横向及角向刚度测试装置[13]Fig.6 Test equipment of lateral and angular stiffness[13]

针对卡箍力学特性中表现出来的非线性特征，考虑金属橡胶卡箍结构和材料的不对称性的影响，李占营等提出描述卡箍分段线性刚度的解析方法(见图7)，图中:和分别为卡箍上、下部刚度,和分别为卡箍上部和材料不对称引起正、负向刚度值;为方向位移。并基于文献[5]的思想搭建柔性卡箍静刚度测试装置(见图8)，以∅14卡箍为例进行试验，试验结果表明在3 N·m拧紧力矩下其横向刚度接近2.5×10N/m。闫辉等对双联金属橡胶卡箍进行了静态试验，获得卡箍刚度随变形幅值呈非线性变化曲线(见图9)，结果表明，卡箍的刚度接近2×10N/m，相对变形较小，不超过金属毡厚度的20%。李鑫等采用3次非线性刚度以及干摩擦记忆恢复力来表征金属橡胶卡箍的非线性支承特性，并建立了金属橡胶隔振数学模型，很多系数后续需要通过试验结果进行反推辨识，因此并未给出卡箍非线性刚度的取值。为了降低高温环境(300 ℃)管路系统的振动，Jiang等提出设计了一种基于金属橡胶材料的对称卡箍阻尼结构，研究了不同温度下卡箍阻尼结构的滞回曲线。通过对迟滞回线的精确分解，建立了包括温度参数的卡箍阻尼结构的非线性能量耗散模型。结果表明，温度在200～300 ℃时，金属橡胶性能趋于稳定。

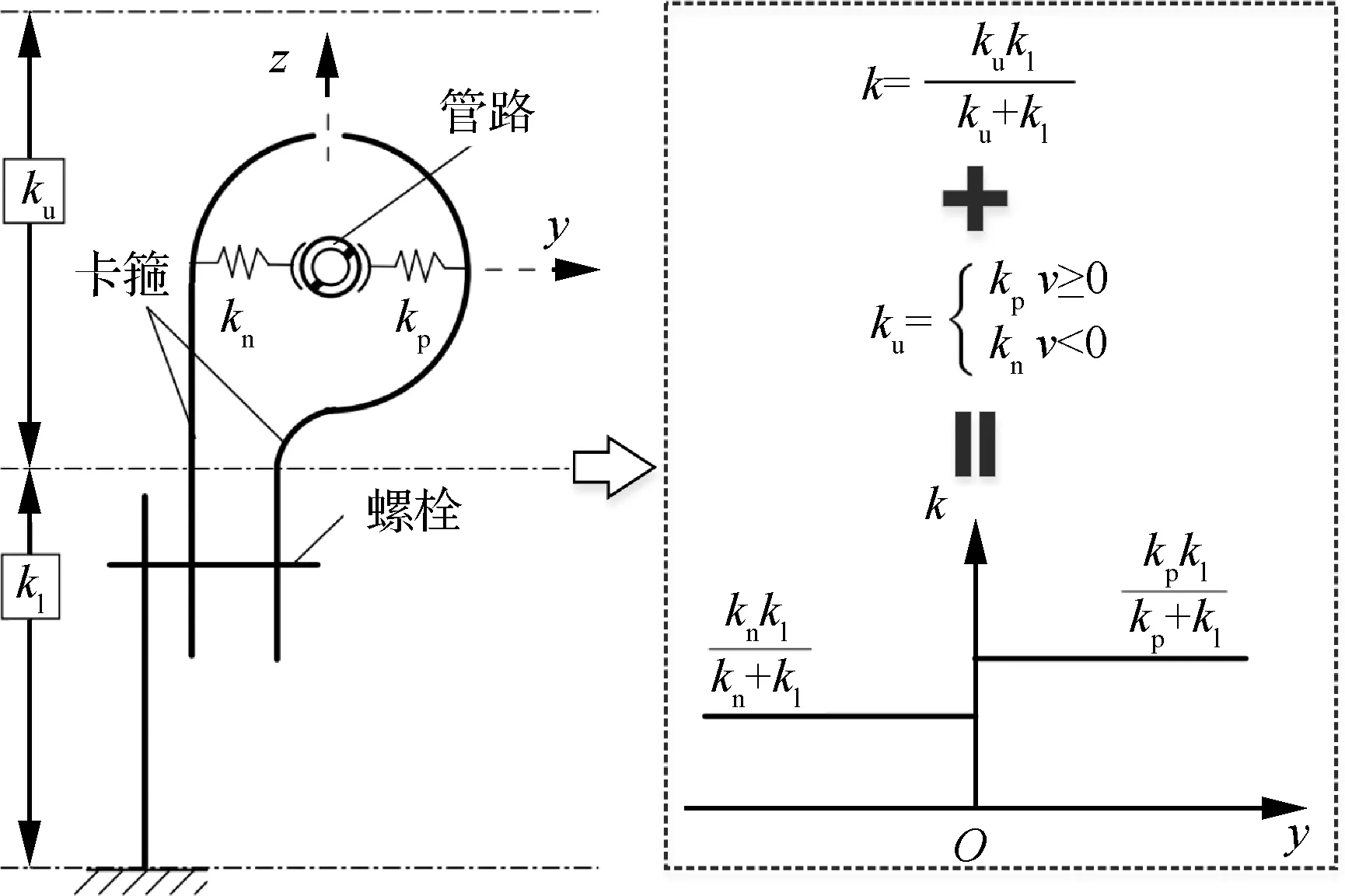
图7 具有分段线性的卡箍刚度解析模型[14]Fig.7 Analytical model of clamp with piecewise linearity[14]

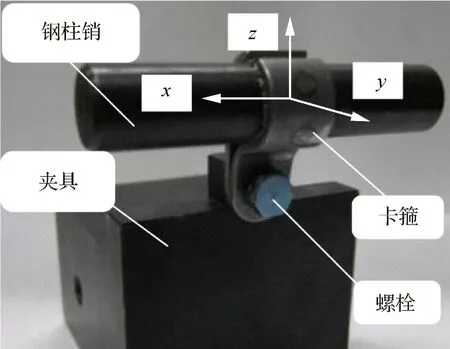
图8 卡箍刚度测试装置[15]Fig.8 Test device of clamp stiffness[15]

图9 金属橡胶刚度-变形关系曲线[16]Fig.9 Relationship curve of metal rubber between stiffness and deformation[16]

针对环抱式橡胶卡箍，考虑温度影响，李枫等建立了卡箍接触有限元模型(见图10)，分析了管径和温度对卡箍刚度的影响规律，并利用带温度箱的电子拉力试验机(见图11)测定了多个管径卡箍在不同温度(-50～125 ℃)下的等效刚度，研究结果表明卡箍不同方向的横向刚度差异较大，常温(20 ℃)下较大的横向刚度接近1.5×10N/m，随着管径的增加横向刚度减小，随着温度增加刚度减小。孙冰江采用ABAQUS软件建立了卡箍有限元模型，其中衬垫采用橡胶材料本构模型(见图12)，分析了卡箍6个自由度平动等效刚度和转动等效刚度，研究结果表明最大横向刚度为7.88×10N/m，最大转角刚度为7 200 N·m/rad。

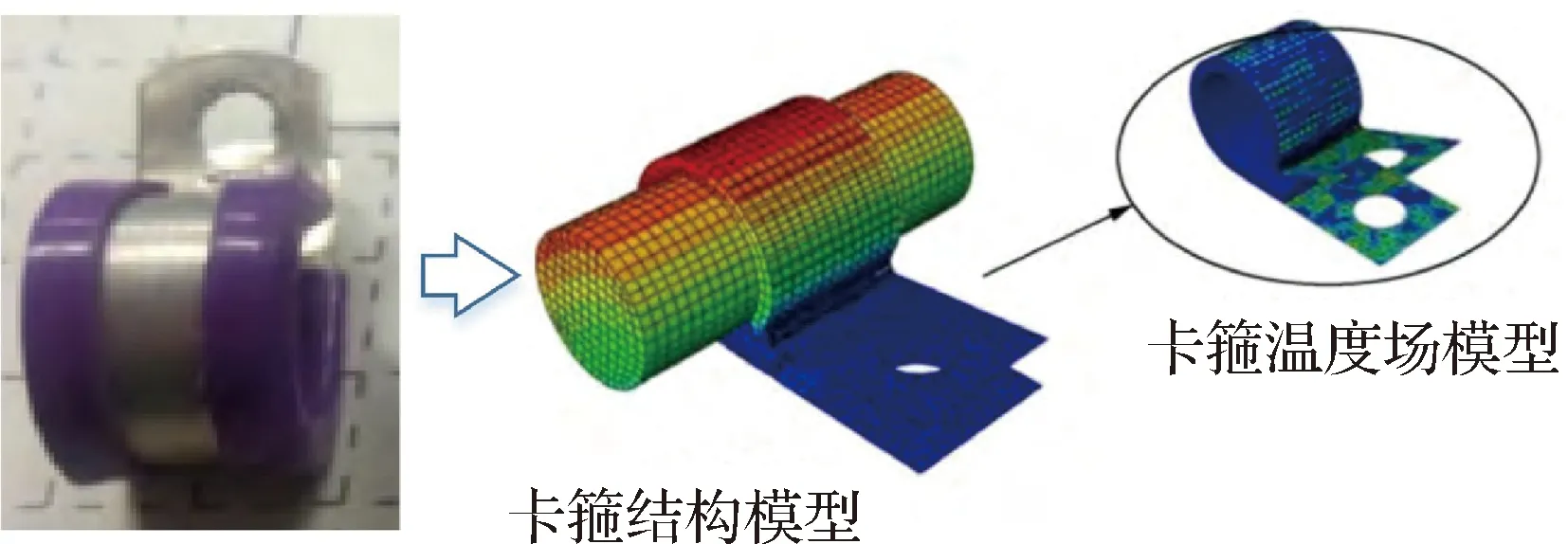
图10 考虑温度影响的橡胶卡箍有限元模型[19]Fig.10 Finite element model of rubber clamp considering temperature effect[19]

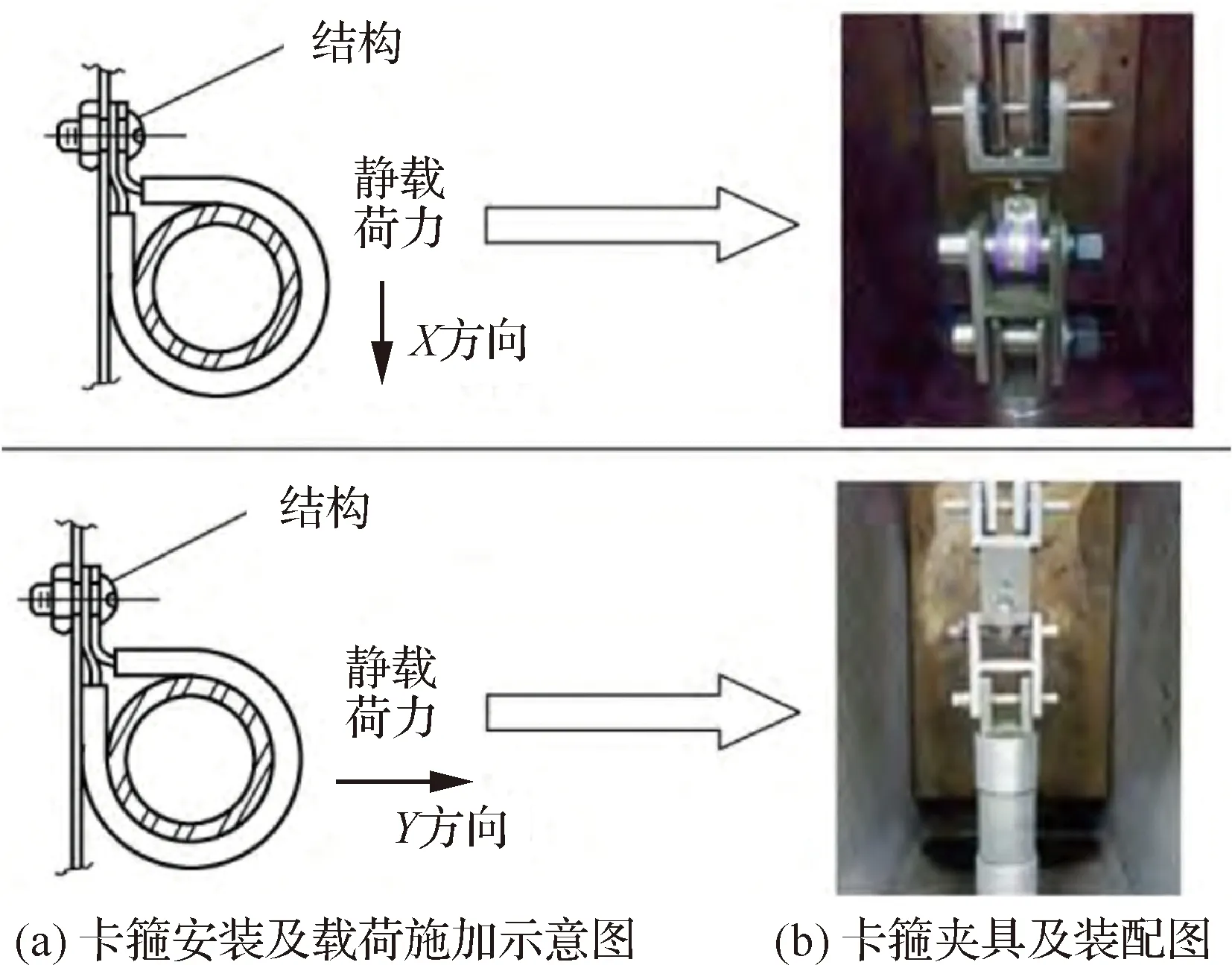
图11 考虑温度效应的卡箍刚度测试装置[19]Fig.11 Stiffness test device for clamp considering temperature effect[19]

图12 基于橡胶本构模型的卡箍有限元模型[20]Fig.12 Finite element model of clamp based on rubber constitutive model[20]

目前对卡箍静态力学特性研究，主要针对金属橡胶卡箍和环抱式橡胶卡箍。以线性化方法表征金属橡胶卡箍力学特性，其横向静刚度的取值量级在10～10N/m，角刚度的取值10～10N·m/rad；非线性方法表征的卡箍刚度随位移幅值变化，卡箍位移幅值较小，卡箍刚度接近2×10N/m；若以分段线性模型表征卡箍刚度，需要准确计算上下半卡箍的静刚度，才能准确描述总体刚度；高温情况下(200～300 ℃)金属橡胶卡箍的力学性能较为稳定。对于环抱型卡箍，温度对其力学特性的影响是关注焦点，其横向刚度量级同样在10～10N/m。

1.2 卡箍动力学特性表征

卡箍的动刚度/阻尼通常是利用反推辨识方法获得，即在给定初值的情况下，将理论建模分析结果利用迭代算法不断逼近动力学测试结果，进而得出卡箍动刚度/阻尼值。

高晔等建立了单联卡箍-直管系统的动力学有限元模型，其中卡箍简化为2自由度线刚度和阻尼单元，并搭建了该模型试验装置，得到仿真和实测的固有频率及频响函数，基于灵敏度法，辨识了卡箍的横向刚度和阻尼(见图13)，卡箍刚度接近2.5×10N/m，阻尼系数177 N·s/m，辨识结果表明卡箍的刚度及阻尼具有频率依赖性，且水平及竖直方向存在差异。其另外一篇文章中，也基于类似的研究方法，辨识了不同拧紧力矩下的卡箍刚度和阻尼，研究表明基于前3阶固有频率辨识的卡箍刚度随着拧紧力矩增大而变大，第1阶固有频率对应的卡箍阻尼随拧紧力矩波动下降，而第2和第3阶对应的卡箍阻尼未见明显变化。高晔等提出了基于实测扫频响应辨识卡箍刚度及阻尼的方法，该方法首先采用响应面法构造了频率和对应响应关于卡箍刚度及阻尼的多项式函数，并采用遗传算法进行了优化(见图14)，辨识出的卡箍横向刚度2×10N/m，横向阻尼系数10N·s/m，对比预测与实测频域响应，共振频率及响应偏差均小于3%，验证了辨识结果的有效性。Ulanov和Bezborodov通过商用软件ANSYS对简单空间管路进行建模，通过经验公式获得初始的刚度与能量耗散系数，进而获得支撑阻尼，通过ANSYS谐响应模块获得频响函数值，进而修正刚度与阻尼，通过不断修正迭代，直至结果稳定，最终获得了单卡箍的刚度1×10N/m与阻尼比为0.007 5。

图13 基于频响函数的卡箍刚度/阻尼辨识流程[21]Fig.13 Identification process of clamp stiffness/damping based on frequency response function[21]

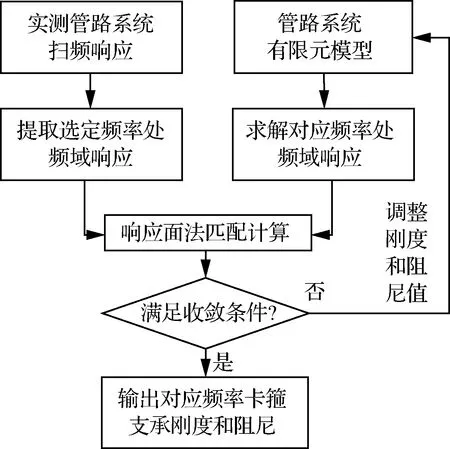
图14 基于扫频响应的卡箍刚度/阻尼辨识流程[23]Fig.14 Identification process of clamp stiffness/damping based on sweep response[23]

吕金华等在考虑卡箍质量的情况下，建立了悬臂直管-单卡箍系统动力学模型，其中卡箍利用双弹簧单元来模拟，搭建该系统测试平台，通过仿真与实测固有特性，对比模态置信准则辨识出单联卡箍水平和竖直方向刚度随拧紧力矩的变化规律，辨识流程见图15；拟合出的卡箍水平刚度接近5×10N/m，竖直刚度接近2×10N/m。Liu等建立了均布多卡箍-直管系统半解析模型，利用欧拉梁模型建立自由边界的管路能量方程，卡箍刚度表达为半周期正弦函数的积分(见图16,图中:为卡箍离散节点)，计算出卡箍变形能，获得系统总能量，并求出系统固有频率，通过与实测固有频率对比，基于遗传算法辨识出卡箍横向刚度6×10N/m和转角刚度145 N·m/rad。

图15 基于固有特性辨识卡箍刚度流程[26]Fig.15 Identification process of clamp stiffness based on natural char-acteristics[26]

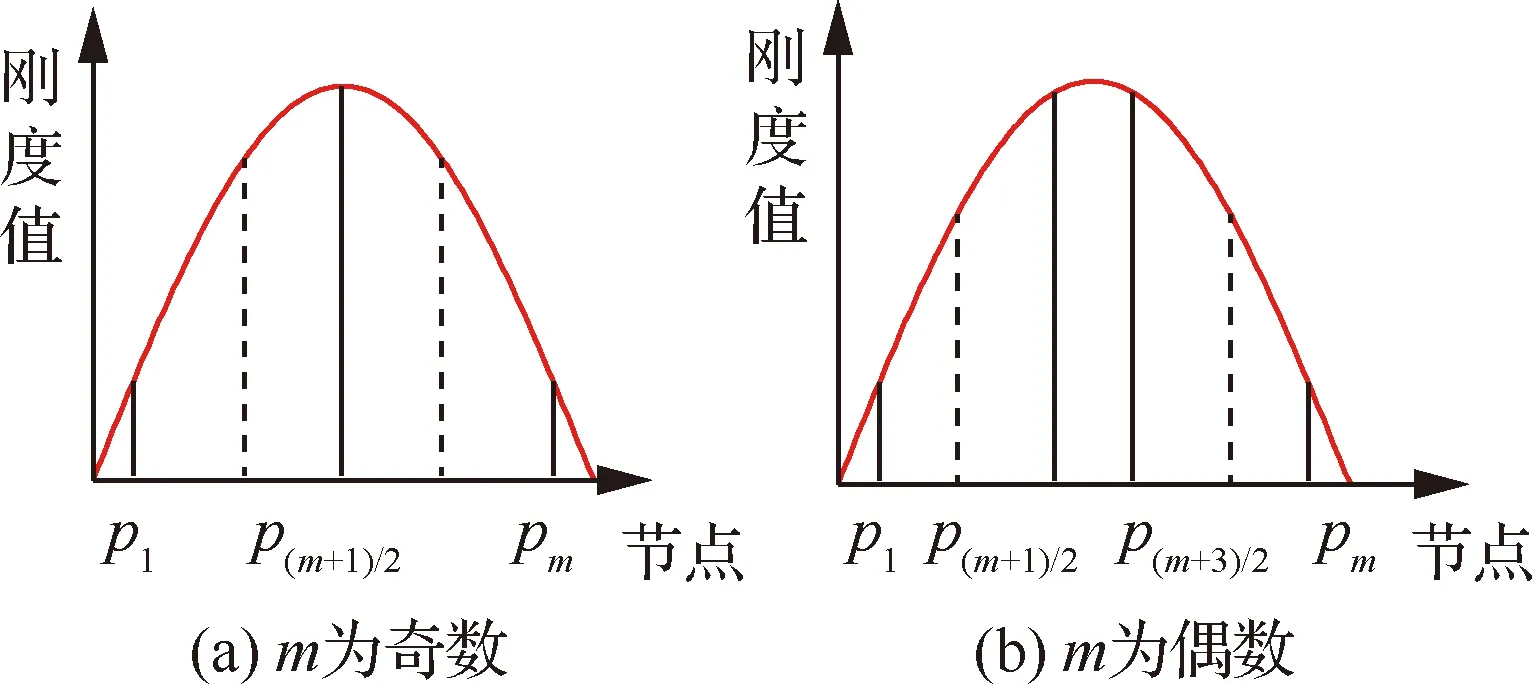
图16 弹簧刚度值正弦分布示意图[27]Fig.16 Sinusoidal distribution schematic of spring stiffness[27]

考虑金属橡胶的非线性力学特性，闫辉等对金属橡胶隔振器的非线性迟滞特性参数进行了反推辨识，首先建立了单自由系统非线性动力学模型，采用双线性迟滞模型来描述非线性迟滞系统的恢复力，基于能量法和最小二乘法对金属橡胶隔振器力学参数进行辨识，结果表明，金属橡胶密度直接影响其滑移刚度，当金属橡胶相对密度为0.24时，辨识出的滑移刚度为4.2×10N/m。吕金华等基于分段样条插值法获得恒位移测试函数及恒速度测试函数，通过频响测试分别建立响应位移与系统第1阶固有频率的关系以及响应速度与频响函数比之间的关系，并通过仿真分析获得卡箍横向刚度与系统第1阶固有频率的关系、卡箍阻尼与频响函数的关系，从而构造出了卡箍横向刚度与位移响应的函数关系，且常数项为1.56×10N/m，与卡箍线性刚度误差2.56%；拟合出卡箍阻尼与速度响应的函数关系，且常数项为4 N·s/m，与卡箍线性阻尼系数7.9 N·s/m 较为接近。

刘中华等以3种规格、每种规格5个样本的金属橡胶卡箍作为试验对象，对卡箍装配应力进行了测试，分析了螺栓拧紧力矩值、加载次数、装配方法对卡箍的应力影响规律，该研究可为带有装配应力的卡箍刚度和阻尼测试提供一定借鉴。考虑到卡箍由于装配和测试导致的分散性影响，Guo等通过反复拆装3次，测试了在5个拧紧力矩下卡箍横向和角向刚度的分散性区间，为后续开展卡箍-管路系统固有特性的分散性研究提供了刚度参数的分散性区间。

目前利用反推辨识方法获得卡箍动力学特性主要存在如下关键问题: ① 需要构建一个准确的卡箍动力学特性模型，对于弹性支撑卡箍，通常简化为刚度和阻尼单元，而忽略单联卡箍质量，该模型是反推辨识的理论基础。② 实验系统本身及边界条件对测试结果的影响较大，以卡箍阻尼为例，目前准确地将管路结构阻尼和测试系统边界阻尼从辨识出的阻尼值中剥离仍存在困难。此外，卡箍刚度和阻尼具有一定的分散性，对于其分散性的辨识也非常必要。③ 辨识匹配算法的效率和精度，也对结果有较大影响。④ 卡箍刚度和阻尼表现出明显的非线性特征，行业内关于卡箍阻尼值的大小缺乏指导性标准，对于已有成果的准确性无法判断。⑤ 目前针对双联卡箍的动刚度/阻尼辨识未见报道。

2 弹支边界管路系统动力学特性

航空发动机在机匣外部有限的空间内排布大量保证发动机及飞机正常运行的管路系统，因此管路布局及管型受空间限制很大；单联卡箍、双联卡箍、支架接头等连接构件使得管路系统存在不同程度的结构耦合。于是在考虑管路系统结构参数、卡箍布局及卡箍力学特性等因素情况下，学者们针对支架-卡箍-管路构成的弹支边界管路系统的动力学特性、耦合振动及性能优化问题进行了研究。本节分别从弹支边界直管路系统动力学特性、弹支边界弯曲管路系统动力学特性及多管路系统动力学特性3个方面的研究成果进行了评述。

2.1 弹支边界直管路系统动力学特性

直管是管路系统中最典型的组成单元，对直管路系统的动力学特性分析是研究其他复杂管路系统动力学特性的基础。

柴清东等利用6自由度Timoshenko梁单元建立了直管-卡箍系统有限元模型(见图17)，其中考虑卡箍宽度，建立双弹簧单元对卡箍刚度进行模拟。通过对比固有频率，验证了静力学试验获得的卡箍刚度的有效性，并分析了卡箍拧紧力矩对系统固有频率的影响，得出当拧紧力矩达到8 N·m时，系统固有特性趋于稳定。吕金华等建立悬臂直管-单卡箍实体有限元模型，将直管-金属毡、金属毡-卡箍之间设置为固定约束，搭建该系统模态测试平台，通过固有频率对金属毡的弹性模量进行修正，并分析卡箍加工误差与金属毡性能退化对系统固有频率的影响。于涛等在实体管路有限元模型基础上，利用缩减方法获得子系统缩减超单元，通过单元装配获得管路系统缩减模型(见图18)，将原模型和缩减模型的固有特性及基础激励响应对比，证明了该缩减方法计算的高效性与准确性。

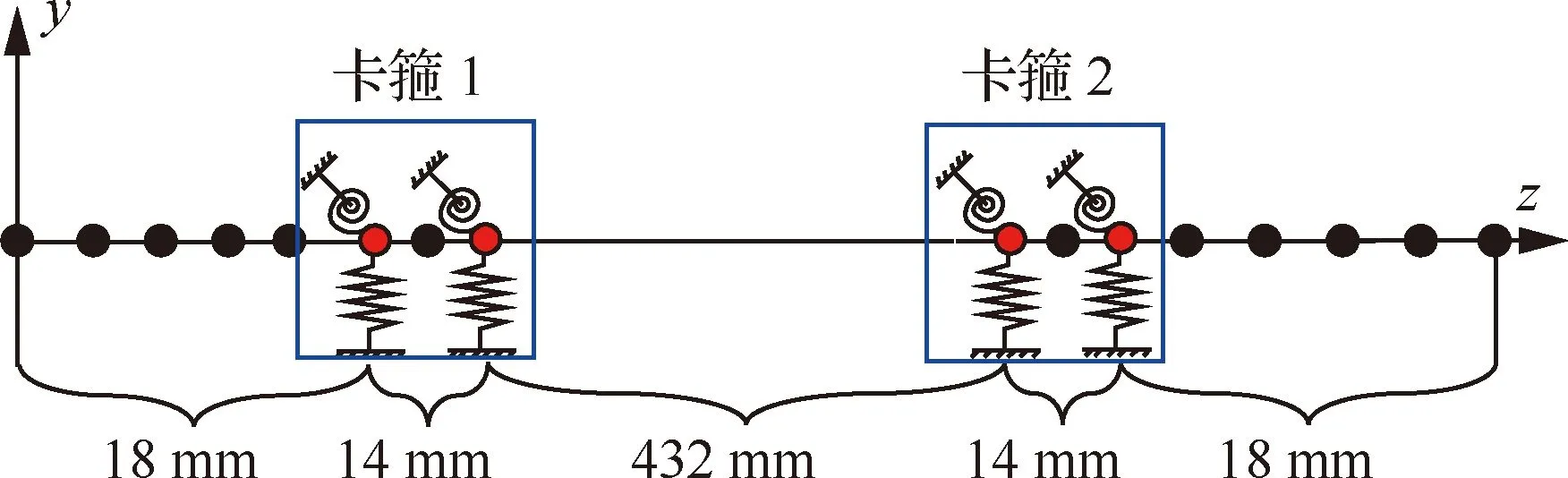
图17 直管-双卡箍有限元模型[13]Fig.17 Finite element model of straight pipe with two clamps[13]

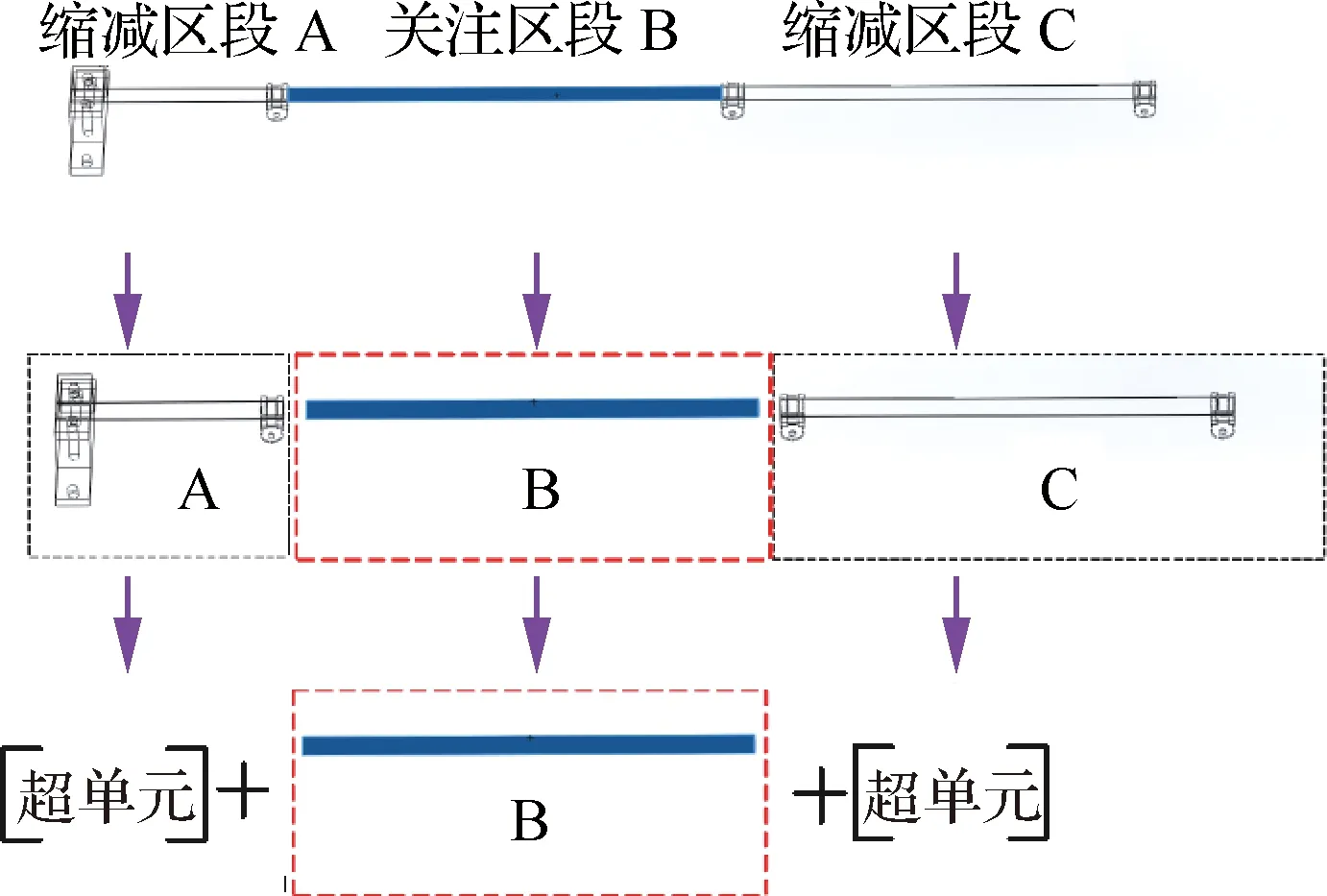
图18 管路系统减缩有限元模型[34]Fig.18 Dimensionality reduction finite element model of pipeline system[34]

针对弹支边界典型直管路的研究主要分为模型的建立及求解效率的研究和弹性支撑卡箍的刚度对直管路系统固有频率的影响研究。由于在真实发动机管路系统中直管路很少单独存在，因此对于直管路的研究侧重在方法的探索。

2.2 弹支边界弯曲管路系统动力学特性

由于布局及空间限制，发动机中存在大量的弯曲管路，包括L型管、U型管、Z型管、凹型管、多弯管路及空间管路等，这些管路通过卡箍或卡箍-支架连接在机匣上，构成弹支边界弯曲管路系统。

孙冰江采用传递矩阵法建立由直管和弯管组成的凹型管路动力学模型(见图19,图中:表示单元;为集中质量点的质量;、、分别为管长度、弹性模量、截面对中心轴的惯性矩;为传递矩阵;为弯管曲率半径;为弯管弯曲角度;为等效直管角度;=,为等效直管个数)，分析其固有特性并与ABAQUS软件结果对比，验证了传递矩阵法建立复杂管路模型的高效性与准确性。

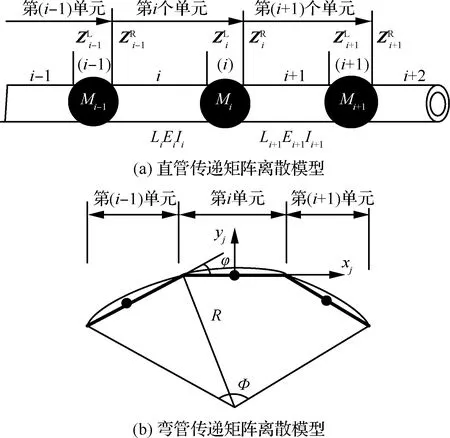
图19 直管和弯管传递矩阵法离散模型[20]Fig.19 Discrete model of straight and elbow pipes based on transfer matrix method[20]

柴清东等建立了L型管-卡箍系统有限元模型(见图20)，其中L型管路单元经过坐标变换实现角度转换，仿真获得其加速度频响函数及基础激励下的加速度响应幅值，通过与模态测试结果、定频激励与扫频激励下的响应结果对比，表明了有限元法建立典型管路-卡箍系统动力学模型并进行振动响应分析的有效性。

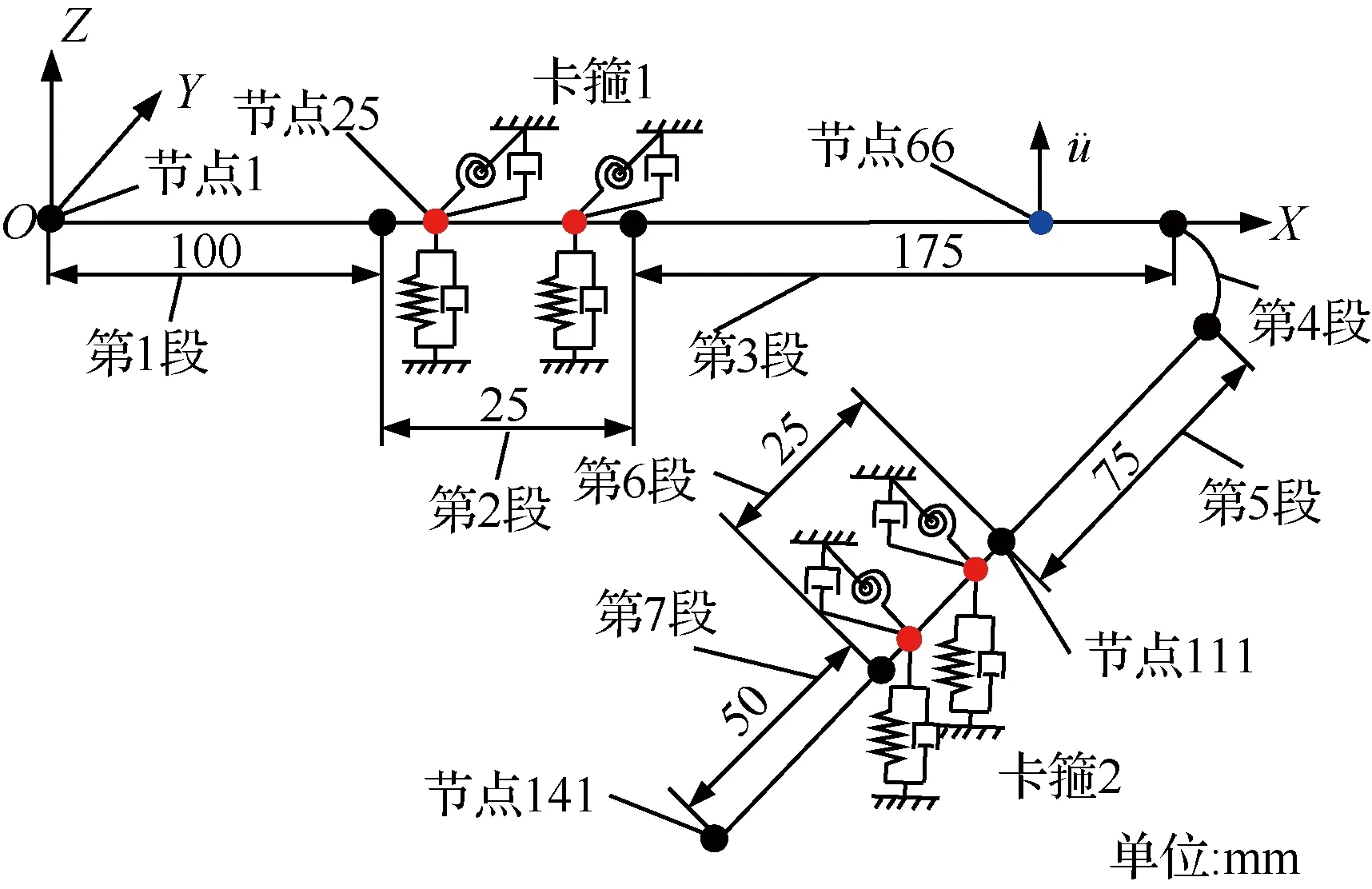
图20 L型管-双卡箍系统有限元模型[35]Fig.20 Finite element model of L-shaped pipe and two-clamp system[35]

刘海年和王桂华等对航空发动机机匣所处振动环境进行了研究，通过可靠性试验、功能性试验、耐久性试验及强化试验获得振动环境测试数据，得出风扇机匣、燃烧室及尾喷口附近的振动特性及激励形式(见图21)。以此为基础，康力等利用真实载荷谱对某发动机空间管路系统进行了振动响应分析，利用工程分析软件，对受典型简谐激励的风扇机匣位置管路进行谐响应分析，对受典型随机激励(见图22)的燃烧室及尾喷口位置管路进行随机振动响应谱分析，获得某点径向位移响应值，绘制功率谱密度曲线(见图23)，从图中可以看出，文中所建立的空间管路结构对1阶振动敏感，为航空发动机外部管路振动响应分析提供依据。

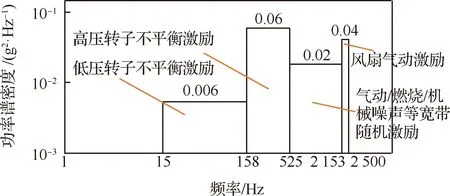
图21 航空发动机振动环境载荷谱[3]Fig.21 Load spectrum of aero-engine in vibration environment[3]

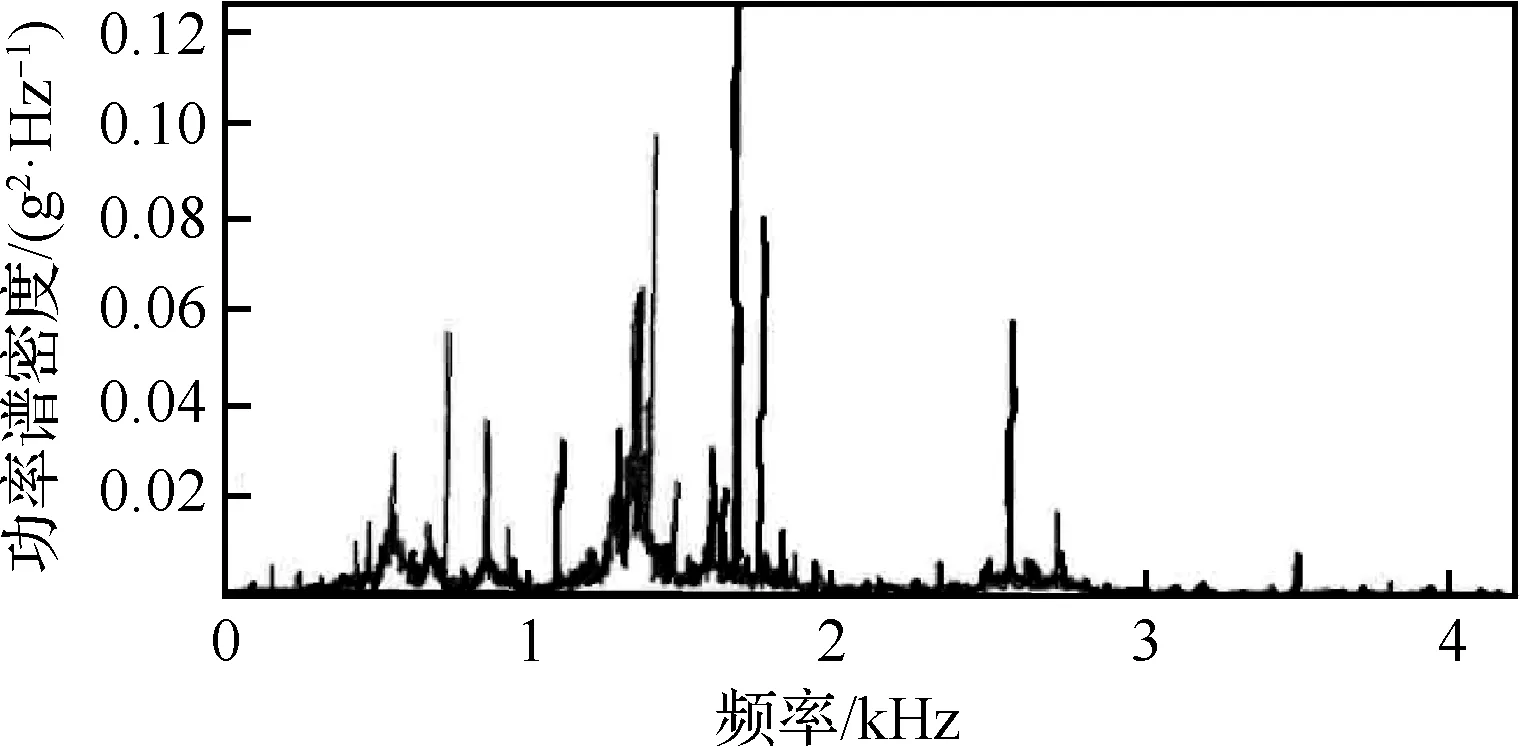
图22 燃烧室及尾喷口位置典型工况的频域特征[36]Fig.22 Frequency characteristics of typical conditions on combustion chamber and tail nozzle[36]

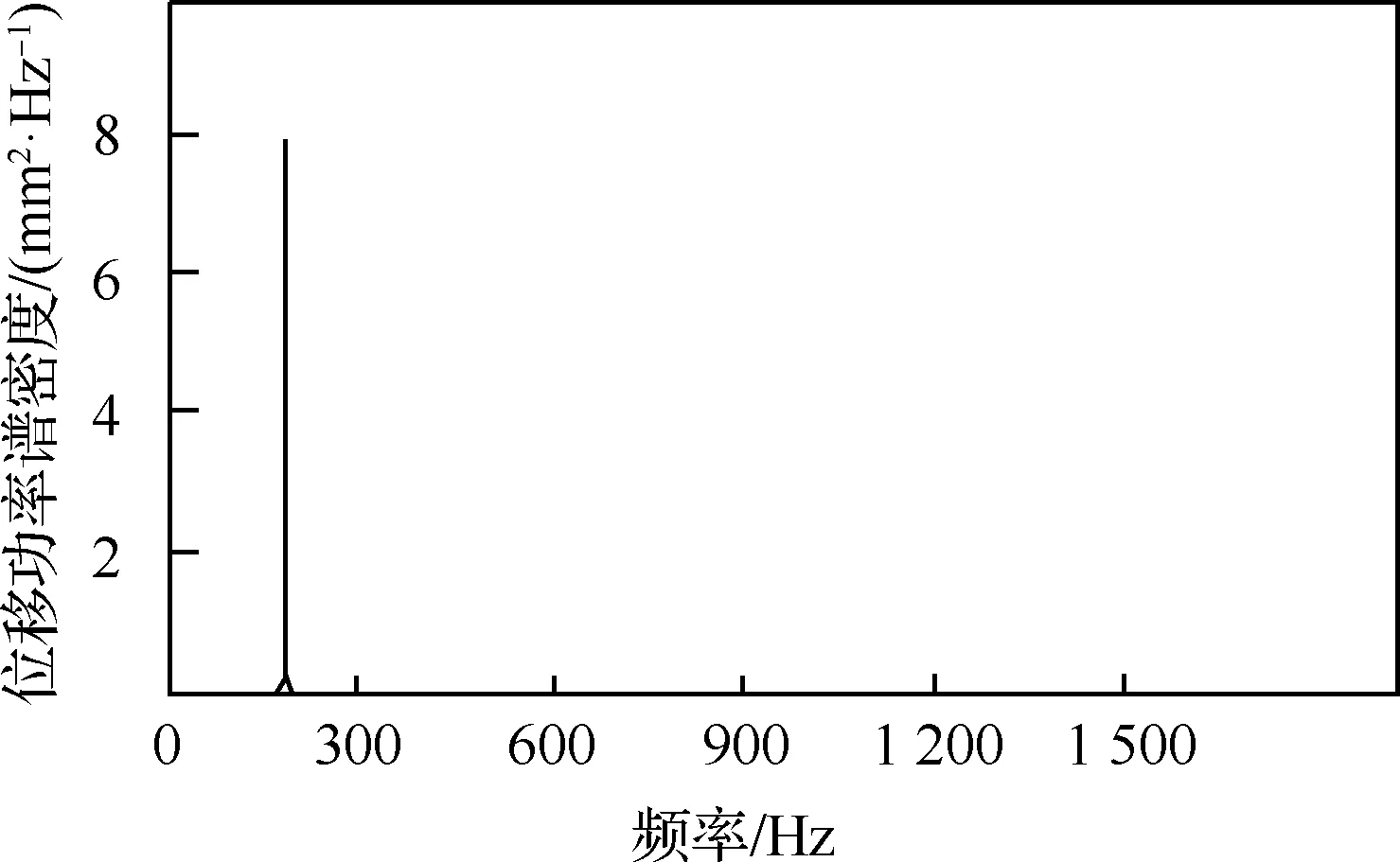
图23 随机载荷作用下的响应曲线[36]Fig.23 Response curve of random load[36]

对于弹支边界的弯曲管路系统，相关学者进行了振动特性的研究，研究方法主要以有限元分析为主，部分学者利用传递矩阵法来提高分析效率；激励形式包括模拟简谐激励和实测随机激励，其中在实测载荷谱作用下空间管路系统的振动响应，对真实发动机管路系统动力学性能优化具有指导性意义。另外，对于设计单位更关注的动应力问题，在研究弯曲管路系统动力学特征的过程中值得更多关注。

2.3 多管路系统动力学特性

多管路系统包括典型管路并联系统、不同管型管路串联系统、典型管路串并联系统、三通连接的分支管路系统等各类复杂管路系统。

多管路系统存在大量的结构耦合，因此其振动形式受到连接件的影响与单一管路存在差异，部分学者首先对多管路系统的固有特性进行研究。赵爽利用直管和Z型管路将某双列带分支管路系统分解，通过模态测试对直管和Z型管路进行“超模型”和“简化模型”的修正，通过刚性连接部件构成修正后的复杂管路系统，并研究了卡箍预紧力和支架刚度对系统固有特性的影响。有学者将双联卡箍简化为同等宽度的弹簧阻尼单元，柴清东等基于6自由度Timoshenko梁理论建立两端固支的单-双联卡箍平行直管路系统动力学模型(见图24)，采用遗传算法结合模态试验搜索未能测定的双联卡箍螺栓拧紧方向线刚度，并对其进行固有特性分析，仿真获得固有频率与各阶振型都与测试结果吻合较好，此研究探索了平行管路的振型规律。赵伟志和陈志英以双路总燃油管路系统为例，建立总体管路系统的有限元模型，其中将双联卡箍及支架作为整体等效为6自由度的支撑刚度，并采用Matrix27单元进行了模拟。仿真结果表明，发动机燃烧室管路系统固有频率呈分族密集特点，管路系统的模态振型主要分为主、副燃油分管主导振型以及分管与总管耦合振动模态。朴玉华建立了双直管并联的多管路系统减缩有限元模型和全模型，研究在冲击载荷、定频激励、变频激励和随机激励作用下，不同支撑条件的平行管路系统动力学响应。

图24 单-双联卡箍管路系统有限元模型[38]Fig.24 Finite element model of pipe system with single-double clamps[38]

多管路系统的振动特性分析包括以下3方面重点：① 多管路系统动力学模型复杂，多管路系统包含的多根管路，多种管型及连接部件，这些都增大了多根路系统建模的难度；② 连接部件的力学特性各异，比如卡箍的弹性支撑，三通和接头的刚性连接，不同的力学特性对多管路耦合系统振动特性的影响不同；③ 目前已有针对单一载荷作用下的多管路系统振动响应分析，但多源载荷耦合作用下的多管路系统振动分析问题仍鲜有涉及。

3 流固耦合管路系统动力学特性

航空发动机外部管路主要流体介质包含液压油、燃油、润滑油等，目前考虑流体介质的发动机管路系统动力学特性研究的相关文献和成果较少，部分文献报道了采用经典的输流管路流固耦合理论以及经典的水锤理论对航空外部管路的振动特性进行了研究。航空发动机外部管路的动力学行为十分复杂，原因在于管路具有复杂的空间构型、外部复杂的机械载荷环境以及管路内部复杂的流体载荷，存在着结构耦合、流固耦合、热固耦合等复杂耦合的综合作用，其动力学机理极为复杂，是目前研究面临的难题。

目前考虑流体介质的管路动力学特性研究已经明确归为流固耦合问题，根据流体的特点主要分为定常流动与管路之间的耦合和非定常流与管路之间的耦合、多源激励与管路结构之间的耦合3部分。针对不同的耦合形式，分别从考虑流体介质的管路动力学建模方法、动力学分析方法和动力学特性3个方面的研究成果进行评述如下。

3.1 定常流动与管路结构之间耦合动力学特性

针对定常流动与管路之间的耦合问题国内外相关学者已经开展了大量的研究工作，重点关注了流体引起管路的失稳问题，多数文献报道了黏弹性管路由于管体刚度较小，在流速增大时引发的系统固有频率下降直到为零，从而导致管路系统产生失稳现象，并出现分叉和混沌特性。对于考虑介质的定常流动与管路之间的耦合动力学问题，航空发动机管路方面的文献报道相对较少，本部分综合了航空发动机和飞机液压管路系统的流固耦合动力学问题进行了总结。

目前部分学者采用定常流动与管路之间的耦合模型开展了考虑介质的航空发动机管路系统动力学特性分析。李占营等采用定常流动与管路之间的耦合模型分析了航空发动机空间管路系统的振动特性，通过空间管路系统振动固有频率和响应特性研究表明，随着流速和内压的增大引起管路固有频率下降(见图25)，流固耦合效应导致了管路系统的刚度减小。航空发动机管路数量众多、结构特征多样，需要在设计阶段重点关注流速对弱支撑、低刚度管路系统的影响，避免其发生屈曲失稳。

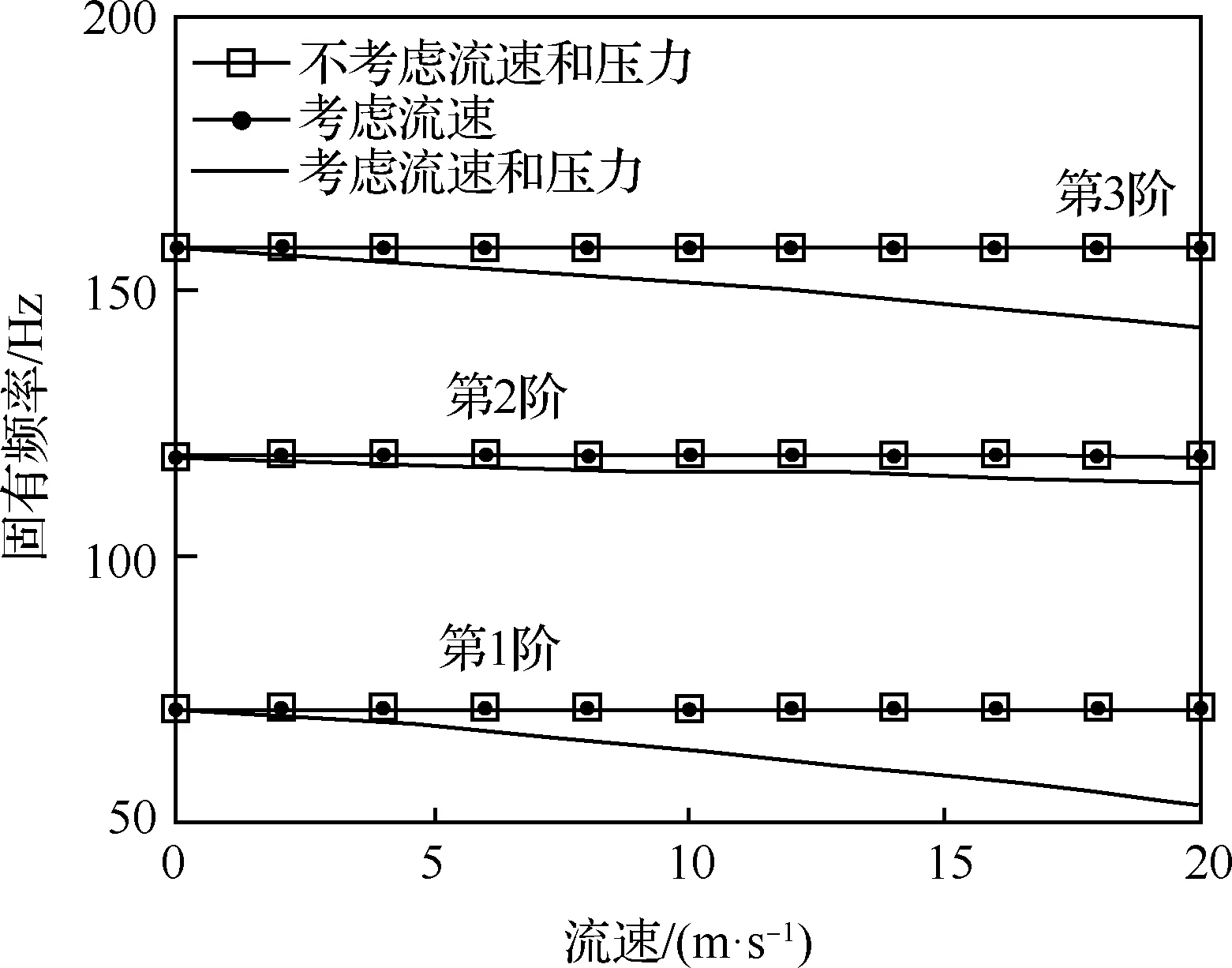
图25 介质流速对管路固有频率的影响[42]Fig.25 Influence of medium flow rate on natural frequency of pipe system[42]

针对考虑介质管路系统流固耦合动力学模型，采取有效的分析方法进行动力学方程求解是管路流固耦合研究的技术难点。目前国内外相关学者提出了多种求解方法。针对定常流动与管路之间的耦合问题主要的动力学分析方法有伽辽金法、有限元法和有限体积法。伽辽金法是将系统的偏微分运动方程对求解函数进行空间与时间变量分离，空间变量函数满足边界条件，得到以时间为变量的常微分方程组。有限元法是先将物体离散化，然后进行单元分析，建立物体所有结点载荷与结点位移组成的线性方程组，并引入边界条件进行求解。有限体积法是将求解域进行离散，并分割成有限大小的离散网格，将控制微分方程式在控制容积内进行积分，再将体积分转化为面积分。李占营等针对航空发动机外部管路流固耦合动力学模型，采用了伽辽金法进行了模态截断求解，通过试验测试数据验证了伽辽金法计算结果的正确性。进一步提出了采用有限元方法建立管路流固耦合模型，考虑了管路横向流固耦合和轴向流固耦合，管路支承采用了非线性弹簧单元进行模拟，数值计算结果与试验测试数据进行了对比验证。在此基础上，对基础简谐激励作用下简单直管路系统时域受迫响应进行了分析，讨论了柔性卡箍支承刚度对系统非线性行为的影响。发现柔性卡箍刚度的不对称性较大时，系统的幅频响应特性曲线出现明显的非线性突跳现象；在特定频率范围，响应中存在激励频率的亚谐和超谐分量，这是由于卡箍非线性支撑引起的。该研究工作综合考虑了复杂空间管路横向、轴向流固耦合以及周向扭转振动，得到了卡箍支承刚度非线性对管路振动响应的影响规律，为后续研究航空发动机空间管路系统的动态行为和振动控制提供了理论依据和方法参考。

李继世等针对航空发动机外部管路的动力学设计需求，应用Timshenko理论和能量法推导了等效流体压强和流速的管路湿模态求解方法，使用Galerkin法得到两端简支、两端固支以及悬臂边界条件下的直管基频表达式；利用ANSYS中现有Pipe289+Matrix27单元模拟流体压强和速度影响的附加刚度和阻尼矩阵，并利用Shell281+Fluid220单元验证Pipe+Matrix组合的准确性。研究表明，流体压强引起的横向压力差会降低管路弯曲刚度，而压强引起的轴向张力会提高弯曲刚度，流速增加会引起管路固有频率下降甚至出现失稳现象。该研究工作通过在有限元软件中引入自定义刚度和阻尼单元等效流体压强项和速度项，提出了一种适用于工程问题的考虑流体介质影响的管路模态特性的求解方法。

在飞机液压管路系统流固耦合动力学特性分析方面，陈果等针对飞机管路系统提出了一种复杂空间管道系统流固耦合动力学模型，采用有限元法计算了流体流速对管路振动的影响，采用数值积分法获得系统流固耦合响应。针对实际液压管路系统，数值计算与实验结果进行了对比验证，获得了管路系统的失稳流速。该研究工作基于有限元分析方法建立了一种复杂空间管路系统流固耦合动力学模型，大大提高了复杂空间管路流固耦合求解效率，为复杂空间管路建模提供了方法参考。

高培鑫等针对飞机液压管路的结构特点，提出了基于模型缩减的管路系统动力学建模方法(见图26,图中为管理第个子结构模态截断阶数)，将管路系统划分为若干子系统，采用有限元法分别对子系统进行建模，选取合理的模态截断阶数进行整体模态组集，建立管路缩减模型，显著地提高了管路系统的计算效率，减小了计算的成本，实现了飞机液压管路系统的高效建模与振动响应的高精度计算分析。在此基础上，采用有限元法建立了带有黏弹性约束层材料的航空管路流固耦合动力学模型，分析了流速、压力以及卡箍支撑刚度对管路系统固有频率和损耗因子的影响，为航空管路系统的振动控制提供了技术参考。

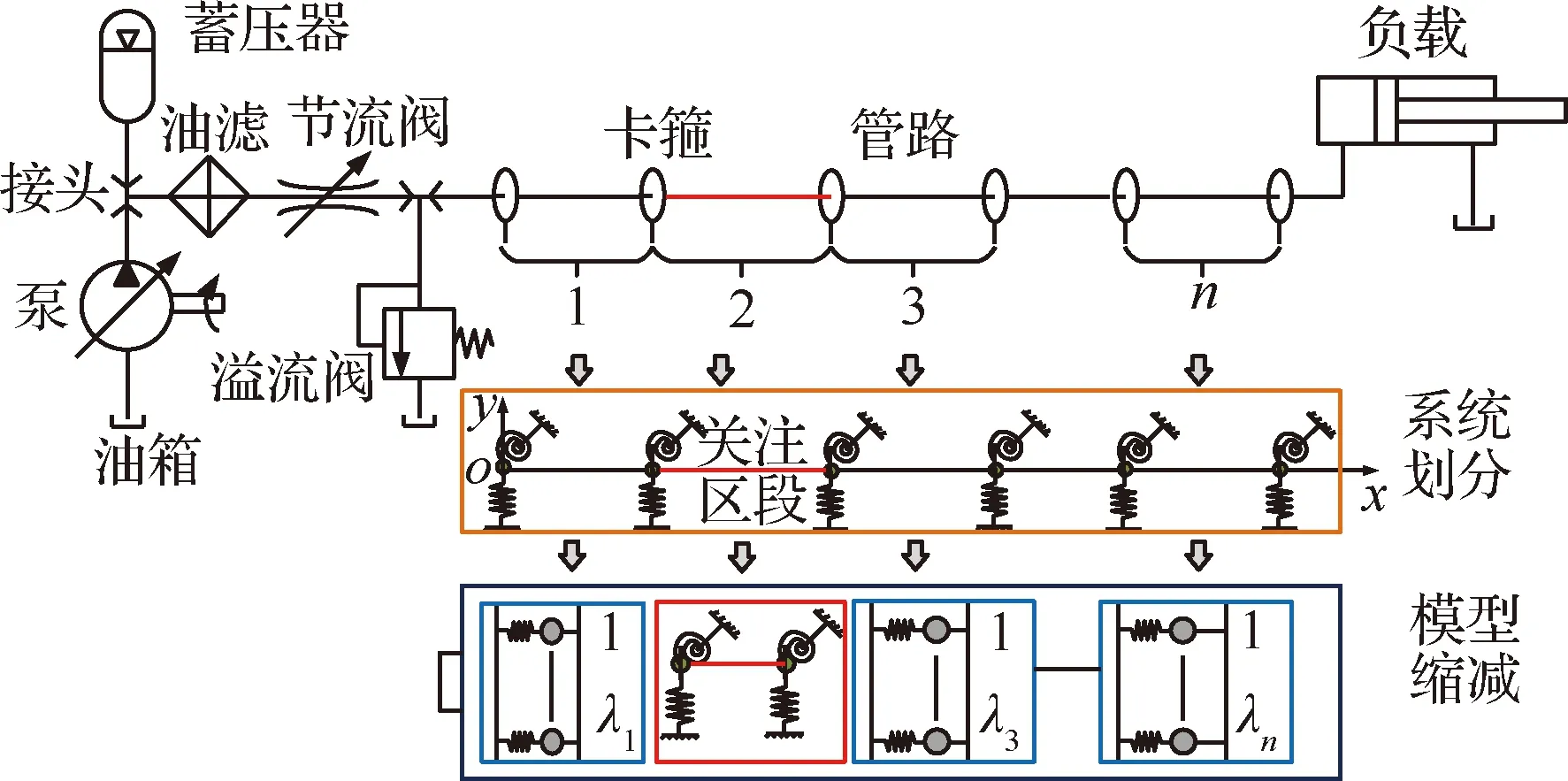
图26 管路系统缩减动力学模型[45]Fig.26 Reduced dynamic model of pipe system[45]

丁虎等基于Timoshenko梁建立了输流管路非线性耦合动力学模型，提出了采用有限差分法进行固有特性和振动响应求解，结果表明当流速或初始位移幅值较大时，非线性系数对非线性频率影响较大。当初始振幅较小时，剪切系数对非线性频率有显著影响。总的来说，大的流速、大的振幅或较短的管道长度使得耦合Timoshenko模型更适合于模拟输流管路耦合振动。在此基础上，进一步研究了准零刚度支撑的管路系统流固耦合动力学特性，准零刚度支撑和流体流动参数可以使管路的多个固有振动频率向低频区偏移。当支撑在垂直方向上的线性刚度为零时，输流管路弯曲振动的前2个模态趋于刚性模态。在实现高频区高效隔振的同时，低频区的振动行为更加复杂，且流体的流速会影响支撑的隔振性能。

定常流动与管路之间的耦合动力学问题的研究工作主要集中在流体引起的管路系统固有频率的改变，研究对象主要针对典型直管和简单弯管，对于基础激励下含介质管路系统振动响应问题，目前仅讨论了卡箍非线性支撑引发的管路振动响应，在接下来的研究中还需要进一步讨论基础激励下所引起的管内流体改变导致管路产生耦合振动，特别是考虑非线性支撑与复杂空间管路的耦合振动。

3.2 非定常流动与管路结构之间耦合动力学特性

针对非定常流与管路之间的耦合动力学问题，目前报道的文献主要针对飞机液压管路系统受到高强液压泵产生的脉动流体作用以及阀门启闭引发的水锤效应。本部分通过对飞机液压管路系统流固耦合动力学特性进行总结，进而为解决航空发动机非定常流与管路之间的耦合动力学问题提供方法和技术参考。

非定常流与管路之间的耦合问题主要基于经典水锤理论发展而来，研究对象为水箱-管路-阀门系统，重点关注了在阀门启闭瞬间所引发的管路内部水锤效应，分析水锤所产生的非常定流体动态特性及对管路系统振动的影响。耦合特性主要包含流体与管路的摩擦耦合效应、泊松耦合效应以及多通和接头的连接耦合效应。描述流固耦合的动力学模型主要包含4方程模型、8方程模型和14方程模型。其中14方程模型全面给出了管路轴向、横向及扭转振动的动力学方程。权凌霄等全面总结了近年来液压管路流固耦合线性化动力学模型和非线性振动模型的研究成果，揭示了考虑多场、多尺度及流固耦合因素影响的液压管路的流固耦合振动机理，在此基础上提出了液压管路系统流固耦合振动机理及振动控制研究的发展趋势。

目前部分学者采用了瞬态流与管路之间的耦合模型开展了飞机液压管路系统的流固耦合动力学特性分析。欧阳小平等针对飞机液压管路系统建立了8方程流固耦合模型，从时域角度重点分析了典型平面弯管的内部流体压力分布，以及管壁的振动应力分布。从频域角度分析了管路出口处的压力脉动响应，以及弯管出口的管壁轴向应力响应。考虑了管路弯曲与摩擦对其频率响应的影响(见图27)，结果表明摩擦耦合效应会影响管路振动应力水平，增加管路的弯曲半径将会降低管路共振频率。Zhang等针对飞机液压管路系统，建立了考虑摩擦效应的14方程流固耦合模型，以典型的飞机Z型管为例，数值计算与试验测试结果进行了对比验证，考虑流固耦合的管路固有频率误差小于5%。权凌霄等针对航空弯曲管路建立其14方程流固耦合模型，分析了弯曲角度对管路固有特性影响，并与模态试验进行了验证。

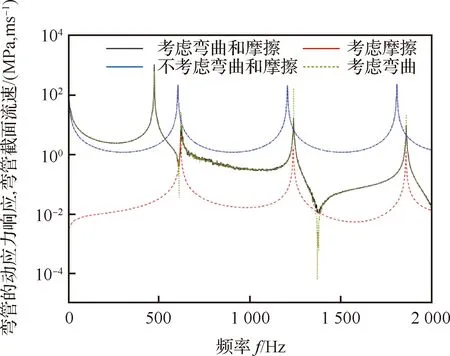
图27 弯管出口的管壁轴向应力响应[54]Fig.27 Axial stress responses of pipe wall at elbow pipe outlet[54]

针对非定常流与管路之间的耦合问题主要的动力学分析方法有传递矩阵法、特征线法、有限元法和特征线-有限元法等。Ferras等针对一维非定常流与管路之间耦合问题的时域求解方法进行了全面的总结，并结合具体的工程案例给出了目前管路流固耦合问题所面临的挑战。

传递矩阵法是一种常用于链式结构模态分析的有效方法，对于流固耦合动力学方程的求解，主要建立管路每一个部件的传递矩阵，并结合边界条件求解方程，是一种典型的频域求解方法。例如，郭长虹等针对国产大飞机C919左侧机翼的一段典型弯曲液压管路，建立了弯管14方程流固耦合模型，采用传递矩阵法求解了管路流固耦合动力学方程，通过试验验证了算法有效性。焦宗夏针对飞机液压能源管路系统，建立了流体传输管路及有关元件的传递矩阵，结合特性阻抗法对系统进行求解，并对飞机液压能源管路系统的动态特性进行了仿真。

特征线法是一种基于特征理论的求解双曲型偏微分方程组的近似方法，通过将流体波动方程转化为常微分方程，从而方便求解管路在流体作用下的瞬态和稳态振动响应，具有计算效率高、成本低和操作简单等特点，对于管路内流体压力和流量的计算具有独特的优势。大量学者采用特征线法求解瞬态流与管路之间的耦合问题。例如，欧阳小平等采用特征线法求解了飞机液压管路的流固耦合动力学方程。Xu和Jiao针对充液管路轴向4方程流固耦合模型提出了一种改进的特征线法，采用时间线插值代替递推算法，在满足精度的同时，大大提高了计算效率。李军等采用特征线法对飞机液压管路系统的瞬态压力脉动进行了数值仿真分析，获得了流量阀的阀口开度对液压系统内水锤冲击波形参数的影响规律。

有限元法是利用微分方程中的精确解来替代多项式插值函数，采用一定数量的单元矩阵模拟复杂空间布局管路的方法。有限元法在复杂构型管路和复杂边界条件的处理方面具有优势。张乐迪和张显余基于有限元仿真软件对某飞机上的一段典型液压管路进行了流固耦合分析，讨论了不同阻尼比对管道结构动态响应的影响，为飞机液压管路的设计及优化提供了依据和参考。周红等利用有限元软件建立了某型飞机液压管路系统的三维模型，分析了流体冲击下管路系统的振动响应，结果表明，液压冲击能引起悬空管束剧烈的振动响应, 在管接头加卡箍和提高管路材料的刚度能较好地改善管路系统的抗振性能。

特征线-有限元法是近年来提出的一种新的分析方法，它综合了特征线法计算流场变化和有限元法计算管路结构的优点。该方法是利用特征线法分析液压管路内流体脉动的瞬态特性，并将瞬态流体各个节点的力施加到管路系统有限元模型相对应的节点。高培鑫等基于实测获得的管路入口压力脉动谐波曲线，采用特征线-有限元法计算了液压直管路系统在泵源激励下的振动响应(见图28)，将总长度为的管路分为段，每段长度为Δ=,为管路节点数，为管路第个节点，特征线斜率为，时间增量步长为Δ=Δ,和分别为左右特征线；和分别为左端入口处压力和流速值；和分别为右端入口处压力和流速值；若已知第-1个节点点和+1个节点点压力和流速，通过特征线差分可以得到第个节点点压力和流速；若已知点和点压力和流速，通过特征线差分结合边界条件可以得到点和点压力和流速。即将瞬态流体各个节点的力施加到管路有限元模型相对应的节点上，然后采用逐步积分法求解了泵源激励下的管路振动响应。理论和试验分析表明，管路系统在泵源激励下产生多个谐波阶次的共振响应(见图29)。当谐波频率位于管路共振区时，管路产生大幅度共振。

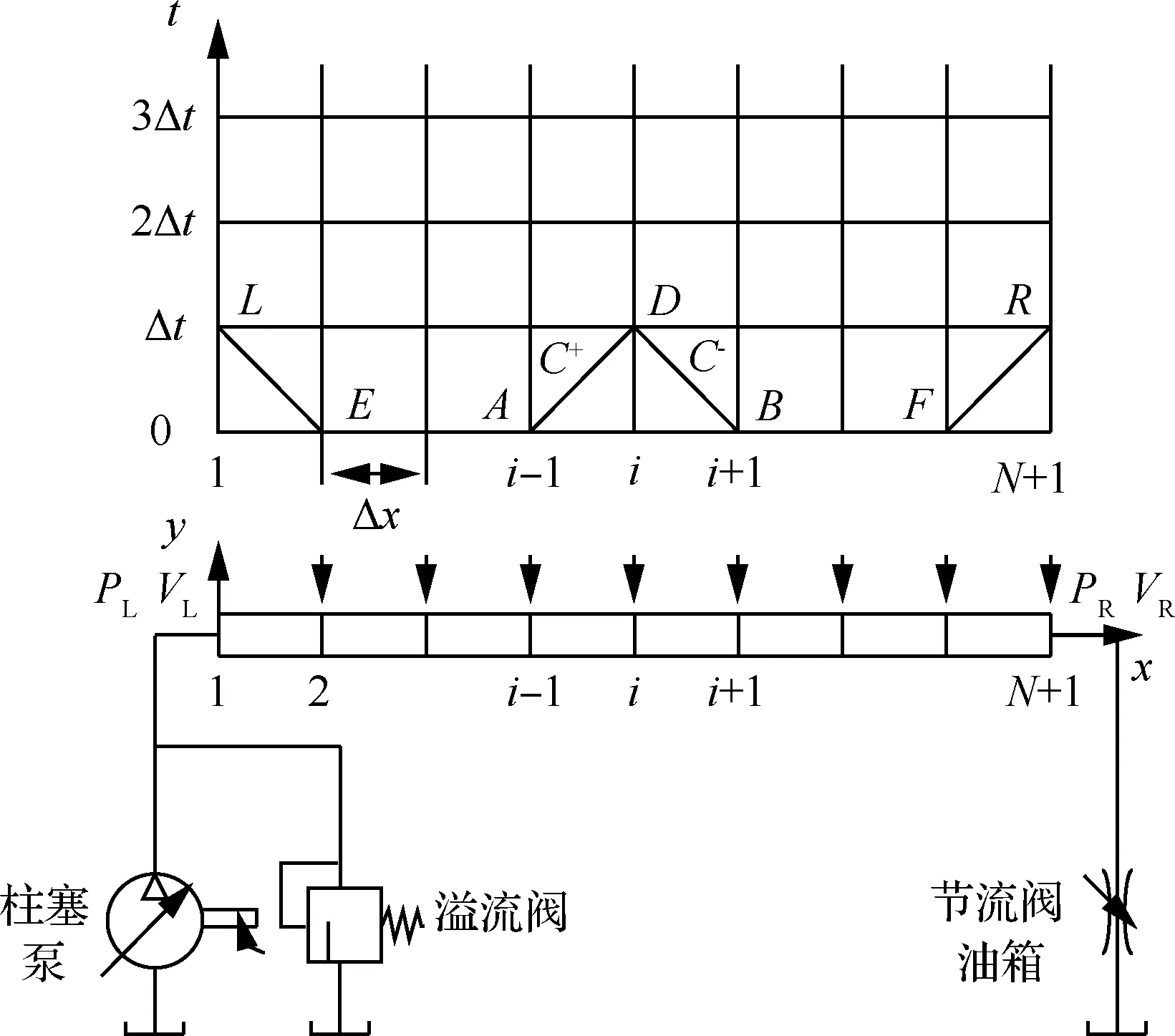
图28 基于特征线法-有限元液压直管路流体求解示意图[64]Fig.28 Solution diagram of hydraulic straight pipeline based on MOC-FEM[64]

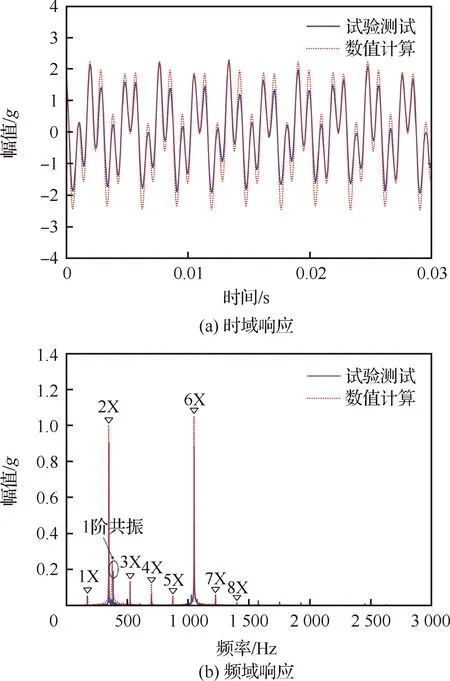
图29 泵源激励下管路系统让振动响应特性[64]Fig.29 Vibration response characteristics of pipeline system under pump source excitation[64]

目前对于非定常流与管路之间的耦合问题的研究工作主要集中在典型管路直管、L型管路等，对于复杂空间构型管路的研究较少，管路系统具有结构耦合与流固耦合的特点，是技术难点。另外对于非定常流与管路之间的耦合动力学模型，有效的计算方法是分析管路系统动力学特性的关键，本文将管路系统流固耦合动力学分析方法进行归纳分类，列于表2。可以看出，伽辽金法对简单构型管路定常流固耦合动力学问题计算效率高，对复杂空间构型管路建模与计算实施较困难。有限体积法可以求解定常流与非定常流固耦合动力学问题，存在复杂空间构型管路求解效率低的特点。传递矩阵法在复杂空间构型管路非定常流固耦合动力学求解效率方面具有优势，但是在管路振动分析中存在数值不稳定的缺点。传递矩阵法在管路振动分析中存在数值不稳定的缺点，特征线法对于管路内流体压力和流量的计算具有独特的优势，但是对于管路结构的计算与分析精度差，其原因是由于流体波速和固体波相差较大导致特征线网格大小不一致从而产生插值误差。有限元法在复杂管路结构系统处理方面具有明显的优势，对于流体的计算与分析存在着效率低的缺点。采用特征线-有限元法可以求解管路系统的流固耦合动力学方程，但是对于复杂空间构型管路，实施较为困难。在接下来的研究中，可以重点考虑采用特征线-CFD-有限元相结合的方法，通过特征线-CFD的方法结合，可以高效求解复杂空间管路流场特性，结合有限元法可以进一步求解复杂空间管路动力学分析。

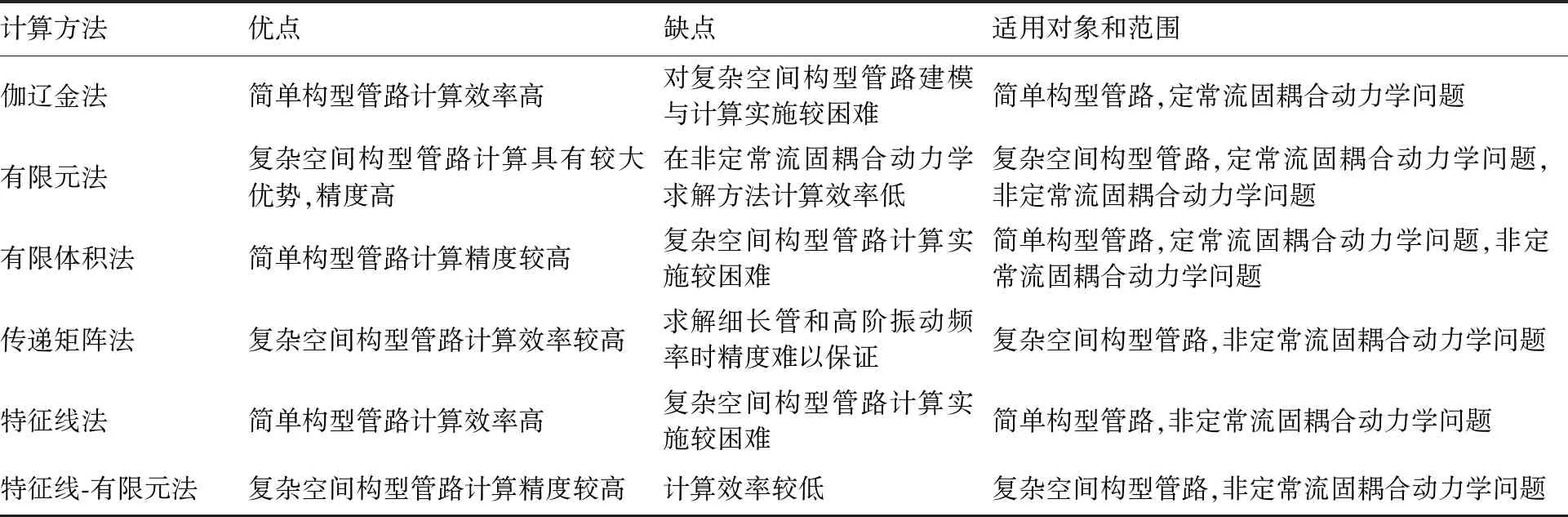
表2 管路系统流固耦合动力学分析方法对比Table 2 Comparison of dynamics analysis methods for fluid structure interaction in pipeline systems

3.3 多源激励与管路结构之间的耦合动力学特性

国内外学者和工程技术人员对于航空管路系统的振动问题已明确认为泵源流体压力脉动和发动机基础振动是导致管路系统产生振动的主要原因。多源载荷主要指流体脉动、流体冲击、基础简谐以及基础随机载荷，目前对于多源载荷作用下航空发动机管路系统振动行为研究成果较少，主要的研究成果集中在单源激励(流体或基础激励)作用下管路系统振动特性方面。

对于基础激励下定常流动与管路之间的耦合动力学问题，目前相关学者仅分析了简谐激励下卡箍非线性支撑引发的管路振动响应，且研究对象为简单直管路，还需要考虑基础激励下管内流体改变所引起的管路耦合振动。

对于基础激励下非定常流动与管路之间的耦合动力学问题，目前研究主要针对飞机液压管路系统，仅考虑了简单直管路在简谐激励的作用下的动力学特性。例如，高培鑫等针对典型液压直管路，采用特征线-有限元法和试验测试对比分析了管路系统在流体压力脉动激励和基础简谐激励的综合作用下振动响应特性。研究发现了当流体的压力脉动谐波频率与机体的基础激励频率接近时会引发拍振现象，管路系统产生拍振后的振动响应表现为低频大幅度振动。在此基础上，进一步讨论了管路系统产生危险拍振的条件。

综合上面的研究成果，航空发动机管路系统在多源激励下的耦合振动行为研究较少，其耦合振动机制目前还不明确。特别是考虑管路空间构型、卡箍弱支撑、大变形、强非线性特点，以及高压、高速流体的耦合影响，揭示其非线性振动强耦合机理是未来需要重点关注的研究方向。另外，目前的研究未考虑基础随机激励，由于航空发动机外部管路处于基础随机叠加简谐激励综合环境下，如何进行流固耦合动力学分析是未来需要重点研究的方向，特别是求解方法在时域和频域之间的转换是研究的重点和难点。

4 管路系统动力学优化

航空发动机管路动力学特性分析是进行管路振动有效控制的基础和前提。高培鑫等全面总结了航空液压管路系统振动控制技术，主要包含被动减振技术和主动减振技术。其中被动减振技术主要有：高阻尼支撑卡箍、卡箍优化布局、管体表面贴敷黏弹性约束阻尼层、管路安装动力吸振器及颗粒阻尼器等，主动减振技术主要包含管体表面贴敷压电复合阻尼层材料、管路内部安装基于压电材料的流体压力脉动消振器等。本部分重点对航空发动机管路系统动力学优化进行总结和评述。

对航空发动机管路系统进行动力学优化的主要目的是避振，首先通过结构参数或卡箍个数及位置，进行调频避振；在调频无法满足设计要求时，进行调幅避振；在调频和调幅都无法避开发动机转频时，可通过增加减振隔振装置进行优化。本节按照典型直管路动力学优化、单根弯曲管路系统动力学优化和多管路系统动力学优化三部分进行论述。

4.1 典型直管路系统动力学优化

对于典型直管路系统，Liu等利用4自由度Timoshenko梁单元建立单直管-多卡箍系统有限元模型，考虑卡箍螺栓预紧的不均匀现象，利用正弦分布函数来描述卡箍接触刚度，以单一激振源避振和双激振源避振为优化目标，基于粒子群优化算法，获得最优的卡箍支撑位置。Liu等利用能量法建立单直管-多卡箍系统半解析动力学模型，以降低共振幅度为目标构建了卡箍布局优化模型，并利用遗传算法对优化模型求解得到了最优卡箍位置。

4.2 单根弯曲管路系统动力学优化

贾志刚和郭家良等将平面典型管路(L型、U型、凹型及多弯管路)结构参数对系统固有频率的影响应用到对空间管路系统的避振研究。李会娜等通过模态测试方法，获得某型航空发动机中长跨距4条典型管路系统的固有频率，针对其在泵源工作转速范围内，管路振动过大发生泄漏的现象，进行避振研究，选择在长跨距管路中部增加一个卡箍，重新测试后系统运行良好。高培鑫等以6自由度Bernoulli-Euler梁单元建立Z型管路-卡箍系统有限元模型，以系统一阶固有频率差异最大化、振动响应位移最小化和动应力最小化为优化目标，通过神经网络建立变量和目标之间的代理模型，利用全局灵敏度Sobol方法确定了卡箍最优布局方案。Zhai等利用ANSYS对某飞机发动机L型管路的三维有限元模型进行了模态与响应分析，通过固有频率与动应力获得卡箍数量与位置的最优解。

冯凯等利用NASTRAN对航空发动机外部空间管路的模态进行计算，以管路系统一阶固有频率高于发动机工作转速频率1.25倍为目标，得出了该空间管路在敷设时卡箍的最佳安装位置和数量。於为刚等以空间管路的基频最大为目标，提出一种基于模态位移的卡箍位置自动优化方法，得出优化后卡箍数量、位置及施加顺序。柳强和焦国帅以空间管路为研究对象，建立了卡箍布局与管路动力学特性之间的Kriging代理模型，以一阶和二阶固有频率为优化目标，基于NSGA-II算法进行卡箍多目标布局优化，以实现系统避振。陈艳秋和朱梓根在NASTRAN平台上，基于遗传算法，开发了以避开共振和响应幅值最小为目标的空间管路优化程序，实现管路系统卡箍位置、数量及刚度的优化。为了避免管路系统产生共振，Zhang等提出了以空间管路系统固有频率远离振源频率和最大动应力及最大加速度响应最小为目标，建立了某空间长距离多点支撑管路系统有限元模型，通过灵敏度分析揭示了不同夹持位置与固有频率的变化关系，获得了卡箍支撑的最佳布局位置，试验结果表明，卡箍支撑位置优化后管路未发生共振，为航空管路的分析和设计提供了指导。李鑫和王少萍以一段包括直管、弯管及附件的飞机空间管路为研究对象，建立14方程的流固耦合模型，以特征阻抗为目标函数，利用粒子群优化算法获得最优的卡箍位置。

4.3 多管路系统动力学优化

对于多管路系统动力学优化方面，彭刚等基于解析法、ANSYS仿真及试验法对空间多管路系统的固有特性进行分析，并得出管路结构参数、安装参数、卡箍刚度对管路基频的影响规律。刘伟等提出了基于ANSYS与离散抽样法相结合，以基频最大和随机振动应力均方差最小为目标，针对空间分支管路进行了结构参数的灵敏度分析，讨论了卡箍数量和刚度对管路系统动力学影响，对复杂管路系统的关键卡箍位置进行了优化设计。徐培原和刘伟建立航空发动机复杂空间管路系统有限元模型，以前4阶固有频率远离避开发动机工作频率和随机振动应力均方根响应最小为优化目标，采用多目标遗传算法对5个关键卡箍参数进行了优化,实现了多阶频率调节和随机振动应力均方值的同步减小。Zhang和Wang等建立了航空液压空间分支管路有限元模型，基于非概率灵敏度法筛选出对于系统最大动应力、最大位移及一阶固有频率不敏感的卡箍，进而利用遗传算法优化了剩余卡箍位置，研究表明，优化后的管路系统动态特性得到改善。Tang等针对飞机复杂多分支液压管路系统，利用ANSYS软件，以系统最大位移、最大应力/应变、卡箍处最大应变及失效概率作为优化目标，对卡箍位置进行优化设计，结果表明优化后液压管路系统振动位移、速度、轴向应力和应变下降十分显著。Kwong和Edge建立了液压多管路14方程流固耦合模型，通过对卡箍的支撑位置进行了优化设计减低了液压管路系统的振动水平。

此外，对于航空发动机外部复杂管路系统的快速敷设与动力学优化问题，柳强等以数字样机为基础平台，以工程准则为约束，以几何拓扑和减振为目标，以UG NX二次开发为手段，开发了更加自动化、智能化专用管路设计仿真平台。该平台基于图论、计算几何以及智能优化等理论，结合管路敷设及卡箍布置工程约束，实现管路快速敷设优化方案求解；基于多目标优化理论及管路敷设规则，研究了管路敷设多方案求解算法。突破了以数字化方法自动实现其外部管路的自动构型、敷设、卡箍布局和自动装配等关键技术。

将管路系统动力学优化文章按照研究对象的基础模型；由目标函数、设计变量和约束条件决定的优化模型；以及求解优化方法进行归纳分类，列于表3。可以看出，管路系统研究对象已经从单根管路发展到分支空间多管路系统，建模方法以有限元法为主，有一些学者建立管路系统半解析模型，以及利用传递矩阵法对流固耦合管路系统进行描述。优化模型中的设计变量，大量学者以卡箍布局为主，部分学者兼顾了管路系统的结构参数；目标函数及约束条件从单纯调频或调幅逐步发展成同时考虑调频和调幅的多目标优化问题；优化算法也从参数优化发展到灵敏度法及遗传算法等。

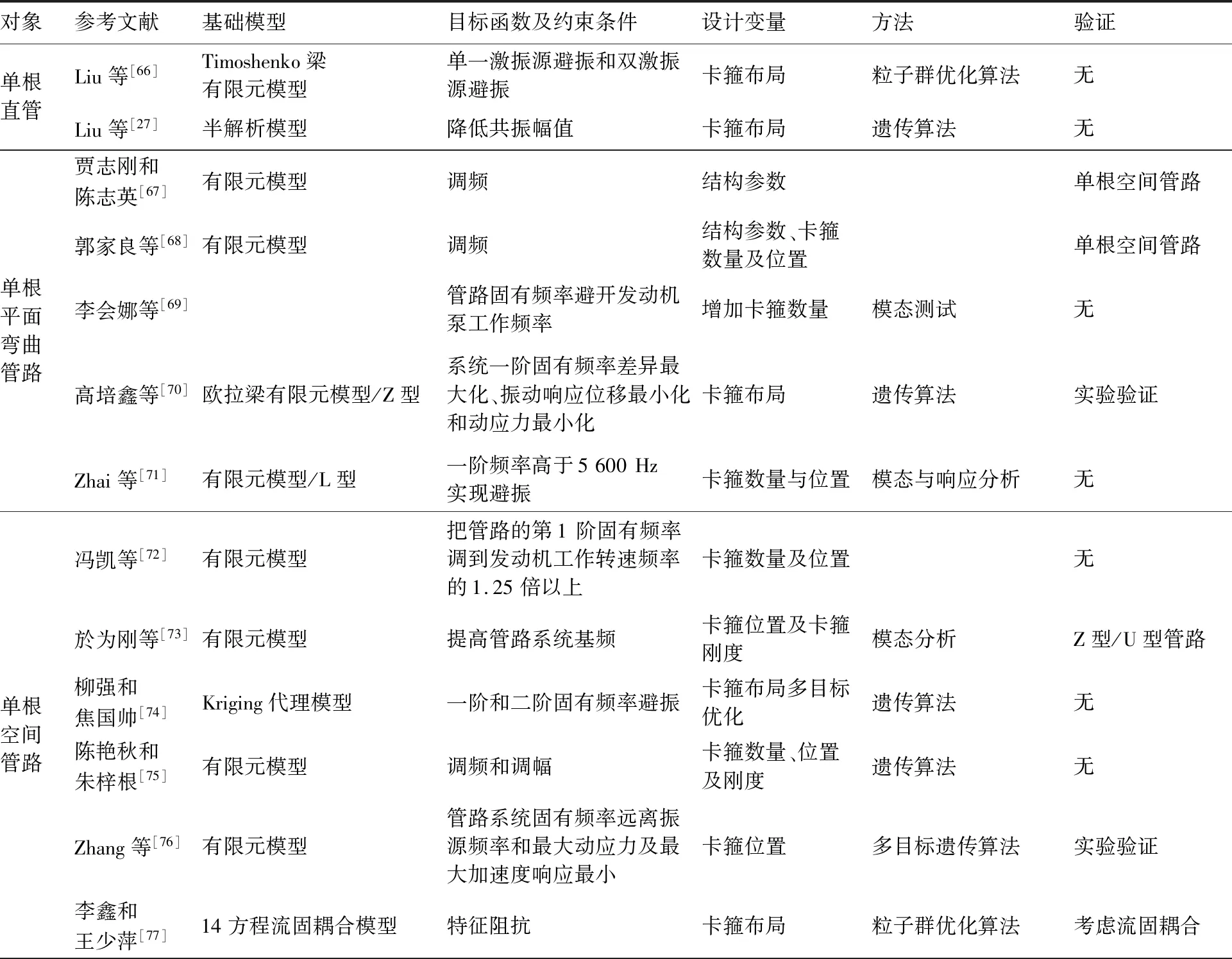
表3 管路系统动力学优化文献解读Table 3 Literature interpretation of pipeline system dynamics optimization

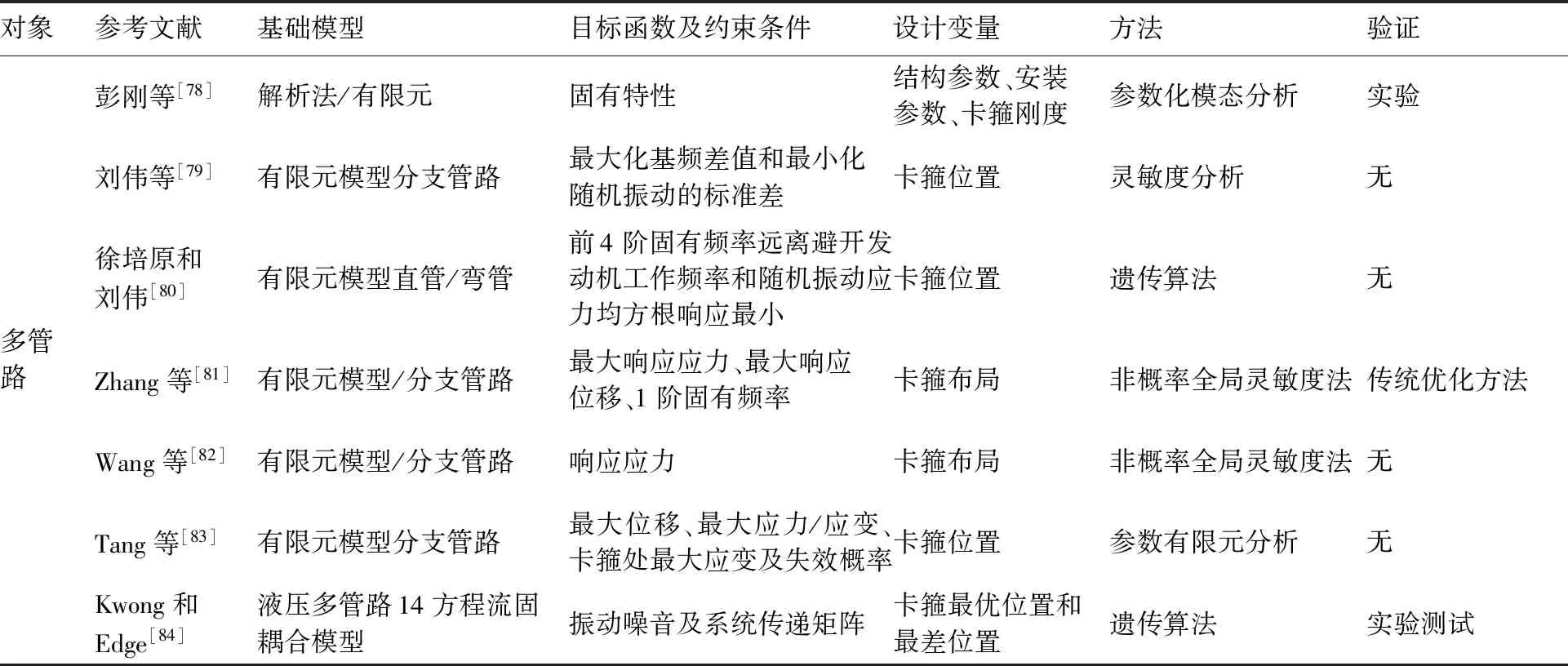
续表3

在弯曲管路及空间管路中，流体对弯管系统的激励作用是确实存在的，如何在考虑实测机匣基础激励和流体耦合作用下，以调频和以动应力为主要指标的调幅多目标优化的基础上，获得最优的卡箍布局及快速优化流程对设计单位具有指导意义。

5 总结与展望

目前管路系统振动特性研究，主要聚焦在关键支撑件如卡箍的刚度、阻尼力学表征；弹支边界管路系统振动特性分析，主要根据研究对象分为典型直管路、弯曲管路(L型、U型、Z型、凹型及空间管路等)、多管路系统；流固耦合管路系统的振动特性分析，主要包括定常流动、非定常流、多源激励与管路系统流固耦合特性分析；管路系统动力学性能优化研究。本文针对上述研究的国内外进展进行了详细的梳理，主要总结如下：

1) 在卡箍力学特性参数计算方面，主要包括静态力学特性和动力学特性2个方面。金属橡胶卡箍通过力和变形关系确定卡箍的力-变形滞回曲线，从而获得卡箍线性近似刚度/阻尼，或者通过滞回曲线获得卡箍非线性刚度随变形的变化关系；环抱型橡胶卡箍的力学特性对温度敏感，而高温状态下金属橡胶卡箍的力学性能较为稳定。卡箍动力学特性的研究主要通过反推辨识法来辨识出卡箍的动刚度/阻尼。

2) 弹支边界管路系统振动特性，针对典型直管路、弯曲管路及多管路系统进行分析。包括卡箍动力学建模方法、卡箍弹性支撑对管路系统动力学特性的影响、基础激励及真实载荷谱下管路系统的振动特性等。针对多管路系统的耦合振动问题及在多源激励载荷谱下的振动响应仍值得关注。

3) 流固耦合管路系统动力学特性，主要聚焦在典型直管路、L型、Z型管路的流固耦合问题，对于复杂空间构型管路的研究较少。大量报道了飞机液压管路系统流固耦合动力学研究，由于飞机液压管路受到高强流体压力(21 MPa及以上)，其流固耦合问题更加突出，对于航空发动机管路系统，介质压力相对较小，对于低压力的管路系统流固耦合动力学问题的研究仍然具有研究价值。定常流动与管路之间的耦合问题的研究工作主要集中在流体引起的管路系统固有频率的改变。非定常流与管路之间的耦合问题，研究工作主要集中在阀门启闭瞬间所引发的管路内部水锤效应以及压力脉动引起的管路多阶次谐波振动。在多源激励下管路结构之间的耦合问题，目前文献仅报道了简单直管路在基础周期激励和流体压力脉动联合作用下的动力学特性。飞机液压管路系统流固耦合动力学建模与分析方法可以为航空发动机管路系统动力学特性分析提供技术参考。

4) 管路系统的动力学优化，管路系统动力学特性分析的目的是对管路进行振动有效控制，对于航空发动机管路系统，动力学优化是实现管路系统振动控制最直接有效的方法。目前动力学优化主要聚焦在通过改变管路结构参数及卡箍布局实现调频避振，有部分学者在调频的同时进行了调幅的研究，目前文献报道了考虑单一基础激励或考虑压力脉动激励下的管路系统调幅，对于同时考虑管内流体脉动激励和机械基础激励的多源耦合激励的管路系统调幅问题少有涉及。

对未来管路系统动力学计算，需要集中在以下几个方面：

1) 卡箍力学特征参数获取

目前主要通过静力学仿真及试验、动力学反推辨识来确定卡箍刚度和阻尼。已有研究表明卡箍力学参数具有明显的非线性特征，因此非线性参数辨识方法和在线辨识方法在卡箍力学特征参数获取的应用是需要关注的一个方向。

同时由于卡箍金属橡胶材料的特点，使其具有较大的分散性，已有的研究并没有考虑卡箍分散性对管路动力学特性的影响，借鉴统计学的方法分析卡箍力学参数的分散性，确定参数分散性特征是未来需关注的另一个方向。

另外，卡箍在长时间服役过程中，其力学性能处于缓慢衰退的过程，有待深入开展卡箍的力学性能退化机制研究，获得性能退化对外部管路动力学特性的影响规律。

2) 复杂管路系统动力学建模

目前管路系统建模工作主要集中在直管、L型、U型、Z型等简单构型的管路，而对于复杂空间构型(空间走向、多通、并联、软硬相接等)管路系统的建模研究较少。管路系统具有结构耦合与流固耦合的独特性，决定了其动力学建模的复杂性，是目前建模方法的技术难点，复杂空间管路通常由多个子部件组成，建立其动力学模型采用三维原理建模和辨识建模相结合的方法，这对未来研究如何有效的建立复杂空间管路模型并分析其动力学行为具有非常重要的价值。

另外，由于卡箍和接头存在装配的不确定性，不同批次之间的差异性，以及管路在工作过程中受到不确定因素影响较大，如何构建有效的区间分析模型，揭示不确定性因素下管路动力学特性也是未来研究的一个方向。

3) 管路载荷确定

管路载荷主要包含流体载荷和机械载荷。确定载荷关系是开展管路动力学分析的重要前提。目前已有工作多是基于假设的流体压力参数代入管路动力学模型，缺少激励源测试与分析的支撑，振动响应的仿真结果往往与实测结果误差较大。如何有效地获得实际流体载荷，建立准确的数学描述是目前需要关注的研究方向。对于转子不平衡、齿轮啮合等机械载荷，如何准确获取传递至管路安装位置的载荷特征，提出有效的分析方法也是接下来需要重点研究的一个方向。

4) 复杂管路流固耦合动力学分析

目前对于基础激励下非定常流与管路结构耦合动力学特性研究较少，特别是考虑弱支撑、大变形、强非线性特点，如何确定基础激励与瞬态流体之间的耦合关系，获得管路系统在多界面上振动能量传递规律和振动激发机制，是未来需要重点突破的研究方向。另外，对于基础随机激励下管路系统动力学分析的计算方法也是目前存在的技术难题，随机激励下的动力学特性主要在频域中进行求解，非定常流体的计算方法是时域法，如何提出一种有效的时频转化方法分析基础随机激励叠加非定常流体作用下管路耦合动力学特性是目前研究的一个新方向。

5) 管路优化布局

目前针对管路系统优化的研究主要集中在卡箍支撑位置优化布局方面，存在管路系统构型简单、约束变量少、忽略卡箍不确定性及卡箍拧紧力矩不均匀性、与具体工程约束因素差别较大、以及优化目标单一等问题。如何在实际约束条件下综合考虑发动机管路空间走向、卡箍不确定性和管路支撑布局优化而提出多目标稳健设计优化方法是目前的研究重点。此外，考虑结构与动力学特性的复杂管路空间优化布局的一体化设计方法，通过构建高效的代理模型，建立管路系统的几何与动力学模型重构与映射关系，提出面向设计迭代优化的高效动力学计算方法，实现管路调频壁免共振，进而降低管路整体振动水平也是一个新的研究方向。