考虑关节回差的工业机器人精度补偿方法

2022-07-04田威程思渺李波廖文和

航空学报 2022年5期

田威，程思渺，李波，廖文和

1. 南京航空航天大学机电学院，南京 210016

2. 南京理工大学机械工程学院，南京 210094

工业机器人由于工作范围广、柔性化程度高的特点在制孔、铆接、喷涂、去漆、增材制造等领域广泛应用，产生了诸多重大效益，包括降低成本、人力和时间以及提高质量和制造效率等。在航空制造领域，以机器人为载体的各类钻铆系统使得飞机部件的装配质量与效率较传统加工方法有较大提升，通过离线编程方法进行孔位任务规划能极大缩短产品生产周期。然而，飞机装配对孔位置的精度要求为≤0.5 mm，工业机器人因绝对定位精度低，对应其理论位置与实到位置的偏差值高，机器人定位误差大，难以进一步应用于飞机装配中的高精度加工制造。

针对上述痛点，国内外研究人员在提高机器人绝对定位精度方面做出了诸多有益的尝试。传统的机器人精度补偿方法是运动学校准。Barker提出了一种基于Denavit-Hartenberg (D-H)参数的运动学误差标定算法。该方法仅需通过测量不同关节角度下末端执行器的位置来估算机器人几何参数误差。Tian等基于该方法提出了优化采样点策略。针对基于D-H参数的运动学误差模型存在奇异性问题，Hayati和Mirmirani提出了一种新的建模方法，在两个平行或接近平行的关节轴之间增加一个绕轴旋转参数，并通过Stanford机械手和6R串联机器人的仿真实验验证了该方法的有效性。Okamura和Park提出了一种基于指数积模型的运动学标定方法，同样解决了奇异性问题。Yang等优化了指数积参数，降低了运算时间并提升了校准精度。上述方法均能有效补偿由几何误差引起的机器人定位误差，然而影响机器人定位误差的因素还包括关节回差、坐标系建立误差和减速比误差等。

因此，近年来许多研究人员通过构造机器人末端位姿或各关节转角与机器人定位误差关联的模型来代替机器人运动学误差模型。周炜等提出了基于反距离加权法的机器人定位误差补偿方法，通过将工作空间划分网格补偿了机器人定位误差。Tian等通过导轨扩展机器人工作空间，并通过反距离加权法提升了机器人绝对定位精度。石章虎等将反距离加权法应用在AGV式移动制孔机器人上，有效降低了机器人定位误差。Zeng等提出了基于误差相似度的机器人定位误差补偿方法，将机器人定位误差与其末端位姿相关联。Cai等在相似度模型的基础上设计了偏移变量对算法进行改进。Chen等将误差相似度与径向基神经网络相结合，进一步提高了机器人绝对定位精度。上述方法无需建立运动学模型，并能有效地提升工业机器人绝对定位精度。然而，该类方法仅考虑机器人末端的位姿变化，忽略了同一位姿下关节回差对其定位误差的影响。

为减小关节回差对机器人定位误差造成的影响，许多学者对此提出不同的方法。Liu等通过试验证明由于关节回差的存在，采用常规精度补偿方法无法进一步提高机器人绝对定位精度。Hovland等描述了一种从转矩和位置测量中自动识别和估计机器人关节回差的方法。Ruderman等在二轴关节上添加一个外部编码器，通过内外编码器的差值确定关节回差的大小。Slamani等提出了一种基于统计检验的方法，通过多项式对轴与轴方向误差进行拟合，同时研究了速度、负载对精度的影响。Lehmann等设计了一种将机器人末端与地面固连的紧锁装置，通过旋转单轴，读取内部控制器的位置、速度、电流信息确定机器人的关节回差。Mousavi等使用千分表测量SCARA机器人的重复性，进而估算关节回差。Liu等在前三轴关节安装光栅，通过伺服反馈消除关节回差。上述方法通过特定的外部装置或通过机器人厂商开放电流等信息数据辨识关节回差，但均未针对机器人绝对定位精度建立一个包含关节回差的精度补偿模型。

针对上述问题，提出了一种考虑关节回差的工业机器人精度补偿方法，使用KUKA KR 500-3、KUKA KR 30HA以及国产埃斯顿ER12-1510三种型号机器人对该方法进行精度补偿试验验证，并搭建制孔试验平台进行制孔试验验证。第1节建立了考虑关节回差的参数辨识模型，第2节建立了考虑关节回差的误差相似度模型，第3节通过试验验证本文方法，并通过对比分析试验数据，第4节进行总结。

1 考虑关节回差的参数辨识模型

1.1 机器人运动学建模

Hayati等提出了MD-H(Modified DH)模型，通过在相邻的平行关节之间增加一个绕轴旋转的运动学参数，解决了D-H模型的奇异性问题。其关节坐标系定义为：轴方向，即旋转关节轴线方向，正方向由右手法则确定；轴方向，与上一关节轴的公垂线方向，正方向为上一关节轴指向当前关节轴；轴，右手法则确定；原点：当前关节轴与上一关节轴平行时，是当前轴与前一关节轴的交点，平行时则为当前轴与当前轴的交点。

以KUKA KR 500-3型工业机器人为研究对象，以MD-H模型构建各关节坐标系，如图1所示，其末端矩阵为

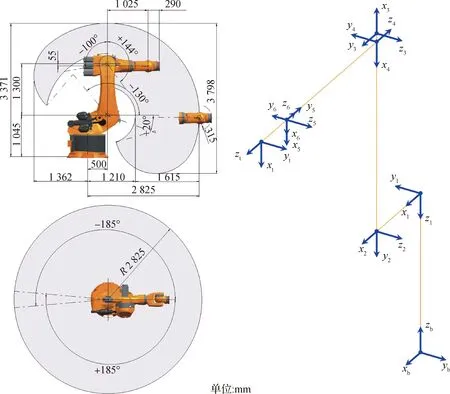
图1 KUKA KR500-3机器人尺寸结构及关节坐标系Fig.1 Size structure and joint coordinate system of KUKA KR500-3 robot

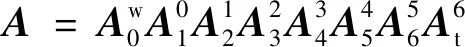
(1)

式中：

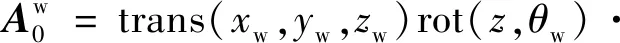
rot(,)rot(,)

(2)

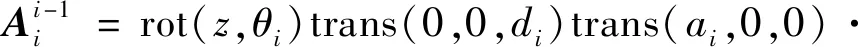
rot(,)rot(,)

(3)

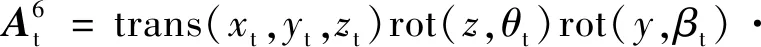
rot(,)

(4)

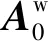
1.2 机器人误差建模

由于机器人装配时产生的关节角度及姿态安装偏差以及制造时产生的连杆长度误差等因素，使得机器人理论几何参数与实际几何参数产生一定偏差，经由一系列连杆传递至末端导致机器人定位误差，因此建立由几何参数误差引起的机器人定位误差模型：

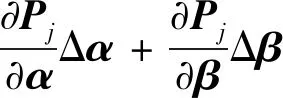
(5)

式中：为工具坐标系位置向量(即矩阵第4列第1～3个元素)；Δ为由于几何误差引起的机器人定位误差向量。对六自由度工业机器人，每个参数误差矢量(即Δ、Δ、Δ、Δ和Δ)有6个元素。

由于坐标系建立过程中不可避免的引入新的误差，该部分误差经由一系列连杆传递至末端或直接作用于机器人末端，导致机器人定位误差，因此建立由坐标转换误差引起的机器人定位误差模型：

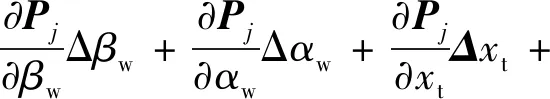
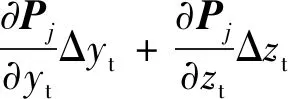
(6)

式中：Δ为由于坐标系建立误差引起的机器人定位误差向量。

RV减速器由于其体积小、扭矩大、振动小和减速比大等诸多优点被广泛应用于高精度机器人中，其内部传动结构如图2所示，从输入轴将动力依次传递到行星齿轮机构和摆线针轮机构，并由输出端传出，实现减速效果。

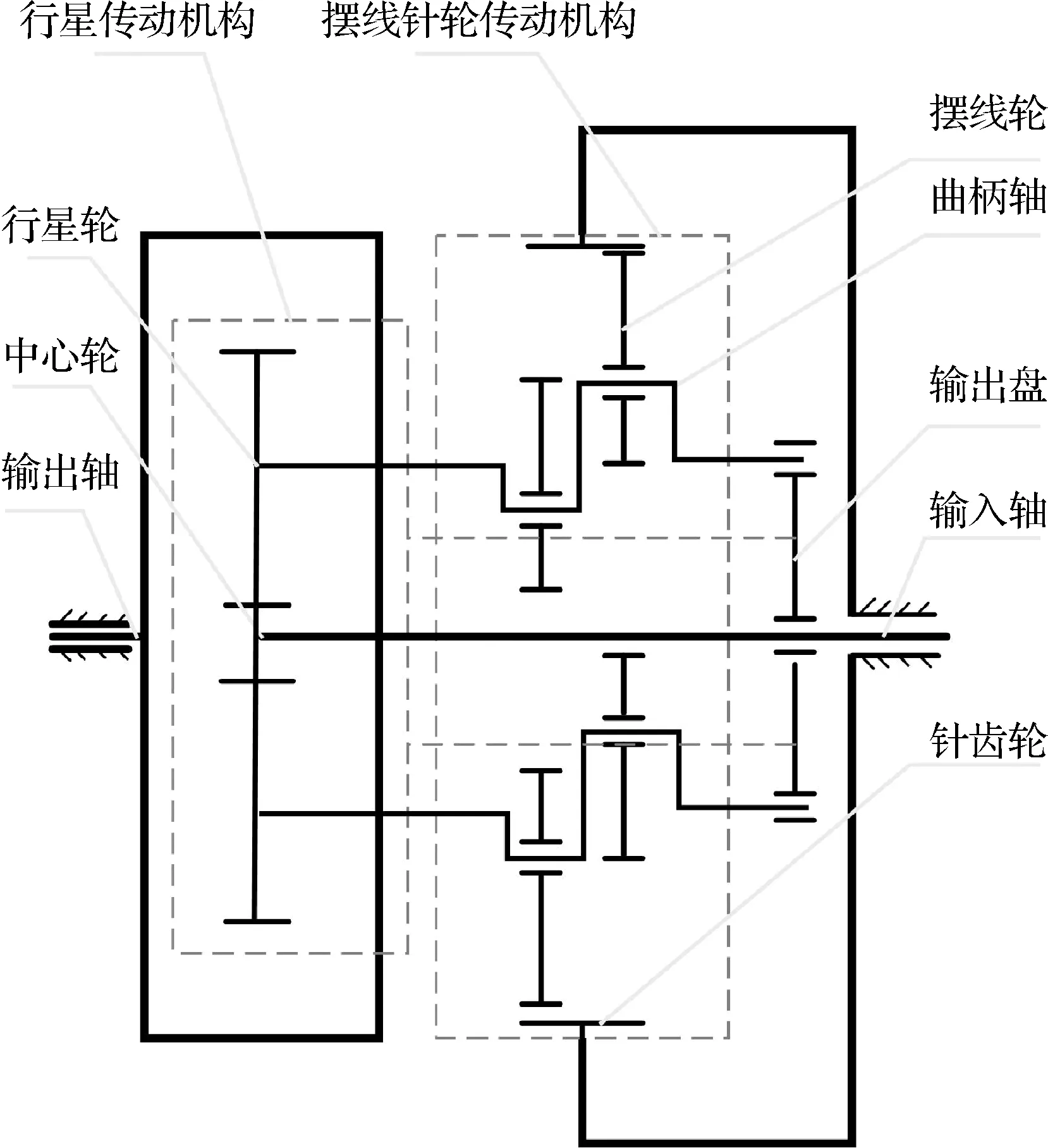
图2 RV减速器内部机构Fig.2 RV reducer internal mechanism

其误差主要体现在：① 装配时关节名义中心与实际中心产生偏差以及安装角度误差，该部分误差可视为几何误差经由一系列连杆影响机器人定位误差，并可以由式(5)补偿；② 加工时齿轮等传动件名义值与实际值间偏差，导致实际减速比与理论减速比误差，该部分误差作用于关节角度，经由一系列连杆传递导致机器人定位误差；③ 磨损及加工误差使得针齿与摆线轮间产生关节回差，导致机器人关节在运动方向相反时产生角度偏差，经由一系列连杆传递导致机器人定位误差。此外，轴承在高速运转中容易产生较大的磨损，但由于飞机装配过程的机器人运动速度相对较慢，该部分误差可忽略不计。

因此对每个关节建立包含关节回差与减速比误差的实到关节角度模型：

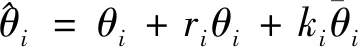
(7)

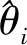
(8)

将传动误差定义为关节回差与减速比误差共同影响产生的误差，建立传动误差引起的机器人定位误差模型：

(9)

式中：Δ为由于齿轮传动引起的机器人定位误差向量，由此建立基于运动学的误差模型：

Δ=Δ+Δ+Δ=Δ

(10)

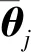
Δ=()Δ

(11)

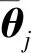
2 考虑关节回差的误差相似度模型

2.1 误差相似性分析

机器人定位误差的相似性体现在机器人在两种相似状态下，比如关节转角相近时，其对应的定位误差也相近。机器人定位误差的相似性可以用半方差函数定量分析，该函数定义为工作空间内两个点位机器人定位误差增量方差的一半，通常由一组样本的机器人定位误差的经验半方差函数得到：

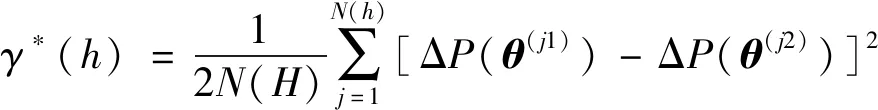
(12)

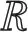
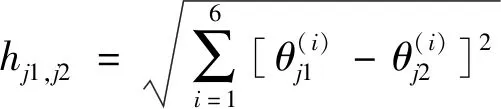
(13)

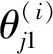
若式(12)中某分割量下机器人定位误差的半方差函数数值越小，则对应定位误差散点图在该分割量下点位越集中，定位误差分散程度越低；反之，则表示其定位误差分散程度越高。若机器人定位误差在分割量数值较小时分散程度低，并在分割量数值较大时分散程度高，则表示机器人定位误差具有相似性，即相似状态下定位误差相似的特征。

已知由几何误差引起的机器人定位误差具有误差相似性。对关节回差引起的机器人定位误差相似性进行研究。仿真环境下机器人结构尺寸如图1所示，以表1辨识得到的关节回差作为仿真环境中的误差参数，以机器人基坐标系为参考坐标系，即以水平向上方向为轴方向，以图1中home位置臂展伸出方向为轴方向，右手法则确定轴方向，同时以KUKA KR500-3精度补偿试验中的数据点作为仿真环境中的理论数据点，并随机生成各点位的关节运动方向，计算可以得到在基坐标下各点位的机器人定位误差，不同点位的两组数据配对，可以得到如图3所示的机器人定位误差散点图，其中，为半方差函数，为分割量

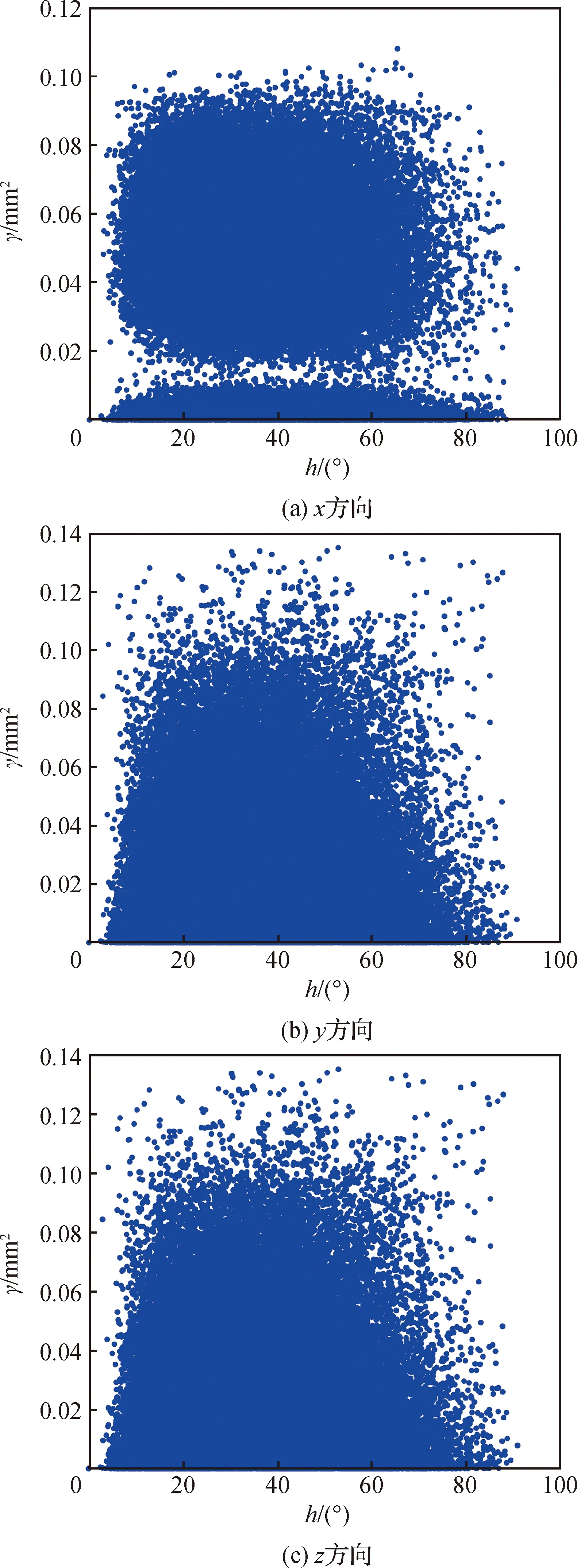
图3 机器人定位误差散点图Fig.3 Scatter plot of robot positioning error

由几何参数误差引起的机器人定位误差在两组关节角度间的欧式距离较小时，对应的定位误差分散程度小，随关节转角的欧式距离增加，定位误差分散程度逐渐增大。由图3误差散点图可以得出由关节回差引起的机器人定位误差与几何参数误差引起的机器人定位误差呈不同的趋势，在两组关节转角欧式距离较小时，机器人定位误差分散程度较大，为进一步分析，使用式(12)建立半方差函数图，将分割量平均分为12组，得到的半方差函数图如图4所示。

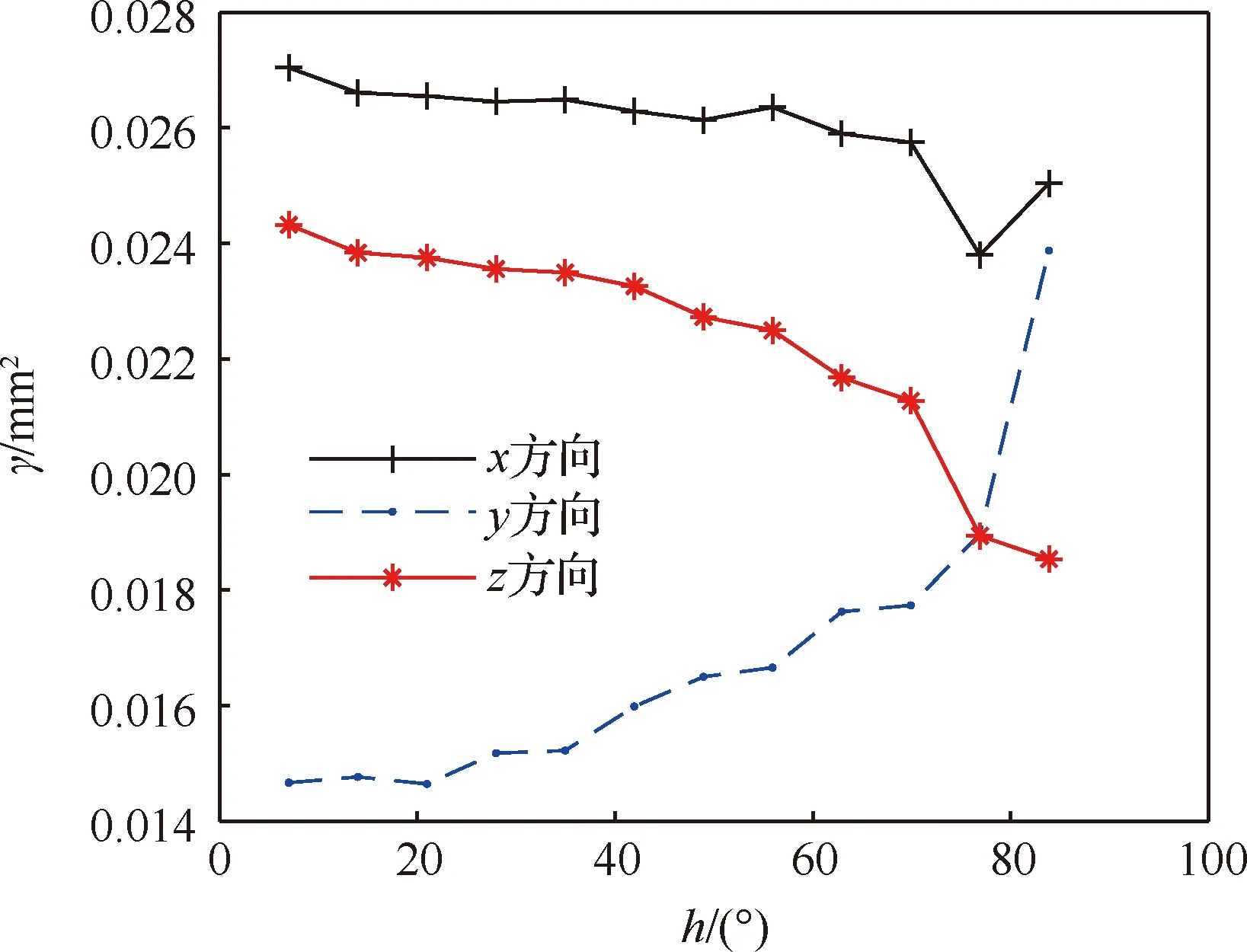
图4 机器人定位误差的半方差函数Fig.4 Semi-variance function of robot positioning error

从图4可以看出，3个方向与图中轴相交点不在原点位置，这是由于理论曲线与图中轴的交点为同一点位下机器人定位误差方差的一半，而同一点位受关节回差影响在机器人基坐标系下不同方向上会产生不同的机器人定位误差；从交点位置的大小可以得到，3个方向从大到小依次为、、，这意味着对于同一点位或相近点位轴误差分散程度更高。这是由于存在对该方向影响误差较大的关节轴，导致该关节运动方向不同时其他关节引起的误差相对较小，使得在分割量较小的情况下误差分散程度较大，而分割量较大时由于该关节运动方向相反时误差叠加作用没有分割量较小时明显，因此图4中随着分割量的增大半方差函数逐渐变小，方向同理。

轴方向的半方差函数与轴和轴呈现相反的趋势，这是由于影响该方向误差的关节轴误差大小相近，相互制约。值得注意的是，尽管制约关系存在，但仍然有小概率事件会产生叠加作用，因此分割量较小的点仍然存在个别较大机器人定位误差差异点。在仿真环境下可以由小分割量情况下，误差散点图中数值较大的散点证明，试验环境中可以对比不辨识回差的模型与辨识回差的模型在轴误差范围上的差异证明。

2.2 误差相似度模型建立

由2.1节可知，由关节回差引起的机器人定位误差呈现一定的规律性，但并不存在必然的空间相似性，仅考虑关节角度不能有效补偿由关节回差引起的机器人定位误差。为进一步提升工业机器人的绝对定位精度，构建考虑关节回差的误差相似度模型。

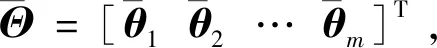
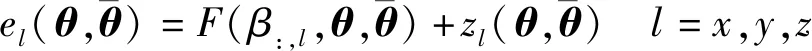
(14)

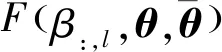
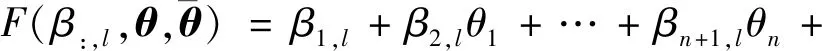
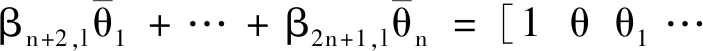
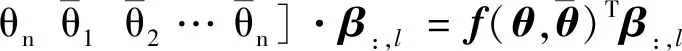
(15)

=,,

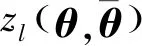
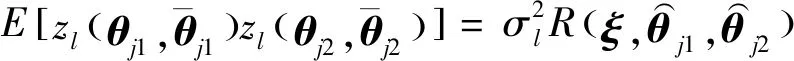
(16)

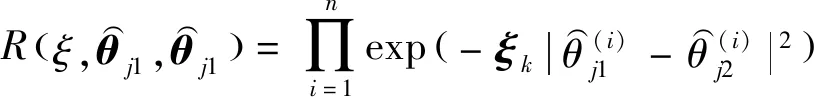
=1,2,…,6

(17)

通过已知样本集合建立误差预测模型

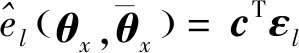
(18)

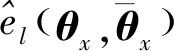
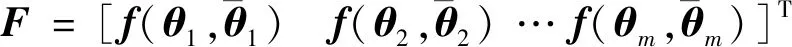
(19)

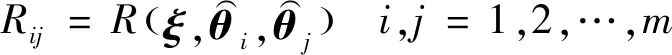
(20)

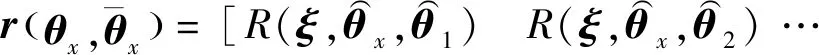
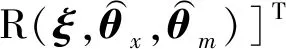
(21)

则预测误差和实际误差的差值可表示为

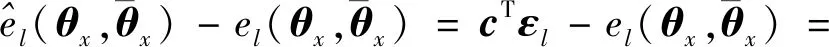
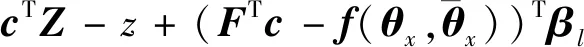
(22)

式中：=[…]，为了保证预测误差无偏性

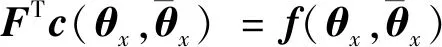
(23)

在此条件下，均方差为

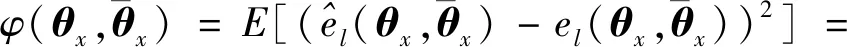
[(-)]=[+-2z]=

(1+-2)

(24)

为获取目标点位的最优估计，应保证预测方差最小，式(23)作为已知条件，使得式(24)数值最小，由此建立拉格朗日方程

(,)=(1+-2)-(-)

(25)

式中：是拉格朗日乘数，方程对的偏导数为

′(,)=2(-)-

(26)

式(26)为0时，式(24)取值最小，将方程的解代入式(18)可得

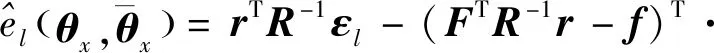
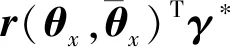
(27)

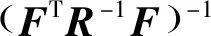
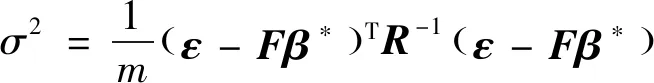
(28)

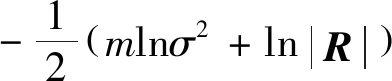
3 试验验证与分析

3.1 精度补偿试验

搭建如图5所示的试验平台对本文提出的机器人定位误差补偿方法进行试验验证。试验目的主要分为: ① 为获取相似度建模方法所需关节回差参数，对工业机器人进行参数辨识；② 为确定本文方法相较传统方法的优越性，对比辨识关节回差方法与不辨识关节回差方法的补偿效果及对比相似度补偿方法和参数辨识方法的补偿效果；③ 为确定本文方法的通用性，通过其他型号机器人重新进行精度补偿试验。

精度补偿试验分为坐标系建立，选取采样空间，采样点规划并采集点位误差，验证点生成并采集点位误差，验证点误差与预测误差对比得到精度补偿结论几个部分。

试验验证载体为KUKA KR500-3型号机器人，其法兰盘上装有制孔装置，测量设备为API Radian激光跟踪仪。靶球安装位置如图5左上角所示，在进行精度补偿试验时，将末端刀具从刀柄换下，将靶标座安装于刀柄处，使得靶球中心点位于刀具旋转轴线上，以便制孔试验时直接测量刀尖点与刀柄上端长度确定刀尖点位置。

图5 KUKA KR500-3机器人精度补偿试验平台Fig.5 Experimental platform of error compensation for KUKA KR500-3 robot

通过旋转机器人关节和拟合关节轴线来构建机器人基坐标系，并在机器人的工作空间中规划了一个尺寸为700 mm×1 200 mm×900 mm的长方体区域作为本次试验验证的测量区域，使用拉丁超立方采样方法随机生成497个点，采样点位置(,,)在该长方体区域内随机选取，三个姿态角(,,)在∈[-15°,15°]∈[-15°,5°]和∈[-15°,15°]内随机选取。控制机器人运动至上述各随机采样点的理论位姿，并用激光跟踪仪测量其实际位置，并重新在预定区域内随机采集300个点位位置数据进行模型验证。

首先，通过第1节方法进行参数辨识，辨识结果如表1～表5所示，并对坐标系建立误差、减速比误差和关节回差对机器人定位误差的影响进行分析。

表1 修正后的关节回差Table 1 Revised joint backlash

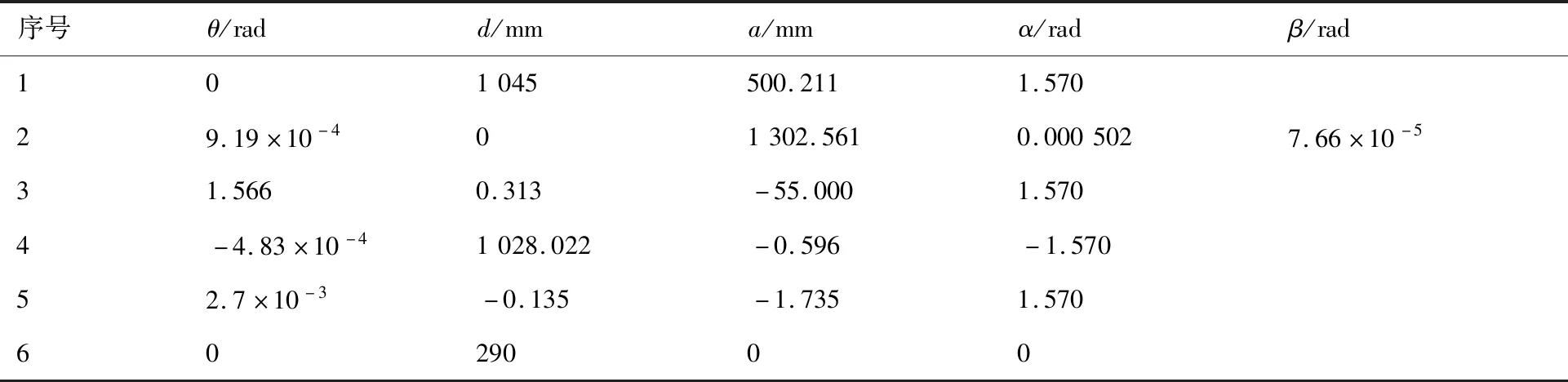
表2 修正后的MD-H参数Table 2 Revised MD-H parameters

表3 修正后的基坐标系误差Table 3 Revised base coordinate system errors

表4 修正后的TCP坐标Table 4 Revised TCP coordinates

1) 由表1得到的关节回差数据可以看出，前三轴的关节回差远小于后三轴关节回差，这是由于前三轴为RV减速器，相较于后三轴的谐波减速器制造更加精密，关节回差更小。但由于前三轴臂展较长，对末端的影响同样不可忽视。尽管单个关节回差对机器人定位误差的影响在0.01 mm 数量级，在6个关节同时运动时误差可能会相互抵消，但在某些特殊情况时会有误差累积效应。因此要进一步提升机器人绝对定位精度必须考虑到关节回差的影响。

2) 由表3得到的基坐标系误差可以看出，由旋转轴线建立的基坐标系在基坐标系下不同方向的偏移相差较大，其中方向偏移最大，轴次之，这是因为拟合得到的二轴轴线受重力影响与实际轴线产生偏差，并且重力主要作用在轴和轴方向。而3个欧拉角数量级较小，仅绕轴方向略大，证明坐标系建立误差主要体现在偏移方向上，且主要影响因素为重力。由此可以得到，通过旋转轴线法拟合出的机器人基坐标系与实际坐标系偏差可用第1节参数辨识方法拟合，且此方法的误差主要集中在轴和轴的平移误差和绕轴方向的旋转误差。

3) 由表5得到的减速比修正误差可以看出，1轴数值可忽略不计，这是由于RV减速器制造精准，同时1轴减速器上几乎不受重力影响，而其他轴该项误差受重力影响产生与角度相关的线性关系，即由重力影响产生的关节变形由式进行了部分补偿，导致三轴和五轴数值偏大，说明重力产生的变形不可忽略，本文通过构建误差相似度模型补偿该部分误差。

表5 修正后的相对减速比Table 5 Revised relative reduction ratio

图6(a)～图6(d)分别表示不考虑关节回差的参数辨识方法和考虑关节回差的参数辨识方法、不考虑关节回差的误差相似度补偿方法和考虑关节回差的误差相似度补偿方法下基坐标系下轴方向、轴方向、轴方向残余误差和机器人综合定位误差。

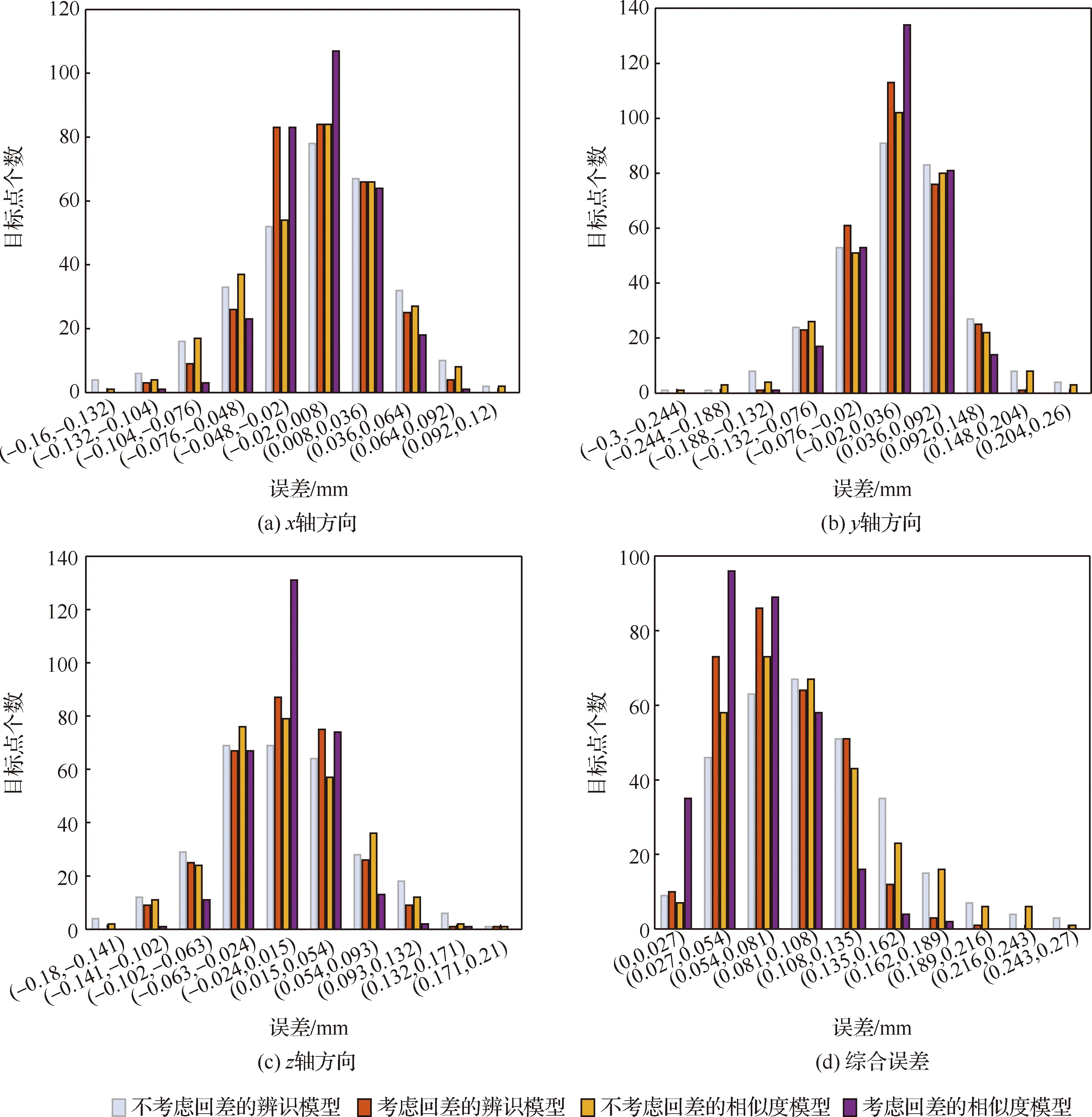
图6 补偿后KUKA KR500-3机器人误差Fig.6 Errors of KUKA KR500-3 robot after compensation

对比补偿后3个方向的残余误差可以看出，本文方法补偿后误差均值趋近于0，且分散程度更低，同时机器人的绝对定位误差最大值更小，体现本文方法相较其他方法的优越性。为进一步分析，将相关数据记录在表6和表7中。

表6和表7分别表示4种补偿方法补偿后及补偿前不同方向和总体误差的均值和标准差。其中表示的是总体误差。

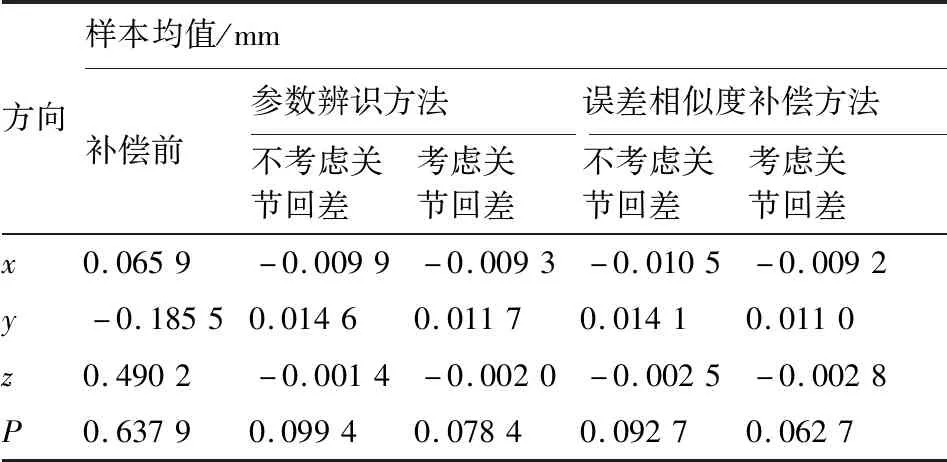
表6 补偿后KUKA KR500-3机器人样本均值Table 6 Sample mean of KUKA KR500-3 robot after compensation

表7 补偿后KUKA KR500-3机器人样本标准差Table 7 Sample standard deviation of KUKA KR500-3 robot after compensation

从图表中可以看出几种精度补偿模型均能有效地预测实际位置，考虑关节回差的参数辨识方法(第1节构建的参数辨识方法)优于不考虑关节回差的参数辨识方法，证明了辨识关节回差的必要性。体现在：① 通过关节回差辨识可以将机器人定位误差最大值由0.25 mm降低到0.20 mm，平均值由0.094 4 mm降低到0.078 4 mm，证明前者具有更好的精度；② 通过关节回差辨识可以将,,方向误差标准差从0.046 3、0.075 1、0.063 8 mm降低到0.035 7、0.057 0、0.051 3 mm, 最为明显的方向体现在轴，误差范围由[-0.25,0.25] mm降低到[-0.13, 0.15] mm，证明前者误差范围更加集中。

考虑关节回差的相似度补偿方法(本文方法)优于考虑关节回差的参数辨识方法，证明了本文方法的优越性。体现在以考虑关节回差的参数辨识模型为参照，通过本文相似度补偿方法可以使机器人定位误差最大值由0.20 mm提升到0.18 mm，平均值由0.078 4 mm降低到0.062 7 mm；提升最明显的方向在于轴，标准差由0.051 3 mm降低到0.036 3 mm，这是由于重力影响主要集中在轴方向，说明了误差相似度模型能够较好地补偿几何误差和非几何误差。

考虑关节回差的参数辨识方法优于不考虑关节回差的相似度补偿方法，证明了现有相似度补偿方法受关节回差限制。由上述结论可知相似度模型可以较好地补偿非几何误差，由表中数据可知，考虑关节回差的误差相似度方法在机器人定位误差集中程度，定位误差范围，绝对定位精度及平均定位精度均优于考虑关节回差的模型，说明了关节回差的存在制约了传统相似度补偿方法的定位精度，这与文献[18]的研究成果相吻合，说明本文提出的方法可以解决这一问题。

最后，通过两种其他型号的机器人验证本文方法的通用性。已知现有误差相似度补偿方法可以对机器人误差进行补偿，在此基础上，Cai等对以往的误差相似度算法进行改进，使用普通克里格法并取得更好的校准效果。但由于该类方法忽略了机器人同一位姿下关节回差对其定位误差的影响，限制了机器人绝对定位精度的进一步提升。为验证本文方法可进一步提升机器人绝对定位精度，选取普通克里格法方法作为对照组(简称方法一)。

为了证明本文方法的通用性，选取KUKA KR30HA机器人作为试验对象，测量设备为API公司生产的T3型号的激光跟踪仪，构建如图7所示的精度补偿试验平台，选取国产埃斯顿ER12-1510机器人为试验对象，测量设备为API Radian型激光跟踪仪，构建如图8所示精度补偿试验平台，两个平台的靶球均安装于机器人末端，试验流程与KUKA KR500-3机器人精度补偿试验相同。

图7 KUKA KR30HA精度补偿试验平台Fig.7 Experimental platform of error compensation for KUKA KR30HA robot

图8 埃斯顿ER12-1510精度补偿试验平台Fig.8 Experimental platform of error compensation for ESTUN ER12-1510 robot

图9和图10分别表示KUKA KR30HA和埃斯顿ER12-1510机器人未补偿、方法一补偿后及本文方法补偿后的综合定位误差，表8和表9分别列举了两种型号机器人定位误差均值和标准差。从试验数据中可以得出：

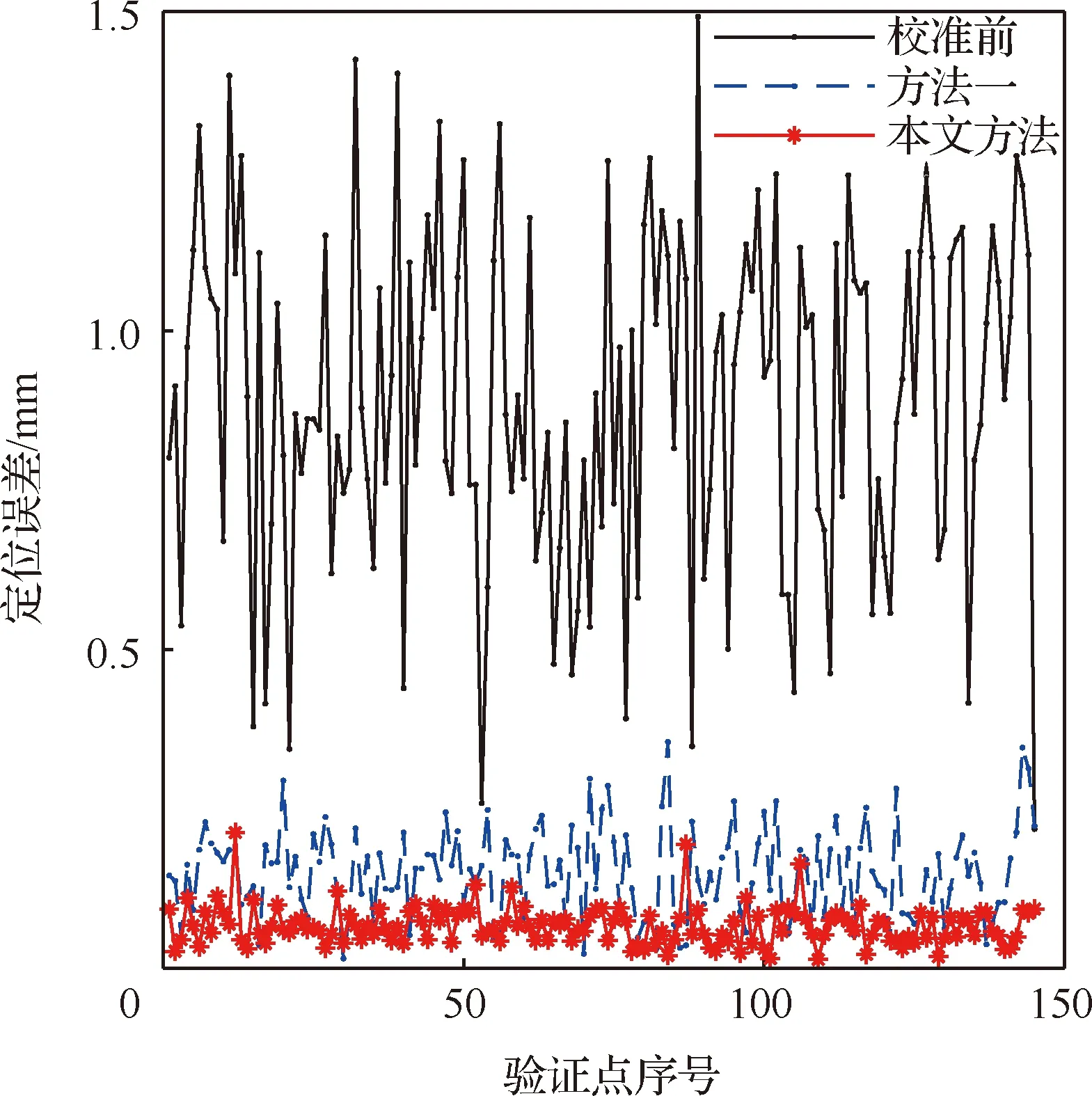
图9 补偿后KUKA KR30HA机器人综合误差Fig.9 Comprehensive error of KUKA KR30HA robot after compensation

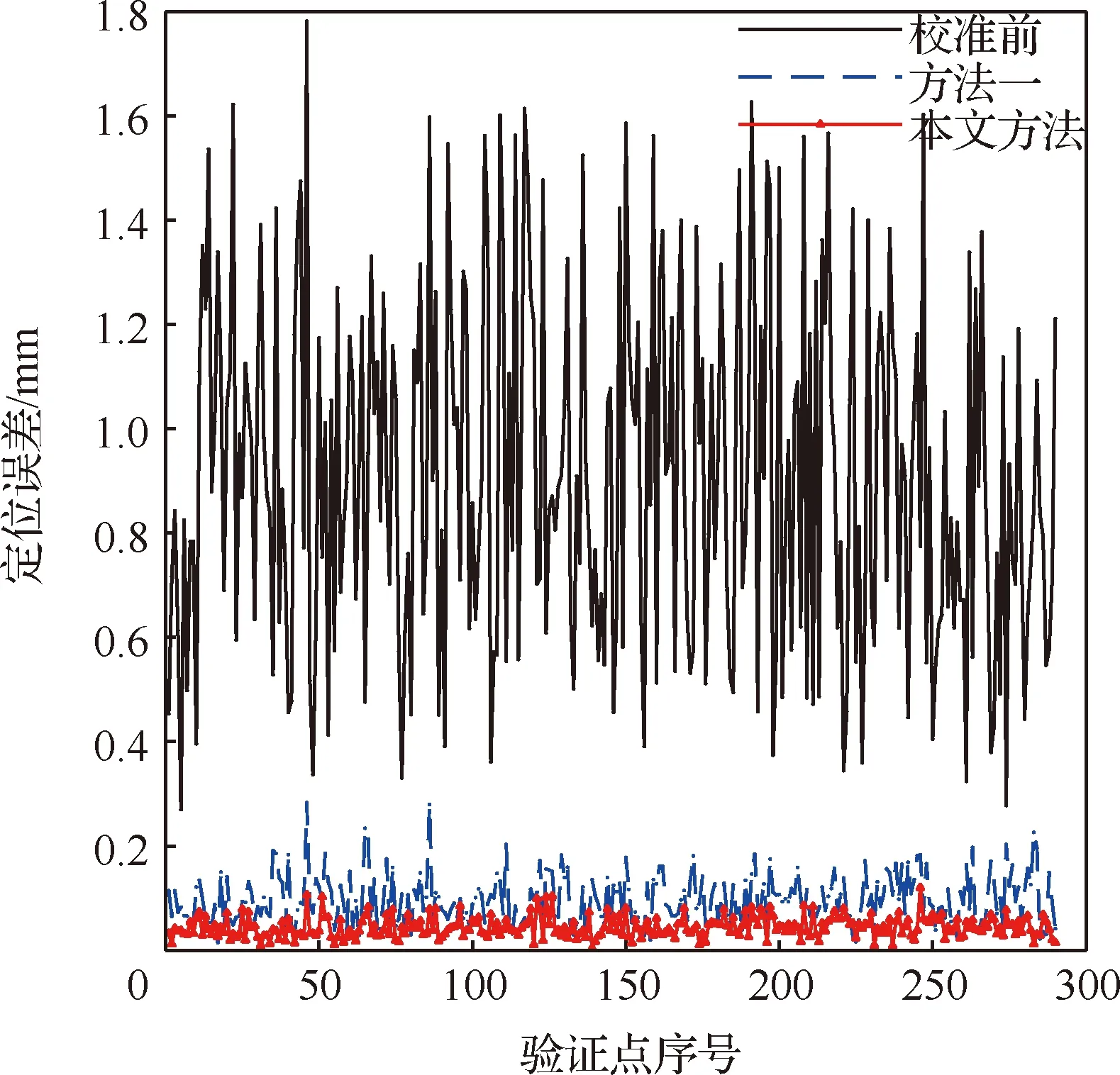
图10 补偿后ER12-1510机器人综合误差Fig.10 Comprehensive error of ER12-1510 robot after compensation

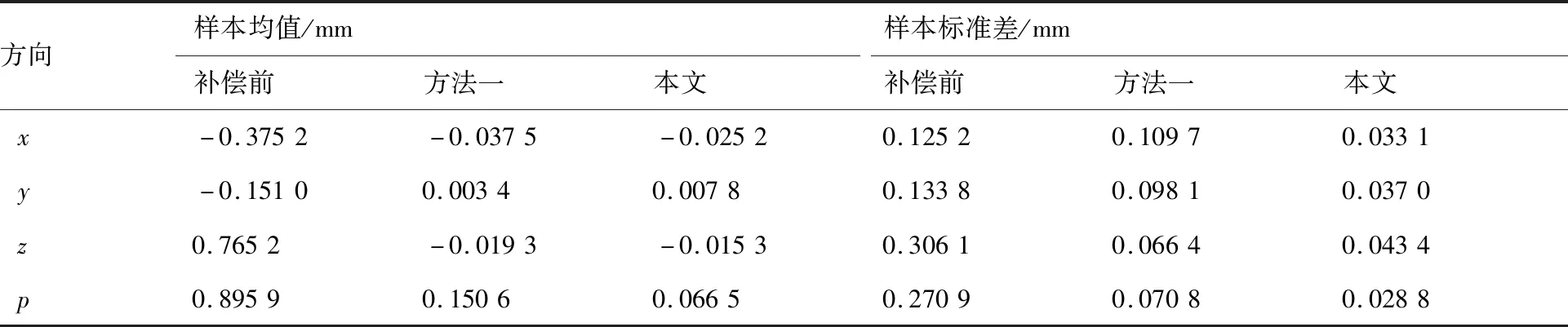
表8 补偿后KUKA KR30HA机器人样本统计Table 8 Sample statistics of KUKA KR30HA robot after compensation

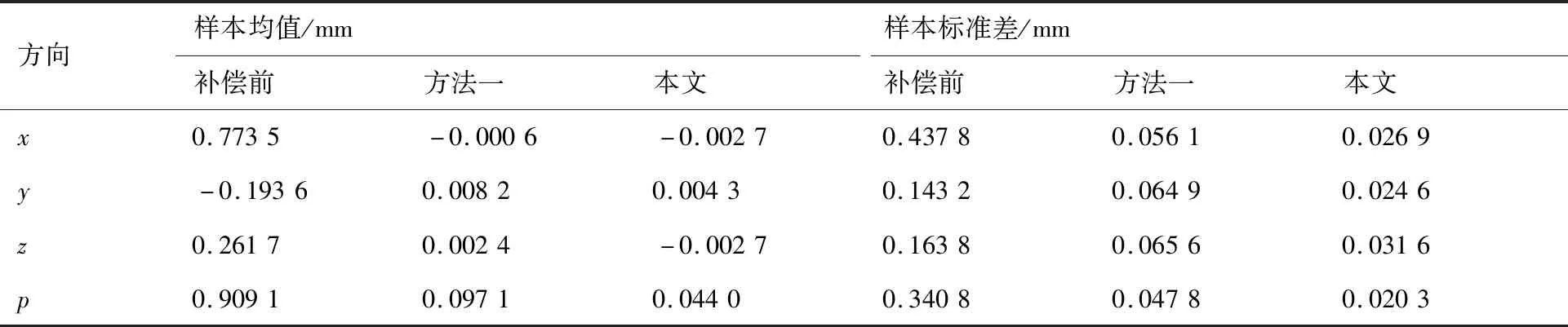
表9 补偿后ER12-1510机器人样本统计Table 9 Sample statistics of ER12-1510 robot after compensation

本文方法在不同机器人上均取得了良好的精度补偿效果，证明了本文方法具有通用性，且相较不考虑关节回差的传统方法具有优越性。体现在：① 对于KUKA KR30HA机器人，本文方法将机器人绝对定位误差由1.492 0 mm降低到0.218 0 mm，精度提升85.38%。且相较于方法一绝对定位精度由0.355 0 mm提升到0.218 0 mm，精度提升38.59%，标准差由0.070 8 mm降低到0.028 8 mm，提升59.32%。② 对于埃斯顿ER12-1510机器人，本文方法将机器人绝对定位误差由1.781 5 mm降低到0.120 0 mm，精度提升93.26%，且相较于方法一本文方法将绝对定位精度由0.283 0 mm提升到0.120 0 mm，精度提升57.59%，标准差由0.070 8 mm降低到0.028 8 mm，提升57.53%。

3.2 自动制孔试验

飞机装配对孔位置的精度要求为≤0.5 mm，为验证本文方法的工程实用性，通过搭建制孔试验平台进行制孔试验，对比补偿前后的制孔孔位精度验证本文方法。

制孔试验分为刀具安装，基准孔制备，离线编程规划验证孔位，验证孔制备，测量孔位误差和数据分析几个部分。

试验以薄壁板作为待加工件，将图5所示精度补偿平台中的机器人末端靶标座拆除，并在刀柄上安装制孔所需刀具进行制孔试验，如图5左下角所示，首先在试件上制备基坐标系下轴方向的2个基准孔作为参照孔位，然后在此基准上规划48个孔作为验证孔，分别制备补偿前后的加工件，通过对比精度补偿前后的制孔孔位精度验证精度补偿效果，精度补偿前后的试件如图11所示。

图11 补偿前(上)后(下)制孔试件Fig.11 Test specimen before (upper) and after (lower)compensation

通过三坐标测量仪测量孔位圆心坐标，并与理论值进行对比得到实际误差，以两基准孔连线方向为理论轴方向，试件表面为轴方向建立坐标系，可以得到两块试板上验证孔在产品坐标系的方向、方向的位置误差以及平面上综合位置误差如图12所示。

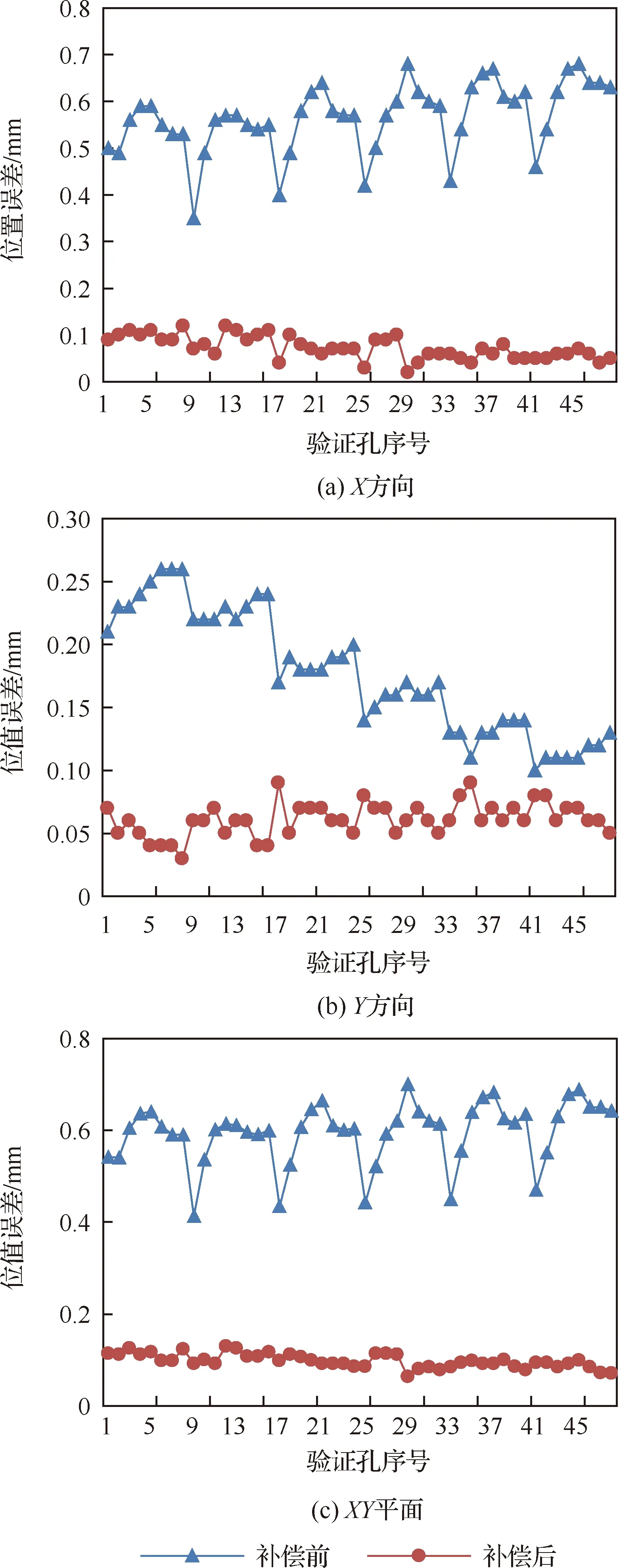
图12 验证孔位置误差Fig.12 Position error of verified holes

其中，工件轴正方向和轴正方向分别接近机器人基坐标系的轴正方向和轴负方向，轴方向接近机器人基坐标系的轴方向。由试验结果可以得到：

1) 关节回差的存在影响了机器人制孔孔位精度。体现在第8个点到第8+1个点位时方向误差和方向误差同时发生跳动，该跳动误差在方向跳动可达0.2 mm，方向可达0.07 mm。这是由于离线编程过程中是沿方向制好8个孔后，再制下一排孔，因此运动方向发生突变导致机器人定位发生偏差。

2) 经由本文方法补偿后，制孔孔位精度有较大提升，且能有效补偿关节回差引起的机器人定位误差。体现在：① 验证孔的最大综合位置误差从0.701 mm降低至0.134 mm，制孔孔位精度提高了81.35%，满足飞机装配对孔位置的精度要求。② 由本文方法补偿后8个点到第8+1个点位时方向误差和方向误差规律性跳动现象不明显。

此外，由于产品坐标系的轴方向与机器人基坐标系的轴方向较为接近，而恰好该方向的突变现象明显且误差更高，证明了3.1节模型对比与分析中的统计数据与相关分析和2.1节仿真统计数据与相关分析中对轴方向的讨论的合理性。