曲率单调的组合二次Phillips q-Bézier曲线

梁吉娜，解 滨，韩力文,3,4

曲率单调的组合二次Phillips-Bézier曲线

梁吉娜1，解 滨2，韩力文1,3,4

(1. 河北师范大学数学科学学院，河北 石家庄 050024；2.河北师范大学计算机与网络空间安全学院，河北 石家庄 050024；3. 河北省计算数学与应用重点实验室，河北 石家庄 050024；4. 河北省数学与交叉科学国际联合研究中心，河北 石家庄 050024)

Phillips-Bézier曲线是一类包含-整数的广义Bézier曲线。针对二次Phillips-Bézier曲线的曲率单调条件，从代数和几何两方面进行了研究，构造出曲率单调的二次Phillips-Bézier曲线及曲率单调递减的组合二次Phillips-Bézier曲线。首先，通过曲线曲率的坐标表示，探究代数形式的曲率单调条件，定义曲率单调包围圆，给出二次Phillips-Bézier曲线具有单调曲率的几何充要条件。当形状参数=1时，Phillips-Bézier曲线退化为经典的Bézier曲线，因此上述曲率单调条件包含经典二次Bézier曲线的结果。其次，讨论二次Phillips-Bézier曲线间的2光滑拼接条件及条件中的各个参数对拼接曲线的影响。再次，对于给定首末控制顶点的曲线，选择合适的中间控制顶点，求得使其具有单调曲率时形状参数的取值范围，构造出曲率单调的单条二次Phillips-Bézier曲线。进而，构造出同时满足2拼接与曲率单调递减的组合二次Phillips-Bézier曲线。最后，利用曲率单调递减的组合二次Phillips-Bézier曲线，构造出具有包含关系的两圆之间的缓和曲线。数值实例显示了组合二次Phillips-Bézier曲线的造型优势和灵活性。

Phillips-Bézier曲线；单调曲率；包围圆；2拼接；缓和曲线

曲率分布能够反映曲线的形状。具有单调曲率的曲线符合美学特征，包含相对少的单调曲率段的曲线被认为是光顺的[1]。在工业设计领域，如道路设计[2]、机器人轨道设计[3]、齿轮齿根设计[4]等方面，曲率单调的曲线有重要应用。

许多学者对Bézier曲线的曲率单调条件进行了研究。1992年，Sapidis和FREY[5]指出，当二次Bézier曲线的中间控制顶点位于指定区域时，曲线的曲率是单调的。2000年，Frey和FIELD[6]分析了标准形式的有理二次Bézier曲线所表示的圆锥曲线段的曲率单调条件。标准形二次有理Bézier曲线同时由控制顶点和权因子控制，与二次Bézier曲线相比，权因子使得曲线中间控制顶点所在的曲率单调区域能够随之调整，从而使二次有理Bézier曲线比二次Bézier曲线的曲率单调条件[5]有所放松。Walton和MEEK[7]给出了具有单调曲率的三次Bézier曲线的构造方法，并用其构造出道路设计中的5种缓和曲线。接着又提出了具有单调曲率的三次Bézier曲线的另外2种构造方法[8-9]。2018年，Ahmad和GOBITHAASAN[10]构造基于曲率导数的单调曲率检验函数，给出使标准形二次有理Bézier曲线曲率单调时，权因子的取值范围。2019年，Wang等[11]通过建立合适的坐标系，给出了曲率单调的次Bézier曲线的构造方法。又利用控制多边形边的旋转与缩放，给出曲率单调的次Bézier曲线的另一种构造方法[12]。2020年，Ahmad等[13]探究了光滑连接点与圆、直线与圆2种情况下的曲率单调二次有理Bézier曲线的构造方法。2021年，CANTÓN等[14]利用矩阵生成Bézier曲线的控制多边形，给出了产生单调曲率平面Bézier曲线的新条件。

近些年来，随着-微积分理论的迅速发展，基于-整数的广义Bernstein算子应运而生[15-17]。其中，研究最为广泛的是文献[15]提出的Lupaş-Bernstein算子与文献[16]提出的Phillips-Bernstein多项式。1998年，Oruҫ[18]证明-Bernstein多项式是多项式空间的一组基；2003年，Oruҫ和PHILLIPS[19]定义Phillips-Bézier曲线，并给出该曲线的升阶算法。2007年，DIŞIBÜYÜK和Oruҫ[20]构造有理Phillips-Bézier曲线，并给出该曲线的-差分定义、细分算法和升阶公式。2008年，DIŞIBÜYÜK和ORUÇ[21]又定义出矩形域上张量积型的Phillips-Bézier曲面，该曲面具有几何不变性和仿射不变性、保凸性等优良几何性质。2012年，Simeonov等[22]为Phillips-Bézier曲线建立-开花形式的定义，开花形式的降阶算法和细分算法。2013年，SIMEONOV和Goldman[23]应用-开花理论构造出-B-样条基和-B-样条曲线，建立了-B-样条理论。

Phillips-Bézier曲线是由控制顶点和Phillips-Bernstein基函数定义的多项式曲线，比起由有理形式的Lupaş-Bernstein算子定义的Lupaş-Bézier曲线[24]与加权Lupaş-Bézier曲线[25]，其在计算时更加简便。与经典Bézier曲线相比，其具有许多与经典Bézier曲线相同的优良性质。与此同时，其含有的形状参数使Phillips-Bézier曲线有了更加灵活的形状调控能力。在≠1时，曲线在末端点处的导矢与控制多边形不相切，与经典Bézier曲线和Lupaş-Bézier曲线有所不同。

为了更好地表达复杂曲线，可以将曲线进行光滑拼接。2019年，JIN等[26]通过调整控制点和在相邻的0连续Bézier曲线之间插入过渡Bézier曲线，构造2连续刀具轨迹。2021年，何川等[27]提出一种可灵活构造满足1插值条件的曲率单调Bézier曲线的算法。在给出经典Bézier曲线的光滑拼接条件[28-29]的基础上，本文将探究二次Phillips-Bézier曲线的光滑拼接条件。

1 预备知识

首先给出Phillips-Bézier曲线的相关定义。

定义1(-整数[30]). 对于任意的自然数，称

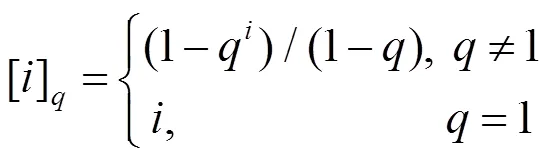
定义2 (-阶乘[30]). 对于任意的自然数，称

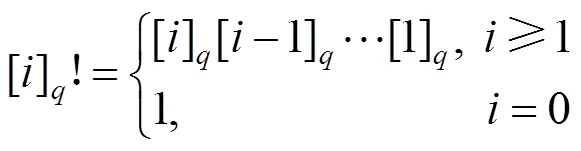
定义3(-二项式系数[30]).对于任意的自然数，称

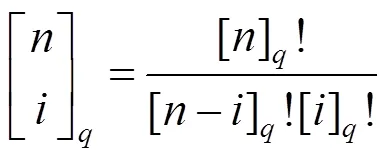
为次Phillips-Bézier曲线。

2 二次Phillips q-Bézier曲线曲率单调的充要条件

二次Phillips-Bézier曲线为

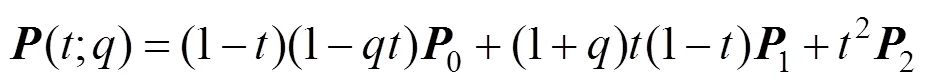
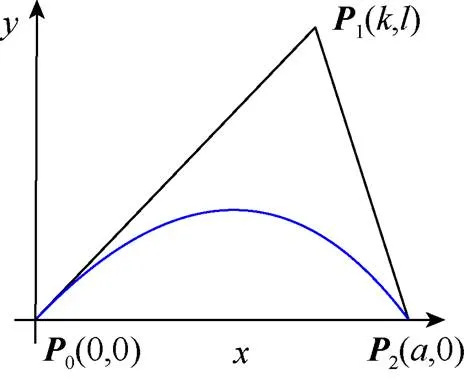
图1 平面直角坐标系中的二次Phillips q-Bézier曲线

结合控制顶点的坐标，可得二次Phillips-Bézier曲线一阶导矢、二阶导矢的坐标表示，因此曲率可表示为

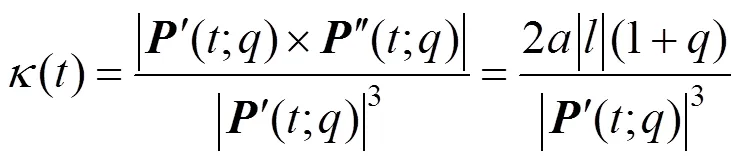
曲率的导数为

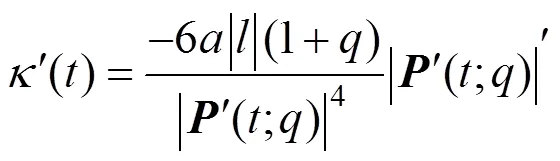
引理：一般来说，沿着曲线的方向，当曲率圆位于曲线左侧时，将曲率的符号定义为正，反之为负。由于二次Phillips-Bézier曲线只有3个控制顶点，所以曲线上任一点的曲率圆始终位于曲线的同一侧。因此将曲率符号均认为是正。

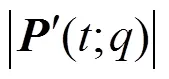
记二次函数()的对称轴为

得

得

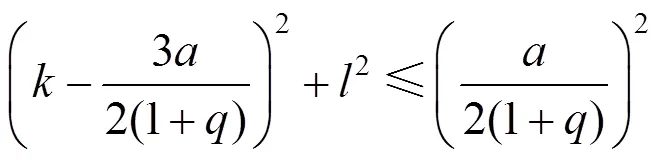
证毕

注：对于首末端点确定的二次Phillips-Bézier曲线，若曲线中的取值从1到0减小，那么曲线左、右包围圆的半径增大，圆心向轴正向移动。

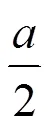
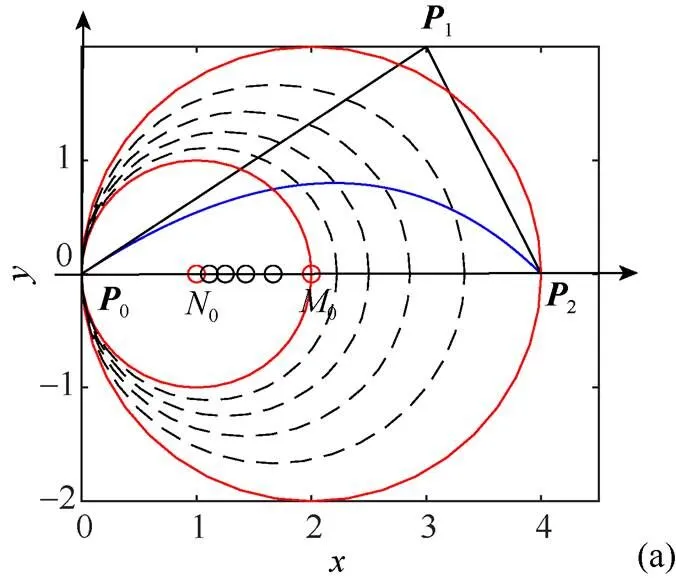
由定义可知，二次Phillips-Bézier曲线的2个单调曲率左、右包围圆是相切的，且具有等长的半径，如图3所示。

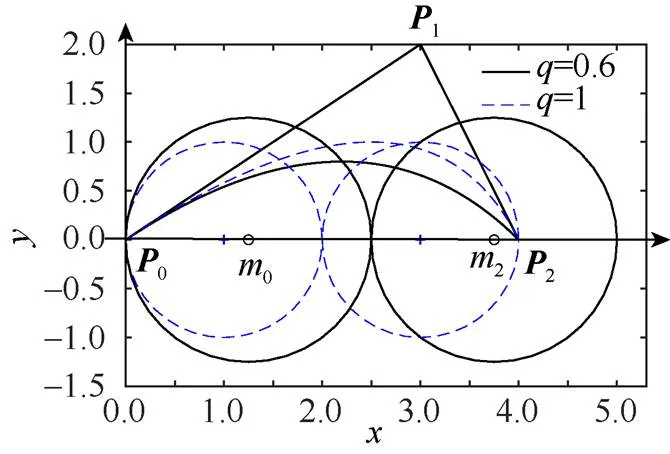
图3 二次Phillips q-Bézier曲线及左、右包围圆

由此可得曲线(;)的曲率单调几何充要条件。

定理1. 由控制顶点0(0,0)，1(,)和2(,0)定义的二次Phillips-Bézier曲线，其曲率单调递减的几何充要条件为：1位于单调递减曲率包围圆0内或圆上；曲率单调递增的几何充要条件为：1位于单调递增曲率包围圆2内或圆上。

3 二次Phillips q-Bézier曲线的光滑拼接

3.1 光滑拼接条件

定理2. 记2条二次Phillips-Bézier曲线分别为(;1)和(;2)，且满足几何连续性的充要条件为：

(1)0连续条件：

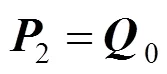
(2)1连续条件：0连续，且

(3)2连续条件：1连续，且

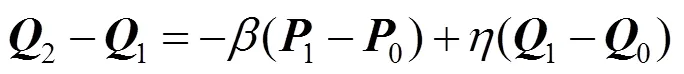
其中，任取，

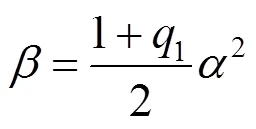
证明：

(1) 由Phillips-Bézier曲线的端点插值性可得：2=0。

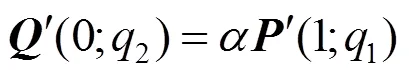
(3) 在满足1连续的基础上，2条曲线在连接点2连续，当且仅当在连接点处有相同的曲率矢。也就是说，在连接点处，曲率矢的方向和大小均要相同。

曲线(;1)在末端点处的曲率矢为

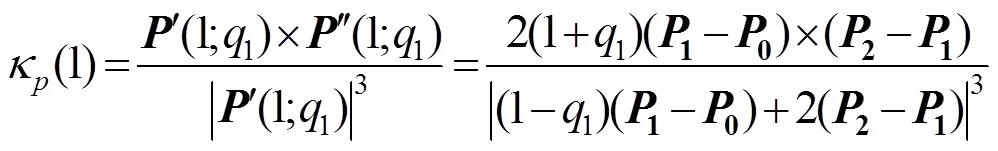
其次，令2个曲率矢的大小相同，即令|(1)|= |(0)|。结合0和1连续条件，有

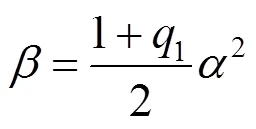
从而得到了二次Phillips-Bézier曲线在端点处2连续的充分必要条件。

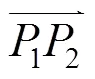
当参数1=2=1时，二次Phillips-Bézier曲线的几何连续条件退化为经典二次Bézier曲线的几何连续条件[31]。

3.2 G2拼接条件中a，h，q2对拼接曲线形状的影响

在二次Phillips-Bézier曲线间的2光滑拼接条件中，拼接曲线的控制顶点同时受给定曲线的控制顶点和变量，及拼接曲线的形状参数2的影响。

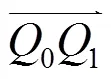
图5 Q(t;q2)的控制顶点随hi的变化

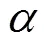
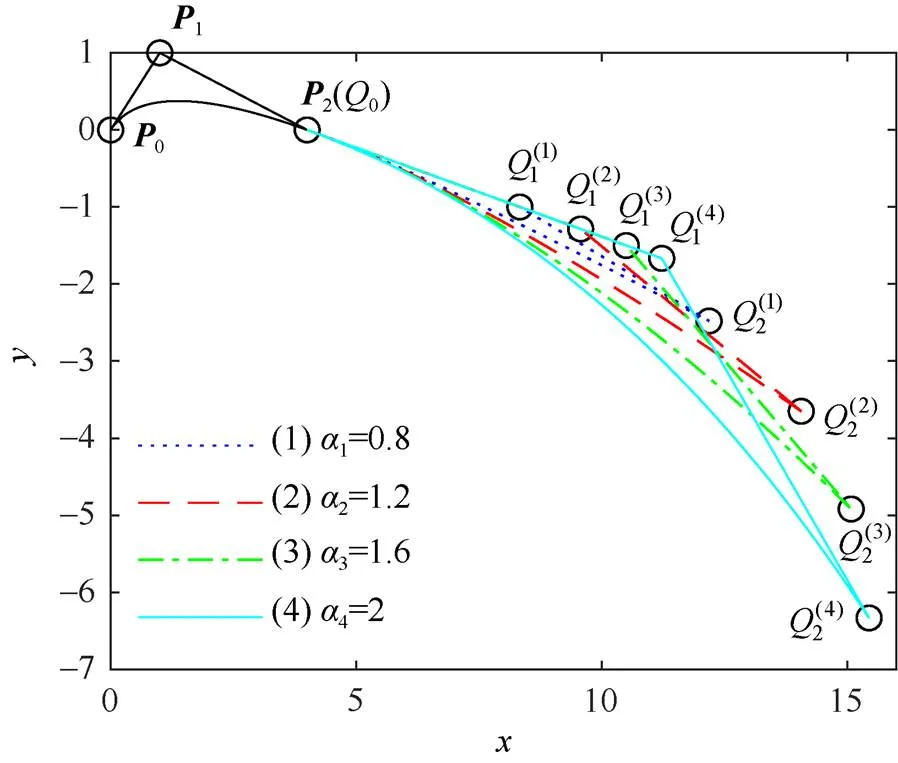
图6 Q(t;q2)的控制顶点和随ai的变化

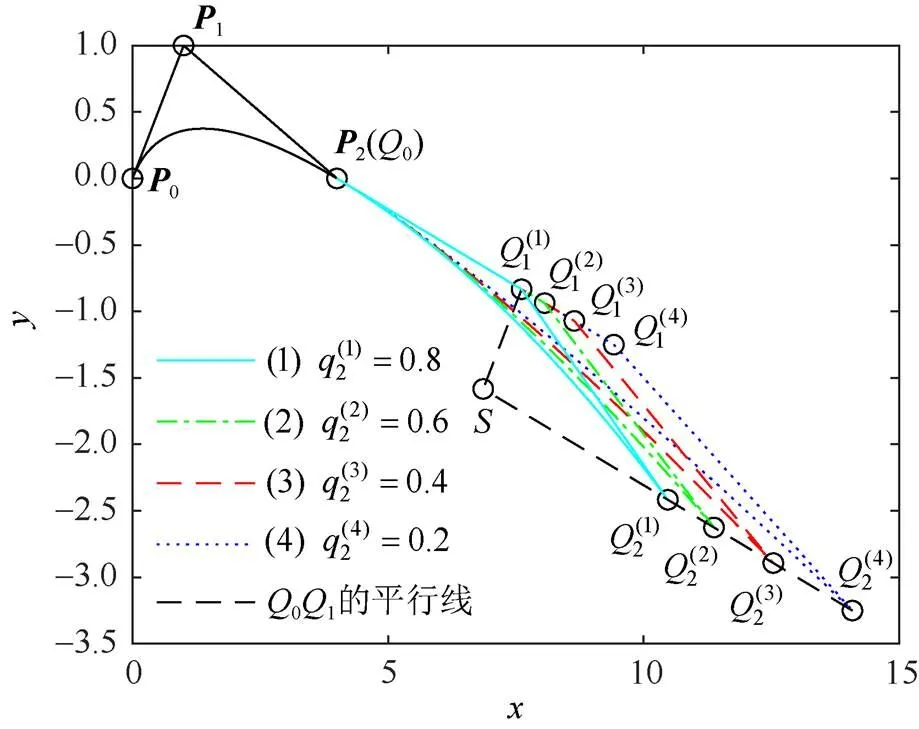
图7 Q(t;q2)的控制顶点和随的变化

4 构造曲率单调的二次Phillips q-Bézier曲线

4.1 具有单调曲率的二次Phillips q-Bézier曲线的构造方法

根据实际需要，在平面上的合适位置选取2个点分别作为曲线的首末控制顶点0和2。按照平面直角坐标系的建立方法建系。则有0(0,0)，1(,)，2(,0)，其中>0，,,均为实数。

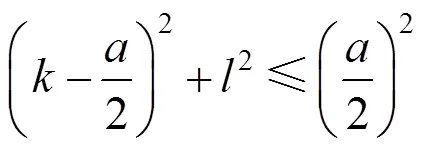
曲线曲率单调递减的充要条件为：控制顶点1位于曲线的左包围圆中，即

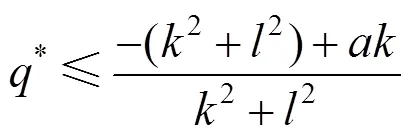
综上，曲线曲率单调递减的充要条件为，形状参数*的取值为

算法1.具体步骤如下：

步骤1.在平面直角坐标系中选择原点与轴上一点，分别记为0(0,0)和2(,0)。

步骤2.确定左包围圆0(趋于0时的左包围圆)，并从中选取控制顶点1(,)。

步骤4.由控制顶点0，1，2和形状参数*确定的二次Phillips-Bézier曲线曲率单调递减。

例1.如图8所示，确定2个控制顶点0和2，建立平面直角坐标系，记0(0,0)和2(4,0)，此时包围圆0的圆心坐标为(2,0)，半径为2。在包围圆中选取1(3,1)，取=0.2，构造出一条曲率单调递减的二次Phillips-Bézier曲线。若取=0.4，则曲线的曲率不单调。

情况2.若控制顶点1在包围圆2的范围内，则控制顶点1(,)满足

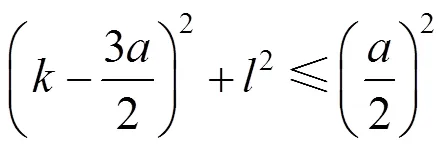
曲线曲率单调递增的充要条件为：控制顶点1位于曲线的右包围圆中，即

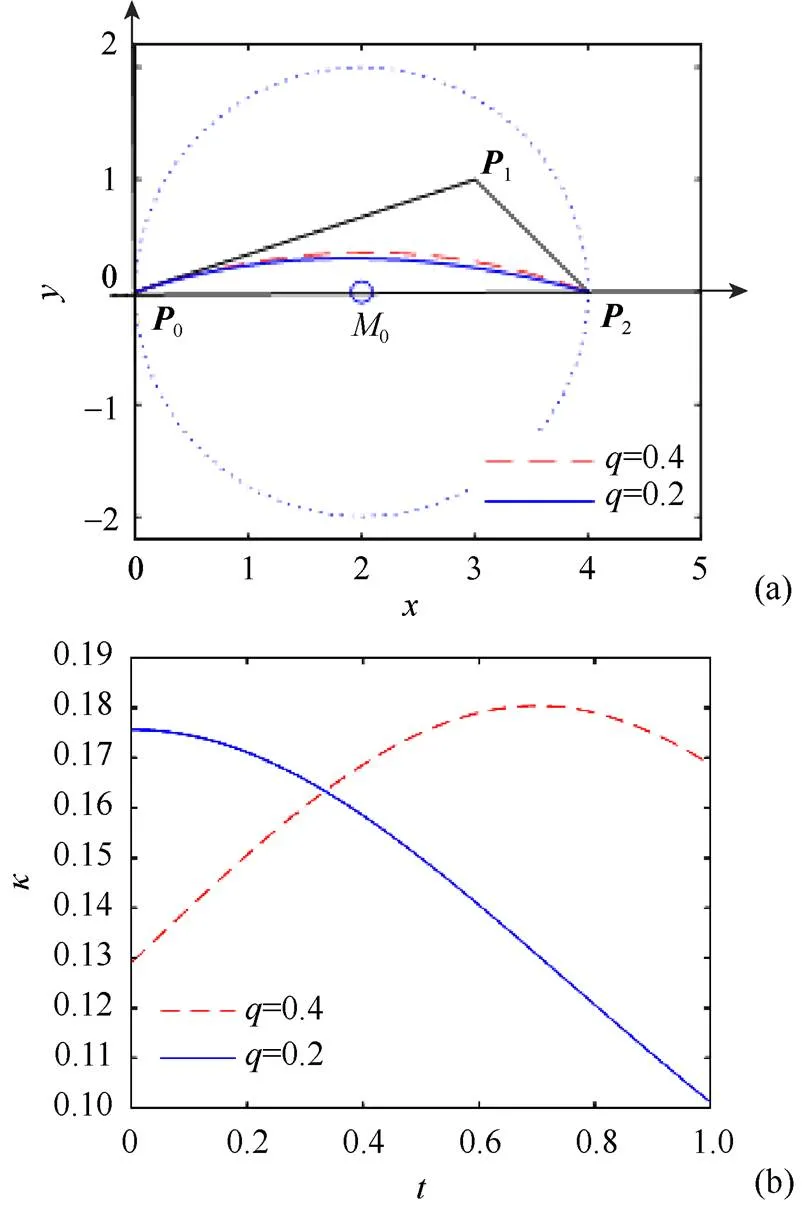
图8 二次Phillips q-Bézier曲线及其曲率图((a) q=0.4与q=0.2的二次Phillips q-Bézier曲线；(b)曲率图)

整理得*的取值需满足

又因的取值范围为(0,1]，综上，曲线曲率单调递减的充要条件为，形状参数*的取值为

算法2.具体步骤如下：

步骤1.在平面直角坐标系中选择原点与轴上一点，分别记为0(0,0)和2(,0)。

步骤2.确定右包围圆2和2(=1和趋向于0时的右包围圆)，并从中选取控制顶点1(,)。

步骤4.由控制顶点0，1，2和形状参数*确定的二次Phillips-Bézier曲线曲率单调递增。

例2. 如图9所示，确定2个控制顶点0和2，建立平面直角坐标系，有0(0,0)和2(4,0)，选取1(6,1)，取=0.259，构造出一条曲率单调递增的二次Phillips-Bézier曲线。若取=0.6，则曲线的曲率不单调。

注1：若一条已有的曲率不单调二次Phillips-Bézier曲线的控制顶点满足算法1或算法2中的前提条件，则可以按照这2条定理中*的取值去改变曲线的形状参数的取值，从而将已有曲线调整为一条曲率单调递增或递减的曲线。

注2：由于一系列右包围圆是不相互包含的，所以不能准确地刻画所有的右包围圆所在的区域。因此在算法2中，要求在半径最小和半径趋于最大的右包围圆2和2中选取控制顶点1，而实际上控制顶点1处于其他右包围圆的范围中，也可以用定理4中的方法找到合适的*值。

图9 二次Phillips q-Bézier曲线及其曲率图((a) q=0.259与q=0.6的二次Phillips q-Bézier曲线；(b)曲率图)

4.2 具有单调递减曲率的组合二次Phillips q-Bézier曲线的构造方法

根据二次Phillips-Bézier曲线曲率单调递减的充要条件，可以构造出一条曲率单调递减的曲线(;)。若能找到这样一条曲线(;0)，其在始端点处与(;)2连续，且曲率是单调递减的，那么就得到了一条曲率单调递减的组合二次Phillips-Bézier曲线。

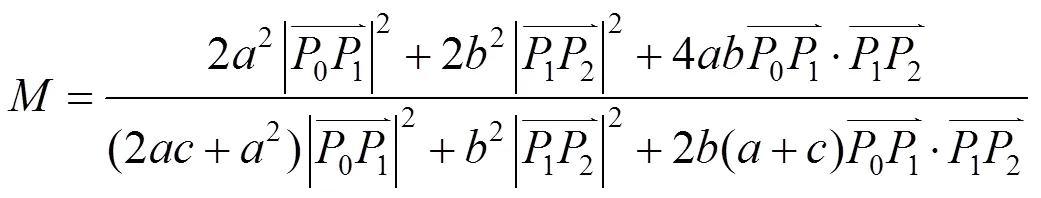
证明：由二次Phillips-Bézier曲线的2连续条件，若(;0)满足式(4)～(7)，则其与(;)在0=2处2连续。

继续证明曲线(;0)的曲率单调递减的充要条件为≥2(1+0)-1。

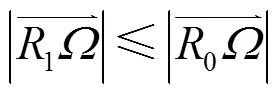
首先表示。

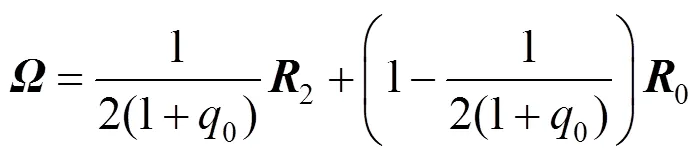
则

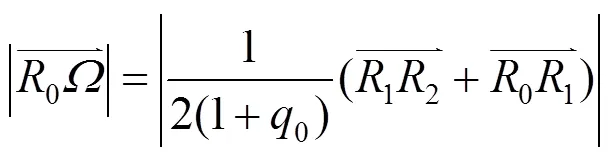
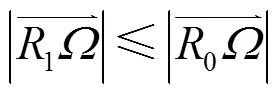
为便于表示，将上式记为

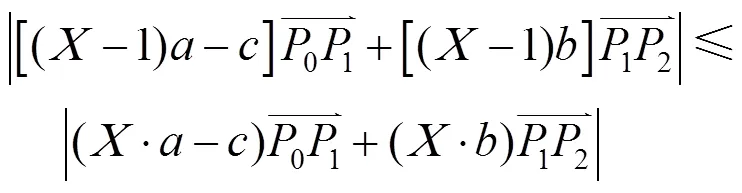
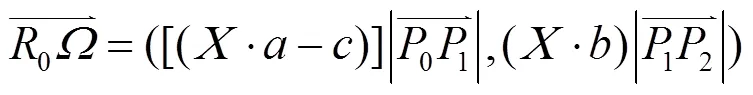
整理得

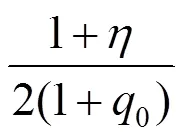
综上所述，曲线(;0)曲率单调递减的充要条件为≥2(1+0)-1。

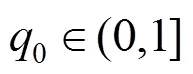
例3.给定一条曲率单调递减的二次Phillips-Bézier曲线(;)，如图10所示，控制顶点坐标分别为0(0,0)，1(1,1)和2(4,0)，参数=0.5。构造出一条与其2连续，且曲率单调递减的曲线(;0)，用实线表示，控制顶点分别为0(4,0)，1(8.33,-1)和2(10.31,-2.38)。取参数0=0.5，=1，=0.63。2条曲线合起来是一条曲率单调递减的组合二次Phillips-Bézier曲线。

在例3中，可取大于0.63的值，此时组合二次Phillips-Bézier曲线中曲线段(;0)的形状稍有变化，但曲率仍然是单调递减的。

在公路设计中，缓和曲线是设置在直线和圆曲线或圆曲线与圆曲线之间的过渡曲线。缓和曲线通过曲率的逐渐变化保证汽车行驶过程中的转向平稳。采用本文方法可以设计出类似的曲率单调递减的过渡路线。

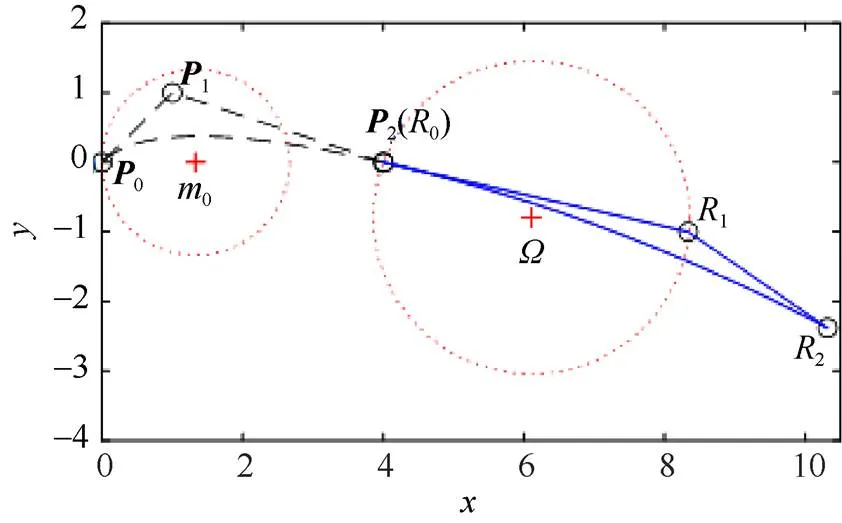
图10 曲率单调递减的组合二次Phillips q-Bézier曲线

例4. 利用本文中曲率单调递减的组合二次Phillips-Bézier曲线设计出具有包含关系的圆到圆之间的缓和曲线。图11中显示了2个具有包含关系的圆(点虚线)；连接2圆的是由曲率单调递减的组合二次Phillips-Bézier曲线表示的缓和曲线(实线)；，Q分别为组合曲线中2段曲线的控制顶点。

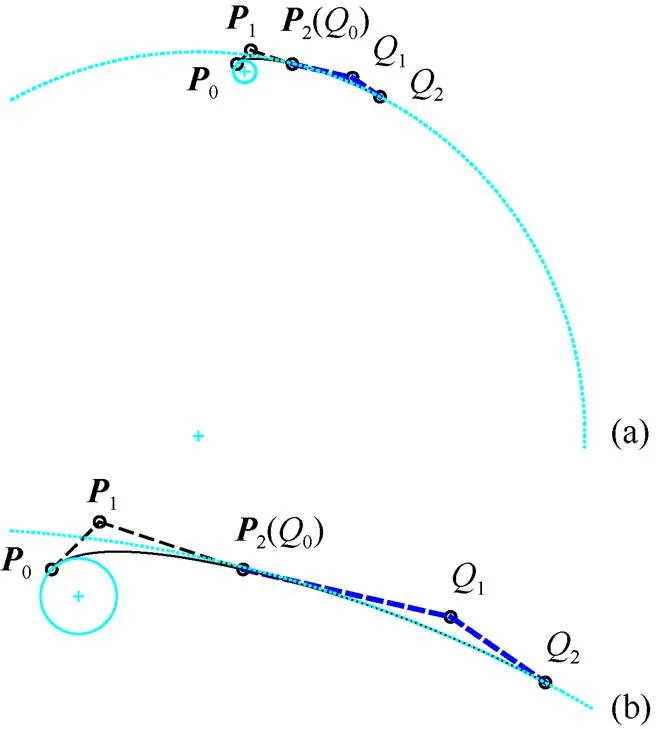
图11 具有包含关系的两圆及圆到圆之间的缓和曲线((a)具有包含关系的两圆及圆到圆之间的缓和曲线整体图；(b)缓和曲线局部图)

5 结束语

本文提出并证明了二次Phillips-Bézier曲线的曲率单调充要条件，指出当曲线的首末端点确定时，中间控制顶点应当处在由首末端点和形状参数值决定的曲率单调包围圆中。包围圆的大小可由参数调整，因此与经典Bézier曲线的曲率单调范围[5]相比，本文中间控制顶点的选择范围更广。当=1时，二次Phillips-Bézier曲线退化为经典二次Bézier曲线，二次Phillips-Bézier曲线的曲率单调条件退化为经典二次Bézier曲线的曲率单调条件。

本文还给出了二次Phillips-Bézier曲线之间的2连续条件，并探究了条件中的3个变量对拼接曲线的影响。最后给出曲率单调曲线的构造方法，及造型上的实例。进一步还可探究具有单调曲率的有理二次Phillips-Bézier曲线。

[1] FARIN G, SAPIDIS N. Curvature and the fairness of curves and surfaces[J]. IEEE Computer Graphics and Applications, 1989, 9(2): 52-57.

[2] BAASS K G. The use of clothoid templates in highway design[J]. Transportation Forum, 1984, 1(3): 47-52.

[3] 杨秀霞, 周硙硙, 张毅. 一种基于PH螺线的避障重规划路径修正方法[J]. 飞行力学, 2016, 34(5): 86-90.

YANG X X, ZHOU W W, ZHANG Y. A re-planning path correction method for collision avoidance based on PH spiral[J]. Flight Dynamics, 2016, 34(5): 86-90 (in Chinese).

[4] 董新华, 马勇, 柳强. 渐开线齿轮齿根过渡曲线最佳线型实现方法[J]. 机械传动, 2013, 37(5): 47-49.

DONG X H, MA Y, LIU Q. Realization method of tooth root transition curve best linetype of involute gear[J]. Journal of Mechanical Transmission, 2013, 37(5): 47-49 (in Chinese).

[5] SAPIDIS N S, FREY W H. Controlling the curvature of a quadratic Bézier curve[J]. Computer Aided Geometric Design, 1992, 9(2): 85-91.

[6] FREY W H, FIELD D A. Designing Bézier conic segments with monotone curvature[J]. Computer Aided Geometric Design, 2000, 17(6): 457-483.

[7] WALTON D J, MEEK D S. A planar cubic Bézier spiral[J]. Journal of Computational and Applied Mathematics, 1996, 72(1): 85-100.

[8] WALTON D J, MEEK D S, ALI J M. Planar G2 transition curves composed of cubic Bézier spiral segments[J]. Journal of Computational and Applied Mathematics, 2003, 157(2): 453-476.

[9] WALTON D J, MEEK D S. A further generalisation of the planar cubic Bézier spiral[J]. Journal of Computational and Applied Mathematics, 2012, 236(11): 2869-2882.

[10] AHMAD A, GOBITHAASAN R U. Rational quadratic Bézier spirals[J]. Sains Malaysiana, 2018, 47(9): 2205-2211.

[11] WANG A Z, ZHAO G, HOU F. Constructing Bézier curves with monotone curvature[J]. Journal of Computational and Applied Mathematics, 2019, 355: 1-10.

[12] 王爱增, 何川, 赵罡, 等. 基于几何方法的曲率单调Bézier曲线的一个充分必要准则[J]. 计算机辅助设计与图形学学报, 2019, 31(9): 1617-1621.

WANG A Z, HE C, ZHAO G, et al. A sufficient and necessary criterion for curvature monotone bézier curves[J]. Journal of Computer-Aided Design & Computer Graphics, 2019, 31(9): 1617-1621 (in Chinese).

[13] AHMAD A, AHMAT N, ADNAN M. Fair transition spiral using a single rational quadratic Bézier curve[J]. Journal of Computer Science & Computational Mathematics, 2020, 10(1): 7-12.

[14] CANTÓN A, FERNÁNDEZ-JAMBRINA L, VÁZQUEZ-GALLO M J. Curvature of planar aesthetic curves[J]. Journal of Computational and Applied Mathematics, 2021, 381: 113042.

[15] LUPAŞ A. A-analogue of the Bernstein operator [J]. Seminar on Numerical and Statistical Calculus, 1987, 9: 85-92.

[16] PHILLIPS G M. A de Casteljau algorithm for generalized Bernstein polynomials[J]. BIT Numerical Mathematics, 1997, 37(1): 232-236.

[17] OSTROVSKA S. The-versions of the Bernstein operator: from mere analogies to further developments[J]. Results in Mathematics, 2016, 69(3-4): 275-295.

[18] Oruç H. Generalized Bernstein polynomials and total positivity [D]. Scotland: University of St. Andrews, 1998.

[19] ORUÇ H, PHILLIPS G M.-Bernstein polynomials and Bézier curves[J]. Journal of Computational and Applied Mathematics, 2003, 151(1): 1-12.

[20] DIŞIBÜYÜK Ç, ORUÇ H. A generalization of rational Bernstein-Bézier curves[J]. BIT Numerical Mathematics, 2007, 47(2): 313-323.

[21] DIŞIBÜYÜK Ç, ORUÇ H. Tensor product-Bernstein polynomials[J]. BIT Numerical Mathematics, 2008, 48: 689-700.

[22] SIMEONOV P, ZAFIRIS V, GOLDMAN R.-Blossoming: a new approach to algorithms and identities for-Bernstein bases and-Bézier curves[J]. Journal of Approximation Theory, 2012, 164(1): 77-104.

[23] SIMEONOV P, GOLDMAN R. Quantum B-splines[J]. BIT Numerical Mathematics, 2013, 53(1): 193-223.

[24] HAN L W, CHU Y, QIU Z Y. Generalized Bézier curves and surfaces based on Lupaş-analogue of Bernstein operator[J]. Journal of Computational and Applied Mathematics, 2014, 261: 352-363.

[25] HAN L W, WU Y S, CHU Y. Weighted Lupaş-Bézier curves[J]. Journal of Computational and Applied Mathematics, 2016, 308: 318-329.

[26] JIN Y Q, ZHAO S, WANG Y H. An optimal feed interpolator based on G2continuous bézier curves for high-speed machining of linear tool path[J]. Chinese Journal of Mechanical Engineering, 2019, 32(1): 1-10.

[27] 何川, 赵罡, 王伟, 等. 曲率单调Bézier曲线G1插值算法及应用[J]. 图学学报, 2021, 42(4): 644-650.

HE C, ZHAO G, WANG W, et al. G1 interpolation algorithm and application of Bézier curves with monotone curvature[J]. Journal of Graphics, 2021, 42(4): 644-650 (in Chinese).

[28] 施法中. 计算机辅助几何设计与非均匀有理B样条[M]. 北京: 高等教育出版社, 2001: 173-186.

SHI F Z. CAGD & NURBS[M]. Beijing: Higher Education Press, 2001: 173-186 (in Chinese).

[29] 王国瑾, 刘利刚. 几何计算逼近与处理[M]. 北京: 科学出版社, 2015: 108-118.

WANG G J, LIU L G. Geometric computation approximation and processing[M]. Beijing: Science Press, 2015: 108-118 (in Chinese).

[30] KAC V, CHEUNG P. Symmetric quantum calculus[M]// Quantum Calculus. New York: Springer New York, 2002: 99-104.

[31] 王仁宏, 李崇君, 朱春钢. 计算几何教程[M]. 北京: 科学出版社, 2008: 102-116.

WANG R H, LI C J, ZHU C G. Computational geometry course[M]. Beijing: Science Press, 2008: 102-116 (in Chinese).

Combinatorial quadratic Phillips-Bézier curves with monotone curvature

LIANG Ji-na1, XIE Bin2, HAN Li-wen1,3,4

(1. School of Mathematical Sciences, Hebei Normal University, Shijiazhuang Hebei 050024, China; 2. College of Computer and Cyber Security, Hebei Normal University, Shijiazhuang Hebei 050024, China; 3. Hebei Key Laboratory of Computational Mathematics and Applications, Shijiazhuang Hebei 050024, China; 4. Hebei International Joint Research Center for Mathematics and Interdisciplinary Science, Shijiazhuang Hebei 050024, China)

Phillips-Bézier curves are a class of generalized Bézier curves containing-integers. The research was conducted on the curvature monotonicity condition of quadratic Phillips-Bézier curve from two aspects of algebra and geometry. Based on this, the following two curves were constructed: a quadratic Phillips-Bézier curve with monotonous curvature and a combined quadratic Phillips-Bézier curve with decreasing curvature. Firstly, through the coordinate representation of curve curvature, this paper explored the condition of monotonic curvature in algebraic form. By defining the curvature decreasing (or increasing) bounding circle, the geometric sufficient and necessary conditions were given to enable decreasing (or increasing) curvature for quadratic Phillips-Bézier curves. In the case of the shape parameter=1, Phillips-Bézier curves would degenerate into classical Bézier curves. Thus, the curvature monotonicity conditions of quadratic Phillips-Bézier curves include the results of classical quadratic Bézier curves. Secondly, the paper examined the2smooth condition of quadratic Phillips-Bézier curves and the influence of parameters on the stitching curve. Thirdly, for the quadratic Phillips-Bézier curve with given initial and final control vertices, the appropriate intermediate control vertex was selected, the range of shape parameters was obtained in the case of decreasing (or increasing) curvature, and a quadratic Phillips-Bézier curve with decreasing (or increasing) curvature was constructed. Furthermore, a combined quadratic Phillips-Bézier curve was constructed, which could satisfy both2smooth condition and decreasing curvature. Finally, using the combined quadratic Phillips-Bézier curve with decreasing curvature, the transition curve between two circles with inclusion relationship was constructed. The numerical examples highlight the advantages and flexibility of the combinatorial quadratic Phillips-Bézier curve in modeling.

Phillips-Bézier curve; monotonic curvature; bounding circle;2blending; transition curve

TP 391

10.11996/JG.j.2095-302X.2022030443

A

2095-302X(2022)03-0443-10

2021-09-23；

2021-10-27

23 September，2021；

27 October，2021

国家自然科学基金项目(62076088)；河北省自然科学基金项目(A2018205103)；河北师范大学科研基金资助项目(L2020Z02)

National Natural Science Foundation of China (62076088); National Natural Science Foundation of Hebei Province (A2018205103); Research Fund of Hebei Normal University (L2020Z02)

梁吉娜(1997–)，女，硕士研究生。主要研究方向为CAGD。E-mail：996953165@qq.com

LIANG Ji-na (1997–), master student . Her main research interest covers CAGD. E-mail：996953165@qq.com

韩力文(1974–)，女，教授，博士。主要研究方向为CAGD、计算几何。E-mail：hanliwen@sina.com

HAN Li-wen (1974–), professor, Ph.D. Her main research interests cover CAGD, computer geometry. E-mail：hanliwen@sina.com