弹性力学与流体力学基本方程的统一性1)

黄忠文 张博文 唐明哲 王发达 徐钦旭

(武汉工程大学机电工程学院，武汉 430205)

弹性力学是研究弹性体在载荷作用下产生应力和弹性变形规律的科学[1]，研究对象一般为弹性固体。流体力学是研究流体平衡和运动规律的科学，研究对象一般为易流动且极易变形的流体[2]。目前，在众多实际工程中普遍存在固体与流体相互作用的现象[3-4]，弹性力学与流体力学的交叉研究越来越深入[5]。弹性力学中的弹性固体与流体力学中的流体均为连续介质模型[6-7]。流体力学中的流体微团是基于流体质点提出的一个重要概念，流体微团是流体中任意小的微元体积[8]。流体微团与弹性力学中的微元体相对应，存在一定的共性，所以在一定程度上可以利用弹性力学的理论去推导流体力学的部分方程。

流体的平衡状态对应弹性力学中弹性体的平衡状态，流体的运动状态对应弹性力学中弹性体的运动状态。利用弹性力学的微元体平衡方程，并结合流体的平衡性质，可以推导出流体静力学的欧拉平衡方程。流体动力学中的不可压缩流体N–S方程具有极其重要的地位，20世纪就有学者针对N–S方程的求解进行了研究[9-10]，但N–S方程的推导较为复杂，需要利用霍姆赫兹定理与斯托克斯假定进行推导。本文直接利用弹性力学的微元体动力学方程、几何方程与应力应变关系，并结合不可压缩黏性流体的性质，推导出N–S方程。

1 流体静力学的静压强

流体静力学中，平衡流体的受力达到平衡，而弹性力学中，任意形状的物体达到平衡状态时，同样受力平衡。不难发现，平衡流体中的微元体主要受压强影响，而弹性力学中的微元体受到了正应力及切应力的影响，那么弹性力学中的正应力可对应于流体力学中的压应力，但需要注意平衡流体具有不存在切应力的特点[11]。

如图1所示，在三个坐标面均有垂直平面的正应力及平行于平面的切应力，斜截面用V表示，斜截面上的应力为PV，该应力可分解为三个沿坐标轴方向的应力分量XV,YV,ZV，也可以分解为正 应 力σV与 切 应 力τV，斜 截 面 的 外 法 线单位矢量为λ(l,m,n) 。为考察一点处的受力情况，微元四面体的体积接近为0，相当于缩小为一个点。

图1 微元体各面受力分析

物体整体达到受力平衡时，微元体也会达到力的平衡。根据微元体在三个坐标方向上的力平衡方程，可得到斜截面的三个应力分量为

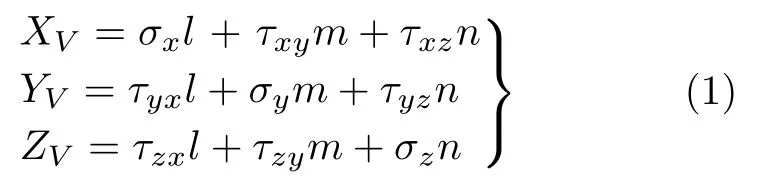
此公式称为弹性力学中的柯西公式。

本文将柯西公式应用于流体时，由于平衡流体的微元体此时不存在切应力，故有

于是得到

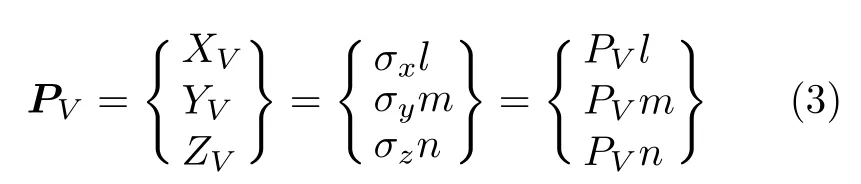
流体微元的压应力对应柯西公式中的正应力，即

结合式（3）和式（4）可以推得

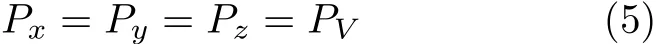
在流体力学中，式（5）表示从任何方向作用于一点上的流体静压强均是相等的，反映了流体静压强的概念。

2 流体静力学的欧拉平衡微分方程

对于微元六面体进行研究分析时，单位体积力分量用Fbi表示。

弹性力学中的平衡微分方程为

根据平衡流体的微元体中切应力不存在的条件，得出

静压强用P表示，则平衡流体的微元体的正应力为

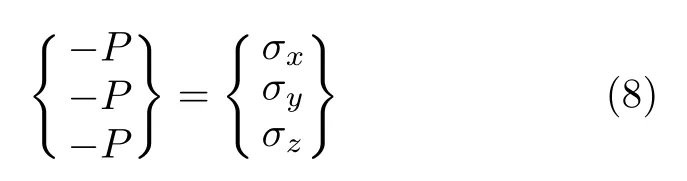
单位质量力的分量用fi表示，密度用ρ表示，则单位体积力与单位质量力的关系为

再将式（8）和式（9）代入到式（7）中可以得到

式（10）即为欧拉平衡微分方程，该方程表明流体在静平衡状态时，其内部的压力分布情况仅与其体积力或质量力有关。该推导过程也表明流体的静平衡状态与弹性体静平衡状态在本质上是一样的。

3 流体动力学的N–S方程

流体动力学问题主要研究不可压缩黏性流体，黏性流体在运动时，其内部的切应力不再为0。位移分量函数分别表示为

速度分量函数分别为

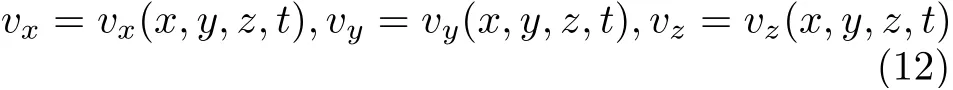
微元体不平衡时采用达朗贝尔原理，加上惯性力后，可以得到弹性体动力学微分方程为

流体微元体所受到的正应力σi为压应力pi，式（13）应用到流体力学微元体中有

弹性力学静力学几何方程为

动力学问题主要研究某个瞬时开始在dt时间段的动力学方程，则动力学的几何方程为

该动力学的几何方程对弹性动力学和流体动力学都是适用的。

弹性力学静力学的本构方程为

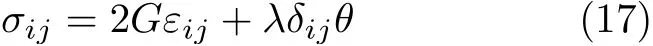
式中，G为剪切模量，λ为拉梅常量，θ为体积应变。

若体积不变，则式（17）中的体积应变θ=0 ，得到

根据流体力学一维运动的牛顿内摩擦定律，切应力与速度梯度成正比[12]，即

又剪切角度即切应变，为

由式（19）和式（20）得到切应力为

即流体力学中运动变形产生的应力与单位时间内的应变即应变速度成正比。

弹性力学中的剪切模量G相当于流体力学中的动力黏度µ，根据式（18）和式（21），可以得到不可压缩流体的应力应变关系为

式（22）是不可压缩流体流动变形时由于黏性的影响而产生的应力，再根据式（16）写成直角坐标形式的方程为

流体微元体与固体微元体不同，其本身还存在一个静压强p产生的应力，那么流体微元体总应力为

将式（24）中总应力的应力分量代入式（14）中第一个方程得到

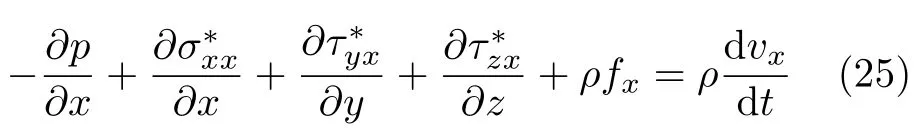
再将式（23）代入式（25）中可以得到

整理得到

同理可得到y,z方向上的公式

联立式（28）和式（29）及式（30）并结合运动黏度υ为动力黏度µ和密度ρ的比值，可以得到不可压缩实际流体的运动微分方程式为

式（31）为流体动力学中不可压缩黏性流体的N–S方程。

4 结论

弹性力学中的弹性体与流体力学中的不可压缩流体具有相同的可变形性，且都符合连续介质模型的假定，但流体的性质与弹性体存在一定的差异。本文利用弹性力学中微元体的受力分析方法结合流体力学中流体在不同状态下的条件，推导出流体力学中静压强概念、欧拉方程以及N–S方程，实际上是把流体微元看成固体微元的一种特殊情况。与弹性固体中体积可变化的微元体相比较，不可压缩流体的微元体是一种体积不变的微元体，将不可压缩流体的这种特性作为一种条件代入到弹性力学的基本方程中，并直接利用弹性力学中的动力学微分方程，几何方程，本构方程，并结合不可压缩流体微元体的特性，可以推导得出N–S方程。该推导过程相较传统流体力学方法更好理解，并将两种学科内在的基本方程联系起来，加深了对弹性体与不可压缩黏性流体的交融程度的理解。由此表明，弹性力学与流体力学的基本方程具有高度的统一性，这种研究结果会极大地促进弹性力学与流体力学两种学科的深度融合统一与相互促进发展，可以进一步改善力学课程教学内容，加深理解力学基本原理，有效提高力学课程教学水平。