掺氢天然气在燃气锅炉和灶具中的回火风险分析1)

王天天 张 海 ,† 张 扬 ,†,2) 周 托 岳光溪

*(清华大学能源与动力工程系热科学与动力工程教育部重点实验室，北京100084)

†(二氧化碳资源利用与减排技术北京市重点实验室，北京 100084)

在“双碳”目标下，氢能的发展与应用成为近年来的研究热点[1]。纯氢的利用受到生产、储存和终端使用的制约，成本较高。将氢气掺混到已有的天然气管网中，形成“掺氢天然气”，再通过管网输送[2]至终端用户燃烧利用，是大规模低成本利用氢能的潜在途径之一[3]。因此，掺氢天然气在燃气终端设备中的燃烧特性受到了学术界和工业界的广泛关注[4-7]。

天然气成分较为复杂，但主要成分是甲烷（>90%）[8]，由于甲烷和氢气的物理性质存在差异，因此，掺氢天然气的燃料特性随着氢气掺混比例的变化而变化。氢气的加入提高了燃料的火焰传播速度[9-11]，降低了燃料的最小点火能量[12]，同时也拓宽了燃料的贫燃极限[13]。掺氢燃料面临的主要问题之一在于易于发生回火，造成安全事故。燃气终端设备中，供暖锅炉和灶具通常安装于住宅、办公楼等民用场所，其安全问题受到格外关注。因此，掌握掺氢天然气在锅炉和灶具中的回火特性，对于判断掺氢天然气使用安全具有重要意义。

目前，一些学者已经关注到掺氢天然气应用于灶具中的回火问题。Zhao等[14-16]研究了掺氢天然气在不同形式灶具上的回火特性，发现在已经稳定燃烧的灶具中（稳态）逐渐增加氢气，不发生回火的最大掺氢比可达50%以上，但是如果在点火前燃料中已经掺混氢气，则在点火的“瞬态”过程中不发生回火的最大掺氢比降为25%。Choudhury等[17]通过实验研究了掺氢天然气对家用燃气热水器的影响，结果表明在低于10%的掺氢比下，燃烧器可以保证燃烧稳定性。Jones等[18]通过分析掺氢天然气火焰传播速度随掺氢比的变化规律，提出在燃料中氢气的摩尔百分比不高于30%时，掺氢天然气在实际燃烧器中的回火风险不会显著增加。

锅炉和灶具的运行工况存在差异，因此掺氢天然气应用于锅炉时，其回火特性也与应用于灶具时不尽相同。为了控制氮氧化物生成，中小型供暖燃气锅炉常采用预混燃烧的方式。Schiro等[19]指出，为了保证掺氢天然气锅炉的安全可靠运行，必须避免回火现象。增加未燃侧的出口流速有助于避免回火现象的发生[20]。de Vries等[21]通过本生灯方法测量了在回火极限下对应的掺氢天然气的最大掺氢比，并讨论了不同掺氢比下燃料的火焰传播速度对回火特性的影响。Colorado等[22]通过在贫燃预混燃烧的表面燃烧器进行实验，获得了不同组分的掺氢天然气在定热流密度下的回火和吹熄特性。

根据上述文献调研可知，国内外已有的相关研究，虽然已经获得了大量掺氢天然气预混燃烧回火基础数据，并且积累了少量灶具、锅炉等设备上的回火实验数据，但仍存在如下的局限性：

首先，文献中已有的关于回火的研究，尚未细致分析燃烧设备入口条件的差异。由于甲烷和氢气物理化学性质差异显著，天然气掺氢后会带来密度、热值等参数的显著变化，这使得掺氢天然气燃烧设备的燃料和空气入口条件（流速、当量比等）发生变化（详见第2节所述），导致火焰传播速度在实际设备中的变化规律较为复杂，进而影响到回火现象。而已有文献缺乏对该问题的关注，导致不同文献中得到的回火极限数据并不一致，缺少通用性的结论。

第二，缺乏设备回火风险的表征方法。针对掺氢天然气在锅炉和灶具上的回火特性，学者们或是采用实验方法获得保证用户侧安全稳定运行、不发生回火的最大掺氢比例；或是通过简单分析掺氢天然气火焰传播速度的变化，来判断发生回火的可能性。已有的研究缺乏天然气掺氢后设备回火风险的表征方法，难以根据已有结论快速判断燃料发生变化的回火风险。

第三，对于已有文献[14]中发现的灶具中“稳态”和“瞬态”回火掺氢比的差异，已有文献无法给出合理的解释。

针对上述问题，本文首先讨论了掺氢天然气的层流火焰传播速度等基本物理化学性质，并校核了本文采用的数值模型的合理性；其次，针对预混燃烧的燃气锅炉和灶具，厘清燃料成分变化引发的运行参数（如燃料流量、空气流量、当量比等）的变化规律；最后，通过将掺氢天然气的基本火焰特性与设备入口参数相结合，提出了掺氢天然气燃烧设备回火风险的表征方法，并使用实验数据对表征方法进行了验证，揭示了灶具中“稳态”和“瞬态”回火掺氢比差异的原因。

1 掺氢天然气基础物理化学性质

天然气的主要成分是CH4，因此本文的理论计算中采用CH4来代替天然气。甲烷和氢气的基本物理化学性质如表1所示。根据《城镇燃气分类和基本特性》（GB/T 13611−2018）[23]，华白数（Wobbe index，W）和燃烧势（CP）是作为燃气互换性判定的评价指标。华白数的计算公式为

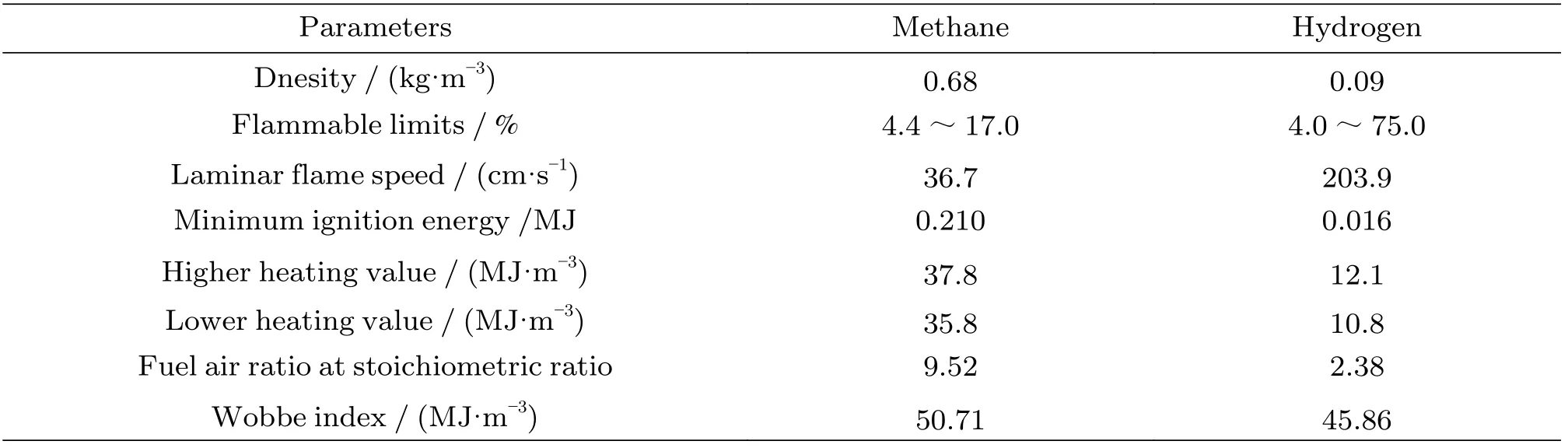
表1 甲烷和氢气的基本物性参数Table 1 Basic characteristics of methane and hydrogen

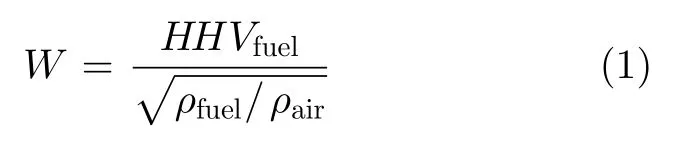
式中，W表示华白数，MJ/m3；HHVfuel表示燃料体积高位热值，MJ/m3；ρfuel和ρair分别表示燃料和空气密度，kg/m3。

燃烧势的计算公式为

式中，k表示燃料中氧气含量的修正系数；XH2,XCmHn,XCO,XCH4,XO2分别表示燃料中氢气、碳氢化合物（除甲烷）、一氧化碳、甲烷和氧气的体积分数，%。

在掺氢天然气中，燃料的体积高位热值、体积低位热值、华白数和燃烧势随着氢气体积分数的变化情况如图1(a)和(b)所示。从图中可以发现，随着氢气体积分数的增加，掺氢天然气的体积热值线性下降，华白数先下降后上升，燃烧势则一直增加。以甲烷作为基准燃料，一般要求掺氢后燃气华白数的变化范围是45.76 ～ 54.78 MJ/m3，燃烧势的变化范围是36.3 ～ 69.3[23-24]。在此范围内，华白数降低至45.76 MJ/m3对应的氢气体积分数约为0.4，燃烧势升高至69.3对应的氢气体积分数约为0.2。考虑到对燃气锅炉来说，华白数是更重要的评价指标，且根据已有文献中的结论，若将燃气锅炉运行条件下的掺氢比限制到0.2，可能会错失一些有意义的结果。因此综合考虑后，本文所研究的掺氢天然气的氢气体积分数在0 ～ 0.4范围内。

图1 掺氢天然气Fig. 1 Hydrogen-enriched natural gas ( HENG )

此外，考虑掺氢天然气在不同终端用户上的回火特性，层流火焰传播速度SL是需要重点关注的燃料燃烧特性。本文通过Premix代码[25]耦合Chemkin Ⅱ程序包[26]和TRANSPORT程序包[27]，选取FFCM-1化学反应动力学机理[28]计算掺氢天然气的层流火焰传播速度，同时与文献[9-11]中的实验数据进行了对比。计算得到的掺氢天然气在氢气体积分数XH2为0～0.4下的层流火焰传播速度SL随着当量比Φ的变化情况如图2所示。从图中可以看出，在氢气体积分数为0和0.4时，与文献[10]的实验结果吻合较好；在氢气体积分数为0.2时，与文献[11]的实验结果吻合较好。整体上，模拟的结果能够反映掺氢天然气火焰传播速度随当量比和掺氢比的变化规律，后面的章节将基于数值模拟的结果进行讨论。

图2 掺氢天然气层流火焰传播速度随当量比的变化Fig. 2 Variation of laminar flame speed of hydrogen-enriched natural gas as a function of equivalence ratio

2 掺氢天然气燃烧设备运行参数变化规律

正如引言中所述，由于甲烷和氢气物理化学性质差异显著，掺氢天然气燃烧设备的燃料和空气入口条件（流量、当量比等）将随掺氢比发生变化，而这种入口条件的变化与燃烧性质相互耦合，进而显著地影响回火规律。因此，在探讨回火特性之前，首先要根据预混燃烧的燃气锅炉和灶具的工作条件，理清因掺氢比变化而引发的入口条件的变化规律。

2.1 燃气锅炉

通常情况下，燃气锅炉处于贫燃状态，即Φ<1。常见的预混燃烧的燃气锅炉进风方式为强制送风式，即通过风机向锅炉送入助燃空气。空气流量通过调节风机频率或阀门开度来控制。

在运行过程中，燃气管道供给的压力通常维持不变，燃料流量通过调节燃气阀门开度（即调节压差）来控制。在燃气锅炉的使用过程中，常常存在两种操作场景，其操作参数的变化规律计算方法如下。

场景#1

当掺氢天然气中XH2变化时，锅炉操作不做任何调整，燃料管道阀门开度、风机频率或阀门开度均保持不变，即供气压差保持不变。在这种场景下，空气流量Vair保持不变。但是，掺氢比变化导致燃料密度发生变化，其计算为

式中，ρCH4和ρH2分别表示CH4和H2的密度，kg/m3，其具体数值见表1。

则掺氢天然气的流量计算公式为

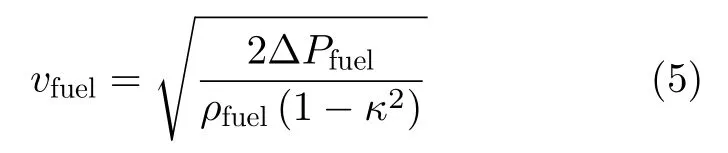
式中，vfuel表示燃料流速，m/s；ΔPfuel表示燃料管道压差，Pa；κ表示阀门最小流动截面和管道主截面的面积比。通常情况下，κ的值较小（<0.2），因此可认为，当获得vfuel，由于掺前后管道截面无变化，可认为燃料流量Vfuel∝vfuel。

预混气体的当量比和总流量可分别根据式（6）和式（7）计算得到。

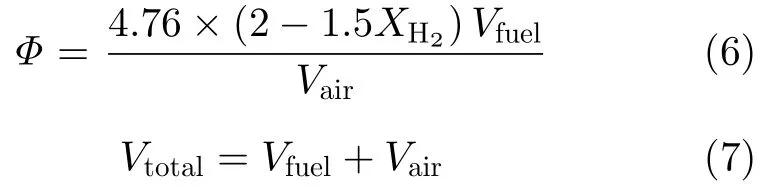
本文将以CH4为燃料的工况运行参数作为基准，把锅炉进口燃料体积流量、空气体积流量、预混气体总流量和当量比随着氢气体积分数XH2的变化进行归一化处理，按照式（8）计算。其结果如图3(a)所示。

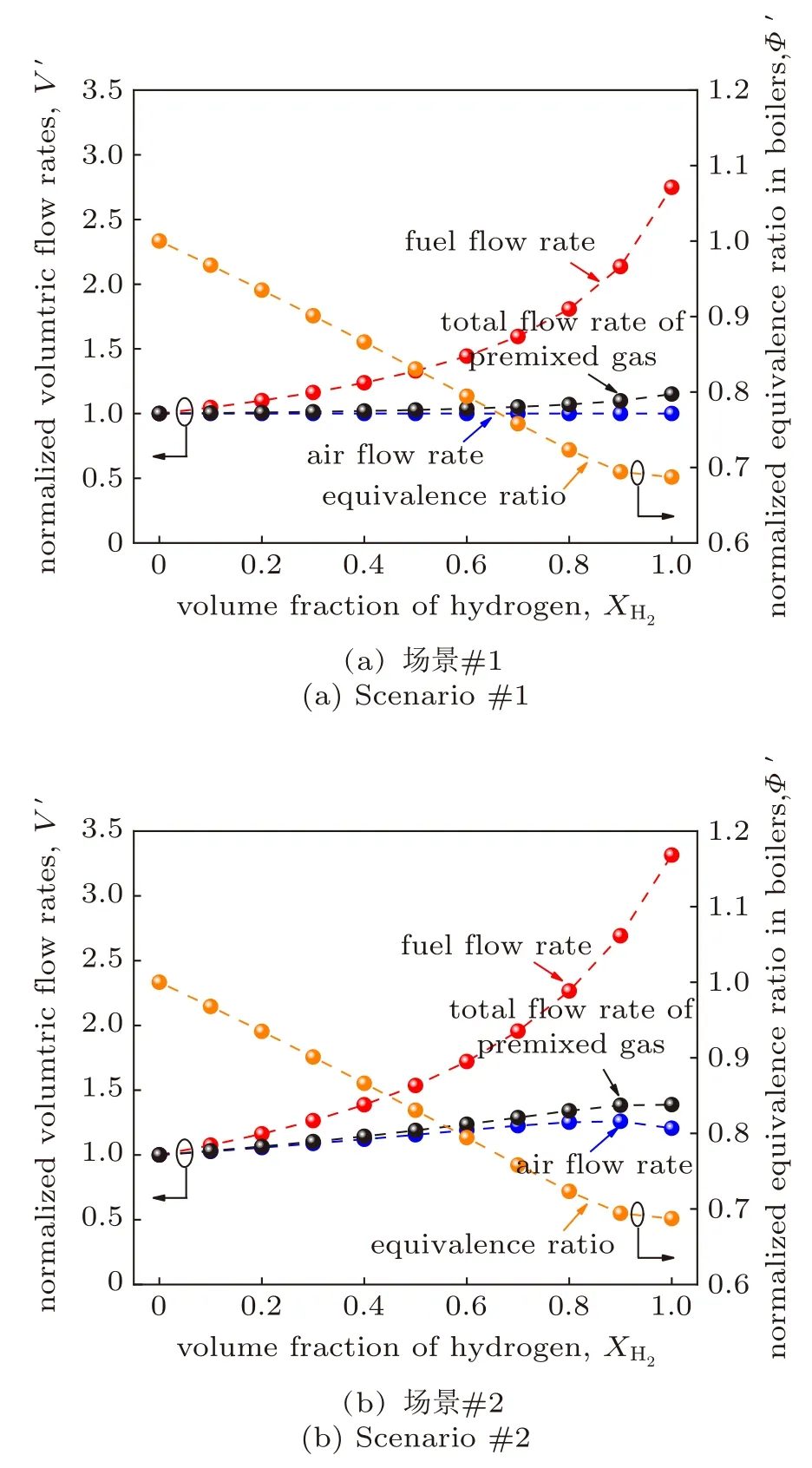
图3 氢气体积分数对锅炉操作参数的影响Fig. 3 Variation of operating parameters in boilers as a function of hydrogen volumetric fraction

式中，Z可指代燃料流量Vfuel，空气流量Vair，总流量Vtotal和当量比Φ。Z′表示归一化之后的运行参数，ZHENG和ZCH4分别表示掺氢天然气燃烧时的运行参数和甲烷燃烧时的运行参数。

以燃气锅炉典型工况（Φ= 0.9）为例，本文重点关注掺氢天然气的氢气体积分数为0 ～0.4范围内，当燃料中氢气体积分数从0变化到0.4时，在保证管道供气压差不变时，由于燃料密度减小，进口流量增加，空气流量保持不变，预混燃料的当量比降低，进口总流量增加2.1%。在不改变燃烧器结构的情况下，锅炉入炉预混气体的流速与进口总流量成正比。也就是说，当氢气体积分数从0增加到0.4时，入炉预混气体流速增加了2.1%。

场景#2

实际锅炉运行中，由于用户常常对热负荷有相应的要求，当掺氢天然气中氢气体积分数发生变化时，需要保证锅炉燃烧热负荷不变。在这种场景下，燃料的体积热值会发生变化，其计算公式为

假定燃料完全燃烧，保证锅炉负荷不变的条件下，燃料流量也会发生变化，其计算公式为

式中，Q表示锅炉燃烧热负荷，MW。

此时燃料流量的变化是用户根据热负荷需求主动采取的调节，即主动改变了燃料阀门开度和风机频率或空气阀门开度。此时，燃料管道的供气压差会发生变化，按照燃烧器预设的控制逻辑，燃料阀门开度和风机频率或空气阀门开度应按照初始当量比设置一一对应。因此，需要首先将掺氢天然气的流量按照等阀门开度原则，等效为甲烷流量，再根据初始设定的当量比，计算得到对应的空气流量。

掺氢天然气体积流量可按照式（11）等效为甲烷体积流量。

在管道截面积不变的情况下，流速v和体积流量V是等价的。同时，进入锅炉的空气体积流量可根据式（12）计算。

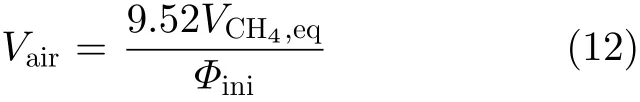
其中，Φini指原燃烧器控制逻辑中，以甲烷为燃料时的固定燃烧初始当量比。

场景#2的燃烧当量比和总流量可以把式（10）和式（12）的结果代入式（6）和式（7）中计算得到。同样地，在场景#2中，把锅炉进口燃料体积流量、空气体积流量、预混气体总流量和当量比进行归一化处理，场景#2的锅炉进口参数的变化情况如图3(b)所示。

同样地，以燃气锅炉典型工况（Φ= 0.9）为例，当燃料的氢气体积分数从0变化到0.4时，在保证锅炉负荷不变时，由于燃料体积热值减小，进口流量增加，空气进口流量随XH2的增大而增加，总流量变化趋势与空气体积流量的变化趋势相近，预混燃料的当量比降低。在不改变燃烧器结构的情况下，当氢气体积分数从0增加到0.4时，锅炉入炉预混气体流速增加了14.4%。

通过比较图3(a)和(b)可知，场景#1和场景#2下预混燃料的当量比随氢气体积分数的变化是一致的，这是因为场景#1和场景#2中进口燃料和空气体积流量的变化都与管道供气压差密切相关。在场景#1中，空气体积流量不变，燃料体积流量由于密度减小而增大，当量比降低；在场景#2中，燃料体积流量由于体积热值减小而增大，但在确定其对应的空气体积流量时，需将其视为在该工况下保证燃料管道供气压差不变，将掺氢天然气替代为甲烷时所需的空气体积流量。这种控制逻辑与场景#1类似，因此两种场景下当量比的变化趋势相同。而两种场景的不同点在于，场景#2中燃料和空气的体积流量相较于场景#1中增长幅度更大，这样才能维持锅炉燃烧热负荷不变。

2.2 燃气灶具

家用燃气灶具一般为大气式燃烧器，其结构如图4所示。首先，燃料通过高速射流引射环境空气，并在预混管中混合，形成预混气体。这部分被燃料引射的空气被称为一次空气，燃料与一次空气混合后形成的预混气体一般为富燃状态，即Φ> 1。富燃的混合物在灶头燃烧形成预混的一次火焰。一次火焰后未燃尽的燃料与周围环境中的空气形成扩散燃烧的火焰。参与扩散燃烧的空气被称为二次空气。

图4 燃气灶具燃烧器结构示意图Fig. 4 Structure diagram of gas stove burner

在常见的家用燃气灶具中，一般情况下燃料管道的供气压差保持不变。当燃料由天然气变成掺氢天然气时，由于密度的变化，燃料的体积流量发生变化，由燃料射流所引射的一次空气量也将随之变化，使得预混气体的当量比发生改变。这种场景在本文中被记为场景#3，其基本的计算过程描述如下。

场景#3

燃气流量变化的计算方法与上述锅炉场景#1类似，式（2）～式（5）可迁移应用。但灶具中引射的一次空气流量需根据式（13）[29]计算得到。

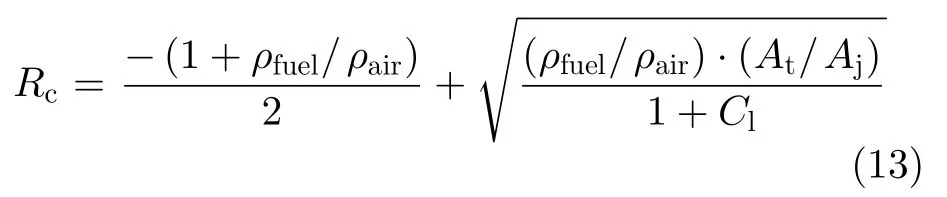
式中，Rc表示引射一次空气量与燃料量的体积比；Cl表示损失系数，本文中取0.2；At和Aj分别表示预混管的截面积和燃料射流出口的截面积，m2。

与锅炉类似，此处也将以甲烷为燃料时的运行参数作为基准，将掺氢后灶具的进口燃料体积流量、空气体积流量、预混气体总流量和当量比进行归一化处理，这些归一化参数随着氢气体积分数的变化情况如图5所示。

图5 场景#3中氢气体积分数对灶具操作参数的影响Fig. 5 Variation of operating parameters in domestic appliances as a function of hydrogen volumetric fraction in Scenario #3

以燃气灶具典型工况（预混气体当量比Φ=1.33）为例，当XH2从0变化到0.4时，管道供气压差不变，燃料进口体积流量由于密度减小而增加，其引射的空气体积流量几乎保持不变。此外，由于氢气在化学计量比下燃烧所需的空气量小于甲烷燃烧所需的空气量，所以预混燃料的当量比下降。马向阳等[24]通过实验手段研究了天然气掺氢比在0 ～ 0.2范围内对家用燃气灶燃烧特性的影响，研究结果表明在额定管道供气压差下，随着掺氢比的增加，燃烧器的一次空气系数逐渐增大，与本文结果一致。在不改变燃烧器结构的情况下，灶具未燃侧气体的流速与进口总流量成正比，当XH2从0增加到0.4时，未燃侧气体的出口流速增加了2.2%。

3 掺氢天然气燃烧设备回火风险的表征方法及验证

3.1 预混燃烧燃气锅炉和灶具回火风险的表征方法

实际生产中，需要快速评估燃料成分变化时设备回火风险。结合本文第1、2节的结果，本节将给出掺氢天然气燃烧设备回火风险的表征方法。

对于燃气锅炉和燃气灶具来说，燃料中XH2从0增加到0.4时，预混燃料的当量比都逐渐降低，但是贫燃状态和富燃状态下对层流火焰传播速度的影响却有很大差别。考虑到实际应用中的工况选择，燃气锅炉选取初始当量比Φini分别为0.9，0.8，0.7三个不同工况，燃气灶具选取初始当量比Φini分别为1.33，1.43，1.54三个不同工况。燃料的层流火焰传播速度随着掺氢比的变化如图6(a)，(b)和(c)所示。需要注意的是，图6中同时考虑了掺氢比变化时燃烧当量比也随之变化的情形，即使用图3和图5中掺氢比和当量比的对应规律。

对于燃气锅炉典型工况，根据前文研究可知，在保证管道供气压差不变（场景#1）和锅炉燃烧热负荷不变（场景#2）的情况下，当量比Φ随XH2的变化一致，因此在图6中，场景#1和场景#2统称为锅炉场景，不做区分。在初始当量比为0.9时（图6(a)），当使用纯CH4时，预混气体的SL值如图中点A所示；当XH2增加到0.4时，由图3可知，其对应当量比Φ降低至纯CH4时的0.87倍，对应的SL变化到图中点B处。由此可知，对该工况而言，当XH2从0增加到0.4时，对应的SL增加5.8%；而在Φini分别为0.8和0.7时，用类似的方法，得出SL反而出现了随XH2的增加而下降的趋势（分别下降了4.6%和14.6%）。由此可以看出，对于锅炉而言，掺氢后预混气体火焰传播速度SL变化规律较为复杂，需要针对具体情况进行分析。

对于燃气灶具来说，与锅炉场景类似，也同时考虑了掺氢比变化时燃烧当量比也随之变化的情形。在初始当量比分别为1.33，1.43和1.54时，XH2从0增加到0.4，SL分别增加124.8%，211.1%和272.1%，如图6所示。相比之下，未燃侧气体的出口流速增长幅度较小（图5）。因此可以预期，灶具在燃料掺氢后，由于掺氢比变化和当量比变化的共同作用，在高掺氢比下的回火风险显著增加。

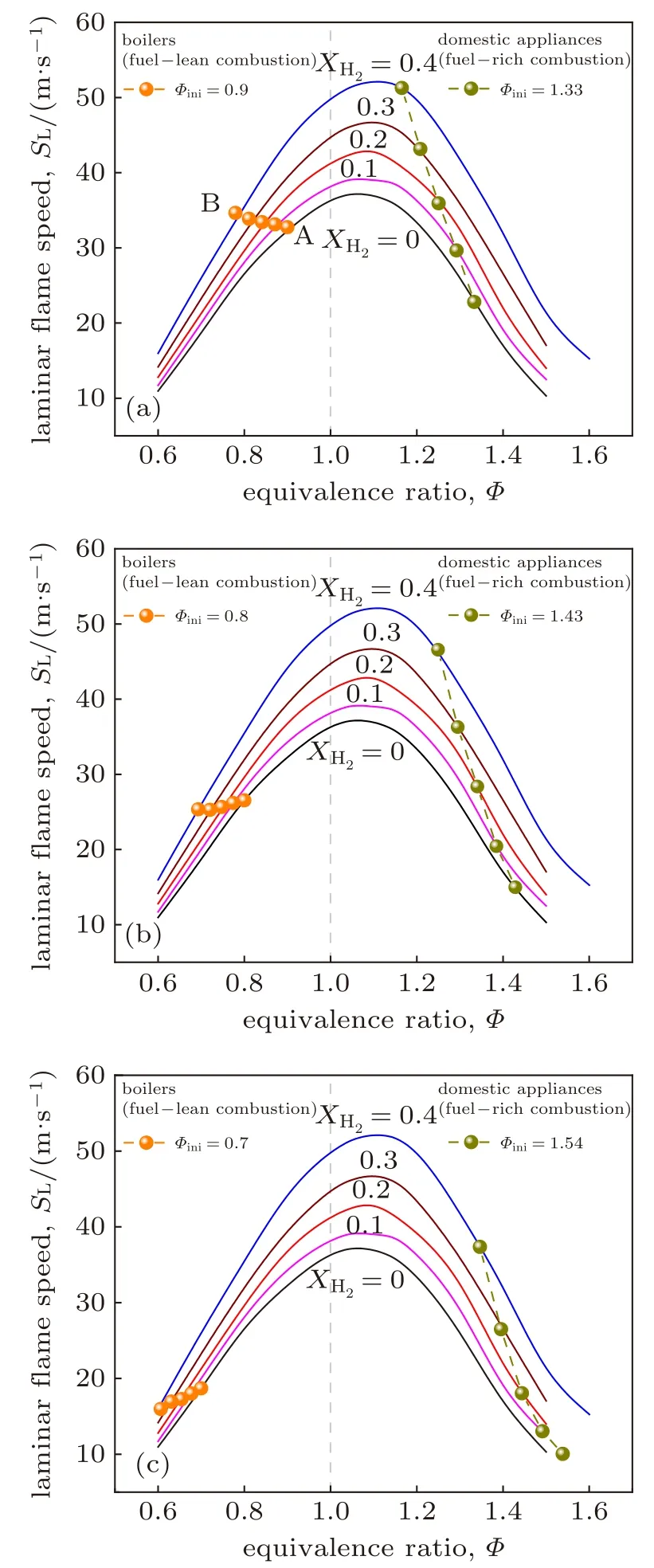
图6 不同典型工况下氢气体积分数对锅炉（ Φ ini = 0.9、0.8、0.7）和灶具（ Φ ini = 1.33、1.43、1.54）层流火焰传播速度的影响Fig. 6 Variation of laminar flame speed as a function of hydrogen volumetric fraction under different typical cases in boilers ( Φ ini = 0.9/0.8/0.7) and domestic appliances ( Φ ini =1.33/1.43/1.54)

设备的回火与燃烧器出口气流速度和当地火焰传播速度两个因素密切相关，已有文献[22,30]通过定义K=vtotal/SL作为设备燃烧稳定性的判据。设备出口预混气体气流速度小于火焰传播速度时，发生回火；而当气流速度过大，火焰无法稳定在喷嘴出口时，可能发生吹熄。但设备中燃烧器的结构和形式对K的具体数值影响较大，对于不同设备来说，其发生回火和吹熄对应的K值可能存在较大差别[22,30]。为了对比不同设备发生回火和吹熄的趋势，本文采用预混气体未燃侧流速vtotal和层流火焰传播速度SL两个参数做归一化处理，定义参数β来表征设备发生回火和吹熄的风险，即

式中，vt0otal表示燃料中XH2= 0时（即甲烷）的未燃侧流速，m/s；SL0表示燃料中XH2= 0时的层流火焰传播速度，cm/s。

使用β值可以判断燃料变化后发生回火和吹熄的风险。β = 1时，即为使用天然气时的设计工况；β < 1代表了燃烧器喷嘴出口气流速度的增大的幅度小于火焰传播速度增大的幅度，这表明发生回火的风险增加，β值越小，发生回火的可能性越高；反之，β > 1代表了燃烧器喷嘴出口气流速度的增大的幅度大于火焰传播速度增大的幅度，这表明发生吹熄的风险增加，β值越大，发生吹熄的可能性越大。

需要注意的是，实际燃烧设备中，燃烧器喷嘴出口速度并非均匀分布，燃烧也并非总是处在层流状态，因此vtotal和SL并非与实际燃烧过程中出口气流速度和当地火焰速度相等。但是，对于同一个设备而言，其燃烧器喷嘴出口的流动具有一定相似性，而vtotal和SL仅与燃料特性相关，因此β值的变化可以在工程上“半定量”地刻画因燃料变化而引发的回火和吹熄发生的趋势。

针对上述燃气锅炉和燃气灶具的典型工况，当掺氢天然气中XH2从0增加到0.4时，β的变化如图7所示。

图7 不同燃烧设备中未燃侧流速与层流火焰传播速度归一化参数之比β随氢气体积分数的变化Fig. 7 Variation of ratio between normalized flow rate and flame speed β as a function of hydrogen volumetric fraction in different combustion devices

对于燃气锅炉来说，在保证管道供气压差不变（场景#1）时，β在0.95 ～ 1.2范围内变化；在保证锅炉负荷不变（场景#2）时，β在1 ～ 1.4范围内变化，这表明对于一般锅炉工况而言，燃料掺氢比在0 ～ 0.4以内时，发生回火的风险较低，但要注意的是，对于场景#2，小当量比（Φ=0.7）时存在一定的吹熄风险（β值高达1.4）。

而对于燃气灶具来说，在燃气管道供气压差不变（场景#3）时，β的变化范围是0.2～1，并且呈现单调下降的趋势。这说明燃气灶具的燃料掺氢后未燃侧气体流速增幅小于火焰传播速度增幅。随着XH2的增加，灶具发生回火的可能性增加，在高掺氢比工况下存在极大回火风险。

3.2 预混燃烧燃气锅炉和灶具回火风险的表征方法验证

基于本文提出的使用β值表征回火风险的方法，本节将文献中已有的掺氢天然气回火实验数据进行了验证。

针对燃气锅炉运行工况，图8展示了其回火风险表征方法的实验验证。García-Armingol等[13]通过单管射流实验台研究了掺氢天然气在贫燃预混状态下氢气体积分数在0～0.5范围内的回火特性，通过实验发现，该范围内无明显回火现象，此时β > 0.6。de Vries等[21]通过本生灯实验获得掺氢天然气在贫燃预混状态下氢气体积分数在0～0.3范围内的回火特性，实验表明在该掺氢比范围内无明显回火现象，此时β > 0.8。Colorado等[22]通过陶瓷纤维表面燃烧实验台得到掺氢天然气在恒定燃烧热功率下受氢气体积分数和当量比影响的回火特性，与本文中锅炉场景#2对应。从图8中可以看出，β值随掺氢比增加先增大后减小。随着β值的增加，火焰有逐渐抬升的趋势，吹熄风险增加；而β值减小，火焰逐渐贴附于陶瓷纤维表面燃烧，回火风险增加。实验表明，在纯氢工况下当量比为0.57时发生回火现象，此时对应的β值为0.58。而在本文重点关注的氢气体积分数为0～0.4范围内，根据实验验证的β值可判断燃气锅炉无明显回火风险。

图8 燃气锅炉回火风险表征方法实验验证Fig. 8 Experimental verification of the flashback risk for gas-fired boilers

针对燃气灶具运行工况，图9展示了其回火风险表征方法的实验验证。Zhao等[15]通过在灶头燃烧器上进行掺氢天然气的回火实验，在掺氢比为0.2时发生回火，此时对应的β值约为0.57。此外，根据Jones等[18]在灶具上的回火实验也可验证，在掺氢比大于0.3时发生回火，此时对应的β值约为0.54。以上实验均与本文灶具场景#3对应。在本文重点关注的氢气体积分数为0～0.4范围内，根据实验验证的β值可判断，若β <0.6时，燃气灶具的回火风险将显著增加。

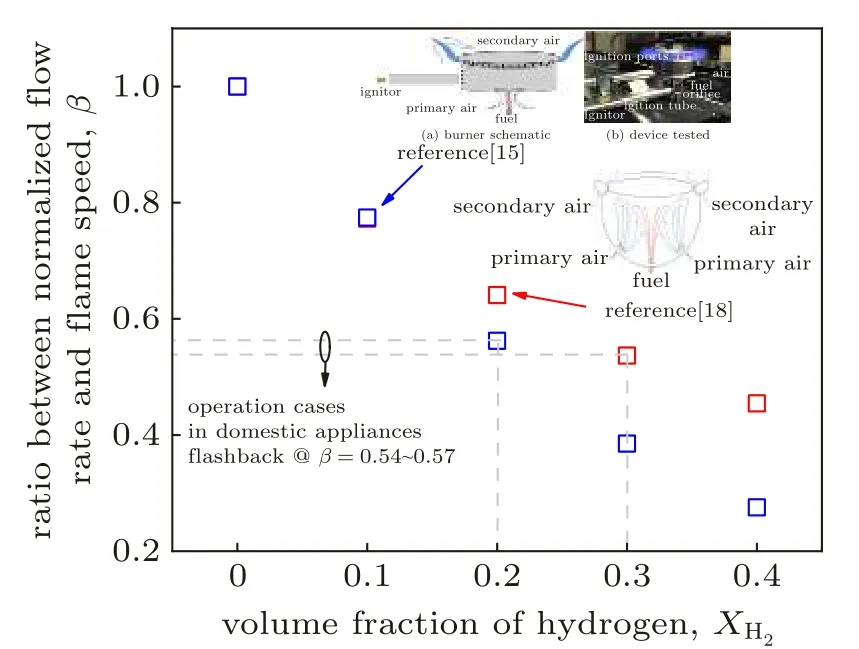
图9 燃气灶具回火风险表征方法实验验证Fig. 9 Experimental verification of the flashback risk for gas-fired domestic appliances

通过对燃气锅炉和燃气灶具回火风险表征方法的实验验证可以发现，通过对β值的分析，可以解释不同燃烧设备发生回火的掺氢比各不相同的原因。但需要注意的是，对于不同的燃烧设备，由于各自的设计运行工况和结构参数各不相同，发生回火时对应的β值也在一定范围内变化。

此外，引言中提到，Zhao等[14]发现在已经稳定燃烧的灶具中逐渐增加氢气，不发生回火的最大掺氢比可达0.5以上，但是如果在点火前燃料中已经掺混氢气，则在点火的“瞬态”过程中不发生回火的最大掺氢比降为0.25。此时也可以从β值的角度来分析这种“稳态”和“瞬态”回火掺氢比差异的原因。

灶具点火过程描述如下：初始时灶具燃烧器预混管内充满空气，如图10左上方小图所示；燃料从射流入口进入后，一方面引射空气，另一方面将预混管内的空气通过灶头排出燃烧器；同时，安装在灶头的火花塞尝试点火。在这段极短时间内，灶头出口处的预混气体当量比逐渐增加，从0到贫燃，越过化学计量比，达到最终的富燃状态。

图10 燃气灶具在点火状态和稳定燃烧状态下氢气体积分数对层流火焰传播速度的影响Fig. 10 Variation of laminar flame speed as a function of hydrogen volumetric fraction in the ignition state and steady combustion state of domestic appliances

此处以燃气灶具典型工况（预混气体当量比Φ= 1.6）为例，其在点火状态和稳定燃烧状态下XH2对SL的影响如图10所示。以甲烷作为基准工况，首先考虑天然气在灶具中稳定燃烧时逐渐增加燃料中XH2的情形。稳定燃烧时灶头出口预混气体处于富燃状态，当燃料中XH2从0增加到0.5时，SL增加约433.6%（图中绿色箭头所示），vtotal增加3.4%，此时对应的β值约为0.2，若此掺氢比为稳定燃烧状态下不发生回火的最大掺氢比，则可认为，该灶具系统设计回火安全阈值为β = 0.2。在图10中作出等β曲线，如曲线C-D所示，此即为回火临界线，C-D曲线之上，将发生回火，反之，曲线之下不回火。

接下来讨论点火前天然气已经掺氢时，灶具点火过程是否会发生回火的情形。由于点火过程燃料成分已经确定，则点火过程中，灶头出口预混气体的SL将随Φ的增加沿着图10中等XH2曲线变化（图中红色箭头所示）。在等XH2曲线上，Φ= 1.0～1.2时SL达到峰值，β值也达到最小值，此时发生回火的可能性最高。将不同的等XH2曲线与回火临界线C-D做对比，若等XH2曲线完全处于曲线C-D之下，则表明点火过程所有时刻都不存在回火风险；若等XH2曲线与曲线CD存在交点（等XH2曲线部分位于曲线C-D之上），即表明该XH2值在点火过程中存在回火风险。从图10中可以看出，等XH2曲线与曲线C-D存在交点的最小XH2值约为XH2= 0.25（相交于D点），这说明点火的瞬态情形不发生回火的最大XH2为0.25。

通过上述分析讨论可知，使用β = 0.2的阈值，对于灶具的“稳态”情形（天然气稳定燃烧后逐渐增加掺氢比）和点火“瞬态”情形（点火前天然气已经掺氢）而言，其对应的不发生回火的最大XH2分别为0.5和0.25，这与文献[14]中的实验现象基本一致。因此，使用β值的分析方法能够定性地解释燃气灶具的“瞬态”和“稳态”回火掺氢比的差异现象。

从上述实验结果可以看出，天然气掺氢后发生回火的工况都出现了β的显著下降，这与理论分析的结果保持一致，证明了利用β判断燃烧设备回火风险的合理性。综合考虑发生回火时具体β值，可以发现当β < 0.6时，燃烧设备发生回火的可能性显著增加，这对于判断天然气掺氢后燃烧设备的回火风险具有重要的指导意义。

4 结论

本文获得了预混燃烧燃气锅炉和燃气灶具的实际入口运行参数及火焰传播速度的变化规律，并定义了参数β用来表征天然气掺氢后燃烧设备回火特性。本文得到的主要结论如下。

（1）在天然气燃烧设备实际运行中，燃料掺氢比变化会影响燃料密度、热值等参数，进而影响燃烧设备中燃料、空气入口条件及燃烧当量比。当掺氢比从0增加到0.4时，对于燃气锅炉（场景#1和场景#2）来说，预混气体的燃烧当量比随掺氢比的增加而下降，进而使掺氢后火焰传播速度的变化规律较为复杂，需要根据初始未掺氢时的当量比具体讨论；对于燃气灶具（场景#3）来说，预混气体的燃烧当量比随掺氢比增加而下降，火焰传播速度随掺氢比和当量比变化均呈现上升趋势，且初始未掺氢时的当量比Φ越高，相同掺氢比下火焰传播速度相比于纯甲烷时的火焰传播速度增幅越大。

（2）β定义为预混气体未燃侧流速归一化参数与层流火焰传播速度归一化参数的比值，用来评估天然气掺氢后设备发生回火的可能性。对于燃气锅炉，当掺氢比在0～0.4范围内变化时，β的变化范围是0.95～1.4，表明锅炉无明显回火风险。对于燃气灶具，当掺氢比在0～0.4范围内变化时，β的变化范围是0.2～1，并且单调下降，在β < 0.6的工况下回火风险显著增加。

（3）对于燃气灶具在“稳态”情形（天然气稳定燃烧后逐渐增加掺氢比）和点火“瞬态”情形（点火前天然气已经掺氢）而言，掺氢比和当量比对这两种情形下火焰传播速度的影响效果不同，在等β值下对应不发生回火的最大掺氢比分别为0.5和0.25，可解释两种情形下回火掺氢比差异的现象。