织构化涂层表面的黏附接触力学行为研究

闵强强，唐雪峰，周青华

摩擦磨损与润滑

织构化涂层表面的黏附接触力学行为研究

闵强强，唐雪峰，周青华

（四川大学 空天科学与工程学院，成都 610065）

建立刚性微球与织构化涂层表面黏附接触数值分析模型，探究织构化涂层属性对微观接触副黏附力学性能的影响。基于Hamaker求和法以及Lennard–Jones势能定律，考虑织构高度对接触体间距离分布的影响以及涂层、织构材料属性对接触体间黏附力的影响，建立织构化涂层表面黏附接触力学模型并验证所提模型。基于所提模型，研究不同Tabor数下织构形貌、密度、高度以及涂层厚度对接触系统黏附力学性能的影响。在相同参数下，圆柱型织构黏附力最大，半椭球型织构次之，四棱锥型织构最小。织构密度从200 μm‒2增加到4 000 μm‒2时，最大黏附力随着织构密度的增加而增加，圆柱型织构增加约5～6倍，四棱锥型织构增加约1.5倍。随着织构高度从1bs增加至30bs，最大黏附力减小，四棱锥型织构减小最多，约为原来的1%，圆柱形织构减小最少，约为原来的90%。涂层厚度能够影响黏附力的大小，但影响规律与织构化涂层的Tabor数及织构高度相关。随着涂层厚度从1bs增加至16bs，大Tabor数时黏附力逐渐增加，小Tabor数时黏附力逐渐减小。Tabor数较大、织构高度较小时，黏附力–接近距离曲线会出现2次峰值。揭示了织构形貌、密度、高度及涂层厚度对接触系统黏附力学性能的影响，总结了黏附力与最大黏附力的变化规律，所得规律可为工程实践中的黏附微纳米结构设计与应用提供理论指导。

织构化涂层；接触力学；范德华力；黏附接触

干黏附现象起源于分子间的范德华力，该作用力不可消除。当接触副的尺寸减小到微纳米尺度，范德华力会变得十分显著，成为引起微纳米机电设备表面黏附磨损与失效的重要因素。与此相对，研究人员尝试揭示干黏附机理并加以利用，设计出具有多尺度微纳米结构的黏附表面，以实现黏结、爬壁等功能。例如，仿壁虎脚掌的干黏附微结构由于具有适应真空与高低温、无需化学介质与电磁场、能够产生高黏附力等诸多优秀特性，成为实现空间未知目标附着与空间巡游的重要途径[1]。表面涂层与织构技术已被证实是调控表面黏附特性的可行手段[2-7]，但采用单一涂层或织构技术对黏附性能的调控能力十分有限，且不能满足对接触界面的综合力学性能需求。因此，综合涂层以及织构2种表面处理工艺，即通过涂层保证界面的强度、抗磨损等力学性能需求，结合织构技术改善界面的黏附特性[8-9]，是有效调控接触系统黏附力学性能的潜在手段之一。

现有针对织构化界面的黏附接触问题研究主要从试验与理论2个方面展开。试验方面，Bhushan等[10]制造出具有微米柱与纳米粒子的两级织构表面，发现分级织构表面能够显著减小黏附力，且只有光滑表面下作用力的27.2%。gorb等[11]制备出PVS仿生蘑菇型织构，发现织构化表面的黏附效果是光滑表面的2倍以上，抗污染性能也更强。Kim等[12]制备出3种不同高度的壁状织构，研究了不同初始切向位移下撕脱角对撕脱力的影响。结果显示，当撕脱位置在撕脱总距离的一半处、撕脱角度为60°～90°时，黏附力最大。Kizilkan等[13]在硅橡胶表面加工出蘑菇状织构，研究发现尽管接触面积减少50%，但黏附力增加了91%。通过高速相机观测接触过程发现，蘑菇状织构在撕脱过程中相比其他类型织构能够保持更大的接触面积，因此黏附性能更佳。上述研究表明，合适的织构形貌设计能够有效地调控界面黏附力。

理论研究方面，Zhang等[14]基于Hamaker求和法[15]以及Lennard–Jones势能定律建立起均质材料单级织构黏附接触模型，探讨了织构形貌及织构密度等对接触系统黏附力学性能的影响。Yang等[16]基于Lifshitz–Hamaker方法及Lennard–Jones势能定律建立起分级织构及绝缘液体介质的黏附接触模型，发现分级织构表现出良好的抗黏附性能，纳米织构效果超过微米级织构。此外，部分学者也研究了表面粗糙度对界面黏附力的影响，如Violano等[17]在Johnson– Kendall–Roberts（JKR）理论[18]的基础上建立了自仿射分形粗糙面黏附接触模型，并通过实验验证了所提模型在多尺度复杂分形几何表面的可适用性。Acito等[19]基于JKR理论研究了光滑玻璃镜面与粗糙橡胶表面的黏附接触问题，发现即使是微小的黏附力也会显著改变接触面积。Li等[4]以及Popov等[20]利用Griffifith能量法建立起各类形状压头与涂层[4]或均质表面[20]的黏附接触模型，发现黏附强度与压头接触面的表面积成正比，而与压头形状无关。关于织构与粗糙表面的黏附接触问题研究还有文献[21-24]等，但仅考虑粗糙度或织构的影响，文献[25]研究了织构与涂层的影响，但未针对2种技术的结合开展研究，无法实现界面高强度、高抗磨等与高黏附性能的统一。为设计出综合力学性能良好的黏附界面，本文提出一种在基体材料上加工涂层，并在涂层表面进行黏附微织构设计的方案。

基于文献[25]的研究，本文综合利用Hamaker求和法以及Lennard–Jones势能定律，建立起刚性微球与织构化涂层表面的黏附接触模型。该模型通过将织构高度引入接触体间的间距分布，从而考虑了织构高度对黏附力的影响，并通过对织构化涂层以及基体的黏附力贡献进行分段积分以求得接触体间总的黏附力。进一步，基于所建立模型研究不同织构形貌、密度、高度以及涂层厚度对织构化涂层表面黏附力学行为的影响，获得织构以及涂层参数对黏附力的影响规律，研究结果可为织构化涂层界面的结构设计与材料选择提供一定的理论参考。

1 织构化涂层表面黏附接触模型及验证

为方便建模分析，选定接触对象为刚性微球与弹性织构化涂层基体系统。图1a为弹性织构化涂层基体系统与刚性微球黏附接触模型三维示意图，将坐标原点设定于未变形涂层表面建立三维坐标系。假设涂层与基体完美固结，织构位于涂层表面上，刚性微球半径为，涂层厚度为c，织构高度分布为t，织构最大高度为t。如图1a所示，点为球面上一点，点c是变形织构化涂层表面上一点，点与c分别为点与c在平面上的投影；角度为与c′的夹角，是c与轴的夹角，为c与轴的夹角。图1b为织构化涂层基体系统在黏附力下的变形示意图（平面），假设整个接触过程中涂层、基体以及织构仅发生弹性变形。织构的引入改变了接触体间的间距分布，进一步影响黏附力的分布与作用规律。

构建任意一个具有无限小角度d的圆锥体，如图1b所示。该圆锥体从刚性微球内部任意一点出发，穿过微球表面点、变形织构化涂层表面点c以及变形基体表面点s，直到无穷远处点结束。该圆锥体的体积dcone可以表示为：

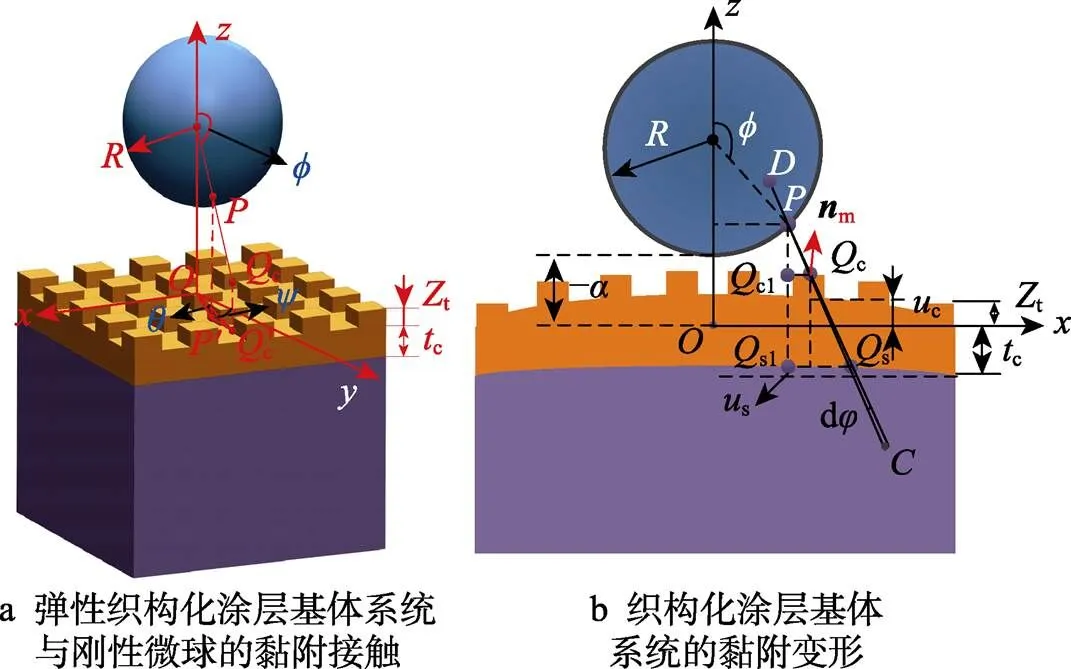
图1 织构化涂层–基体系统与刚性微球的黏附接触模型

a) adhesive contact of elastomeric textured coating substrate system with rigid microspheres; b) adhesion deformation of textured coating-substrate systems

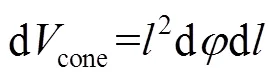
式中：为沿着圆锥体轴线的长度，即点与点之间的距离。由图1b可知，织构化涂层–基体系统中，存在物质分子的圆锥体体积由织构化涂层内体积dc与基体内体积ds两部分组成，即：

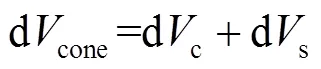
由Hamaker求和法可知，任意两物体之间的相互作用可以通过对两物体内部所有分子之间的相互作用进行体积积分得到[15]。因此，位于点的体积单元db作用在织构化涂层–基体系统内部圆锥体dcone上的黏附力矢量c为：

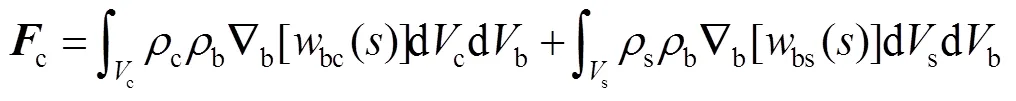
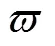
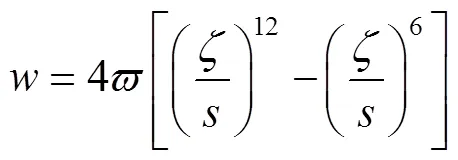
式（1）中，角度d可以通过圆锥体轴线上单位向量与织构化涂层表面的单位外法向向量m建立起与织构化涂层表面单元dm的关系，即：

点、c皆为任意点，故刚球上点的位置向量为b，涂层上点c的位置向量为m，则单位向量有：

式中：c为点与点c间的距离。同理可得点与点s间的距离s。将式（1）、式（5）、式（6）代入式（3）可得：

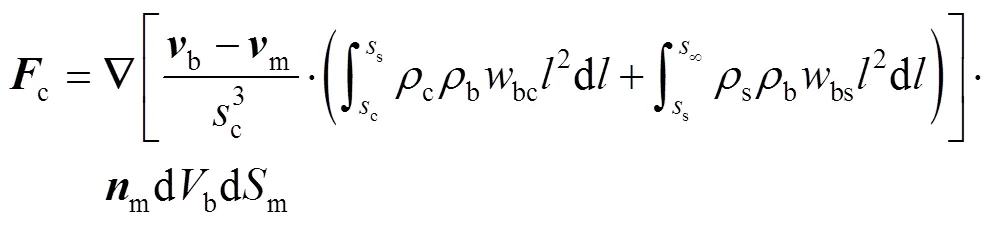
当所构建圆锥体从织构侧面射入时，依次穿过涂层与基体，此处穿入点纵坐标按照织构最大高度计算。考虑到织构高度处于微纳米尺度，该处理方式仅会对c与s的数值产生细微影响，通过加密计算网格，可以减小该误差的影响。由式（7）可知，作用力矢量c主要与距离c与s相关。参考文献[25]对散度定理的运用，距离c与s可以转变为球面上点到织构化涂层表面点c与基体表面点s间的距离，具体求解过程如下。

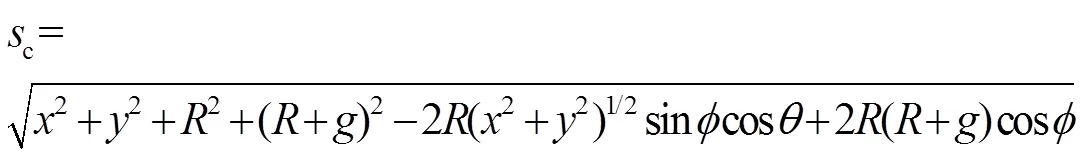
由图1b可知：

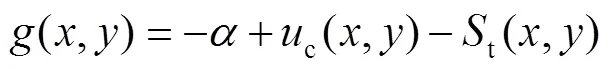
根据相似三角形法则有：

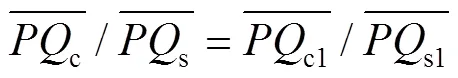
故点与点s之间的距离s可以表示为：

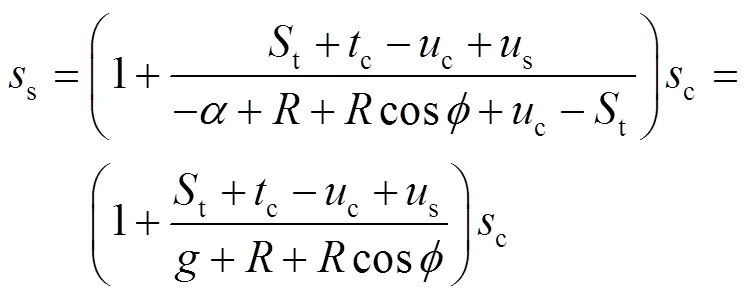
式中：s(,)为基体表面点c处的法向弹性变形。引入比例系数见式（12），则式（11）可以简成式（13）。

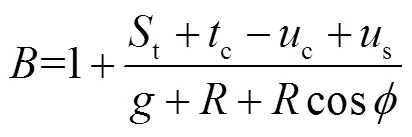
s=c(13)

本文所提模型为轴对称模型，与方向的黏附力相互抵消，仅余法向作用力。参考文献[14,25]的方法，结合式（4）与式（7）—（13），可得刚性微球作用在弹性织构化涂层表面点c处单位面积上的法向黏附力(,)，见式（14）。

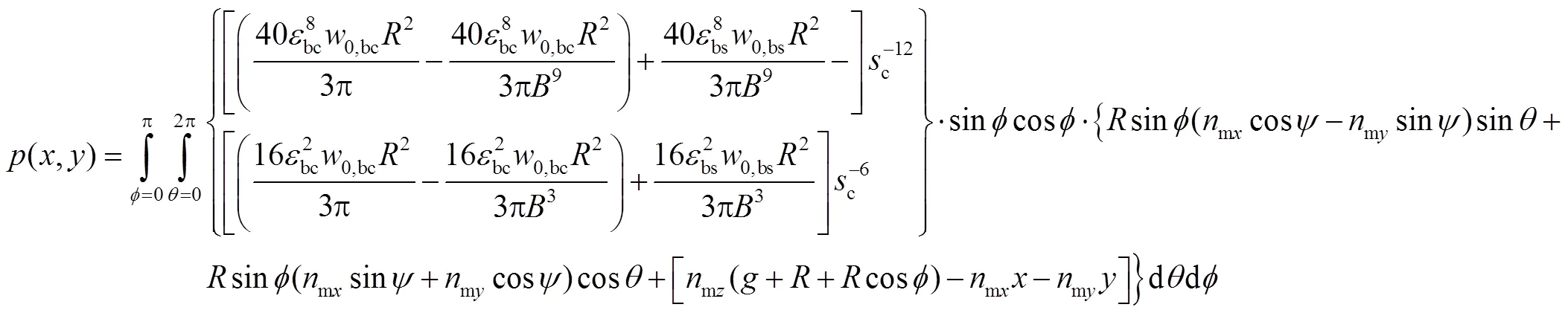
式中：mx、my、mz分别为向量m在、与方向上的分量；0,bc与0,bs分别为微球与织构化涂层以及与基体之间的Dupré黏附功；bc与bs表示不考虑变形且黏附力为零时两平行平面间的距离，满足条件：

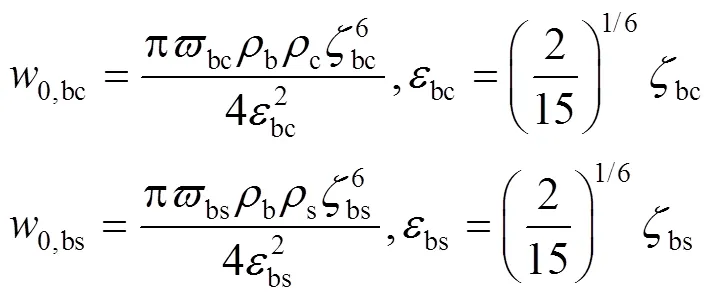
对单位面积的黏附力进行面积积分，可得刚性微球与弹性织构化涂层基体系统间总的黏附力：

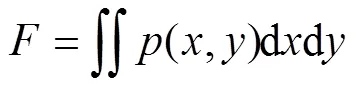
>0时黏附力表现为排斥力，<0时表现为吸引力。由于工程应用中主要利用黏附吸引力，因此后文对黏附力的讨论只描述<0时的数值，不描述符号。定义<0时所能达到的最大数值为最大黏附力pull-off。类似地，接近距离‒仅讨论数值。织构化涂层基体系统弹性变形c、s的求解方法见文献[26]。

为验证所提黏附接触模型的有效性，选取半球型织构为研究对象，设置织构半径t=50bs，织构高度t=50bs，织构密度tex=4 356 μm‒2。将本文模型中基体与涂层材料参数设置一致，所得结果与文献[25]建立的均质织构黏附接触模型结果进行对比。如图2a所示，2种模型所得不同下微球与织构的黏附力s-t、与基体的黏附力s-s以及与织构–基体系统的总黏附力total吻合较好。将本文模型所得不同织构半径t下最大黏附力pull-off，与文献[23]的分子动力学计算结果进行对比，如图2b所示。可见二者变化趋势一致，但数值上存在差异，这主要是因为本文模型采用Lennard–Jones势来描述分子间的相互黏附作用，忽略了其他分子对2个相互作用分子的影响。上述结果表明，本文所提模型可以用于计算织构化涂层基体系统与刚性微球间的黏附力。

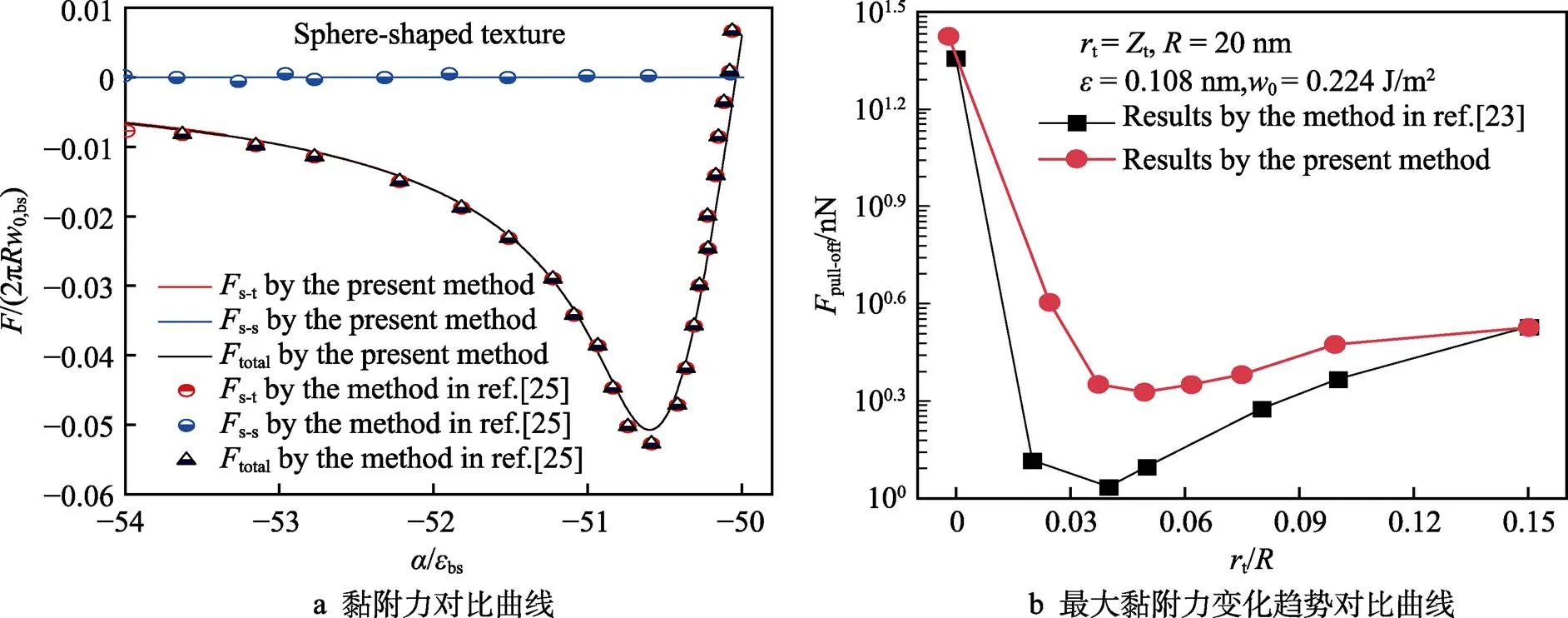
图2 织构化涂层表面黏附接触模型的验证

2 织构化涂层表面参数影响分析

参考现有均质织构化表面黏附接触相关研究[14,25,27-28]，选择半椭球型、四棱锥型以及圆柱型织构为研究对象，为方便讨论，设置四棱锥型织构的底边宽度相同。求解接触系统黏附力时，通过散度定理的运用将式（7）中接触体间的体力转换为接触体相对两表面间的面力，进而给出表面单位面积的黏附力表达式，从而显著降低计算复杂度[29]。故织构与球体间相对的表面面积，即织构在平面上的投影面积，是决定接触体间黏附力的关键。因此，后续研究对比不同织构形貌的影响时，需确保不同类型织构在平面上的投影面积相同。

织构半径t、织构底面宽度及织构高度t的定义如图3所示。假设任意单个织构中心点坐标为(t,t)，平面上任意一点坐标为(,)，则3种织构三维示意图及数学表达式如表1所示。对圆柱型以及半椭球型织构，平面上的投影面积tex=πt2，对四棱锥型织构，投影面积tex=2，刚性微球与基体间的Tabor数s[20,bs(s*23bs)]1/3，其中等效弹性模量s*=s/(1‒2s)，s为基体的弹性模量，s为基体的泊松比。

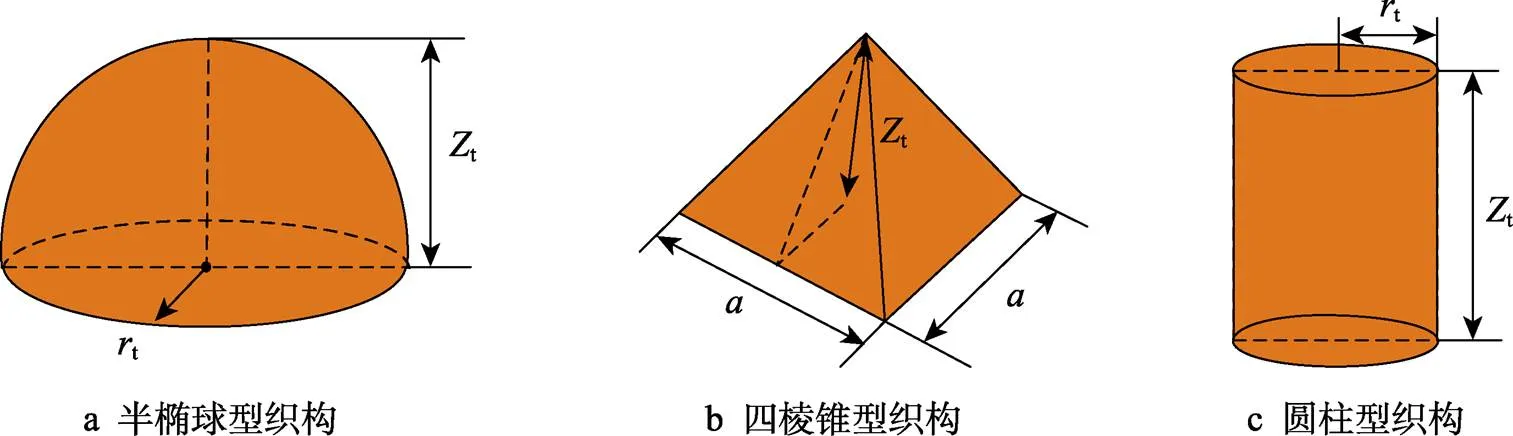
图3 织构参数示意图

表1 织构三维示意图及数学表达式

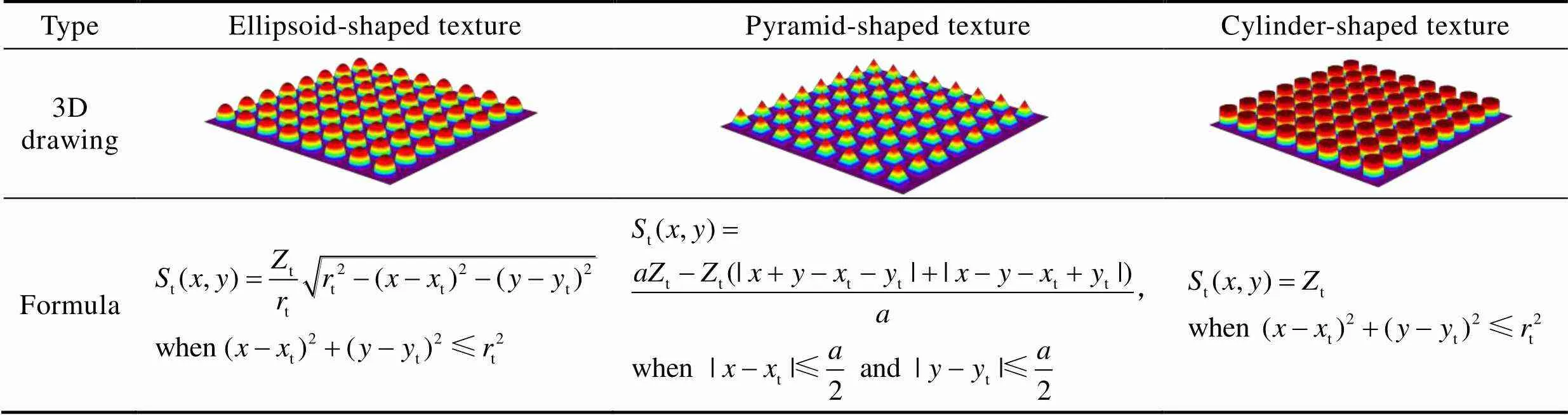
Tab.1 The three-dimension sketch and mathematical expression of textures

由已有研究可知，织构化涂层与微球间的Tabor数、织构密度、织构高度以及涂层厚度都会影响接触系统的黏附力学性能，因此本文将进行参数化讨论，研究本模型中上述因素的作用规律。除特殊说明外，设置微球半径=5 000bs，涂层厚度c=200bs，平衡距离bs=0.15 nm，弹性模量s=115 GPa，泊松比s=0.3，织构密度tex=4 356 μm‒2，基体与微球间的Tabor数s=0.518 2（0,bs=0.1 J/m2）。织构化涂层与微球间的Tabor数分2种情形进行讨论，即c=0.205 6（0,bc=0.025 J/m2）和c=0.822 5（0,bc=0.2 J/m2）。文献[25]研究表明，当Tabor数约大于0.7时，接触系统将发生突跳不稳定现象，因此本文所选2个c足够探讨大Tabor数（>0.7）与小Tabor数（<0.7）时接触系统下黏附力的变化规律。

2.1 织构密度的影响分析

选定5种不同织构密度（tex=200、500、1 000、2 000、4 000 μm‒2）探讨织构密度对黏附力的影响。设定织构高度t=50bs，织构半径t=50bs，织构底面宽度=88.6bs。图4a—c给出了2种Tabor数下3种不同织构黏附力随着接近距离的变化关系。图4d给出了织构密度由tex=200 μm‒2增加到tex=4 000 μm‒2时3种织构最大黏附力的增加比例。

由图4可知，在2种Tabor数下，最大黏附力都随着织构密度的增加而逐渐增大，织构密度由tex= 200 μm‒2增加到tex=4 000 μm‒2时，圆柱型织构最大黏附力的增长倍数最多，四棱锥型织构与半椭球型织构的增长倍数相对较小，说明圆柱型织构对织构密度的变化最敏感。如图4a—c所示，随着织构密度的增加，达到最大黏附力的接近距离也在增加，即更容易达到最大黏附力。相同Tabor数与织构密度下，圆柱型织构的黏附力最大，半椭球型织构次之，四棱锥型织构最小。织构密度tex=4 000 μm‒2时，半椭球型织构在c=0.822 5时最大黏附力无量纲化数值为0.1，几乎是c=0.205 6时数值（0.012）的8.3倍，而四棱柱型织构为8倍，圆柱型织构为7.6倍。由此可见，Tabor数越大，黏附力越大。由图4d可知，随着织构密度的增加，圆柱型织构最大黏附力的增加倍数最大，四棱锥型织构次之，半椭球型织构最小；c=0.822 5时的增加倍数小于c=0.205 6时，但是差值不大。总之，Tabor数以及织构形貌共同影响织构密度对黏附力的影响规律。

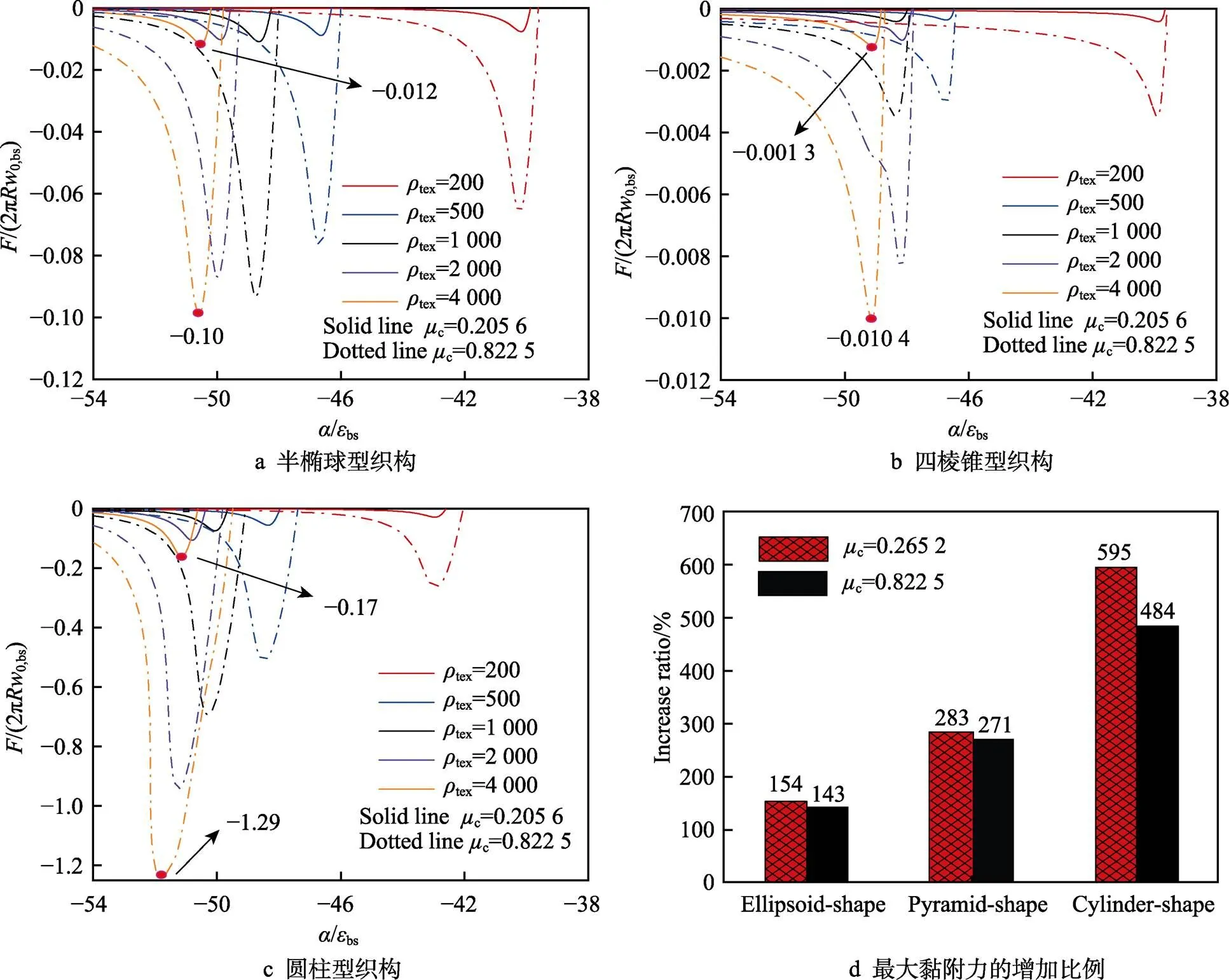
图4 织构密度对黏附力的影响

2.2 织构高度的影响分析

选用7种不同织构高度（t/bs=1、5、10、15、20、25、30）探讨织构高度对黏附力的影响规律，结果如图5所示。设定织构半径t=50bs，织构底面宽度=88.6bs。图5a给出了不同织构的最大黏附力pull-off/(2π0,bs) 随织构高度的变化关系。图5b给出了织构高度由1bs增加到30bs时最大黏附力减小的比例。

由图5可知，最大黏附力随着织构高度的增加而减小，减小比例与织构类型明显相关，而与Tabor数无明显关系。如图5a所示，2种Tabor数下，最大黏附力的数值随着织构高度的增加逐渐减小，随后不再变化，说明织构高度对黏附力的调节能力是有限的。任意织构高度下，c=0.822 5时的最大黏附力大于c=0.205 6时的数值，这说明Tabor数越大，最大黏附力越大。同一Tabor数同一织构高度下，圆柱型织构的最大黏附力最大，四棱锥型织构最小。如图5b所示，2种Tabor数下，四棱锥型织构随着织构高度的增加，最大黏附力的下降比例最大，几乎为原本的1%，下降2个量级；半椭球型织构次之，下降1个量级；圆柱型织构下降比例最小，最大黏附力数值几乎为原本的90%。这说明四棱锥型织构对织构高度的变化最敏感。

图6给出了3种不同织构达到最大黏附力时织构化涂层表面的压力分布bs/0,bs。压力数值大于零时表现为排斥力，数值小于零时为吸引力。由图6可知，半球型织构与四棱锥型织构在织构的顶点位置有排斥力区域集中分布，圆柱型织构靠近区域中心位置有排斥力区域分布，但3种织构的排斥力区域面积远小于吸引力区域。圆柱型织构吸引力区域最大，半椭球型织构次之，四棱锥型织构最小，这也解释了相同织构高度下圆柱型织构最大黏附力最大、四棱锥型织构最小的结论。

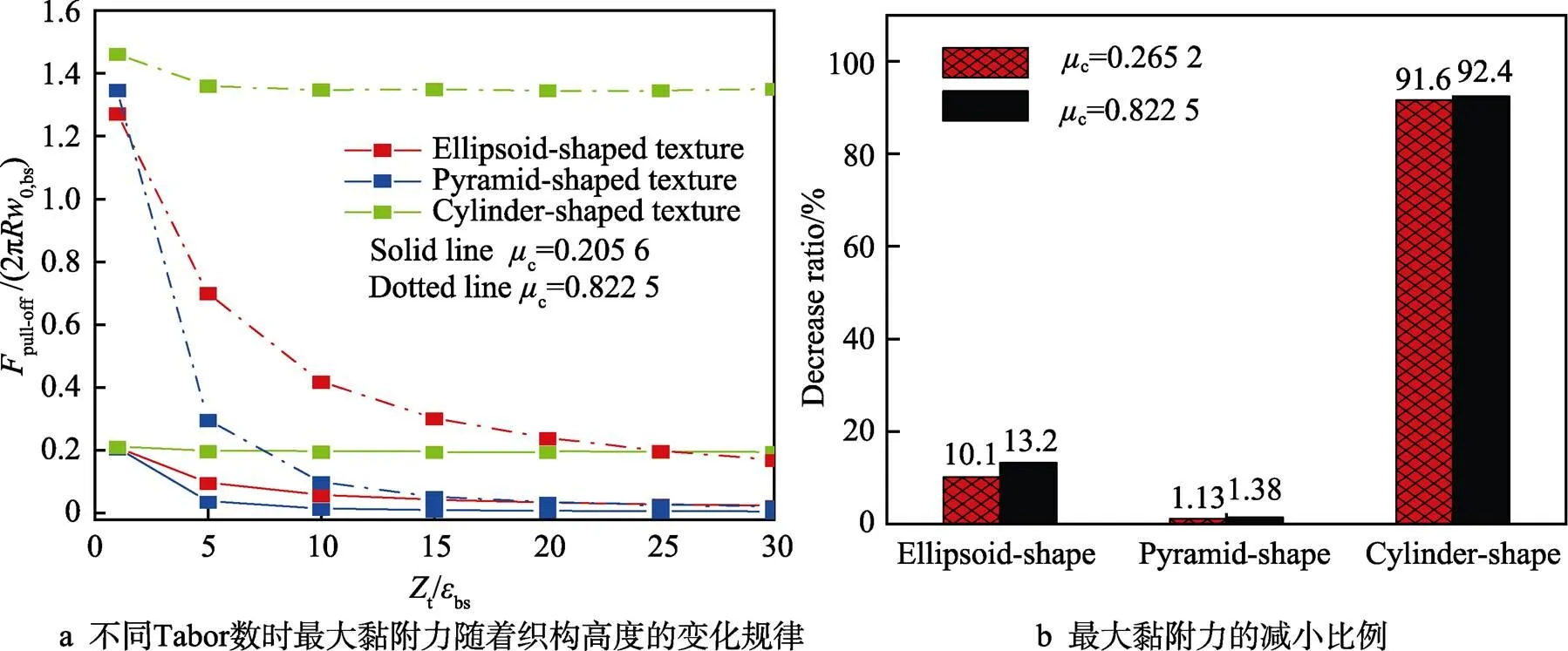
图5 织构高度对黏附力的影响

图6 μc=0.205 6、Zt=5εbs时3种织构发生黏附分离时中心区域的压力分布

Fig.6 The pressure distributions of three kinds of textures when pulling off atc=0.205 6 andt=5bs: a) ellipsoid-shaped texture; b) pyramid-shaped texture; c) cylinder-shaped texture

2.3 涂层厚度的影响分析

接触体间的黏附力主要来源于有限空间区域的分子数，涂层厚度决定了涂层对黏附力贡献的分子数。为研究涂层厚度对织构化涂层表面黏附力学性能的影响，设定织构高度t=1bs，织构半径t=50bs，织构底面宽度=88.6bs。图7a—c给出了c=0.205 6与c=0.822 5时不同涂层厚度下3种织构的黏附力随接近距离的变化规律。图7d进一步给出了不同Tabor数下最大黏附力随涂层厚度的变化规律。

由图7可知，3种织构在相同涂层厚度下，Tabor数越大，黏附力越大，出现最大黏附力数值时的接近距离更远。随着涂层厚度的增加，c=0.205 6与c=0.822 5时的最大黏附力数值的变化规律相反。图7a—c中，当c=0.822 5时，不同涂层厚度时，半椭球型织构与四棱锥型织构的黏附力–接近距离曲线均出现二次峰值，圆柱型织构却无此现象；当c= 0.205 6时，涂层厚度越大，最大黏附力的数值越小，但是出现最大黏附力时的接近距离几乎没有区别。而当c=0.822 5时，黏附力随着涂层厚度的增加而增大，出现最大黏附力数值时的接近距离也在缓慢增大。图7d中，2种不同Tabor数下最大黏附力随涂层厚度的变化规律相反，但两者都在c=8bs时几乎不再变化，可见涂层厚度调控黏附能力也是有限的。综上所述，通过改变涂层厚度来调节织构化表面黏附力学性能是有效的也是有限的。对于小Tabor数（小于球体与基体的Tabor数）织构化涂层，增大涂层厚度能有效减小最大黏附力；但对于大Tabor数黏附接触系统，最大黏附力随着涂层厚度的增加而增大。

为探讨半椭球型织构与四棱锥型织构黏附力出现二次峰值的原因，图8给出了织构高度t=20bs时不同厚度下黏附力随接近距离的变化规律。可见二次峰值现象消失，随着涂层厚度的增加，2种Tabor数下最大黏附力都在增大，出现最大黏附力数值的接近距离也在增加。相比织构高度t=1bs，t=20bs时的黏附力对涂层厚度的变化更敏感。这说明二次峰值的出现与织构高度相关，Tabor数较大，织构高度较小时，黏附力–接近距离曲线会出现二次峰值。此外，涂层调控黏附力的能力受到织构高度的影响，织构高度越大，调控作用越明显。

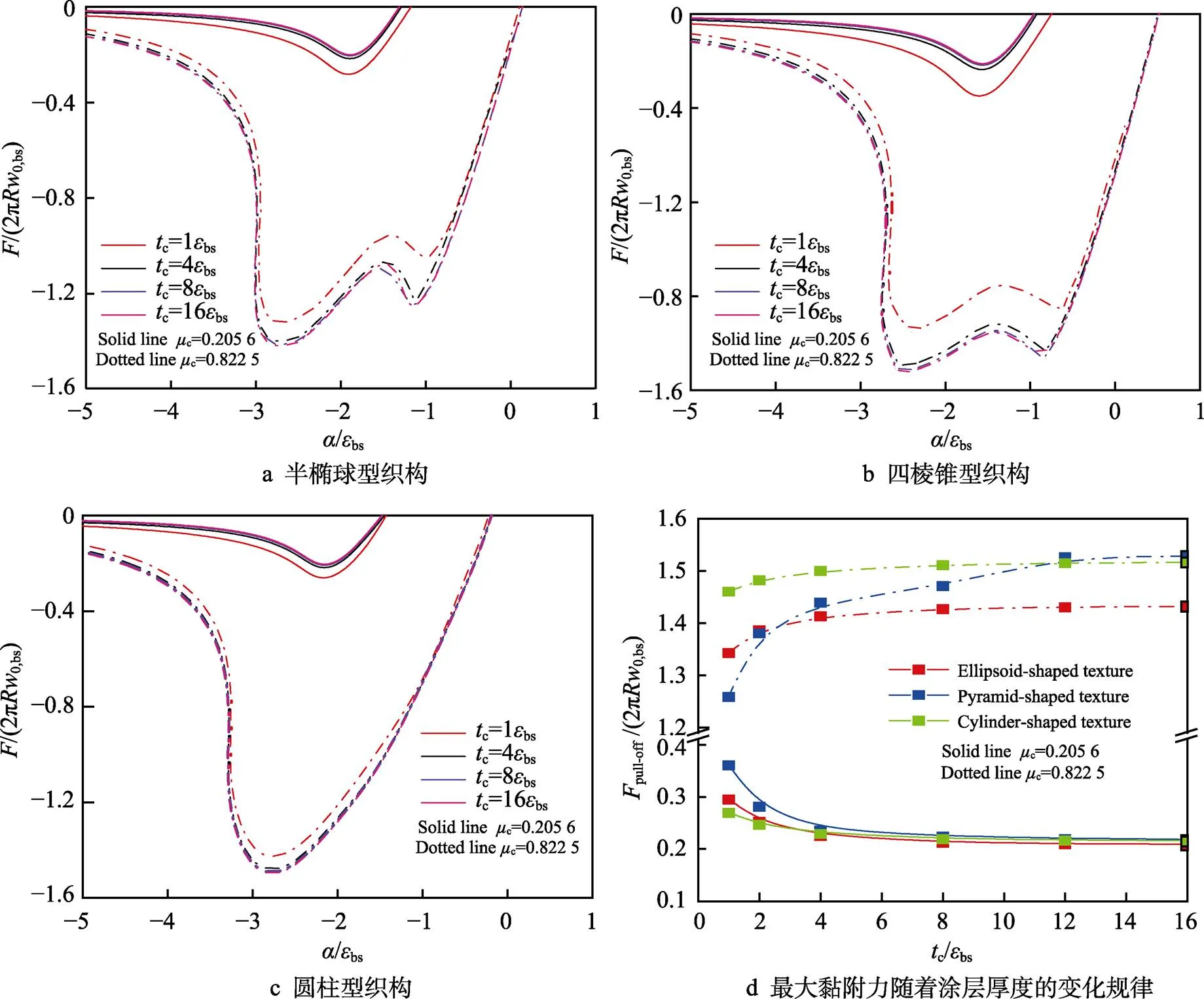
图7 不同涂层厚度下黏附力随接近距离的变化规律

图8 织构高度Zt=20εbs时不同涂层厚度下黏附力随接近距离的变化规律

3 结论

1）本文建立起刚性微球与织构化涂层基体系统黏附接触数值模型，所建模型准确可靠，可用于探讨织构化涂层属性对接触系统黏附力学性能的影响。

2）织构密度越大，最大黏附力越大，且发生黏附分离的接近距离越远。Tabor数越大，黏附力越大；相同密度下，圆柱型织构黏附力最大，半椭球型织构次之，四棱锥型织构最小。

3）织构高度越大，最大黏附力越小，减小幅度与织构类型以及Tabor数相关，四棱锥型织构对织构高度的变化最敏感，但织构高度对黏附力的调控能力有限。

4）涂层厚度会明显影响最大黏附力，调控能力与织构高度相关。小织构高度下，小Tabor数时增大涂层厚度会减小黏附力，大Tabor数时增大涂层厚度会增大黏附力；大织构高度下，增大涂层厚度会增大黏附力。

[1] 沈丹妮. 基于范德华力的仿壁虎机器人在模拟空间环境下的黏附和运动仿真研究[D]. 南京: 南京航空航天大学, 2016.

SHEN Dan-ni. Adhesion Test and Motion Simulation Analysis in Simulated Space Environment of Gecko Mi­mi­cking Robot Based on van Der Waals’ Force[D]. Nan­jing: Nanjing University of Aeronautics and Astronautics, 2016.

[2] ZHANG Xiao-liang, ZHONG Xiao-hua, MENG Xu, et al. Adhesion and Friction Studies of Nano-Textured Surfaces Produced by Self-Assembling Au Nanoparticles on Sili­con Wafers[J]. Tribology Letters, 2012, 46(1): 65-73.

[3] LI Pei-xing, LIU Tie-jun. Two-Dimensional Adhesive Con­tact Problem for Graded Coating Based on a New Multi-Layer Model[J]. IOP Conference Series: Materials Science and Engineering, 2018, 301: 012043.

[4] LI Qiang, POPOV V L. Adhesive Contact between a Rigid Body of Arbitrary Shape and a Thin Elastic Coating[J]. Acta Mechanica, 2019, 230(7): 2447-2453.

[5] SRIDHAR I, SIVASHANKER S. On the Adhesion Mech­anics of Multi-Layer Elastic Systems[J]. Surface and Coa­tings Technology, 2003, 167(2-3): 181-187.

[6] SRIDHAR I, ZHENG Z W, JOHNSON K L. A Detailed Analysis of Adhesion Mechanics between a Compliant Elastic Coating and a Spherical Probe[J]. Journal of Physics D: Applied Physics, 2004, 37(20): 2886-2895.

[7] SMALLWOOD S A, EAPEN K C, PATTON S T, et al. Performance Results of MEMS Coated with a Conformal DLC[J]. Wear, 2006, 260(11-12): 1179-1189.

[8] 吕延军, 方重阳, 邢志国, 等. 仿生织构图案的设计、加工及应用的研究进展[J]. 表面技术, 2021, 50(2): 112-122, 159.

LYU Yan-jun, FANG Chong-yang, XING Zhi-guo, et al. Research Progress in Design, Processing and Application of Bionic Texture Patterns[J]. Surface Technology, 2021, 50(2): 112-122, 159.

[9] 裴阳阳, 宋青, 李鹏. 仿生微纳结构抗菌表面研究进展[J]. 表面技术, 2019, 48(7): 200-210.

PEI Yang-yang, SONG Qing, LI Peng. Research Progress of Biomimetic Micro/Nano-Structured Antibacterial Sur­faces[J]. Surface Technology, 2019, 48(7): 200-210.

[10] BHUSHAN B, KOCH K, JUNG Y C. Nanostructures for Superhydrophobicity and Low Adhesion[J]. Soft Matter, 2008, 4(9): 1799.

[11] GORB S, VARENBERG M, PERESSADKO A, et al. Biomimetic Mushroom-Shaped Fibrillar Adhesive Micro­structure[J]. Journal of the Royal Society, Interface, 2007, 4(13): 271-275.

[12] KIM J K, VARENBERG M. Biomimetic Wall-Shaped Adhesive Microstructure for Shear-Induced Attachment: The Effects of Pulling Angle and Preliminary Displace­ment[J]. Journal of the Royal Society, Interface, 2017, 14(137): 20170832.

[13] KIZILKAN E, GORB S N. Bioinspired Further Enhanced Dry Adhesive by the Combined Effect of the Microstru­cture and Surface Free-Energy Increase[J]. ACS Applied Materials & Interfaces, 2018, 10(31): 26752-26758.

[14] ZHANG Yu-yan, WANG Xiao-li, LI Han-qing, et al. Adhesive Behavior of Micro/Nano-Textured Surfaces[J]. Applied Surface Science, 2015, 329: 174-183.

[15] HAMAKER H C. The London—Van Der Waals Attra­ction between Spherical Particles[J]. Physica, 1937, 4(10): 1058-1072.

[16] YANG Wei-xu, WANG Xiao-li, LI Han-qing, et al. Eff­ects of Hierarchical Structures and Insulating Liquid Me­dia on Adhesion[J]. Applied Surface Science, 2017, 423: 891-899.

[17] VIOLANO G, AFFERRANTE L. Modeling the Adhesive Contact of Rough Soft Media with an Advanced Asperity Model[J]. Tribology Letters, 2019, 67(4): 1-7.

[18] Johnson K L, Kendall K, Roberts A D. Surface Energy and the Contact of Elastic Solids[J]. Procrso­c­londa, 1971, 324(1558): 301-313.

[19] ACITO V, CIAVARELLA M, PREVOST A M, et al. Adhesive Contact of Model Randomly Rough Rubber Surfaces[J]. Tribology Letters, 2019, 67(2): 1-10.

[20] POPOV V L, POHRT R, LI Qiang. Strength of Adhesive Contacts: Influence of Contact Geometry and Material Gradients[J]. Friction, 2017, 5(3): 308-325.

[21] MILANESE E, BRINK T, AGHABABAEI R, et al. Role of Interfacial Adhesion on Minimum Wear Particle Size and Roughness Evolution[J]. Physical Review E, 2020, 102(4-1): 043001.

[22] RADHAKRISHNAN H, AKARAPU S. Two-Dimensio­nal Finite Element Analysis of Elastic Adhesive Contact of a Rough Surface[J]. Scientific Reports, 2020, 10: 5402.

[23] SI Li-na, WANG Xiao-li. Nano-Adhesion Influenced by Atomic-Scale Asperities: A Molecular Dynamics Simula­tion Study[J]. Applied Surface Science, 2014, 317: 710- 717.

[24] ZHANG Yu-yan, SI Li-na, ZHANG Xiao-qing, et al. Inve­stigations of the Adhesive Contact Behavior of Ela­stic Layered Media with Surface Roughness[J]. Jour­nal of Tribology, 2019, 141(4): 258.

[25] 张玉言. 微/纳尺度黏附接触及其滚动摩擦特性研究[D]. 北京: 北京理工大学, 2016.

ZHANG Yu-yan. Researches on the Adhesive Contact and Rolling Friction at Micro and Nano Scales[D]. Beijing: Beijing Institute of Technology, 2016.

[26] LIU Shuang-biao, HUA D, CHEN W W, et al. Tribolo­gical Modeling: Application of Fast Fourier Transform[J]. Tribology International, 2007, 40(8): 1284-1293.

[27] 杨潍旭, 王晓力, 陈平. 摩擦纳米发电机表面织构的优化设计[J]. 机械工程学报, 2020, 56(3): 130-136.

YANG Wei-xu, WANG Xiao-li, CHEN Ping. Optimal De­sign of Surface Texture in Triboelectric Nanogenera­tors[J]. Journal of Mechanical Engineering, 2020, 56(3): 130-136.

[28] YANG Wei-xu, WANG Xiao-li, LI Han-qing, et al. Fundamental Research on the Effective Contact Area of Micro-/Nano-Textured Surface in Triboelectric Nano­gen­erator[J]. Nano Energy, 2019, 57: 41-47.

[29] ARGENTO C, JAGOTA A, CARTER W C. Surface For­mu­lation for Molecular Interactions of Macroscopic Bo­dies[J]. Journal of the Mechanics and Physics of Solids, 1997, 45(7): 1161-1183.

Adhesive Contact Mechanical Behaviors of the Textured Coating Surface

,,

(School of Aeronautics & Astronautics, Sichuan University, Chengdu 610065, China)

Dry adhesion is demonstrated as one of the best ways to realize attachment on space irregular objects and space cruise, as a result of its reliable adhesive ability when exposed to the vacuum and high or low-temperature atmosphere, and its unnecessity of chemical medium or electromagnetic filed. Traditional measures, including coating and texture technique, are utilized to realize higher adhesive force, however, interface high adhesion and mechanical reliability are difficult to realize at the same time. Hence, a new method named textured coating technique trying to process textures on the coating is proposed in this paper such that the interface comprehensive mechanical properties can meet the requirements. Furthermore, a new numerical adhesive contact model of textured coating surface was established to explore the influence of the textured coating on the adhesive mechanical properties of micro contact pairs. The results can be utilized to help instruct the design of the proposed textured coating technique.

Based on the Hamaker summation method and Lennard-Jones potential law, the adhesion contact model of textured coating surface was constructed by considering the effects of textures height on the approach distribution between two contact bodies and the effects of coating and texture properties on the adhesive force. The model was validated with the numerical results from existing literature. Based on the proposed model, the effects of texture types, texture density, texture height, and coating thickness on the adhesive properties under two typical Tabor parameters are investigated. The influences of different materials represented by two kinds of Tabor parameters on the adhesive force are revealed. Three different kinds of textures, including ellipsoid-shaped texture, pyramid-shaped texture and cylinder-shaped texture are selected to explore the effects of texture types on adhesive behaviors. Results showed that cylinder-shaped texture corresponds to the biggest pull-off force, followed by ellipsoid-shaped texture and pyramid-shaped texture under the same conditions. When the texture density increases from 200 μm‒2to 4 000 μm‒2, the pull-off force of three kinds of textures increases gradually. Cylinder-shaped texture increases by about 5～6 times and pyramid-shaped texture increases by about 1.5 times of the original. With the increase of texture height from 1bsto 30bs, the pull-off forces of three kinds of texture decrease gradually. Pyramid-shaped texture decreases to 1% of the original with the largest decrease proportion and the cylinder-shaped decreases the least, about 90% of the original. The coating thickness has an influence on the adhesion force but the effects are related to the Tabor parameters and texture height. The pull-off force increases gradually at a large Tabor parameter but decreases gradually at a small Tabor parameter with the coating thickness increasing from 1bsto 16bs. At larger Tabor parameter and bigger texture height, a secondary peak occurs in the adhesive force versus approach curves.

All in all, the effects of texture types, density, height and coating thickness on the adhesive mechanical properties are revealedand the variation law of adhesive force and the pull-off force are summarized. The obtained results can provide theoretical guidance for the design and application of the adhesion mechanical structure of micro or nano texture surfaces in engineering practice.

textured coating; contact mechanics; Van der Waals forces; adhesive contact

Th117

A

1001-3660(2022)06-0194-10

10.16490/j.cnki.issn.1001-3660.2022.06.016

2021–05–15；

2021–12–06

2021-05-15；

2021-12-06

国家自然科学基金（51875373）

National Natural Science Foundation of China (51875373)

闵强强（1996—），男，硕士生，主要研究方向为空间机构表界面力学。

MIN Qiang-qiang (1996-), Male, Postgraduate, Research focus: surface and interface mechanics of space mechanical components.

周青华（1986—），男，博士，研究员，博士生导师，主要研究方向为空间摩擦学与可靠性工程、空间大型结构机构/传动系统动力学。

ZHOU Qing-hua (1986- ), Male, Doctor, Professor, Doctoral tutor, Research focus: space tribology and reliability engineering and space large structure mechanism/transmission system dynamics.

闵强强，唐雪峰，周青华. 织构化涂层表面的黏附接触力学行为研究[J]. 表面技术, 2022, 51(6): 194-203.

MIN Qiang-qiang, TANG Xue-feng, ZHOU Qing-hua. Adhesive Contact Mechanical Behaviors of the Textured Coating Surface[J]. Surface Technology, 2022, 51(6): 194-203.

责任编辑：万长清