Thermodynamics of the black holes under the extended generalized uncertainty principle with linear terms

He Su(苏贺)and Chao-Yun Long(龙超云)

College of Physics,Guizhou University,Guiyang 550025,China

Abstract In this paper,we employ the extended generalized uncertainty principle with linear terms(LEGUP)to investigate the thermodynamics properties of the Schwarzschild and Reissner–Nordström(RN)black holes.Firstly,by constructing the theoretical framework of LEGUP,the minimal temperature of the Schwarzschild black hole and the modified mass–temperature function for the black hole are calculated.Furthermore,the heat capacity function for the Schwarzschild black hole is obtained.After that,we compare LEGUP black hole thermodynamics with EGUP black hole and with the usual forms.Besides,the modification of black hole entropy is discussed,which involves a heuristic analysis of particles absorbed by the black hole.Finally,we derive the LEGUP-corrected temperature,heat capacity and entropy functions of the RN black hole.

Keywords:black hole thermodynamics,generalized uncertainty principle,black hole entropy

1.Introduction

In the early 1970s,black hole thermodynamics was born,and Hawking and Bekenstein combined thermodynamics with general relativity to explore the thermodynamic properties of black holes.On the basis of Hawking’s black hole area theorem[1],Bekenstein proved the existence of black hole entropy[2].On the other hand,based on semi-classical quantum field theory,Hawking showed that black holes not only absorb objects but also emit thermal radiation[3,4],which is called Hawking radiation.As is known to all,Hawking radiation proved the existence of black hole temperature and established the law of black hole thermodynamics,which laid the foundation for the study of black hole thermodynamics[2,5].Black hole thermodynamics reflects the deep inner connection between general relativity and quantum theory,revealing the quantum nature of black holes.

Since there are still some problems with the semi-classical quantum tunneling radiation,researchers began to try to introduce generalized uncertainty principle(GUP)[6,7]into the classical Hawking radiation theory and discuss the modification of black hole thermodynamics by GUP.The GUP is an amendment to the Heisenberg uncertainty principle(HUP),which mainly describes the existence of a non-zero‘minimum observable length’.The minimum length effect has also given rise to many quantum gravitational effects,such as string theory[8,9],non-commutative geometries[10],and black holes physics[11],the most striking of which is GUP.More recently,in a study of black hole physics with GUP,Adler found that the black hole does not completely evaporate with the GUP modification,leaving a residual mass[12].Won Sang Chung also investigated the thermodynamic properties of the Schwarzschild black hole and the Unruh effect by using the simplest form of the extended uncertainty principle(EUP)[13].In[14],Hassan Hassanabadi studied the thermodynamic properties of the Schwarzschild and Reissner–Nordström(RN)black holes by taking into account the extended generalized uncertainty principle(EGUP).And the lower bound for the Schwarzschild black hole temperature was obtained by the minimal momentum of EGUP.

Recently,there has been a lot of discussion about the generalized uncertainty principle with linear terms(LGUP).In[15],the authors proposed LGUP on the Planck scale and solved the problems related to the discreteness of space by this LGUP.Very recently researchers used LGUP to modify the Friedman equation and found that the linear formulation is more suitable for researching gravitational waves[16,17].In both five and seven dimensions,linear GUP is able to obtain the correct form of the black hole entropy correction.In other words,the entropy of the LGUP correction yields an acceptable result that the first-order entropy correction is logarithmic[18].In addition,LGUP can reduce the critical and remnant mass of the black hole,thus providing a possible explanation for the formation of black holes at energies higher than the energy scales of LHC[19].Therefore,the application of GUP with linear terms to the correction of the thermodynamic properties of black holes is a very interesting study.

In this paper,we will use linear extended generalized uncertainty principle(LEGUP)to correct the thermodynamic properties of Schwarzschild and RN black holes to obtain thermodynamic corrections for the mass,temperature,heat capacity,and entropy of the black holes,and compare them with the existing corrections.This paper is organized as follows:In section 2,we briefly introduce the HUP,GUP,EUP,EGUP,LGUP,and LEGUP formalisms.In section 3,we calculate the corrected mass–temperature relation,heat capacity,and entropy of Schwarzschild black holes under LEGUP and compare them with known data.In section 4,we discuss the thermodynamic properties of the charged RN black holes under LEGUP.Finally,the discussion proceeds in section 5.

2.The LEGUP

3.Thermodynamics of Schwarzschild black hole

3.1.Mass–temperature relation for LEGUP black hole

Next,by considering the mass–temperature relation given in equation(15),the heat capacity corresponding to the uncertainty relation generated by the EGUP black hole can be obtained as

Figure 1.Plot of the mass–temperature relation for the ordinaryblack hole,the EGUP black hole with α=β=0.5 and the LEGUP black hole with α=β=0.5 where we set c=kB=1,8πG=1.

Similarly,we take the limit for the parameters in equation(24).We first let β=0,and we obtain

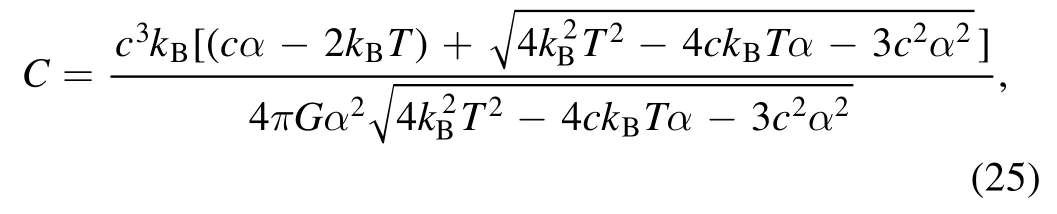
then,we apply L’Hopital’s rule to the limit of α in equation(25),and we get

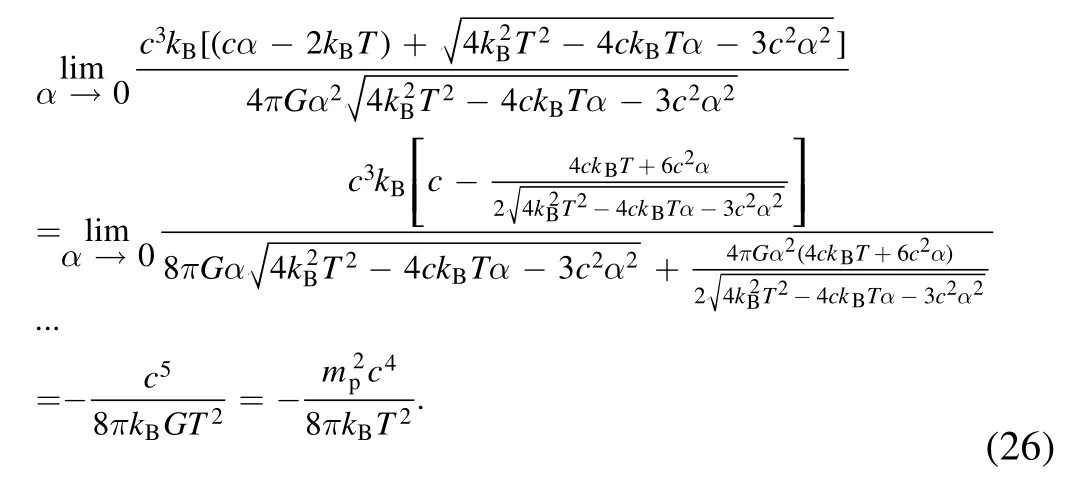
Hence,the modified heat capacity in the absence of LEGUP are consistent with the semiclassical heat capacityobtained in[13,30].

3.2.Comparison and analysis

In the EGUP black hole[31,32]we know the mass–temperature relation as

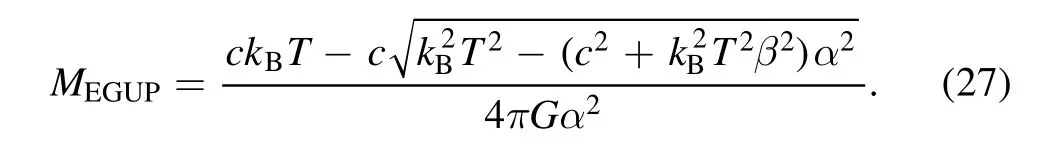
Obviously,the mass of the EGUP black hole is missing the result of the linear term,which will cause the minimum mass of the black hole to decrease.Using LEGUP,the above disadvantages are well corrected by adding linear terms figure 1 describes the plot of the mass–temperature relation for the ordinary black hole,the EGUP black hole and the LEGUP black hole.It is obvious from the figure that the ordinary black hole does not give the lower bound on the mass while EGUP black hole and LEGUP black hole do.By comparing the curves of LEGUP and EGUP black holes,it can be seen that due to the linear terms of position and momentum,the lower mass limit of black holes becomes larger,which is similar to that LGUP can change the critical and remnant mass of the black hole in[19].

In the EGUP black hole,the temperature is

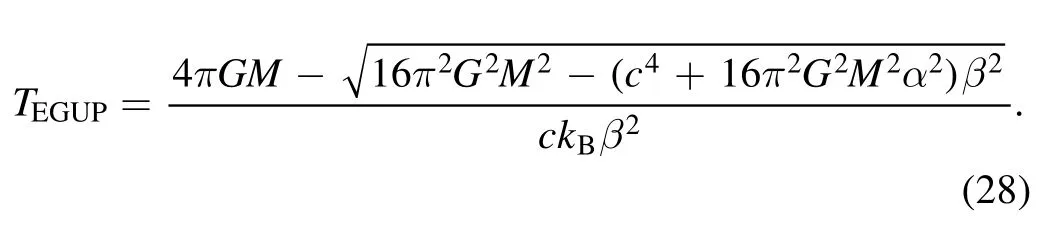
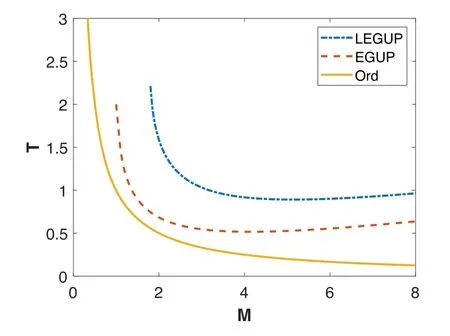
Figure 2.Plot of the temperature-mass relation for the ordinary black hole,the EGUP black hole with α=β=0.5 and the LEGUP black hole with α=β=0.5 where we set c=kB=1,8πG=1.

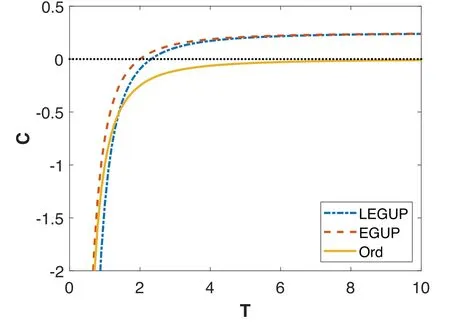
Figure 3.Plot of the capacity-temperature relation for the ordinary black hole,the EGUP black hole with α=β=0.5 and the LEGUP black hole with α=β=0.5 where we set c=kB=1,8πG=1.

Comparing this with equation(20),we know that the temperature of the LEGUP black hole increases the linear term,which will cause the lower limit of black hole temperature to change.As can be seen from figures 1 and 2,the truncation point in the left part of the image is due to the lower limits of temperature and mass given by the LEGUP black hole.The lower limits of both values are lower than those of the EGUP black hole,as a result of equations(12)and(19).Due to the symmetry of LEGUP,the curves trends in figures 1 and 2 regarding the temperature and mass of the black hole are essentially the same.

From figure 2,we can see that the temperature of the(L)EGUP black hole increases with increasing mass in the case of large masses.This implies that macroscopic black holes in our Universe could be hotter than the CMB and we should be able to detect their Hawking radiation.Considering that we do not detect such radiation,the mass of the most massive black holes we see clearly places a bound on the acceptable values of the(L)EGUP parameter α.Recent surveys have revealed that supermassive black holes rarely exceed a mass ofM≃a few×1010M⊙during the entire cosmic history[33].Taking the massive black hole withM=1010M⊙as an example,we consider estimating the value range of LEGUP parameter α.On substituting equation(12)into(20)we obtain the following black hole maximum mass

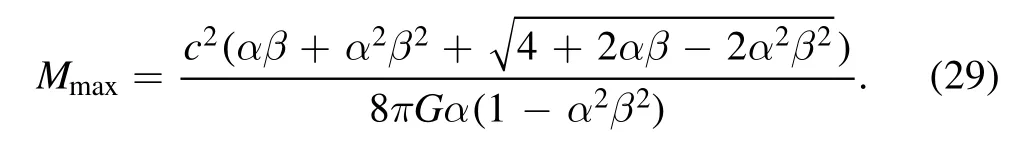
So,the mass of the massive black hole(M=1010M⊙)should satisfy the following relationship

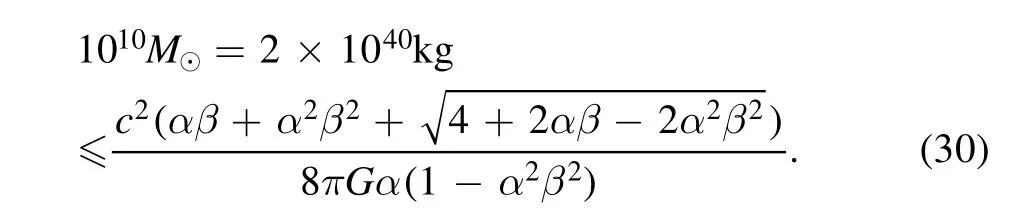
SubstituteG=6.67×10−11N·m2kg−2,c=3×108m s−1and β=0.5 into the equation(30)above,and the range of the parameter α is obtained

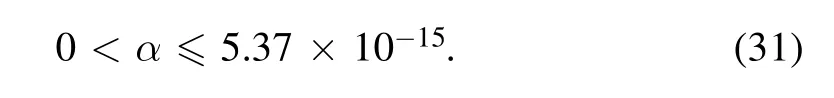
Comparing the curves in figure 3,we find that the heat capacity of black holes increases as the temperature increases.While the heat capacity of the ordinary black hole is always negative,so there is no point at which the heat capacity disappears.In contrast,for LEGUP and EGUP black holes,the specific heat has vanishing points.That is,when the temperature is set at a certain value,the heat capacity of the black hole is zero,which can also provide a possible solution to the black hole remnant.

3.3.LEGUP black hole entropy

Next,we will calculate the entropy of the black hole,whose calculation was proposed by[34].The entropy of a black hole is related to its area by Bekenstein’s entropy expression.We consider a particle that is captured by a black hole,and when this particle disappears,its information disappears from the view of the observer.Then,the minimum increase in the area of the black hole is given by

whereband μ are the particle’s size and mass.A particle is described as a wave packet,and the width of the wave packet is defined as the standard deviation of thexdistribution,i.e.the position uncertainty(b∼Δx).In addition,the momentum uncertainty cannot be greater than the mass of the particle(Δp≤μ).Thus,equation(32)can be deduced as

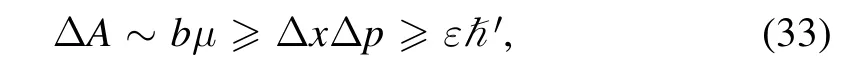
where ε is the calibration factor and ′ħis the effective Planck constant.In order to obtain the effective Planck constant in equation(33),the minimum position and minimum momentum in equation(7)are substituted into equation(6),and the uncertainty relations for position and momentum are rewritten as

The effective Planck constant can be calculated as

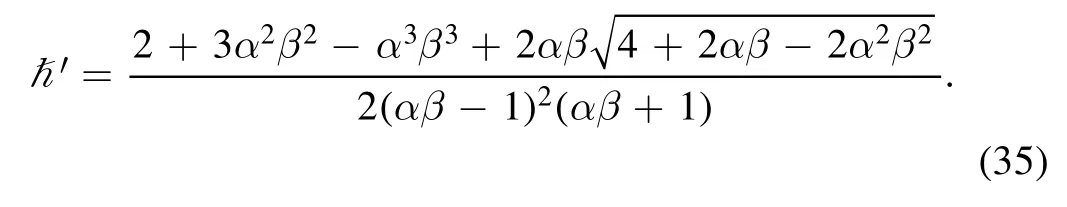
When the particle vanishes,the information of one bit is lost and the black hole acquires the increase in entropy(ΔS)min=ln 2.We obtain

The Benkenstein–Hawking entropy of a black hole isIn general,let’s takeS=A/4(ħ=c=G=kB=1).Also,from the consistency of the thermodynamic information of the black hole in absence of LEGUP with the semi-classical case,we can defineε= 4 ln 2.So equation(36)can be rewritten as

Hence,the LEGUP-corrected black hole entropy is given by

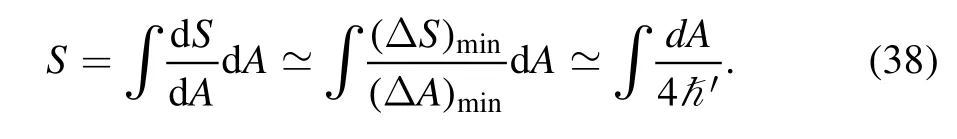
Considering(35)and(37),we obtain

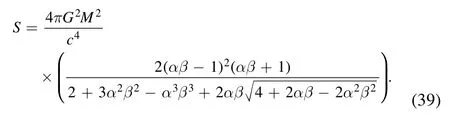
When the correction for LEGUP disappears(α=β=0),we have

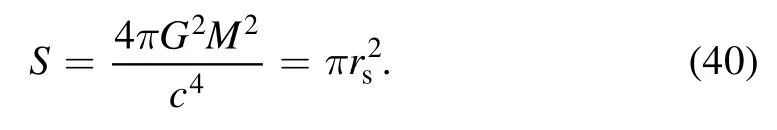
We can see in the absence of correction due to LEGUP,the relationship obtained for entropy reduces to the semi-classical Bekenstein-Hawking entropy for the Schwarzschild black hole asS=A/4.

4.Thermodynamics of RN black hole

In this section,let us consider an RN black hole with massMand chargeQ[35,36].In this case,near the horizon of the black hole,the position uncertainty of a particle will be of the order of the RN radius of the black hole

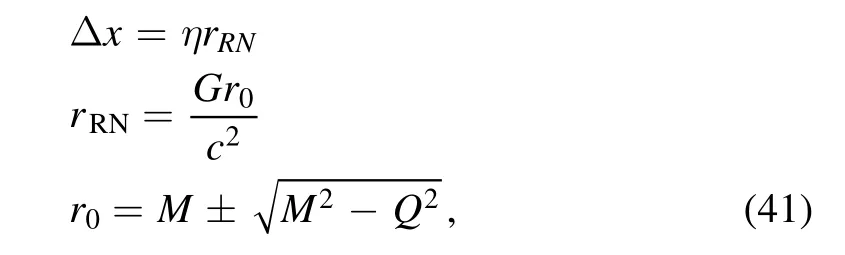
where η andrRNdenote a scale factor and the horizon radius of the RN black hole.The above two values forr0are corresponding to the outer and inner horizons.In the limitQ=0,the radius of the RN black hole should return the Schwarzschild radius,so we take the plus sign in equation(41)to consider only the radius of the outer horizon

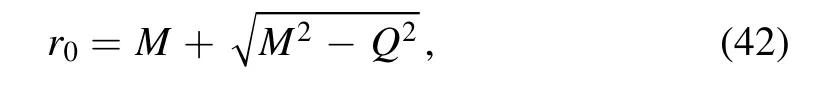
then we find

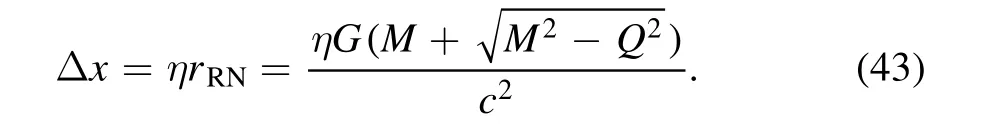
Substituting the value of Δpand Δxfrom equations(10)and(41)the equation(11)can be rewritten a quadratic equation ofr0andTin the form of

Once again,in the absence of correction due to LEGUP,equation(44)reduces to

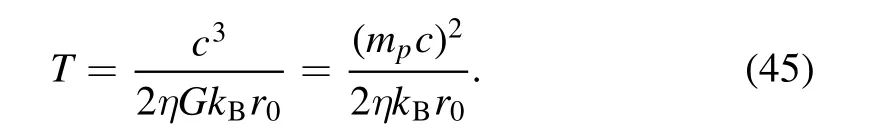
Comparing the above relation with the semi-classical Hawking temperature,the value of η is seen to be

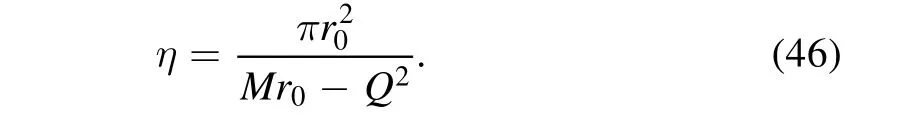
By inserting equation(46)into(44),we obtain the following mass–charge–temperature relation corresponding to the RN black hole

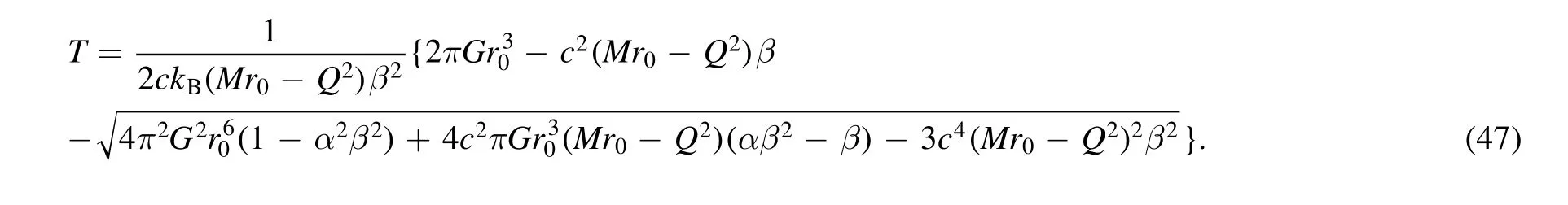
By the identityMr0−Q2=r0(r0−M),we take the limit for the parameters in equation(47).We first let α=0,and we obtain

then,we apply L’Hopital’s rule to the limit of β in equation(48),and we get

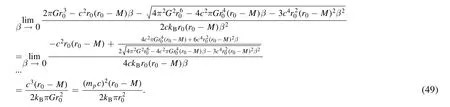
This equation is consistent with the usual semi-classical Hawking temperature in the absence of correction due to LEGUP[30].

Now the heat capacity of the RN black hole can be calculated as

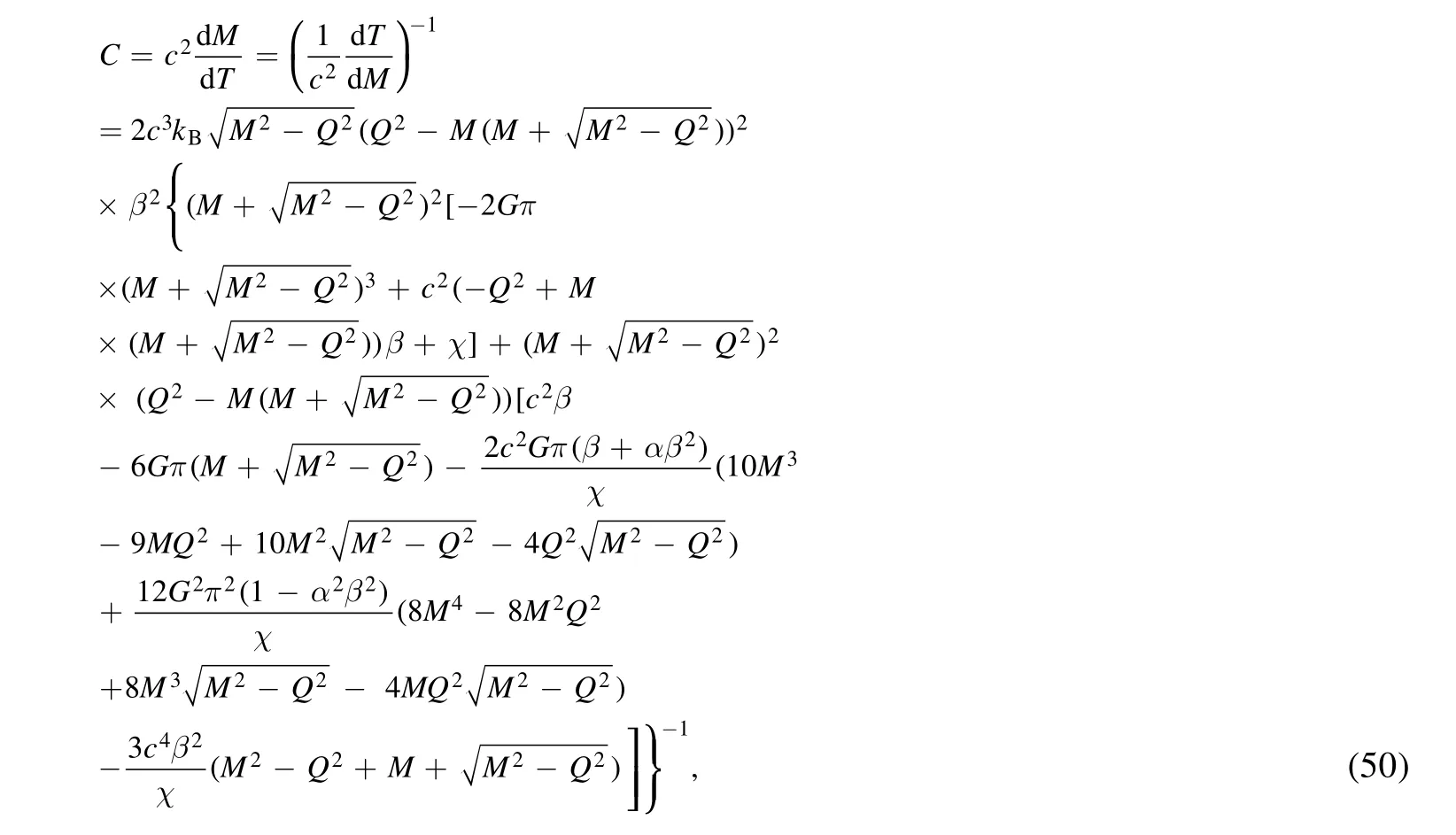
where

If we consider equation(42),the heat capacity of the RN black hole can be rewritten as

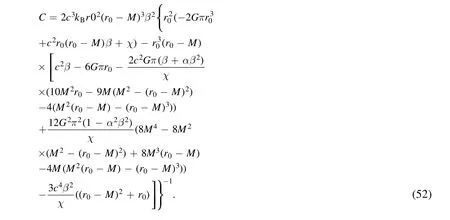
For the parameters of LEGUP go to zero and in the absence of correction due to LEGUP,the obtained heat capacity for the charged black hole is consistent with results obtained previously in the absence of correction due to GUP[30].In order to obtain the entropy of the RN black hole,we use the same method as we used to calculate the entropy of the Schwarzschild black hole in section 3.We obtain

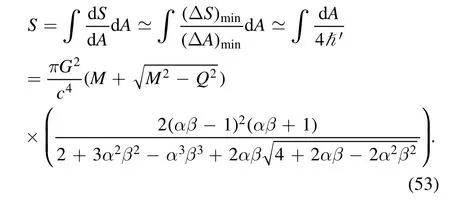
From equation(53),it is not difficult to find that in the caseQ=0,the RN black hole entropy is recovered to the calculated entropy of the Schwarzschild black hole in equation(39).Also we can see in the absence of correction due to LEGUP for α=β=0,equation(53)reduces to the semi-classical entropy for the black hole.

5.Conclusions

In this paper,we have investigated the modifications of the various thermodynamic properties of Schwarzschild and RN black holes by using the LEGUP.Considering the minimal momentum of LEGUP,the minimal temperature of the Schwarzschild black hole has been obtained.And this minimum temperature is a new result of the LEGUP correction.The modified mass–temperature function for the Schwarzschild black hole and the corrected mass–charge–temperature functions of the RN black hole have been obtained.And we have compared corrected Schwarzschild black hole thermodynamic curves with the usual forms,that is,without corrections to the LEGUP.By comparison,it is obvious that the temperature and mass expressions of LEGUP black holes add linear term results,and the lower limits on the temperature and mass of a black hole are raised.Then,we have followed a heuristic method to derive the entropy function of the two black holes after obtaining the heat capacity function of Schwarzschild and RN black holes.Moreover,the thermodynamic properties of the two black holes have been compared.In particular,we hope to apply LEGUP to more questions about black holes or the Universe.

Acknowledgments

Project supported by the National Natural Science Foundation of China(Grant No.11565009).

ORCID iDs