Systematic study of α decay half-lives for even–even nuclei within a deformed twopotential approach

Hai-Feng Gui(桂海峰),Hong-Ming Liu(刘宏铭),Xi-Jun Wu(吴喜军),Peng-Cheng Chu(初鹏程),Biao He(何彪) and Xiao-Hua Li(李小华),5,6,7

1 School of Nuclear Science and Technology,University of South China,421001 Hengyang,China

2 School of Math and Physics,University of South China,Hengyang 421001,China

3 The Research Center for Theoretical Physics,Science School,Qingdao University of Technology,Qingdao 266033,China

4 College of Physics and Electronics,Central South University,Changsha 410083,China

5 National Exemplary Base for International Sci &Tech.Collaboration of Nuclear Energy and Nuclear Safety,University of South China,Hengyang 421001,China

6 Cooperative Innovation Center for Nuclear Fuel Cycle Technology &Equipment,University of South China,421001 Hengyang,China

7 Key Laboratory of Low Dimensional Quantum Structures and Quantum Control,Hunan Normal University,410081 Changsha,China

Abstract In this work,we systematically study the α decay half-lives of 196 even–even nuclei using a two-potential approach improved by considering nuclear deformation.The results show that the accuracy of this model has been improved after considering nuclear deformation.In addition,we extend this model to predict the α decay half-lives of Z=118 and 120 isotopes by inputting the α decay energies extracted from the Weizsacker–Skyrme-type(WS-type)mass model,a simple nuclear mass formula,relativistic continuum Hartree–Bogoliubov theory and Duflo-Zuker-19(DZ19)mass model.It is useful for identifying the new superheavy elements or isotopes for future experiments.Finally,the predicted α decay energies and half-lives of Z=118 and 120 isotopes are analyzed,and the shell structure of superheavy nuclei is discussed.It shows that the shell effect is obvious at N=184,while the shell effect at N=178 depends on the nuclear mass model.

Keywords:α-decay,deformed two-potential approach,superheavy nuclei,magic number

1.Introduction

In 1899,Rutherford firstly discovered the natural α radioactivity phenomenon from uranium and uranium compounds.Later on,Gurney and Condon[1]and Gamow[2]proposed the quantum tunneling theory to explain this process independently.α decay is the main decay mode of the unstable nuclei,the study on α decay can provide abundant nuclear structural information,such as the ground-state properties,level structure,shell closure effect and so on[3–7].In addition,α decay plays an important role in identifying the new elements and synthesising superheavy nuclei[8–17].Therefore,α decay has become one of the hottest topics in nuclear physics.Based on the description of Gamowet al,up to now,a lot of empirical formulas or theoretical models have been developed to study α decay,such as Coulomb and proximity potential model[18],density-dependent cluster model[19,20],universal decay law[21],Royer formula[22],Gamow-like model[23],two-potential approach(TPA)[24]and others[25,26].

The study of superheavy nuclei has always been a hot topic[27–39].In recent years,the effect of deformation has attracted more and more attention to the study of superheavy nuclei[40–50].Some research shows that the deformation has a certain influence on the calculation of α decay half-lives[46,47,51].Recently,Hassanzadet al[52]systematically studied the favored α decay half-lives of deformed nuclei with 93 ≤Z≤118 using deformed Coulomb and proximity potential model.Their results indicated that the deformation has a certain effect on α decay half-lives.Therefore,it is necessary to modify the TPA by considering the effect of nuclear deformation,this is our first motivation of the article.In addition,the magic numbers of superheavy nuclei has also attracted the attention of researchers.Recently,by exploring the properties of α decay ofZ=118 and 120 isotopes,an obvious shell effect atN=178 is found besides that atN=184.It is well known that the model dependence on the shell effect atN=184[17,53–55]is not strong.However,the new magic numberN=178 has not been confirmed by other models.In order to test whetherN=178 is a new magic number,it is necessary to use the improved TPA to study the alpha-decay properties ofZ=118 and 120 isotopes.This is the second motivation of this paper.Driven by the two above motivations,we will improve the TPA by taking into account the nuclear deformation and further investigate the α decay properties of unstable nuclei,especially for the case of the superheavy nuclei.

The article is organized as follows.The theoretical framework of the deformed TPA is briefly presented in section 2.The detailed calculations and discussion are given in section 3.A summary is given in section 4.

2.Theoretical framework

Figure 1.The difference in logarithmic form of α decay half-lives between experimental data and calculated ones.The abscissa is the mass number A and the ordinate is the value of .The black square and red dot represent the theoretical value calculated by using the TPA without considering deformation and after considering deformation,respectively.

Table 1.Comparison of the experimental data for α decay nuclei with calculated results.The deformation parameters β2,β4 and β6 are take from FRDM2012[78].The Qα are taken from the AME2020[72].The experimental α decay half-livesare taken from the NUBASE2020[71].is the logarithm of half-life calculated by TPA without considering deformation,andis the logarithm of half-life calculated by TPA considering deformation.

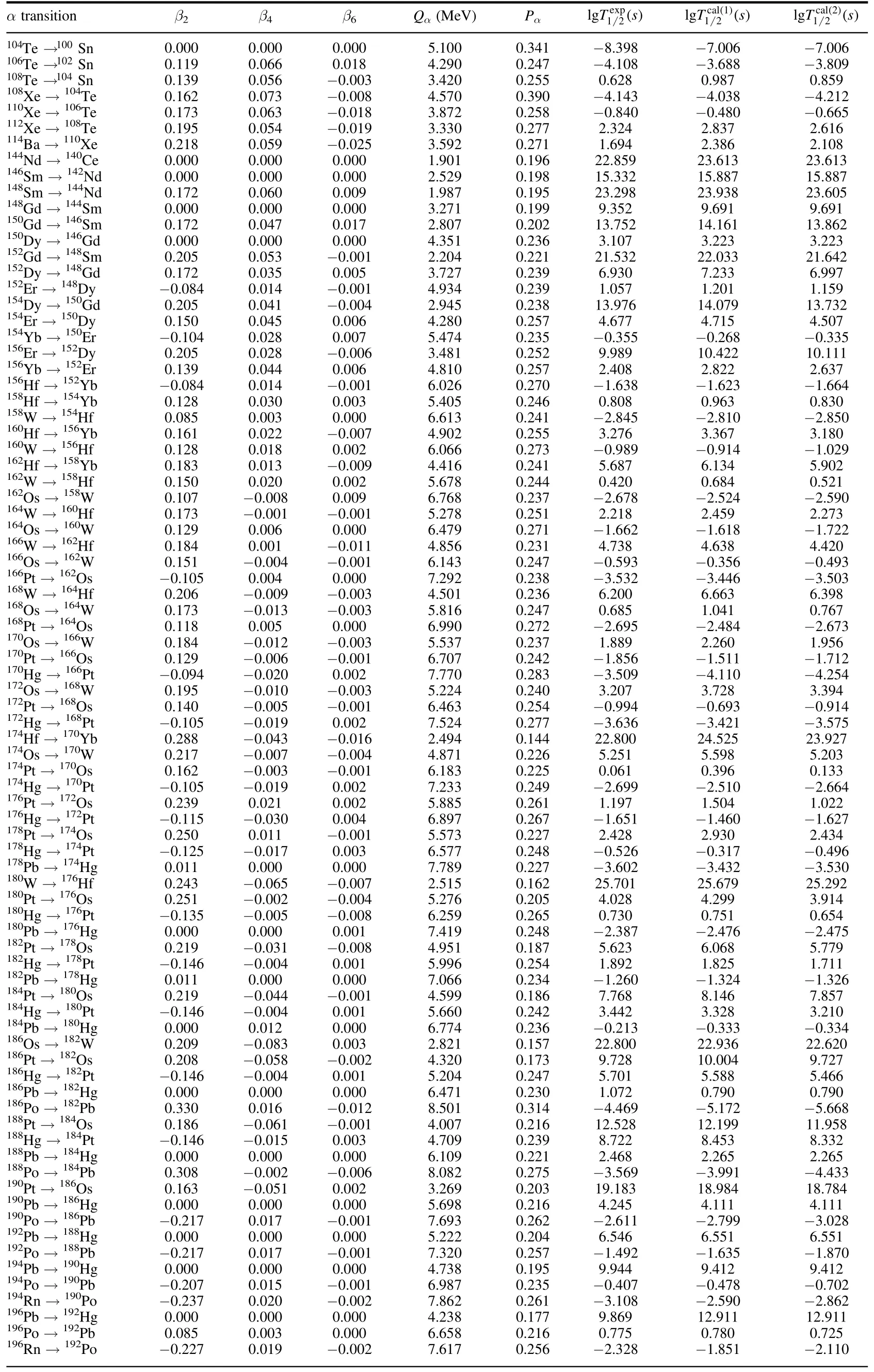
Table 1.Comparison of the experimental data for α decay nuclei with calculated results.The deformation parameters β2,β4 and β6 are take from FRDM2012[78].The Qα are taken from the AME2020[72].The experimental α decay half-livesare taken from the NUBASE2020[71].is the logarithm of half-life calculated by TPA without considering deformation,andis the logarithm of half-life calculated by TPA considering deformation.

α transitionβ2β4β6Qα(MeV)Pα exp lg 1 2 Ts()cal 1()cal 2()lg 1 2 Ts()lg 1 2 Ts()1041000.0000.0000.0005.1000.341−8.398−7.006−7.006→TeSn→1061020.1190.0660.0184.2900.247−4.108−3.688−3.809→TeSn 1081040.1390.056−0.0033.4200.2550.6280.9870.859 108Xe →104Te0.1620.073−0.0084.5700.390−4.143−4.038−4.212 110Xe →106Te0.1730.063−0.0183.8720.258−0.840−0.480−0.665 112Xe →108Te0.1950.054−0.0193.3300.2772.3242.8372.616 114Ba →110Xe0.2180.059−0.0253.5920.2711.6942.3862.108 144Nd →140Ce0.0000.0000.0001.9010.19622.85923.61323.613 146Sm →142Nd0.0000.0000.0002.5290.19815.33215.88715.887 148Sm →144Nd0.1720.0600.0091.9870.19523.29823.93823.605 148Gd →144Sm0.0000.0000.0003.2710.1999.3529.6919.691 150Gd →146Sm0.1720.0470.0172.8070.20213.75214.16113.862 150Dy →146Gd0.0000.0000.0004.3510.2363.1073.2233.223 152Gd →148Sm0.2050.053−0.0012.2040.22121.53222.03321.642 152Dy →148Gd0.1720.0350.0053.7270.2396.9307.2336.997 152Er →148Dy−0.0840.014−0.0014.9340.2391.0571.2011.159 154Dy →150Gd0.2050.041−0.0042.9450.23813.97614.07913.732 154Er →150Dy0.1500.0450.0064.2800.2574.6774.7154.507 154Yb →150Er−0.1040.0280.0075.4740.235−0.355−0.268−0.335 156Er →152Dy0.2050.028−0.0063.4810.2529.98910.42210.111 156Yb →152Er0.1390.0440.0064.8100.2572.4082.8222.637 156Hf →152Yb−0.0840.014−0.0016.0260.270−1.638−1.623−1.664 158Hf →154Yb0.1280.0300.0035.4050.2460.8080.9630.830 158W →154Hf0.0850.0030.0006.6130.241−2.845−2.810−2.850 160Hf →156Yb0.1610.022−0.0074.9020.2553.2763.3673.180 160W →156Hf0.1280.0180.0026.0660.273−0.989−0.914−1.029 162Hf →158Yb0.1830.013−0.0094.4160.2415.6876.1345.902 162W →158Hf0.1500.0200.0025.6780.2440.4200.6840.521 162Os →158W0.107−0.0080.0096.7680.237−2.678−2.524−2.590 164W →160Hf0.173−0.001−0.0015.2780.2512.2182.4592.273 164Os →160W0.1290.0060.0006.4790.271−1.662−1.618−1.722 166W →162Hf0.1840.001−0.0114.8560.2314.7384.6384.420 166Os →162W0.151−0.004−0.0016.1430.247−0.593−0.356−0.493 166Pt →162Os−0.1050.0040.0007.2920.238−3.532−3.446−3.503 168W →164Hf0.206−0.009−0.0034.5010.2366.2006.6636.398 168Os →164W0.173−0.013−0.0035.8160.2470.6851.0410.767 168Pt →164Os0.1180.0050.0006.9900.272−2.695−2.484−2.673 170Os →166W0.184−0.012−0.0035.5370.2371.8892.2601.956 170Pt →166Os0.129−0.006−0.0016.7070.242−1.856−1.511−1.712 170Hg →166Pt−0.094−0.0200.0027.7700.283−3.509−4.110−4.254 172Os →168W0.195−0.010−0.0035.2240.2403.2073.7283.394 172Pt →168Os0.140−0.005−0.0016.4630.254−0.994−0.693−0.914 172Hg →168Pt−0.105−0.0190.0027.5240.277−3.636−3.421−3.575 174Hf →170Yb0.288−0.043−0.0162.4940.14422.80024.52523.927 174Os →170W0.217−0.007−0.0044.8710.2265.2515.5985.203 174Pt →170Os0.162−0.003−0.0016.1830.2250.0610.3960.133 174Hg →170Pt−0.105−0.0190.0027.2330.249−2.699−2.510−2.664 176Pt →172Os0.2390.0210.0025.8850.2611.1971.5041.022 176Hg →172Pt−0.115−0.0300.0046.8970.267−1.651−1.460−1.627 178Pt →174Os0.2500.011−0.0015.5730.2272.4282.9302.434 178Hg →174Pt−0.125−0.0170.0036.5770.248−0.526−0.317−0.496 178Pb →174Hg0.0110.0000.0007.7890.227−3.602−3.432−3.530 180W →176Hf0.243−0.065−0.0072.5150.16225.70125.67925.292 180Pt →176Os0.251−0.002−0.0045.2760.2054.0284.2993.914 180Hg →176Pt−0.135−0.005−0.0086.2590.2650.7300.7510.654 180Pb →176Hg0.0000.0000.0017.4190.248−2.387−2.476−2.475 182Pt →178Os0.219−0.031−0.0084.9510.1875.6236.0685.779 182Hg →178Pt−0.146−0.0040.0015.9960.2541.8921.8251.711 182Pb →178Hg0.0110.0000.0007.0660.234−1.260−1.324−1.326 184Pt →180Os0.219−0.044−0.0014.5990.1867.7688.1467.857 184Hg →180Pt−0.146−0.0040.0015.6600.2423.4423.3283.210 184Pb →180Hg0.0000.0120.0006.7740.236−0.213−0.333−0.334 186Os →182W0.209−0.0830.0032.8210.15722.80022.93622.620 186Pt →182Os0.208−0.058−0.0024.3200.1739.72810.0049.727 186Hg →182Pt−0.146−0.0040.0015.2040.2475.7015.5885.466 186Pb →182Hg0.0000.0000.0006.4710.2301.0720.7900.790 186Po →182Pb0.3300.016−0.0128.5010.314−4.469−5.172−5.668 188Pt →184Os0.186−0.061−0.0014.0070.21612.52812.19911.958 188Hg →184Pt−0.146−0.0150.0034.7090.2398.7228.4538.332 188Pb →184Hg0.0000.0000.0006.1090.2212.4682.2652.265 188Po →184Pb0.308−0.002−0.0068.0820.275−3.569−3.991−4.433 190Pt →186Os0.163−0.0510.0023.2690.20319.18318.98418.784 190Pb →186Hg0.0000.0000.0005.6980.2164.2454.1114.111 190Po →186Pb−0.2170.017−0.0017.6930.262−2.611−2.799−3.028 192Pb →188Hg0.0000.0000.0005.2220.2046.5466.5516.551 192Po →188Pb−0.2170.017−0.0017.3200.257−1.492−1.635−1.870 194Pb →190Hg0.0000.0000.0004.7380.1959.9449.4129.412 194Po →190Pb−0.2070.015−0.0016.9870.235−0.407−0.478−0.702 194Rn →190Po−0.2370.020−0.0027.8620.261−3.108−2.590−2.862 196Pb →192Hg0.0000.0000.0004.2380.1779.86912.91112.911 196Po →192Pb0.0850.0030.0006.6580.2160.7750.7800.725 196Rn →192Po−0.2270.019−0.0027.6170.256−2.328−1.851−2.110 TeSn

Table 1.(Continued.)

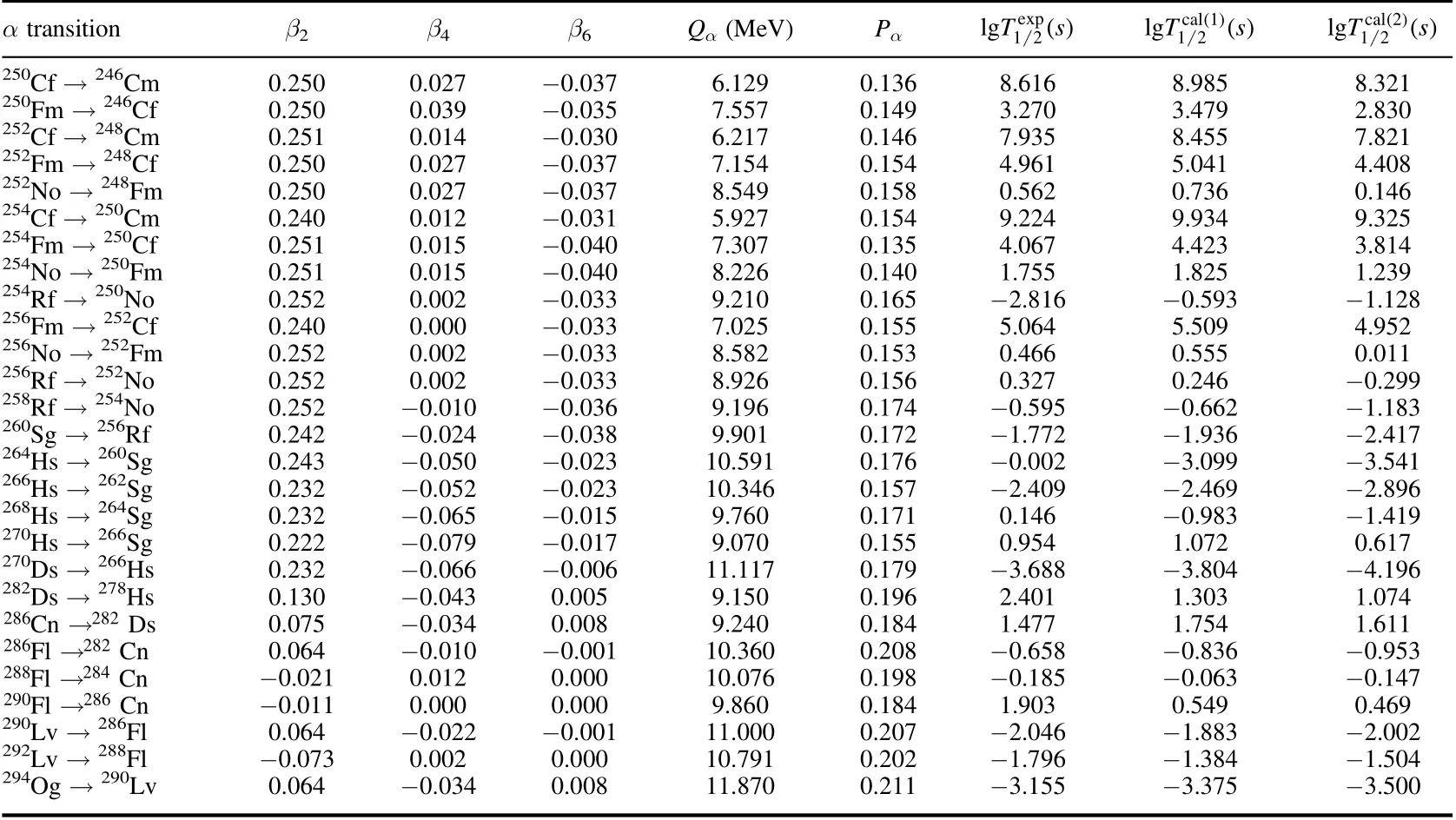
Table 1.(Continued.)

Table 2.The Qα and prediction half-lives of α decay in even–even nuclei with Z=118 and Z=120.The deformation parameters β2,β4 and β6 are take from WS4[77],and the binding energy or mass excess required to calculate the Pα and Qα are respectively from each mass table.indicate that the data are from mass tables WS-type[73],SNMF[74],RCHB[75]and DZ19[76],and the unit is MeV.are the logarithms of the corresponding calculated half-life,in s.

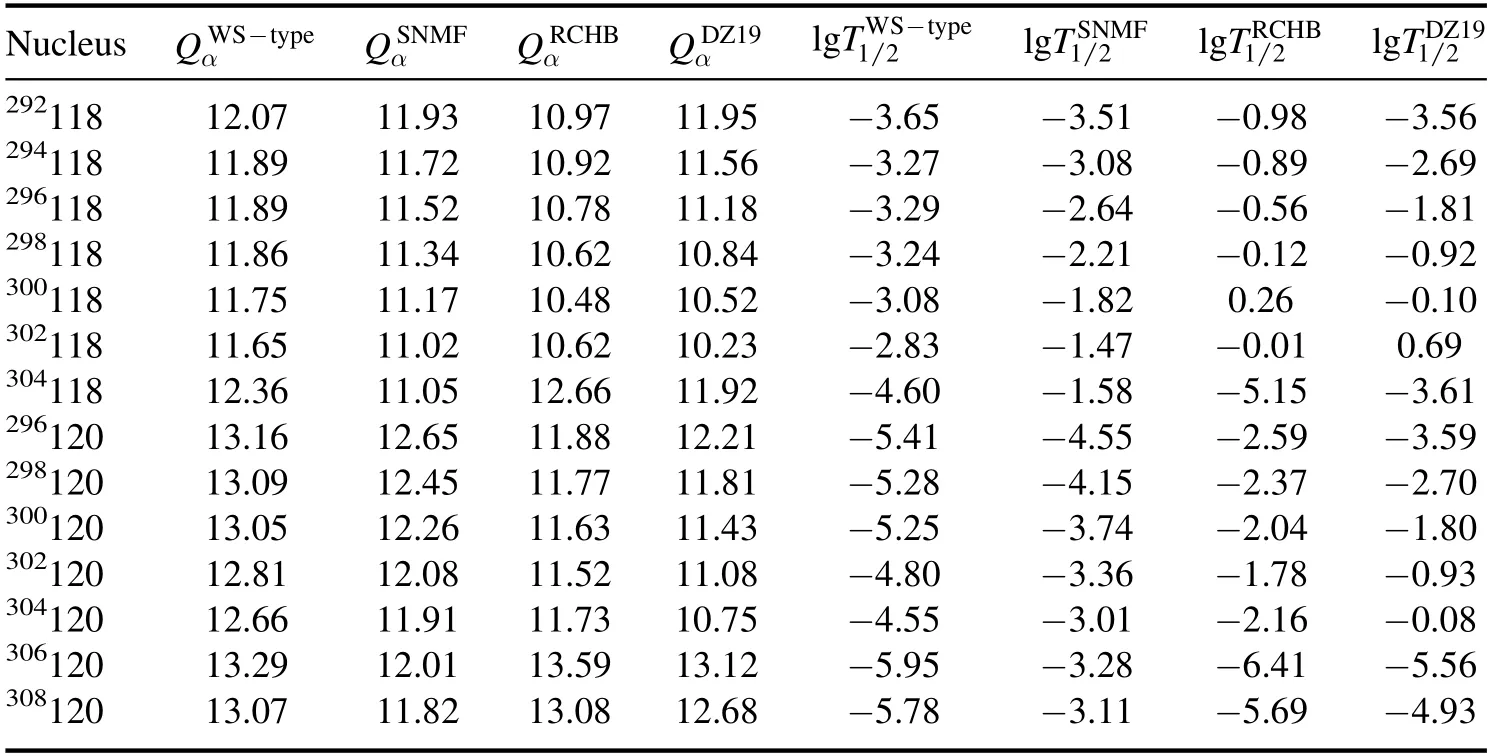
Table 2.The Qα and prediction half-lives of α decay in even–even nuclei with Z=118 and Z=120.The deformation parameters β2,β4 and β6 are take from WS4[77],and the binding energy or mass excess required to calculate the Pα and Qα are respectively from each mass table.indicate that the data are from mass tables WS-type[73],SNMF[74],RCHB[75]and DZ19[76],and the unit is MeV.are the logarithms of the corresponding calculated half-life,in s.

Nucleusα−QWStypeQαSNMFQαRCHBQαDZ19−T lg 1 2 WS type T lg 1S 2NMF T lg 1R 2CHB T lg 1D 2Z19 29211812.0711.9310.9711.95−3.65−3.51−0.98−3.56 29411811.8911.7210.9211.56−3.27−3.08−0.89−2.69 29611811.8911.5210.7811.18−3.29−2.64−0.56−1.81 29811811.8611.3410.6210.84−3.24−2.21−0.12−0.92 30011811.7511.1710.4810.52−3.08−1.820.26−0.10 30211811.6511.0210.6210.23−2.83−1.47−0.010.69 30411812.3611.0512.6611.92−4.60−1.58−5.15−3.61 29612013.1612.6511.8812.21−5.41−4.55−2.59−3.59 29812013.0912.4511.7711.81−5.28−4.15−2.37−2.70 30012013.0512.2611.6311.43−5.25−3.74−2.04−1.80 30212012.8112.0811.5211.08−4.80−3.36−1.78−0.93 30412012.6611.9111.7310.75−4.55−3.01−2.16−0.08 30612013.2912.0113.5913.12−5.95−3.28−6.41−5.56 30812013.0711.8213.0812.68−5.78−3.11−5.69−4.93

3.Results and discussion

Based on the experimental data,using TPA,we obtain σ(1)=0.573 without considering nuclear deformation,and σ(2)=0.506 after considering nuclear deformation.These results show that there is indeed some improvement after considering deformation.In other words,the calculation results of TPA are in better agreement with the experimental data.For a more intuitive comparison of this standard deviations,the difference in logarithmic form of α decay half-lives between experimental data and calculated one is shown in figure 1.From this figure,we can see that the deviations in the two regions i.e.158 ≤A≤180 and 222 ≤A≤254 are obviously larger.This clearly shows the influence of nuclear deformation on the calculation results.The overall calculation result is better,although there is a slight deviation at some points,such asA=254,256 and 258.We speculate that this may be caused by the difference between the theoretical value and actual value of the deformation parameters(β2,β4and β6).In other words,if the experimental data and the model formula used are reliable,we may be able to take the experimental value as the input and use this model to reverse the deformation parameter.We will consider making an attempt in this regard and expect experimenters to measure these nuclei.

In order to provide a reference for the synthesis of new elements,we extend this model to predict the α decay halflives of 14 even–even nuclei withZ=118 andZ=120 in the following.As we all know,in the α decay,the half-lifeT1/2is extremely sensitive toQα.Therefore,to obtain the precise predictions of α decay half-lives for the heavy and superheavy nuclei,the method of selecting a more preciseQαis at the heart of the matter.In this work,we use four mass tables i.e.WS-type[73],simple nuclear mass formula(SNMF)[74],relativistic continuum Hartree–Bogoliubov(RCHB)[75]and DZ19[76],to obtainQα.The calculated results are listed in table 2.In this table,the first column is α decay parent nucleus,and the second to fifth columns are the differentQαfrom the four mass tables,respectively.The last four columns are the logarithmic form of α decay half-lives corresponding to the four mass tables.To see more intuitively,the value ofQαand predicted α decay half-lives for even–even nuclei withZ= 118 and 120 are drawn in figure 2.In this figure,we can clearly see thatN=184 has an obvious shell effect.However,the shell effect ofN=178 is not observed.TheQαin this figure are from the mass tables:WS-type[73],SNMF[74],RCHB[75]and DZ19[76].Combined with the mass table quoted by Cuiet al:WS4[77],FRDM[78],KTUY[79]and GHFB,it is not difficult to draw a conclusion:N=184 is a magic number,but the shell effect ofN=178 is dependent on models.This information may help to provide a reference for future work.

Figure 2.The value of Qα and predicted α decay half-lives for even–even nuclei with Z=118 and 120 isotopes.The black square and red dot indicate Z=118 and Z=120,respectively.The abscissa is neutron number N,the ordinate in the left column is Qα in Mev,and the ordinate in the right column is logarithmof calculated half-life in s.The mass tables used from top to bottom in this figure are WS-type[73],SNMF[74],RCHB[75]and DZ19[76].

4.Summary

In this work,the TPA is extended to the study of deformed nuclei.Through a systematic study of α decay half-lives for 196 even–even nuclei,we find that TPA after taking deformation into account are in better agreement with the experimental data.In addition,the α decay half-lives of 14 even–even nuclei withZ=118 andZ=120 isotopes are predicted by using the four mass tables of WS-type,SNMF,RCHB and DZ19.Combining the mass tables(WS4,FRDM,KTUY,GHFB)used in Cuiet alʼs work,we can conclude thatN=184 is a magic number andN=178 is dependent on models.This work will help to provide reference to the future research.

Acknowledgment

Supported by the National Natural Science Foundation of China(Grants No.12 175 100 and No.11 975 132),the Construct Program of the Key Discipline in Hunan Province,the Research Foundation of Education Bureau of Hunan Province,China(Grant No.18A237),the Innovation Group of Nuclear and Particle Physics in USC,the Shandong Province Natural Science Foundation,China(Grant No.ZR2019YQ01),Hunan Provincial Innovation Foundation For Postgraduate(Grant No.CX20210942 and No.CX20200909),the Opening Project of Cooperative Innovation Center for Nuclear Fuel Cycle Technology and Equipment,University of South China(Grant No.2019KFZ10).

Appendix.Calculation formula of coulomb potential

ORCID iDs