Variable viscosity effects on the flow of MHD hybrid nanofluid containing dust particles over a needle with Hall current—a Xue model exploration
2022-06-29MuhammadRamzanandHammadAlotaibi
Muhammad Ramzan and Hammad Alotaibi
1 Department of Computer Science,Bahria University,Islamabad,44000,Pakistan
2 Department of Mathematics,College of Science,Taif University,PO Box 11099,Taif 21944,Saudi Arabia
Abstract This study scrutinizes the flow of engine oil-based suspended carbon nanotubes magnetohydrodynamics(MHD)hybrid nanofluid with dust particles over a thin moving needle following the Xue model.The analysis also incorporates the effects of variable viscosity with Hall current.For heat transfer analysis,the effects of the Cattaneo–Christov theory and heat generation/absorption with thermal slip are integrated into the temperature equation.The Tiwari–Das nanofluid model is used to develop the envisioned mathematical model.Using similarity transformation,the governing equations for the flow are translated into ordinary differential equations.The bvp4c method based on Runge–Kutta is used,along with a shooting approach.Graphs are used to examine and depict the consequences of significant parameters on involved profiles.The results revealed that the temperature of the fluid and boundary layer thickness is diminished as the solid volume fraction is raised.Also,with an enhancement in the variable viscosity parameter,the velocity distribution becomes more pronounced.The results are substantiated by assessing them with an available study.
Keywords:hybrid nanofluid,dusty fluid,variable viscosity,Cattaneo–Christov heat flux model,Hall current
Nomenclature


Introduction
The use of liquid flow for cooling in a range of applications for instance automobiles,metallic plate cooling,and electronics has gained great popularity.In all of these cooling systems,various convectional fluids such as water,ethylene glycol,water mixtures,and other basic fluids are exercised as coolants.Several researchers have made significant contributions to improving the thermal conductivity of coolants for many years.Choi and Eastman[1]proposed the utilization of nanoparticles to increase the thermal conductivity of base liquids.Nanofluids are essentially a mixture of solid nanoparticles and liquid coolants that have been combined.The introduction of this new kind of coolant completely transformed the current manufacturing world.The ability of nanoparticles to enrich the heat transfer phenomena of the base fluid is quite remarkable.Many studies followed up on the pioneering work of Choi and Eastman[1]by looking into the impression of putting different solid nanoparticles into a variety of working fluids along with different geometries and finding interesting results[2–6].The cuttingedge nanofluid,‘hybrid nanofluid,’has recently been the subject of several discreet research using two kinds of nanoparticles submerged in a base fluid.To maximize the heat transfer rate of a hybrid nanofluid,a proper combination of nanoparticles must be used.Hybrid nanofluids have a wide variety of applications in medical,lubricating,solar heating,microfluidics,nuclear system and cooling,and thermal management of vehicles.In comparison to ordinary nanofluid,the hybrid nanofluid is more efficient as a cooling agent.The concept of a hybrid nanofluid is discussed in several scholarly works.Wainiet al[7]demonstrated the flow of the hybrid nanofluid with(PHF)prescribed heat flux over a thin needle erected vertically.It is noticed that rising the volume fraction of copper(Cu)nanoparticles and lowering the needle size results in a rise in the skin friction coefficient and the heat flux rate on the needle.Additionally,Sulochanaet al[8]scrutinized the Al–Cu/menthol flow of the nanofluid(hybrid)across a thin needle with(thermal)radiation effects.It is discovered that increasing the needle thickness has a substantial effect on the heat transfer rate of hybrid nanoliquid.Mousaviet al[9]established the hybrid nanofluid flow comprising TiO2–Cu/H2O along a thin needle accompanying the radiation effects.The results reveal that dual solutions exist for the reverse direction of the free stream of the thin needle.Rameshet al[10]deliberated the heat transmission of a hybrid liquid across a thin needle in a spongy medium with different effects.Further literature on hybrid nanofluids is available in the[11–18].
It is well established that heat transfer happens between two bodies or inside the same body as a result of a temperature difference.Heat transfer is a tremendously important phenomenon in industrial,technical,and biological applications.Fourier was the first to explain the heat transmission process[19].However,it has the drawback of producing a parabolic energy equation for the temperature distribution.Cattaneo[20]solved this problem by adding the thermal relaxation period to the basic Fourier formula of heat conduction.Finally,Christov[21]replaced the Cattaneo law with an Oldroyd upper convected derivative in the Maxwell–Cattaneo model to preserve the formulation’s material invariance.Cattaneo–Christov(C–C)heat flux model consistency concerns have been examined by Ciarletta and Straughan[22]in both specific and systematic approaches.The latest research has highlighted the significance of the C–C heat flux in varied models[23–27].
Numerous researchers have devoted years to studying the heat transfer properties of dusty fluid flow,which is a two-phase fluid,to better understand a variety of real-world challenges,particularly in the meteorological,medical,and engineering domains.Dust particles are employed in a diverse application,including the petroleum industry,soil erosion caused by natural winds,crude oil purification,aerosol and fluidization,paint spraying,dust entrainment after nuclear explosions in clouds,and wastewater management[28–30].Saffman[31]developed the first dusty fluid flow equations and analyzed the stability of the laminar flow of a dusty gas with equally distributed particles.Later,Chakrabarti[32]studied dusty gas utilizing boundary layer theory.Numerous scholars have since worked on dusty fluid flow on different geometries.Recently,Kumaret al[33]considered the flow of suspended carbon nanotubes(CNTs)in a dusty nanofluid across a stretched porous rotating disk.The results indicate that SWCNT-water-based fluid exhibits a higher rate of heat transfer than MWCNTs water-based fluid in both the dust and fluid phases.Gireeshaet al[34]used numerical simulations to investigate the significance of nonlinear thermal radiation and hall currents on a dusty fluid on a heated stretched sheet,whereas Abbaset al[35]investigated dusty fluid flow in a spongy media while taking slip and MHD into account.More work on dust phase fluid can be found in[36–39].
The main contribution of this investigation is to deal with the MHD nanofluid flow with CNTs in engine oil with thermal slip across a thin moving needle in two dimensions.Dust particles are also studied concerning Hall current and varying viscosity.C–C theory and heat generation/absorption are also cogitated in the temperature equation for heat transfer analysis.CNTs-based hybrid nanofluid’s thermal conductivity is analyzed using a new model named the Xue model.Using the relevant similarity transformations,the resultant system of a highly nonlinear system is numerically resolved.The findings are presented using graphs.The leading objective of the present exploration is to look for the answers to the ensuing questions:
•What are the consequences of solid volume fraction on the dust and hybrid nanofluid phases?
•How does solid volume fraction affect the temperature of the hybrid nanofluid and dust phases?
•What is the impact of fluid particles’ interaction parameters on the fluid velocity and dust phases?
•How hybrid nanofluid particle interaction parameter affects the fluid and dust phases?
•What is the consequence of the Eckert number on the fluid temperature?
Mathematical modeling
We consider a hybrid nanofluid flow past a moving needle with temperature-dependent viscosity(figure 1).The Xue model is adopted with single-wall and multi-wall CNTs immersed into the engine oil(base fluid).The radius of the cylindrical needle is presumed asR=r(X).Here,the needle’s leading edge is along theX-axis andR,Xare assumed as the radial and axial coordinates.Here,the transverse curvature is considered nevertheless the pressure gradient in the body direction is ignored.The wall temperatureTwand the temperature far away from the wall∞Tare taken as constant withTw>T∞.The movement of the needle is observed with a constant velocityVw.
Nanofluid phase:[5,43]

Dust phase:[42]
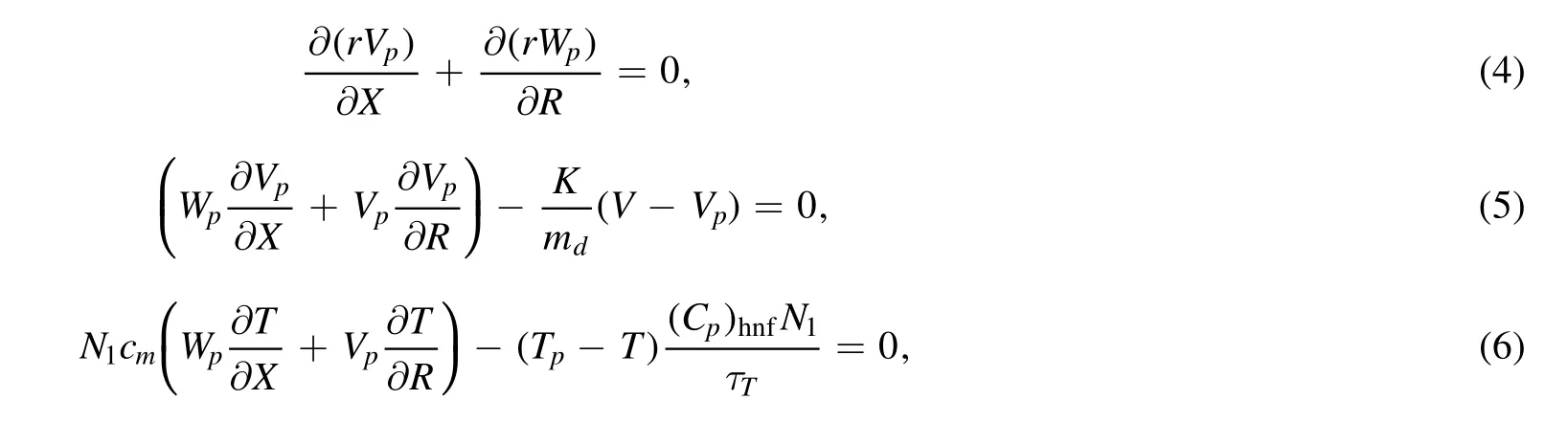
the stretching velocity and thermal slip boundary conditions are given as:

Table 1 presents the attributes of the CNTs and the engine oil(base fluid).
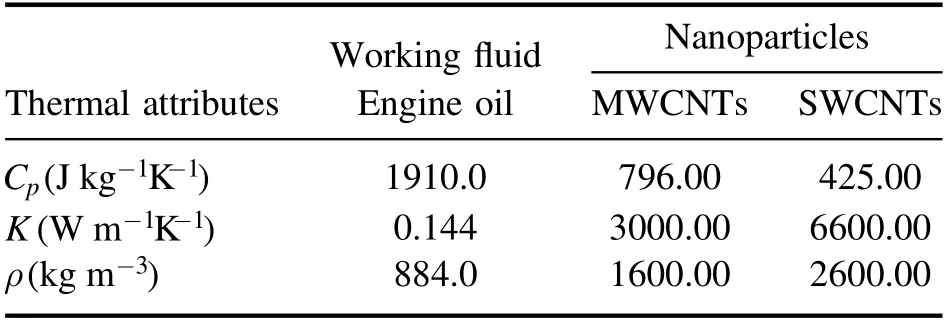
Table 1.Thermal and physical traits of engine oil and CNTs(SWCNTs and MWCNTs)[44].
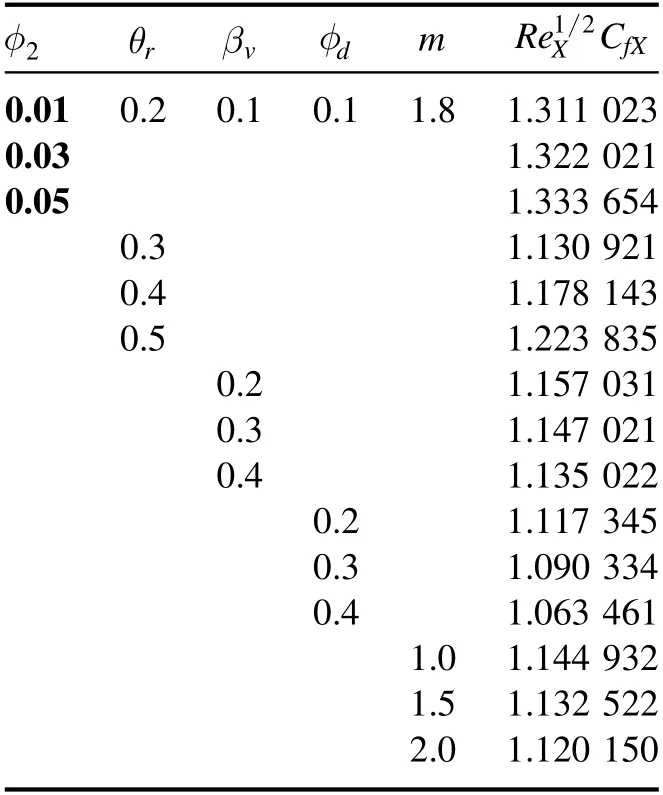
Table 2.Numerical calculations of skin friction whenPr=6.2,M=0.2,φ1=0.03,α=0.2.

Table 3.Verification of the current problem for the varied values of c whereφi,d= 0= λ =βv= m =M with Ishak et al[40],Afridi et al[41],and Tlili et al[42].
The variable viscosity,thermal conductivity,density,and specific heat for SWCNTs/engine oil(nanofluid)and SWCNTs-MWCNTs/engine oil(hybrid nanofluid)are specified as[44,45]:

Simple nanofluidHybrid nanofluid()α=ρ k C,pnf nfnf()()μ μ=−−φ θθ 11,nf f 2.5 r()()()()αρC,μ μ φφ==−−−θθ k 111,p f hnfhnf hnf hnf 12.522.5 r()()()()ρρφ ρφ=+−CC C1,pp p nfSWCNT f()()(){()()()}ρρφφ φ ρφ ρC=−−×−+CC C 1 1,ppT p fp hnfSWCN22 1 1MWCNT()ρφρφ ρ=+ 1−,nfSWCNTf(){()}ρφ ρφ φ ρφ ρ=+ −×−+1 1,hnf2 SWCNT2 1 f1 MWCNT()()()()()()φφ φφ=−+−+−+−+kk 12ln 12ln.k kk kk k k kk kk k nf f T NT f f SWCNTf SWCNT SWCNf SWCf SWCNTf f()()()()()()φφ φφ=−+−+−+−+kk 12ln 12ln,k kk kk k k kk kk k hnf nf 22 22 Tnf bf SWCNT SWCNnf SWCNTnf SWCNTnf SWCNTnf nf()()()()()()φφ φφ=−+−+−+−+k kk 12ln 12ln.k kk kk k k kk k k nf f 11 11 T T T T MWCNT MWCNf MWCNf f f MWCNf MWCNf f
The solid volume fraction of SWCNTs is denoted byφ2and that of the MWCNTs is clarified byφ1,specific heat and thermal conductivity of regular fluid are correspondingly defined byCpandkf.
Similarity analysis
Using the similarity transformation[46]:
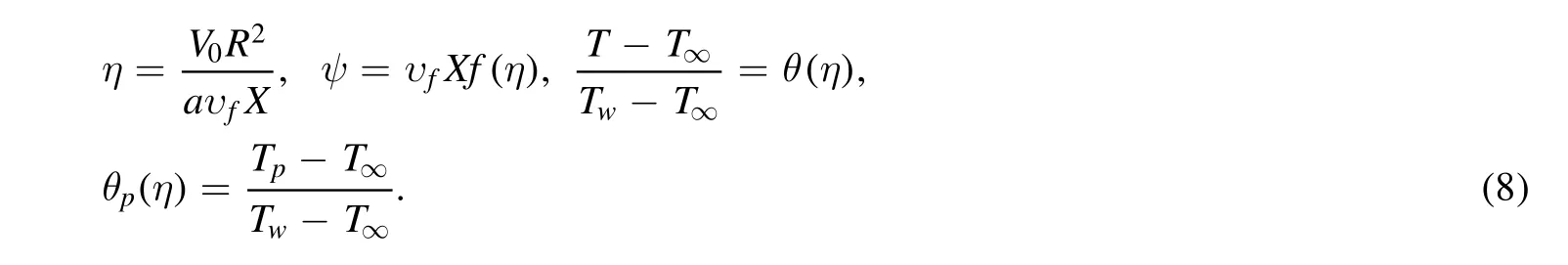
Applying equation(8),the above nanoparticle phase equations are transmuted to:
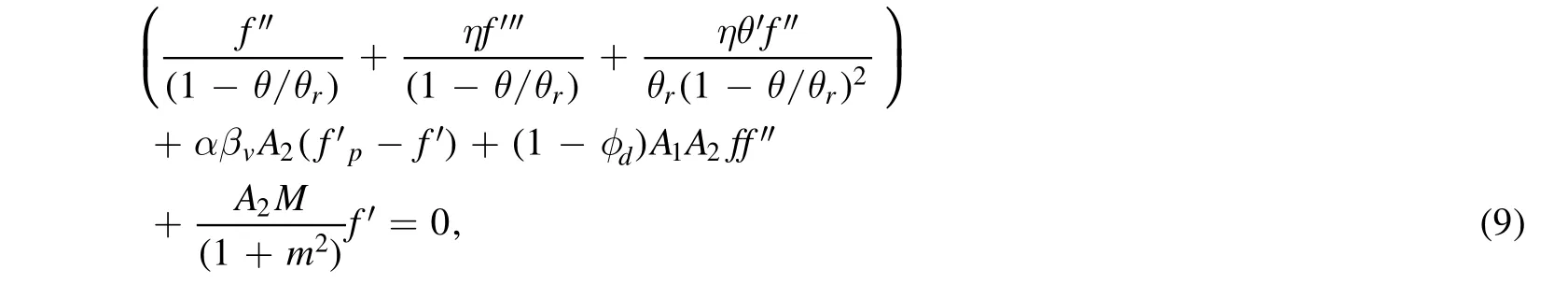
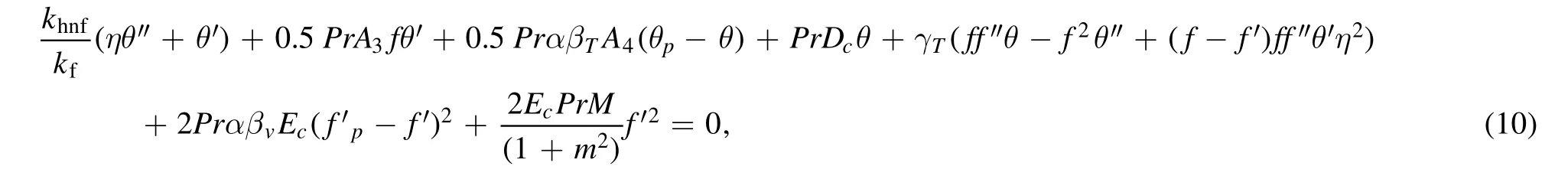
and the dust phase equation becomes:

with the transformed conditions:

The parameters involved in equations(9)–(13)is identified as:

Physical engineering quantities
The surface drag coefficient and the rate of heat flux are identified as:

Using equation(10)in(17)we gained,
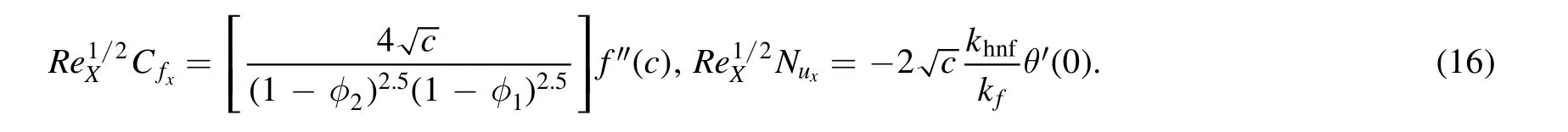
Numerical appraisal
By implementing the Runge–Kutta-based MATLAB function bvp4c,the existing problem solution is found numerically.In addition,we ‘shoot’ directions in this method in different ways until we have the appropriate boundary value.This is a technique that is very simple and effective.We take the convergence criterion to reach the solution,which is10−5.The solution is achieved graphically concerning different variables for the velocity and temperature for both the fluid phase and the dust phase.

Outcomes and discussion
This section describes the salient parameters’correlation with the associated profiles.The values of the involved parameters are taken as:m=2,θr=0.1,βv=0.3,α=0.2,γT=0.5,δ=0.1,λ=0.2,M=0.2,Pr=6.2,βT=3,Ec=0.01,Dc=0.1,c=0.01.Figures 2–5 demonstrate the significance of solid volume fraction of SWCNTs and MWCNTs on velocity and temperature fields of fluid and dust phase.Figures 2 and 3 scrutinized the impact of solid volume fraction on velocity distribution for fluid and dust phases.It is found that the velocity of the fluid and dust phases is enhanced with an increase in the solid volume fraction.The thermal conductivity of the fluid is directly proportionate with the volume fraction that improves the fluid velocity for both fluid and dust phases.Nevertheless,the temperature profile and its related boundary layer thickness diminish for enlarged estimation of solid volume fraction(see in figure 4).While the dust phase temperature and their accompanying boundary layer thickness are enhanced(figure 5).To identify the influence of fluid particles’ interaction parameterβvon both velocities figures 6 and 7 are sketched.It is seen that both the velocities are diminished forβ.vThis is owing to intensified fluid particles interaction that creates an opposing force to the fluid flow.This phenomenon continues till the dust phase fluid velocity accesses the fluid phase velocity.That is why declined velocities are seen here.Figures 8 and 9 are plotted for both velocity profiles for varied values of dust particles mass concentrationα.Velocity distribution for both fluid and dust phase reduces for enlarged values ofα.The accumulation of the dust particles into the fluid strengthens the surface drag force that eventually resists the fluid motion.That is why diminished velocities for both phases are observed.The temperature of the fluid and dust phase is an escalating function of the fluid particle interaction parameterβT(figures 10 and 11).It is understood from the figures that increasing values ofβTsimmer down the fluid.Thus,βTacts as a controlling agent for the flow behavior.The influence of the Eckert numberEcon the fluid temperature is exhibited in figure 12.It is concluded that the temperature profile enhances for significant estimates ofEc.The physical explanation for this outcome is an improvement in kinetic energy and the collision among nanofluid molecules because of its direct association with the Eckert number.Figure 13 examines the impact of the thermal relaxation parameterγTon the temperature field.It is comprehended that the temperature of the fluid is on the decline for numerous values ofγT.Higher estimates of theγTspecify the qualities of the insulating material that lowers the fluid temperature.That is why we see a diminishing thermal profile.Figure 14 highlighted the impression of the heat generation parameterDcon the temperature profile.It is inspected that the temperature and its correlated thermal boundary layer thickness enhance with the large estimation of heat generation parameter.It is because excessive energy is produced for large estimates of heat generation that eventually boosts the fluid temperature.
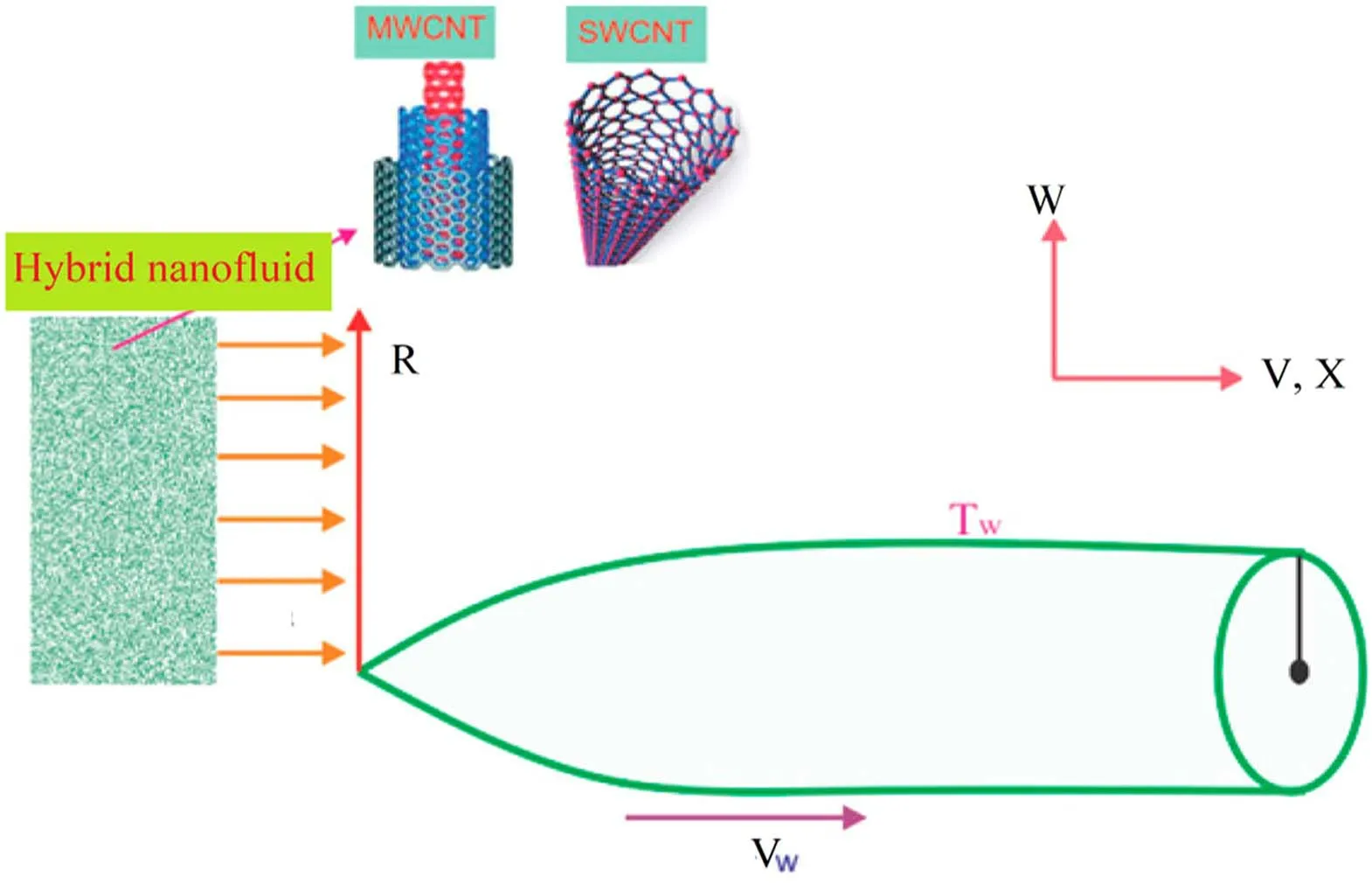
Figure 1.Flow problem model.
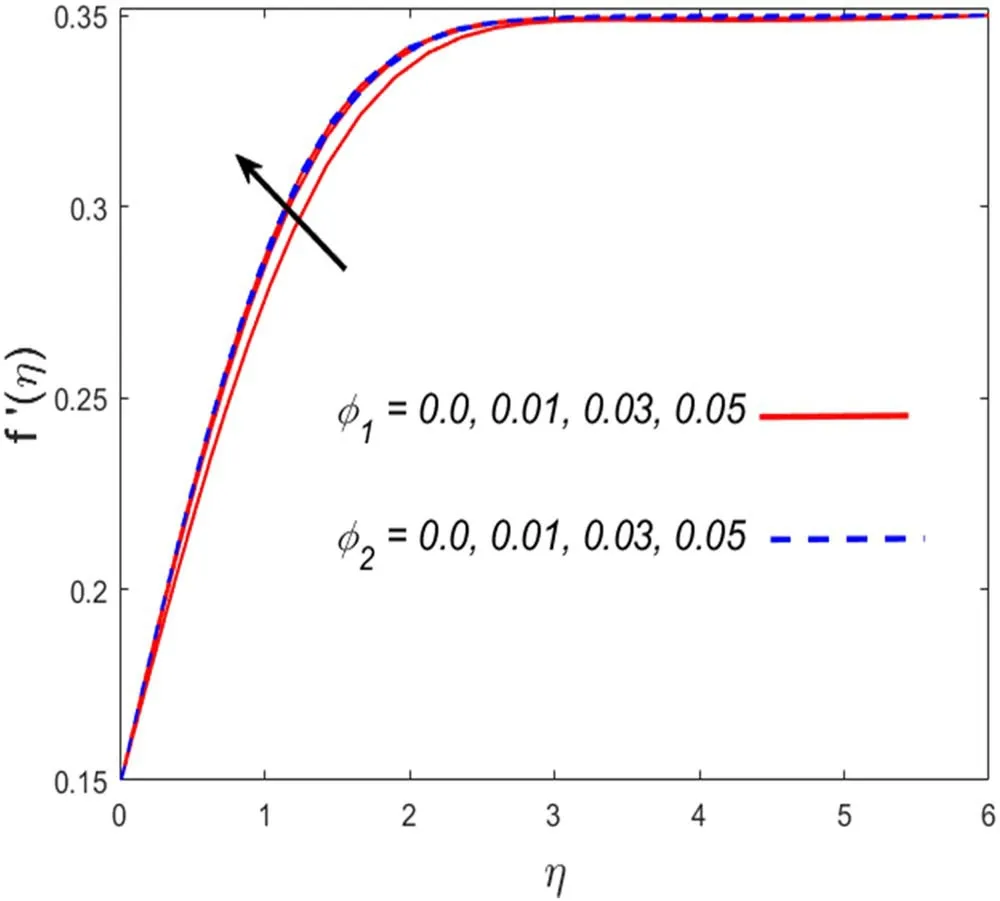
Figure 2.Association ofφ 1,φ2 and f′(η).

Figure 3.Association ofφ 1,φ2 andfp′(η).

Figure 4.Association ofφ1,φ2 and θ (η).
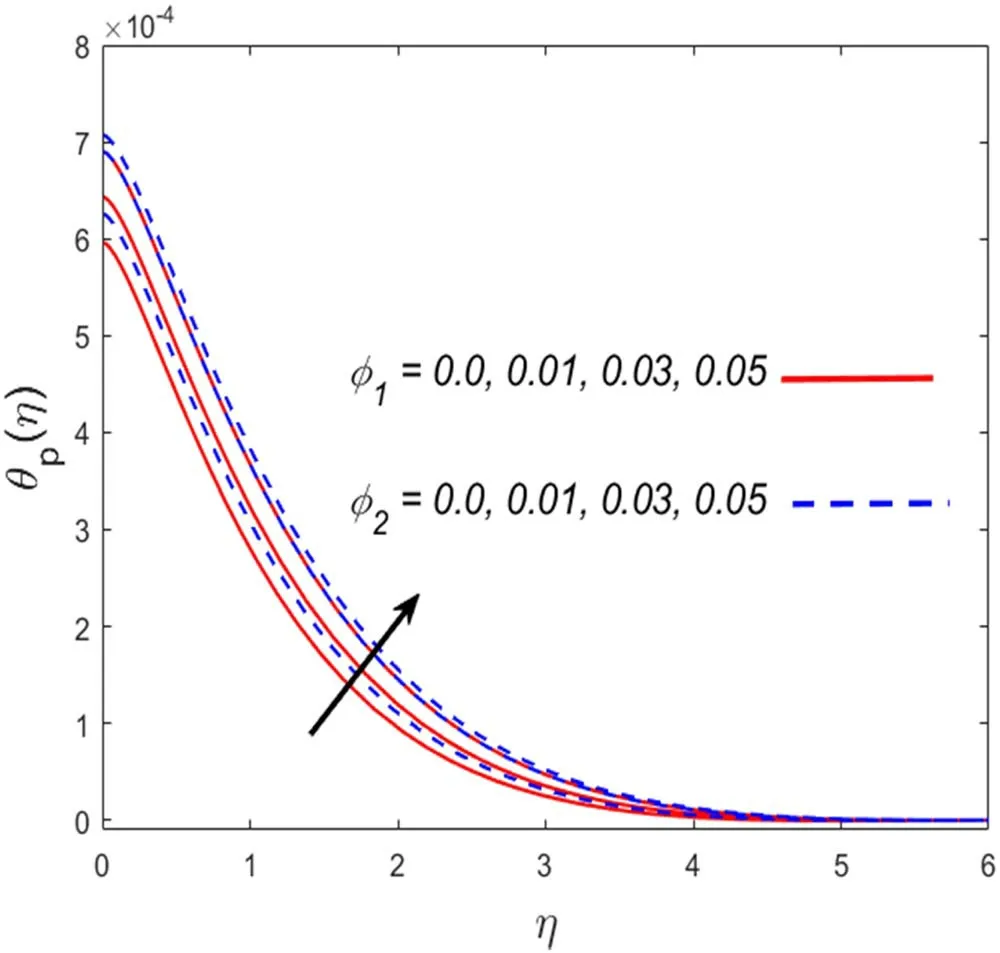
Figure 5.Association ofφ 1,φ2 and θp (η).

Figure 6.Association of βv and f′(η).
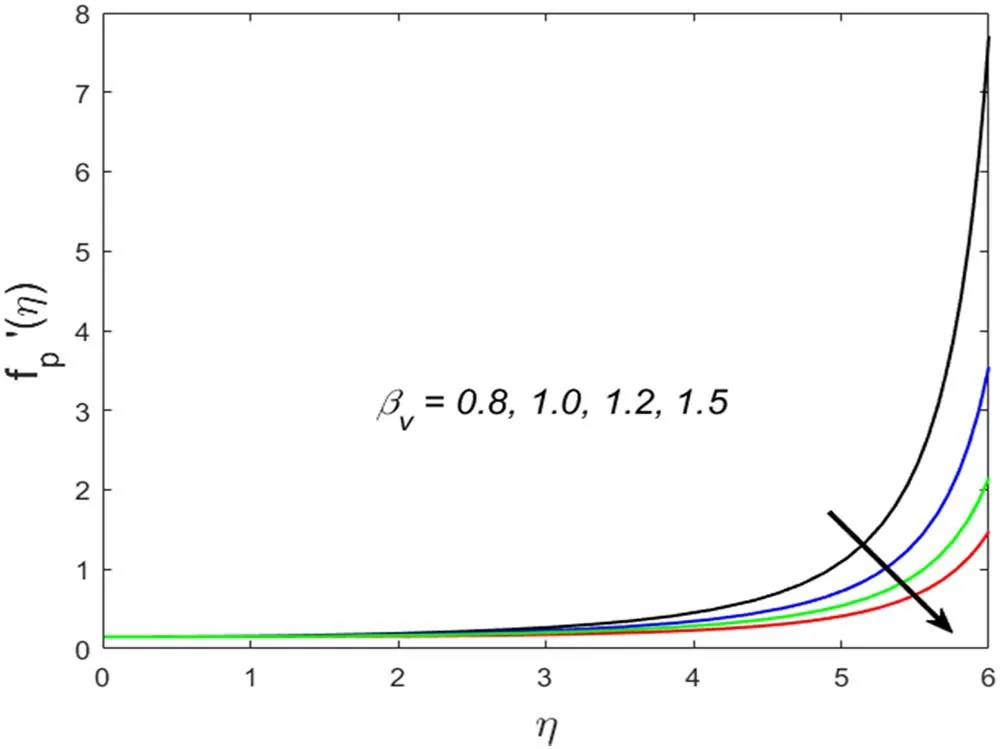
Figure 7.Association of βv andfp′(η).
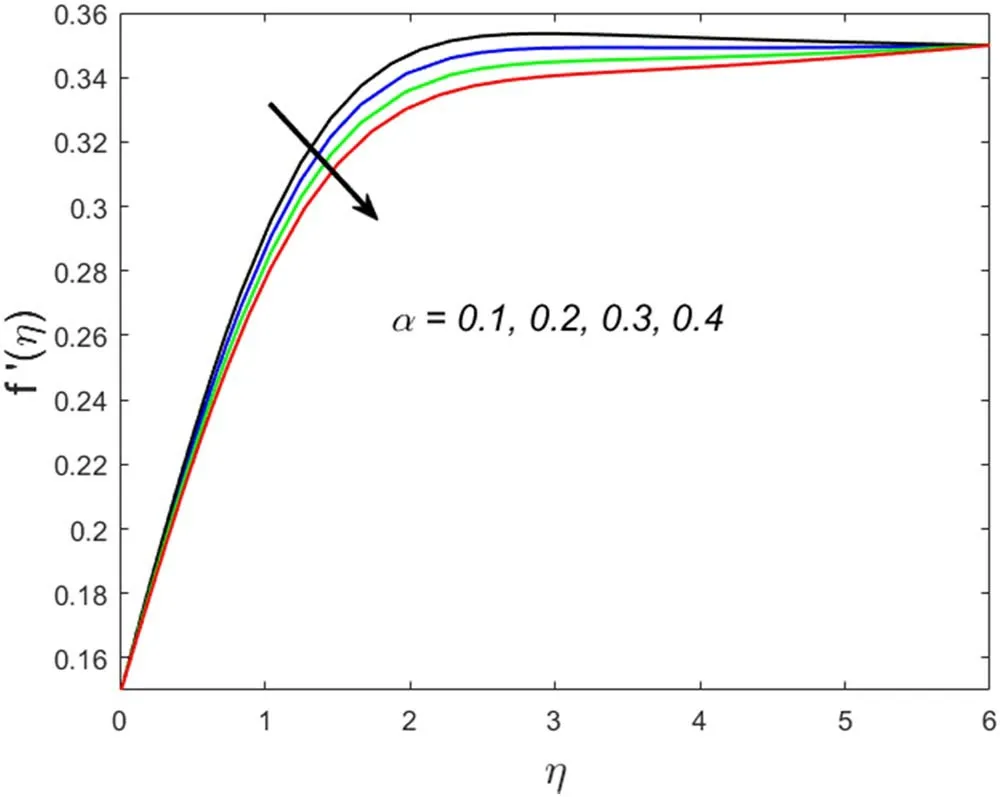
Figure 8.Association of α and f′(η).
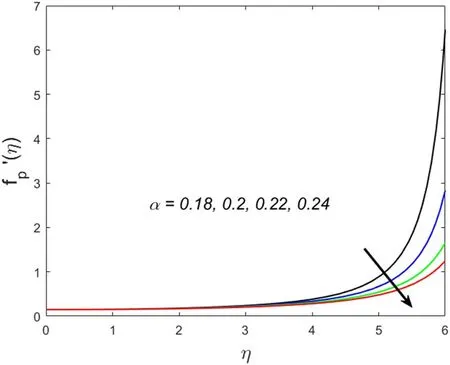
Figure 9.Association of α andfp′(η).
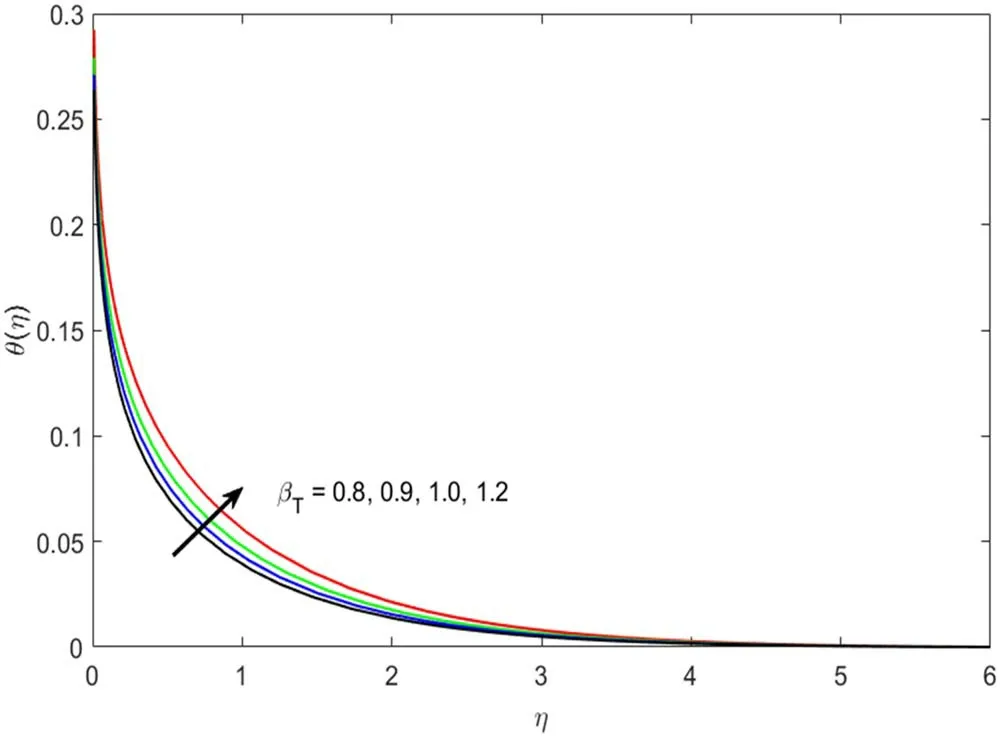
Figure 10.Association of βT and θ (η).
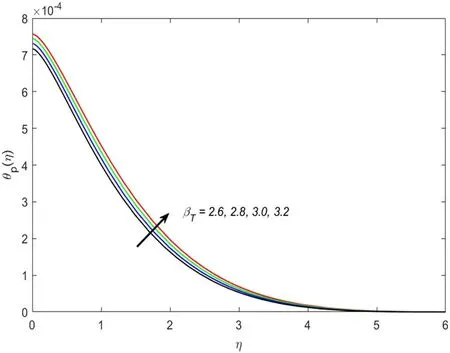
Figure 11.Association of βT and θp (η).

Figure 12.Association of Ec and θ (η).

Figure 13.Association of γT and θ (η).
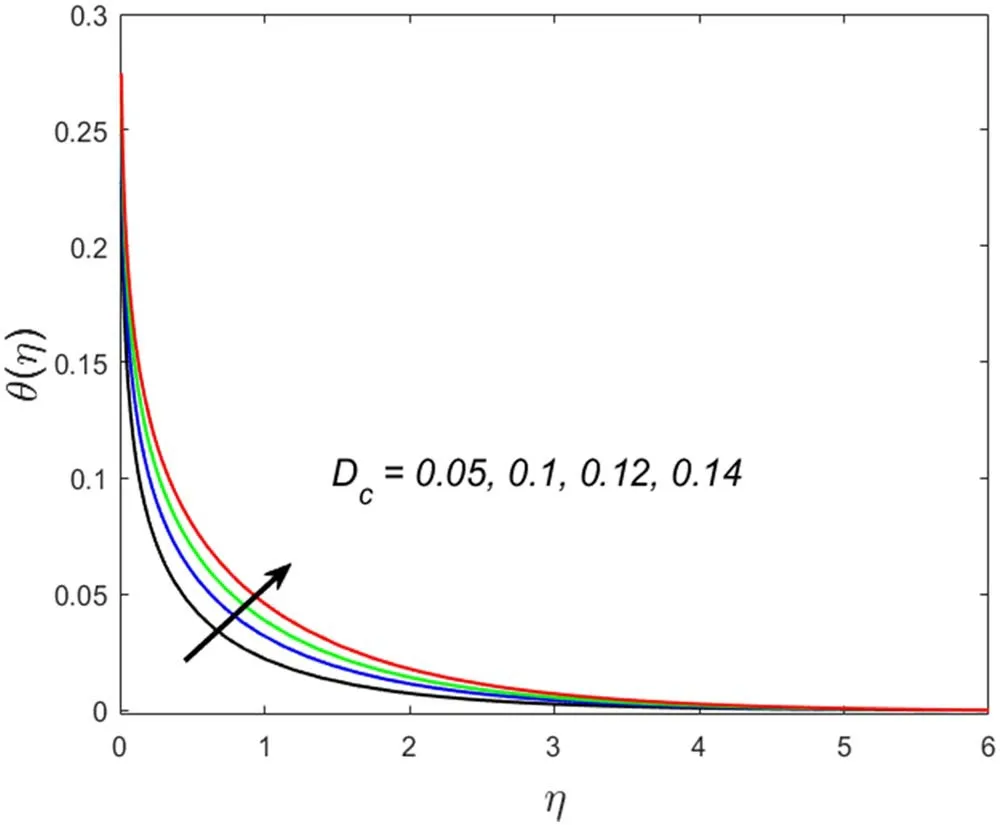
Figure 14.Association of Dc and temperature field θ (η).
Table 2 demonstrates the surface drag coefficient for numerous values of varied parameters.It is demonstrated that the drag coefficient augments with higher the estimation of solid volume fraction and variable viscosity parameter while its declines with higher the estimation of Hall current parameter,fluid particles interaction parameter,and volume fraction of dust particles.
The current result shows good accord with earlier published findings Ishaket al[40],Afridiet al[41],and Tliliet al[42](see in table 3).
Concluding remarks
This research has been established to explore the impact of the magnetohydrodynamics(MHD)2D,nanoliquid flow of engine oil as a working fluid.CNTs were inserted with thermal slip over a thin moving needle following Xue model.Variable viscosity and thermal C–C heat flux and the heat generation/absorption were supported by the thermal slip.The constructed model has been numerically handled using the bvp4c function of MATLAB software.The corresponding profiles are plotted against their relevant parameters and the findings are described coherently.The following are the most significant outcomes:
•The fluid phase and dust phase velocities are boosted as the estimates of solid volume fraction increase.
•For larger solid volume fraction estimation,temperature distribution and boundary layer thickness dwindled,while dust phase temperature raised.
•The fluid and dust phases velocities have dwindled for the improved fluid particles interaction parameter.
•Velocity distribution for fluid and dust phase reduces for enlarged values of dust particles mass concentration.
•The temperature distribution heightens for greater estimates of the Eckert number.
Acknowledgments
The authors are thankful for the Taif University research supporting project number(TURSP-2020/304),Taif University,Saudi Arabia.
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Author contribution statement
MR supervised and conceived the idea;HA wrote the manuscript.
杂志排行
Communications in Theoretical Physics的其它文章
- Less is more:a new machine-learning methodology for spatiotemporal systems
- Thermodynamics of the black holes under the extended generalized uncertainty principle with linear terms
- Potential energy surface and formation of superheavy nuclei with the Skyrme energy-density functional
- Systematic study of α decay half-lives for even–even nuclei within a deformed twopotential approach
- Magnetic correction to the anomalous magnetic moment of electrons
- Friedberg-Lee neutrino model with μ–τ reflection symmetry
