Magnetic correction to the anomalous magnetic moment of electrons
2022-06-29FanLinandMeiHuang
Fan Lin and Mei Huang
School of Nuclear Science and Technology,University of Chinese Academy of Sciences,Beijing 100049,China
Abstract We investigate the leading order correction of anomalous magnetic moment(AMM)to electrons in a weak magnetic field and find that the magnetic correction is negative and magnetic field dependent,indicating a magnetic catalysis effect for the electron gas.In the laboratory,to measure the g −2,the magnitude of the magnetic field B is several T,and correspondingly the magnetic correction to the AMM of electron/muon is around 10−34/10−42,therefore the magnetic correction can be safely neglected in the current measurement.However,when the magnitude of the magnetic field strength is comparable with the electron mass,the magnetic correction of the electron’s AMM will become considerable.This general magnetic correction to the charged fermion’s AMM can be extended to study quantum chromodynamic matter under a strong magnetic field.
Keywords:anomalous magnetic moment,magnetic correction,magnetic field
1.Introduction
Recently,the anomalous magnetic moment of the quark[1–10]has attracted much interest in investigating quantum chromodynamic(QCD)matter under a strong magnetic field created through non-central heavy ion collisions[11,12].It has been known that the magnetic field catalyzes the chiral condensate of a spin-0 quark–antiquark pair which carries a net magnetic moment and triggers a dynamical anomalous magnetic moment(AMM)of quarks[13–15].The exact value of a quark’s AMM under a magnetic field is unknown but very important for magnetized QCD matter.In this work,we will gain some experience by investigating the AMM of electrons in a magnetic field,which can be calculated from theory and measured experimentally with high precision.
It is well known that a charged fermion can interact with an external magnetic field through an intrinsic magnetic momentum(ħ=1,c=1)

whereq,m,and s are the charge,mass,and spin of the fermion,respectively.For an electron,theLandéfactorgeis believed to be exactly equal to 2 according to Dirac relativistic quantum mechanics.Until a small derivation is observed in an elaborate experiment[16],the deviation ofgefrom 2 is defined as the anomalous magnetic momentae=(ge−2)/2.Meanwhile,quantum electrodynamics(QED)was in its ascendancy and has deepened our understanding of the physical vacuum,where the creation and annihilation of virtual particles contribute additional loop-diagram corrections.The leading order correctionae=α/2π(α ≃1/137 is the fine structure constant of QED)calculated by J.Schwinger[17]with renormalizable QED matches the experimental measurement perfectly,powerfully manifesting the validity of quantum field theory.
In the standard model,the theoretical contribution toaecomes from three types of interactions,electromagnetic,hadronic,and electroweak:
ae(theory)=ae(QED)+ae(hadronic)+ae(electroweak),
where the QED contribution can be expressed with perturbative expansion:

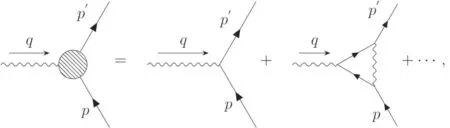
Figure 1.The Feynman diagram of total electron–photon vertex.
J.Schwinger’s consequence givesand the latest calculation from Aoyamaet al[18,19]has reached up to the tenth-orderae(10)with the help of the automatic code generator numerically.The accuracy of experimental electron’s AMMae(experiment)also enhances continually with measurements in a one-electron quantum cyclotron[20–22],which provides us with surprising consistency[19,22]
ae(experiment)−ae(theory)= −1.06(0.82)×10−12.
In essence,the emergence of the electron’s AMM is related to slightly broken chiral symmetry because of electron massme[13],implying any dynamical mechanisms can further break the chiral symmetry always inducing an extra AMM.Naturally,the external magnetic field existing in a one-electron quantum cyclotron is worthy of consideration,for the study of massless spinor QED explicitly shows that a magnetic field reinforces chiral symmetry breaking by endowing the electron with a dynamical mass,known as the magnetic catalysis effect[23],which suggests that the magnetic field could provide an electron with an extra correction.Recently,the latest experimental measurement of muongμ−2 confirms the disagreement between experiment and theory[24–28],for the potential possibility as a window to pry into new physics,attracting much attention.All of these motivate us to investigate an electron’s AMM in a magnetic field and extend to general fermions,which can deepen our understanding of quantum field theory in a magnetic field.
In this work,we investigate the leading order correction of the magnetic field on the AMM of an electron,which can be calculated with relatively high precision.There have been some relevant works to calculate the magnetic correction of an electron by the mass operator and the eigenfunction method[29–32],but these do not consider the Feynman diagram of photon–electron vertex correction as done in usual quantum field theory[33].The motivation of this work is twofold:firstly,we would like to check how the magnetic field will modify the AMM of electrons;secondly,the magnetic field dependent on an electron’s AMM will shed light on the AMM of quarks under a magnetic field.
2.The leading order correction of electron–photon vertex

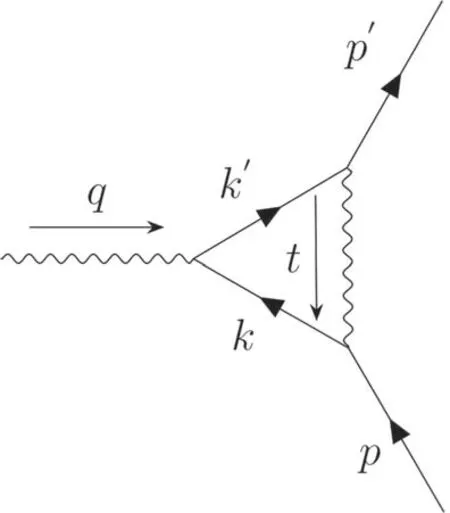
Figure 2.Leading order correction of electron–photon vertex.


this formula explicitly exhibits mass term,causing the lefthanded fermion to entangle with the right-handed one.If we naively setm=0,it leads to the massless spinor QED,which is an infrared-free theory,where the photon and electron are not coupled[34],then there will be no observable AMM,i.e.,F2≡0.Nevertheless,this does not conflict with the perturbative and mass-independent consequenceF2(0)=α/2π in the one-loop calculation,because QED is not an asymptotically free theory and does not possess a well-defined chiral limit,so the perturbative expression and computation ofF2(0)cannot be applied to the case ofm=0.In contrast,the QCD is asymptotically free,whose chiral limit could be rigorously defined nonperturbatively,so a quark’s AMM as a continuous function in the chiral limit is expected.This has been confirmed by the Dyson–Schwinger equation calculation[13],which reveals a dressed-quark with a mass ofMq∼0.5 GeV possessing an AMM κq∝Mq.In addition,κq∼0.1 is much bigger than an intrinsic one due to the strong breaking of the QCD’s chiral symmetry,dramatically changing the nature of quark matter in the magnetic field[10].The presence of a magnetic field induces a magnetic catalysis effect[35],but it is unknown how this would affect the AMM of quarks.It is quite challenging to do the direct calculation in QCDs because of the nonperturbative nature,therefore we will check the magnetic field-dependent behavior of an electron’s AMM and use it for reference in the case of quarks.
To calculate the magnetic field correction to the AMM of an electron,we put the Lagrangian density of QED in an external magnetic field,




2.1.The phase factor part



2.2.The momentum integral part


2.3.The AMM term extracted from Θμ(r,s)



3.Conclusion and discussion




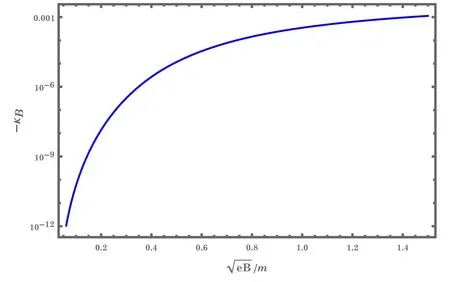
Figure 3.The magnetic correction to the AMM of electron/muon as a function of the dimensionless quantity ,with m=me or mμ.

As addressed in the introduction,the AMM of a quark plays a vital role for QCD matter under a strong magnetic field when the magnitude of the magnetic field becomes comparable with the quark mass square,such as in the early evolution of cosmological phase transition[43],non-central heavy ion collisions[12],and neutron-star merger[44].The exact value of the AMM of quarks under a magnetic field remains unknown because of its nonperturbative nature.In most literature,the AMM of quarks under a magnetic field was taken as a positive constant.We can extend the magnetic field-dependent AMM of electrons to the case of quarks and investigate its effect on the magnetized QCD matter.We will report the results in the forthcoming work[42].
Acknowledgments
We thank Xinyang Wang and Anatoly V.Borisov for their helpful discussions.This work is supported by the NSFC under Grant Nos.11 725 523 and 11 735 007,Chinese Academy of Sciences under Grant No.XDPB15 and XDB34000000,the start-up funding from University of Chinese Academy of Sciences(UCAS),and the Fundamental Research Funds for the Central Universities.
Appendix A.Calculation details in section 2.1
In order to to manage the Schwinger phase Φ(x,y)Φ(y,z),we have

and the only non-zero terms ofFμνareF12=−F21=−B,which gives
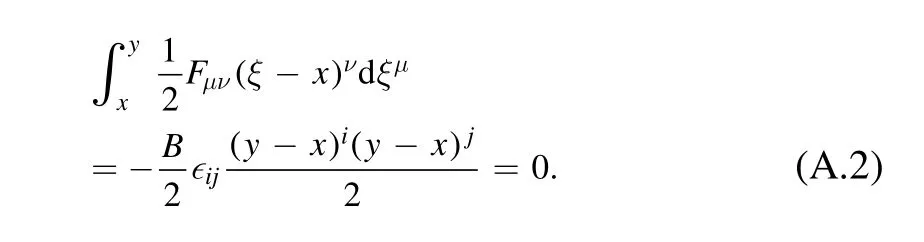
Then


Appendix B.Calculation details in section 2.2







Appendix C.Calculation details in section 2.3
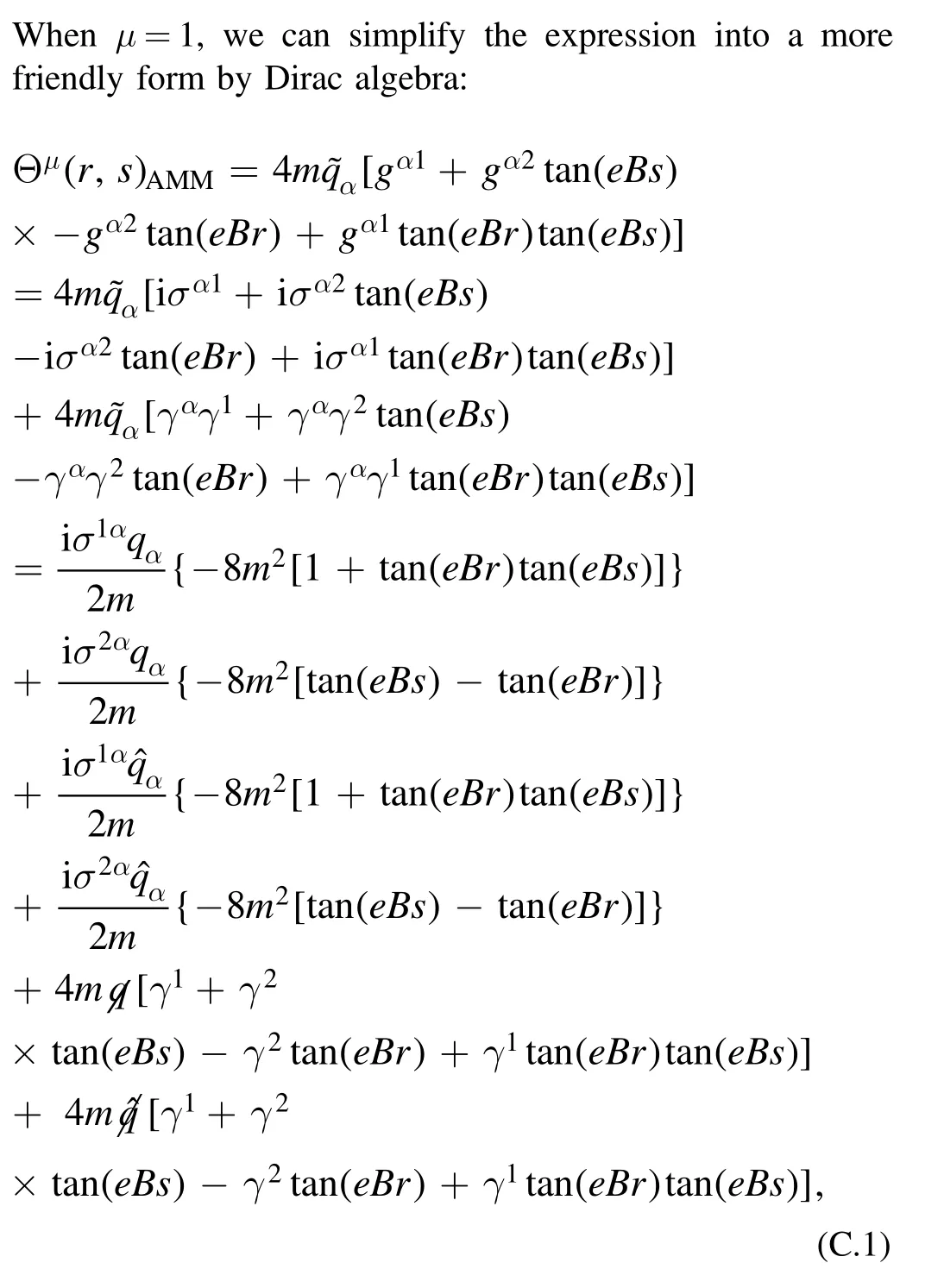




杂志排行
Communications in Theoretical Physics的其它文章
- Variable viscosity effects on the flow of MHD hybrid nanofluid containing dust particles over a needle with Hall current—a Xue model exploration
- Less is more:a new machine-learning methodology for spatiotemporal systems
- Thermodynamics of the black holes under the extended generalized uncertainty principle with linear terms
- Potential energy surface and formation of superheavy nuclei with the Skyrme energy-density functional
- Systematic study of α decay half-lives for even–even nuclei within a deformed twopotential approach
- Friedberg-Lee neutrino model with μ–τ reflection symmetry
