加速度载荷信息部分缺失下船舶机械噪声快速预报
2022-06-29刘西安杨德庆刘见华
刘西安, 杨德庆, 刘见华
(1. 上海交通大学 船舶海洋与建筑工程学院,上海 200240; 2. 上海交通大学 海洋工程国家重点实验室,上海 200240;3. 中国船舶与海洋工程设计研究院,上海 200011)
船舶作为水中弹性结构,在运行过程中不可避免受到设备激振载荷的作用而引起结构的振动,进而产生水下辐射噪声。船舶水下辐射噪声是衡量舰船隐身性能最重要的指标,随着声呐探测技术的迅速发展,对海军舰艇的声学隐身性能要求更加严格[1]。此外,由船舶产生的水下辐射噪声已经成为改变海洋环境噪声的主要因素。大量研究表明由船舶产生的水下辐射噪声对海洋生物特别是哺乳动物是个巨大的威胁,影响该类动物通讯、捕食、躲避天敌和繁殖,甚至导致该类生物逃避栖息地或者死亡[2-5]。而且随着全球化的深入发展,目前船舶水下辐射噪声仍以每年 0.2 dB 的速度增长[6]。因此,准确预报由设备激振力产生的水下辐射噪声对提高船舶声学性能和改善海洋声学环境具有重要的意义。
设备作为船舶水下辐射噪声的重要激振源,其加载方法直接影响预报的精度。设备激励载荷形式主要包括加速度载荷、激振力载荷与功率流载荷。由于安装环境和测量方法的限制,很难直接测量设备运行时传递到基座的激振力载荷和功率流载荷[7],而基座面板的响应加速度载荷具有测量方便、容易获取的优点,因此常常被用于表征设备的输入载荷。在工程实践中常通过载荷识别方法将加速度载荷转化为激振力载荷[8-9]用于结构振动及水下辐射噪声的预报。国内外学者对载荷识别方法进行了大量的研究,包括设备运行时的传递函数[10]、测量结果的可靠性[11]和载荷识别的方法[12]。此外,病态矩阵的处理[13]是载荷识别的重要的问题,一般通过奇异值分解方法[14]、截断奇异值分解方法[15]、总体最小二乘方法[16]、Tikhonov正则化方法[17]等可以有效地降低矩阵条件数,提高识别的精度。
现阶段对船舶机械噪声仿真计算和水声测量的研究已经取得了大量成果,但对设备加速度载荷的加载方法仍需进一步研究。首先,由于加速度载荷信息缺失,很难通过传统的载荷识别方法获得准确的设备激振力载荷;其次,载荷识别的核心问题是反演模型的选取,由于船用设备激励成分比较复杂,各个载荷分量对水下辐射声功率影响规律也不尽相同,选取合适的等效反演模型对识别设备激振力载荷与预报船舶机械噪声具有重要的影响。最后,在船舶设计阶段,设备载荷通常以平均加速度形式给出,如何考虑加速度载荷信息缺失对机械噪声的影响。因此,本文基于结构动力学基本原理,建立加速度载荷与设备激振力载荷之间的转化关系。基于声学边界元法,研究加速度载荷和激振力载荷对船舶机械噪声的影响规律。根据计算结果提出等效反演模型和能量叠加法以解决加速度载荷信息缺失情况下结构水下辐射声功率预报的问题,并将数值与试验结果进行对比,验证本文基于等效载荷模型快速预报方法的合理性和可靠性。
1 设备载荷类型对机械噪声影响
本章基于声学边界元法[18-19],研究了加速度载荷信息部分缺失对船舶机械噪声的影响,并讨论了激振力载荷分量对水下辐射噪声的影响规律。在进行振动和水声分析时,经常采用级的概念表征物理量,如下所示
AL=20lg(a/a0)
(1)
(2)
FL=20lg(F/F0)
(3)
(4)
WL=10lg(W/W0)
(5)
(6)
式中,AL为加速度级,dB;a为响应加速度,m/s2;a0=1×10-6m/s2为参考加速度;AOL为合成加速度级,dB;f1为频率下限,Hz;f2为频率上限,Hz;FL为力载荷级,dB;F为激振力,N;F0=1 N为参考力载荷;FOL为合成力载荷级,dB;WL为声功率级,dB;W为辐射声功率,W;W0=1×10-12W为参考声功率;WOL为合成声功率级,dB。
1.1 舱段计算模型
舱段模型如图1所示,模型的总长11.2 m,型宽5.2 m,吃水1.2 m,型深3.2 m,排水量48.5 t。材料为Q235普通钢。在Hypermesh中进行有限元建模,龙骨和板材结构均采用四边形或三角形板壳单元模拟。横梁、纵骨、扶强材采用两节点带偏置梁单元模拟。用实体单元和质量点单元模拟各设备,并施加到相应位置。采用实体单元模拟液舱中的压载水。单元大小依据一个波长至少有6个单元原则,单元大小为100 mm。计算舱段模型在给定激振力载荷下的船体湿表面速度响应,并将其作为机械噪声计算的声学边界条件,导入Virtual.Lab中采用声学边界元法求解舱段的水下辐射声功率。
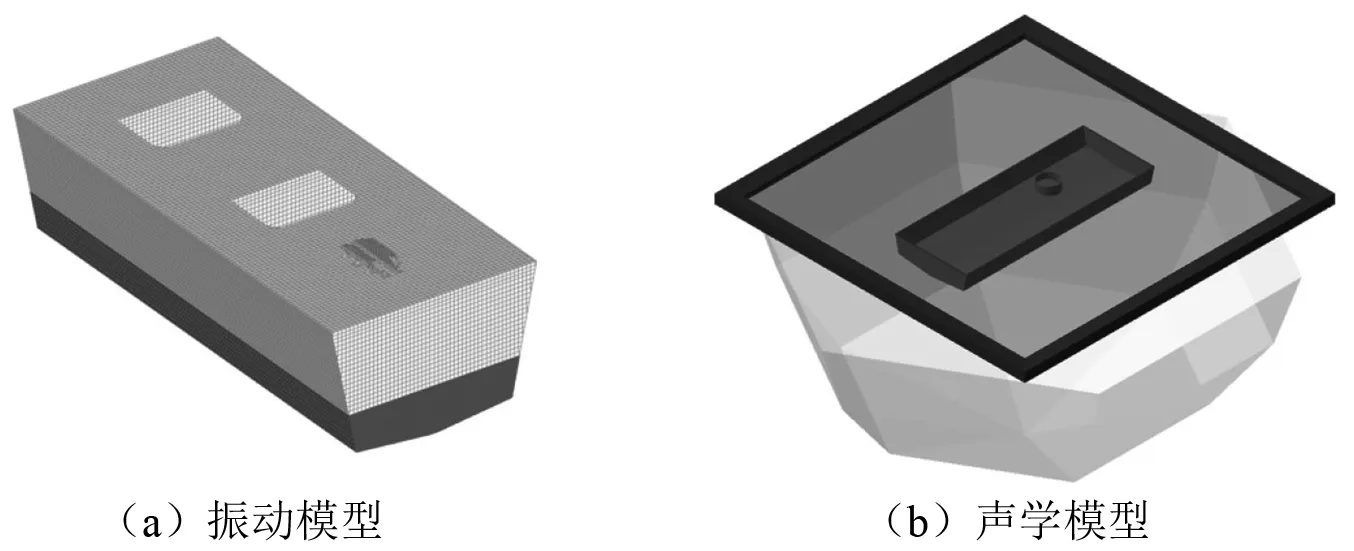
图1 舱段模型的振动与声学数值模型Fig.1 The compartment numerical model of vibration and acoustics
1.2 加速度载荷信息缺失对机械噪声的影响
设备激振力载荷通过隔振器传递到基座面板,振源设备引起的船体振动可以等效为基座面板的垂向加速度载荷(Az)引起的船体振动[20]。加速度载荷信息缺失时,会影响结构机械噪声的预报结果。本节主要研究加速度载荷幅值分布和相位信息缺失对船舶机械噪声的影响。假设设备安装于双层底短基座,设备的激振力载荷如图2所示,在整个频段内分别施加Fx=30 N,Fy=80 N,Fz=10 N,Mx=10 Nm,My=30 Nm,Mz=60 Nm的简谐载荷,采用声学边界元法计算舱段模型的水下辐射声功率,并获得基座与机械设备连接处的垂向加速度响应(Az)。然后,将该加速度响应作为水下辐射噪声的激励载荷,再次计算舱段模型水下辐射声功率。加速度载荷分为3种工况:LC1加速度载荷幅值和相位信息完整,采用幅值和相位加载;LC2加速度载荷相位信息缺失,采用幅值加载[21];LC3加速度载荷幅值分布信息缺失,采用平均加速度和相位加载。舱段模型在3种加速度载荷下水下辐射声功率线如图3~图4所示。
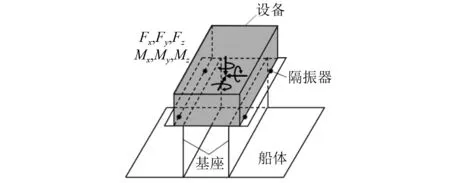
图2 设备的受力模型Fig.2 The mechanics model of the equipment
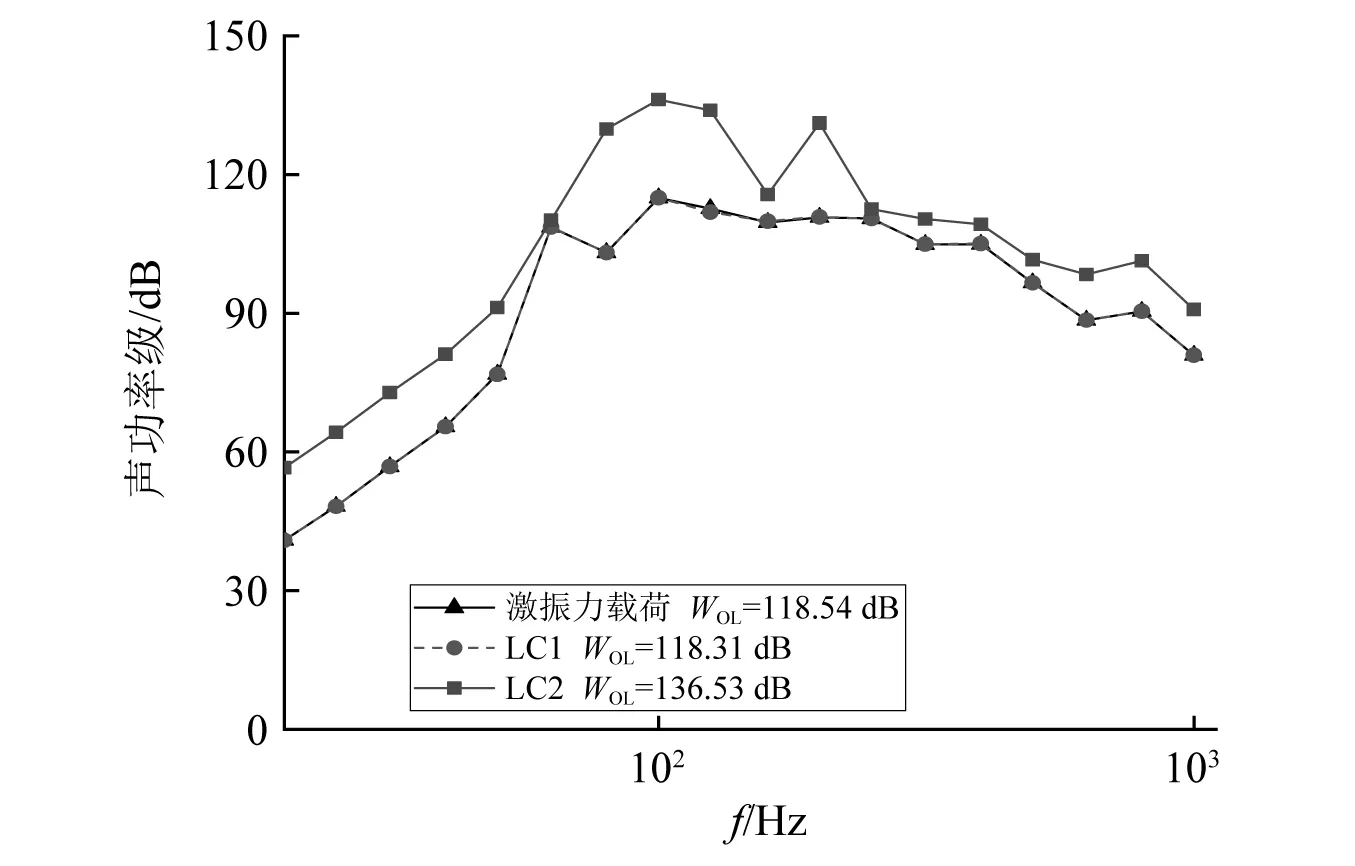
图3 加速度载荷相位信息对机械噪声影响Fig.3 The effect of acceleration phase on the mechanical noise

图4 加速度载荷幅值分布对机械噪声影响Fig.4 Effect of acceleration amplitude distribution on the mechanical noise
由图3、图4可知,与激振力载荷工况相比,加速度载荷信息完整时,水下辐射声功率总级的误差仅为0.23 dB;当加速度载荷幅值的分布信息缺失而相位信息完整时,水下辐射声功率总级的误差为0.14 dB,但低频段误差较大;当加速度载荷相位信息缺失时,水下辐射声功率总级的误差超过10 dB。上述结果表明,采用加速度载荷加载时,仅考虑加速度幅值的加载方式计算误差较大。这是因为基座与设备连接点处各点的加速度之间存在相位差,船体振动和水下辐射声功率不仅与连接点处加速度幅值有关,也与各点加速度间相位差有关。
1.3 力载荷分量对机械噪声影响规律
由理论力学可知,基座面板的垂向加速度载荷Az主要受到激振力分量Fz,Mx和My的影响,而上述研究表明Az是引起结构机械噪声的主要加速度载荷分量。本节主要计算4种激振力作用下的机械噪声,研究设备激振力的简化模型。4种工况分别为:①工况FxyzMxyz为模型在研究频段内X,Y和Z方向受到单位力矩简谐载荷和单位力简谐载荷;②工况FzMxy为模型在研究频段内X和Y方向受到单位力矩简谐载荷和Z方向受到单位力简谐载荷;③工况Fz为模型在研究频段内仅Z方向受到单位力简谐载荷;④工况Mxy为模型在研究频段内X和Y方向受到单位力矩简谐载荷;舱段模型的基座面板垂向响应加速度Az以及水下辐射声功率的计算结果如图5、图6所示。
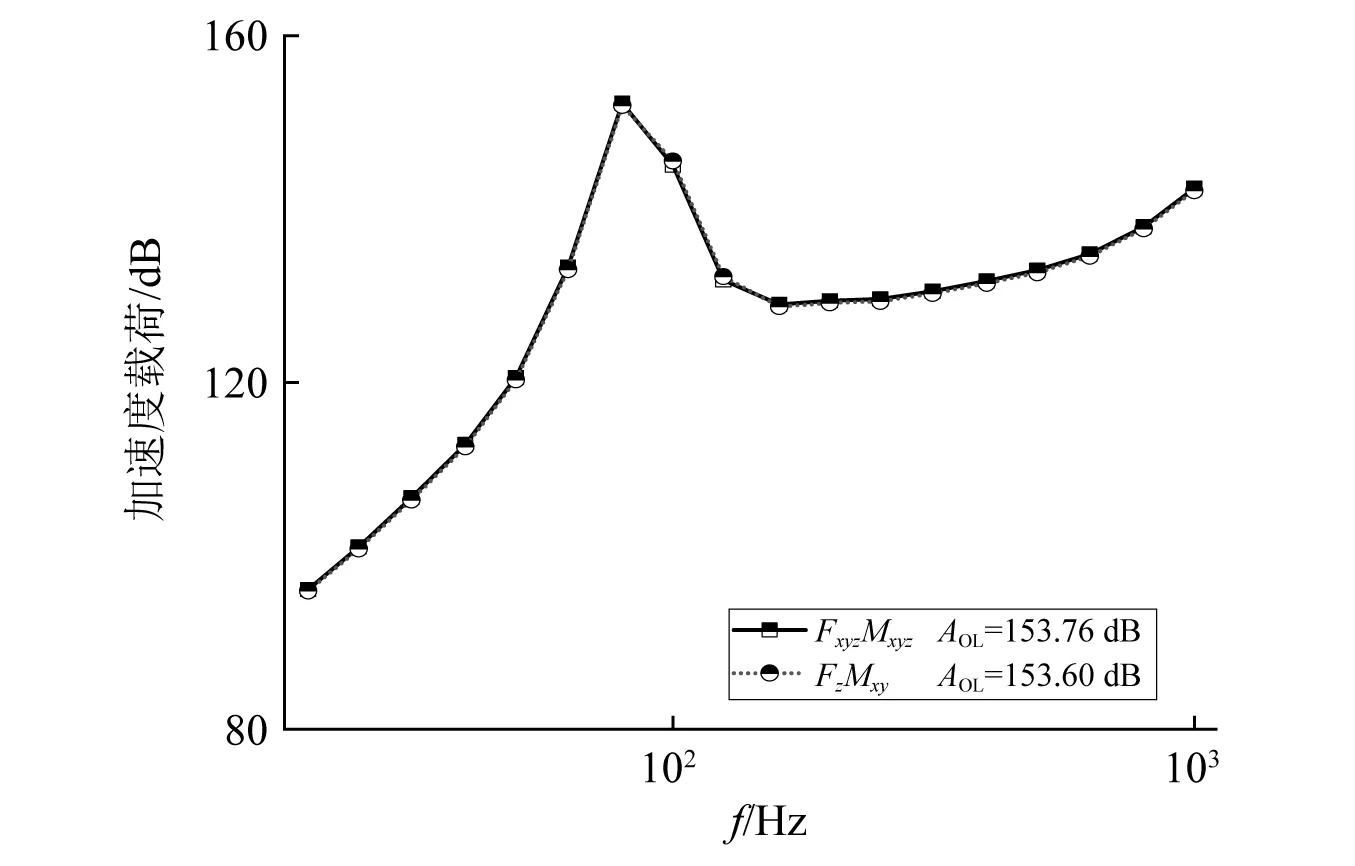
图5 2种工况下基座面板响应加速度AzFig.5 The response acceleration (Az) of the base panel under two working conditions
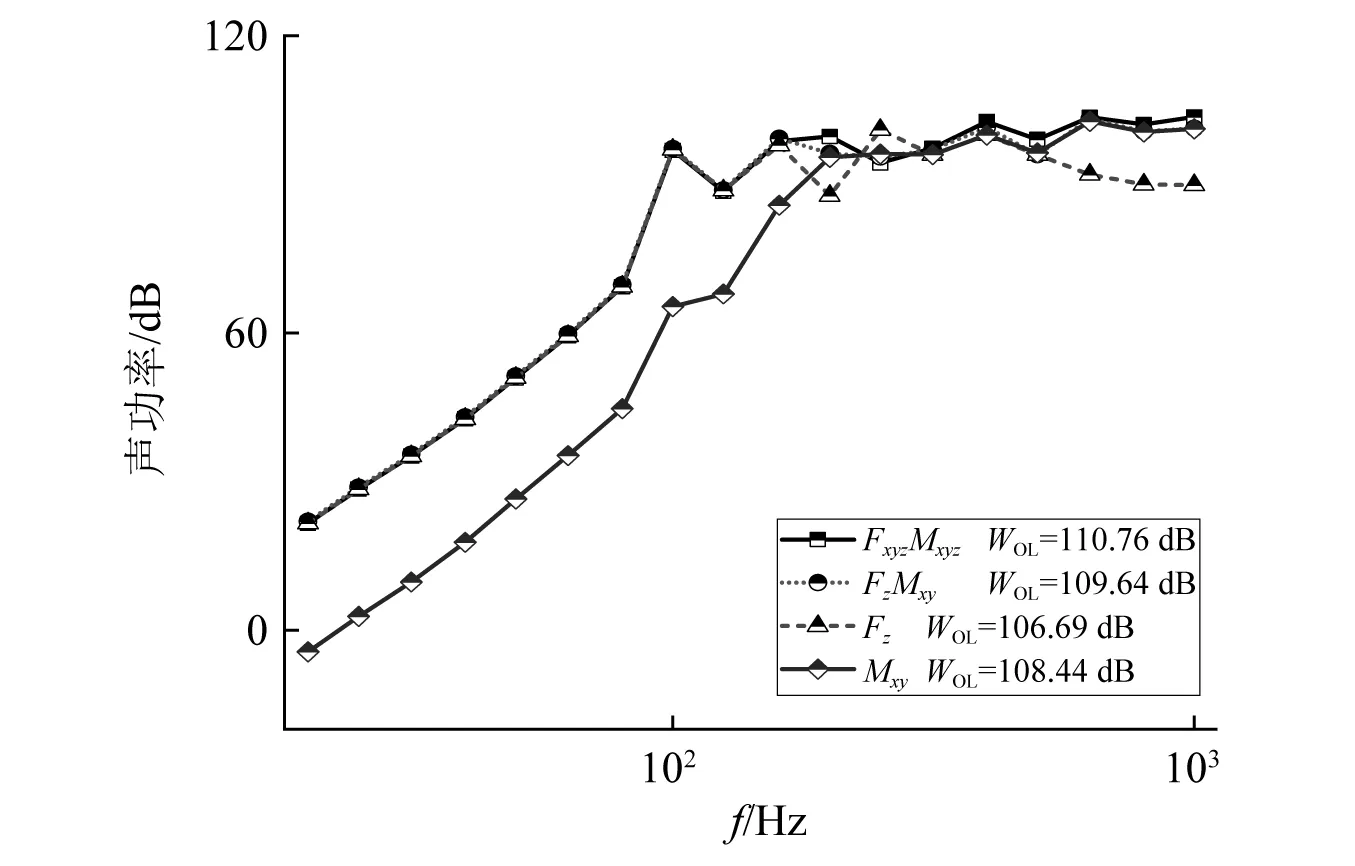
图6 4种工况下辐射声功率结果Fig.6 The radiation sound power under the four working conditions
由图5可知,工况FxyzMxyz和工况FzMxy引起的基座面板垂向加速度Az一致,误差为0.16 dB。这表明基座面板响应加速度Az仅与激振力载荷分量Fz,Mx和My有关。由图6可知,工况FxyzMxyz和工况FzMxy的声功率曲线变化趋势吻合,引起的水下辐射声功率总级的误差为1.12 dB,主要因为结构辐射噪声是由振动产生的,振动在结构中主要以弯曲波的形式传播,而产生弯曲波的加速度形式载荷是Az,对应的激振力载荷是Fz,Mx和My。因此,对于复杂设备的力学模型FxyzMxyz可简化为FzMxy。此外,工况Fz和工况Mxy的水下辐射声功率合成级与工况FzMxy的计算结果接近,误差仅为1.02 dB,这表明载荷分量产生的机械噪声基本满足能量叠加原理。
2 基于等效载荷模型的船舶机械噪声计算方法
本章基于载荷识别的基本原理,通过等效载荷模型FzMxy实现加速度载荷向激振力载荷的反演,并提出在加速度相位缺失条件下船舶机械噪声的计算方法。
2.1 等效载荷模型
任意激励作用下设备的等效载荷模型如图7所示。

图7 设备载荷识别的力学模型Fig.7 The mechanical model for equipment load identification
对上述振动系统,结构受到激振载荷Fz,Mx和My作用,基座面板的响应加速度分别为a1,a2,a3,…,an,由系统的动力学方程可得
an=Hn×mFm
(7)
式中:Hn×m为传递函数矩阵(频率响应函数矩阵);Fm为设备激振力载荷的列向量(FzMxMy)T;an为基座面板响应加速度的列向量。
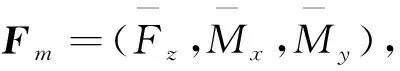
(8)
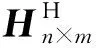
2.2 加速度载荷信息缺失时机械噪声快速预报方法
载荷识别的本质就是通过响应加速度和振动传递函数确定激振力分量的各个载荷系数,进而确定各个激励源之间的相位信息。由声学理论可知,复杂载荷激励下的辐射声场可以看作每个简单源激励下辐射噪声的相干声波叠加。相干声波叠加意味着各激励源的相位关系以及单源激励下辐射噪声与激励源的相位关系必须已知。通过等效载荷模型虽然可以确定各个载荷的相位关系,但是相干叠加方法在实际计算中较为复杂。大量的研究表明,复杂激励作用下船体的结构响应和辐射声场可近似为单源激励下结构响应和辐射声场的能量叠加[22-23],因此复杂激励作用下船体结构的水下辐射声功率可以通过式(9)计算
WFxyzMxyz≈WFzMxy≈WFz+WMx+WMy
(9)
式中:WFxyzMxyz为任意复杂力系作用下结构的水下辐射声功率;WFzMxy为激振力载荷Fz,Mx和My共同作用时结构的水下辐射声功率;WFz,WMx和WMy为激振力载荷Fz,Mx和My单独作用时所产生的声功率。
对于“设备-隔振器-基座-船体”构成的振动系统,结构中基座面板的加速度满足
a=AFz+AMx+AMy
(10)
式中:a为基座面板的响应加速度;AFz,AMx和AMy分别为激振力载荷分量Fz,Mx和My单独作用时基座的响应加速度。
由结构动力学可知
AFz=αaFz
AMx=βaMx
AMy=γaMy
(11)
式中:α,β和γ分别为激振力分量Fz,Mx和My的载荷系数;aFz,aMx和aMy为激振力分量Fz,Mx和My的加速度传递函数。对于确定结构,aFz,aMx和aMy是常数,与载荷的大小无关。
对于单源激励下,结构的辐射声功率满足[24]
(12)
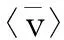
由式(10)~式(12)可知,各个载荷分量产生水下辐射声功率为
(13)
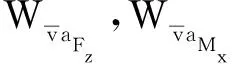
根据能量叠加原理,则复杂载荷同时作用下的水下辐射声功率WA满足
(14)
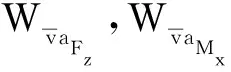
(15)
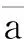
(16)
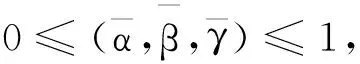
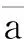
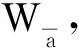
(17)
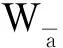
(18)
(19)
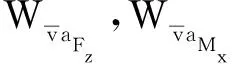
声功率总级满足
(20)
即基于等效载荷模型的方法可以确定船舶机械噪声的变化范围。
3 试验验证
为了验证本文提出的基于等效载荷模型计算船舶机械噪声方法的可靠性,在规定湖区进行舱段模型振动及水声测量试验。通过振动测试可得柴油机基座面板响应加速度载荷、设备激振力载荷及船体振动加速度响应。采用垂直水听器阵的方法对舱段模型的水下辐射声功率进行测量。试验舱段模型及其振动与水声测量试验原理图如图8所示。
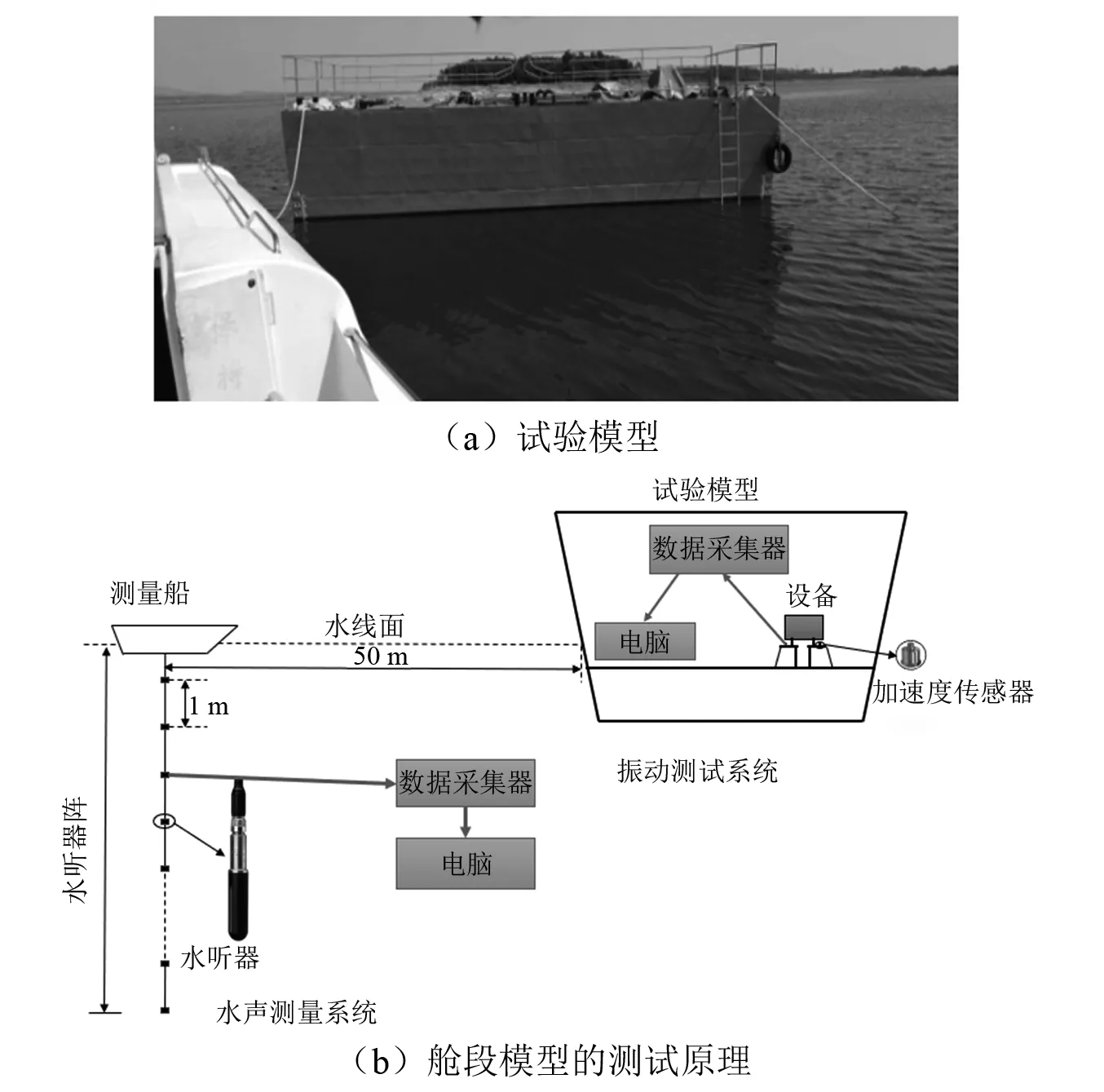
图8 试验舱段及测试原理Fig.8 The experimental model and testing principle
试验工况为柴油机刚性安装在双层底短基座和尾部圆基座。试验步骤如下:首先将柴油机安装于基座,以额定功率运转;其次通过加速度传感器测量基座面板响应加速度,通过力环传感器测量设备激振力,通过垂直水听器阵测量柴油机运行时的水下辐射声功率;最后将试验与数值结果进行对比,验证了该方法的可靠性。
柴油机载荷以完整加速度信息给出时,基于等效载荷模型计算两组工况下舱段模型水下辐射声功率,与试验测量结果的对比如图9所示。
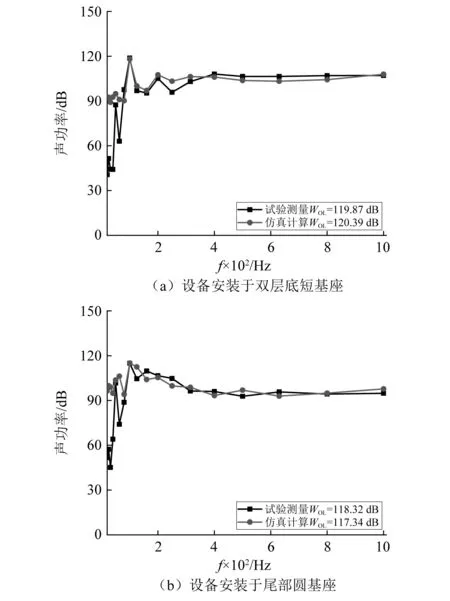
图9 基于完整加速度信息的水下辐射声功率对比Fig.9 Comparison of underwater radiation sound power between experiment and simulation based on complete acceleration information
柴油机激励以平均加速度的形式给出时(缺少幅值分布及相位分布信息),其试验测量结果如图10所示。通过等效载荷模型预测的舱段模型水下辐射声功率的变化范围与试验测量结果对比如图11所示。
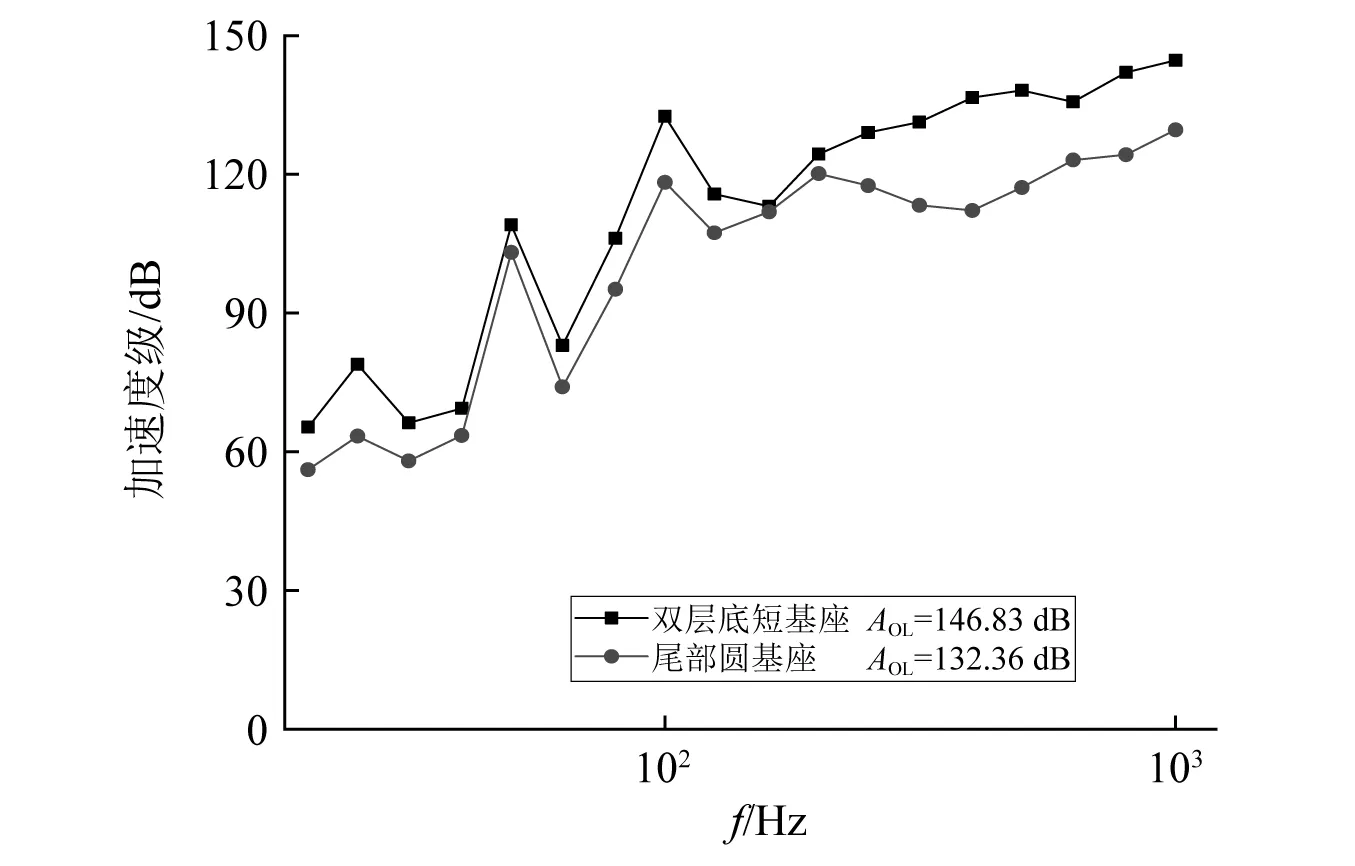
图10 基座面板平均加速度载荷Fig.10 The average acceleration load under the diesel engine working conditions
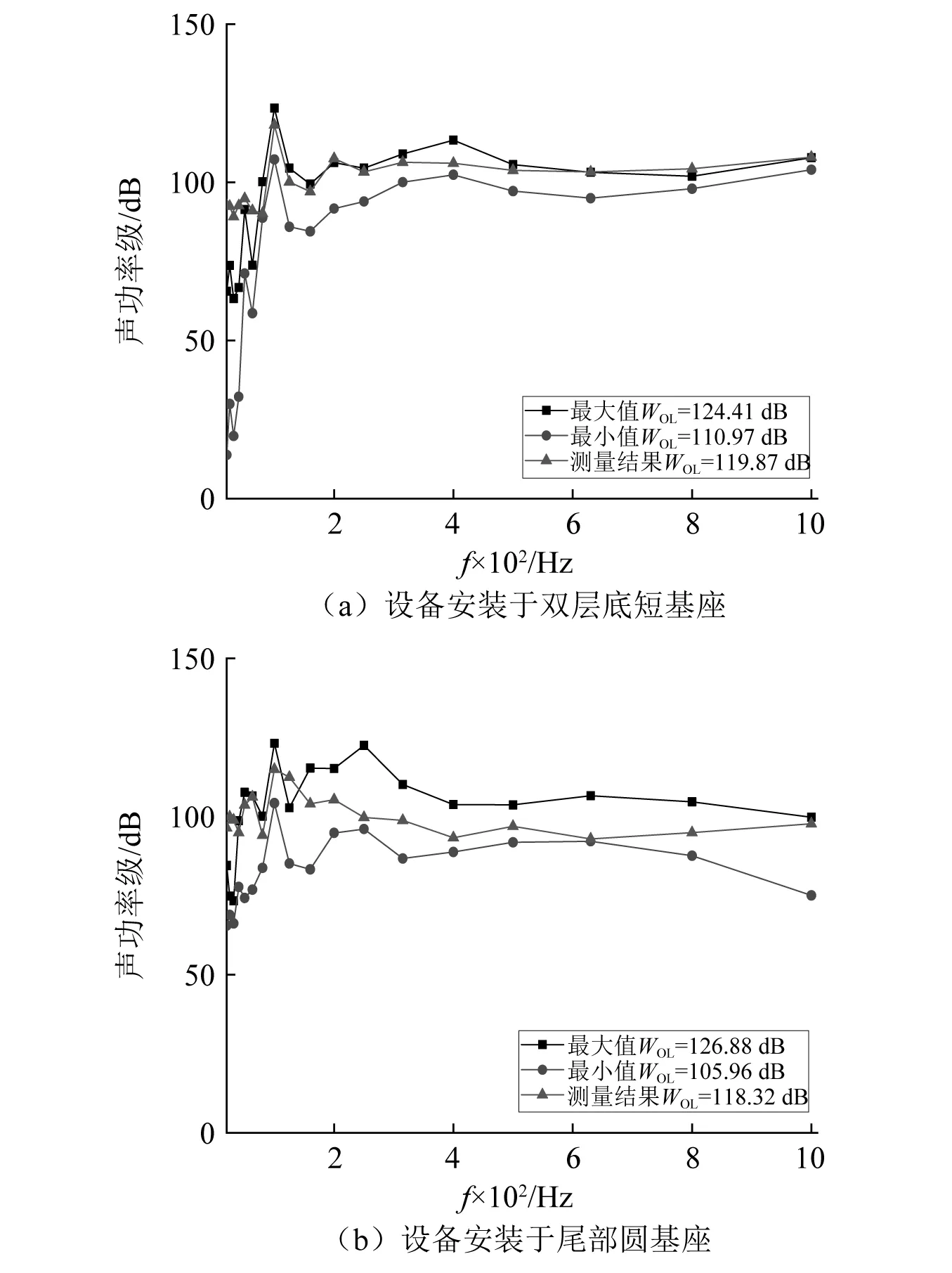
图11 基于平均加速度载荷的声功率预报Fig.11 The results of sound power based on average acceleration load
由上述计算结果可知,柴油机激励以完整加速度信息给出时,通过等效载荷模型预报水下辐射声功率总级的误差在1 dB左右。柴油机激振以平均加速度(缺少幅值分布及相位分布信息)给出时,试验测试得到的水下辐射声功率位于本文方法确定的声功率波动范围之内。
因此,该舱段模型试验验证了本文所提方法的可靠性。此外,根据水下辐射声功率曲线可知,在低频段,数值仿真与试验测试结果相差较大。主要由于水声测量不满足远场条件,导致低频辐射声功率的测量值与仿真值之间存在误差。
4 结 论
本文主要研究了设备加速度载荷信息部分缺失情况下船舶机械噪声的快速预报方法,并通过模型试验验证了该方法的合理性与可靠性。现将本文所得结论归纳如下:
(1)设备在任意激振力载荷作用下的力学模型可简化为仅包含Fz,Mx和My的等效载荷模型,通过该等效载荷模型实现设备激振力反演以及振动噪声的预报。
(2)对于设备加速度载荷信息缺失情况,若可以确定激振力分量(Fz,Mx和My)的载荷系数,则基于能量叠加原理可较为准确地预报船舶机械噪声;若无法确定激振力分量的载荷系数,则可通过等效载荷模型快速预报船舶机械噪声的变化范围。
Vol.41 No.12 2022
