多重不确定性下的电气设备地震失效风险评估
2022-06-29王社良江力强
何 畅, 王社良, 江力强
(1. 西京学院 陕西省混凝土结构安全与耐久性重点实验室,西安 710123;2. 中南大学 土木工程学院,长沙 410075)
变电站中安装有大量的绝缘子、避雷器、隔离开关等电气设备。变电站中,电气设备量大、功能广,电气设备在地震下的失效风险对区域电网的灾害抵御能力有重要影响。
变电站电气设备多由陶瓷、玻璃钢纤维复合材料等材料构成,地震及其次生灾害易使电气设备发生脆性破坏[1]。国内,在2008年的汶川地震中,大量陶瓷制开关类电气设备断裂,影响当地电力系统的震后恢复[2]。2013年的芦山地震造成芦山、天全、宝兴三县的电网全部垮网,电力负荷损失达2×105kW[3]。2014年鲁甸地震、2017年九寨沟地震也均造成了电气设备的损坏及变电站的断电失效。强地震也造成了许多国外变电站的损伤及失效。1995年美国Northridge地震、1999年日本Kobe地震中,许多电气设备倒塌[4-5]。2007年的日本新潟地震引起了电气设备的漏油失火而造成核电站的停运[6]。2010年,智利[7]、墨西哥[8]及海地[9]均发生了造成电气设备地震破坏的地震。2011年的日本“311”地震中,共621个电气设备失效[10]。
变电站中的电气设备多安装在支架上,支架对电气设备的地震响应有一定的放大作用[11]。Mohammadi等[12]研究发现支架的动力特性能显著影响安装其上的电气设备的地震响应,且给出了体系基频的拟合公式。何畅等[13]研究了安装在阀厅山墙上穿墙套管的地震响应,提出通过增加阀厅刚度,可提高穿墙套管的抗震性能。林森等[14]对安装在支架上的特高压电容式电压互感器进行了抗震及减震振动台试验研究,验证了减震装置对支柱类设备的有效性。Li等[15]通过敲击试验及振动台试验探究了复合材料电气设备的在地震下的失效模式及其应力、位移、阻尼变化等判别指标。孙宇晗等[16]对170 kV中性点电抗器进行了地震模拟振动台试验,提出需考虑设备位移对连接导线的影响。Koliou等[17-18]研究了加劲肋对安装在支架面板上的套管类设备的地震响应的影响,通过数值与试验研究的方法优化了加劲肋的布置形式。另外,研究发现管母线可减小其耦联的电气设备支架的放大效应,提高体系的抗震性能[19]。
电力设施中,针对水电站、核电站结构地震易损性的研究较多。汶川地震后,针对电气设备的震害情况的统计易损性研究也逐渐展开[22],贺海磊等[23]绘制了汶川地震中电气设备的统计地震易损性曲线。基于地震加速度峰值(peak ground acceleration,PGA),杨长青[24]研究了汶川地震中电力设施的地震易损性。熊明攀[25]探究了以地震烈度、仪器烈度等参数对电气设备地震易损性的影响。由于基于震害统计的地震易损性分析方法具有较强的局限性,计算分析法也逐渐应用于电气设备易损性分析中。Zareei等[26]研究了地震动不确定性对变压器地震易损性的影响。除地震动不确定性外,材料力学性能对电气设备的抗震性能也有影响。刘振林等[27-28]考虑了陶瓷材料的强度不确定性,研究了避雷器及隔离开关的地震易损性。Dolsek等[29]考虑不同研究人员的建模分析质量,研究了建模不确定性对结构地震易损性的影响。由于进行电气设备地震易损性研究的计算分析量较大,基于地震动聚类等高效易损性分析方法也逐渐提出[30]。
Cornell[31]提出了基于概率的地震危险性分析方法,研究结构在地震下的破坏风险。不同学者提出了对房屋、桥梁等结构的地震破坏风险的评估方法,并逐渐应用于基于性能的结构设计中[32]。电力系统方面,闫路鹏[33]评估了中国大陆电网设施的整体地震灾害风险。另外,针对变电站电气设备系统的抗震韧性的研究也逐渐开展。
目前,对电气设备的地震失效风险的研究较少,且仍然采用强度准则对电气设备进行抗震设计,未考虑不同烈度地震的发生概率及电气设备地震易损性对变电站整体抗震性能的影响。变电站中,电气设备的种类及数量多,且不同电气设备在造价、运输时间等方面有较大区别。评估变电站电气设备的地震破坏风险,对于变电站不同设备在强度取值、备品数量等设计方面具有指导意义,能有效缩短变电站震后停电时间,提高区域电力系统的可靠性。本文考虑了地震动不确定性、结构不确定性、性能指标不确定性及分析质量不确定性的影响,基于我国GB 50260—2013《电气设施抗震设计规范》[34]及我国地震区划图,提出了考虑多重不确定性的变电站电气设备地震失效风险评估方法。对某真型特高压气体绝缘开关(gas insulated switchgear,GIS)套管进行振动台试验,并以该型GIS套管为算例,探讨了多重不确定性对电气设备地震易损性的影响,分析了我国不同地区该型套管的地震失效风险,以期为我国变电站的抗震设计提供参考与依据。
1 电气设备地震失效风险评估方法
1.1 多重不确定性下的电气设备地震易损性
1.1.1 电气设备的地震易损性
电气设备的地震易损性是指在一定强度地震下,电气设备达到某种地震失效模式的概率,如式(1)所示。
Pf(x)=P(D≥C|IM=x)
(1)
式中:Pf为电气设备在强度指标IM(intensity measure)为x时的地震失效概率;D为电气设备的地震响应;C为该响应的失效限值。对于常见工程结构,其地震易损性与地震动强度IM的关系曲线一般符合标准对数正态分布函数曲线,如式(2)所示
(2)
式中:Φ(·)为标准正态分布函数;mR,βR分别为地震动强度指标的中位值及对数标准差(logarithmic standard deviation,LSD)。进行结构的地震失效风险评估时,为充分考虑地震动频谱特性对结构的影响,式(2)中,IM通常用电气设备第一周期(T1)对应的加速度反应谱[Sa(T1)]表示。
1.1.2 多重不确定下的电气设备地震易损性
由于影响结构地震易损性及地震失效风险的随机变量较多,评估结构的地震易损性及地震失效风险时,需考虑多重不确定性的影响。针对变电站电气设备,需考虑以下不确定性的影响
(1) 地震动不确定性。地震动具有强烈的随机性,地震动的PGA、频谱特性等因素对电气设备的地震响应有重要影响。评估电气设备的地震易损性时,需考虑地震动不确定性的影响。由地震动不确定性引起的易损性函数对数标准差记为βr-r。
(2) 结构不确定性。由于变电站电气设备多为单支柱结构,结构的尺寸因素不确定性对电气设备的地震响应影响较小。因此,对电气设备的结构不确定性进行分析时,本文考虑材料弹性模量、密度及结构阻尼比对电气设备地震响应的影响。由结构不确定引起的易损性函数中的对数标准差记为βr。
(3) 性能指标不确定性。灾害现场调查结果表明,地震多引起电气设备根部截面断裂,继而引起电气设备的地震失效。电气设备多由陶瓷、复合材料等脆性材料制成,故材料强度随机性产生的性能指标不确定性影响电气设备的地震易损性。由电气设备性能指标不确定性引起的易损性函数中的对数标准差记为βLS。
(4) 认知不确定性。对电气设备进行地震易损性及地震失效风险分析时,需要建立电气设备的数值分析模型。不同研究人员所建立的分析模型质量不一致。另外,电气设备内部一般含有大量的元器件。元器件的力学性能与部件之间连接件的力学参数尚不明确,进一步影响了数值模型的模拟质量。认知不确定性主要通过已有报道的统计得到。由分析模型认知不确定性引起的易损性函数中的对数标准差记为βm。
对于符合标准对数正态分布的随机变量,可表示为[35]
(3)
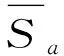
(4)
则当第i个随机变量的对数标准差为βi时,有
(5)
多重不确定性下电气设备易损性函数的对数标准差可由式(5)确定。
1.2 电气设备地震失效风险
1.2.1 地震危险性函数
地震危险性函数是指IM为x的地震年发生概率。我国目前尚无具体地区及场地地震危险性函数相关规范。Cornell于1968年指出场地的地震危险性函数可拟合如式(6)所示。
(6)
式中,k0,k为相关系数,可由式(7)~式(8)拟合得到[36],即
ln(k0)=ln{pDBE·[Sa(T1)DBE]k}=
(7)
(8)
式中:pDBE及pMCE分别为设计基本地震(design based earthquake,DBE)和最大考虑地震(maximum considered earthquake,MCE)的年发生概率,我国分别取pDBE=0.002 1及pMCE=0.000 4;Sa(T1)DBE及Sa(T1)MCE分别为电气设备第一周期所对应的设计基本地震(设防烈度)和最大考虑地震(罕遇烈度)加速度反应谱。
考虑GB 50260—2013《电力设施抗震设计规范》中推荐的加速度反应谱,当电气设备的第一周期为T1时,Sa(T1)为
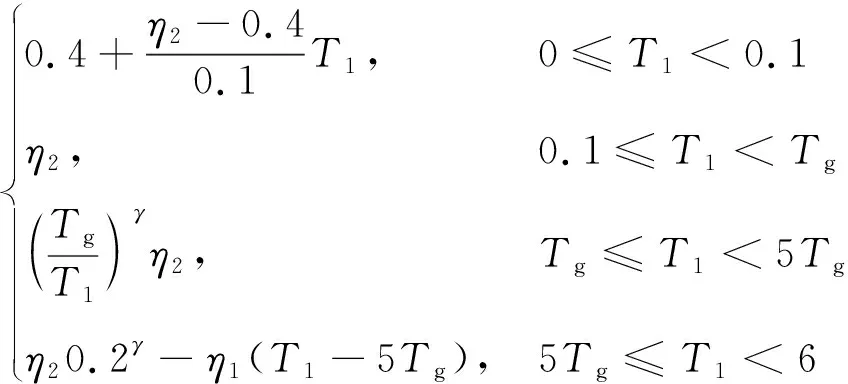
(9)
式中,APG为地震加速度峰值。
考虑结构阻尼比ξ的影响,式(9)中
(10)
(11)
(12)
对于国内不同场地的DBE及MCE下的PGA,本文采用CECS 160:2004《建筑工程抗震性态设计通则》给出的数值[37]。
1.2.2 电气设备的地震失效风险
电气设备的地震失效风险是指该设备的在一年内发生地震失效的概率,该参数受到电气设备的地震易损性函数及场地地震危险性函数的影响,即
(13)
式中,Pl,1为电气设备的年地震失效概率。将式(2)、式6)代入式(13),可得[38]
(14)
对于设计使用年限为50年的电气设备,其在设计使用期内的地震失效概率为
Pl,50=1-(1-Pl,1)50
(15)
由1.1节和1.2节分析可知,考虑多重不确定性时,电气设备的地震失效风险评估流程如图1所示。
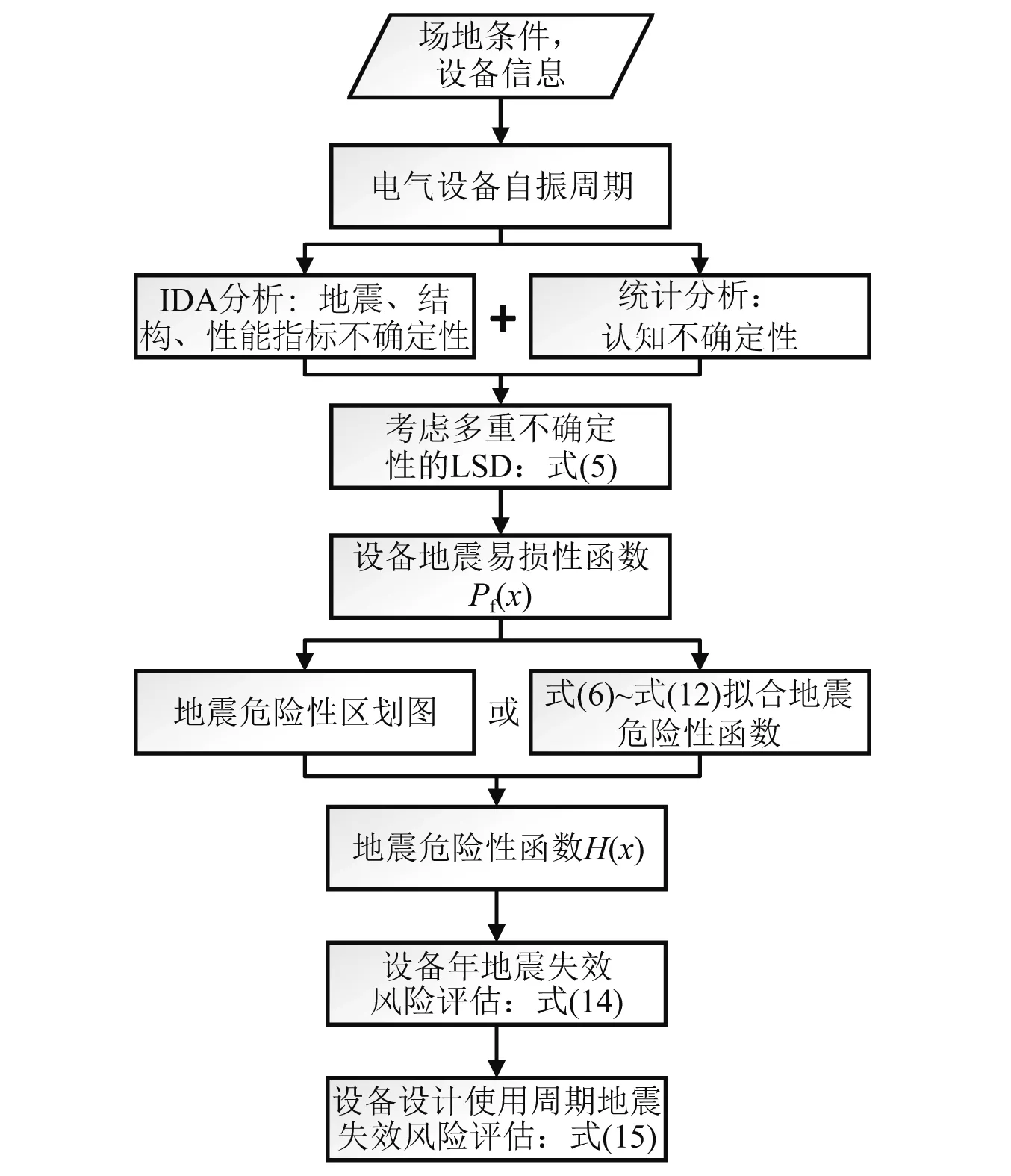
图1 电气设备地震失效风险评估流程Fig.1 Assessment flowchart of electrical equipment seismic failure risk
2 算例简介
2.1 特高压GIS套管及数值分析模型
2.1.1 特高压GIS套管简介
本文以某型安装在支架上的特高压瓷制GIS套管为例,对其进行考虑多重不确定性的地震易损性及地震失效风险评估。特高压瓷质GIS套管总长12.02 m,为内部充填SF6气体的空心结构,其根部截面外径为960 mm。瓷套管通过铜制法兰安装于钢支架上。安装在支架上的特高压GIS套管如图2所示。
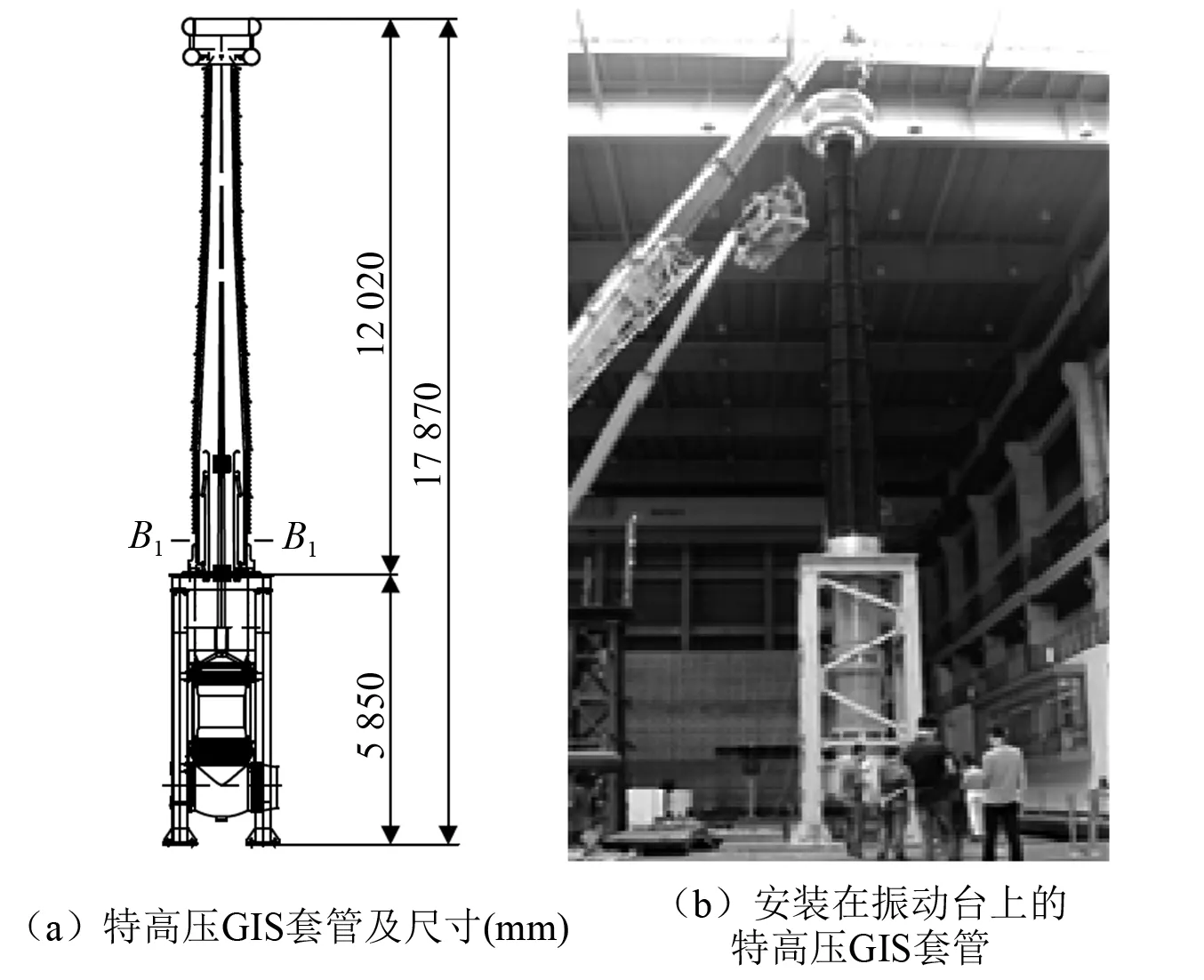
图2 安装在支架上的GIS套管Fig.2 GIS bushing mounted on the supporting frame
GIS套管钢支架由宽翼缘H型钢梁柱及等边角钢支撑构成,支架各节点间采用螺栓连接。钢支架立面如图3所示。考虑现场安装条件及精度要求,钢支架采用长螺栓孔,如图4(a)所示。在该型GIS套管支架中,梁柱节点梁腹板未采用连接板件与柱连接,如图4(b)所示。套管及支架具体结构信息可见文献[39]。
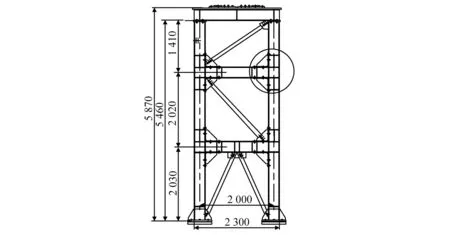
图3 GIS套管支架立面(mm)Fig.3 Side views of the GIS bushing frame (mm)
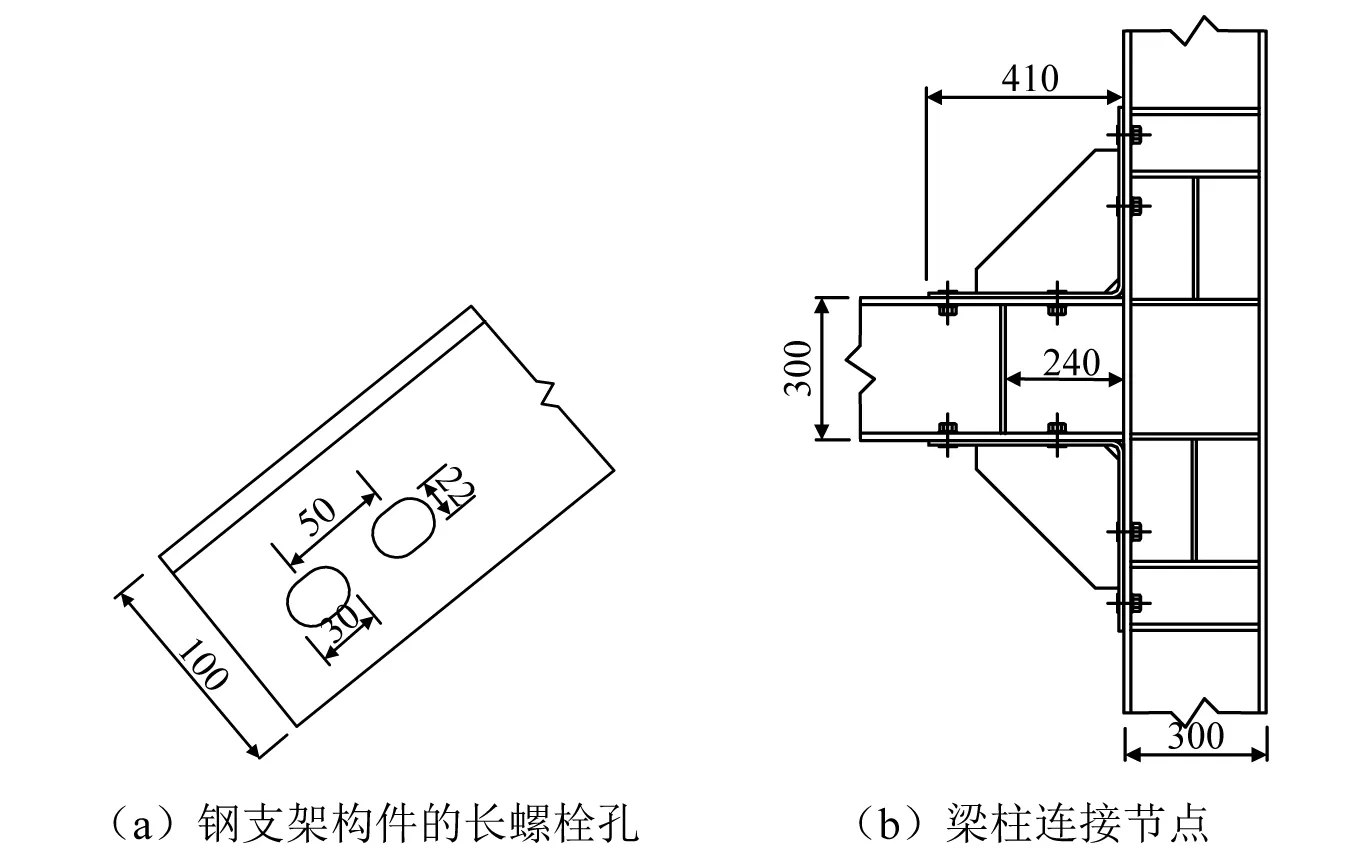
图4 GIS套管支架螺栓节点(mm)Fig.4 Bolt connections of the GIS bushing frame (mm)
2.1.2 特高压GIS套管数值分析模型
由振动台试验研究可知,梁柱节点的刚度对安装在其上的GIS套管地震响应有较大影响。因此,采用ABAQUS软件平台分析梁柱节点刚度曲线。采用C3D8I六面体实体单元模拟梁、柱、加劲肋、连接板及节点螺栓。梁柱节点采用M20高强螺栓连接,螺栓预紧力取108 kN。节点有限元模型中,不同部件的界面之间设置为硬接触,部件界面切向摩擦因数取0.15。梁柱节点有限元模型如图5(a)所示。由于梁腹板未与柱连接,节点发生变形时,梁柱之间出现间隙(见图5(b)),影响节点刚度。由数值分析,该型支架梁柱螺栓节点弯矩—转角曲线如图6所示。由图6可知,支架梁柱节点的弯矩—转角曲线基本呈线性关系,其拟合刚度曲线刚度k为2.84×106N·m/rad。
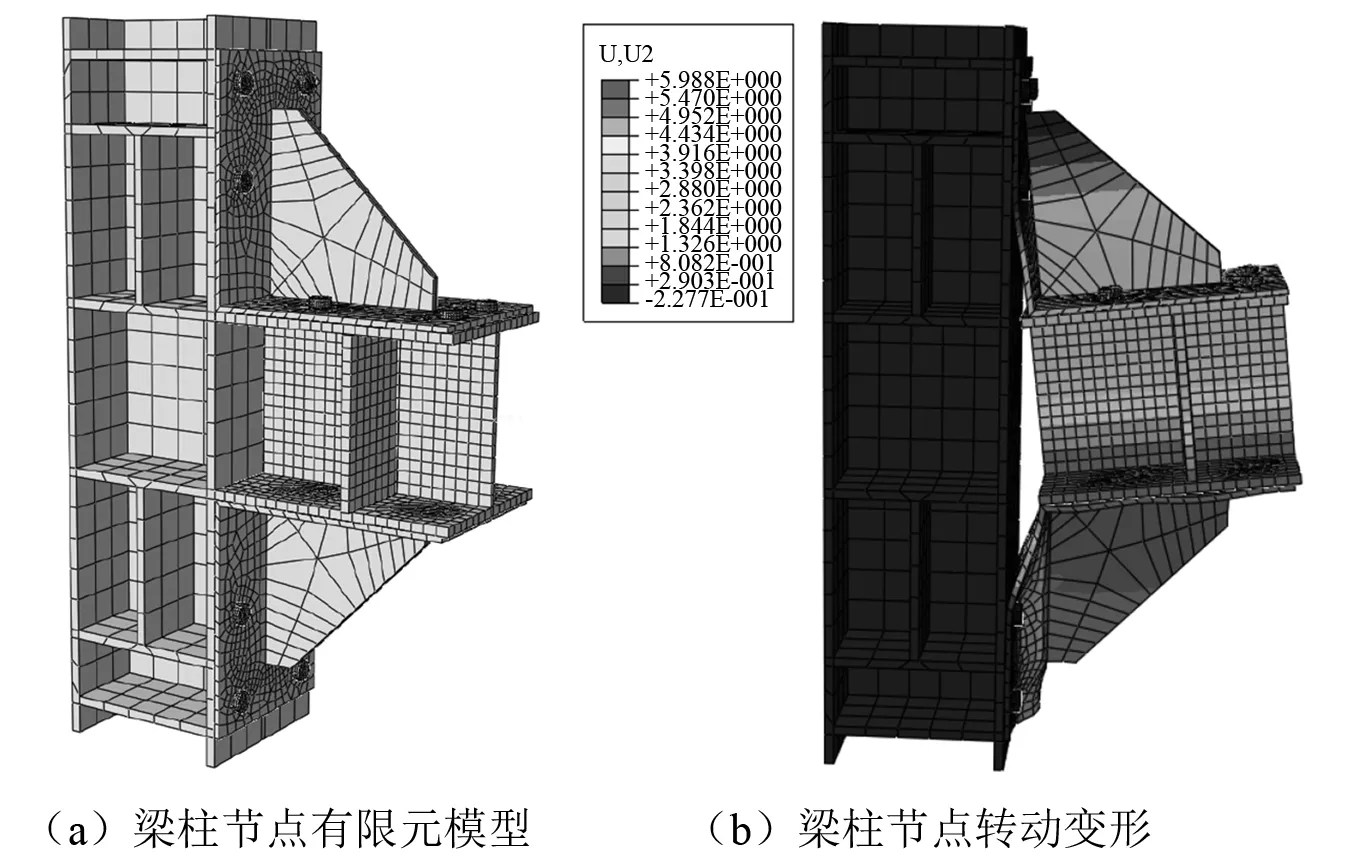
图5 支架梁柱节点及其转动变形Fig.5 Beam-column connection and its rotational deformation
进一步地,利用Hinge连接模拟该节点的弯矩-转角关系曲线,利用B31三维梁单元模拟支架梁、柱及支撑,分别利用C3D8R三维六面体实体单元和S4R三维壳单元模拟GIS瓷套管及其均压环,建立套管-支架体系的数值分析模型。
2.2 数值分析模型的振动台试验验证
对该型特高压GIS套管进行振动台试验以验证数值分析模型的有效性,振动台试验具体信息可见何畅等的研究。安装在振动台上的真型GIS套管如图2(b)所示。由数值分析模型与振动台试验获得的GIS套管前两阶自振频率如表1所示。在PGA为0.4g的人工波下,由数值分析模型及振动台试验获得的GIS套管根部截面(图2(a)B1-B1截面)最大应力响应、套管顶部最大位移及加速度响应分别列于表2中。由表1及表2可知,数值分析模型所获得的GIS套管动力特性及地震响应结果与振动台试验结果一致,验证了该数值分析模型的有效性。

表1 前两阶自振频率数值分析与振动台试验对比Tab.1 Comparison of the first-two resonance frequencies between the numerical analyses and test results
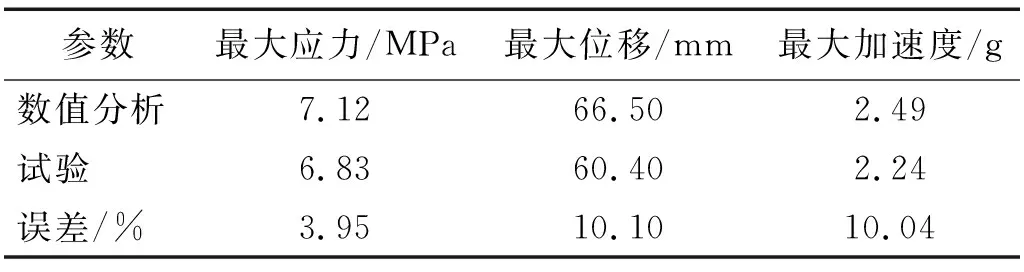
表2 套管最大应力与位移数值分析与振动台试验对比Tab.2 Comparison of the maximum stress and displacement results between the numerical analyses and tests
有限元分析与振动台试验中,GIS套管顶部加速度反应谱如图7所示。由图7可知,GIS套管有限元分析曲线与试验结果曲线类似,进一步验证了该有限元模型的有效性。
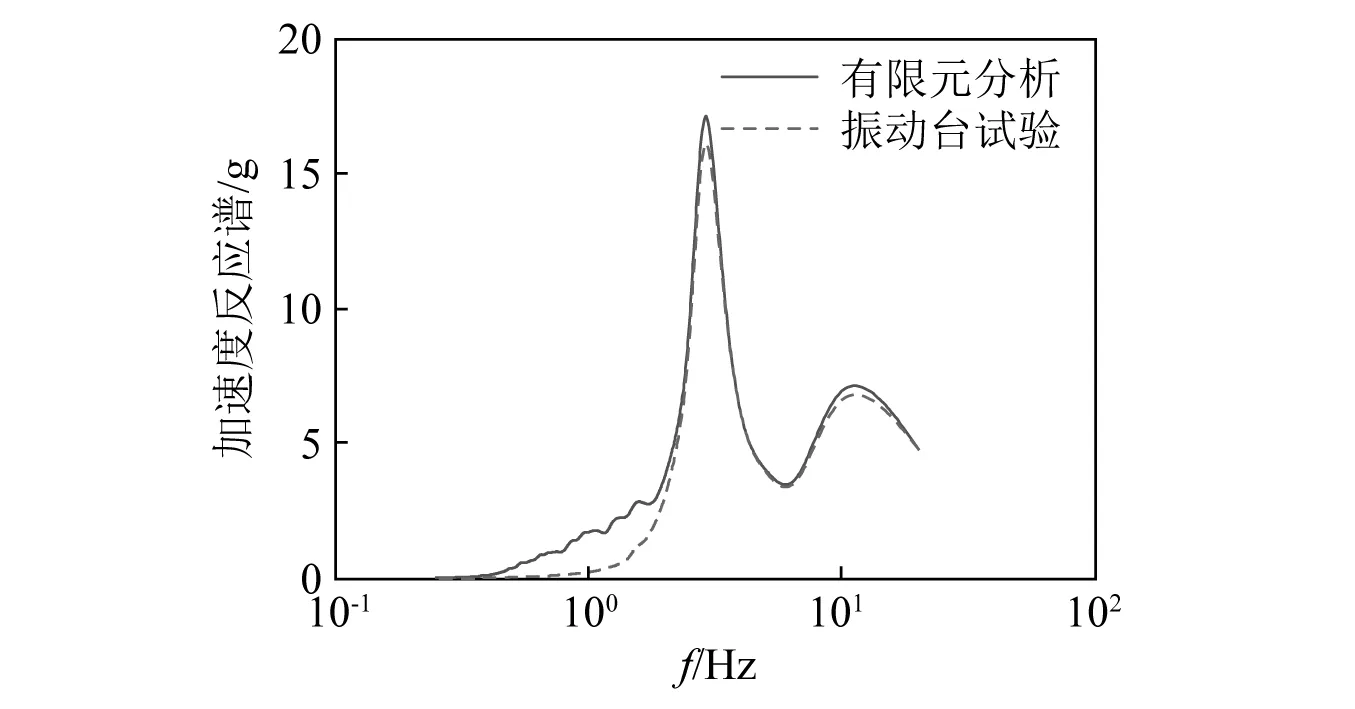
图7 GIS套管顶部加速度反应谱Fig.7 Acceleration response spectra at the top of the GIS bushing
3 多重不确定性下的特高压GIS套管地震易损性
3.1 地震动不确定性
地震动具有强烈的随机性,Cornell指出,考虑地震动不确定性时,结构地震响应与地震强度指标IM之间近似符合幂函数关系,即
σD|IM=a[Sa(T1)]b
(16)
式中:σD|IM为套管根部截面最大地震应力的拟合值;a,b为拟合系数,则在不同地震动激励下有
(17)
式中:σmax为套管在地震下的最大地震应力响应;ε为由地震动不确定性引起的随机参数,则由地震动不确定引起的易损性函数中的对数标准差为
βr-r=σ[ln(ε)]
(18)
式中,σ(·)为标准差函数。
本文选用FEMA/SAC项目推荐的20条天然地震动(LA01~LA20)作为特高压GIS套管地震易损性分析的地震激励。20条天然地震动记录的加速度反应谱及平均反应谱如图8所示。
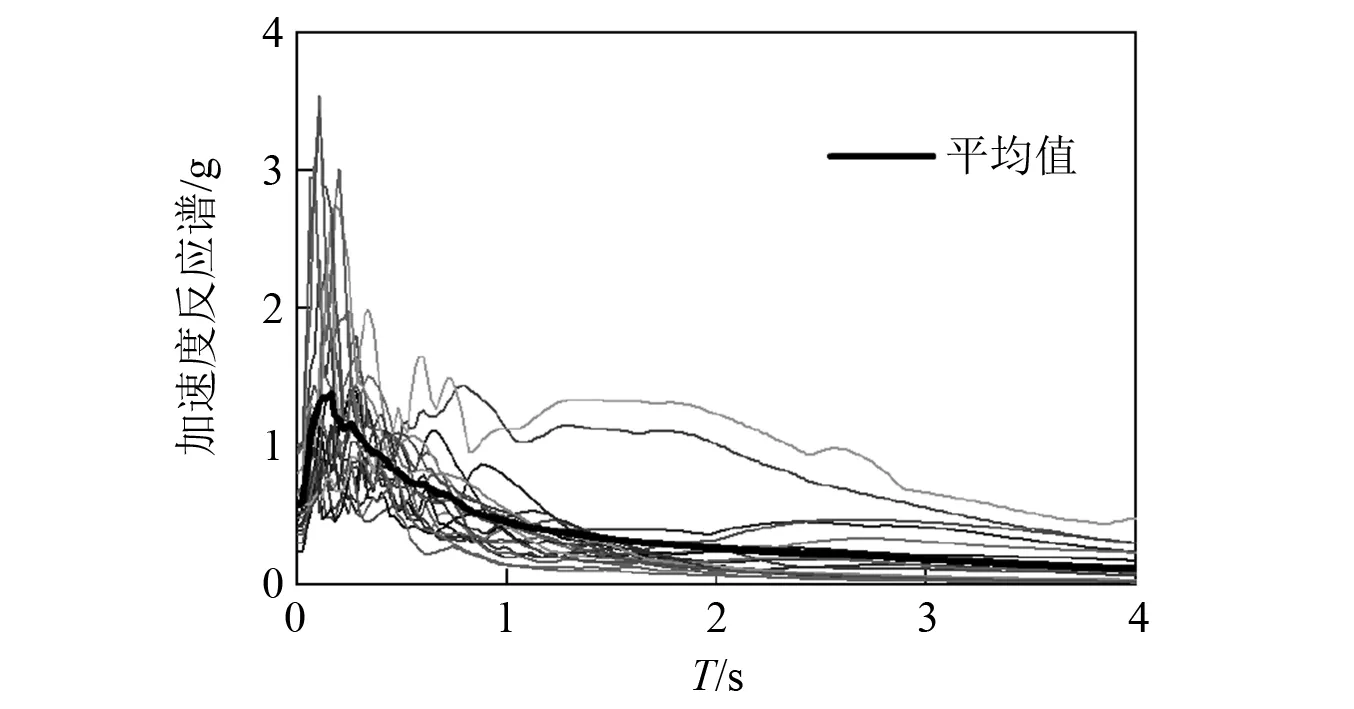
图8 地震动加速度反应谱Fig.8 Acceleration response spectra of the earthquake time histories
在未调幅天然地震动激励下,特高压GIS套管根部地震应力响应如图9所示。由图9可知,天然地震动下,特高压GIS套管根部最大应力响应可拟合为
(19)
由式(18)可知,地震动不确定性引起的对数标准差βr-r为0.43。对于该型特高压GIS套管,由地震动随机性引起的不确定性较大。
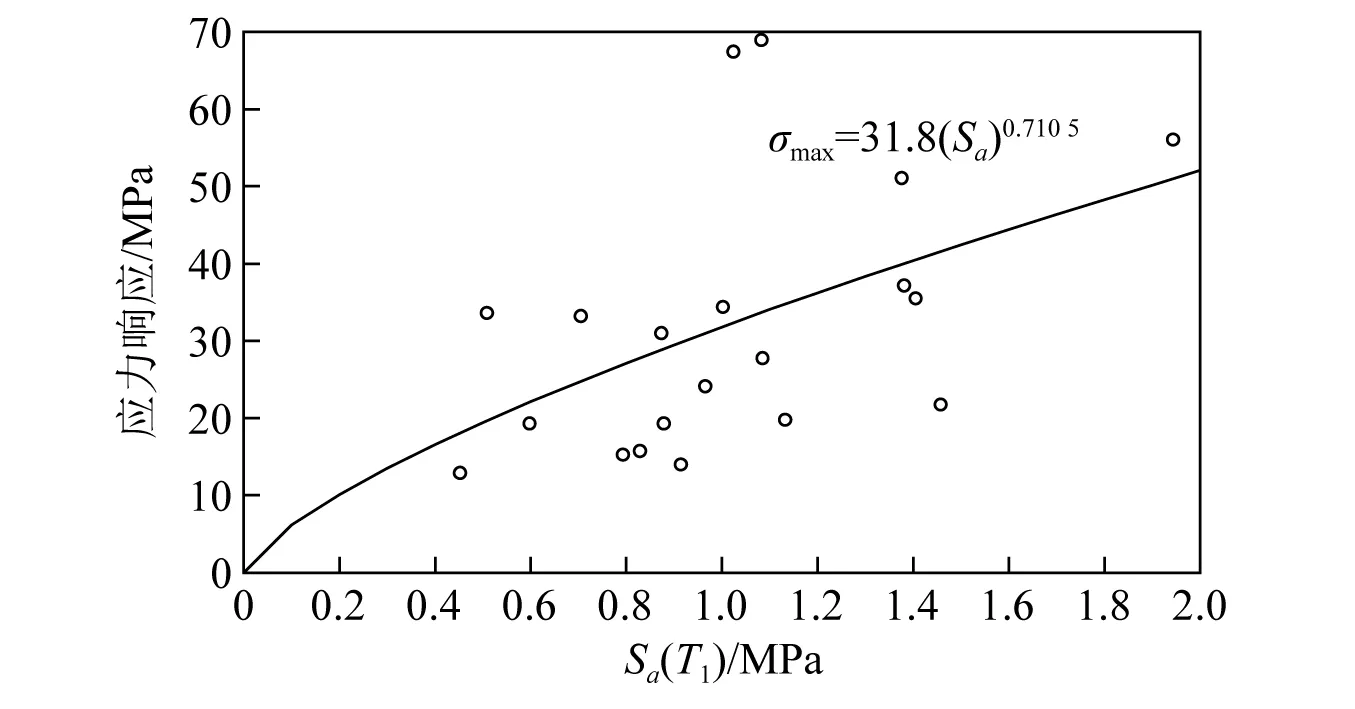
图9 未调幅地震下套管根部最大应力响应Fig.9 Maximum stresses of the bushing under unscaled earthquake time histories
对该型特高压GIS套管进行增量动力分析(incremental dynamic analysis,IDA),可获得套管在地震失效时对应的加速度反应谱值Sa(T1)。当套管根部应力响应达到陶瓷材料抗拉强度值时,IDA曲线截断。在LA01~LA20共20条地震动作用下,变压器套管根部最大应力响应的IDA曲线如图10所示。由图10可知,套管应力IDA曲线基本呈现线性关系。陶瓷材料在破坏前呈线性,对于电气设备地震响应的分析,多采用线性模型。该型GIS套管支架梁柱节点的弯矩—转角曲线如图6所示,其接近线性关系。由图10可确定在套管根部应力响应达到陶瓷抗拉强度极限值时,多条地震动作用下,套管地震失效的第一周期加速度反应谱Sa(T1)均值mR为1.01g。
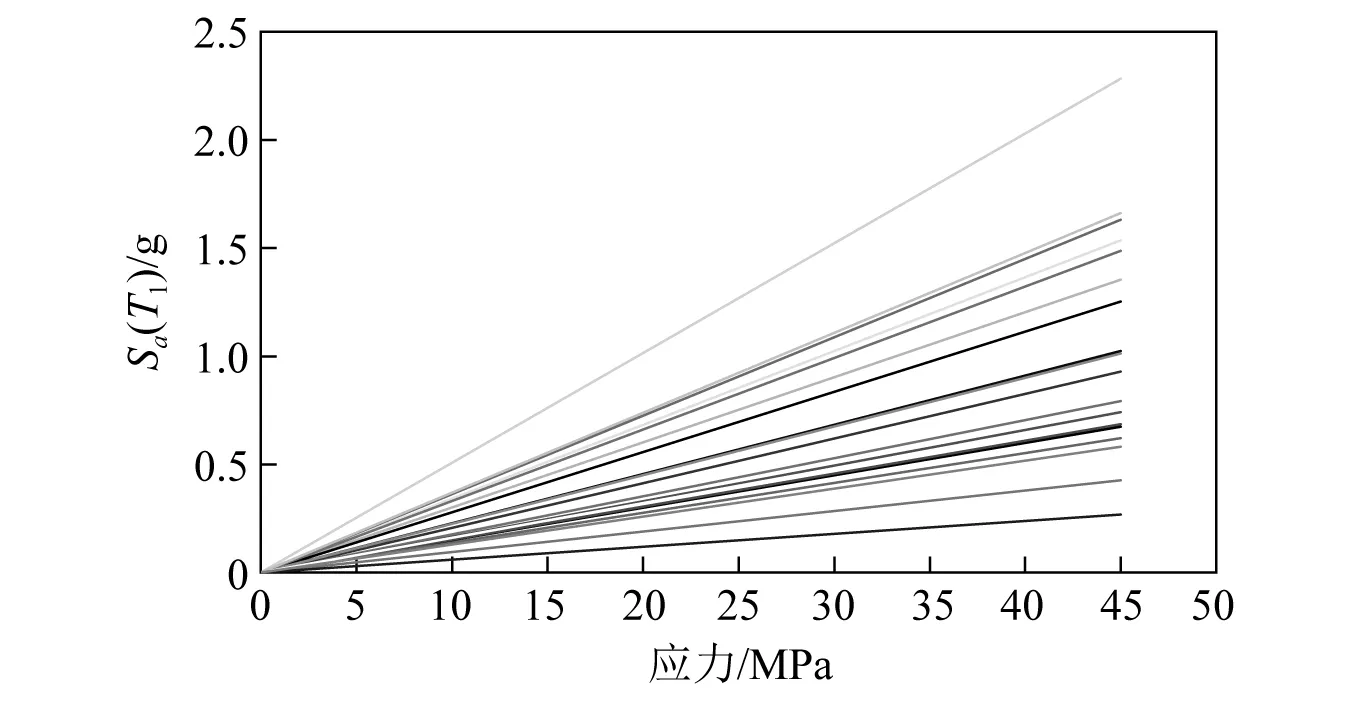
图10 不同地震动下套管根部应力IDA曲线Fig.10 IDA curves of the stress at bushing bottom cross section under different earthquake time histories
3.2 结构不确定性
对于特高压GIS套管,其地震响应主要受套管陶瓷材料弹性模量Ep、陶瓷材料等效密度mp及结构整体阻尼比ξ的影响。另外,支架动力特性对套管地震响应也有较大影响,故本文在评估结构不确定性对GIS套管地震易损性及地震失效风险的影响时,考虑钢支架钢材弹性模量Es及支架梁柱节点(见图5)转动刚度k离散性的影响。本文考虑的参数、其中位值、变异系数(coefficient of variation,COV)及分布如表3所示。
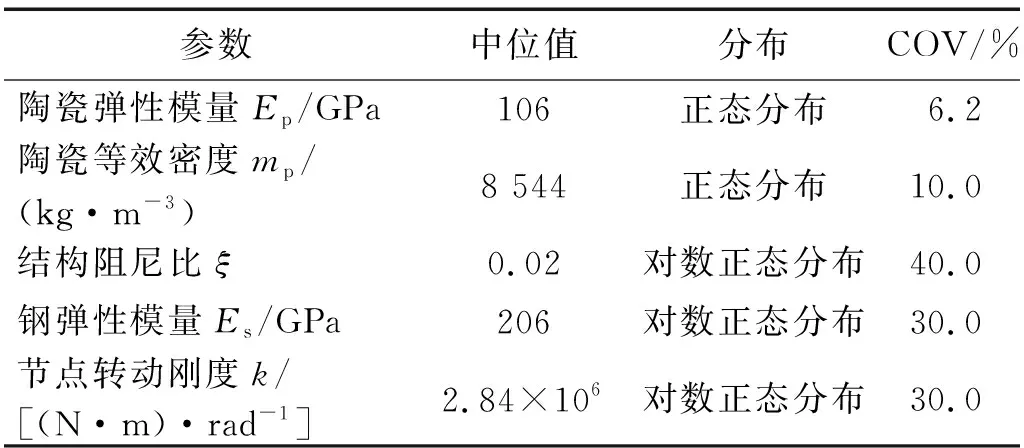
表3 特高压GIS套管的结构参数及其分布Tab.3 Structural parameters and distributions of ultra-high voltage GIS bushing
本文共考虑5个结构参数的不确定性,见Dolsek的研究,当各随机变量的样本数量大于样本总数两倍时,样本数量对统计中位值及标准差的影响较小。本文采用拉丁超立方法抽样法(Latin hypercube sampling,LHS)对各随机变量分别抽取30个样本。
假设表3中各变量独立,考虑各变量随机性引起的对数标准差βi,则该特高压GIS套管的结构不确定性引起的对数标准差βr可由式(5)计算。对于第i个结构不确定性变量,其引起的对数标准差为
(20)
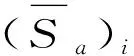
在进行结构地震易损性分析及地震失效风险分析时,可认为不同地震动作用下结构地震响应是相互独立的。因此,本文仅分析在LA01地震激励下的GIS套管地震响应。
在LA01地震动作用下,对于表3中5种变量,由式(20)计算的对数标准差及式(5)计算的结构不确定性对数标准差如表4所示。对于该型特高压GIS套管,由陶瓷弹性模量不确定性βEp、套管整体质量不确定性βmp、结构阻尼比不确定性βξ、支架钢材弹性模量βEs及支架梁柱节点转动刚度不确定性βk引起的结构不确定性对数标准差βr为0.215。另外,由表4可知,支架节点转动刚度的离散性对GIS套管地震易损性的对数标准差影响较其他结构不确定性参数的影响小。

表4 特高压GIS套管的结构不确定性对数标准差Tab.4 Logarithmic standard deviation caused by the structural uncertainties of ultra-high voltage GIS bushing
3.3 结构性能指标不确定性
瓷质电气设备主要表现为地震下断裂的地震失效模式,故在评估性能指标不确定性的影响时,主要考虑陶瓷强度不确定性对套管地震易损性及地震失效风险的影响。对于该型特高压GIS套管陶瓷材料,其抗拉强度中位值为45 MPa,COV为6.2%,且陶瓷强度服从正态分布。
进行性能指标不确定性分析时,GIS套管结构参数均取其中位值。采用LHS法对陶瓷抗拉强度进行抽样,并由图10计算在GIS套管陶瓷应力响应达到陶瓷抗拉强度时的第一周期加速度反应谱Sa(T1)。由此可得陶瓷强度离散性的性能指标不确定性引起的GIS套管地震易损性的对数标准差βLS为0.060。
3.4 认知不确定性
评估电气设备地震易损性及失效风险时,多采用数值分析法。电气设备数值模型的准确性对评估结果有一定的影响。ATC-63规范指出,可根据研究人员水平、模型详细程度、参数准确性等要求将结构数值分析模型分为质量优、良及一般3个等级,由模型质量不确定性(认知不确定性)引起的对数标准差βm可分别取0.2,0.4及0.6。
由于电气设备内部结构较传统结构复杂,采用ATC-63规范推荐的认知不确定性对数标准差不能较准确的反应电气设备数值分析模型的准确性及离散程度。因此,本文收集整理现有文献报道中关于电气设备地震响应的数值分析结果与振动台试验结果,并以振动台试验结果为基准,对比获得电气设备地震应力响应数值误差。利用对数正态分布统计数值分析误差的对数标准差,并以此作为现阶段电气设备地震易损性及地震失效风险分析的认知不确定性对数标准差βm。
根据现有文献报道,本文收集统计共40个地震应力响应分析工况的数值分析结果与振动台试验结果误差。误差的累积概率及其拟合分布曲线如图11所示。由图11可知,考虑现有数值分析技术水平及结构参数精细化水平、结构简化方法等因素,由认知不确定带来的误差中位值为5.93%,其对数标准差βm为1.03。由此可知,对于电气设备,数值分析模型质量离散性引起的电气设备地震易损性及地震失效风险的不确定性远大于其他随机参数引起的不确定性,且该值大于ATC-63规范推荐的βm取值。电气设备内部等元器件较多、连接复杂,增大了数值模拟的难度,继而引起了较大的误差离散性。另外,由于目前对比电气设备振动台试验与数值分析应力响应结果的报道仍较少,对于数值分析模型质量不确定性引起的对数标准差,仍需进一步研究。
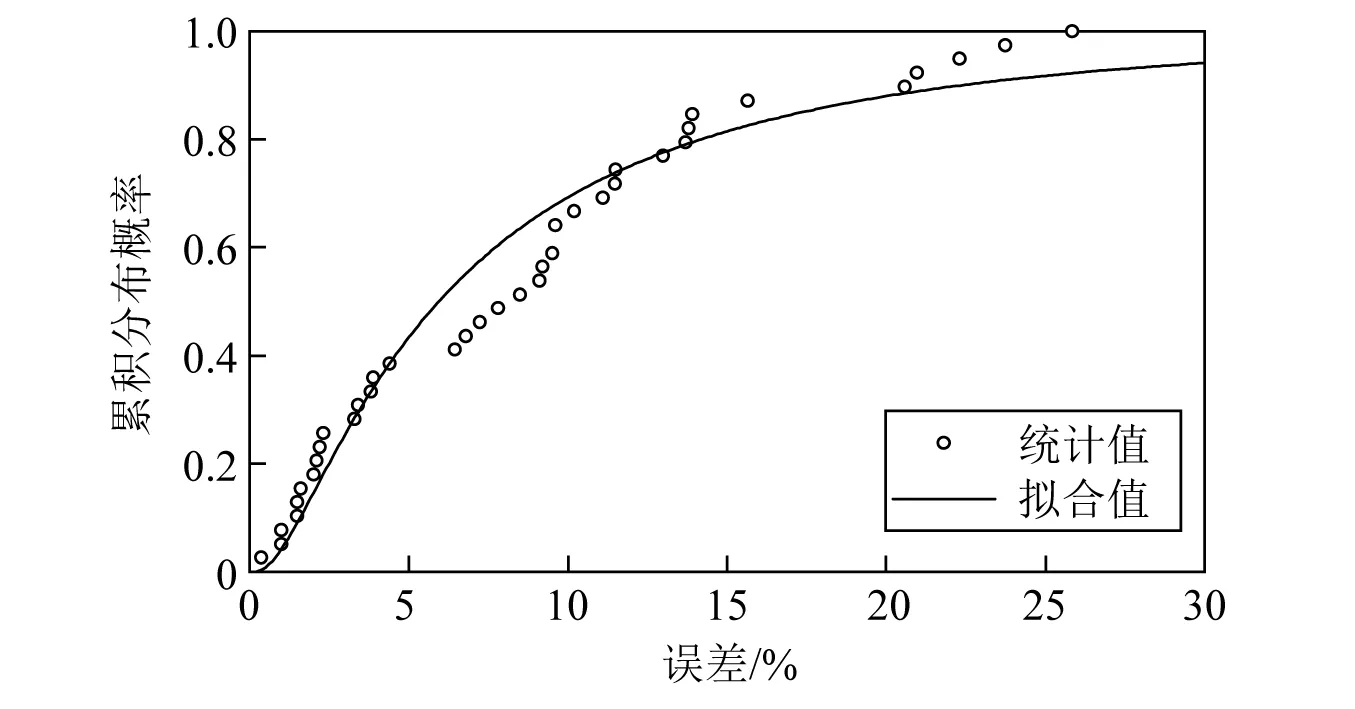
图11 电气设备数值分析误差统计及其分布Fig.11 Errors and their distribution of numerical analyses of electrical equipment
3.5 特高压GIS套管地震易损性
本文考虑多种不确定性组合对特高压GIS套管地震易损性及地震失效风险的影响。多重不确定性的组合方式如下:
(1) 仅考虑地震动不确定性。
(2) 考虑地震动不确定性及套管结构不确定性。
(3) 考虑地震动不确定性、套管结构不确定性及套管性能指标不确定性。
(4) 考虑地震动不确定性、套管结构不确定性、套管性能指标不确定性及电气设备认知不确定性(βm分别为0.2,0.4,0.6及1.03)。
由式(5)可得,不同不确定性组合下,该型特高压GIS套管地震易损性的对数标准差如表5所示。由表5可知,随着考虑的不确定性因素增加,GIS套管地震易损性函数的对数标准差增加。对于该型GIS套管,地震动不确定性对其地震易损性函数对数标准差的影响较大。现有材料参数条件下,结构不确定性及性能指标不确定性对该参数的影响较小。
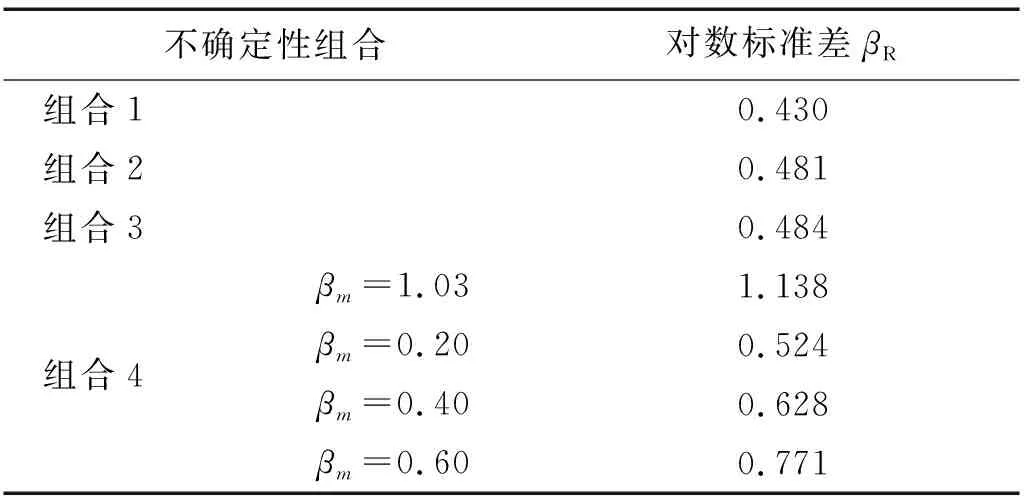
表5 多重不确定下特高压GIS套管的对数标准差Tab.5 LSD of the GIS bushing considering different sorts of uncertainty
不同对数标准差下,该型特高压GIS套管的易损性曲线如图12所示。由图12可知,在电气设备地震易损性曲线中,当地震动强度小于易损性函数中地震动中位值时,考虑较少的不确定性因素易低估电气设备的地震易损性。当地震动强度大于易损性函数的中位值时,考虑较少的不确定性因素易高估电气设备的地震易损性。另外,由于电气设备的结构特殊性,数值分析模型的质量对电气设备地震易损性分析的准确性有较大影响,在分析电气设备地震易损性及地震失效风险时,应考虑此影响。

图12 多重不确定下特高压GIS套管的地震易损性曲线Fig.12 Seismic fragility curves of the GIS bushing considering different sorts of uncertainty
4 多重不确定性下的特高压GIS套管地震失效风险
4.1 适用于特高压GIS套管的场地地震危险性函数拟合
考虑我国水电、风电资源分布及用电负荷区域分布情况,本文共选取5个不同地区的场地为研究对象。各场地的地震烈度、场地类别、特征周期及地震危险性分区等参数如表6所示。表6中,场地设防地震烈度、设防地震加速度、场地特征周期及场地危险性分区可由CECS 160:2004《建筑工程抗震性态设计通则》确定。另外,不同场地在DBE及MCE水准下的PGA也可由该规范确定,如表6所示。对于算例GIS套管,不同PGA对应的第一周期加速度反应谱由式(9)~式(12)确定。由式(7)~式(8),不同场地地震危险性函数中的k及k0如表7所示。
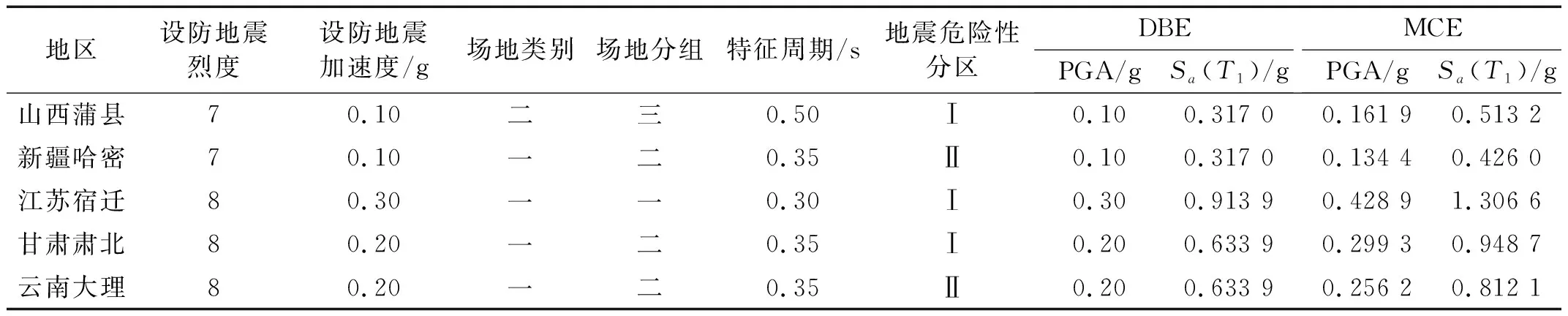
表6 场地地震动设防参数Tab.6 Seismic fortification parameters of the sites

表7 场地地震危险性函数Tab.7 Seismic hazard functions of the sites
4.2 GIS套管地震失效风险
电气设备年地震失效风险如式(14)所示。对于该型特高压GIS套管,不同场地下,其年地震失效风险如表8所示。随着对数标准差βR的增加,套管的年地震失效风险逐渐增加,此结论与图12一致。电气设备地震响应的多重不确定性影响电气设备的地震失效概率,在评估电气设备地震失效概率时,应考虑此多重不确定性的影响。由于认知不确定性造成的对数标准差较大,继而使一些考虑建模不确定的组合下该型套管年地震失效概率达到100%。该现象表明,在评估电气设备的地震失效风险时,应注意控制电气设备分析模型的质量,使地震失效风险的评估更准确。

表8 GIS套管年地震失效风险Tab.8 Annual seismic failure probabilities of the GIS bushing %
由于分析模型的准确性对电气设备地震失效风险有较大影响,本文选取βm为0.2(分析模型质量较好)时分析该型GIS套管在50年设计使用周期内的地震失效风险。由式(15),可得不同场地下该型GIS套管50年设计使用周期内的地震失效风险如图13所示。由图13可知,对于甘肃肃北及云南大理,两地设防烈度及设备地震加速度相同,但该型GIS套管在云南大理的地震失效风险远大于在甘肃肃北的相应风险值。另外,云南大理的设防地震加速度小于江苏宿迁相应值,但在50年设计使用周期内,该型GIS套管在云南大理的地震破坏风险大于江苏宿迁相应值。由此可知,在进行变电站电气设备抗震设计及评估设备抗震性能时,需考虑多重不确定性及设备地震失效风险的影响。另外,由于我国水电基地大多集中在西南地区,该区域电气设备有较高的地震失效风险,对于该区域变电站进行抗震设计时,需评估其在设计使用周期内的地震失效风险,优化变电站内该设备备品数量,以期缩短由该设备地震失效导致的震后停电时间。
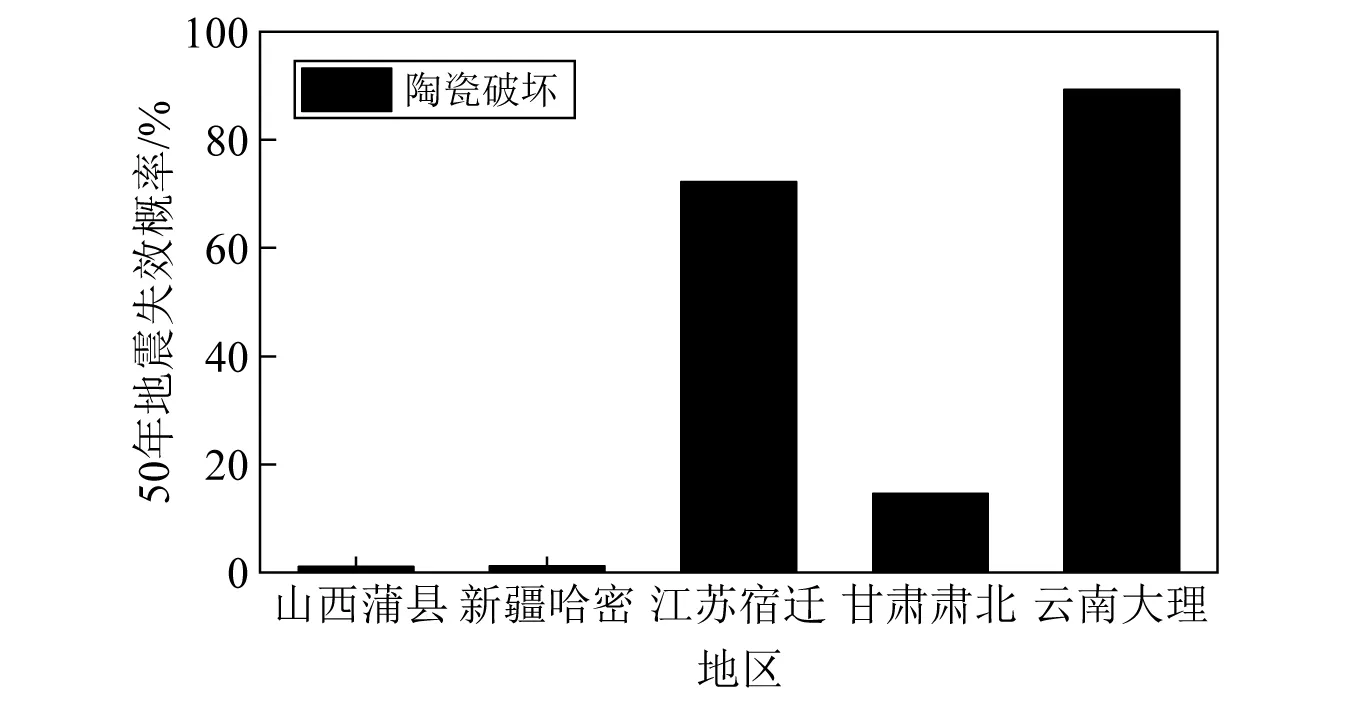
图13 GIS套管50年内地震失效风险Fig.13 Seismic failure probabilities of the GIS bushing in 50 years
5 结 论
本文考虑地震动不确定性、电气设备结构参数不确定性、电气设备性能指标不确定性及认知不确定性,提出了考虑多重不确定的电气设备地震易损性及地震失效风险评估方法,并对某型特高压GIS套管进行了地震易损性与地震失效风险评估,其结论如下:
(1) 多重不确定对电气设备的地震易损性及地震失效风险有较大影响,在评估电气设备地震易损性及地震失效风险时,应考虑地震动、结构参数、性能指标及分析模型质量等多重不确定性的影响。
(2) 当地震动强度小于易损性函数中位值时,考虑较少的不确定性因素易低估电气设备的地震易损性。
(3) 当不同场地的抗震设防烈度及设防地震动PGA相同时,其地震失效风险仍可能不一致。设防地震动PGA较小的地区,电气设备地震破坏风险仍可能大于设防地震动PGA较大的地区。对变电站电气设备进行抗震设计时,需考虑此影响。
