血液黏性对脉搏波传播特性影响的定量分析
2022-06-29卢意成李本森缪馥星龚文波
卢意成 李本森 缪馥星 龚文波
0 引言
在心脏周期性收缩和舒张过程中,血液压力、血流速度和血流量的脉动以及血管壁的变形在血管系统中的传播统称为脉搏波[1]。脉搏波蕴含着丰富的人体生理和病理信息[2],临床上应用于评估高血压、冠心病等疾病患者的心血管状况[3-4]。已有临床研究表明[5-6],长期血液黏性过高会诱发心脑血管病、高血压、糖尿病等疾病。可见,对血液黏性进行检测可为某些疾病提供一定的预判依据。当前已有研究提出利用脉搏波信号光容积描记法估算血液黏度[7],该方法可以克服传统测量方法存在的侵入损伤且操作复杂等缺点。因此定量分析血液黏性对脉搏波传播特性的影响,将对促进血液黏性的无创检测研究具有重要的研究意义。
调研国内外相关文献得知,关于脉搏波和血液黏性的研究已有较多成果。譬如,Kim等[8]测量并分析了814例冠状动脉疾病患者的脉搏波速和血液流变学参数,得到全血黏性等血液流变学参数对脉搏波速的影响并不独立,但其研究并未定量地给出血液黏性与脉搏波速之间的关系。Alastruey等[9]通过对黏弹性血管中一维血流方程的线性分析,研究了血液黏度等因素对脉搏波传播的影响,但其研究涉及动脉的一维假设。李滚等[10]建立了脉搏波波形特征的数学表达式,发现改变血液黏度等参数后发现所得的脉搏图能较好地反映生理信息,但其主要研究单个脉图中波形信息未考虑到脉搏波传播的过程。姚大康等[11]将动脉中脉搏波复波速所满足的频率方程推广到黏弹血液情形,讨论了血液黏弹性对动脉中脉搏波波速和波的衰减的影响,但其主要研究血液的弹性和黏性分别对脉搏波传播的影响程度强弱,未具体给出血液黏性对脉搏波传播的影响规律。潘一山等[12]将血管简化成弹性管,建立血液流过血管壁的力学模型,分析了血液黏性等参数对波的传播的影响,但其在分析黏性项对脉搏波传播的影响时忽略了血液流动惯性项。总之,计及不同血液动力黏性系数对脉搏波传播特性影响的定量分析尚未见报道。
依据当前研究现状,本文假设血管为弹性薄壁等壁厚圆管,血液为均质牛顿流体,且不考虑血管壁的微观结构特点,建立三维血液-血管系统的有限元模型。依据流体力学理论与弹性薄壁管理论,采用双向流固耦合方法模拟血液流动过程中脉搏波的传播。本文在模拟血液流动过程中,考虑了血液流动惯性项的影响,计及不同血液动力黏性系数,分析压力和轴向速度脉搏波的传播特征,从脉搏波峰值和波速的变化情况,定量地分析血液黏性对脉搏波传播特性的影响,以期通过检测脉搏波波形特征进而对血液黏性的无创检测提供帮助。
1 血液-血管系统的双向流固耦合有限元模型
1.1 几何模型
肱动脉处是测量血压最常用的部位,且该位置的脉搏波具有较高的研究价值[13-14]。因此以人体肱动脉部分为研究对象,在多物理场仿真软件COMSOL Multiphysics中建立薄壁圆管几何模型,红色部分表示血液,绿色部分表示血管壁。分别用l、D0、h0表示血管长度、血管内径、血管壁厚度。以血管上游端面的圆心为原点,血管的轴向为x轴建立空间直角坐标系,如图1所示。根据人体肱动脉的平均几何尺寸[15-16],本文血管几何模型取D0=5 mm,h0=0.5 mm,径厚比D0/h0=10,且为避免模拟中过早发生波的反射而对脉搏波波形的影响,取l=1 m。
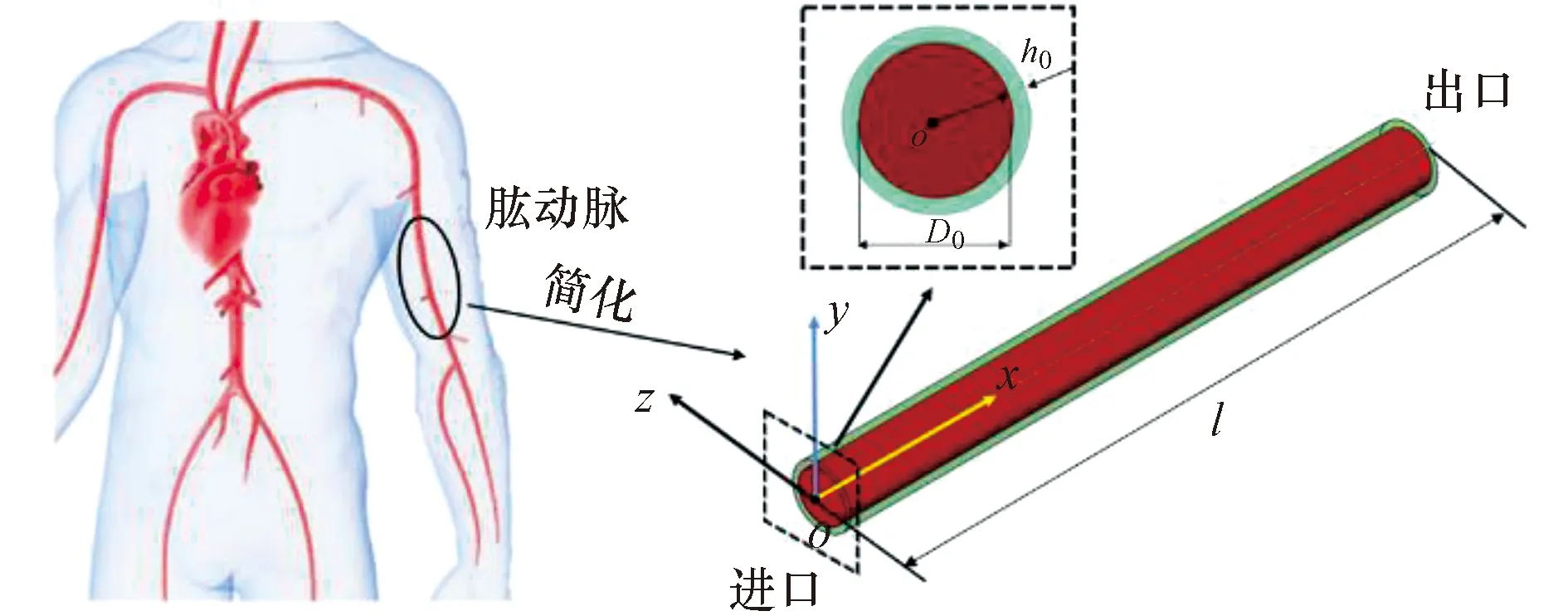
图1 血管几何模型示意图Figure 1 Schematic diagram of blood vesselgeometric model
1.2 材料属性
假设血管壁为各向同性的线弹性材料,密度ρv=1150 kg/m3,弹性模量Ev=2.5 MPa,泊松比υ=0.45[17],即血管壁为弹性薄壁管;假设血液为绝热的、不可压缩的黏性牛顿流体[18],密度ρb=1050 kg/m3;假设血液体积力矢量、流动速度矢量、压力分别为Fb、vb、p,下标b、v分别代表血液和血管壁。血液流动的控制方程为:
(1)
(2)
τb=μ[▽vb+(▽vb)T]
(3)
式中:ρbvb▽vb为血液流动惯性项;I为二阶单位张量;ρb为血液密度;μ为血液动力黏性系数;t为血液流动时间;τb为黏性应力张量。
人体平均动力黏性系数约为0.004 Pa·s[18],为研究肱动脉中不同的血液动力黏性系数对脉搏波传播特性的影响,分别取血液动力黏性系数0、0.002、0.004和0.006Pa·s进行计算分析,定量地探究血液黏性与脉搏波传播规律之间的联系。
1.3 边界条件
模拟计算分析中,在血液进口边界处加载如图2所示脉冲压力,出口边界处控制相对压力为0 Pa。进口压力脉搏波波形是通过脉象仪临床实测采集得到的,用作模拟中的加载波形。另外,为了在有限硬件配置条件下提高计算效率,根据无量纲数据分析,将加载波形周期缩短10倍进行模拟计算。在双向流固耦合分析模型中,血液流动为其与血管壁内表面无滑移的层流流动,血管壁的两端不设约束条件,外表面为自由壁面。
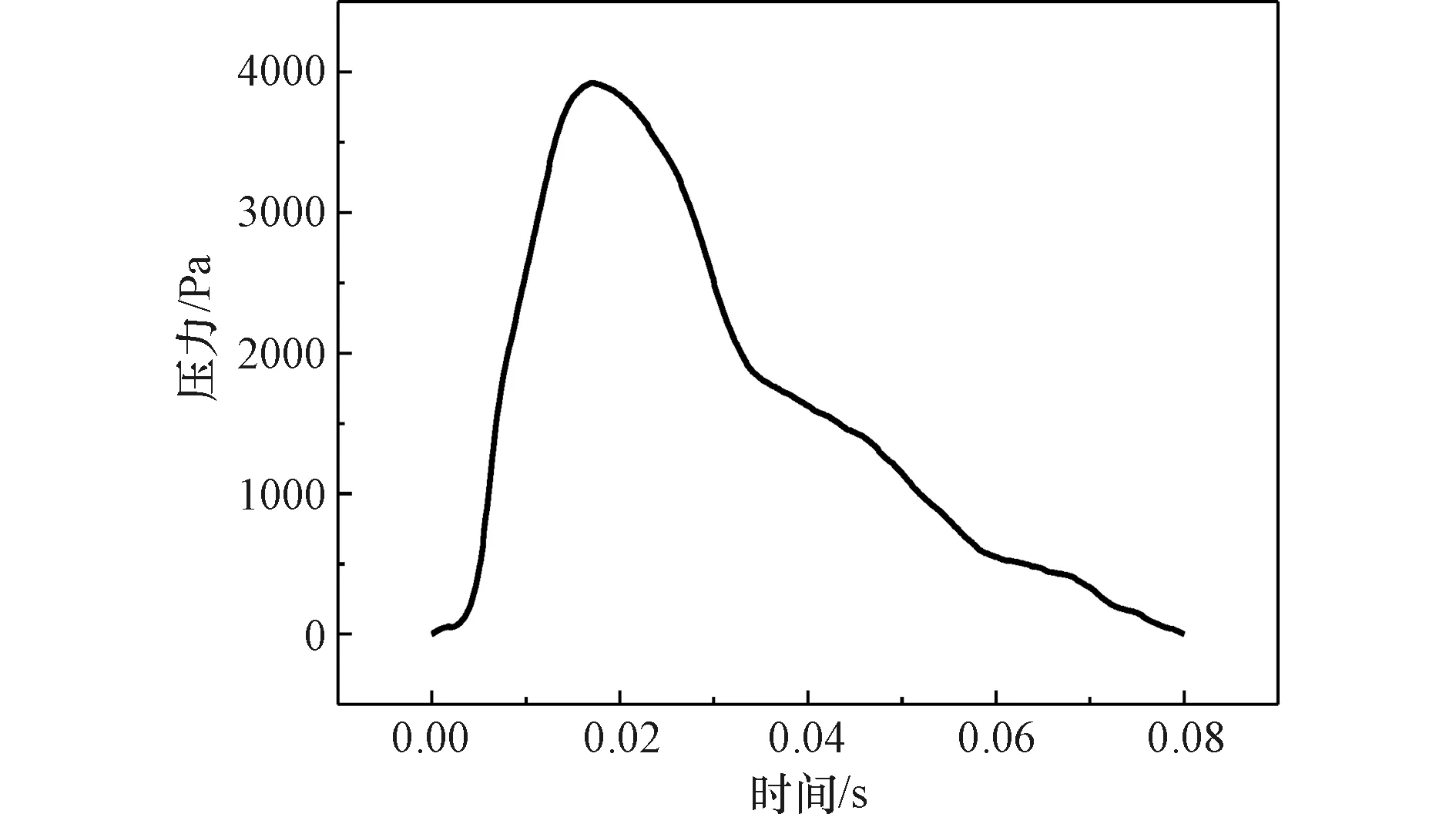
图2 血管进口处加载的压力脉冲历程Figure 2 Pressure pulse history loaded at the inletof the vessel
根据连续介质力学理论,在血液和血管壁耦合界面处,血液和血管壁应满足位移连续和应力连续边界条件:
ub=uv
σb=σv
(4)
式中:ub、uv分别表示血液和血管壁的位移矢量;σb、σv分别为血液和血管壁上的应力。
1.4 网格划分
应用COMSOL Multiphysics模拟分析中,血液和血管壁均采用六面体单元。本文几何模型下,共有六面体单元786 000个,网格顶点833 055个。这里要说明的是,以计算结果的数值上的稳定性为准,经过了网格无关性验证,所选的单元数满足本文计算分析的收敛要求。
1.5 求解设置
在本文的双向流固耦合计算中,将血液流动与血管壁变形两者之间的相互作用结合起来,集合血液和血管壁每个节点处的控制方程组形成的大型矩阵,应用任意拉格朗日-欧拉方法(arbitrary Lagrangian-Eulerian,ALE),采用瞬态求解器的全耦合方法进行大型矩阵的解耦求解,并结合边界条件求解血液和血管壁的控制方程。设定计算周期为0.1 s,时间步长为10-4s,每个时间步长内最大迭代次数为50。
在血管进口脉动压力的作用下,血液的流动会呈现出脉动性。选取肱动脉中心轴线上4个不同位置点作为监测点,坐标分别为A(x1,0,0)、B(x2,0,0)、C(x3,0,0)和D(x4,0,0)。为避免反射波以及血管出口位置边界条件的影响,令x1=l/20,x2=l/10,x3=3l/20,x4=l/5。为分析血液动力黏性系数对脉搏波传播的影响程度,本文提取4个监测点处的压力和轴向速度脉搏波曲线对脉搏波峰值以及波速进行着重分析,另外给出了血管壁位移云图和血液流线图。
2 结果与分析
2.1 脉搏波传播特征
压力脉搏波与轴向速度脉搏波的传播规律如图3所示。
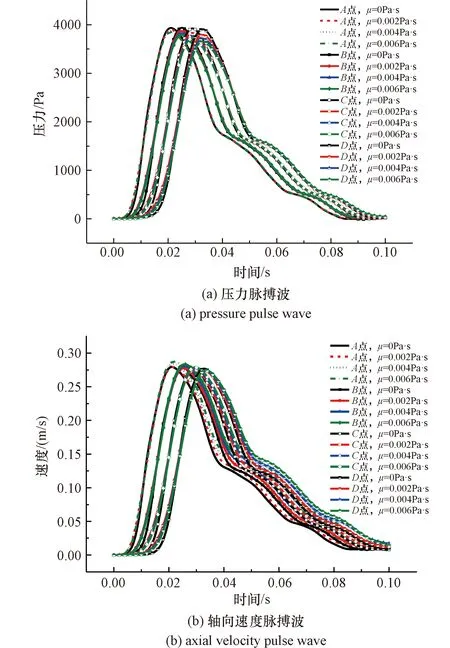
图3 不同监测点处脉搏波曲线Figure 3 The curve of pulse wave at different monitoring points
由图3(a)可知,本文模型中不计脉搏波传播过程中波的反射影响,波形几乎与加载波形一致。在同一个监测点,不同血液动力黏性系数下,压力脉搏波的波峰幅值明显不同,随着黏性系数的增加,压力脉搏波波峰值减小。这是由于血液黏性使得脉搏波在传播过程中,发生能量耗散现象,表现为压力波波峰值减小。另外,沿着血流方向,随着血液动力黏性系数的增大、脉搏波传播距离的增大,血液黏性引起的压力脉搏波波峰值衰减越明显。若以不考虑血液黏性时的波峰值为基准,在监测点A处,血液动力黏性系数为0.006 Pa·s时波峰值降低了约0.69%。而在监测点B、C和D处,压力脉搏波波峰值之间的差距更为明显,当血液动力黏性系数为0.006Pa·s时波峰值分别降低了约2.80%、4.46%和5.69%。
由图3(b)可知,对于不同的血液动力黏性系数,其速度脉搏波曲线在升支阶段几乎完全重合,主要差别是波峰幅值略有不同。在降支阶段,血液动力黏性系数越大,速度波形曲线下降越平缓。另外发现:在监测点A、B、C处,血液动力黏性系数较大时的速度波波峰值最高;而在监测点D处,不考虑血液动力黏性时的速度波波峰值最高。还可以看出,沿着血流方向,脉搏波传播距离越远,血液黏性引起的速度波波峰值衰减程度越明显,且血液的动力黏性系数越大,速度波峰值的衰减幅度越大。在速度波从监测点A传播至监测点D的过程中,不计血液动力黏性系数时,速度波峰值衰减幅度最小,约为0.90%;当血液动力黏性系数为0.006 Pa·s时,速度波峰值衰减幅度最大,约为4.50%。由此可见,血液黏性对速度脉搏波的传播具有较为明显的影响。
2.2 脉搏波波峰点分析
为进一步分析血液动力黏性系数对脉搏波传播的影响程度,4个不同血液动力黏性系数下,各个监测点处的压力脉搏波和速度脉搏波的波峰分布情况如图4所示。
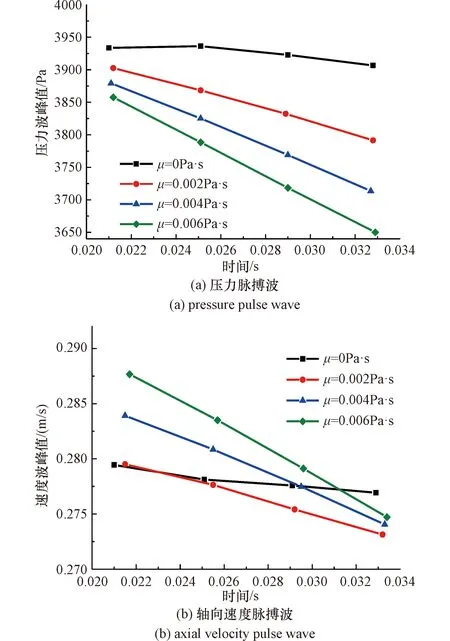
图4 不同监测点处的脉搏波的波峰幅值Figure 4 The peak amplitude of pulse wave at different monitoring points
血液黏性对脉搏波传播规律的影响较为明显,同一血液动力黏性系数下,在脉搏波从监测点A传播至监测点D的过程中,血液动力黏性系数分别为0、0.002、0.004和0.006 Pa·s时,压力脉搏波峰值的衰减幅度分别为0.68%、2.85%、4.27%、5.38%,轴向速度脉搏波峰值的衰减幅度分别为0.90%、2.28%、3.47%、4.50%。整体上看,黏性系数每增大0.002 Pa·s,压力脉搏波峰值衰减幅度增加约1.76%,轴向速度脉搏波峰值衰减幅度增加约1.20%。由此可见,血液黏性越大,压力脉搏波的波峰值越小,血液黏性是压力脉搏波幅值衰减的原因之一,且血液黏性的作用会随着脉搏波传播距离的增大而越加明显。
本文通过监测点之间的距离和波峰点的时间差,计算脉搏波的传播速度。以每个波形的波峰点作为标记分析点,对于不同血液动力黏性系数0、0.002、0.004和0.006 Pa·s情形,根据图4,可以计算得到压力脉搏波的平均波速分别为12.71、12.93、12.93和12.82 m/s;速度脉搏波的平均波速分别为12.61、12.82、12.71和12.82 m/s。压力脉搏波和速度脉搏波几乎是以相同的速度在血液-血管系统中传播,而速度脉搏波在每个监测点达到峰值的时刻略晚于压力脉搏波情形的。另外,血液动力黏性系数越大,速度脉搏波达到峰值的时间越晚。由计算可知,血液黏性对速度脉搏波的强弱有较大影响,而对其波速的影响比较微弱,不同动力黏性系数下的波速差距仅在1%左右。
2.3 血管壁变形分析
脉冲压力作用下,伴随血液的流动,弹性血管壁产生涨缩变形,随着血液中压力波的传播,血管壁上的变形也沿着血管壁传播。为直观起见,通过径向位移的大小观测血管壁的变形程度。比如,当t=0.04 s时,将模型放大100倍,不同血液动力黏性系数下,血管壁外表面变形后的位移波如图5所示。血管壁在血液内压作用下,向外膨胀变形,对于4种不同的血液动力黏性系数0、0.002、0.004和0.006 Pa·s,血管壁的最大径向位移分别为23.5、22.7、22.1和21.7 μm。显然,随着血液黏性的增大,血管壁的径向位移减小。若以血液动力黏性系数为0 Pa·s时的最大径向位移为基准,血液动力黏性系数分别为0.002、0.004和0.006 Pa·s时,其最大径向位移分别减小了3.40%、5.96%和7.66%。
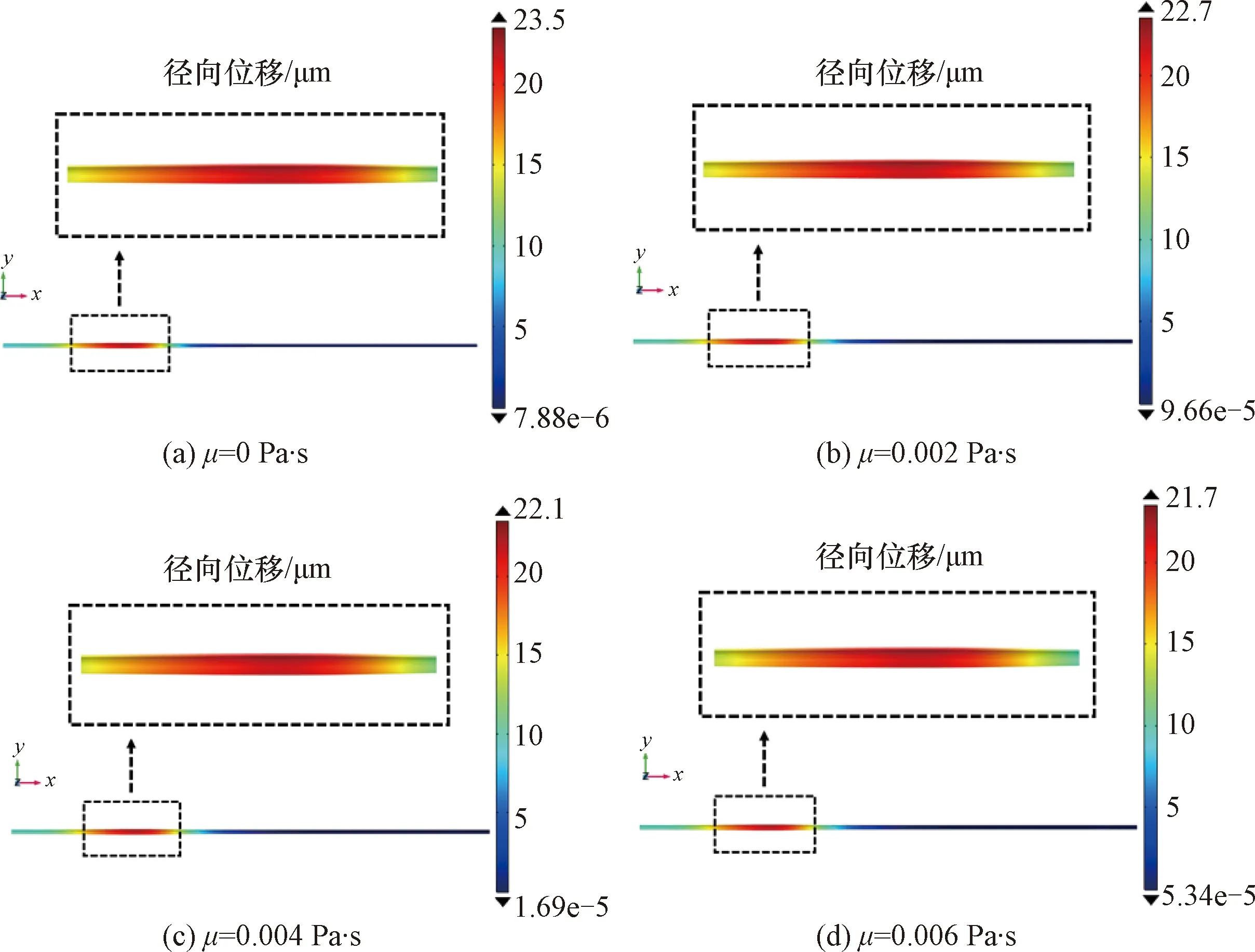
图5 t=0.04 s时动脉径向位移波Figure 5 The radial displacement wave of the artery at t=0.04 s
3 讨论
本文所得到的结果显示,在不考虑血液黏性情况下,波峰衰减幅度最小但仍存在一定的衰减,而文献[12]通过血液流过血管壁的力学模型,得出,在不考虑血液黏性时,脉搏波传播过程中波峰幅值保持不变。本文结果与文献[12]的存在较明显差别。
为分析不考虑血液黏性时脉搏波峰值衰减原因,对于血液动力黏性系数为0 Pa·s情形,截取血管进口处l/5长度作为分析对象,提取血液流动的流线图如图6所示。当t=0.06 s时,压力脉搏波向血管出口处传播,最大流动速度为0.11 m/s,血管进口端面附近出现微弱的回流现象。当t=0.08 s时,血管进口端面压力脉冲加载结束,最大流动速度为0.05 m/s。血液中流线分布较为杂乱,回流现象变得更为明显。血液回流使得血液质点间相互撞击,产生一定的能量损耗,压力脉搏波和轴向速度脉搏波的波峰幅值随之衰减。
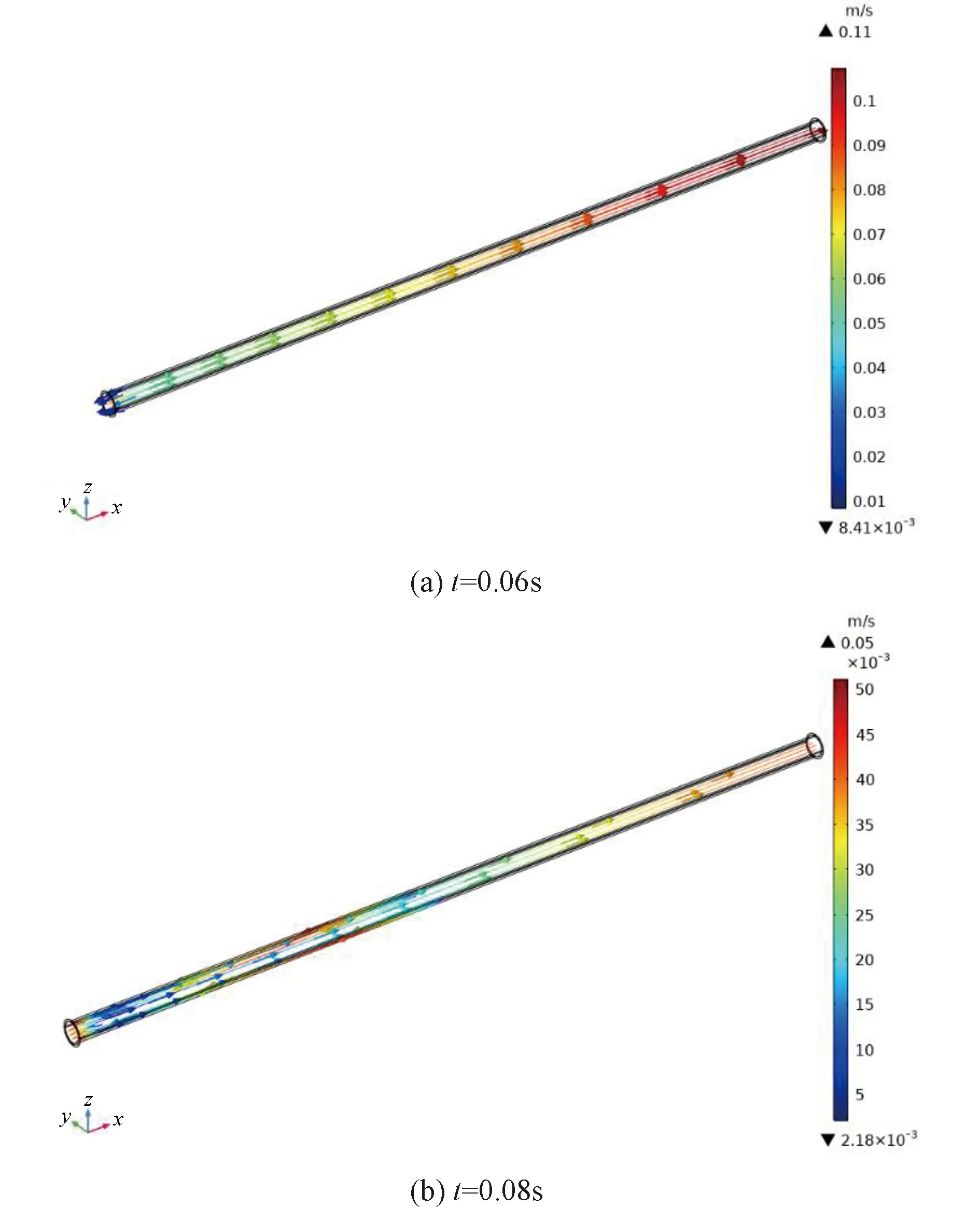
图6 μ=0 Pa·s时不同时刻血流速度场流线图Figure 6 Blood flow velocity streamlines at different time with 0 Pa·s
另外,对于脉搏波的传播速度,本文计算所得结果为血液黏性对脉搏波波速的影响比较微弱,不同动力黏性系数下的波速差距仅在1%左右。此结果与王礼立等[19]认为脉搏波传播速度主要依赖于两个无量纲参数(血液-血管模量比和薄壁血管径厚比),血液的黏性并不是主要影响因素的观点相一致。
本文应用双向流固耦合的有限元数值模拟方法,研究了血液黏性大小对脉搏波传播特性的影响。然而,此分析模型也存在一定的局限性,如将肱动脉简化成规则的圆管模型,血液的非牛顿流体特性可能会对结果产生一定的影响。这些均需要在后续的研究中加以深入分析和探讨。
4 结论
本文应用多物理场仿真软件COMSOL Multiphysics,建立了血液-血管壁系统的双向流固耦合分析模型,定量分析了4个不同血液动力黏性系数下,肱动脉中血液黏性对压力和速度脉搏波的传播特性的影响。通过计算分析发现,血液黏性对脉搏波波速的影响比较微弱,不同动力黏性系数下的波速差距仅在1%左右。而血液黏性对脉搏波的波峰幅值影响较大。血液动力黏性使血液-血管壁系统的能量耗散较大,使压力脉搏波、速度脉搏波以及径向位移波的峰值均降低。另外,血液黏性引起的波峰值的衰减程度随着传播距离的增大变得越明显,如在血管1/20长度处,黏性引起的峰值衰减幅度在0.8%~2%之间,而在血管1/5长度处,黏性引起的峰值衰减幅度在2.5%~7%之间。当血液动力黏性系数在0 ~ 0.006 Pa·s范围内时,血液动力黏性越大,脉搏波峰值衰减幅度越大,且黏性系数每增大0.002 Pa·s,压力脉搏波峰值衰减幅度增加约1.76%,轴向速度脉搏波峰值衰减幅度增加约1.20%,血管壁的变形程度减小约2.98%。本文研究结果可以为通过脉搏波进行血液黏性的无创检测研究提供参考依据,为血液黏性的无创检测提供一种新的思路。
致谢:本文是在宁波大学王礼立教授多次悉心指导下完成的,非常感谢王礼立教授对本文提出的重要意见,同时也感谢宁波大学杨黎明教授对本文的有益讨论,特此致谢!
