DOA Estimation Based on Root Sparse Bayesian Learning Under Gain and Phase Error

Dingke Yu,Xin Wang,Wenwei Fang,Zixian Ma,Bing Lan,Chunyi Song,Zhiwei Xu

Abstract—The direction of arrival (DOA) is approximated by first-order Taylor expansion in most of the existing methods,which will lead to limited estimation accuracy when using coarse mesh owing to the off-grid error.In this paper,a new root sparse Bayesian learning based DOA estimation method robust to gain-phase error is proposed,which dynamically adjusts the grid angle under coarse grid spacing to compensate the off-grid error and applies the expectation maximization (EM)method to solve the respective iterative formula-based on the prior distribution of each parameter.Simulation results verify that the proposed method reduces the computational complexity through coarse grid sampling while maintaining a reasonable accuracy under gain and phase errors,as compared to the existing methods.

Keywords—direction of arrival estimation,gain-phase error,root sparse Bayesian learning,off-grid error

I.INTRODUCTION

Low earth orbit (LEO) satellite communication (SATCOM) is considered as one of the few solutions to realize sufficient communication coverage and bandwidth in the ocean[1].Phased antenna arrays (PAA) have a wide range of applications in LEO SATCOM and we therefore made efforts on the phase-array receiver integrated circuit (IC)[2]and pattern synthesis[3].Direction of arrival (DOA) estimation plays an important role in the array signal processing of PAA[4]in various areas of radar[5],communications[6],sonar[7],seismic detection[8],and medical engineering[9],etc.The tradition high-resolution DOA estimation methods whose great performance is not suitable for the condition of low signal-to-noise ratio (SNR),and limited snapshots and correlated signals mainly include Capon method[10],maximum likelihood method[11,12],and subspace-based method[13,14].With the development of compressed sensing theory[15],the method based on sparse reconstruction provides a new solution for DOA estimation[16],including thel0norm-based greedy method[17],the minimum oflpnorm-based optimization methods[18],and the sparse Bayesian learning (SBL)based algorithms[19].However,in practical engineering applications,the array sensors suffer from gain-phase disturbances due to the changes of climate and environment,which will cause the large bias in the DOA estimation[20].

The incipient DOA estimation methods in the presence of array errors were achieved by direct discrete measurement,interpolation,and storage of the array manifold[21,22],which are costly on computation leading to limited effectiveness.By modeling the array disturbance,the array error calibration is transformed into the parameter estimation problem and can then be roughly divided into two categories:active calibration and self-calibration.The active calibration methods can offline estimate the array perturbation parameters[23].It requires prior knowledge on the number and position of the calibration source and therefore cannot always be applied in practice.By contrast,self-calibration does not require additional auxiliary source,but the original self-calibration method had high requirements on the initial value of iteration to guarantee global convergence[20].To avoid the suboptimal convergence,Liu et al.proposed an eigenstructure method[24],which realizes DOA estimation by the dot product of the array output vector and its conjugate.To relax the requirements on condition that at least two signals are spatially far from each other,Cao et al.proposed a Hadamard product-based method[25],which realizes DOA estimation by the Hadamard product of the covariance matrix and its conjugate.However,this method suffers from high computational complexity.Wang et al.devised a DOA estimation method from a phase retrieval perspective[26],which transform the DOA estimation problem into a phase retrieval formulation with sparse constraint.Analogously,a DOA estimation method that takes the squared magnitude of the elements in the compensated covariance matrix to avoid the effect of phase errors was proposed[27].With the development of SBL in array signal processing,a great number of DOA estimation methods under gain-phase error are proposed.Liu et al.proposed a unified framework and sparse Bayesian perspective for DOA estimation in the presence of array imperfections[28],which can realize array calibration and DOA estimation by exploiting the spatial sparsity of the arrival signals.Based on this method,Lu et al.proposed a DOA estimation method via coarray with model errors[29].Similarly,Chen et al.proposed a robust sparse Bayesian learning-based DOA estimation method with phase calibration in multiple-input multiple-output (MIMO)radar[30].However,these methods only consider the condition that the arrival signal strictly falls on the divided grid in the presence of gain-phase errors.To better estimate the off-grid error,Yang et al.proposed off-grid DOA Estimation using sparse Bayesian inference[31],which use the first-order Taylor expansion to linearly approximate the deviation angle error.Using the sample covariance matrix,Zhang et al.further gave an improved off-grid SBL method to reduce the effect of noise variance[32].Yu et al.proposed a novel sparse reconstruction based DOA estimation method under grid mismatch[33],which also use the first-order Taylor expansion.However,according to the characteristics of first-order Taylor expansion,the approximate direction can only be used when the mesh angle is small,otherwise the approximate error is large.In order to further improve the approximate effect of off-grid method based on SBL,Dai et al.proposed root sparse Bayesian learning for off-grid DOA estimation[34],which considered the sampled locations in the coarse grid as the adjustable parameters.However,it is worth noting that whether the model is effective when considering gain and phase error.

In this paper,we aim at improving the DOA estimation computational efficiency by using coarse grid spacing for offgrid case.A new DOA estimation method under gain and phase error is proposed.First,it is assumed that the parameters are satisfied as a certain sparse prior,and combined with the gain-phase error model,a sparse Bayesian model with different parameters is formed.Secondly,sparse Bayesian inference is performed on different parameters using hierarchical prior probability to obtain iterative update formulas for different parameters,and the expectation maximization(EM)algorithm is used to iteratively optimize and solve each parameter to obtain the iterative estimated value of each parameter.Then,using the grid angle as a variable,through the operation of matrix transformation,the grid angle iterative update formula is converted into a polynomial form,and the grid angle is solved and updated by using the root-finding method to obtain the final estimated value of the source angle.

The rest of this paper is organized as follows.Section II gives the formulation of the problem.The proposed method is presented in section III.Section IV evaluates the performance of the proposed method via simulations.Section V draws the conclusion.

Notation:Vectors and matrices are denoted by boldface lowercase and uppercase letters,respectively.CN(μ,Σ) denotes joint complex Gaussian distribution with the mean beingμand covariance matrix beingΣ.E{·}denotes the expectation operation.(·)-1is the inverse,(·)*is the complex conjugate,(·)Tis the transpose,and(·)His the complex conjugate transpose.Inrepresents then×nidentity matrix.tr{·}denotes the trace of a matrix.diag{a}means a diagonal matrix with the entries of vectoraon the diagonal.

II.PROBLEM FORMULATION

Consider a uniform linear array (ULA) withMomnidirectional sensors labeled 1,2,···,M,where the distance between adjacent sensors is half-wavelength.Let the first sensor be placed as the reference sensor at the origin of coordinates,i.e.(x1,y1)(0,0),and the coordinates of themth(m1,···,M)sensor are denoted by(xm,ym).Assume thatKnarrowband far-field signalsxk(t)(k1,···,K;t1,···,T)impinging on the array from directionsθk(k1,···,K).The array output vector can be modeled as

By taking the gain-phase errors into consideration,the model(1)should be modified as

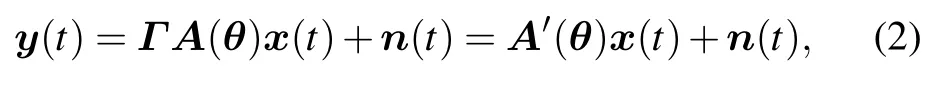
whereA′(θ)Γ A(θ)P ΦA(θ)is the modified manifold matrix after considering gain and phase errors.PandΦare the gain and phase error matrices,which have the forms of

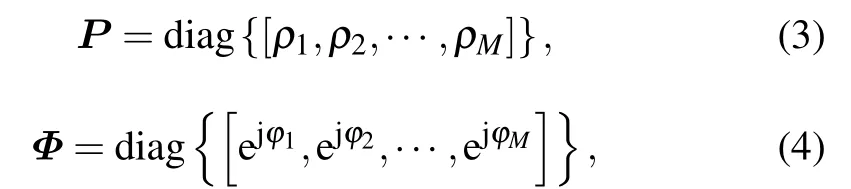
whereρmandφmare the corresponding gain error and phase error of themth sensor,respectively.

Although the modified array manifold matrix still retains the information of the arrival signal,the specific value of the modified array manifold matrix cannot be directly obtained due to the unknown gain and phase error,so it is difficult to directly obtain the arrival information from the data received by the array.To better highlight the ideal signal components and make the relationship between the array output and the gain and phase error parameters more intuitive,we consider using the following array output model under the gain and phase error

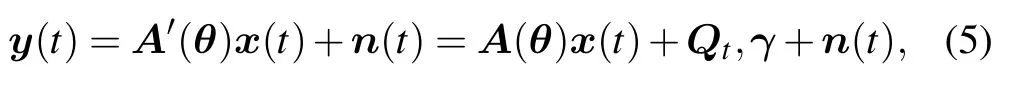
whereγ ∈C(M-1)×1represents a column vector composed of gain and phase error parameters,specifically expressed as

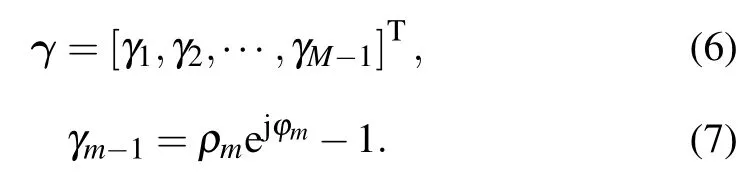
The matrix containing the gain and phase error parameters is expressed as

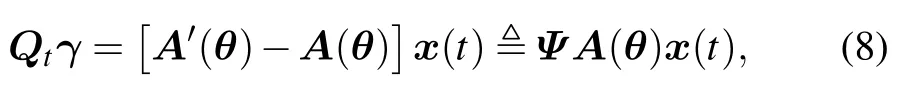
whereΨdiag([0,γT]T)is the matrix of the gain-phase error parameter matrixγindependent of the arrival angle.

AboutQt ∈CM×(M-1)can be expressed as

where only the elements at(m,m)of the matrixGm-1are the non-zero value of 1.

To better highlight the spatial sparsity of the arrival signal,the array output model should be reformulated in an overcomplete form.The arrival signal space is discrete sampled to form a direction setΘ[θ1,···,θL],where the direction set contains the true arrival signal angle.Therefore,the previous parameters aboutθcan be extended to overcomplete models by zero-padding,which are expressed as

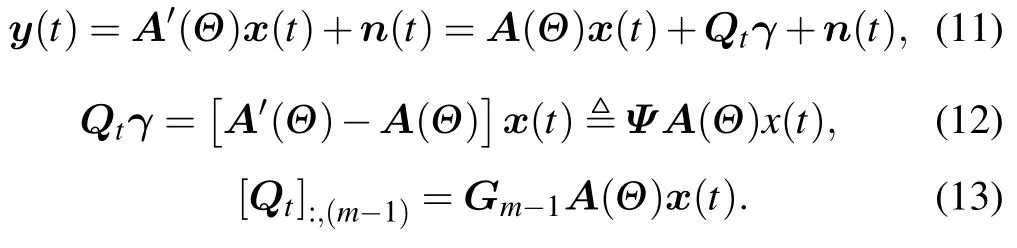
However,the assumption that the true DOAs are located on the predefined spatial grid is not always valid in practical implementations.To solve this off-grid problem,called deviation angle error,the common method used the first-order Taylor expansion to linearly approximate the deviation angle error,so as to realize the estimation and compensation of the deviation angle error.Obviously,this method can alleviate the effect caused by the deviation angle error,but it cannot be fully eliminated.When the coarse grid is set,this linear approximation method may still lead to high modeling error,while the finer grid is set,the massively involved computation could make the linear approximation method unfavorable for real applications.In this regard,we analyze the grid sampled location characteristics,and a new method suitable for coarse grid sampling to estimate the direction of arrival under the gain and phase error is proposed.

III.THE PROPOSED METHOD

A.Sparse Bayesian Formulation

For parameter that satisfy the complex Gaussian distribution,withμrepresenting the mean value of parameters andΣrepresenting the covariance of parameters,the parameter then satisfies the probability density function(PDF):

Therefore,the PDF for the gaussian distribution noiseNwith mean value of 0 and covariance ofσ2can be expressed as

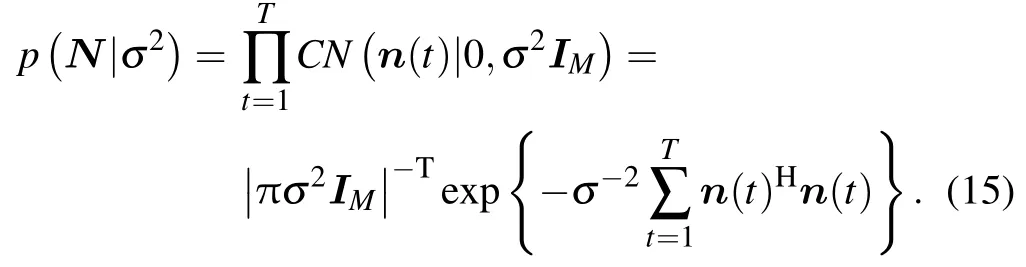
The unknown covarianceσ2of the noise is assumed satisfying the conjugate prior gamma superprior of the Gaussian distribution,whose PDF can then be expressed as

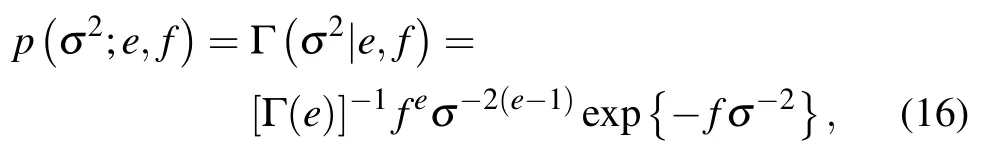
where Γ(·) denotes the Gamma function,and the parameters are sete,f →0 as in Refs.[35,36] to obtain a broad hyperprior.

According to(11),the received signalYsatisfies the Gaussian distribution with mean value ofA(Θ)x(t)+Qtγand covariance ofσ2.Its PDF can then be expressed as

The corresponding row vector of the sparse signal matrixXis represented as the arrival signal power distribution atΘ.Therefore,we can let the power parameter of arrival signal beα,and then,the PDF of sparse signalXin the over-complete model regarding the arrival signal power parameterαcan be expressed as

whereα ∈RN,Λdiag(α),and‖α‖0K,which represents that there areKnon-zero values corresponding to the actual number of signals.The prior distribution function of arrival signal power parameterαcan be expressed as

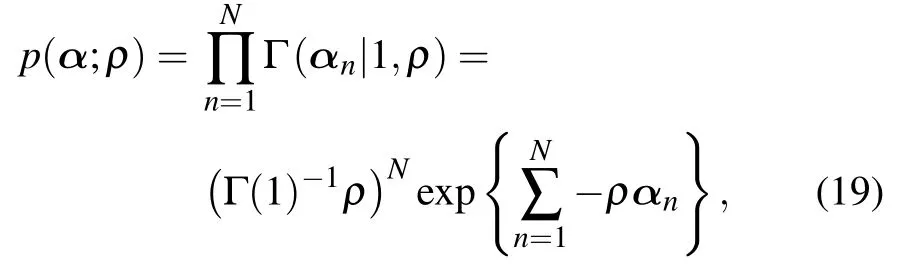
whereρ ＞0,and satisfies that whenρ →0,the value of this prior distribution function reaches the peak at the origin.

Combined with the Bayesian model at all levels,the PDF of joint estimation can be obtained as

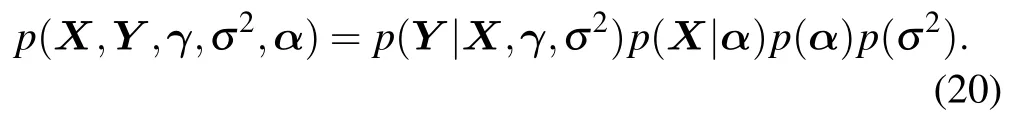
Each distribution function of(20)can be obtained from(16),(17),(18),and(19),respectively.

B.Bayesian Inference

To jointly estimate each parameter,the array receiving signal based on Bayesian principle can be used to represent a parameter with maximum posterior probability,as shown below

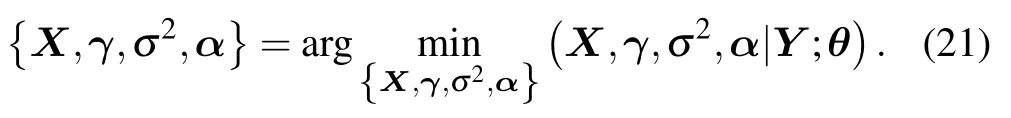
The EM algorithm is applied to perform sparse Bayesian inference since the exact posteriori probability function ofp(X,γ,σ2,α|Y;θ)cannot be obtained directly.The principle behind the EM algorithm is to repeatedly construct a lowbound on the evidence functionp(γ,σ2,α|Y;θ),or equivalently,firstly compute the expectation of the complete probability (E-step),and then update the unknown parameters by maximizing the complete probability(M-step).

Among all parameters,Xis the intermediate hidden variable and is solved first.According to the probability dependence of each parameter,the posterior distribution ofXcan be obtained by

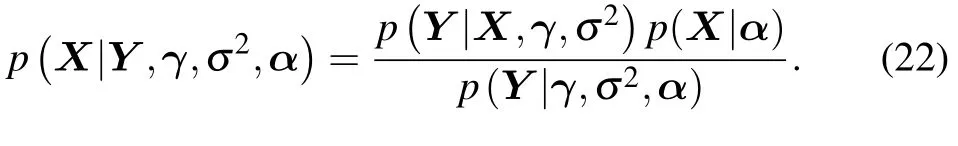
We consider the denominator part of (22) first,and the following (23) can be regarded as the convolution of two functions satisfying the complex Gaussian distribution.According to the properties of the Gaussian function,the result of the convolution of the two Gaussian functions is still a Gaussian function.Thus we only need to solve the mean and covariance matrix of the Gaussian function after deconvolution,which is equivalent to solving the integral in(23).

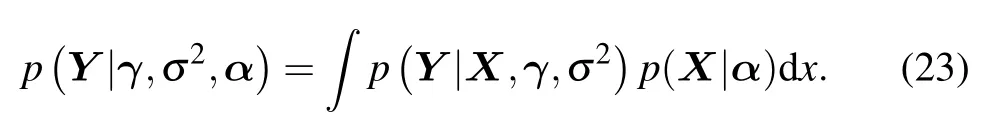
Then we take the exponential part of the convolution Gaussian function and let it as

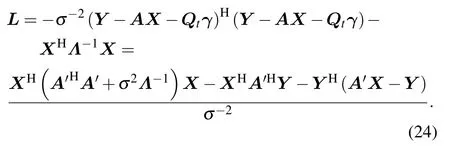
By solving the partial derivative of the exponential part with respect toXand letting it be 0,we can get the expression forXas

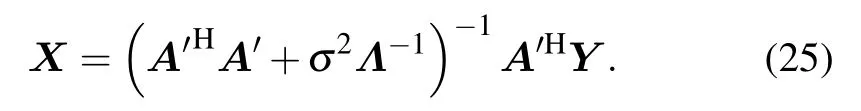
By substituting(25)into(24),we can rewritten the expression ofLas

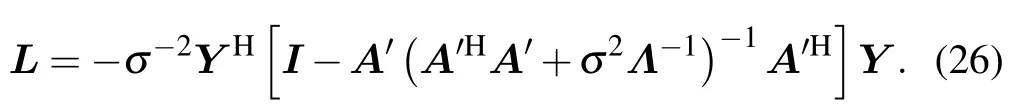
It can be seen that for thep(Y|γ,σ2,α)the mean value is 0 and the covariance matrix isΣy,where

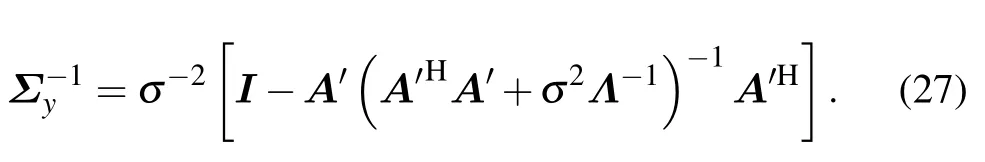
The matrix inverse formula is given by

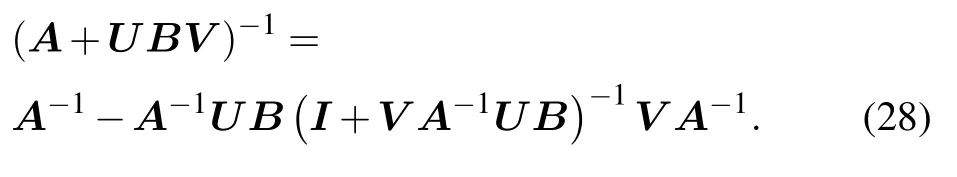
The covariance matrixΣyis then obtained,as

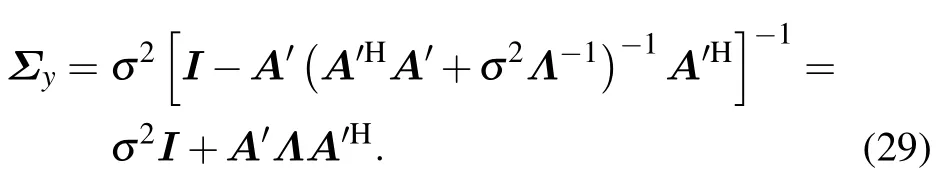
At this time,in(22),the denominator part is known,and the numerator part is the product of two PDF satisfying the complex Gaussian distribution,thus the results still follow Gaussian distribution,so we have the exponential part of(22)obtained by adding(24)and(26).

By ignoring the constant part of (22),the inverse of the covariance matrix is computed as the second derivative of the exponential part with respect toX

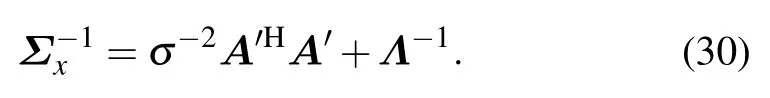
The inverse of the covariance matrix is further inverted to get the covariance matrix

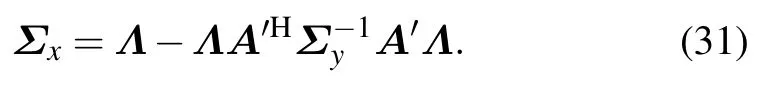
And the mean ofXis calculated as the zero point of the first derivative of the exponential part

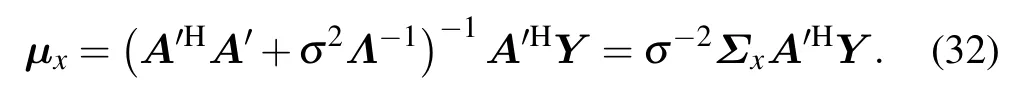
At this point,the mean and covariance matrix ofXhave been obtained,and there are several other variables left to be estimated.Due to takingXas a hidden variable,the lower bound given by lnp(Y,γ,σ2,α)can be expressed as

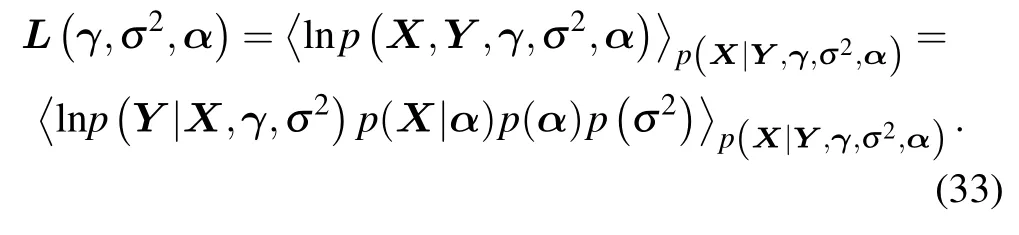
Ignoring other independent terms in the parameter estimates,the likelihood function is obtained for the variableγ,as

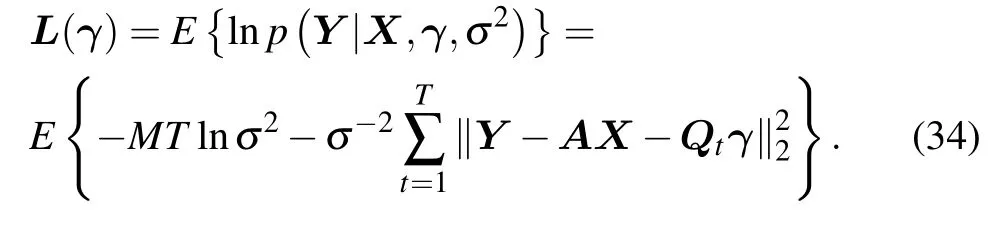
By solving the partial derivative of the likelihood function in(34)with respect toγand setting it to 0,the iterative estimation of the gain-phase error parameterγcan be obtained by

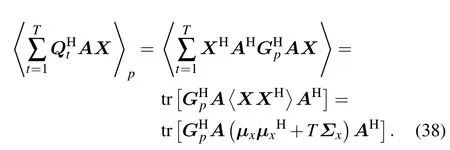
And ignoring other independent terms in the parameter estimates,the likelihood function is obtained for the variableα,as

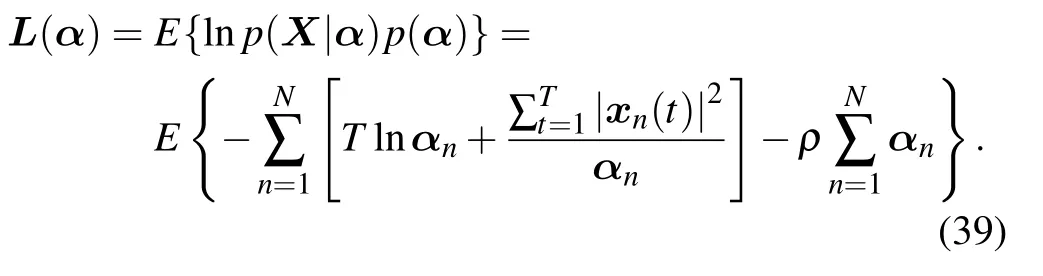
By solving the partial derivative of the likelihood function in(39) with respect toαnand setting it to 0,the iterative estimated value of the arrival signal power parameterαncan be obtained using the root-finding formula by

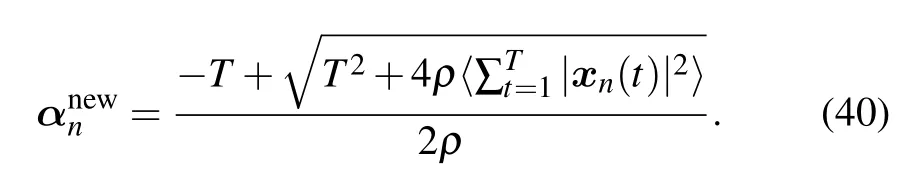
Similarly,ignoring other independent terms in the parameter estimates,the likelihood function is obtained for the variableσ2,as

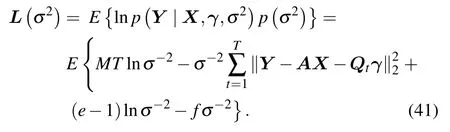
By solving the partial derivative of the likelihood function in(41) with respect toσ2and setting it to 0,the iterative estimation of the noise covariance parameterσ2can be obtained by

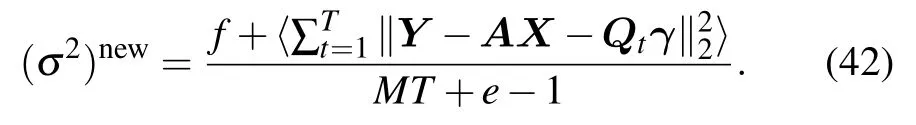
To optimize the estimation accuracy,we also take the grid angleθas a variable.By estimating all the other variables above and ignoring the items that are not related to the grid angle,we only need to optimize the following likelihood function

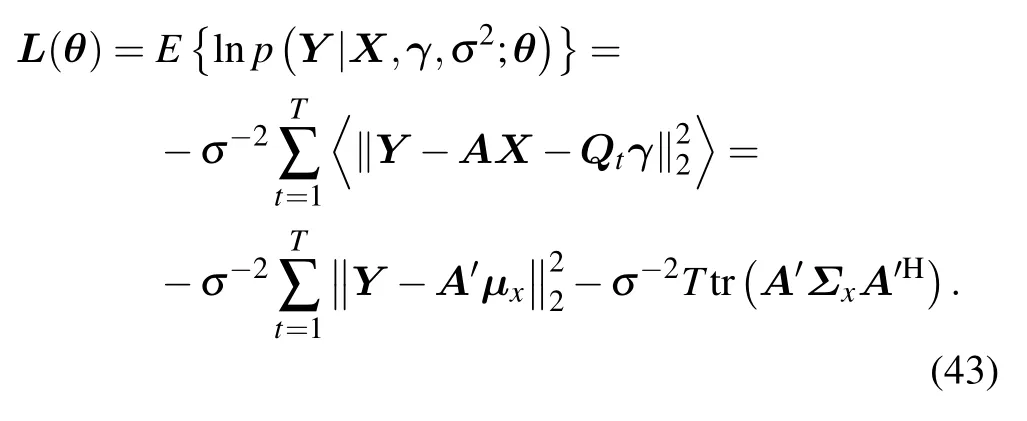
We use the following exponential form to refine each sampled location

The results of solving the partial derivatives of the parts of the likelihood function in(43)with respect toare shown as

To simplify the expression,we make

The order of this polynomial is (M-1),so it has (M-1)roots in the complex plane.According to the definition ofits root value should be precisely selected as a unit absolute value.But due to the existence of noise,its root cannot exactly fall on the unit circle.So we refer to the root-MUSIC algorithm,and select the root closest to the unit circle to represent its value,so that the refined grid update angle can be obtained by

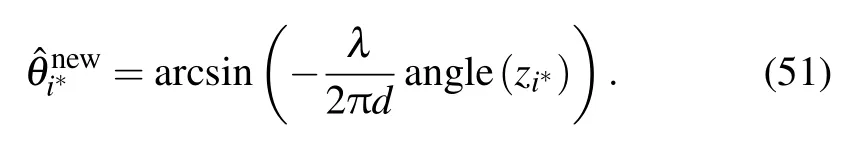
According to the above (51),the grid angleθis updated by solving the roots of the polynomial,so the method can work on coarse grids.However,due to the limitation of the actual polynomial root finding efficiency and the number of coarse grid points,if the angle is updated for each grid point,the complexity of the method is still high,so only the angles that satisfy the following formula are updated

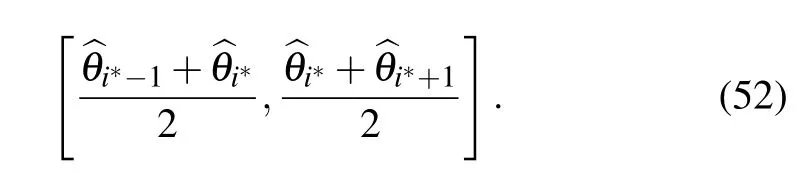
In the actual operation process,some suitable active grid points are selected by setting a threshold.We can letftbe the Frobenius norm ofμx,that is,ft‖μx‖F,then obtain the updated index of the grid point by the firsti(K≤i≤M)maximal values offt,and setitoM.If a smalliis used,the true DOA estimate may be missed during the grid point iteration process,but since the Frobenius norm itself will change with the iteration,the missed DOA estimation may be recovered in the next iteration step.Fig.1 and Tab.1 show the logic diagram of the dependencies of each parameter of the method and the specific implementation steps of the method,respectively.In Fig.1,the circles represent the iterative parameters or signals,and the rectangles represent the hyperparameters.

Fig.1 The logic diagram of the dependencies of each parameter of the method

C.Computational Complexity

According to the operating process of the proposed method shown in Tab.1,the computational complexity of the proposed method is mainly produced by the following operation:calculation of the mean valueμx,calculation of the covarianceΣxandΣy,update of the gain and phase error parametersγ,update of the signal power parameterαn,update of the noise covariance parameterσ2and update of the grid angleθ.Their computational complexity in each iteration isO(MTL2),O(ML2),O(ML+L2+M2),O(M2L),O(TL),O(MTL),respectively.The total computational complexity then equals toO(i(MTL2+2ML2+ML+L2+M2+M2L+TL+MTL)),withirepresenting the number of iterations in the DOA estimation process.Since the number of grid pointsLis much larger than that of array elementsM,the total computational complexity of the proposed method can be approximately expressed asO(i(MTL2+ML2)).The conventional method under the convex optimization framework[26]and that un-der the SBL framework[30]are chosen for comparison,and the complexity equals toO(M2T+2M3+(L+3M)3.5) andO(i(L3+MTL2+MTL)),both are larger than that of the proposed method.Therefore,the proposed method obtains lower computational complexity as compared to the conventional ones.

Tab.1 The specific implementation steps of the proposed method

IV.SIMULATION RESULTS

In this section,the performance of the proposed method is illustrated by experimental simulations.We compare the simulation results with the methods proposed in Ref.[20](called the WF method),Ref.[33] (called the OCOGP method),Ref.[28](called the SBAC method),and Ref.[30](called the SBLPE method).Considering the deviation angle error,the arrival signal angles are modified by the following formula

whereθdenotes the actual angle in the case of deviation angle error,denotes the grid angle closest to the actual angle,εdenotes the deviation angle distributed uniformly over [-Δ/2,Δ/2].Therefore,in the simulation of this paper,the number of arrival signals is 2,whose angle range is[-25°±Δ/2,0°±Δ/2]and the number of the element array is 8.The gain errors and phase errors are generated as follow

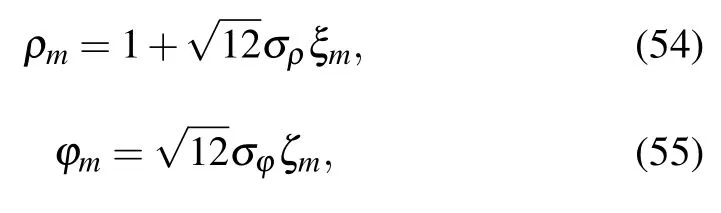
whereξmandζmare independent and uniform random variables in interval[-0.5,0.5],σρandσφare the standard deviations of gain errors and phase errors,respectively.Since the gain errors only affect the peak value of the spatial spectrum,the standard deviation of gain errors is set as 0.1.The performance of the DOA estimation is measured by the root mean square error(RMSE),which is defined as

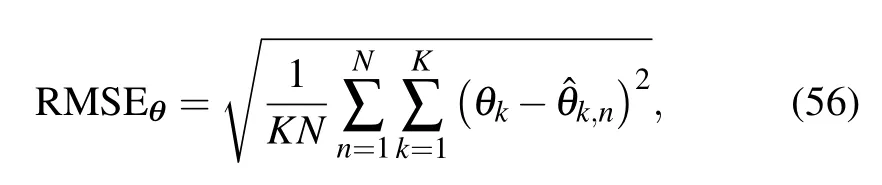
whereN500 represents the number of Monte Carlo experiments,Krepresents the number of signal sources,θkandare the actualkth arrival angle and the estimatedkth angle in thenth Monte Carlo experiment,respectively.

The size of the grid spacing will directly affect the estimation accuracy and computational complexity of the method.Selecting the appropriate grid spacing will maximize the estimation efficiency of the method.To study the influence of grid spacing,we set grid spacing from 1°to 5°with 0.5°interval as a variable.And the performance comparison of DOA estimation under different grid spacing is produced and shown in Fig.2.The estimation accuracy of the proposed method is not the optimal one when setting the grid spacing to 1°.This is probably because the grid angle used as a variable parameter may cause the updated grid angle deviate from the correct direction when setting the finer grid spacing.The proposed method has the minimal increase of the estimation error when the grid spacing becomes larger,and is always in the state with the highest estimation accuracy when the grid spacing is equal or greater than 2°,as compared to the other methods.The results demonstrate that in the case of coarse grid spacing,iterative updating of the grid angle has a better effect,and the computational complexity is reduced due to the increase of the grid spacing.

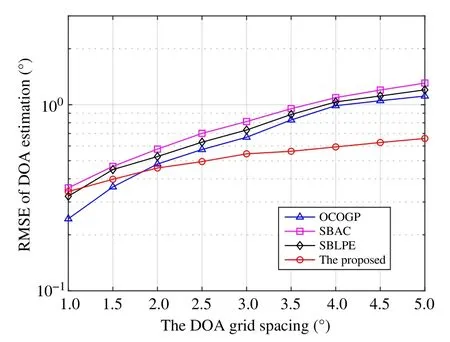
Fig.2 Performance comparison of DOA estimation under different grid spacing,when SNR10 dB,snapshots100,σφ 40°

To comprehensively demonstrate the effectiveness of DOA estimation under different grid spacing,we randomly select two signals coming from-25.3°and 0.8°and for each signal set grid spacing to 1°,2°,and 5°,respectively.The spatial spectrum is produced and shown in Fig.3.The results demonstrate that the proposed method is not the optimal one when setting the grid spacing to 1°,and obtains the slight advantage when setting the grid spacing to 2°,and achieves significant advantage when further increasing the grid spacing to 5°,as compared to the other methods.These comparison results are consistent with that shown in Fig.2.Some spurious peaks are also observed for the proposed method,which may be caused by the adjustment of grid angle parameters and are reasonably expected to have slight impact to the estimation since they all below-20 dB.The results also verify that thanks to the good sparsity based on sparse representation,the coarse grid spacing will not necessarily lead to significant performance degradation of DOA estimation as compared to the finer grid spacing.

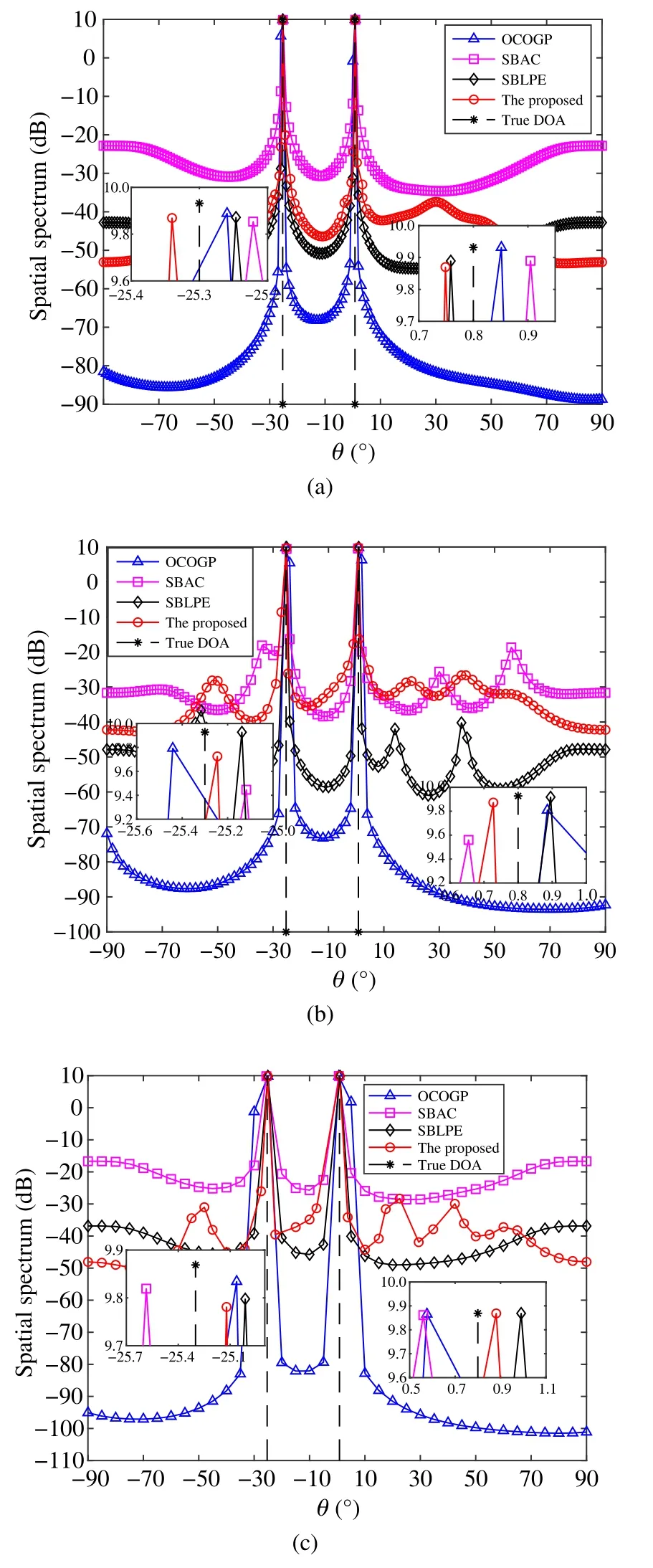
Fig.3 Comparison of spatial spectrum when SNR10 dB,snapshots=100,σφ 40°:(a) the grid spacing is 1°;(b) the grid spacing is 2°;(c) the grid spacing is 5°

Fig.4 shows the DOA estimation performance when varying the SNR from-5 dB to 20 dB.The estimation error of the all methods decreases with the increase of SNR.Among the three conventional methods,the SBLPE shows the best performance.As compared to the SBLPE,when setting the grid spacing to 2°,the proposed method achieves the similar performance when the SNR is set to below 10 dB and slightly better performance by further increasing the SNR.The proposed method obtains significant superiority over the all conventional methods within the investigated range of SNR by setting the grid spacing to 5°.We also notice that the different methods converge at different levels of SNR:the performance of the SBLPE tends to converge at SNR5 dB,both the performance of the SBAC and the proposed method tend to converge at SNR10 dB,the performance of the OCOGP fails to converge when setting SNR＜20 dB.

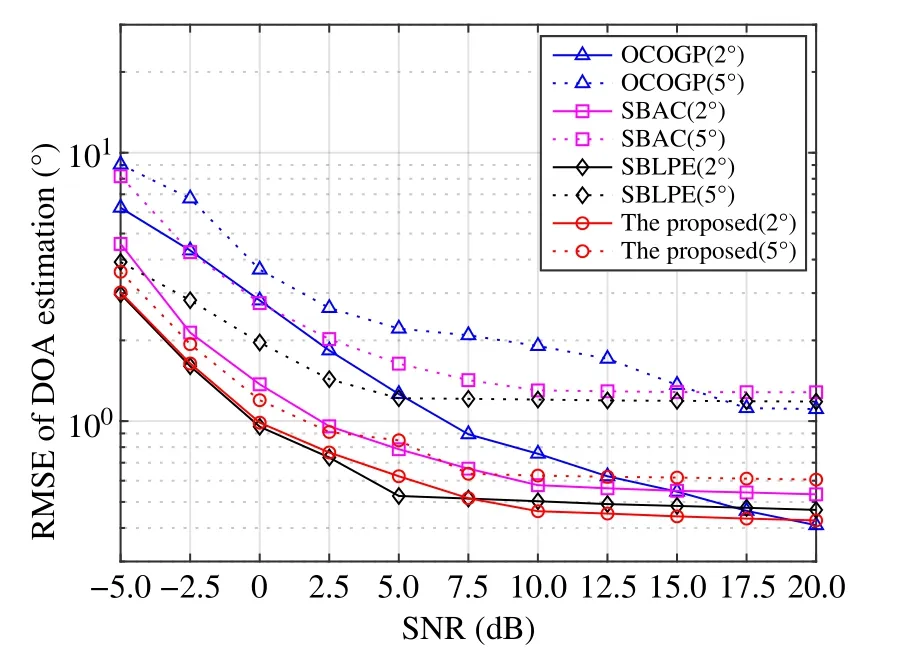
Fig.4 Performance comparison of the DOA estimation under different SNRs when snapshots100,σφ 40°

Fig.5 gives the DOA estimation performance when varying the number of snapshots from 10 to 500.The estimation error of the all methods decreases with the increase of the number of snapshots.When setting the grid spacing to 2°,the proposed method achieves the similar performance when the number of snapshots is set to below 70 and slightly better performance by further increasing the number of snapshots,as compared to the SBAC and the SBLPE,and all of these three methods have good estimation accuracy under the low number of snapshots.The proposed method obtains significant superiority over the all conventional methods when the number of snapshots is set to above 20 by setting the grid spacing to 5°.The different methods converge at different levels of the number of snapshots:the performance of the SBAC tends to converge atT50,both the performance of the SBLPE and the proposed method tend to converge atT100,the performance of the OCOGP fails to converge when settingT ＜500.

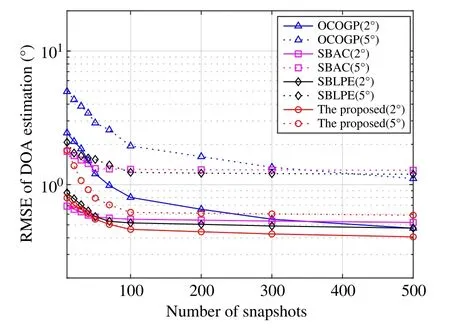
Fig.5 Performance comparison of the DOA estimation under different number of snapshots when SNR10 dB,σφ 40°

In Fig.6,the performance comparison of the DOA estimation when varying phase error standard deviations from 10°to 40°is given.The phase error standard deviations affect the DOA estimation accuracy directly,compared with the gain error standard deviations,which only affect the DOA estimation peak value.The OCOGP method has good robustness to the change of phase error due to its own theoretical method,while the estimation accuracy of the other three algorithms will decrease with the increase of phase error.When setting the grid spacing to 2°,the proposed method achieves the similar performance as the SBAC and the SBLPE,and obtains significant superiority when the phase error standard deviations is set to above 15°by setting the grid spacing to 5°.

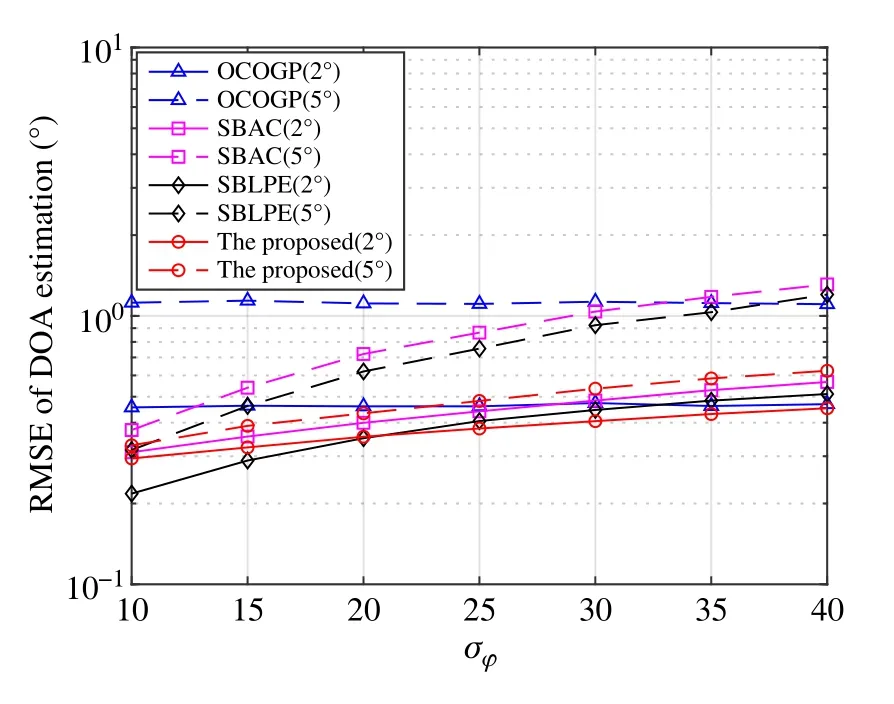
Fig.6 Performance comparison of the DOA estimation under different phase error standard deviations when SNR10 dB,snapshots100

Fig.7 and Fig.8 respectively show the change curve of the gain error and phase error with the increase of the number of iterations,while Tab.2 and Tab.3 are the gain and phase errors estimation results after the iteration is completed.Since the first element array is the reference array,the gain and phase errors of it do not need to be taken into account.The change curves show that the gain and phase errors tend to converge when the number of iterations reaches 500～600,which meets the iterative characteristics of the EM algorithm.Combining the error curves and data tables,when the standard deviation of the gain error is 0.1,the gain error of the element array can converge to within 0.05,where the minimum is close to 0,and the maximum is 0.041 6.And when the standard deviation of the phase error is 40°,the phase error of the element array can converge to within 5°,where the minimum is 0.0068°and the maximum is 3.5866°.

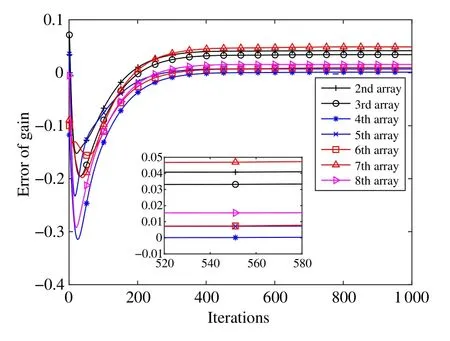
Fig.7 The performance of gain error estimation under different number of iterations

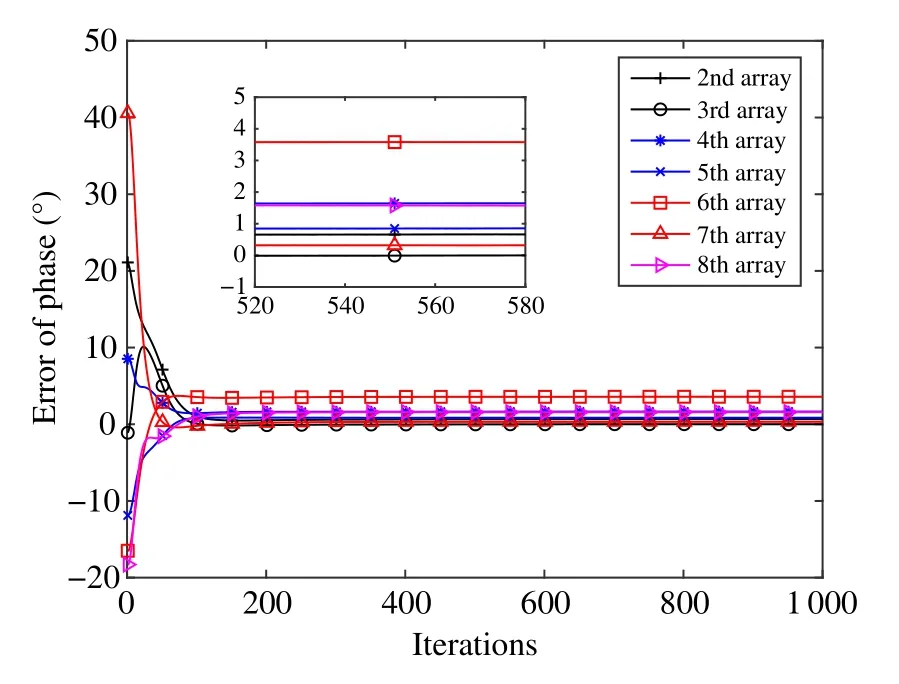
Fig.8 The performance of phase error estimation under different number of iterations

Tab.2 The gain error estimation results

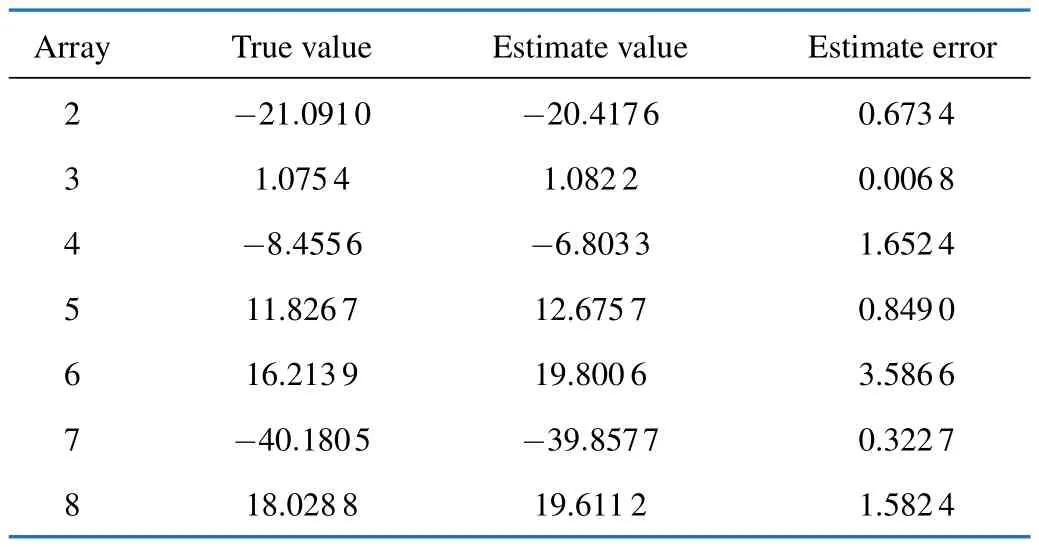
Tab.3 The phase error estimation results

In order to better reflect the performance of the gain andphase error estimation of the proposed method,the gain and phase error estimation deviations of each element array after 500 Monte Carlo experiments are processed.The following(57)and(58)represent the RMSE of the gain and phase error estimation respectively.

In the process of DOA estimation,the gain error affects the peak value while the phase error affects the peak position.Therefore,the performance of gain error estimation and that of phase error estimation are also indicators of the DOA estimation performance.The RMSE of the gain error estimation and that of phase error estimation by each array element are shown in Fig.9 and Fig.10,respectively.According to the results,the proposed method obtains a RMSE of the gain error estimation that is worse than that of the OCOGP and is better than that of the other two conventional methods,and the RMSE slightly varies within the range between 0.02 and 0.03.It simultaneously obtains a RMSE of the phase error estimation that is very slightly worse than that of the OCOGP and is much better than that of the other two conventional methods,and the RMSE increases with the increase of the distance from the reference array while maintaining below 5°.

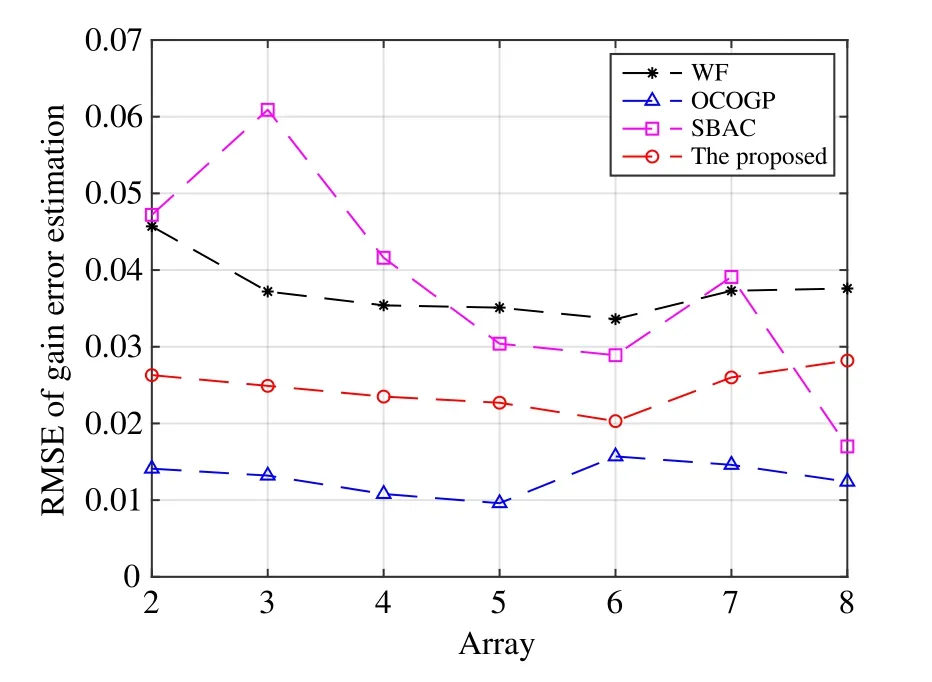
Fig.9 Performance comparison of the gain error estimation by different element arrays

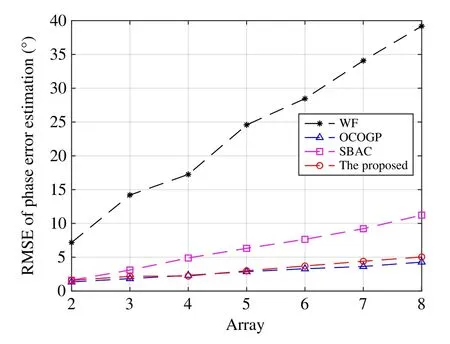
Fig.10 Performance comparison of the phase error estimation by different element arrays

V.CONCLUSION

In this paper,a new DOA estimation method based on root sparse Bayesian learning is proposed,which realizes the compensation of the deviation angle error by adaptively adjusting the grid angle,and utilizes the expectation maximization to jointly and iteratively estimate gain-phase error and arrival signal power.The simulation results verify the superiority of the proposed method over the conventional methods when both use coarse grid,in terms of computational complexity and robustness to gain-phase error.