Local Observations-Based Energy-Efficient Multi-Cell Beamforming via Multi-Agent Reinforcement Learning
2022-06-29KaiwenYuGangWuShaoqianLiGeoffreyYeLi
Kaiwen Yu,Gang Wu,Shaoqian Li,Geoffrey Ye Li
Abstract—With affordable overhead on information exchange,energy-efficient beamforming has potential to achieve both low power consumption and high spectral efficiency.This paper formulates the problem of joint beamforming and power allocation for a multiple-input single-output (MISO) multi-cell network with local observations by taking the energy efficiency into account.To reduce the complexity of joint processing of received signals in presence of a large number of base station (BS),a new distributed framework is proposed for beamforming with multi-cell cooperation or competition.The optimization problem is modeled as a partially observable Markov decision process (POMDP)and is solved by a distributed multi-agent self-decision beamforming(DMAB)algorithm based on the distributed deep recurrent Q-network (D2RQN).Furthermore,limited-information exchange scheme is designed for the inter-cell cooperation to boost the global performance.The proposed learning architecture,with considerably less information exchange,is effective and scalable for a high-dimensional problem with increasing BSs.Also,the proposed DMAB algorithms outperform distributed deep Q-network(DQN)based methods and non-learning based methods with significant performance improvement.
Keywords—distributed beamforming,energy efficiency,deep reinforcement learning,interference-cooperation,POMDP
I.INTRODUCTION
Although a variety of energy-saving methods have been designed in the fifth generation (5G) standard,e.g.,3GPP TS 28.310,its energy consumption is still huge[1].The future generation wireless communications will demand ultrahigh throughput and ultra-massive ubiquitous wireless nodes to meet various applications.Therefore,numerous base stations(BS)will be deployed densely,which results in tremendous energy consumption if designed using the existing methods,and thus will cause an unbearable burden on the environments and operators[2,3].As a result,designing spectrumefficient(SE)and energy-efficient(EE)networks turns to be a critical issue[4].
Distributed multi-cell joint beamforming is effective to eliminate inter-cell interference and improve system capacity,which has attracted tremendous attention in recent years.However,distributed beamforming requires multi-cell collaboration and the traditional methods based mathematical models cannot be used anymore.This inspires us to perform distributed beamforming enabled by multi-agent deep reinforcement learning(MARL),where multiple agents cooperate with each other to perform appropriate beamforming based on historical processing experience and their local observations.
Recently,there are a lot of works concentrated on beamforming techniques[5-11].Jiang et al.have proposed a secrecy EE maximization (SEEM) method in Ref.[5] for heterogeneous cellular networks through jointly optimizing the beamformers of confidential signals and artificial noise at BSs.A1-Obiedollah et al.have developed two beamforming methods in Ref.[6] for the multiple-input single-output (MISO)non-orthogonal multiple access system where the EE fairness among multiple users is considered.Shi et al.have investigated EE optimization in Ref.[7]for a power splitting based MISO downlink system.Wang et al.have designed an algorithm in Ref.[8]based on the alternating optimization to solve the EE problem in millimeter wave systems with an advanced lens antenna array.Moghadam et al.have developed a statistical model for transmitted signal in Ref.[9]and investigated the tradeoff between SE and EE in multiple-input multipleoutput(MIMO)millimeter wave systems.Shen and Yu have used fractional programming algorithm in Ref.[10]to address the continuous beamforming problem,which achieves nearoptimal performance but required the global channel state information (CSI).Joshi et al.have developed a branch-andbound algorithm for sum-rate maximization in MISO downlink cellular networks[11].
Different from the traditional mathematical model-based approaches,deep learning (DL)[12],which can be a modelfree,extracts features and makes decisions based on the historical data and the current observation.It has been used to address many issues in communications[13-17].For example,Lin and Zhu in Ref.[14]have developed a beamforming scheme for a system with a large-scale antenna array by exploiting the collected data to extract features.Alkhateeb et al.have used DL for beamforming in Ref.[15]for the networks with high mobility.Hojatian et al.have designed a novel hybrid beamforming algorithm in Ref.[16],which greatly increases the SE in frequency-division duplex(FDD)communication by using partial CSI feedback.Shen et al.have proposed a DL-based adjustable beam number training method in Ref.[17]to flexibly select beam training candidates considering the mobilities of different users under hybrid line-of-sight (LOS) and nonline-of-sight(NLOS)scenarios.
Deep reinforcement learning (DRL) for communications[18-22]has received tremendous attention.Li et al.have investigated EE beamforming in Ref.[19]based on the DRL algorithm for a cell-free network.However,centralized DRL requires to collect the edge information,which is a huge overhead and causes delay.Therefore,beamforming based on MARL has been studied recently in Refs.[20,21].Especially,Ge et al.have considered multi-cell interference cooperation in Ref.[21],where MARL network obtains near optimal beamforming strategy with information exchange among agents.Lizarraga,Maggio,and Dowhuszko have investigated millimeter-wave hybrid precoding in Ref.[22],where DRL is used to obtain better hybrid beamforming with lower signaling overhead.
Deep Q-network (DQN) in Ref.[23] constructs a value function model for DRL by measuring how good state-action pair is,effectively solving the problem of limitation of Qlearning network due to the size of the Q-value table.Google’s DeepMind team feeds four-frames of game pictures to DQN for learning,which is modeled as a Markov decision process(MDP) and gets the better scores in the game[24,25].However,the state of the object cannot be judged when only one game frame feeding to the network,e.g.,movement speed and direction,which makes the system a partially observable MDP(POMDP),and DQN unable to work perfectly[26].Hausknecht and Stone in Ref.[26] have proposed deep recurrent Q-network (DRQN) by introducing recurrent neural network (RNN) in DQN to deal with the partially observable problem and get better performance.There has been also some work on POMDP issues in communications[27-29].Naparstek and Cohen developed a distributed learning algorithm in Ref.[27]for dynamic spectrum access,considering partial observability of the problem.Xie et al.utilized DRQN to deal with the computation offloading in the Internet of things(IoT)fog systems with imperfect CSI in Ref.[28].Baek and Kaddoum in Ref.[29]have combined DQN with gated recurrent unit (GRU) to solve the task offloading and resource allocations in partial observable multi-fog networks.
In most of the existing works,the beamforming schemes are conventionally based on mathematical models.As a result,it is difficult for the traditional iterative algorithms to quickly adapt to the dynamic and time-varying characteristics of the wireless network.On the other hand,distributed beamforming needs information exchange to get optimal performance.It is especially hard for distributed DRL to reach the global optimal beamforming because of the limited capacity of backhaul,transmission delay,and information privacy.Consequently,it is reasonable to consider distributed dynamic beamforming with local observations through DRL methodology.
In this paper,we design a distributed multi-agent selfdecision beamforming algorithm(DMAB)to maximize longterm EE,which is enabled by a desired multi-agent cooperative or competitive framework.The major contributions of this paper are summarized as follows.
·To decrease signaling overhead,we design a new distributed multi-agent beamforming strategy with local observations to accommodate the time-varying channel conditions and diverse cells interference,where the BSs perform the beamforming and power allocation only based on their local information.The codebook-based beamforming is based on the statistical characteristics of the propagation channel,so it can save the overhead on the high-dimensionality instantaneous CSI feedback.We formulate a POMDP problem and develop a DMAB algorithm based on the distributed DRQN(D2RQN),which can deal with the fuzzy observation and is robust.
·To speed up convergence,we design cooperative and competitive reward functions,which are correlated with the EE difference between adjacent time slots.We verify that the two reward functions can get equilibrium and the cooperation reward can boost the agents to get the near-optimal EE through a designed limited-information exchange mechanism.
The rest of the paper is organized as follows.Section II introduces the system model and formulates the optimization problem.Section III introduces the basic of POMDP and DRQN,discusses the design of multi-cell cooperation and competition reward functions,and information exchange mechanism,and describes the proposed optimization algorithm.Section IV presents and analyzes the simulation results.Finally,the conclusions of this paper are given in section V.
II.SYSTEM MODEL AND PROBLEM FORMULATION
After introducing the system model,local observations,power dissipation model,we will formulate the problem of distributed beamforming and power allocation with MARL.
A.System Model
Consider a typical scenario of downlink multi-cell communications as shown in Fig.1.In each cell,the BS transmits signals to multiple users in the cell at different frequency bands and therefore there is no intra-cell interference.But there is still inter-cell interference since the same frequency is used at different cells.Assume that thereMcells with the corresponding BSs indexed{1,2,···,M}M.The BS is withNtransmit antennas while each user terminal (UT) is with one antenna,The received signal received for the UT in cellmat time slottcan be expressed as,
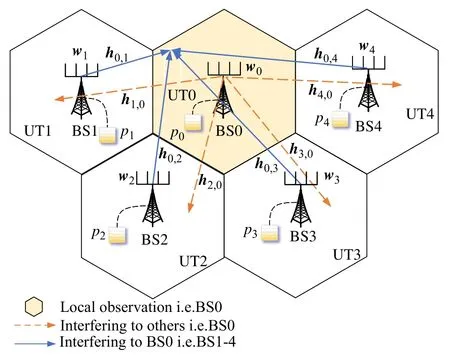
Fig.1 Multi-cell MISO interference channel model with local observations

Assume that there areLpaths for each channel.Therefore,the channel response vector at timetcan be expressed as,
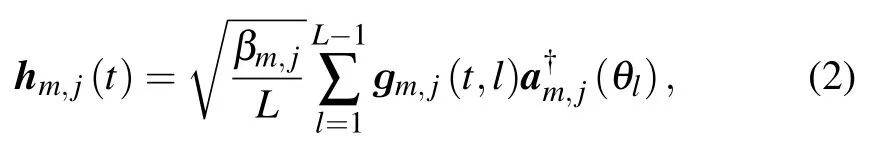
whereβm,jdenotes the large-scale factor,gm,j(t)[gm,j(t,1),gm,j(t,2),···gm,j(t,L)]T∈CL×1is the Rayleigh fading vector composed of the small-scale fading coefficients between BSmand UTj,andam,j(θl) is the steering vector corresponding to thelth path array,If the distance between adjacent antennas is half wavelength,the steering vector can be expressed as
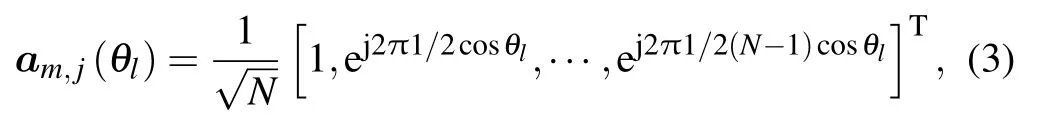
whereθl ∈[0,2π] is the angle of departure (AoD) at thelth path and is assumed to be uniformly distributed(withϑbeing the angular spread andbeing nominal AoD.As in Ref.[30],we use the first-order Gauss Markov process to approximate the Rayleigh fading vectorgm,j(t+1) at time slott+1.For block fading channel model[21],it remains constant in each time slot and varies between continuous time slots.Therefore,the Rayleigh fading vector can be expressed as
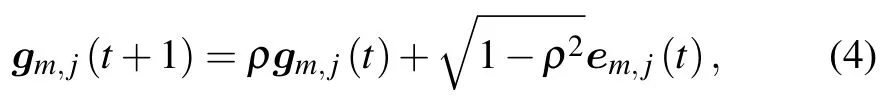
wheregm,j(t+1)∈(0,IL)andem,j(t)∈(0,IL)are both with complex Gaussian distribution andρis the correlation coefficient for the Rayleigh fading vectors between successive time slots.
To reduce the complexity of action,we employ discrete Fourier transform (DFT) based on codebook,denoted asNCB∈CN×N,where the element at thenth row and theqth column of the beamforming matrix is
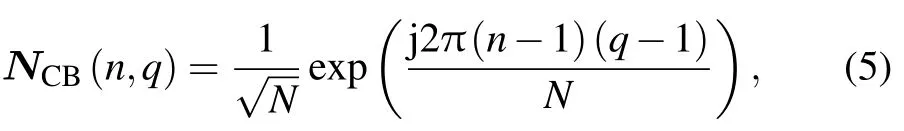
Denote the power level set asTpmax},whereQpowis the quantization level andpmaxis the maximum transmitting power of the BS.If the beamforming vector and transmission power corresponding to themth user at timetarewm(t)∈Candpm(t)∈T,respectively,the instantaneous signal-to-interference-and-noise ratio(SINR)at timetin cellmwill be
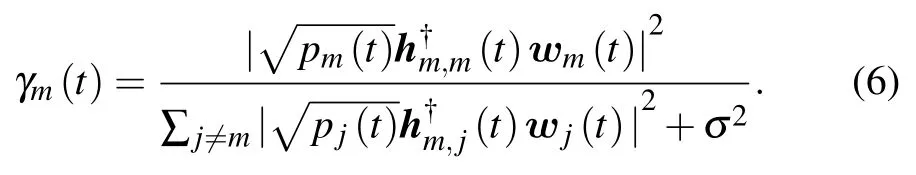
Fromγm(t),we can determine the achievable transmission rate as
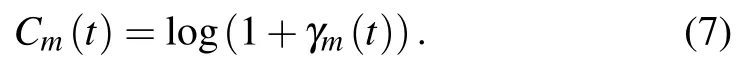
B.Local Observations
For a multi-cell system,BSs located in different positions need to get global information to select a beamforming vector and transmit power to maximize the overall rate.As the scale of the system increases,this information exchange will cause a huge signaling congestion and turn impractical.To avoid this problem,we consider the dynamical decisions with limited information exchange.
The local information observed by the BS at time slottin cellmis defined as
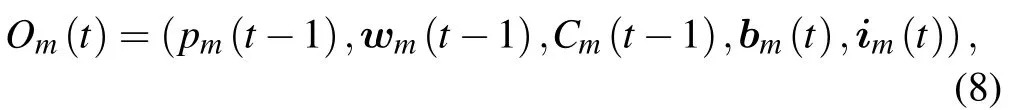
wherebm(t)andim(t)are the equivalent channel gain set and the total interference-plus-noise power set,respectively,in cellm,denoted as
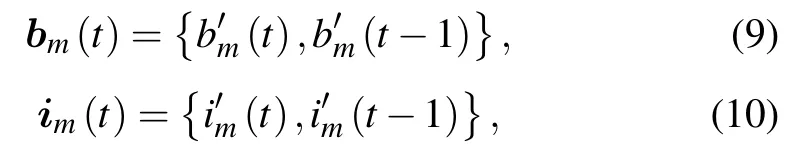
with
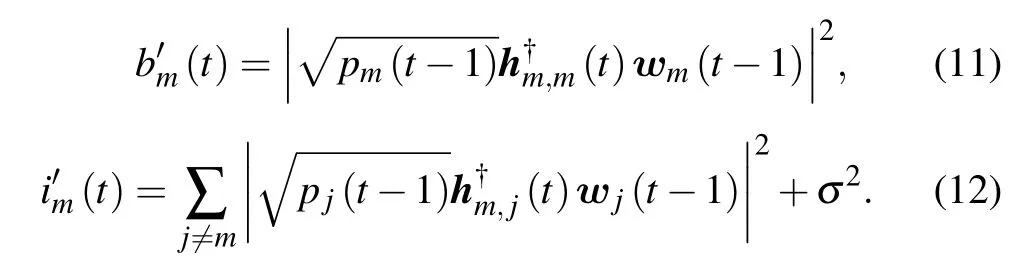
A BS does not have prior information on power allocation,beamforming,achievable rate,and power dissipation about other cells.Therefore,it is impossible for a BS to perform beamforming and power allocation to maximize the global system EE,which is a POMDP.In the presence of uncertainties on dynamic channel environments and other cells’ interference,we formulate the POMDP issue across the time horizon as a stochastic game in which each BS chooses beamforming vector and transmission power as a function of their own local observations.Especially,the power allocation and beamforming strategy of BSs are independent of each other.
C.Problem Formulation
In this paper,we maximize the long-term EE of each cell,which is the ratio of the sum-rate accumulated over all time slots and the total energy consumption accumulated over all time slots[31].But in order to facilitate the deployment of intelligent algorithms,we define EE as the average ratio of the system achievable sum rate and the total energy consumption in Joule over all time slot,as in Refs.[19,32].The total power dissipation of the overall system attcan be expressed as,
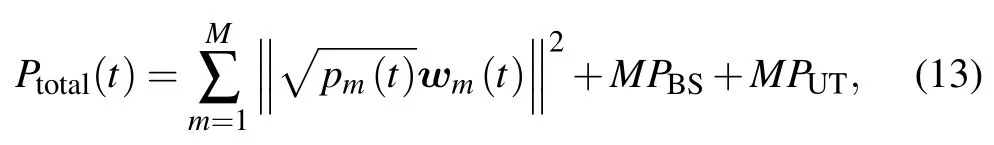
wherePBSrepresents the total hardware energy dissipation in each BS andPUTdenotes the total energy dissipation of each UT.Codebook-based beamforming can be realized by using a structure based on switches and fixed phase shifters[33,34].The(i,j)-entry in beamforming matrix is just like theNCBin equation (5).From the power consumption,the maximizing long-term EE problem can be formulated as follow:
Before the fiddler had time to think, he was ushered9 into a little room by invisible hands, and there a table was spread for him with all the delicious food he had seen cooking in the kitchen
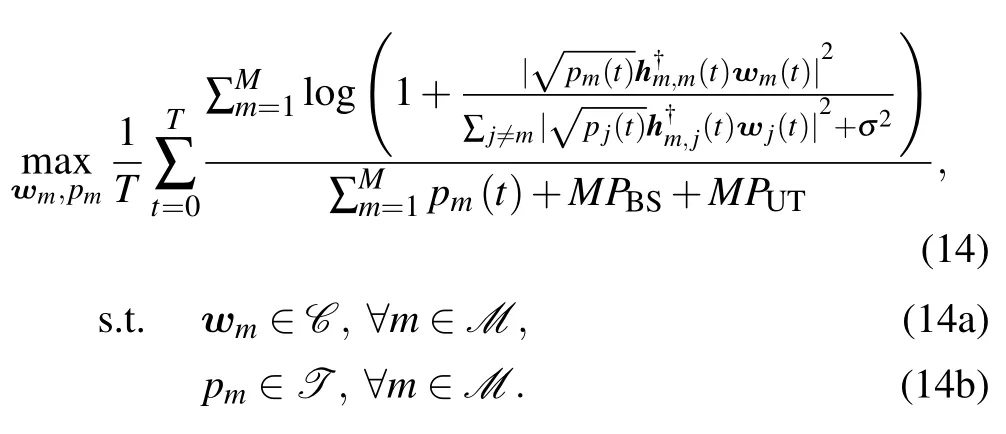
We aim to perform the optimal beamforming and power allocation strategy based on the subsequent response from the environments.Traditional convex optimization methods based on mathematical models are no longer adequate due to the unknown and dynamic environment.On the other side,algorithms based on the historical statistics may fail to generalize to all environments since the local topology can significantly differ from statistical prediction[35].To overcome the dynamic environment and fuzzy observation,BSs are supposed to learn by interacting with the environment and adapt the beamforming and power allocation policy based on the feedback of environment.More explicitly,BSs based on the DRL can learn from the current dynamic environment,historical processing data,and reward feedback to correct their mistakes for maximizing system performance in a foresight manner over the long-term instead of myopically optimizing current benefits[35].Therefore,the DRL method will be used to solve the optimization problem in the next section.
III.EE BEAMFORMING FRAMEWORK BASED ON LOCAL OBSERVATIONS
In this section,we will propose a DMAB scheme to solve the joint problems of beamforming and power allocation,which is illustrated in Fig.2.In this figure,the black dotted line denotes the agent offline training part by itself,colorful solid lines denote the online interaction parts with environment in real time,in which red solid line denotes actions,blue solid line denotes local observation process and green solid line denotes the reward calculation.Green cycle denotes the information exchange mechanism,which is designed for the multi-cell cooperation to guarantee the global optimal solution.For the multi-cell competition,the green cycle is not needed.Memory pool collects the state-action pair in the past few time slots.In the offline training part,memory pool takes out a mini-batch experience and feeds it to the target Q-network.The target Q-network will transmit trained network weightφmto the main Q-network after everyTrtime slots.In the online decision process,main Q-network chooses the optimal beamforming codeword and power level according to the local observation information and its policy,which is determined by the received network weightφmandε-greed criterion.At the same time,information exchange mechanism is triggered,agentmexchanges local states e.g.,local SE and energy consumption,and finally calculates the common reward.
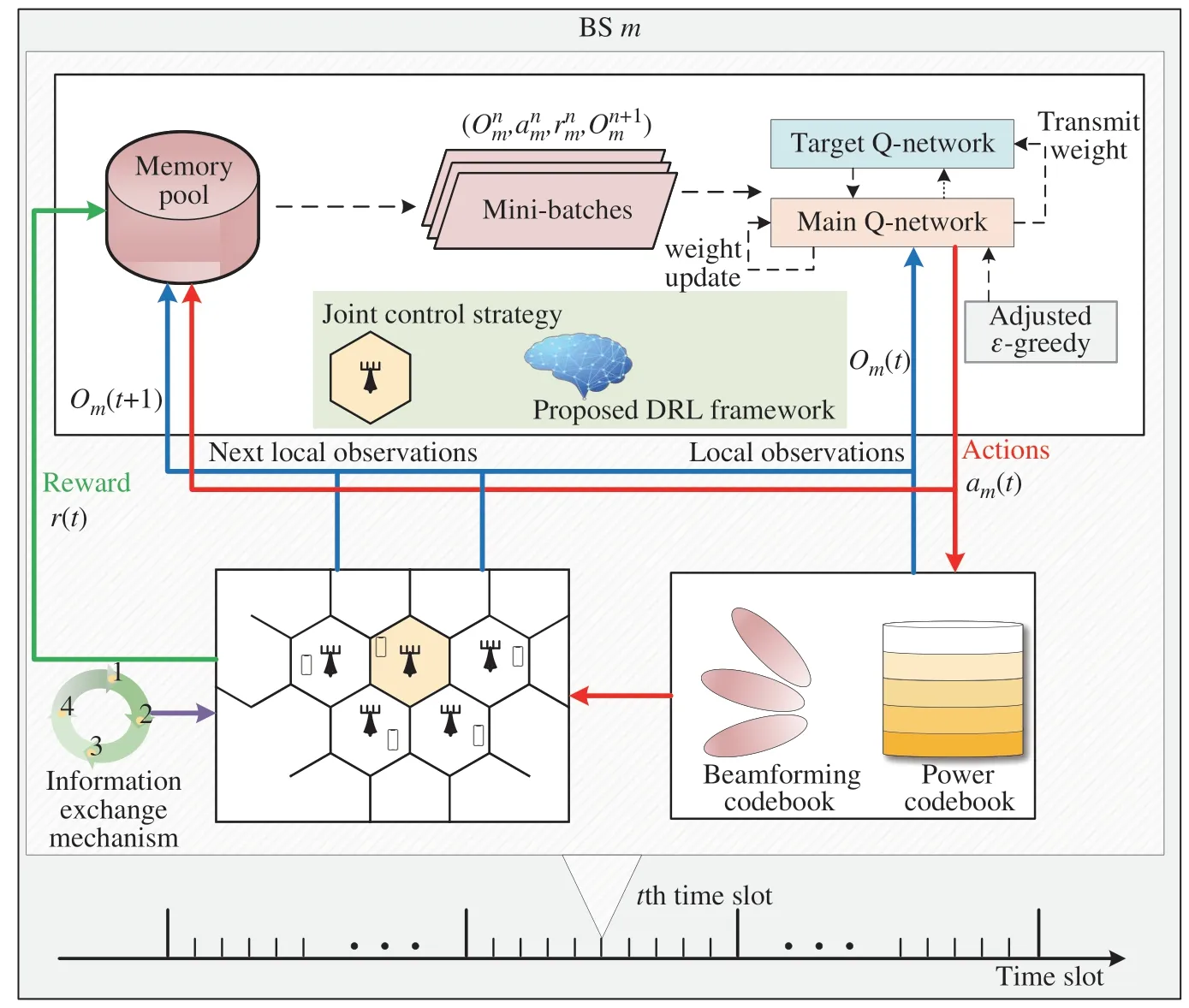
Fig.2 Illustration of the proposed DMAB strategy in Multi-cell MISO interference channel model with local observations
A.POMDP for DMAB
We briefly introduce the concept of POMDP as shown in Fig.3 from Ref.[36].A POMDP consists of five-tuple(S,A,P,O,R),finite set of statesS,set of all possible actionsA,set of all possible partially observationsO,reward functionR,and probability transition function between statesP.The state transition probability can be expressed asP(s,a,s′)Pr(s′|s,a),the probability to transfer to a new states′for given actionaand previous states.The BS learns the optimal policy in offline manner and updates it to online network at fixed period,takes actions based on the current observations according to the policy.We can use the POMDP to formulate the problem of beamforming and power allocation with local observations as follows.
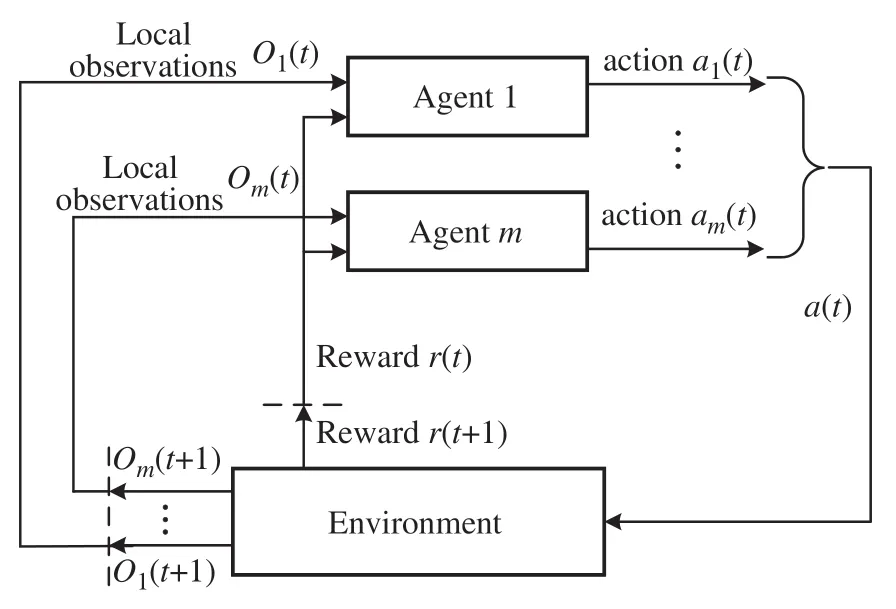
Fig.3 The multi-agent observation-action cycle diagram
State:states include achievable rate and total energy consumption in the global system.However,for the specific BSmat time slott,the states can be represented byOm(t)in(8).
Action:As mentioned earlier,the action spaceAincludes the beamforming and transmission power.The size of the action space will be|A|NQpowas discussed in section II,BSmchooses an appropriate entry of beam direction and power level and results in immediate rewards to evaluate its actions.
Reward:The reward functions are designed to be highly correlated with EE to encourage the multi-agent network to learn toward maximizing EE performance.The specific design is shown later.
B.Why Does DRQN Work with Local Observations?
The local observations for each BS can be regarded as partial information of the overall system and large errors will naturally occur when using the traditional DQN to estimate the Q value.DRQN can use the RNN network to improve the Q value estimation.To overcome gradient explosion in the process of backpropagation through time[37,38],the long shortterm memory (LSTM) network is developed and embedded into DRQN to maintain the internal state and aggregate observations over time,which can learn which information is relevant to keep or forget during training in the recurrent work.This structure allows the DRQN to use the historical information to obtain an optimal policy for each BS.During online real-time decision,the agent gets the local observation state and takes the actions according to the optimal policy,resulting in corresponding reward.The framework of the DRQN is shown in Fig.4.
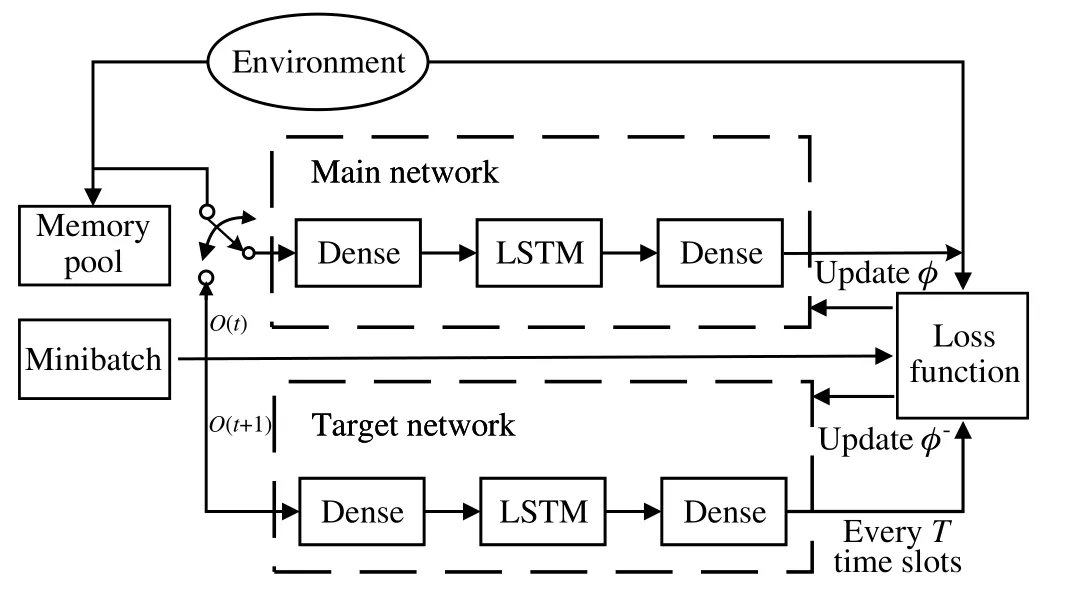
Fig.4 The framework of DRQN
C.Reward Design for DMAB
The reward function plays a key role in the final performance,especially for the distributed multi-agent problem.The reward should be designed to guide the BSs to action towards maximizing equation(14).Here,we will consider two reward functions for multi-cell competition and multi-cell cooperation,respectively.
1) Multi-Cell Cooperation with Limited Information Exchange:For multi-cell cooperation,the primary mission for each BS is to maximize its local cell EE,and the long-term global performance is decided by all BSs.All BSs must still coordinate on interferer to achieve a globally optimal solution.The process,called the Markov game,follows a cooperative network to have a common goal that takes its actions to maximize the EE of the global system[39].BSs take actions based on the local observation at the beginning of time slott.They share their current results with others as feedback information at the end of time slot.This decision-making process shows that independent BSs pursue a common reward,that is related to the actions of all BSs.
At the same time,BSs evaluate their individual actions based on the global reward,which can be expressed as
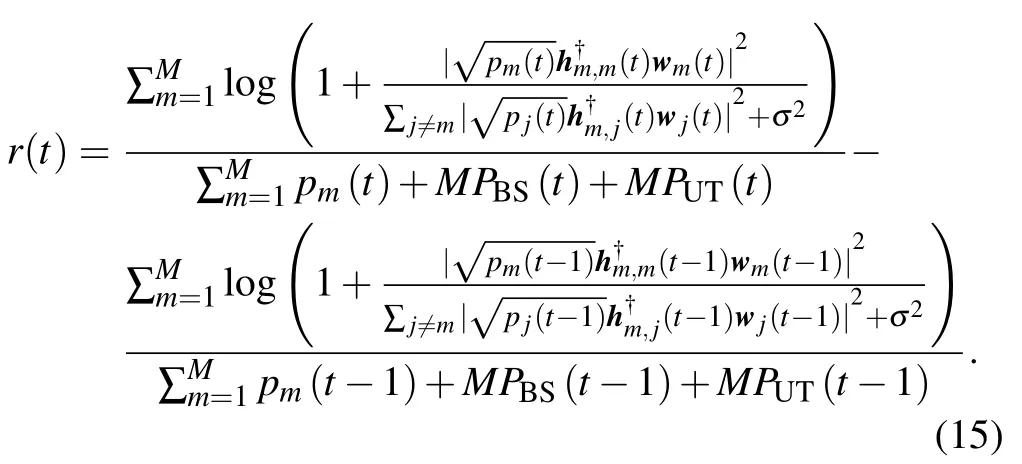
Moreover,if the current global EE at time slottis less than the previous EE at time slott-1,the agent gets a negative evaluation of current actions at time slott.The agent will try to improve its actions at the next decision to get positive reward.At the end of each time slot,only SE and energy consumption information at each cell are exchanged through pre-defined interfaces,e.g.,X2 interface in eNodeBs,which significantly reduces the signaling overhead and information cache.The information interaction mechanism is shown in Fig.5 and the D2RQN-based DMAB scheme with multi-cell cooperation is summarized in Algorithm 1.
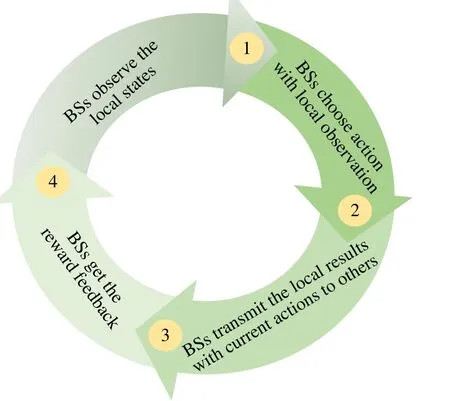
Fig.5 The process of a communication round in cooperative scenes
According to Ref.[40],the multi-cell cooperative strategy will converge to the equilibrium if the following four conditions are satisfied.
1)The learning rateδgradually decreases over time,e.g.,∑tδ →∞,∑tδ2<∞.
2)Each agent has an unlimited visit to action,e.g.,s ∈A.
3)The probability of agentmchooses actionais nonzero,e.g.,P(t,x)/0.
4) The exploration strategy of each agent is exploitative,e.g.,
Therefore,the multi-cell cooperative strategy will get the optimal equilibrium.
2) Multi-Cell Competition without Information Exchange:For multi-cell competition,each BS pursues a higher reward and does not care about interfering others.The local reward about BSmat time slottis defined as
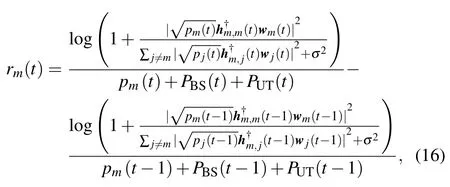
which maximizes the local EE of agentm.The interference items in the reward function are obtained by the agent’s own local observations and there is no information exchange among BSs.This strategy can save signaling overhead significantly.Next,we will prove the convergence of the competitive reward.For convenience,we first define the Nash equilibrium as a strategy for all agents,in which there is no incentive for any agents to unilaterally deviate from their current strategy given the current states.
It can be argued that the multi-cell competitive strategy will converge to a Nash equilibrium no matter whether the current cell’s interference with others is considered or not.Even though the multi-cell competitive strategy can converge to a Nash equilibrium,the equilibrium is not necessarily optimal from the global networks’ EE perspective in considering interference condition,which will be verified in the simulation later.
D.Complexity Analysis
In this section,we will discuss the complexity of observation,memory,computing,and information exchange of our proposed DMAB strategy.In terms of the observation and information exchange complexity,the number of input ports of the proposed DMAB is|Om(t)|7,that is,only local information states are fed to the neural network.This method requires no information about other cells before the local agent makes decisions,which effectively reduces signaling overhead and can quickly respond to the environment without being affected by signaling congestion.On the other hand,local observations based DMAB only require exchanging the local states’ information among agents at the end of the time slot,which is 2Mmessage exchanges.But centralized approaches need toM2Ndimensional complex-valued vectors.Furthermore,the DMAB through parallel computing alleviates the overhead of the network infrastructure.

In terms of the memory and computing complexity,DMAB requires the replay experience,which comprises the observationsOm(t),actionsam(t),rewardrm(t),and the next statesOm(t+1).Assuming agentmperforming once interacts with the environment at time slott,the replay pool requires storing a|Om(t)|+|rm(t)|+|Om(t+1)|7+1+715 size array of float numbers and|am(t)|1 integer number (due to keep the index of codebook).On the other hand,the computing complexity of DQN and DMAB both are O(|Om(t)|χ1+,whereχiis the number of units in theith layer.The training complexity of DMAB isbut the training complexity of DQN iswhereψsis memory step andψbis the mini-batch.The DMAB requires the higher complexity calculations than DQN.But this processing does not affect the real-time decision delay since it is only completed offline.
IV.SIMULATION RESULTS
In the section,we leverage a Tensorflow2.0-based simulator to evaluate the performance of the proposed DMAB-based beamforming and power allocation in a multi-cell network.We consider a multi-cell network where the BS is located at the center of each cell,is BS 0,BSs 1~6 are located in the first tier,and BSs 7~18 are located in the second tier.The path loss between BSmand UTkisβm,k120.9+37.6lgdm,kdB,wheredm,kis the distance between BSmand UTkin kilometers.The maximum transmitting power for each BS is 38 dBm and the total hardware energy dissipation at each BS isPBS9 dBW and the total energy dissipation of UT isPUT10 dBm[32,41,42].The major simulation parameters are included in Tab.1.In addition to the proposed approach,wecompare with four different beamforming schemes as baseline.

Tab.1 Basic environment parameters
·Centralized greedy beamforming:In this algorithm,each BS chooses beamforming and power allocation strategy to maximize the current EE based on the instantaneous wireless channel,instead of considering long-term optimal efficiency.
·Distributed random beamforming:Each BS randomly chooses an action from the pre-defined codebook and there is no information exchange among BSs.
·Distributed DQN with multi-cell competition:In this scheme,each BS has its own DQN neural networks,which can select appropriate actions from the pre-defined codebooks according to the changes in the environment to maximal its own cell’s EE.
·Distributed DQN with multi-cell cooperation:Different from the distributed DQN with multi-cell competition,each cell adopts a cooperative approach to maximize overall system performance,which consists of an input layer,two fullyconnected hidden layers,and an output layer.
We use the dense neural network to construct the model,which consists of a fully connected layer as an input layer,a fully connected layer and an LSTM layer as hidden layers,a fully connected layer as an output layer.The total number of input ports is|Om(t)|7.The number of output port isNQpow.All hyperparameters are included in Tab.2.The EE performance metric is used to evaluate efficiency of different algorithms and each value in the following figures is average of over 500 time slots to get more smooth curves.
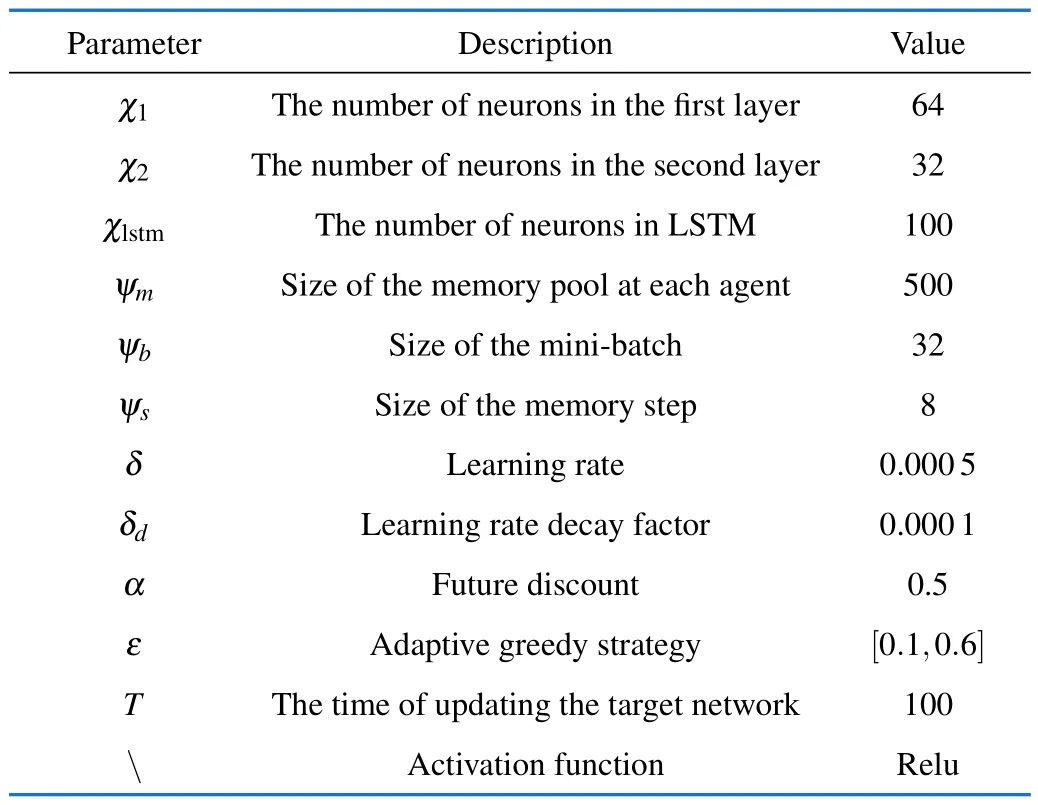
Tab.2 Model parameters of DRQN
A.Convergence
Fig.6 shows the EE of different algorithms with different time slots and different reward functions.From the figure,the EE of the intelligent algorithms is poor at the beginning compared to the greedy algorithm,but increases with the number of time slots and finally stay at a relatively stable level because they need multiple interactions with the environment to save experience and train their own network weights.On the other hand,the DMAB performs better EE than DQN.Comparedwith distributed DQN,DMAB exploits an LSTM to tackle the local-observability by maintaining internal states and aggregating temporal observations.The distributed DQN needs more observations to take more accurate action.As the training progresses,DQN can also get better performance.These figures verify that the cooperative reward can get better performance when considering interference.Therefore,multicell cooperation gets higher EE performance than competition since BSs just improve their own strategies regardless of interference with others for multi-cell competition.
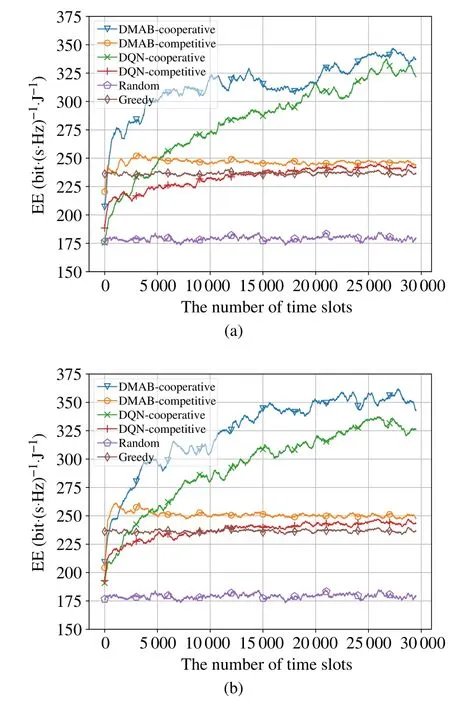
Fig.6 EE comparison for different algorithms with different time slots:(a)Qpow5;(b)Qpow10
Fig.7 shows the global network’s EE with different numbers of considered interfering cells.From the figure,the EE of the four strategies decreases as the number of interfering cells increases.The larger the number of interferences,the lower the global EE performance will be,mainly because the interference reduces the global SE.On the other hand,the EE of the first seven cells declines the fastest while that of the last 12 cells declines slowly.The reason is that interference is always large among the adjacent cells and is small among non-adjacent cells due to regional isolation.Take cell 0 as an example,its neighboring cell,cells 1~6,will cause strong interference to cell 0,while cells 7~18,the non-neighboring cells of cell 0,just cause weak interference to cell 0.
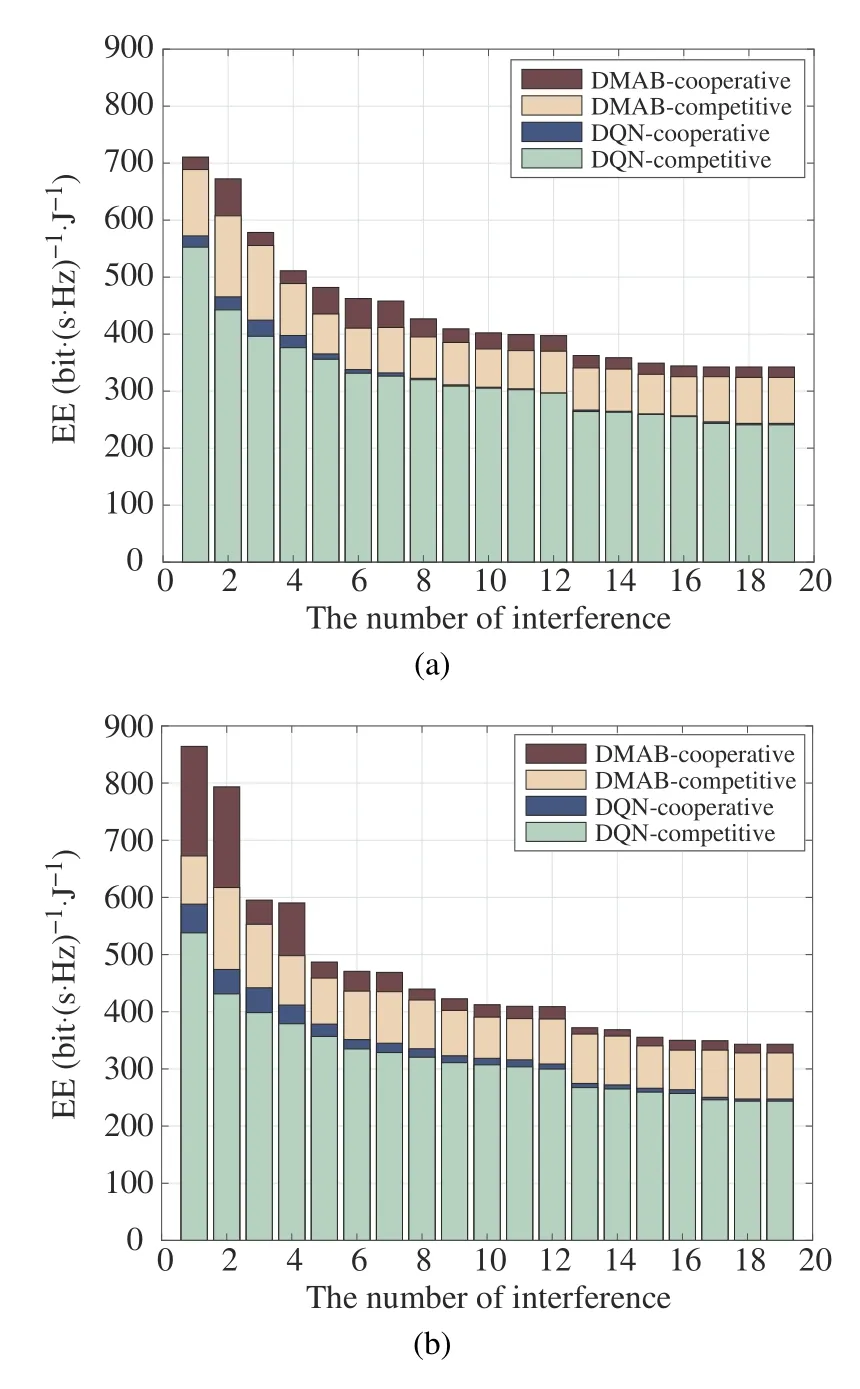
Fig.7 The relationship between the number of interference cells and the EE:(a)Qpow5;(b)Qpow10
B.EE Versus Maximum Transmitting Power
Fig.8 demonstrates the EE of the multi-cooperative and multi-competitive system versus the maximum transmit power of the BS.All based on the average over 100 independent channel realizations.For multi-cooperative,the EE of the global networks raises sharply,as the maximum transmit power increases from 30 dBm to 50 dBm.However,the curve raises slowly in the range of 10 dBm to 30 dBm and gets stable in the range of 50 dBm to 70 dBm.The reasons for these phenomena are different.The maximum transmission power determines the value of codewords in the power codebook.When the transmission power is in the range of 10 dBm to 30 dBm,the slow growth of the curves is mainly caused by the low total achievable rate due to less available transmit power.When it is in the range of 50 dBm to 70 dBm,the reward function based on EE prompts the BS’s policy to select the appropriate power codeword although the BSs can obtain higher transmission power.With competition,the curves climb slowly with the increase of the maximum transmit power and finally get poor EE performance.Therefore,the competitive reward can not guide the agents to get good policy and is inefficient.
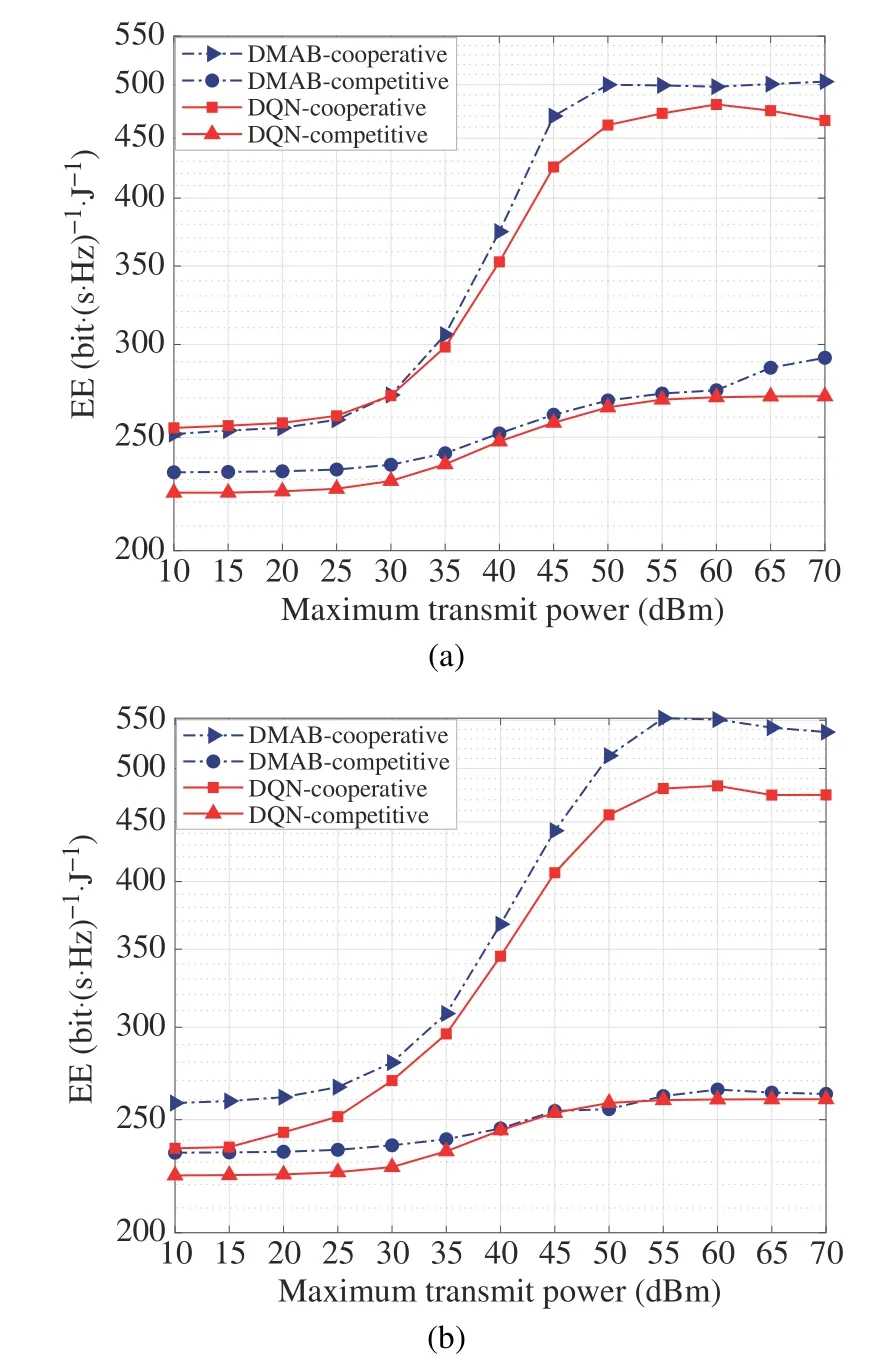
Fig.8 The relationship between the number of interference cells and the EE:(a)Qpow5;(b)Qpow10
Although intelligence algorithms can improve their EE once they are properly trained,the training of the neural network usually requires significant computation and consumes lots of power,which will increase dramatically as the scale of the network increases.Due to the rapid expansion of training datasets and hyperparameters,AI’s electricity consumption has increased 300 000 times from 2012 to 2018,which doubles resource consumption every 3.4 months[43].This extension inspired us to consider the computing consumption of AI,in the future.The model of computing consumption of AI can refer Ref.[44].
V.CONCLUSION
This paper has investigated the joint beamforming and power allocation in multi-cell MU-MISO interference systems with local observations to maximize the overall EE.The two reward functions,multi-cell cooperation,and multi-cell competition,have been discussed.To tackle the problem POMDP formulation,a DMAB algorithm has been proposed for determining the beamforming and power allocation policy.Simulation results have proved that proposed DMAB algorithm outperforms the baseline algorithms.Our method can be applied to the distributed multi-decision system,e.g.,smart factories,unmanned aerial vehicle detection,etc.,where global information is difficult to obtain.
杂志排行
Journal of Communications and Information Networks的其它文章
- Channel Estimation for One-Bit Massive MIMO Based on Improved CGAN
- DOA Estimation Based on Root Sparse Bayesian Learning Under Gain and Phase Error
- Multi-UAV Trajectory Design and Power Control Based on Deep Reinforcement Learning
- A Lightweight Mutual Authentication Protocol for IoT
- Rethinking Data Center Networks:Machine Learning Enables Network Intelligence
- RIS-Assisted Over-the-Air Federated Learning in Millimeter Wave MIMO Networks
