Multi-UAV Trajectory Design and Power Control Based on Deep Reinforcement Learning

Chiya Zhang,Shiyuan Liang,Chunlong He,Kezhi Wang

Abstract—In this paper,multi-unmanned aerial vehicle(multi-UAV) and multi-user system are studied,where UAVs are served as aerial base stations (BS) for ground users in the same frequency band without knowing the locations and channel parameters for the users.We aim to maximize the total throughput for all the users and meet the fairness requirement by optimizing the UAVs’trajectories and transmission power in a centralized way.This problem is non-convex and very difficult to solve,as the locations of the user are unknown to the UAVs.We propose a deep reinforcement learning(DRL)-based solution,i.e.,soft actor-critic(SAC)to address it via modeling the problem as a Markov decision process (MDP).We carefully design the reward function that combines sparse with non-sparse reward to achieve the balance between exploitation and exploration.The simulation results show that the proposed SAC has a very good performance in terms of both training and testing.

Keywords—multi-UAV and multi-user wireless system,UAV,power control,trajectory design,throughput maximization,SAC

I.INTRODUCTION

In recent years,unmanned aerial vehicles (UAV) have attracted significant attention in various fields.For example,it can be used for pesticide spraying and crop monitoring in the agricultural and searching for people that are trapped.In particular,UAVs have been extensively investigated in wireless communication serving as aerial base stations (BS)[1-7],mobile relays[8-10],mobile edge computing[11,12]and wireless power transfer[13,14].UAVs can enhance the probability of line-of-sight(LOS)links and reliably communicate with users by dynamically adjusting their locations[15].There are mainly two different types of studies called static-UAV and mobile-UAV for wireless communications.

For static-UAV,or quasi-stationary,the altitude or horizontal position of the UAV can be optimized to meet different quality of service (QoS) requirements.In Ref.[16],it maximized the convergence by optimizing the height of UAV given the UAV’s horizontal position.In Ref.[2],by fixing the UAV’s altitude,it optimized the UAVs’horizontal positions to minimize the number of UAVs which can meet the communication service of a given number of users.

On the mobile-UAV side,the UAV can be more flexibly deployed,e.g.,for emergency cases[17].In the past years,convex optimization algorithms have been used to optimize the trajectory of UAV.In Ref.[8],the studies have considered a mobile relay,which has a more significant throughput gain than traditional static relaying.Ref.[18] has studied maximizing UAV throughput by optimizing UAV trajectory,UAV transmit power,and UAV-to-user scheduling,while considered the flight energy consumption of the UAV.In Ref.[19],the authors considered a multi-user communication system and proposed a novel cyclical time-division-multiple-access(TDMA)protocol.And the authors have also shown that,for delaytolerant applications,throughput gains can be significantly increased in static-UAV system.Also,the authors in Ref.[19]considered a single-UAV communication system,where one UAV flies with the constant speed and the ground users are assumed to be uniformly located in a one-dimensional (1D)line.In Ref.[3],the authors considered a multi-UAV and multi-user system,where multiple UAVs are served as aerial BSs for ground users in the same frequency band.

For most of the above works,the traditional algorithms such as block coordinate descent(BCD)and successive convex approximation(SCA),are applied to obtain the optimal or suboptimal solutions,e,g.,trajectory design and resource allocation.However,the traditional algorithms require plenty of computational resources and take much time[20].To address this problem,many studies are proposed to adopt deep reinforcement learning(DRL)to solve joint trajectory design and power allocation (JTDPA) of the UAV[21-28].The authors in Ref.[21]have considered a single-UAV communication system,which optimizes 3D UAV trajectory and band allocation to maximize the throughput.In Ref.[22],the authors considered a multi-UAV and multi-user communication system and proposed a distributed multi-agent DRL framework,where each agent makes the best decision following its individual policy through a try-and-error learning process.They aimed to reduce the number of user’s handover to maximize the total throughput,where the UAV-BSs fly in a pre-designed mobility model.The studies in Ref.[24]optimized UAV trajectory to maximize the energy efficiency,which considers communication coverage,equity,and energy consumption.In Ref.[23],by using multi-agent to solve JTDPA,the authors considered the UAVs communication on the same frequency band and the agent may not know the users’locations and channel parameters in advance.

In this paper,we develop a novel multi-UAV-enabled wireless communication system.For security and practicability,the UAVs don’t know the information of users’locations and channel parameters,they only know the achievable rate of users.We assume that the UAVs need to return to initial point and aim to maximize the total throughput for all the users as well as keeping the fairness in communication by optimizing the UAV’s trajectory and transmission power in a centralized way.The means of fairness is all ground users can get minimum total throughput.Our contributions are as follows.

(1)We develop a novel wireless communication system and model it as an MDP and propose a DRL-based framework to solve it.

(2)We carefully design the reward function that combines sparse with non-sparse reward to achieve communication fairness.We also compare our solution with other DRL algorithms to show the performance improvement.

The rest of this paper is arranged as follows.In section II,we introduce the multi-UAV communication system.Section III introduces the principle of soft actor-critic(SAC)[29,30]algorithm and the framework to solve the trajectory optimization problem.In section IV,we present the simulation results and then we conclude the paper in section V.

Notations:In this paper,we use italic letters to represent scalars,bold-face to represent vectors.For a vectorsS,|S|dimmeans the dimensional ofS.

II.SYSTEM MODEL AND PROBLEM FORMULATION

A.System Model

We consider a wireless communication system containsMUAVs as BSs andNground users in Fig.1.The UAV is represented bydm ∈M,1 ≤m≤Mand the user is represented byun ∈N,1 ≤n≤N.Generally,N ＞M,means that the system is an information broadcast system enabled by UAVs.We assume that the UAVs do not have the location information of the grounds users,but they have the received signal strength indicator (RSSI) which is the total achievable rate of the ground user.In this communication system,the UAVs,on the same frequency band,communicate with ground users over consecutive periodsT ＞0.Then,the ground users communicate with one of the UAVs using TDMA protocol.We consider that the UAV flies at fixing altitudeH,so that the UAV trajectory can be expressed asqm(t)[xm(t),ym(t)]T∈R2×1,1 ≤m≤M.we assume that the time interval isδt1 s,where the UAV completes the flight and communication process inδt,and the UAVs need to return the origin point after completing the mission.

Fig.1 The system model

B.Problem Formulation

The coordinate of thenth user is represented byun[xn,yn]T∈R2×1,1 ≤n≤N.Note thatunmay not be accessible for the UAVs.Note that no matter what kind of channel model we adopt,our proposed algorithm only needs RSSI of the ground user.We adopt a typical channel model that the UAV communicates with the group user by using the LoS links,the Doppler shift caused by UAV movement can be compensated at the receivers,and the communication link is only related to the distance between the user and UAV as

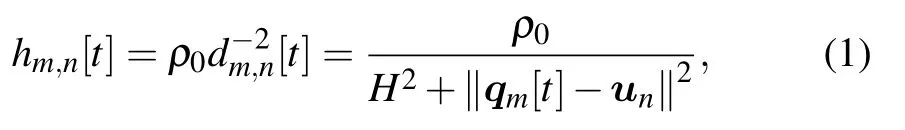
whereρ0denotes the channel power at the reference distanced01 m.We define the downlink UAV transmission power aspm[t],then we have,

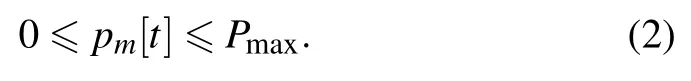
If themth UAV communicates withnth user in time slott,the signal-to-interference-plus-noise ratio (SINR) atnth user is

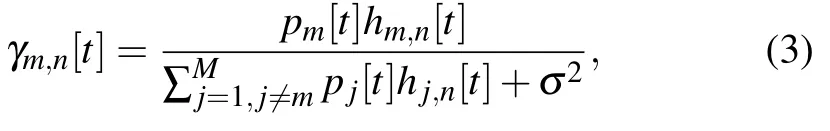
the denominator of (3) represents the noiseσ2which is the power of the additive white Gaussian noise(AWGN)and the interference signal by other UAVs in time slott.

We define a group of binary variables asam,n[t],wheream,n[t]1 denotes thenth user is served bymth UAV in time slott,otherwise,am,n[t]0.We assume that each user can communicate with only one UAV and each UAV can only serve one user at any time,which as following

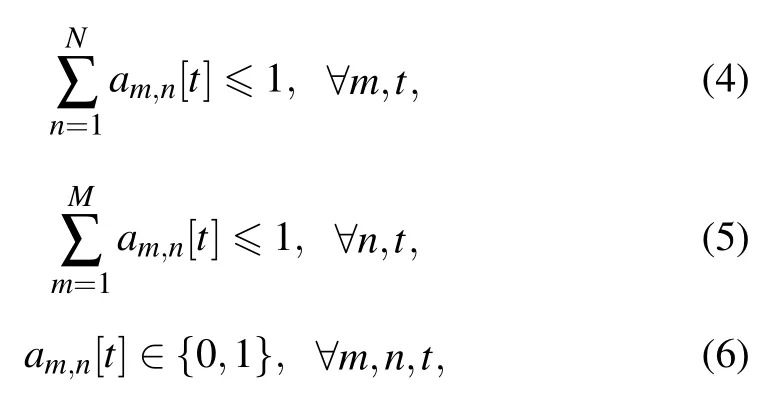
We assume that UAV communicates with the nearest ground user.Moreover,for UAVs trajectory,the maximum flying distance of the UAV in the interval time isSmax,and UAV needs flying back to origin point by the end of each periodT,then we have,

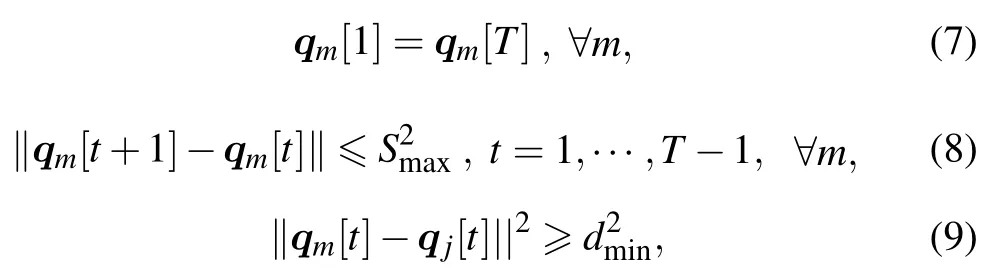
where(9)represents the collision constraints of UAV.We Set the maximum speed of the UAV motion asVmax,andSmaxδt×Vmax.

Hence,the achievable rate ofnth user in time slottcan be expressed as

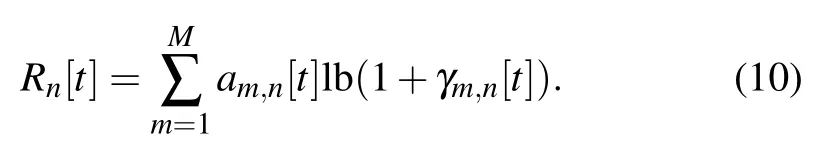
The UAV-user association,trajectory and transmission power of the UAVs are denoted asA{am,n[t],∀m,n,t},Q{qm[t],∀m,t},and P{pm[t],∀m,t},respectively.For fairness,we set the minimum valueRminfor each user.We aim to maximize the total throughput for all users by optimizing the UAV-user associationA,UAV trajectoryQ,and UAV transmission powerPover all time slots.The optimization problem is formulated as

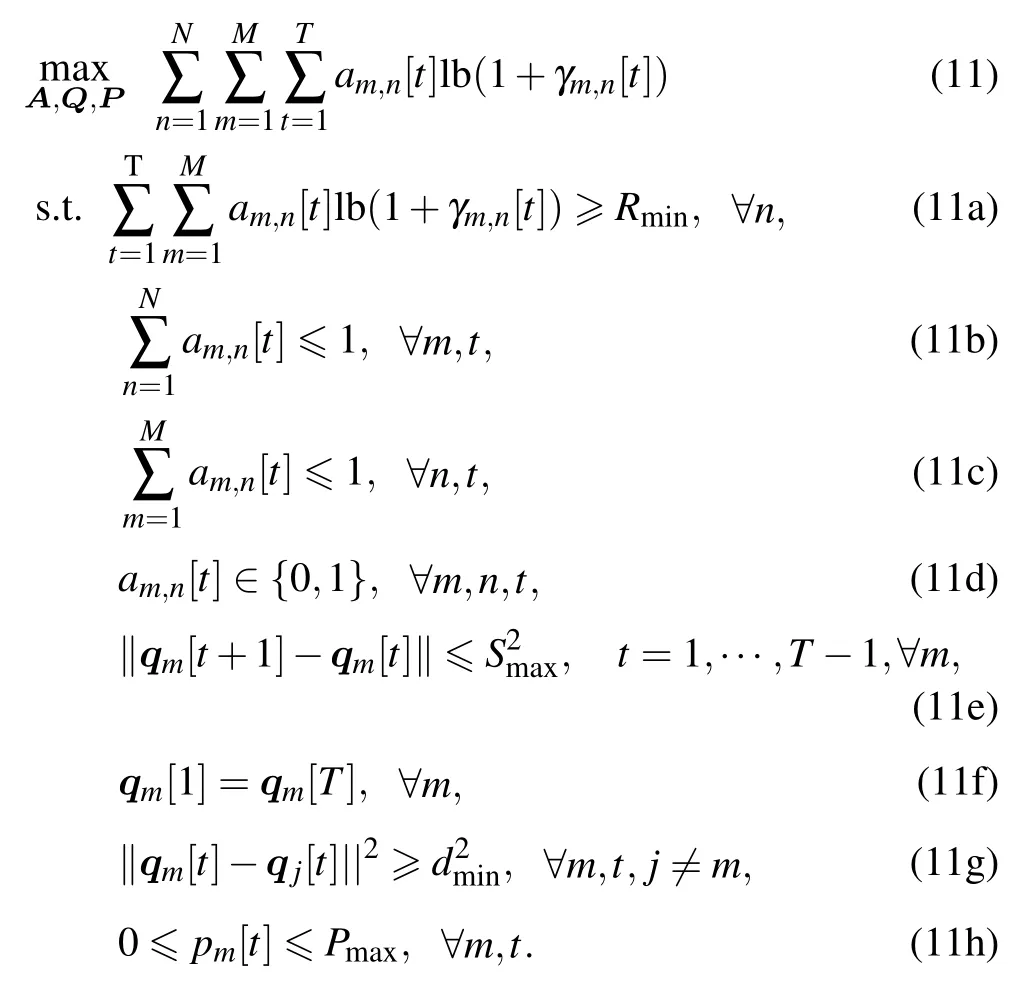
Problem(11)cannot be solved by traditional algorithms,as the UAV does not have the users’ locations and channel parameters.To solve the problem,we model the communication system as the Markov decision process (MDP) and address it by DRL,where the UAVs act as the agent and learn their optimal policies of trajectory and power.

III.SOFT ACTOR-CRITIC

In this section,SAC is adopted to solve the joint trajectory optimization problem.SAC has been proposed by Ref.[29].SAC belongs to the off-line reinforcement learning,which can transfer the learned model to UAV after learning the previous experience without on-line process.At the same time,compared with other traditional machine-learning-based solutions,e.g.,deep deterministic policy gradient(DDPG)and twin delayed DDPG (TD3),it is more stable,where the results are similar for different random seeds.Moreover,the action space is continuous,which leads to a more flexible trajectory.

A.Preliminaries

In order to facilitate the following description,we give a brief introduction to SAC.Firstly,MDP can be defined by a tuple (S,C,P,Z).The state transition probabilitypsatisfiesS×C×S →[0,+∞),which means that the current statest ∈Sand the current actionct ∈Care given,andst+1∈Sis obtained.Define the environment reward asz:S×C →[zmin,zmax] on each transition.Also,we defineρπ(st)andρπ(st,ct)respectively as the state and action distribution under the policyπ(ct|st).Different from the traditional reinforcement learning,SAC adds the maximum information entropyHin the objective function to solve the problem of poor exploratory.

whereπ*represents the optimal strategy andαis the temperature parameter,indicating the importance of information entropy to the loss function.

SAC adopts soft iteration which includes soft policy evaluation and soft policy improvement.In the soft policy evaluation,we add the maximum information entropy to Q-valuesQ(st,ct)which is also called soft Q-values and can be iterated through the modified Bellman backup operatorT π,which is as follows

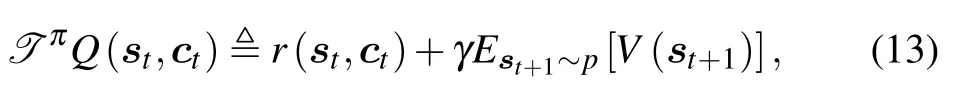
where

Moreover,γ ∈[0,1]is the discount factor which makes the sum of expected rewards finite.The larger the discount factor,the greater the influence of previous actions on subsequent decisions.In particular,whenγ1,the agent can see all the previous information,andγ0,otherwise.We defineQk+1T πQk,then the sequenceQkwill converge to the soft Q-funcation ofπask →∞[29].

In the soft policy improvement,we assume thatπnew∈Π.For optimizing theπ,we introduce Kullback-Leibler(KL)divergence,which means that making the distribution of policy similar to the distribution of soft Q-values,which is as follows

The full soft iteration algorithm alternates between the soft policy evaluation and the soft policy improvement steps.Then,we can get a policyπ* ∈Π,where(st,ct) ≥Qπ(st,ct)for allπ ∈Π and(st,ct)∈S×C,with|C|＜∞.The convergence of soft iteration has been proved in Ref.[29].

B.Problem Definition

As described in section II.B,it is difficult to explicitly formulate the problem as deterministic optimization with the users’ locations and channel parameters.Fortunately,SAC(model-free RL algorithms) can train the agent to make the best decision according to environment.To solve (11),we model it as an MDP,with the following information.

1) State:We assume that themth UAV can get its own location as

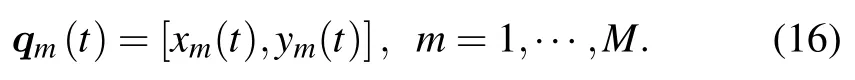
We also assume that the UAV receives the data rate from the ground users as

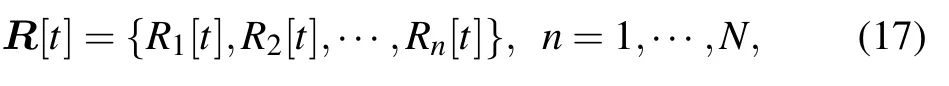
where each entryRn[t]represents the RSSI ofnth user beforet,whereRn(t) can be calculated by (10).RSSI can help the UAV know which user need communication and get the significant achievable rate.We also add the current slot timetto the state space.The state space needs to be normalized before inputting into the neural network.We use the total throughput of continuous communicationDmax,which a UAV is directly above a user,as a normalization of the user throughput.

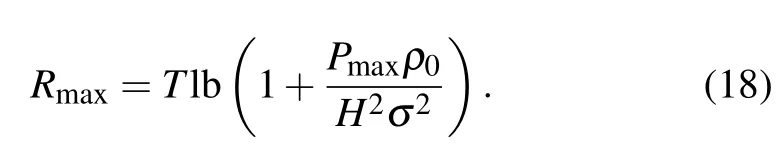
Therefore,the state space can be defined as

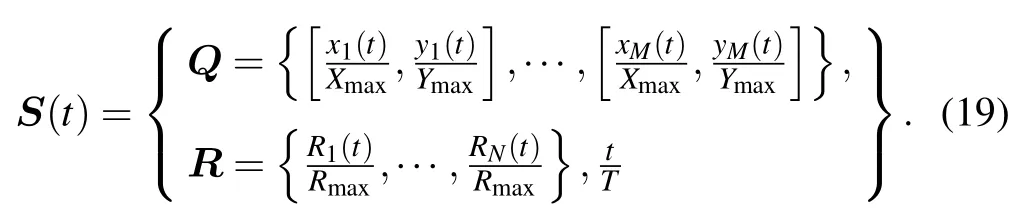
We then define the space size of the model as[Xmax,Ymax]and the maximum power asPmax.At the same time,|S|dim2M+N+1.

2) Action:According to (11),we set the action spaceCas the speed,the flight direction and the UAV transmission power

Wherevm(t)∈{0,Vmax},θm(t)∈{0,2π},andpm ∈{0,Pmax}.We aim to maximize the total throughput for all the users,so we set theam,n[t] as the user with the most achievable rate.For the UAV speed,only the maximum speedVmaxand the minimum speed 0 m/s are employed.Also,one has|C|dim3M.

3) Reward:For solving (11),we consider all the constraints defined in the optimization problem,especially(11a),which reflects the fairness of UAV communication.This brings a great challenge to the design of reward function.We propose a reward function,which not only solves the problem that sparse rewards may not address,but also overcomes the loss of fairness of UAV communication caused by non-sparse rewards.Five sub-reward parts{z1(t),z2(t),z3(t),z4(t),z5(t)}are proposed.z1(t)represents the reward of throughput.z2(t)represents the reward of UAV returning to the origin for constraint (11f).z3(t) represents the non-sparse reward corresponding to constraint (11a).z4(t) represents the sparse reward corresponding to constraint (11a).z5(t) represents the sparse reward corresponding to constraint(11g).We also define two time nodesT1andT2,whereT1means that the UAV starts to consider constraints(11a)andT2means that the UAV begins to consider returning to the origin.

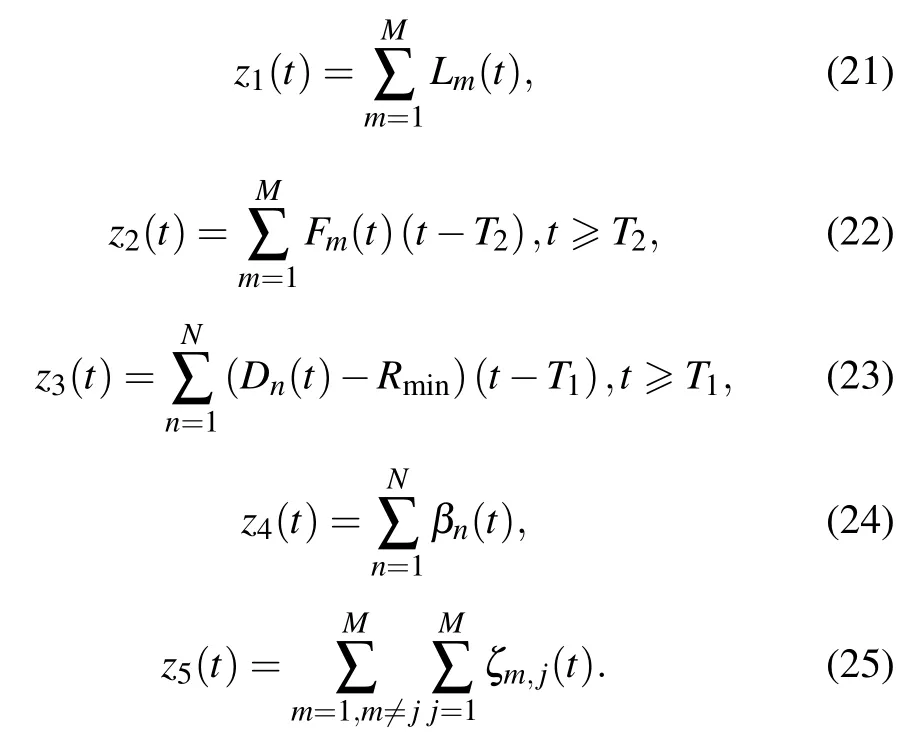
In the above equation,Fm(t) represents the distance ofmth UAV between origin at timet,Lm(t)represents the throughput ofmth UAV at timet,and one has

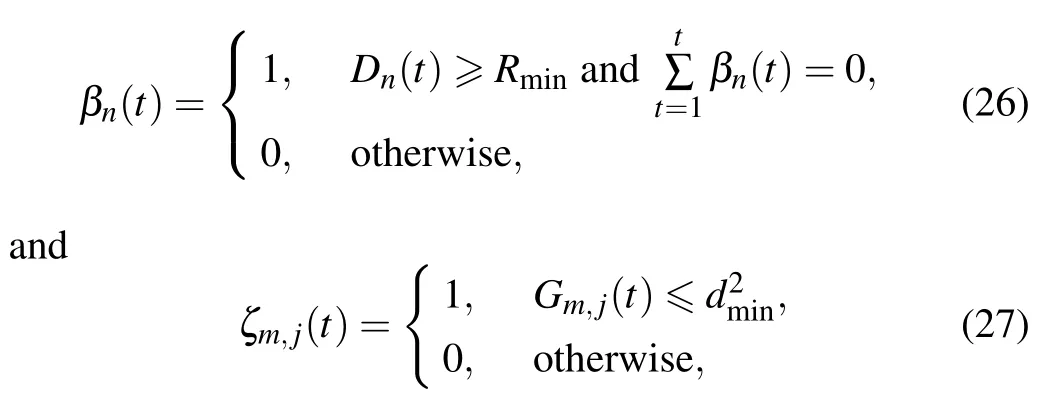
whereGm,j(t)means the distance betweenmth andjth UAVs.

In summary,the complete expression ofz(t)is as

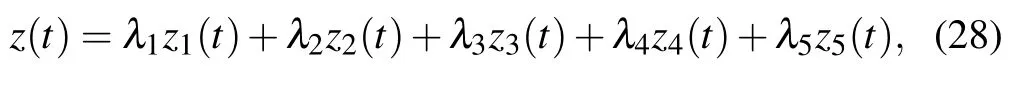
whereλ1,λ2,λ3,λ4,andλ5denote the weight coefficients ofz1(t),z2(t),z3(t),z4(t),andz5(t) separately.Specifically,λ1is a positive constant that is used to adjust the reward of total throughput byMUAV,λ2is a negative constant coefficient to punish non-arrival,λ3andλ4are the positive constant coefficient likeλ1,λ5is the negative constant coefficient likeλ2.

C.SAC

As discussed above,the convergence of SAC is proved in section III.A.Specifically,we use two loss functions to approximate both the soft Q-value and the policy.Then,we adopt stochastic gradient descent (SGD) in training process.

We use an actor-critic framework which contains a critic network and an actor network to solve the problem with continuous actions.

For the critic network,we define the parameters of the critic-evaluation network and critic-target network asθand,respectively.Then,we optimize the soft Q-values by minimizing the following loss function

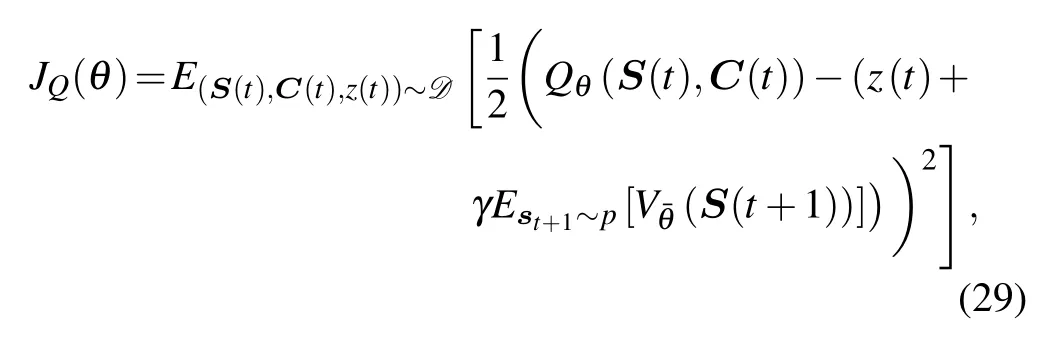
whereDmeans the experience pool andis given by(14).

The critic network takes the stateS(t)and actionC(t)as input,and outputs the soft Q-valueQ(S(t),C(t)).As shown in Fig.2,we use the activation functionrelu(·)in the hidden layers.The role of the critic network is to measure the value ofC(t) at theS(t),which means the higherQ(S(t),C(t)),the moreC(t)will be at theS(t).

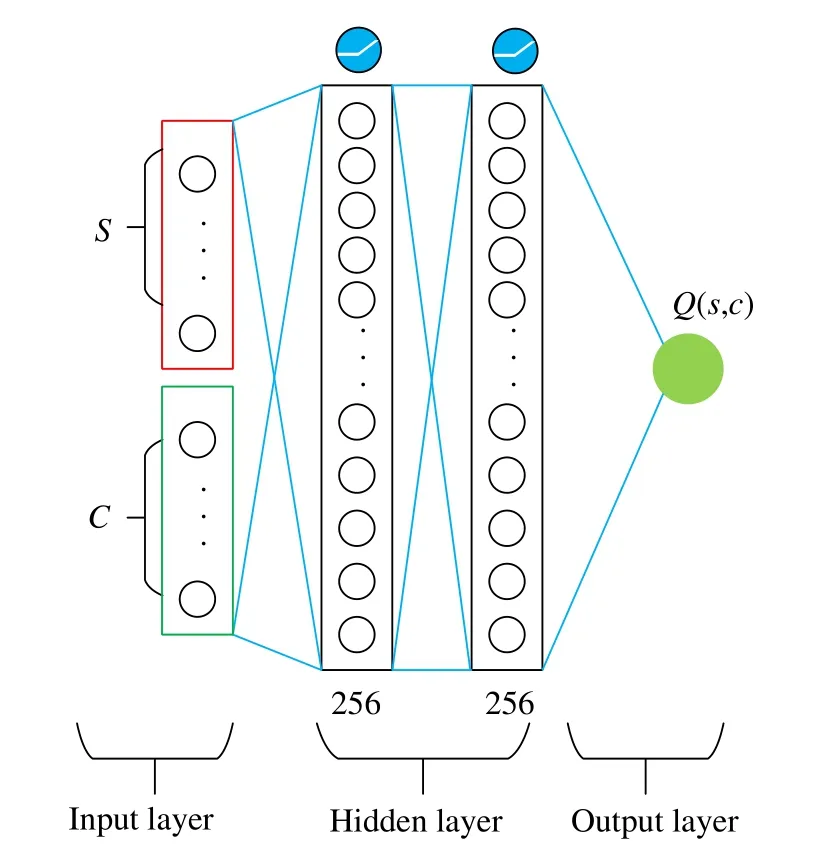
Fig.2 The critic network architecture

For the actor network,we define the parameter of the actor network asφ.BecauseZπold (st) does not contribute to the gradient,we optimize the policy by minimizing the following loss function

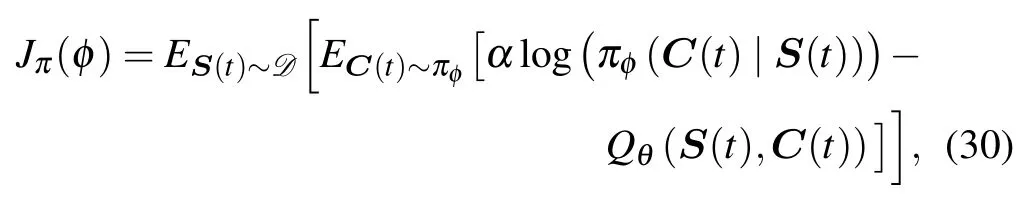
To the end,we reparameterize the policy using actor network transformation as

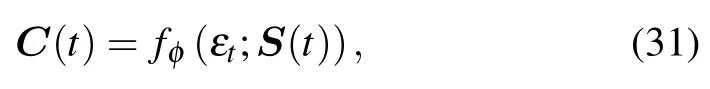
whereεtrepresents noise,sampled from some fixed distribution,such as the spherical Gaussian distribution.Then,by taking(31)into(30),the loss function can be transformed into the following

whereπφis the policy of the agent and defined implicitly in terms offφ.

The input of actor network contains the stateS(t),and the output is the actionC(t).As shown in Fig.3,the hidden layer architecture of actor network is the same as the critic network.Specially,we get the actionC(t)by sampling from 6Mneurons which means the mean and variance of the actionC(t),respectively.The role of actor network is to get the actionC(t)which maximizes the total rewardZ(t)at the stateS(t).

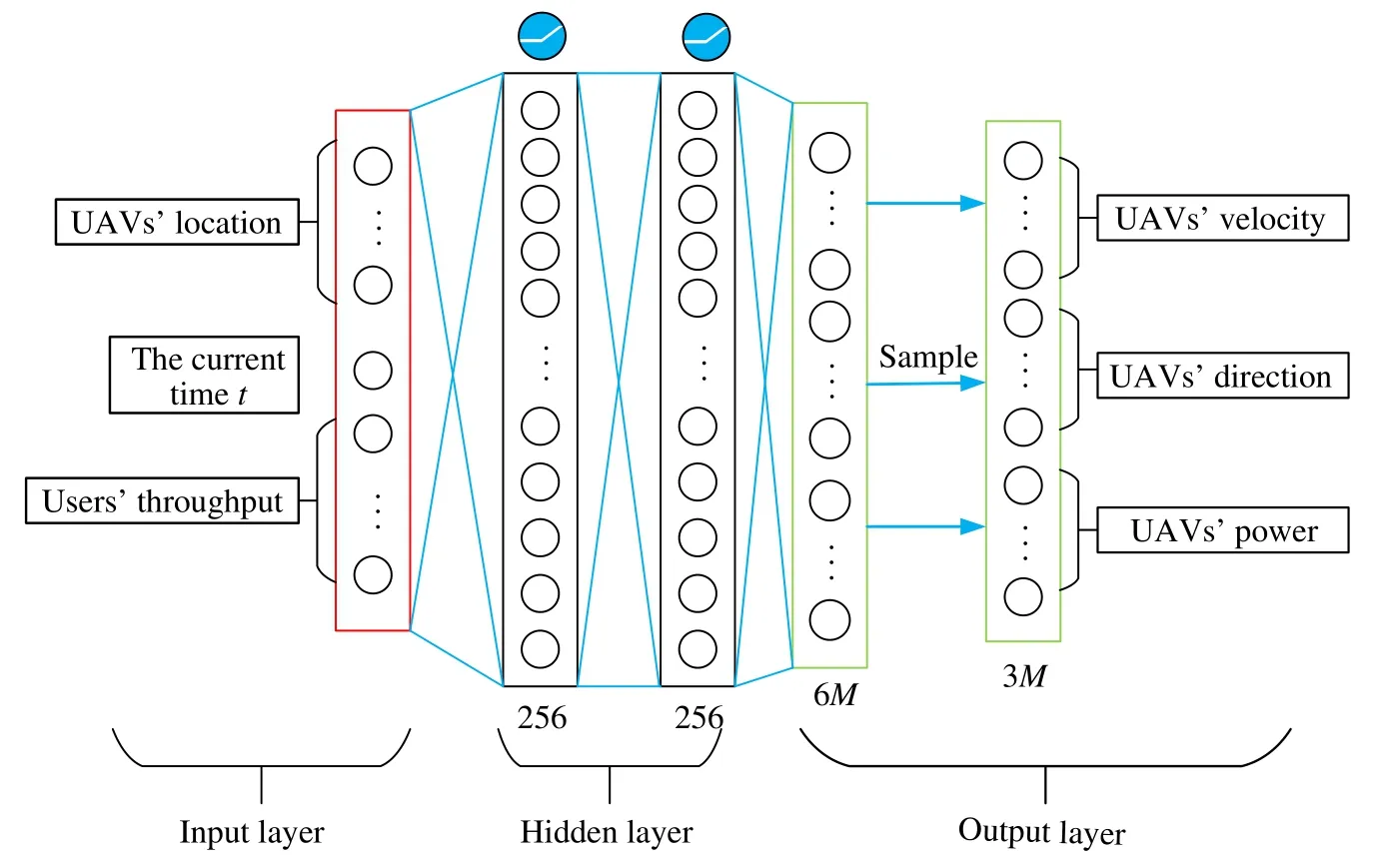
Fig.3 The actor network architecture

The SAC introduces the temperature parameterα.Unfortunately,it’s usually difficult to set its numerical value.To solve the problem,we propose self-adaptingα,which optimizesαby SGD.In the SAC,we aim to find thewhich maximizes the total rewardZ(t)and makes the entropy of actionC(t) greater than the expected entropyTo achieve this,its duality problem has been given in Ref.[29],which is as follows

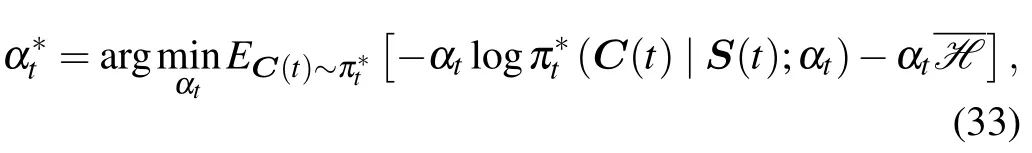
then,we optimize the temperature parameterαby minimizing the following loss function

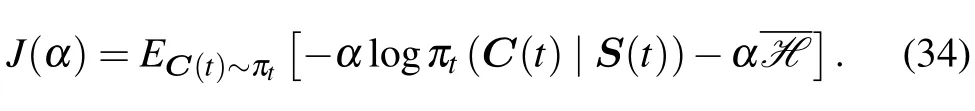
Although the temperature parameterαcan be obtained by the methods above,it also introduces a new parameterFortunately,we can set-|S|dim.

In Algorithm 1,we use two critic-target and two criticevaluation networks to mitigate positive bias.In particular,we parameterize two critic-target networks with parametersand train them independently to optimizeAs shown in Fig.4,SAC has 6 networks,including two Q-evaluation(critic) networks,two Q-target (critic) networks,one Actor network,and oneαnetwork.Q-target networks adopt soft update,whichfori ∈{1,2},whereτis the soft update coefficient.TheDrepresents experience pool,which can make the states independent of each other.TheDminmeans the minimum experiences needed to start the training process.

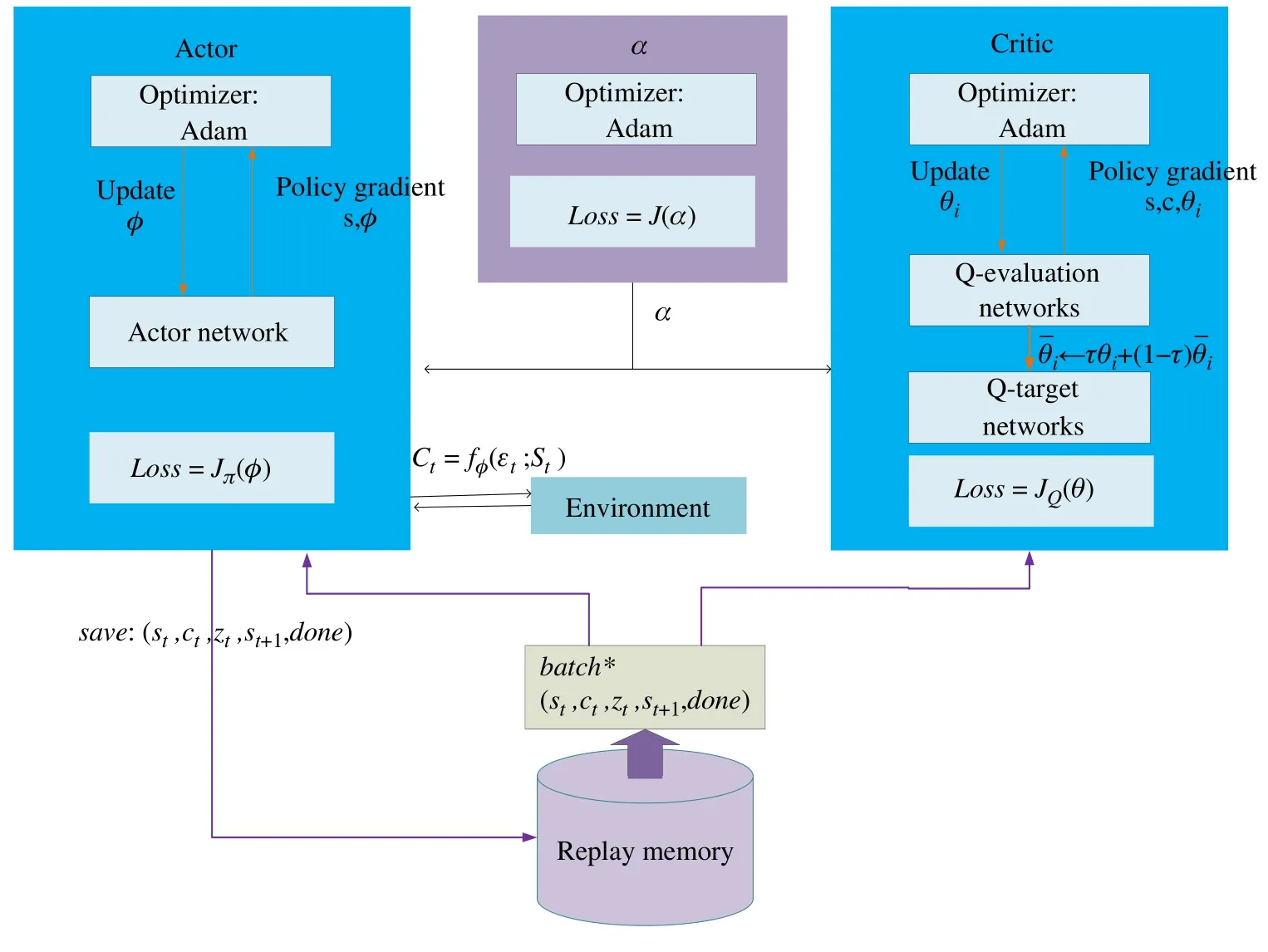
Fig.4 The actor network architecture

IV.NUMERICAL RESULTS

In this section,we provide numerical results with SAC in JTDPA of the multi-UAV system where we consider there areM2 UAVs andN6 ground users which are randomly and uniformly distributed within a 2D area of (3×2) km2.The altitude of the UAVs isH100 m.The noise power at the receiver isσ2-110 dBm.The channel gain isρ0-60 dB at the reference distanced01 m.The maximum transmission power,the minimum distance of UAV,and maximum speed of the UAV arePmax0.1 W,dmin100 m,andVmax50 m/s,respectively.The initial locations of theMUAVs are randomly generated in (3×2) km2.In this paper,the initial locations of the two UAVs are set above the 4th user and the 1st user respectively.For hyper parameters of the SAC,we setλ3×10-4,γ0.98,τ0.001.For other DRL algorithms,such as DDPG,PPO,TD3,we set the reward function and learning rate the same as the SAC.The specific reward function settings are shown in Tab.1.All hyper parameters of other DRL algorithms are as following:the DDPG and TD3 belong to the deterministic policy gradient algorithms,which need to add noise.In our simulations,we use a Gaussian action noise.The mean and variance of the noise are set as 0 and 0.1,respectively.Moreover,the variance will reduce with thetraining.The PPO belongs to on-policy algorithms.We adopt clipped surrogate objective[31],whereε0.2.

Tab.1 Reward setting

Fig.5 demonstrates 105-episode training processes of SAC,SAC without power control (SACNP) (pm(t)Pmax) and other DRL algorithms.We setT90 s andRmin100 bit/Hz.One can see that all the algorithms converge at about 4×104-episode and the SAC,as well as SACNP,have better performance than other DRLs.As for DDPG,TD3,and PPO,their rewards increase quickly at first,but as the number of iterations increase,all of which fall into the local optimal solution.The DDPG and TD3 belong to deterministic policy gradient algorithms,where the actor network outputs a deterministic action,and the PPO is an online algorithm,which cannot solve the problem of smaller experience than off-line algorithm.In contrast,SAC considers the action entropy in Q-value,which encourages the agents to explore,so that SAC may jump out of the local optimal and find the optimal solution as the number of iterations increases.Compared with the SACNP,SAC can change their transmission power to reduce the interference from other UAVs and get more reward,so that the total reward of SAC may be higher than SACNP.

Fig.5 Average rewards of Algorithm 1

In Fig.6,we compare the optimized UAVs’trajectories obtained by the SACNP in Fig.6(a) and SAC in Fig.6(b) with the time periodT90 s andRmin100 bit/Hz.The total throughput of ground users are shown in Tab.2.Note that the user’s locations and channel parameters are inaccessible for the UAVs,and SAC outputs action by applying sampling.As a result,the trajectories of the UAV may not be smooth.

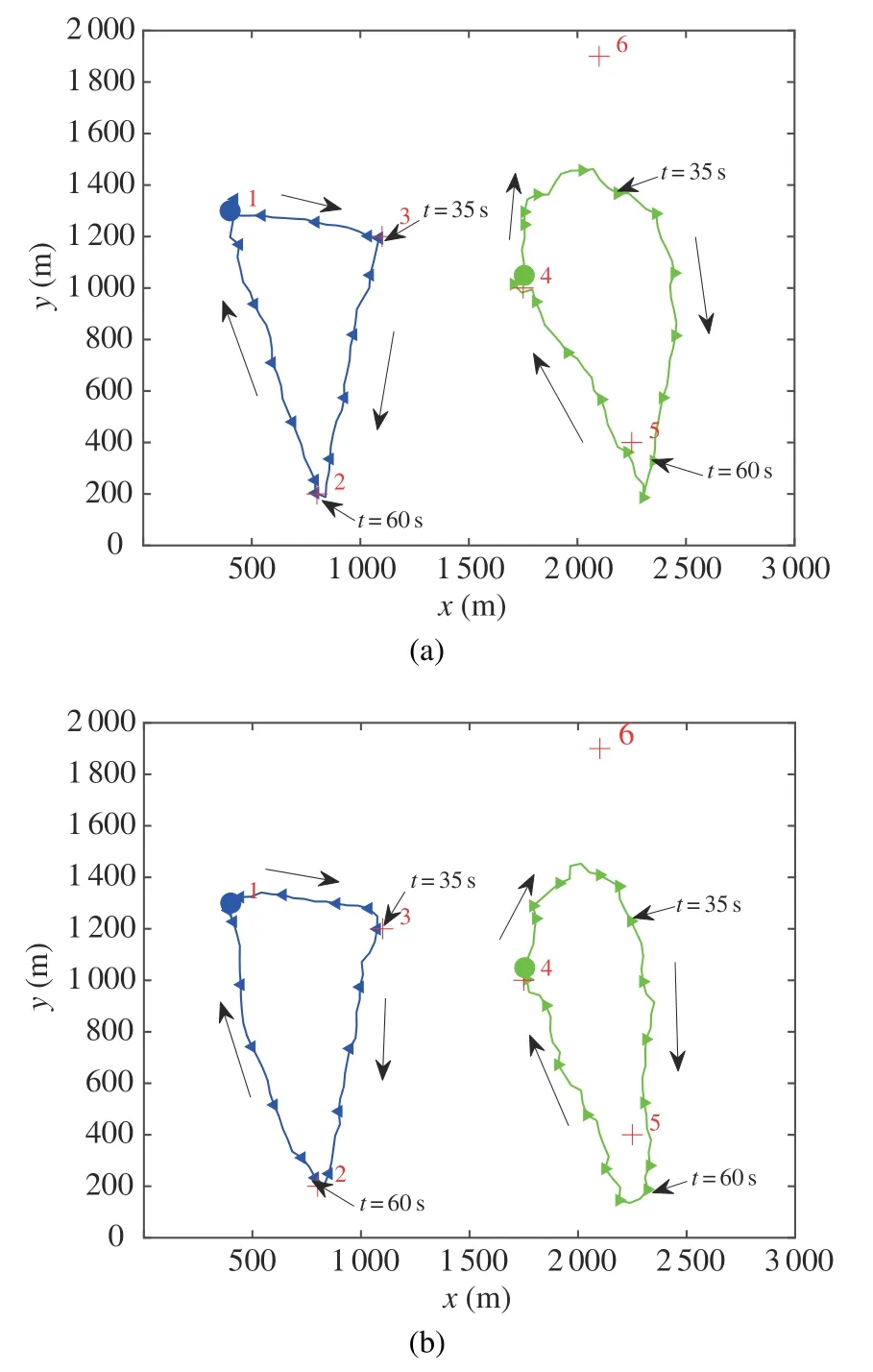
Fig.6 The trajectories of two-UAV and six-user communication system under T 90 s and Rmin 100 bit/Hz.Blue circle ‘·’ and green cricle ‘·’represent the inital locations of two UAVs trajectories,respectively.Black arrows represent the directions of UAV.We sample every 5 s on each UAV’s trajectory and the sampling points are marked with blue‘◀’and green‘▶’as their corresponding trajectories:(a)Optimized UAV trajectories by SACNP;(b)Optimized UAV trajectories by SAC

Tab.2 The total throughput of ground users

It can be observed from Fig.6(a) that two UAVs tend to keep away from each other as far as possible to reduce cochannel interference fromt35 s tot60 s.However,UAVs sometimes sacrifice the favourable direct communication links,especially when they serve two users which are close to each other.As a result,the SAC can dynamically adjust the transmission power of the UAVs to reduce the interference from other UAVs.

Both Fig.6(a) and Fig.6(b) show that the UAVs will not visit the 6th user.The 6th user is far away from the other users,if the UAV visits the 6th user,the total throughput will reduce.However,the UAV will move to the 6th user to ensure it achieves the minimum RSSI.As a result,the SAC can dynamically adjust the trajectory to maximize the total throughput for all users and ensure all users achieve the minimum RSSI.The initial locations of the two UAVs are set above the 4th user and the 1st user respectively,so the 4th user and 1st user will get more throughput.Meanwhile,the UAVs will fly to other users to ensure them achieve the minimum RSSI.

In contrast,in Fig.7,the transmission power of the UAVs are complementary at certain time slots,such as 30～40 s and 15～25 s,when the two UAVs communicate to two nearby users.Therefore,strong direct links and weak co-channel interference can be achieved at the same time,which may improve the total received data rate in the periodT.Therefore,without transmission power control,the interference signal by other UAVs can only be mitigated by adjusting the UAV trajectory to keep away from other UAVs,where jointly optimizing transmission power and trajectory of the UAVs provide more flexibility and the higher throughput.In Fig.8,we compare the maximum throughput of three optimizations for trajectories:1)the SAC,which uses Algorithm 1;2)the SACNP,applying Algorithm 1 but without power control;3)Circular,which is obtained by Ref.[32]withM2 and only optimizes user scheduling and association.Especially,the SAC optimizes the UAVs’ trajectories and transmission power at the same time.We can get several important observations from Fig.8.First,as expected,the total throughput of the three algorithms increases as the periodTbecomes larger.Second,the performance gap between the SACNP and Circular increases with increasingT.Third,comparing the SAC and SACNP,by using power control,it shows that more flexibility can be obtained,result in better throughput.

Fig.7 UAV transmission power versus time for SAC

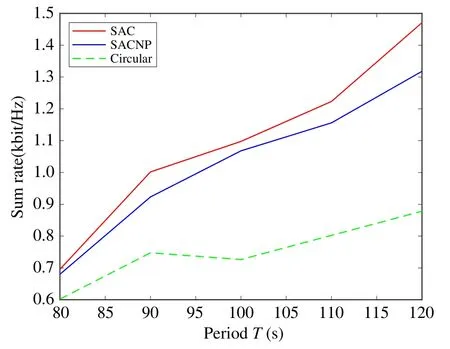
Fig.8 Sum rate versus period T with different algorithms

V.CONCLUSION

In this paper,multi-UAV and multi-user system have been studied,where UAVs serve multiple ground users.We aim to maximize the total throughput for all users as well as meeting the fairness by optimizing the UAVs’ trajectories and transmission power in a centralized way,without knowing users’locations and channel parameters.Note that no matter what kind of channel model we adopt,our proposed algorithm only needs RSSI of the ground user.To solve this problem,we model it as an MDP and adopt DRL-based SAC to address.Meanwhile,the design of our reward function combines both sparse and non-sparse reward,which not only solves the problem that sparse rewards may not address,but also overcomes the loss of fairness of UAV communication caused by nonsparse rewards.Simulation results have shown that the proposed algorithm,in terms of convergence and performance,is better than other DRL-based solutions.