三维点云关键点局部坐标系重构方法研究

2022-06-29许振瑛晁建刚胡帅星

载人航天 2022年3期

许振瑛，何宁，晁建刚∗，胡帅星

（1.中国航天员科研训练中心，北京 100094； 2.中国航天员科研训练中心人因工程重点实验室，北京 100094）

1 引言

航天员利用混合现实系统进行在轨空间操作及地面训练，获取场景重构模型与数字模型的准确匹配关系是混合现实场景实现虚实融合的关键。为获取场景重构模型，可采用点云匹配的方式融合混合现实系统深度传感器各视角下的点云数据。点云匹配的本质是估计传感器的位姿变换，采用基于优化的方法或基于特征点匹配的方法，其中基于特征点匹配的方法需要在关键点处计算特征描述符，由于传感器姿态未知，关键点处的特征描述符易受角度影响，导致匹配失败。

为提高特征点匹配成功率，文献［6－8］采用在关键点处构建局部坐标系（Local Reference Frame，LRF）以克服传感器姿态的不确定性，描述子的旋转不变性优于不构建LRF 的方法。受制于点云噪声、遮挡、分辨率等因素，目前并不存在同时满足健壮性和可重复性的LRF 构建方法。

构造LRF 最直观的方法为主成分分析法，但由于获取各点云片段的视角不同，对应同一关键点处的邻域点云分布不一致，导致该方法计算LRF 的可重复性仅约30%。文献［7－10］分别就LRF 构建中的轴和轴计算提出了不同的改进方法，其中Novatnack 等首次以关键点处法向量为LRF 的轴，轴则通过对邻域点云协方差矩阵特征值分解的方法获得，该方法计算快捷，但计算轴的点云范围过小，对噪声敏感；Yang等仍然使用关键点法向量为轴，将计算法向量的邻域范围扩大了到邻域点云半径的13，并且用邻域点云投影向量的加权和计算轴，由于计算轴依赖于点云均匀采样，不规则分布的点云严重影响该方法的可重复性；Petrelli 等提出了在关键点邻域半径为5 mr（Mean Resolution，点云平均分辨率）的范围内拟合平面的方法计算轴，轴则与邻域内法向量与轴夹角最大的点有关，并且针对点云遮挡问题提出了解决办法，该方法对离群点敏感；Ao 等计算轴的方法与Yang 等一致，但通过对点云进行变换创新了轴的计算方法，轴的可重复性限制了该方法的性能。鉴于上述方法，为提升LRF 的可重复性，本文提出了基于法向量 DBSCAN聚类（Density⁃Based Spatial Clustering of Applications with Noise，DBSCAN）的关键点邻域点云LRF 重构方法，实现稳定可靠的LRF 估计，进而为后续计算具有旋转不变特性的特征描述子提供前提，实现特征的准确匹配。

2 局部坐标系重构

2.1 重构方法概述

本文提出如下方法重构关键点处局部坐{p∈R‖p－p‖，＝1，…，n；标系：

1）在含有n个点的点云片段内随机取一点为关键点，其中＝｛p∈R＝1，…，n｝；

2）利用KDTree方法提取点处半径为的球形邻域点云P，共n个点，其中P ＝

3）计算P中各点p的法向量n，并记P的法向量集为N；

4）利用DBSCAN 方法对法向量集N聚类，元素最多的非噪声类其均值即为轴；

5）结合轴对P进行变换后求得的第一主成分即为轴。

通过上述步骤，可以获得关键点处的局部坐标系L ＝［，×，］，选择邻域点并构建局部坐标系的过程如图1 所示。

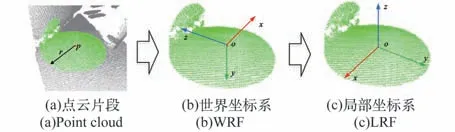
图1 选择邻域点云并构建LRFFig.1 Selection of neighborhood point and LRF con⁃struction

2.2 基于KDTree 方法的邻域点云提取

本文采用KDTree 方法选择关键点的球形邻域点云。点云数据构建KDTree 的步骤为：

1）分别对点云的，，轴数据计算方差，并获取最大方差对应的坐标轴，记为axis；

2）以axis轴数据为参考对点云数据排序，且令中位数为父节点，以垂直于axis轴且过父节点的平面为超平面平分点云数据，将小于父节点的点云列为左子节点，其他为右子节点；

3）对左右子节点递归执行步骤1）和2），直至所有数据被划分完毕。

KDTree 能够加快搜索速度，记KDTree 根节点，关键点，查找范围，则查找KDTree 的步骤为：

1）计算关键点到根节点分割超平面的距离；

2）若，则步骤3），否则步骤4）；

3）计算关键点到根节点的距离d，若d ＜r，则符合查找要求；否则4）；

4）查找的左（右）子节点，若左（右）子节点存在，则以左（右）子节点为，递归执行步骤1）～3），直至不存子节点。

通过上述方法，可以查找出关键点处范围为的所有邻近点p。

2.3 法向量估计

计算cov 的特征值并排序，其最小特征值为，对应的特征向量v，公式（2）计算了点p处的单位法向量：

图2 法向量估计Fig.2 Normal vector estimation

2.4 基于法向量DBSCAN 聚类的Z 轴估计方法

图3（a）、图3（b）和图3（c）分别列举了平面、折角和散乱点云和法向量及其在单位球面上的分布，平面和折角点云存在大量方向基本一致的法向量，其法向量在单位球上的分布相对集中；散乱点云法向量分布相对广泛，其核心较为模糊。因此可以通过法向量的集中程度推测某方向的重要性。

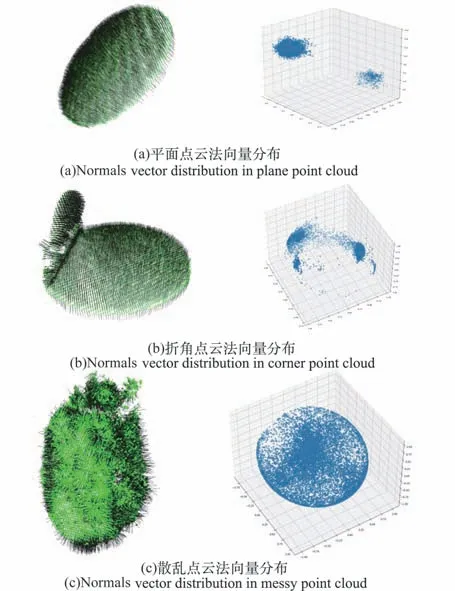
图3 点云的法向量估计及其分布Fig.3 Normal vector estimation of point cloud and its distribution

DBSCAN 是一种基于密度的聚类方法，簇的数量只与点云密度分布相关，由于单位法向量在单位球面上的分布可看做点云，故步骤描述如下：

1）任选一个未经处理的法向量n，若其邻域r内点的个数小于min，则被标记为噪声，否则被标记为核心样本，并分配一个新的簇标签C，将其所有邻域法向量加入候选集C；

2）对于候选集C中所有未处理的法向量n，若其邻域r内的法向量数小于min，则标记为噪声，否则将其邻域加入候选集C且将法向量n加入簇C；

3）重复步骤2），直至候选集C为空；

4）重复步骤1 ～3，直至处理完毕所有法向量。

将上述过程标记为DBSCAN，如公式（3）所示，

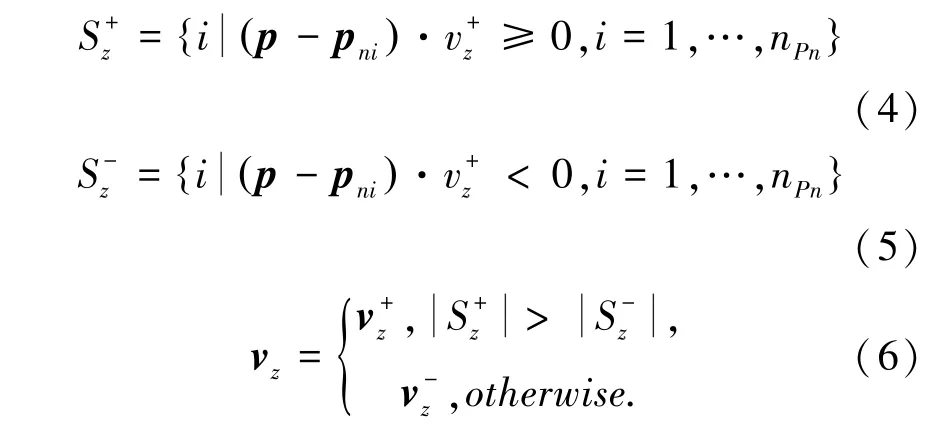
DBSCAN 聚类方法存在缺陷，即：若法向量分布过于散乱而不满足聚类条件，则方法失效。此时采用协方差矩阵特征值分解计算轴。

2.5 局部坐标系x 轴估计

由于噪声、遮挡等原因，轴的确定较轴复杂许多。本文采用对球形邻域点云进行变换后求第一主成分的方法确定轴，解决局部点云有效信息不足导致的轴估计一致性差的问题

为降低数据的复杂度，首先将球形邻域点云P投影到轴的切平面，记为′，如图4所示。

图4 邻域点云在z 轴切平面上的投影Fig.4 Project points on orthogonal plane of z－axis

其中，p为邻域中某点，′为p在上的投影，〈·〉为向量内积，假定球形邻域点云中心为原点，则：

投影后失去了立体特征，本文提出3 种权重因子将点′进行变换，分别表示为、和′。代表了p到中心点的距离（此处为避免‖′‖ 为0 的情况设定‖′‖ 最小为0.001），即距离越远的点越能为轴的方向做出贡献：

为点的法向与轴的内积，即轴越大的点越能为轴的方向做出贡献：

′是′的集合，′是点的法向在轴切平面上的投影，加强与轴方向不相同的点对轴方向估计的权重为式（10）：

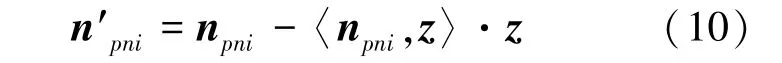
p转换后的点为式（11）：

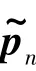
局部坐标系可表示为式（12）：

3 实验验证

3.1 实验目标、比判准则与数据选择

1）实验目标。评估上述方法在局部坐标系构建中的重复性。

为实现上述目标，本文在与点云片段有重叠区域的点云片段＝{q∈R|＝1，…n} 中获取关键点的对应点并分别构建局部坐标系L和L，已知和间的转换为，即＝·，则L＝·L ＋，其中为残差。本文采用公式（13）计算轴和公式（14）计算局部坐标系间的绝对误差。

其中，ε为轴间的旋转误差角度，为局部坐标系间的旋转误差角度，误差角度越小则匹配精度越高。

2）比判准则。本文以10°为标准统计匹配正确率，误差角度小于该标准即认为匹配正确。

3）数据选择。本文选用 3DMatch、SpaceTime 和Registration 数据集评估轴和局部坐标系重构的重复性。

针对空间站舱内三维重建场景匹配问题，上述所选数据集包含了色彩和深度信息，符合重建匹配应用场景需求；其中3DMatch 数据集为室内场景，保证验证数据与应用背景具有相似性；SpaceTime 数据集采用SpaceTime Stereo 技术获取，为双目立体视觉，Registration 数据集由Kinect设备获取，为ToF 深度，保证验证数据适用不同数据来源。

3.2 关键参数设置

分别对各数据集随机取1000 对重合点测试并统计正确率，每次测试的参数保持一致：邻域点云半径取15 mr；估计法向量邻域范围＝10，即附近10 个点； DBSCAN 聚类扫描半径r ＝sin (5·π180) ，最小包含点数 min ＝max（［n］100，5）。

3.3 z 轴重复性测试与对比

以图5 为例，左右侧分别为空间内同一点处不同视角下的球形邻域点云，图5（a）为点云原始数据，可见不同视角下的点云存在差异；图5（b）估计了点云所有点的法向量；图5（c）对法向量进行了聚类，其中属同簇的法向量颜色相同，黑色为离群点；图5（d）将点云中心移至原点并添加了轴（向上轴为轴，其余轴未约束，仅用于表征轴切平面）。