卧式加工中心空间误差预测与验证

王调品，侯益波，何 兵

（1.成都工业职业技术学院装备制造学院，四川 成都 610218；2.成都优拓优联万江科技有限公司，四川 成都 610218）

1 引言

精密数控加工机床精度预测分析始终是国内外研究的热点，其中数控机床加工精度是衡量机床工作性能的重要指标[1]，而由机床几何误差复合而成的空间误差是影响加工精度的主要因素。所以，搭建数控机床完整模型及开展空间误差预测研究，具有较重要的科研理论研究意义与实际工程价值，亦为机床精度设计技术层面提供完整几何误差参数指标。

国内外众多学者围绕数控机床空间误差建模[1-2，9]方面进行了相关研究。国内，文献[3]以多体系统结合齐次坐标转换为理论研究基础，分析了串并混联机床的几何误差。考虑各运动轴几何误差的综合影响，提出了一种串并混联机床综合误差建模方法研究系统。

文献[4]以INTEGREX 200 型九轴五联动车铣复合机床为研究对象，借助多体系统动力学搭建了机床空间误差模型。国外，文献[5]为提高机床整机加工精度，同样多体系统理论提出了基于齐次变换和微分运动矩阵的机床几何误差建模与补偿方法。文献[6]利用均质矩阵变换构造相对坐标系的运动矩阵。其次，基于齐次变换推导了空间误差模型。然后通过计算机数控程序重构，提出了一种误差补偿算法。

最后，在软件中建立的虚拟机床上进行了仿真，验证了模型和补偿算法的有效性。但是传统机床空间误差建模结果并未包含全部几何误差，并少有给出机床空间误差模型预测结果。对此，以卧式加工中心为例，采用旋量指数积分析空间误差并构建机床误差模型，基于传统辨识技术识别各项误差，同时给出空间误差模型预测结果，开展基于ISO230-6的体对角线对比验证实验，为进一步深入研究机床空间误差补偿手段提供必要的理论基础支撑。

2 旋量理论分析

2.1 刚体运动学

任意刚体运动：刚体从某一位置到另一位置的运动可通过绕某一定轴的转动加上沿平行于该直线的移动实现。旋量运动[7]的无穷微小运动称为运动旋量，以几何形式描述，如图1所示。

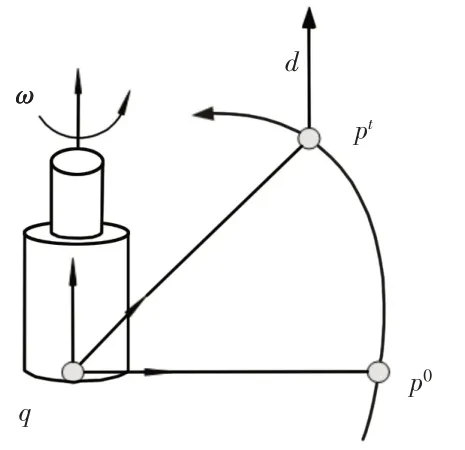
图1 旋量运动Fig.1 Screw Motion

2.2 旋量指数积

定义了机器人相关坐标系，将参考坐标系R取在固定在基座上，末端坐标系E固定于机器人手臂末端，设末端坐标系在参考系R中的初始位形为E0，各关节单位旋量在参考系R中分别表示为：φ1、φ2、…、φn，γn为各关节单位旋量，φn为相对参考坐标系的关节微小变量，如图2所示。

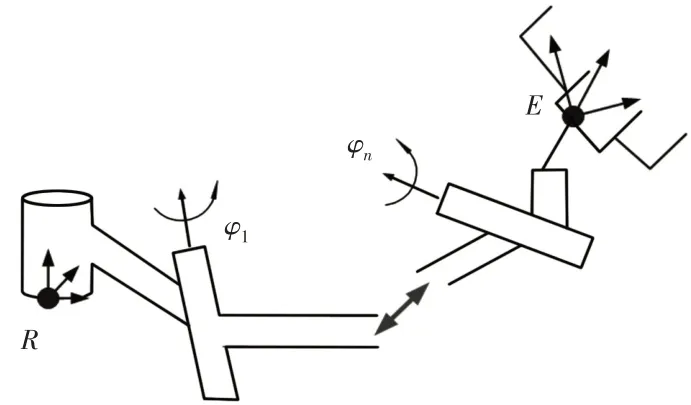
图2 开链机器人手臂Fig.2 Open Chain Robot Arm Crew Motion

机器人手臂终止位形Eφ以旋量指数积形式输出为：

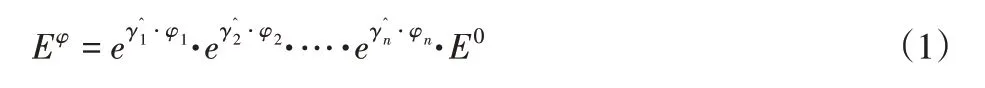
值得注意的是，旋量运动中所有矢量和点均以机床坐标系为参考。

3 数控机床空间误差建模

3.1 几何误差源

影响机床加工精度的因素一般有几何误差、热误差、伺服系统误差、力误差以及载荷误差[8]等，其中几何误差主要包括定位误差、直线度误差、垂直度误差、滚角误差、偏摆误差以及俯仰误差，因其易于测量、受环境影响因素较小，且同样能够以旋量指数形式输出等特点，在恒温条件下，一般以几何误差作为机床加工精度主要误差来源，主要分为与位置无关误差和与位置相关误差共计21项，如表1、图3所示。

表1 几何误差Tab.1 Geometric Error

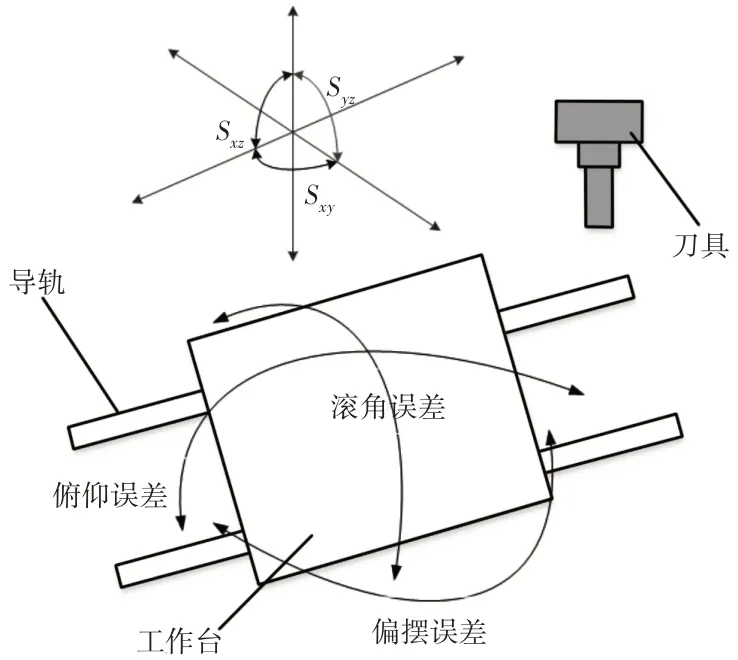
图3 几何误差原理Fig.3 Principle of Geometric Error

3.2 运动链拓扑结构

一般情况下，数控机床机床运动链可分为：刀具链和工件链，刀具链、工件链分别为从刀尖、工件切削点到机床坐标系的运动链。

设定机床坐标系C_xyz为参考坐标系，其坐标原点CO一般为机床回零位置；工件坐标系W_xyz依据实际对刀来确定，刀具坐标系T_xyz设置于刀尖位置，如图4所示。几何误差未参与时，得出刀具运动链与工件运动链末端理想运动矩阵为：

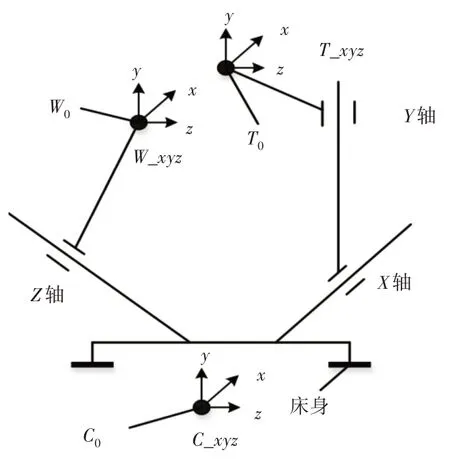
图4 机床运动链简图Fig.4 Kinematic Chain Diagram of Machine Tool

式中：ECT—刀尖相对机床坐标系的理想无误差运动矩阵；ECW—工件切削点相对机床坐标系的理想无误差运动矩阵。

为保证机床空间误差模型的完整性，需确定刀尖点与工件切削点在机床坐标系下的初始位形，参考前文中各坐标系定义，得出在机床坐标系下的位置坐标分别为：

式中：xT、yT、zT—刀尖点在机床坐标系下各轴的投影位置坐标；xW、yW、zW—工件切削点在机床坐标系下各轴的投影位置坐标。

根据以上分析，基于旋量理论将几何误差视作机床各轴旋量运动，推导建立刀具运动链与工件运动链末端实际运动矩阵分别为：

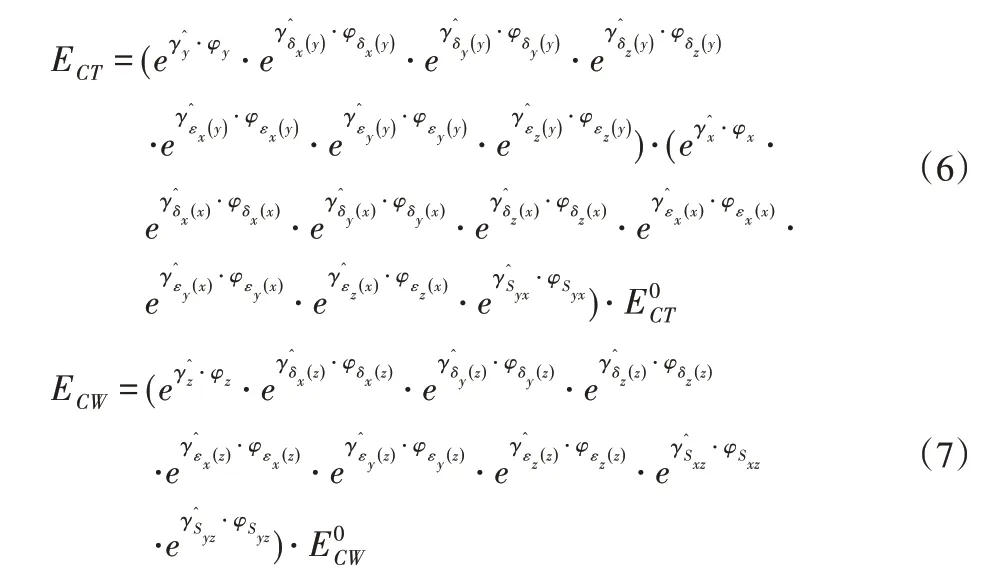
式中：ECT—刀尖相对机床坐标系的实际运动矩阵；ECW—工件切削点相对机床坐标系的实际运动矩阵。

3.3 空间误差模型

在机床坐标系下，根据机床空间误差定义[9]：机床进给时，刀具运动链末端（刀尖点）与工件运动链末端（切削点）实际运动位形间的偏差就是机床空间误差。综上所述，推导该卧式加工中心空间误差模型ΔE：

式中：x、y、z—各轴在机床坐标系下的进给值；Δx、Δy、Δz—空间误差在x、y、z各轴向分量。

综上所述，分析了21几何误差，定义了机床坐标系、工件坐标系与刀具坐标系，明确给出了刀尖点与工件切削点在机床坐标系下的初始位置坐标，利用旋量指数积推导了工件运动链、刀具运动链理想与实际运动矩阵，借助空间误差基本定义建立了机床空间误差模型。从式（8）中可以看出，该误差模型包含了21项几何误差，实现了基于旋量指数积推导机床空间误差完整模型的目的。后续只需在完成辨识各项几何误差后，任取加工空间中某一点即可预测该点在机床坐标系下的空间误差。

将旋量指数积引入机床建模中有以下优点：（1）因其参考坐标系设定特点，减少了机床运动轴局部坐标系的建立；（2）避免了传统建模中因多个局部坐标系建立导致可能产生奇异性的问题。

4 空间误差模型预测

4.1 几何误差辨识

以卧式加工中心为测试目标，基于“12线法”[10]规划实验测量轨迹，选用雷尼绍激光干涉仪为实验测量设备，为保证实验的可靠性，每条测量轨迹均选取16个测量点，重复测试5次并取平均数，测量加工空间设定为600*600*600（mm），采用十二线法完成机床21项几何误差辨识。给出十二线测量结果与21项几何误差辨识结果，如图5、图6所示。

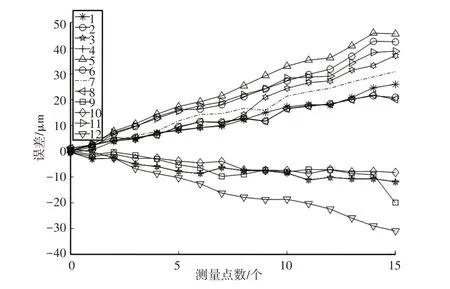
图5 12线法测量结果Fig.5 Measurement Results of 12 Wire Method

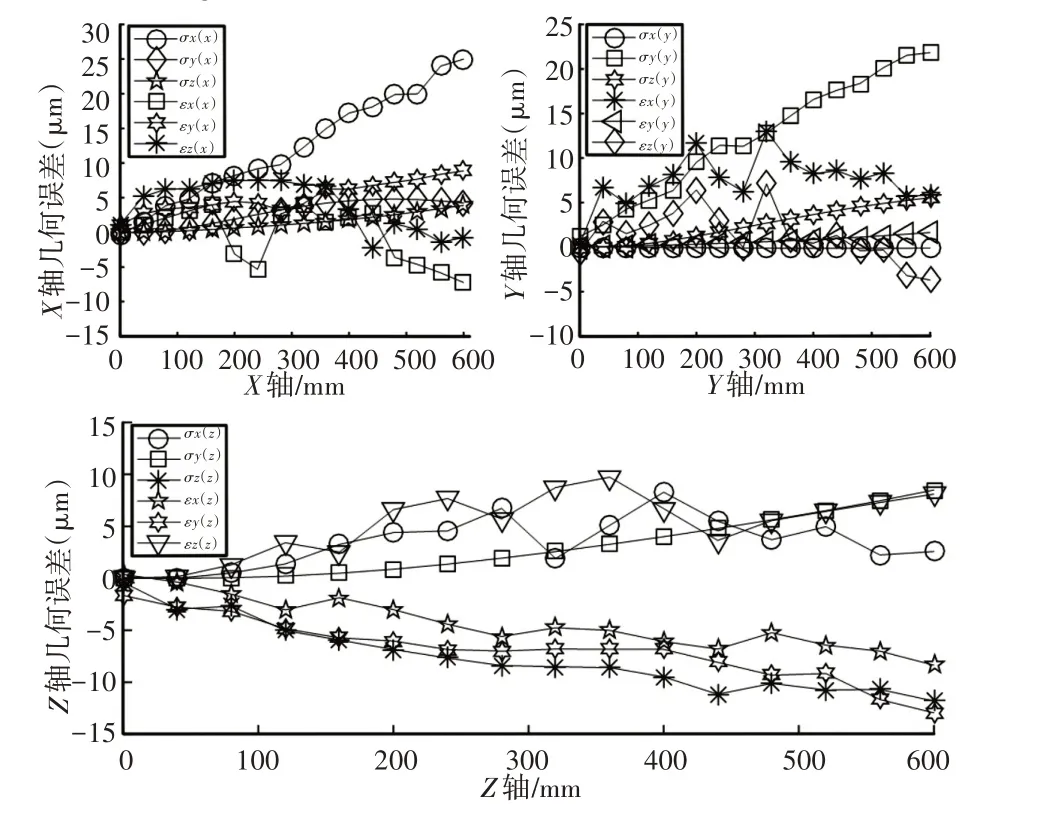
图6 18项几何误差辨识结果Fig.6 18 Geometric Error Identification Results

3 项Sxy、Syz、Sxz垂直度误差辨识结果分别为-1.18μ/m、-3.56μ/m、-6.31μ/m。

4.2 预测模型分析

机床空间误差模型的准确性间接决定了后续误差补偿效果良好的可能性，而模型的准确性体现在加工空间中各点模型预测结果与实验测量结果的对比。

为直观表达机床空间误差模型预测结果，结合前文中21项几何误差辨识结果，带入式（8）中，基于Matlab软件输出该卧式加工中心空间误差预测结果，一种颜色代表空间误差最弱区域，另一种颜色代表空间误差反应强烈区域，如图7所示。

图7 加工空间空间误差预测图Fig.7 Prediction Diagram of Machining Volumetric Error

任意给定加工空间任意一点即可直接该点空间误差显示结果。可以看出，该机床越靠近行程正向位置，则反映了空间误差对机床加工精度影响越大。不仅有利于看出加工空间中各点空间误差对机床的影响趋势，更有利于为后续机床误差补偿提供强有力的预测理论模型。

4.3 实验验证

为了验证基于旋量指数积的卧式加工中心空间误差预测模型的可行性，以及采用十二线法辨识技术手段的有效性，基于ISO230-6[11]展开四条对角线测量实验。规划四条体对角线测量轨迹，同时结合式（8）及其21项几何误差结果给出四条体对角线各点预测值，如图8所示。给出实验测量结果与模型预测数据对比，如图9、表2所示。

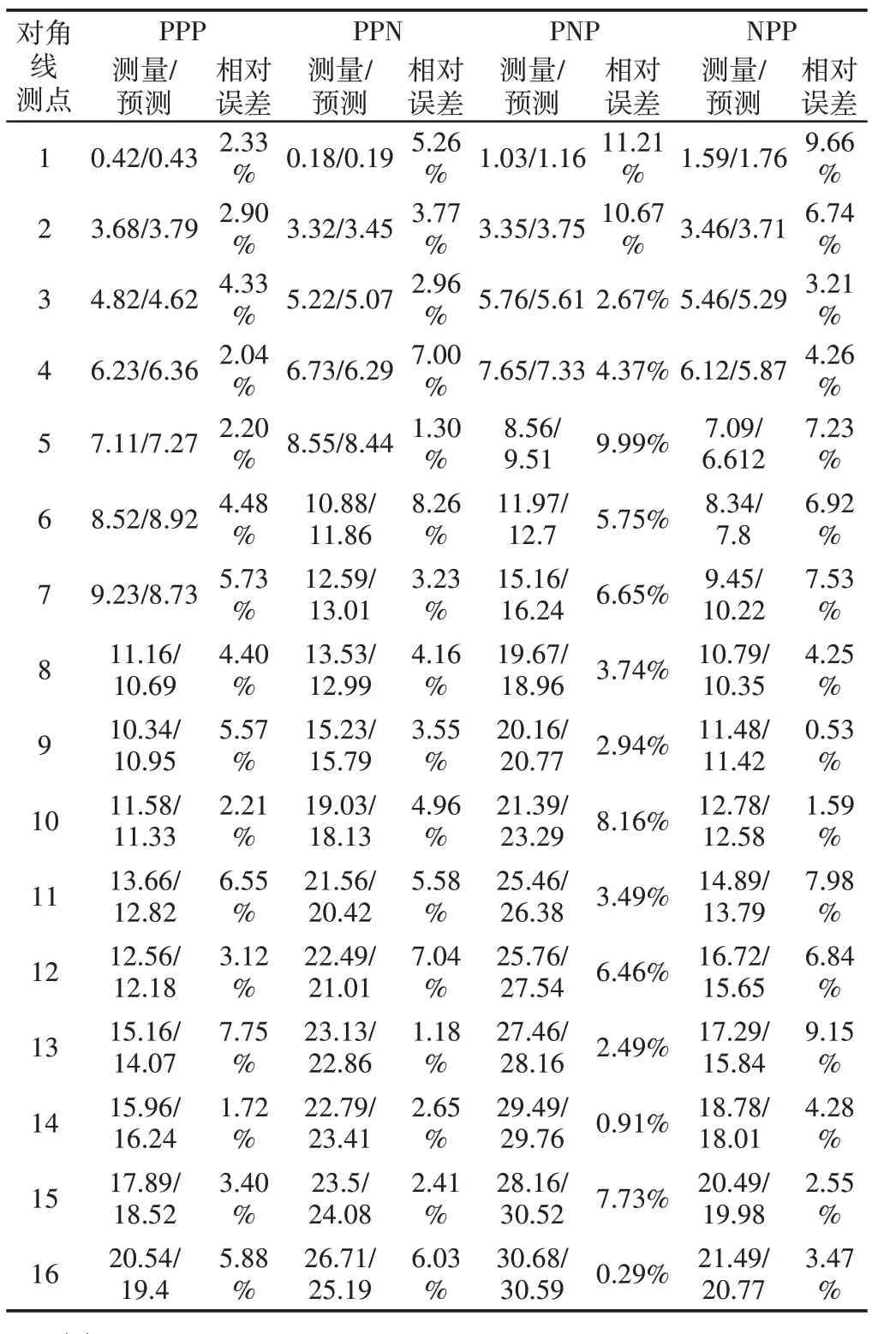
表2 测量值与预测值对比图Tab.2 Comparison Between Measured Value and Predicted Value

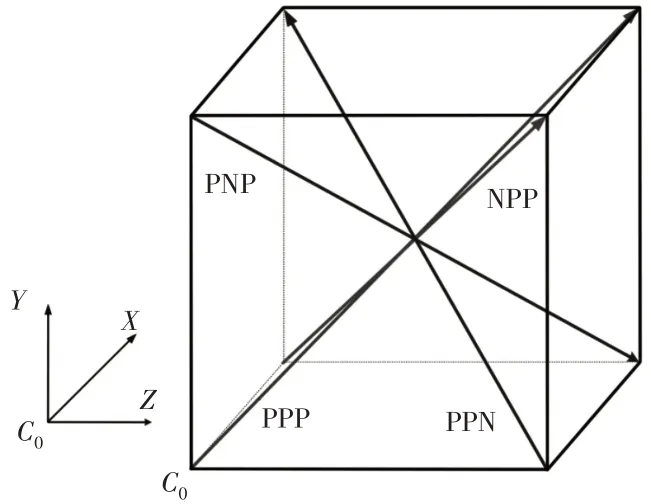
图8 体对角线测量路径Fig.8 Body Diagonal Measurement Path

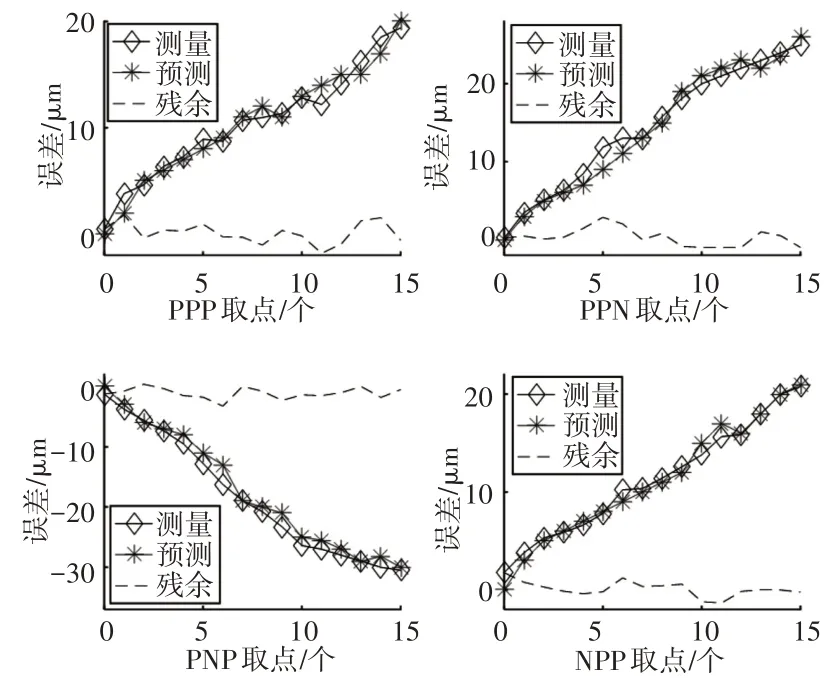
图9 体对角线模型预测值与实验测量值对比Fig.9 Comparison Between Predicted Value of Body Diagonal Model and Measured Value of Experiment

结果表明：最小相对误差为0.29%（对应残差为0.09μm），且最大相对误差为11.21%（对应残差为0.13μm），因此四条体对角线实验测量值与模型预测值符合程度较高，充分验证了基于旋量指数积的卧式加工中心空间误差完整建模及其预测分析方法正确、有效。

5 结论

（1）借助旋量刚体运动理论描述了机器人手臂关节轴线微小运动，从而建立机器人末端实际位形旋量指数积数学模型。（2）分析了机床21项几何误差及其几何形式，同时输出该卧式加工中心运动链拓扑简图，因首先确定了刀尖点与工件切削点在机床坐标系下的初始位形，从而建立了包含21项几何误差的机床完整数学模型。（3）利用十二线法辨识了21项几何误差，输出空间误差预测结果，基于ISO2002-6对角线空间误差评定标准，对比了对角线模型预测值与实验测量值。结果显示四条体对角线符合程度较高，最小相对误差为0.29%（对应残差为0.09μm），且最大相对误差为11.21%（对应残差为0.13μm），不仅充分验证了基于旋量指数积的机床空间误差完整模型正确、有效，更为后续机床空间误差补偿技术提供坚实的理论基础与数据参考。