起重机吊钩失效的双重响应面联动分析方法

胡俊逸，金初云，贾相武，程文明

（1.浙江交通职业技术学院轨道交通学院，浙江 杭州 311112；2.西南交通大学机械工程学院，四川 成都 610031）

1 引言

吊钩是起重机的重要执行机构和承载机构，其应力和变形与安全生产息息相关，故应对吊钩的可靠性设计格外重视。在传统的机械设计方法中，对吊钩等部件采用较大的安全系数进行设计，如今有限元方法（FEM，Finite Element Method）被广泛应用于结构设计领域，国内外也有许多学者对吊钩的受力分析进行过详细研究[1-4]。而在以上研究中通常未考虑能影响吊钩应力的随机性影响因素，而起重机吊钩一旦受随机因素影响发生故障，将对生命和财产安全造成严重后果。也曾有学者将应力作为唯一输出要素进行多随机因素输入条件下吊钩的可靠性研究[5]，而在实际使用中，因长期形变导致的装配关系改变从而影响吊钩正常使用，也属于吊钩的失效类型；而有关吊钩在应力和变形双重输出响应下的可靠性研究，还未有相关报道。

响应面法（Response Surface Method，RSM）作为结构优化和可靠性分析的有效方法，已被应用于交通运输、土木工程等[6-7]多个行业；根据所研究的问题模型复杂程度对响应面法进行改进，也是许多学者的重要研究思路：与不同抽样方法和优化算法的结合，如文献[7]；增加考虑模型时间维度，应用于非线性领域，如文献[5]；针对多输出要素采用多重响应面法进行分析，研究问题模型在多失效模式下的可靠性，如文献[8]采用双重极值响应面法（Dual Extremum Response Surface Method，DERSM）对航空发动机叶盘进行流-固耦合分析和失效模式联动抽样，证明该方法的可行性。采用拉丁超立方抽样与文献［8］的双重响应面方法相结合，应用于起重机吊钩多失效模式可靠性分析中，也不失为一种有益的尝试。

2 结合拉丁超立方抽样双重响应面法

2.1 拉丁超立方抽样（LHS）

LHS 是一种分层抽样技术[9]，若抽样数为n，则在n个K维度的样本产生过程中，每个维度的分量根据样本数n以等概率划分为n个分区间，因此n个样本共有K*n个分区间；然后在K*n个分区间内随机选出的分量组成n个样本。其数学公式如:

式中：P和R—n×K的矩阵，R—（0～1）之间的随机数；P—（1～n）的自然数，且同一列内互不重复；sij—S的第i行第j列的分量，也就是第i个维度的概率分布函数在1到n个样本之间的随机取值，因此，sij取值必然在0到1之间变化，式（1）实现等概率均分取样区间；式（2）中，Ftj—第j维度的概率分布函数，因此，将sij带入到第j维度概率分布函数的逆函数中，就能取得具体的第j维度属于第i次取样的结果tij。

正因为其等概率抽样原理，因此能得到较为均匀的样本分布，应用于结构可靠性分析，具有较好的各区间代表性，进而提高结构可靠性分析结果精度与效率。

2.2 双重响应面法

响应面方法主要原理是通过构造多项式方程来近似模拟问题的本构关系，得到输入变量与输出响应之间的近似显式函数关系，并方便快速求解；通过对问题进行实验设计与抽样分析，得到初始样本点，对样本点进行回归分析，得到显式函数关系式，对非线性问题具有较好的求解效果。一般多采用完全二次、交叉、纯二次非线性或线性方程作为拟合的目标方程［8］。其一般表达式如：

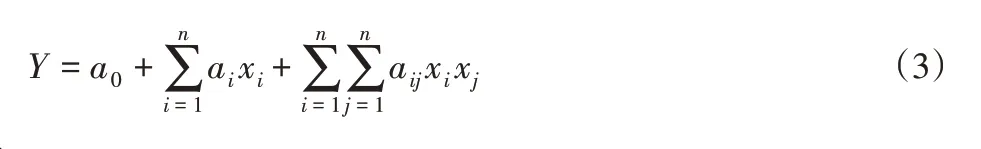
式中：a0—常数项；n—输入随机变量个数；xi—输入随机变量；ai—一次项系数；aij—二次项系数；i、j—1到n的自然数。以上为单一响应面法方程。若将LHS抽样得到的tij以及Yi带入到式（3）的xi和xj中，就能通过最小二乘法得到a0、ai、aij的取值，即完成响应面方程的构建。

双重响应面法即针对多个输出因素进行拉丁超立方的实验设计，每一次取样对应着多个输出因素，并构建出多个响应面方程。

如选取材料密度、重力加速度、起吊物质量作为输入变量，以吊钩最大应力σ、吊钩最大变形ξ作为输出因素。所对应的双重响应面方程如下：

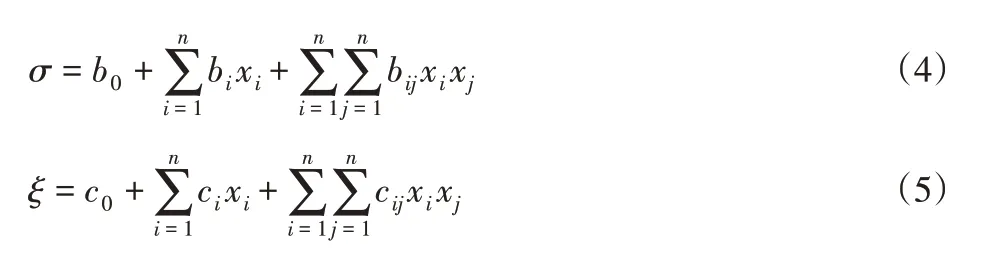
式中：x1—密度ρ；x2—重力加速度g；x3—吊物重量u。在双重响应面法的可靠性分析过程中，代入每一次抽样数据，得到两个输出响应值，与各自的失效条件进行比较，只要任意一个输出响应值达到失效条件，即判定吊钩失效一次，最终累计失效次数得到吊钩的可靠性。此方法对影响吊钩失效的最大应力和最大变形进行联动抽样，避免单独抽样时因样本不同可能导致的计算误差。

3 吊钩静力学条件下可靠性分析

3.1 吊钩静力学分析

以10吨级起重机吊钩为研究对象，其主要受力部位为与绳索接触以及吊钩顶部的螺纹装配位置。对于螺纹接触部位采用固定端约束，同时，在与绳索接触部位划分出接触面用于施加绳索压力。在有限元分析软件中，采用六面体单元划分网格，同时对接触部位以及应力较大部位进行网格细分处理，保证模型求解的质量。材料选用船用级船板D级钢，弹性模量210GPa，泊松比0.3，网格划分后共产生105486个单元和343410 个节点模型，如图1所示。通过带入一组抽样数据进行有限元分析，得到吊钩的最大应力和最大变形，如图2、图3所示。可见，最大应力在吊钩内侧拐弯处，最大变形在吊钩外侧钩尖处。

图1 吊钩有限元模型Fig.1 Grid of Hook

图2 最大应力云图Fig.2 Distribution of Stress

图3 最大变形云图Fig.3 Distribution of Deformation

3.2 吊钩可靠性分析流程

可靠性分析采用以下流程：LHS抽样得到样本的输入因素→有限元计算得到样本输出结果→最小二乘拟合得到双重响应面方程→采用蒙特卡洛进行1×104次联动抽样计算→对蒙特卡洛抽样结果进行可靠性分析。采用Solidworks建立吊钩的三维模型，并用Ansys workbench［10-11］进 行 有 限 元 分 析。采 用MATLAB 编 写 了LHS和蒙特卡洛抽样以及抽样数据结果可靠性分析的程序。

3.3 吊钩可靠性分析算例

选取材料密度ρ，重力加速度g，吊物重量u为三个随机输入变量，统计特征，如表1所示。

表1 输入变量概率分布Tab.1 Radom Input Variables

假设表中三个随机输入变量均服从正态分布。通过LHS抽样，得到30组初始输入样本数据，样本数据的空间分布，如图4所示。

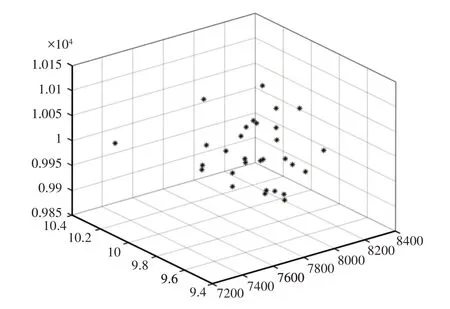
图4 三随机输入要素LHS抽样分布Fig.4 LHS for 3 Input Variables

经过将输入样本数据代入Ansys 计算，并经过最小二乘拟合，得到以下双重响应面方程（应力σ和应变ξ方程，分别为式（6）和式（7），拟合结果与本静力学问题的线性特征一致，x1，x2，x3分别表示密度（kg/m3）、重力加速度（m/s2）和起吊质量（kg）:

随后用响应面函数代替有限元模型，用蒙特卡洛抽样方法对变形与应力的响应面模型进行1×104次联动抽样，并且对其进行可靠性分析，得到叶片变形与应力的输出响应正态分布直方图，如图5所示。应力与变形的蒙特卡洛抽样历史仿真图，如图6所示。

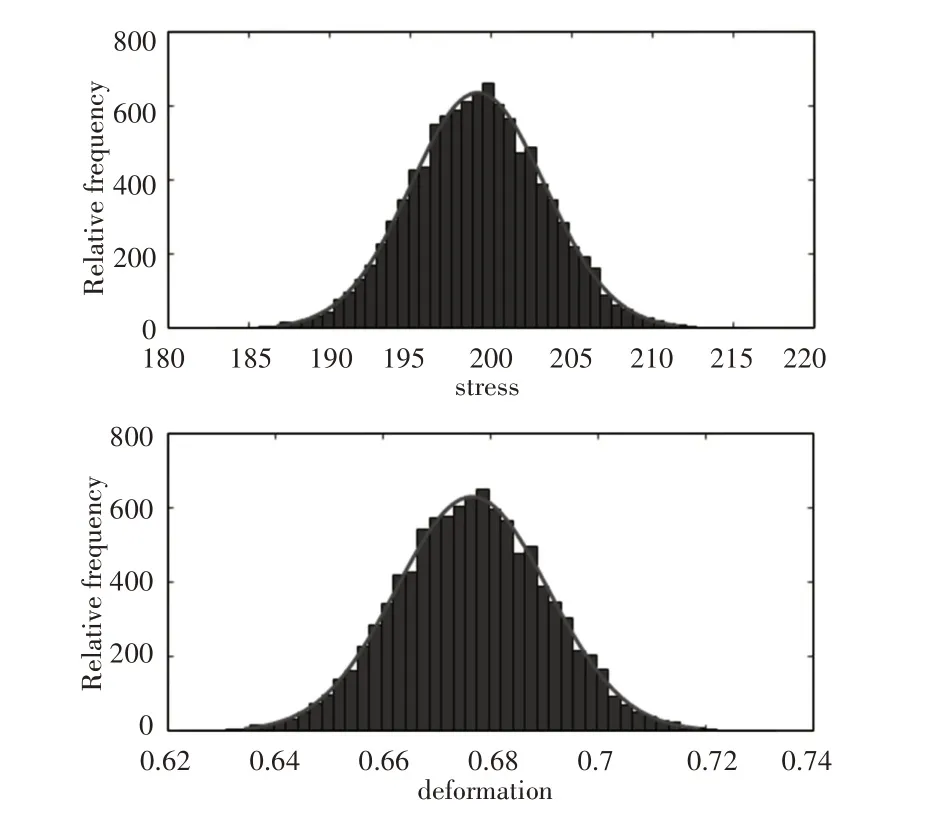
图5 应力和变形正态分布直方图Fig.5 Frequency Distribution of Stress and Deformation

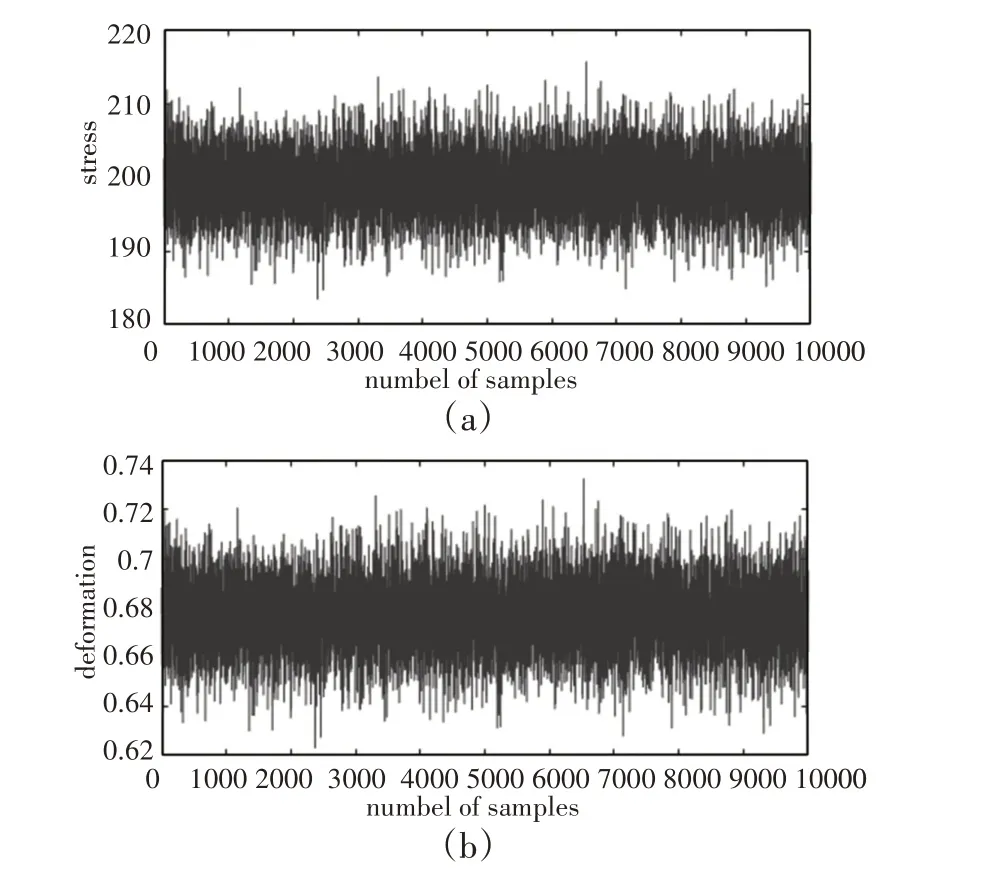
图6 蒙特卡洛抽样应力和变形结果仿真图Fig.6 Simulation Samples of Stress and Deformation

应力σ和变形ξ均值分别为199.1516MPa，0.67647mm；标准差分别为16.3822MPa，0.00018899mm。若吊钩的允许变形量ξ为1mm，许用应力σ为210MPa，总体失效数53，失效概率0.0053，可靠性概率为0.9947，蒙特卡洛抽样1×104次所用时间仅为0.329s。

为验证基于双重响应面法（DRSM）的应力应变联动抽样优越性，设置标准响应面法（RSM）对应力和应变分别抽样的计算方法进行对比分析，如表2所示。由表2可知DRSM联动抽样速度优越较显著。联动抽样的整体失效概率结果与分别抽样后再计算整体失效的概率结果对比，单一失效模式下（σ≥210MPa，ξ≥0.8mm），DRSM与RSM计算结果相近；当存在双重失效模式下（σ≥210MPa，ξ≥0.7mm），DRSM联动抽样下的整体失效概率更准确[8]。

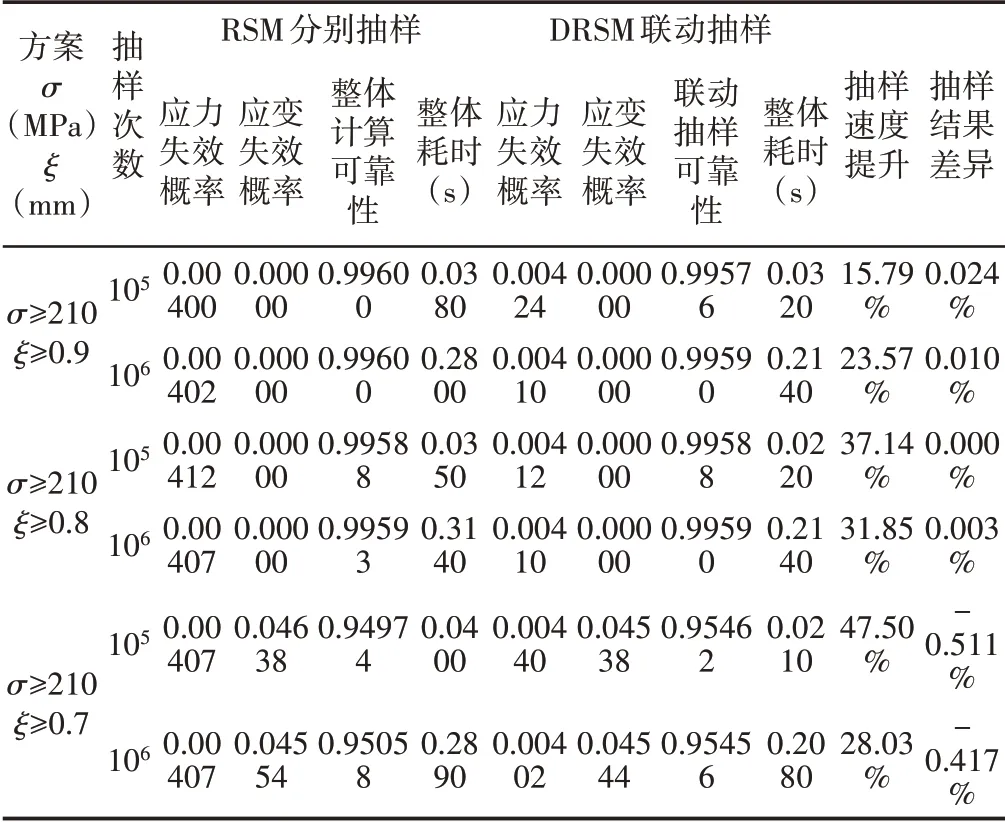
表2 DRSM蒙特卡洛联动抽样和RSM蒙特卡洛分别抽样复合计算结果对比（未含直方图/抽样仿真图时间）Tab.2 Reliability Analysis Results of Hook Based on Two Methods（the Timing for Drawing the Figure is Not Included）

4 结论

（1）针对单响面法在起重机吊钩可靠性分析的不足，采用结合拉丁超立方抽样技术的双重响应面可靠性分析方法，对吊钩进行可靠性分析，得出当吊钩许用应力为210MPa，许用变形为1mm时，吊钩的总可靠度为99.47%；（2）采用结合拉丁超立方抽样技术的响应面法，能在有限的样本容量条件下，快速得到响应面方程，之后再结合蒙特卡洛抽样，仅用0.326s（含直方图/抽样仿真出图时间）即完成1×104次抽样计算和结果分析；因此，响应面法能极大提升计算速度；（3）通过双重响应面法实现对应力和变形的联动抽样，解决吊钩变形和应力的失效相关性问题。