伺服平台消隙齿轮刚柔耦合动力学特性的研究与分析
2022-06-28高志峰钟小兵
鲁 强,高志峰,钟小兵,戴 军
(西南技术物理研究所,四川 成都 610000)
1 引言
消隙齿轮系统广泛应用在精密机械传动[1]中,尤其在制导、光电成像等领域,能够很好地提高伺服平台转动的位置精度[2]。其原理为,消隙齿轮在拉簧拉力下,主齿轮与副齿轮错开一定角度,主齿轮和副齿轮分别与啮合的传动齿轮接触,这样无论齿轮系统正向或反向转动,都能保证消隙齿轮与传动齿轮接触良好,从而达到消除间隙的目的。在伺服平台中,消隙齿轮系统的输入端为力矩电机,输出端为电位计齿轮,转角由电位计测量读出。拉簧的刚度、拉伸长度、齿轮轴间安装偏差等参数都会对消隙效果产生很大影响,直接影响系统传动的精度和动力学特性。消隙齿轮系统的错位关系和接触关系,如图1所示。
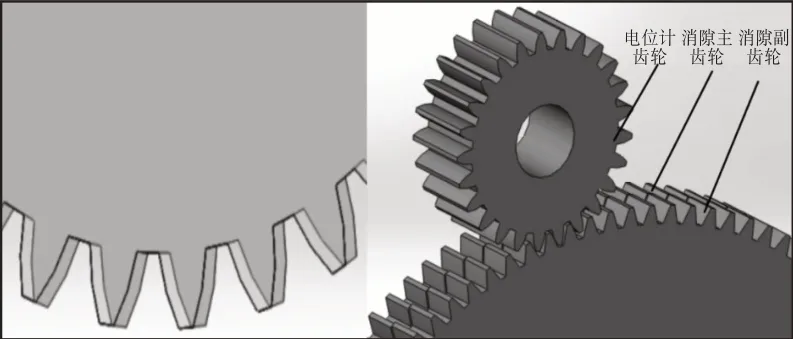
图1 消隙齿轮错位和接触关系Fig.1 Misalignment and Contact for Anti-Backlash Gears
目前,许多学者对消隙齿轮相关特性进行了分析和研究,文献[3]分析了消隙齿轮传动刚度对齿轮谐振频率的相关影响;文献[4]基于仿真软件ADAMS 研究了齿轮啮合力随转速变化的关系;文献[5]基于有限元法的齿轮啮合进行了仿真分析,研究了接触力与负载之间的相关关系;文献[6]对拉簧进行了优化设计,建立了多种弹簧的力学模型并推导出弹性力矩及相关参数的计算公式。
现有文献研究的消隙齿轮系统的负载较大,多用于角度和速度的传动环节,对动力学的相关特性研究不够深入和全面。研究的消隙齿轮系统其特点是负载轻、灵敏度高,用于速度的传动和角度的测量环节,要求齿轮系统传动精度高。这里先对消隙齿轮拉簧参数进行分析和研究,在合理设计拉簧相关参数的基础上,对消隙齿轮系统进行刚柔耦合的动力学研究,全面深入地研究了消隙齿轮系统的动力学特性。
2 消隙齿轮拉簧设计
消隙齿轮系统要达到理想的消隙效果,要保证装配过程中消隙齿轮与电位计齿轮啮合接触良好,齿轮间接触遵循经典赫兹理论[7],其接触应力呈半椭圆柱体分布且最大接触应力分布在接触面中心[8],设计时应保证其工作时的接触应力小于材料的许用应力;同时,要确保消隙齿轮拉簧提供的力矩大于系统工作的负载力矩,即需要满足如下公式:

根据拉簧在平台消隙齿轮中的结构尺寸及安装空间等要求,将参数带入式(1)有:

式中:N1、N2—消隙齿轮和电位计齿轮齿数;n—拉簧数量;k—拉簧刚度系数;x—拉簧拉伸长度;d—拉簧到回转中心的距离;θ—拉簧与水平方向的夹角。
传动比系数为4,拉簧数量为3,拉簧刚度系数为0.3N/mm,拉簧拉伸长度为5mm,拉簧到回转中心的距离为10mm,拉簧拉伸方向与到回转中心方向之间夹角为15°。
由于研究的伺服平台空间尺寸较小,负载较轻,必须选择合适的齿轮来满足设计要求,消隙齿轮和电位计齿轮的相关参数,如表1所示。

表1 消隙齿轮和电位计齿轮参数表Tab.1 Parameters of Anti-Backlash Gear and Potentiometer Gear
将拉簧和齿轮参数带入公式(2)有:

消隙齿轮系统转动过程中,电位计齿轮的负载力矩主要包括电位计回转摩擦力矩、轴承回转摩擦力矩、线扭转力矩等。
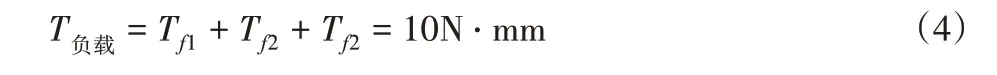
结合式(3)和式(4),拉簧参数满足式(1)的设计要求。消隙齿轮系统传动时,当拉簧产生的力矩小于电位计齿轮负载力矩时,拉簧受到压缩方向的力,导致齿轮之间的接触状态变差,从而影响齿轮系统的传动精度和动力学特性。
3 消隙齿轮刚柔耦合动力学模型
纯刚性体与刚性体仿真研究时,输出结果过于理想,不能反应真实的工况;刚性体和柔性体的耦合既可以得到与实际工况条件相符合的精度要求,又具有较高的仿真计算效率,因此采用刚柔耦合对伺服平台消隙齿轮系统进行多体动力学分析。
3.1 多体系统建模理论
对于求解多体系统,常见的数学建模方法为拉格朗日方法和笛卡尔方法[9]。拉格朗日方法是一种相对坐标方法,其动力学方程的形式为拉格朗日坐标阵的二阶微分方程组:

式中:q—位置坐标矩阵。
笛卡尔方法是一种绝对方法,系统动力学模型的一般形式为微分代数方程组,也称欧拉-拉格朗日方程组,其形式:

式中:q—位置坐标矩阵;Φ—位置坐标阵q的约束方程;Φq—约束方程的雅克比矩阵;λ—拉格朗日乘子;A、B—常数矩阵。
3.2 齿轮柔性体模型的建立
消隙齿轮与电位计齿轮传动过程中,其接触类型严格意义上是柔体与柔体的接触;文中将电位计齿轮看作柔性体,消隙齿轮视为刚性体,尽可能地保证齿轮系统接触类型的真实性,同时简化了计算模型,便于仿真计算。用UG三维建模软件建立消隙齿轮系统模型,然后将电位计齿轮导入ANSYS APDL中建立其刚性区域和约束点,生成mnf 柔性体文件。电位计齿轮柔性体模型,如图2所示。
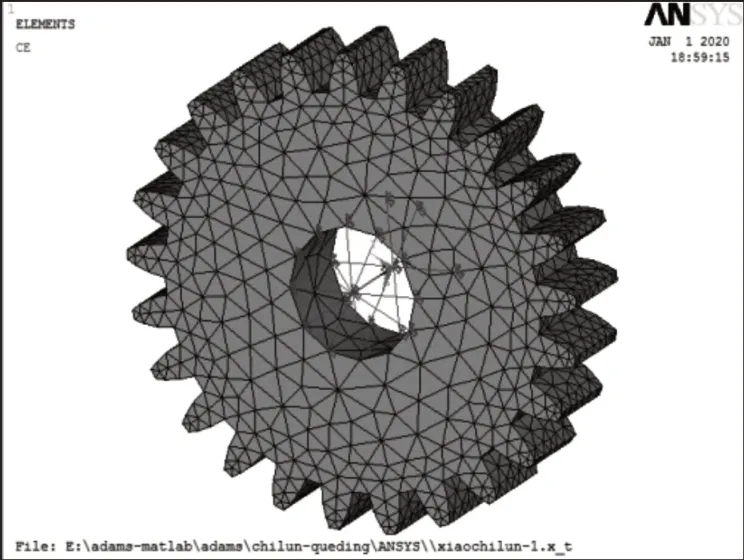
图2 电位计齿轮柔性体模型Fig.2 Flexible Body Model for Potentiometer Gear
将消隙齿轮系统模型导入ADAMS中,再将其电位计刚性齿轮替换成上述生成的柔性体文件,完成消隙齿轮刚柔耦合模型的建立。
3.3 刚柔耦合模型中接触力的设置
Adams接触力的计算方法有两种:一种是基于回归的接触算法,另一种是基于碰撞函数的接触算法。刚柔接触采用基于碰撞函数的接触算法,ADAMS/Solver 运用函数库中IMPACK 函数来计算接触力[10],碰撞函数的理论公式为:

式中:F—法向接触力;K—赫兹接触刚度;δ—接触点的法向穿透深度;e—力的指数,即刚度项的贡献因子;C—阻尼系数。
4 消隙齿轮动力学分析
理想情况下,消隙齿轮系统输出转速与输入转速的比值等于齿轮的传动比,但考虑齿轮柔性接触、负载扭矩、转动摩擦等因素,其输出转速以及其它动力学特性会受到很大影响。
4.1 输入转速对系统动力学特性的影响
在满足文中消隙齿轮拉簧参数的要求下,电位计齿轮负载力矩为10mN/m,齿轮轴间偏移为0mm时;研究消隙齿轮系统输入转速为0.5°/s、2°/s和5°/s三种情况下,系统电位计齿轮的输出特性。输出转速理想情况下分别为:2°/s、8°/s和20°/s,分别对应低速、中速、高速的工况。
4.1.1 系统输出转速与输入转速关系
消隙齿轮输入转速为0.5°/s、2°/s和5°/s三种情况下,如图3所示。电位计齿轮的输出与输入之间的关系,曲线采取(0~1)s内的10个数据点绘制而成。从图中可以看出,电位计齿轮输入转速0.5°/s时,输出曲线很平稳;输入转速2°/s时,输出曲线有较小波动;输入转速增大为5°/s时,输出曲线波动较大。
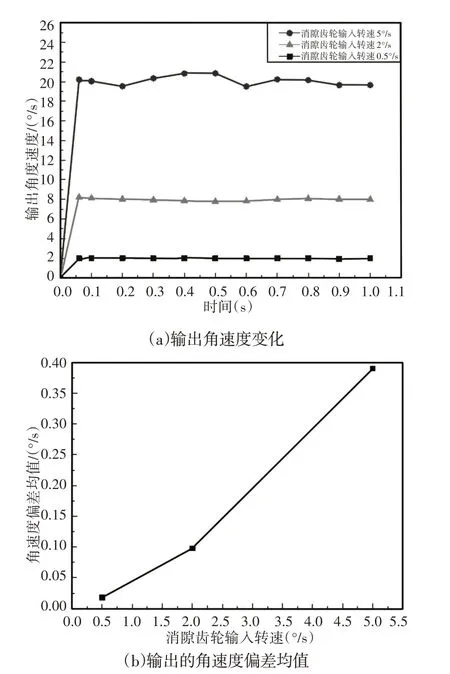
图3 不同输入转速下系统的输出转速Fig.3 System’s Angular Velocity at Different Input Speeds
从图3中可知,随着系统输入的角速度增加,输出角速度的偏差均值不断变大。当输入转速为0.5°/s,输出角速度偏差均值为0.02°/s;输入转速为2°/s,输出角速度偏差均值为0.1°/s;当输入转速为5°/s,输出角速度偏差均值增加到0.39°/s。随着输入转速的增加,消隙齿轮系统输出的角速度相对理论值的波动越厉害。
4.1.2 系统输出的角度偏差与输入转速关系
在上述三种不同输入转速工况下,得到电位计齿轮在1s内的输出转角,计算其转角的偏差均值变化,如图4所示。
从图4中可知,消隙齿轮系统输入转速为0.5°/s、2°/s和5°/s时,输出转角偏差分别为0.008°、0.037°和0.048°。由此可见,随着输入角速度的增加,输出的转角波动越大,其输出转角的偏差均值变大。
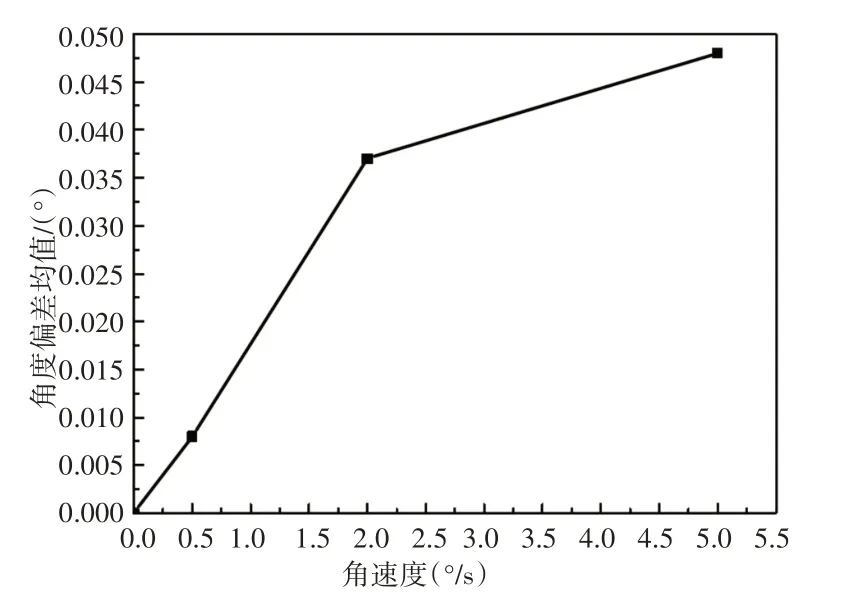
图4 不同输入角速度下输出角度偏差均值Fig.4 Mean Deviation of Output Angle at Different Input Angular Speed
4.1.3 齿轮接触力与输入转速关系
不同输入转速下,系统转动平稳后,消隙齿轮和电位计齿轮接触力变化情况,如图5所示。
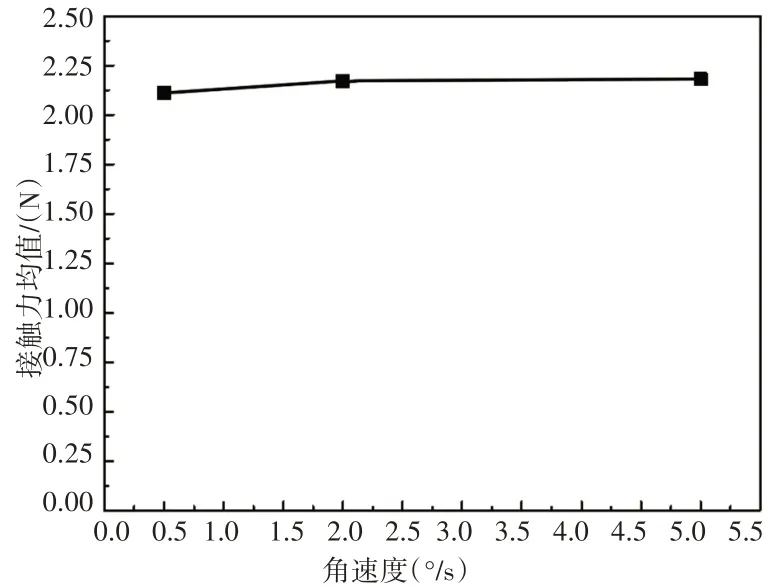
图5 不同输入转速下电位计齿轮接触力Fig.5 Potentiometer Gear’s Contact Force at Different Input Speeds
从图5中可以得知,接触应力变化与消隙齿轮输入转速关系不大,输入角速度增加,接触力略微有所增加。输入转速为较低转速0.5°/s时,其接触力均值为2.1N;输入转速为较高转速5°/s,其接触力均值为2.2N;可见转速对齿轮接触力的影响很小。
4.1.4 系统消隙时间与输入转速关系

图6 消隙时间与输入转速的关系Fig.6 Relationship Between Backlash Time and Input Speed
4.2 轴间偏移对系统动力学特性的影响
消隙齿轮与电位计齿轮轴间距的变化直接影响齿轮的啮合接触关系,系统输出的动力学特性也将会受到影响。
4.2.1 轴间偏移量对系统输出转速的影响
系统输入转速为2°/s,齿轮轴间偏移量为y=0mm 和y=0.1mm时,系统输出的角速度波动曲线,如图7所示。
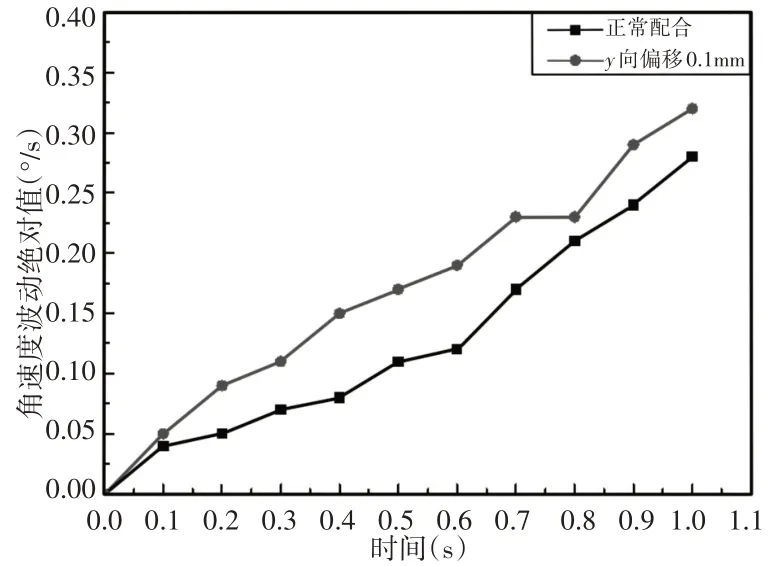
图7 轴间偏移量对输出角速度波动的影响Fig.7 Influence of the Offset Between Shafts on the Fluctuation of Output’s Angular Velocity
从图7中可以看出,轴向偏移量使输出的角速度波动明显增大。齿轮轴间偏移量为y=-0.05、y=0mm 与y=0.1mm 时,系统输出的角速度,如图7所示。根据齿轮的传动比关系,系统输入转速为2°/s时,输出的理论值值为8°/s,如图8所示。从图8可知,偏移量为y=-0.05时,输出角速度为7.9°/s;偏移量为y=0时,输出角速度为7.98°/s;偏移量为y=0.1时,输出角速度为8.26°/s。系统的输出转速随轴间偏移量的增大而变大。

图8 轴间偏移量对输出角速度的影响Fig.8 Influence of the Offset Between Shafts on the Output’s Angular Velocity
4.2.2 轴间偏移量对输出转角的影响
齿轮轴间偏移量会使得齿轮之间的接触状态、接触位置、接触时间等都会发生变化。输入转速为2°/s,时间0.4s内系统输出转角与轴间偏移量之间的关系,如图9所示。
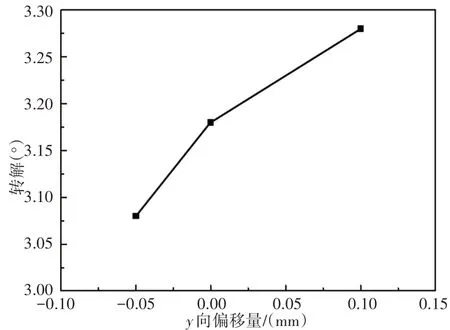
图9 轴间距偏移量与输出转角的关系Fig.9 Relationship Between Shaft Offset’s Distance and Output’s Angle
从图9中可知,移量为y=-0.05时,输出角度为3.08°/s;偏移量为y=0时,电位计输出角速度为3.18°;偏移量为y=0.1时,电位计输出角速度为3.28°。理想情况下0.4s内输出转角应该为3.2°,系统输出转角随轴间距的增加而增大。
4.2.3 轴间偏移量对系统消隙时间的影响
齿轮轴间距的改变,齿轮接触位置发生变化,对消隙时间也会产生很大影响。偏移量对消隙时间的影响,如图10所示。
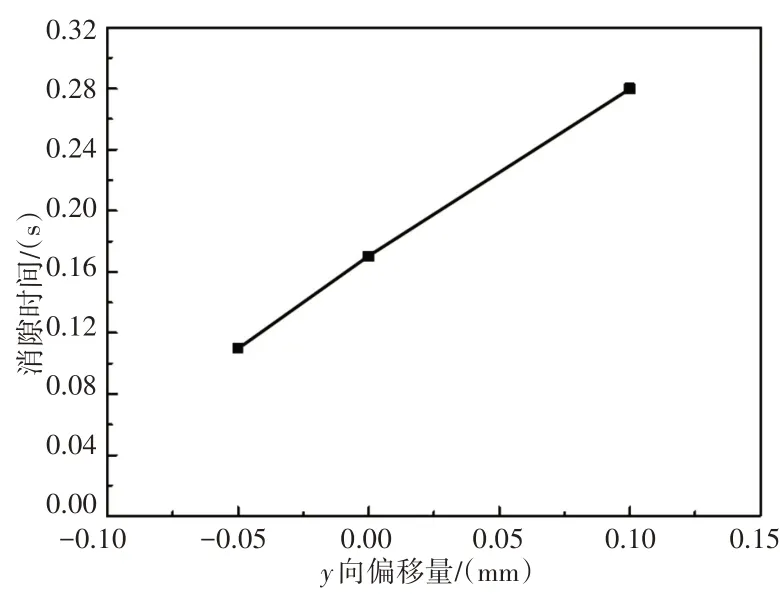
图10 轴间偏移量对消隙时间的影响Fig.10 Effect of Offset Between Shafts on Backlash Time
从图10 中可以看出,y=-0.05mm 时,消隙时间为0.11s;y=0mm时,消隙时间为0.17s;y=0.1mm时,消隙时间为0.28s。轴间距增大,齿形接触轮廓之间的距离增大,消隙时间随之增大。
4.2.4 轴间偏移量对齿轮谐振频率的影响
谐振频率反应齿轮系统的相关固有力学特性,对系统随机相应、震动冲击等特性有着重大影响。不同的轴间偏移量,齿轮系统的谐振频率也会有很大差异,偏移量对谐振频率的影响关系,如图11所示。从图11中可以看出,齿轮轴间距变小,系统的谐振频率增大;齿轮轴间距增大,系统谐振频率减小。在相同的偏移量下,轴间距变小对系统的谐振频率影响比轴间距变大对系统的影响更大。轴间距正向偏移量从(0~0.1)mm时,其一阶谐振频率由495Hz 减小到185Hz;轴间距负向偏移由(0~-0.05)mm时,其一阶谐振频率增加到1376Hz。

图11 轴间偏移量对谐振频率的影响Fig.11 Influence of Shafts’Offset on Resonance Frequency
4.3 拉簧刚度对输出转速的影响
拉簧刚度对系统的刚性有很大影响,拉簧刚度系数减小时,拉簧提供的力矩小于负载力矩,齿轮系统输出特性变差。消隙齿轮拉簧刚度对系统输出转速的影响,如图12所示。在本伺服平台中的工作情况下,消隙齿轮拉簧提供的力矩大于负载力矩时,将此时拉簧的刚度设定为1k值,根据前面拉簧的设计,本系统中k=0.3N·mm。从图12中可以看出,当拉簧刚度从1k减小为0.025k时,角速度偏差均值由0.02°/s增加到0.1°/s。可见,拉簧刚度减小,消隙齿轮系统输出的转速偏差将明显增加。

图12 拉簧刚度对输出转速的影响Fig.12 Effect of Tension Spring’s Stiffness on Output’s Speed
5 实物试验与仿真实验对比
对消隙齿轮系统输出的角速度和角度精度进行了实物试验,并与仿真实验进行了比较。装配完整后的消隙齿轮实物,如图13所示。

图13 消隙齿轮装配体Fig.13 Assembly of Anti-Backlash Gear
其主要由主齿轮、副齿轮以及拉簧组成。在拉簧的作用下,主齿轮和副齿轮错开一定角度,与啮合齿轮接触配合。伺服平台物理样机以及消隙齿轮系统在伺服平台中的工作位置,伺服平台主要包括负载、消隙齿轮、电位计齿轮、电位计、平台框架等,如图14所示。消隙齿轮与负载连接形成回转轴系,电位计齿轮安装在平在框架上;负载在电机驱动下转动,经过消隙齿轮系统,将输出转角传给电位计进行角度测量。

图14 伺服平台消隙齿轮传动系统Fig.14 Transmission System of Servo Platform for Anti-Backlash Gears
5.1 不同输入转速下试验和仿真的输出比较
5.1.1 实物试验与仿真实验的输出转速比较
在消隙齿轮拉簧刚度系数k=0.3N·mm,中心距偏移量y=0时,对消隙齿轮系统输入转速分别为0.5°/s、2°/s和3.75°/s三种工况下,得到1s内实物试验和仿真实验的输出转速曲线,分别计算两者的输出转速偏差均值,如图15所示。

图15 实物试验和仿真实验的输出转速偏差均值比较Fig.15 Comparison of Mean Value of Output Speed’s Deviation Between Physical and Simulation Test
从图15中可以看出,实物试验与仿真实验输出的角速度偏差均值差别不大,两者很接近。输入转速从0.5°/s增加到3.75°/s时,仿真试验的输出转速偏差均值由0.02°/s变到0.22°/s,而实物试验的输出转速均值偏差由0.06°/s变到0.19°/s。仿真实验与实物试验的结果差别很小。
5.1.2 实物试验与仿真实验的输出角度比较
在上述三种输入转速下,仿真实验与实物试验的输出转角比较,如图16 所示。从图16 中可知,输入转速从0.5°/s 增加到3.75°/s时,实物试验的输出转角由5.1°变到21.1°,而仿真实验的输出转角由4.88°变到19.9°。

图16 实物试验与仿真实验的输出转角比较Fig.16 Comparison of Output Angle Between Physical and Simulation Test
5.2 不同拉簧刚度下试验和仿真的输出转速
在物理样机中,齿轮系统中心距偏移量y=0mm,输入转速为2°/s时,通过改变拉簧的刚度系数,研究拉簧刚度系数对输出转速的影响,不同拉簧刚度系数下试验和仿真的输出转速,如图17 所示。消隙齿轮拉簧刚度从1k 减小为0.025k 时,角速度偏差均值由0.02°/s 增加到0.1°/s;实物试验角速度偏差均值由0.01°/s增加到0.22°/s。

图17 不同拉簧刚度系数下试验和仿真的输出转速Fig.17 Output Speed for Different Stiffness Coefficient of Tension Spring
5.3 不同轴间偏移量下试验和仿真的输出转速
在物理样机中,输入转速为2°/s 时,拉簧刚度系数k =0.3N/mm,改变消隙齿轮与电位计齿轮中心距偏移量,研究其对输出转速的影响,不同轴向偏移量下试验和仿真的输出转速,如图18所示。偏移量为y=-0.05增加到y=0.1时,仿真输出角速度为由7.9°/s增加到8.26°/s;实物试验由7.88°/s增加到8.15°/s。

图18 不同轴向偏移量下试验和仿真的输出转速Fig.18 Output Speed of Test and Simulation Under Different Axial Offset
6 结论
这里在合理设计拉簧参数的基础上,对伺服平台消隙齿轮系统进行刚柔耦合的动力学研究。研究了不同输入转速、拉簧刚度系数以及齿轮轴间偏移量等参数,对齿轮系统动力学特性的相关影响。在仿真中,将电位计齿轮进行柔性体处理,且充分考虑拉簧拉力以及相关负载力矩等因素,进行刚柔耦合下的动力学分析,仿真结果与试验结果误差很小。由于该仿真设置充分考虑了齿轮的变形、拉簧拉力、负载力矩等诸多真实的因素,因此该仿真能很好地反应伺服平台中消隙齿轮物理样机的动力学特性。相关结论如下:(1)消隙齿轮系统输出的转速和转角偏差均值随输入转速的增加而增大,消隙时间随之则快速减小,输入转速对接触力的影响不大。(2)轴间偏移量使输出的角速度波动明显增大,消隙时间随轴间偏移量的增加而增大,谐振频率则随之而减小。(3)系统输出转速偏差随拉簧刚度的减小而明显增大。(4)伺服平台实物和仿真实验的输出结果差别很小,验证了动力学仿真实验参数设计的合理性和准确性,对消隙齿轮以及伺服平台系统动力学的研究和优化有较大的帮助和指导。
