SOA优化PID控制在磁流变悬置系统中的应用

潘道远，程自力，肖 平，高清振，2

（1.安徽工程大学机械工程学院，安徽 芜湖 241000；2.汽车新技术安徽省工程技术研究中心，安徽 芜湖 241000）

1 引言

磁流变悬置具有阻尼力连续可调的特性，能够显著地改善车辆NVH性能。适合的控制策略能极大地提升磁流变悬置系统的隔振性能[1]。

目前，研究者针对磁流变悬置系统设计了多种控制策略，并取得良好的隔振效果。针对带有多个惯性通道的磁流变悬置，文献[2]建立了二自由度仿真模型，并采用PID控制研究磁流变悬置系统的隔振效果。文献[3]引入模糊控制理论，设计了模糊控制规则用于发动机磁流变悬置系统。为了进一步提高磁流变悬置系统的宽频隔振效果，文献[4]设计了一种变论域模糊控制器。针对磁流变悬置系统采用单一控制策略控制效果有限的问题，部分学者提出了一些复合控制策略。在模糊控制和PID控制的基础上，引入切换控制策略，文献[5]提出了一种Fuzzy-PID切换控制方法。将模糊控制与神经网络相结合，文献[6]设计了神经模糊控制器，并采用粒子群算法对控制参数进行了优化，结果表明神经模糊控制比模糊控制效果更好。

复合控制策略虽取得了良好的控制性能，但计算复杂，不利于工程应用。PID控制具有算法简单、鲁棒性好、可靠性高等优点[7-8]，仍是磁流变悬置系统广泛采用的控制方法。PID控制的效果主要取决于参数的整定，基于人群搜索优化算法实现磁流变悬置系统的PID控制参数优化，以实现精度高、稳定性好的磁流变悬置控制，为提高磁流变悬置系统的隔振性能提供应用基础。

2 磁流变悬置设计

2.1 磁流变悬置结构

根据磁流变液的流变特性以及普通液压悬置的结构，设计一种新型磁流变悬置，如图1所示。

图1 磁流变悬置结构图Fig.1 Structure Diagram of MR Mount

上连接杆（17）与动力总成刚性连接，并随动力总成振动而上下振动。隔磁盘（4）与橡胶主簧（1）下表面构成上液室（3），与橡胶底膜（9）构成下液室（12）。挤压盘（16）与铁芯（7）上表面形成的间隙为挤压通道，浮动活塞（13）与铁芯隔磁板（8）直表面形成的间隙为流动通道。上连接杆（17）受到力的作用而产生上下振动时，磁流变液经阻尼通道在上下液室之间流动。下液室（12）中的橡胶底膜（9）利用自身弹性形变的能力承担由橡胶主簧（1）变形产生的上下液室体积变化。当动力总成处于低频振动时，磁流变液经过挤压通道和流动通道在上下液室流动。励磁线圈（14）输入电流控制磁场大小，磁流变液流经挤压通道径向切割磁感线产生可控阻尼力使磁流变悬置产生不同的动刚度。当动力总成处于高频振动时，磁流变液通过解耦模（5）通道在上下液室流动，此时磁流变悬置相当于普通液压悬置。

2.2 磁流变悬置的磁路设计

考虑所设计的磁路结构为对称形式，因此选取1/2模型进行分析[9-10]。设计的磁路结构，如图2所示。

图2 磁路结构示意图Fig.2 Structure Diagram of Magnetic Circuit

各区域磁阻为：

式中：m0—空气磁导率；m1、m2、m3、m4、m5、m6—R1、R2、R3、R4、R5、R6区域的相对磁导率。忽略漏磁影响，磁极板间隙的外环区域和内环区域的磁感应强度分别为：

式中：S2—磁极板间隙外环的磁力线穿过磁流变液的有效面积；

S6—磁极板间隙内环的磁力线穿过磁流变液的有效面积；

N—励磁线圈的匝数；I—励磁线圈的电流。为了简化计算过程，将磁极板间隙外环磁感应强度和内环磁感应强度在大小上保持一致。因此若要则必须使S2=S6。由于磁力线与上极板垂直，则有：

综合考虑磁路横截面积、零件装配等多种因素，确定磁路结构尺寸参数为：r0=5mm，r1=12 mm，r2=18mm，r3=23mm，L1=5 mm，L2=20 mm，L3=4 mm，f=3mm，h0=2 mm。

2.3 磁路有限元分析

采用Ansoft Maxwell 软件对磁流变悬置磁路进行分析。当励磁线圈匝数为120匝，通电电流I=3A时，磁路结构中磁力线和磁感应强度分布，如图3、图4所示。

图4 磁感应强度云图Fig.4 Magnetic Induction Intensity Cloud Map

由图3可知，磁力线在挤压通道处较均匀穿过，并与磁流变液流动方向垂直，同时磁力线在流动通道处几乎没有穿过，因此所设计的磁路结构满足设计要求。当输入电流为3A时磁极板间隙中的磁感应强度，如图5所示。

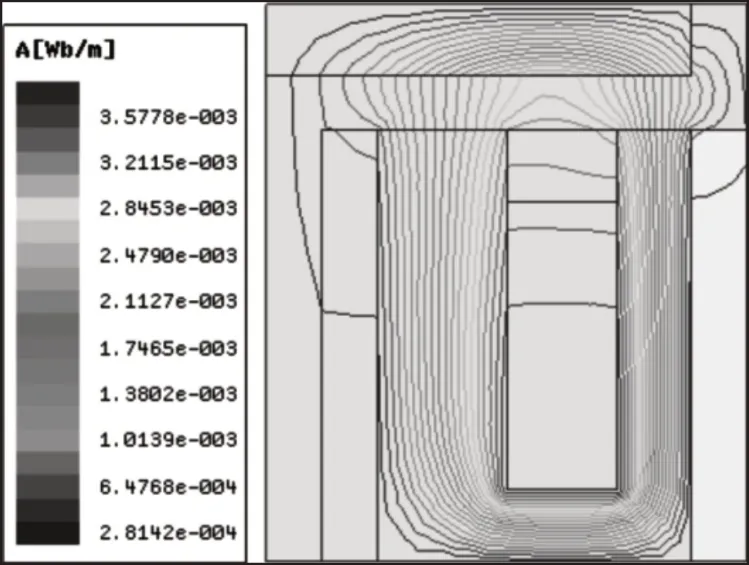
图3 磁力线分布图Fig.3 Distribution of Magnetic Field Lines

图5 极板间隙的磁感应强度Fig.5 Magnetic Induction Intensity at Plate Gap

考虑到在设计磁路结构时，根据式（10）确定磁路的结构参数r0、r1、r2、r3，因此可用磁极板间隙外环中的磁感应强度表示磁极板间隙中的平均磁感应强度。输入电流分别为0.5A、1A、1.5A、2 A、2.5A、3A时，磁极板间的磁感应强度，如图6所示。由图6可知，磁感应强度与励磁线圈中的输入电流呈现抛物线关系，根据计算数据可以拟合成二阶曲线。

图6 磁感应强度与外界输入电流的关系Fig.6 Relationship Between Magnetic Induction Intensity and Input Current

3 磁流变悬置系统建模

3.1 磁流变悬置力学模型

根据图1的磁流变悬置结构，建立其力学模型，如图7所示。

图7 磁流变悬置力学模型Fig.7 Mechanical Model of MR Mount

由图1可知，挤压通道与流动通道相连接，因此可以将挤压通道和流动通道的液体惯性与液阻分别用If与Rf表示。Qf—流经挤压通道和流动通道的液体质量；Qd—流经解耦通道的液体质量。

磁极板间的液体粘性系数为：

磁极板间的库伦阻尼力为：

式中：A—系统矩阵；B、D—输入矩阵；C—输出矩阵；U—系统输入量。

3.2 磁流变悬置系统力学模型

磁流变悬置作为新型隔振元件，对由动力总成引起的振动具有良好的隔振效果。为建立磁流变悬置系统半车六自由度力学模型，如图8所示。

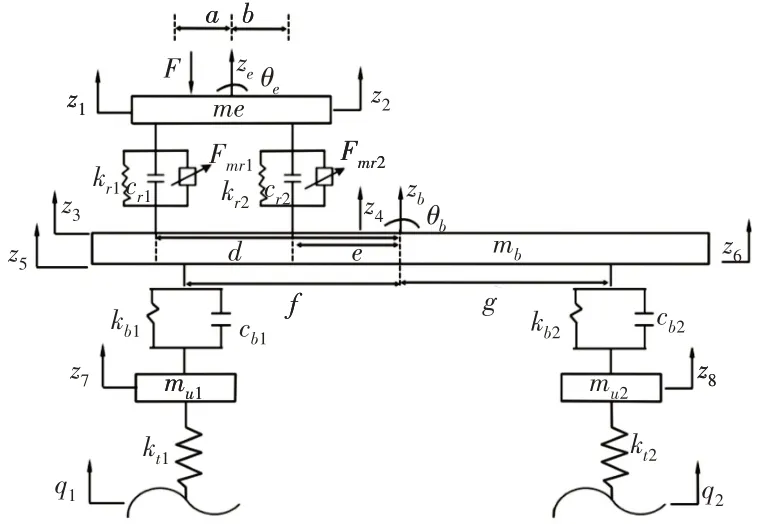
图8 磁流变悬置系统的力学模型Fig.8 Mechanical Model of MR Mounting System

根据图8所示的磁流变悬置系统力学模型，应用牛顿第二定律建立系统的动力学方程[11]。动力总成、车身垂向动力学方程分别为：

非簧载质量垂向动力学方程为：

动力总成、车身俯仰动力学方程为：

其中，z1=ze-aqe，z2=ze+bqe，z3=zb-dqb，z4=zb-eqb，z5=zbfqb，z6=zb+gqb。

4 基于SOA优化的PID控制系统设计

4.1 PID控制

PID控制不需要精确的数学模型，通常由控制器和控制对象组成。磁流变悬置系统PID控制图，如图9所示。

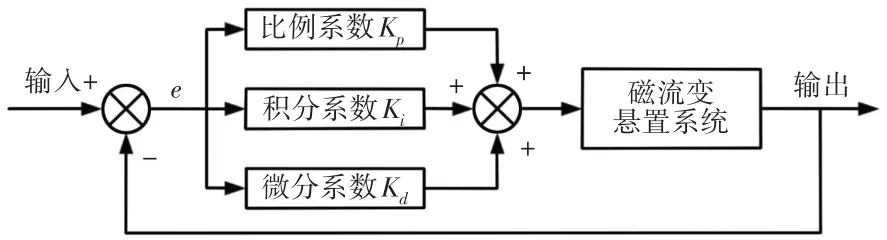
图9 磁流变悬置系统PID控制图Fig.9 PID Control Chart of MR Mounting System

将PID控制器中偏差的比例、积分和微分以线性组合的方式组合[12]，得到PID的控制规律为：

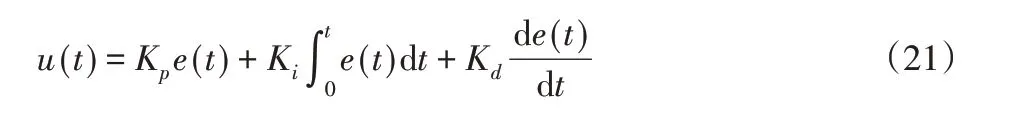
式中：e（t）—系统误差；u（t）—控制输出。

PID控制器的Kp、Ki和Kd对改善磁流变悬置系统的隔振性能具有重要作用。磁流变悬置系统采用传统方法整定PID控制参数难以起到良好的隔振性能，因此需要通过优化算法对PID控制参数进行整定来改善控制效果。

4.2 SOA优化PID控制

SOA算法属于一种新型的智能算法[13-14]，通过模拟人类在进行搜索行为时对位置和方向等的推理判断完成问题的最优求解。SOA算法具体描述为：假定在D维空间中有S个搜寻个体，则个体i的位置为Xi=[xi1xi2…xiD]T。PID 控制器的控制性能由参数Kp、Ki、Kd决定，故设定SOA算法的个体维度为3，从而实现对PID控制参数的优化整定。选取车身垂向加速度作为适应度指标，具体表达式为：

约束条件为：

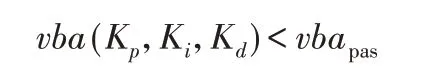
式中：vba（Kp，Ki，Kd）—车身加速度；vbapas—被动悬置工作下的车身加速度。

个体i在第j维空间的搜索步长为：

式中：dij—高斯隶属度函数；uij—个体i在第j维空间的隶属度。

个体i的搜索方向为：

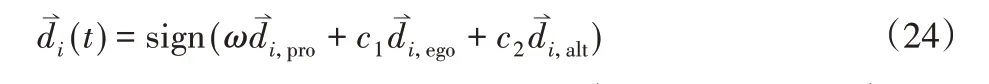
式中：sign（）—符号函数；w—惯性权值；d⇀i，pro—预动方向；d⇀i，ego—利己方向；d⇀i，alt—利他方向；c1、c2—区间［0 1］中的随机实数。

个体i在第j维空间的位置更新为：

式中：Δx（ijt+1）—位移量；dij—个体i在第j维空间的搜索方向；xij（t）、x（ijt+1）—个体i在第j维空间中t、t+1时刻的位置。

基于SOA优化PID控制参数的流程为：（1）计算在动力总成被动悬置下的车身垂向加速度vbapas值。（2）初始化给定种群中S个搜寻者的个体位置，随机矩阵会产生一个称为S×D的个体所在位置的矩阵。（3）在每次记录进行优化后，将每个搜寻者的最佳位置与其历史最佳位置的平均值相比较，如果此次的位置平均值优于其历史最佳的位置，则将此次的位置记录为历史最佳。（4）在每次位置优化后，将每个种群搜寻者的最佳位置与某个种群的一次历史最佳的某个位置比较平均值进行作一次位置比较，如果此次的最佳位置比较平均值远远优于某个搜寻者在该种群一次历史最佳的某个位置，那么将此次位于历史最佳的该位置的每个搜寻者位置记录为这个种群的一次历史最佳。（5）如果不能满足结束条件，返回（2）。根据上述算法原理设计基于SOA优化PID控制的磁流变悬置系统，如图10所示。

图10 基于SOA优化的PID控制图Fig.10 PID Control Chart Based on SOA Optimization

4.3 仿真结果分析

为验证现代车辆磁流变悬置系统采用基于SOA优化PID控制的先进性，与磁流变悬置系统采用PID控制、传统车辆采用被动悬置系统的性能指标进行对比分析。仿真模型参数为：动力总成质量me为156kg，车身质量mb为500kg，轮胎质量mu1和mu2为45kg，悬置刚度Kr1和Kr2为200 kN/m，悬架刚度Kb1为200kN/m、Kb2为210kN/m，轮胎刚度Kt1和Kt2为210kN/m，悬置阻尼cr1和cr2为520kN/m，悬架阻尼cb1和cb2为1200 kN/m，前后悬置距动力总成质心距离a为0.26m、b为0.22m，动力总成激振力距动力总成质心处距离c为0.13m，前后悬置距车身质心距离d为1.49m、e为1.11m，前后悬架距车身质心距离f为1.22m、g为1.5m，往复运动部件的质量m0为0.39kg，曲柄半径r为0.0385m，曲柄半径与曲柄连杆长度的比值l为0.316，曲柄连杆长度l为0.122m。选取车辆在怠速工况和行驶工况下的车身俯仰角加速度和垂向加速度作为评价指标，其中发动机在怠速工况和行驶工况下的转速分别为750r/min 和2500r/min。利用Matlab/Simulink 建立磁流变悬置系统仿真模型，如图11所示。

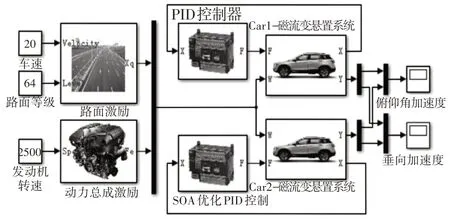
图11 磁流变悬置系统的仿真模型Fig.11 Simulation Model of MR Mounting System

现代车辆磁流变悬置系统分别采用PID 控制（图中PID 控制）和基于SOA优化PID控制（图中SOA优化PID控制），与传统车辆采用被动悬置系统（图中无控制）在怠速工况下的车身俯仰角加速度和车身垂向加速度，如图12、图13所示。为了进行量化比较分析，将怠速工况下车身俯仰角加速度和垂向加速度的峰值和均方根值，如表1所示。

图12 怠速工况下车身俯仰角加速度Fig.12 Body Pitch Angle Acceleration Under Idle Condition

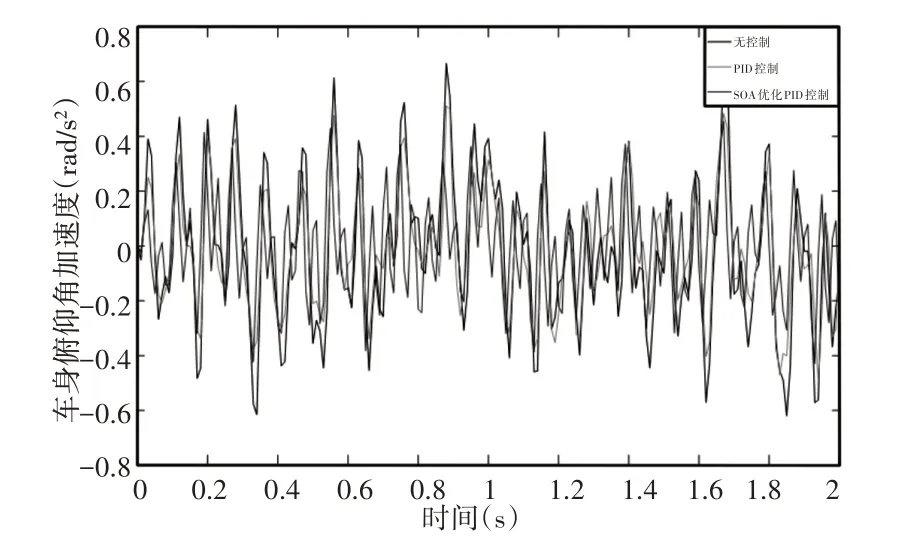
图13 怠速工况下车身垂向加速度Fig.13 Vertical Acceleration Under Idle Condition

表1 怠速工况下仿真数据Tab.1 Simulation Data Under Idle Condition

由图12、图13和表1可知，采用磁流变悬置系统的现代车辆与采用被动悬置系统的传统车辆相比，车身俯仰角加速度的峰值和均方根值分别由0.955rad/s2减小到0.591rad/s2和0.377rad/s2减小到0.291rad/s2，降低了38.12%和22.81%。车身垂向加速度的峰值和均方根值分别由0.768m/s2减小到0.545m/s2和0.277m/s2减小到0.203m/s2，降低了29.04%和26.71%。磁流变悬置系统采用PID 控制和采用基于SOA 优化PID 控制相比，车身俯仰角加速度的峰值和均方根值分别由0.591rad/s2减小到0.571rad/s2和0.291rad/s2减小到0.212rad/s2，降低了3.38%和27.15%。车身垂向加速度的峰值和均方根值分别由0.545m/s2减小到0.456m/s2和0.203m/s2减小到0.183m/s2，降低了16.33%和9.85%。在行驶工况下的车身俯仰角加速度和车身垂向加速度，如图14、图15所示。

车身俯仰角加速度和垂向加速度的峰值和均方根值，如2所示。由图14、图15和表2可知，采用磁流变悬置系统的现代车辆与采用被动悬置系统的传统车辆相比，车身俯仰角加速度的峰值和均方根值分别由5.784rad/s2减小到5.699rad/s2和3.186rad/s2减小到2.534rad/s2，降低了1.47%和20.46%。车身垂向加速度的峰值和均方根值分别由6.281m/s2减小到5.382m/s2和2.802m/s2减小到2.087m/s2，降低了14.31%和25.52%。磁流变悬置系统采用PID控制和采用基于SOA优化PID控制相比，车身俯仰角加速度的峰值和均方根值分别由5.699rad/s2减小到3.620rad/s2和2.534 rad/s2减小到1.329rad/s2，降低了36.48%和47.55%。车身垂向加速度的峰值和均方根值分别由5.382m/s2减小到3.685m/s2和2.087 m/s2减小到1.222 m/s2，降低了31.53%和41.45%。

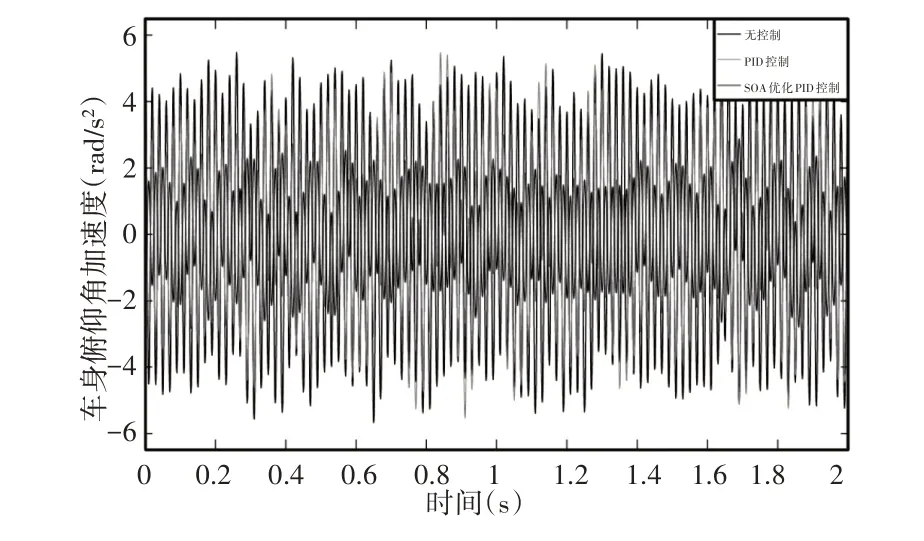
图14 行驶工况下车身俯仰角加速度Fig.14 Body Pitch Angle Acceleration Under Driving Condition

图15 行驶工况下车身垂向加速度Fig.15 Vertical Acceleration Under Driving Condition

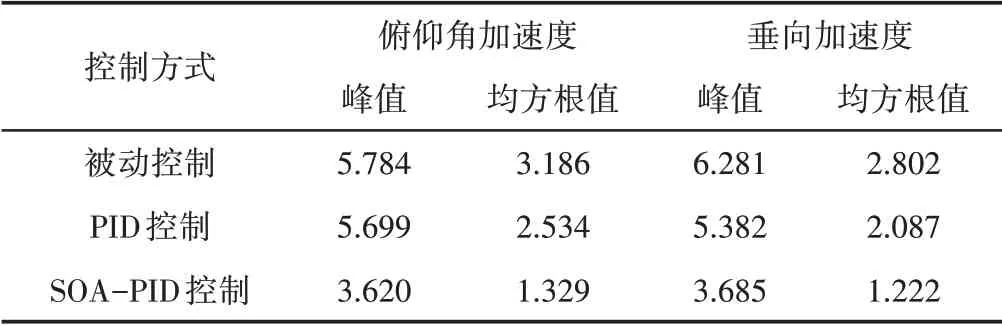
表2 行驶工况下仿真数据Tab.2 Simulation Data Under Driving Condition

5 结论

首先根据磁流变液的流变特性以及普通液压悬置的结构，设计了一种新型磁流变悬置，并采用Ansoft Maxwell软件对其磁路结构进行分析。然后根据磁流变悬置结构，建立了反映其动态特性的力学模型，并采用数据拟合方法得到磁感应强度与输入电流的关系，为磁流变悬置的工程应用提供了控制基础。最后建立了含磁流变悬置的半车六自由度力学模型，利用Matlab/Simulink搭建磁流变悬置系统采用基于SOA优化PID控制的仿真模型。

为验证SOA 优化PID 控制的实际效果，与磁流变悬置系统采用PID控制进行比较。怠速工况下的车身俯仰角加速度的峰值和均方根值降低了3.38%和27.15%，车身垂向加速度的峰值和均方根值降低了16.33%和9.85%；行驶工况下的车身俯仰角加速度的峰值和均方根值降低了36.48%和47.55%，车身垂向加速度的峰值和均方根值降低了31.53%和41.45%。仿真实验结果表明，磁流变悬置系统采用基于SOA优化PID控制具有良好的隔振效果，能够改善车辆平顺性。