圆锥破碎机破能的分析与腔型优化
2022-06-28潘伟桥马立峰吴凤彪姚振强
潘伟桥,马立峰,吴凤彪,姚振强
(太原科技大学机械工程学院,山西 太原 030024)
1 引言
圆锥破碎机是选矿厂的大型设备之一,在世界能源短缺的情况下,有人提出“多碎少磨”的要求,需要圆锥破碎机为磨机提供更为细粒级的原料,因此圆锥破碎机不断向高能化方向发展,通过对破碎机进行研究及市场调研,发现如今矿山上对于圆锥破碎机的使用类型已逐步转向多缸液压高能圆锥破碎机的使用[1]。圆锥破碎机的基本工作原理,如图1所示。由图可知圆锥破碎机的动锥、定锥形成了圆锥破碎机的几何腔型,从圆锥破碎腔中下落的破碎产品是破碎机锥体与岩石材料相互挤压作用的结果。与此同时,圆锥破碎机的性能也依赖于破碎腔的几何形状、破碎机的工作参数以及岩石材料的特性。它的优点是动锥摆动速度快,具有超高的作业率、较少的检修工作以及可互换组件、大偏心距等,由于其高摆速的特点,破碎腔沿高度方向衬板磨损不均匀,特别是平行区,导致腔型发生变化,严重影响生产率下降,产品质量恶化。因此需要对多缸液压高能圆锥破碎机进行腔型优化设计,提高破碎机生产率和产品质量[2]。
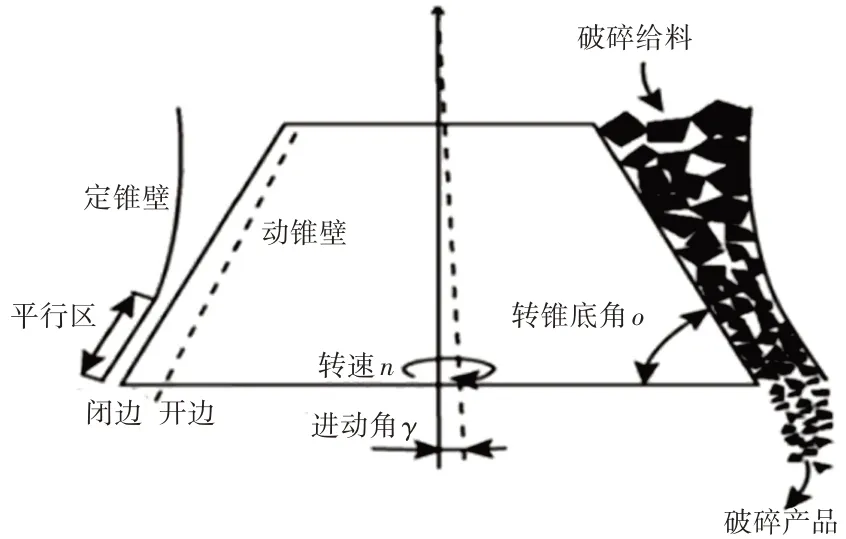
图1 圆锥破碎机工作原理Fig.1 Working Principle of Cone Crusher
2 圆锥破碎机细碎腔型的设计
2.1 动锥衬板曲线的设计
传统破碎机腔型设计未考虑衬板磨损的影响,但是衬板磨损对生产率等影响较大,所以根据衬板磨损曲线设计腔型是合理的。研究表明,衬板磨损曲线的函数式[3]:

式中:V—破碎物料体积;m、n—物料与衬板的硬度系数;y—物料平均直径,即动定锥工作间距。
如图2所示,在破碎物料体积dV的期间内,衬板表面(动锥)任意点A,由于磨损产生的位移AB=dh,求得位移度为:
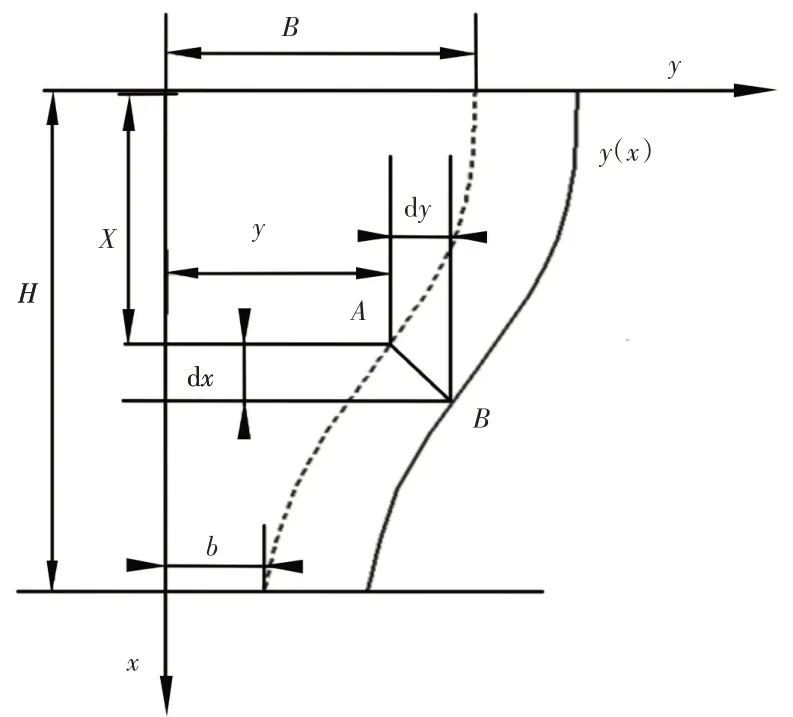
图2 动锥衬板曲线数学模型Fig.2 Mathematical Model of the Moving Cone Liner Curve

AB弧的微分式:
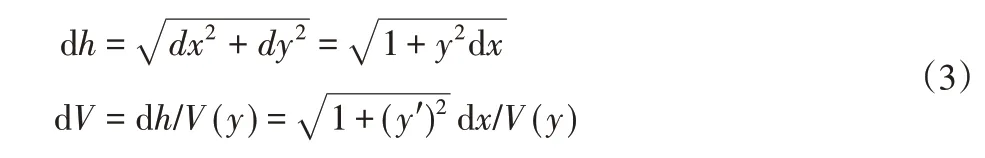
当衬板表面上点的位移最小时,则衬板磨损量最小。在这种情况下:
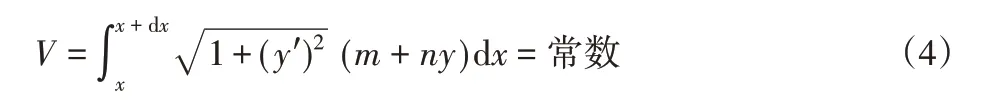
若要使得衬板位移量最小则有积分:
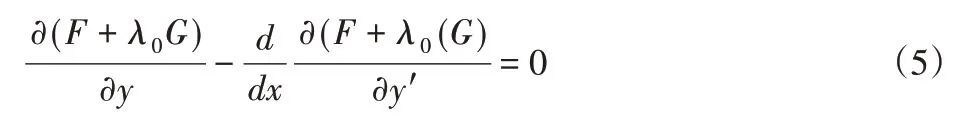
经过对欧拉方程的三角换元与微分运算可得到动定锥间距y与破碎腔高度x的方程:
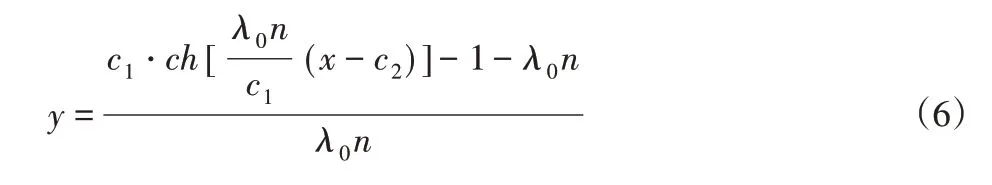
积分常数c1和c2根据进、排料口处的边界条件确定。动锥表面曲线在排矿口处切线平行于x轴,所以y′|x=H=sht= 0 即t=λ0n(H-c2)/c1= 0 求解得c2=H。当x=0 时y=B,x=H时y=b即有:

联立求解即可得c1和λ0。
2.2 定锥衬板曲线的设计
定锥腔型,如图3所示。
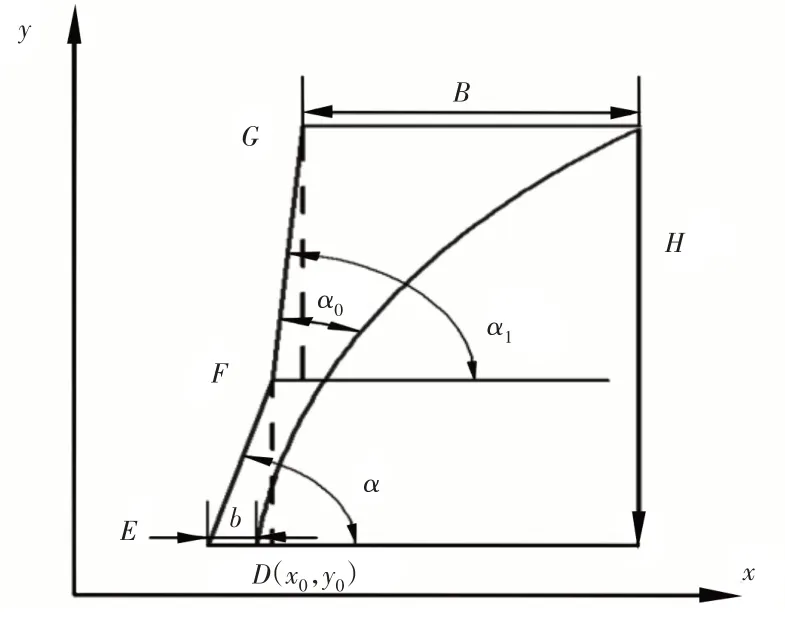
图3 定锥腔型数学模型Fig.3 Mathematical Model of Fixed Cone Cavity
E-F-G段表示定锥腔型,设动锥底角处D点坐标为(x0,y0),动锥底角为α,啮角为α0,已EF段为平行区,长度为l,排矿口距离b,可知E 点坐标(x0-b,y0),则F点坐标为(x0-b+lcosα,y0+lsinα),由两点式直线方程可确定EF段直线方程,所以有:

已知啮角和给料口尺寸B和破碎腔高度H可知G点坐标:所以FG段直线方程为:
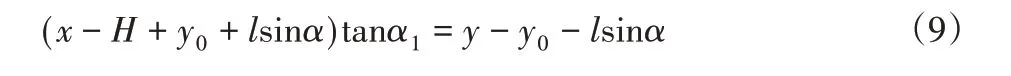
综上可以分别得到动锥与定锥的函数驱动方程:
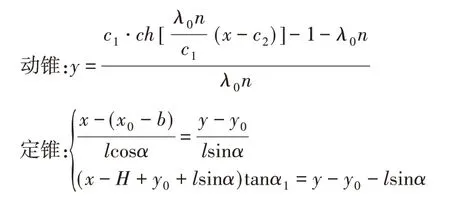
3 圆锥破碎机破碎性能分析与研究
圆锥破碎机破碎性能主要包括生产率和破碎产品质量两个重要因素,结合这两个重要的生产指标,建立以生产率和破碎产品质量为目标的的优化模型,探究不同技术结构参数对生产率和产品质量的影响规律,求解最优腔型和与之匹配的最佳技术结构参数,从而达到提高生产率和产品质量的目的[4]。
3.1 生产率理论模型的优化
生产率的理论计算试是设计破碎机腔型的基本方程式。生产率是指在一定的给料粒度和排料粒度的条件下,单位时间破碎机所处理的物料量,单位是t/h。求破碎机生产率[5],如图4所示。生产率的理论计算式是根据动锥摆动一次从破碎腔排出的物料体积求得。即:V=ΔbΔlDcπ
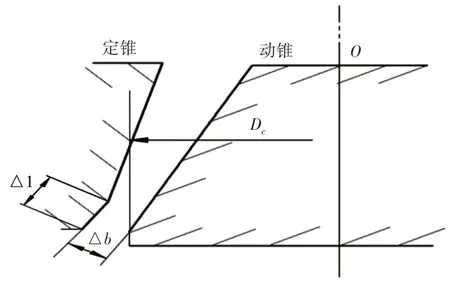
图4 求破碎机生产率Fig.4 Crusher Productivity
式中:Δb—物料被压缩时料层厚度(m);Δl—动锥摆动一次物料位移(m);Dc—物料压缩层平均直径(m);物料压缩层平均直径近似认为Dc≈D(动锥底部直径)。
影响生产率的因素还有很多,包括不同给料粒度、物料性质、腔型等。选取影响较大的两个因素:物料硬度粒度给料粒度,进行修正得到:

式中:ρ—物料堆密度;n—动锥每分钟摆动次数(r/min);μ—松散系数,μ≈0.55~0.7;KQ—物料硬度系数;Kt—给料粒度系数。
经过生产现场验证,通过此计算方法得到的生产率高于实际生产率,这是因为破碎机在实际工作中存在堵塞层,动锥靠近定锥时,物料会有上拱现象,并不能完全随排料口排出,因此需要计算出物料的上拱率。现对破碎机物料上拱率进行理论计算模型推导,如图5所示。当动锥体靠近定锥体时,物料容易发生上拱现象,即在A、D区域是物料的上拱区,对该区域进行积分运算,求得上拱区的物料质量[6-8]。
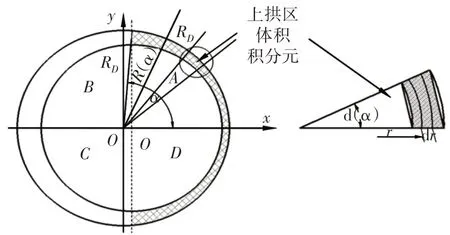
图5 物料上拱区数学模型Fig.5 Mathematical Model of the Arch Area on the Material
上拱区的积分式:
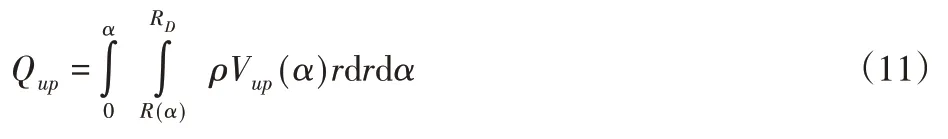
式中:α—上拱边界与坐标轴所围夹角;R(α)—定锥圆心到动锥边的距离;RD—定锥半径;Vup—上拱区物料的速度。
综上,破碎机生产率计算模型为:
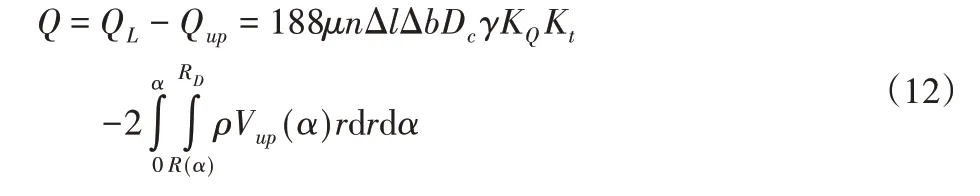
3.2 优化模型的建立
基于推导的生产率计算模型,可知影响参数有动锥转速n,平行区长度l,动锥底角α,综合以上影响参数,以某型号液压标准细碎破碎机为研究对象,建立以生产率和破碎产品质量为优化目标的计算优化模型,破碎产品质量以破碎产品中小于闭边排料口尺寸css(16mm)的破碎产品占总体破碎产品的百分数PCS(S%)表示[9-11]。如式(13)所示:
设计变量:
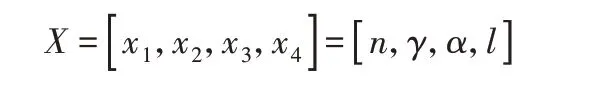
目标函数:
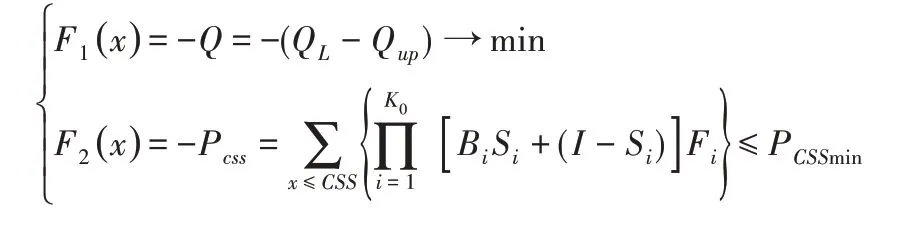
约束条件:

4 算例与仿真分析
4.1 算例分析
为验证优化设计的正确性以某型号液压圆锥破碎机标准细碎型为设计优化算例,建立如式(13)的优化计算模型,通过MATLAB中相关优化算法程序得到的优化计算结果,如表1所示。
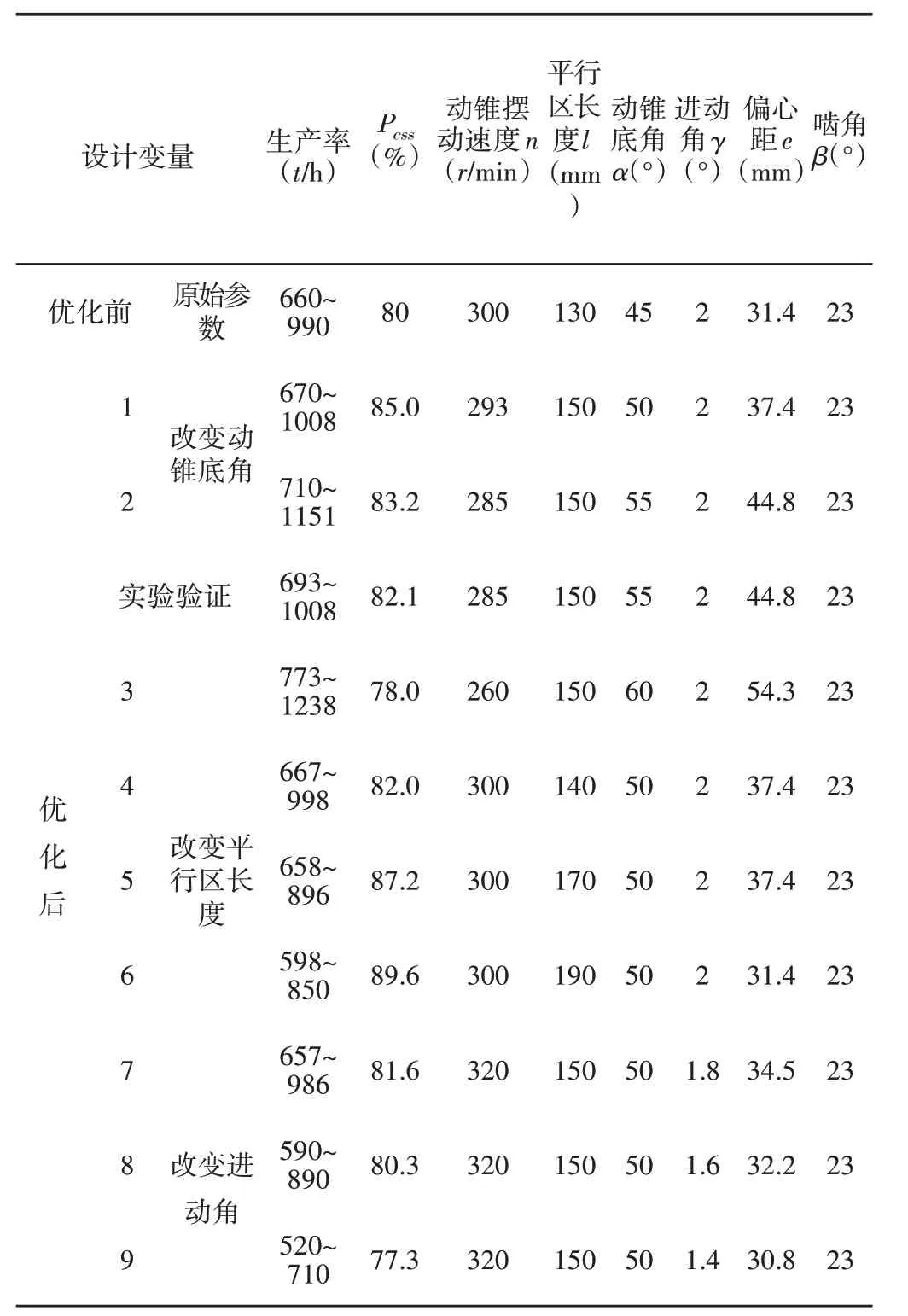
表1 优化计算结果Tab.1 Optimization Calculation Results
表1中第1组到第3组数据是改变动锥底角后的优化结果,第4组到第6组数据是改变平行区后的优化结果,第7组到第8组数据是改变进动角后的优化结果。分析表中数据可知当动锥底角由50°增加到60°时,破碎机产量由1008t/h 提高到1238t/h,提高了约23%,但是破碎产品质量下降,小于闭边排料口尺寸颗粒占破碎产品百分数由85%下降到78%,这是由于随着动锥底角的增大,破碎腔破碎层总数减少,散体物料受到更少次数的破碎作用。此外,随着动锥底角的增大,选矿设备的破碎腔各破碎层空行程增加,实际进动压缩量减小,因而相应选择函数和破碎函数减小,从而导致标定排料粒度减小。
保证动锥底角不变,改变平行区长度,平行区减少,生产率有所提高,平行区增大,生产率下降,但小于闭边排料口尺寸颗粒占破碎产品百分比提高约9.6%,这是因为随着平行区增大,物料破碎更为充分,但破碎时间增长导致生产率下降。改变进动角大小,影响的是偏心距和行程,进动角越小,偏心距和动锥行程越小,整机的动力性能改善,但是破碎机的生产率和产品破碎质量都下降,因此需要提高转速以满足生产和质量的要求。
根据给出的动锥方程式(6)和式(7),与该型号破碎机相关参数B=252mm、b=16mm、H=750mm,选取合适的物料与衬板的表面特征系数,求得λ0=0.0001,c1=1.03678[12]分别代入式(6)中得到圆锥破碎机的动锥腔型曲线方程:

结合表1 中优化后的结构参数,可绘制出相对应的破碎机腔型。
该型号圆锥破碎机的原始腔型,如图6(a)所示。动锥和定锥分别是由两段直线段组成。根据动锥和定锥的腔型曲线数学方程结合表1得到的优化后参数由MATLAB得到,如图6(b)~图6(d)所示。
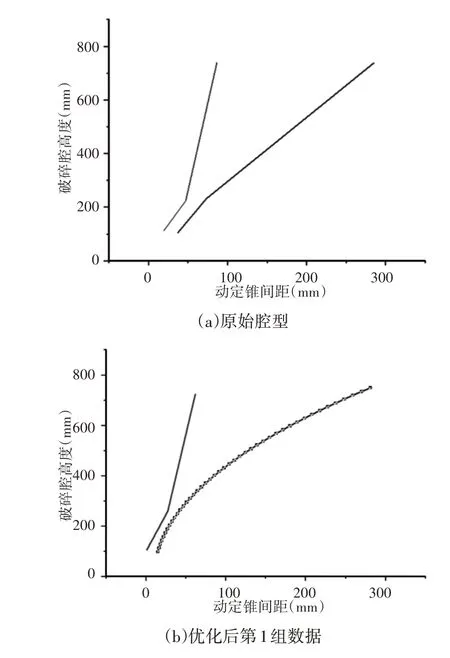
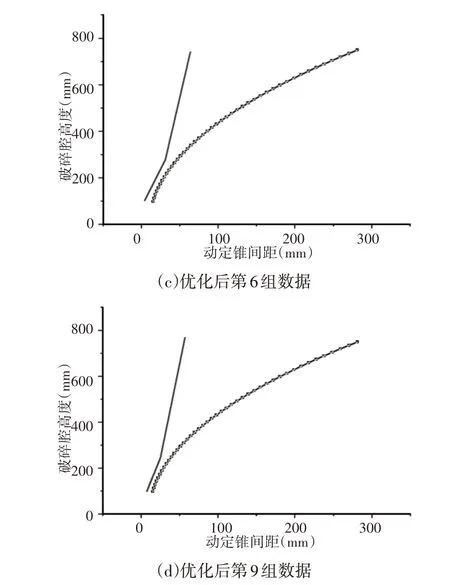
图6 破碎机腔型结构Fig.6 Cavity Structure of Crusher
由图可知,由曲线段代替了传统直线段,采用优化后第一组结构参数绘制,动锥底角角度是50°,较原腔型增加了5°,平行区长度由130mm增加到150mm,如图6(b)所示。采用的优化后第六组和第九组的结构参数绘制,如图6(c)、图6(d)所示。目的是为了探究不同结构对破碎性能的影响规律,为下一步三维建模与离散元仿真提供一定的理论基础。
4.2 仿真分析
根据优化后的破碎机腔型结构建立对应的三维模型,将其导入EDEM仿真软件进行破碎仿真分析,仿真破碎过程,如图7所示。根据物料粘结键总数N和断裂建数目M的比值即破碎百分比来表征物料的破碎效果,断裂建数目所占比例越大,表明破碎效果越好。通过此仿真过程来验证优化后结构参数对破碎效果影响规律的可靠性。
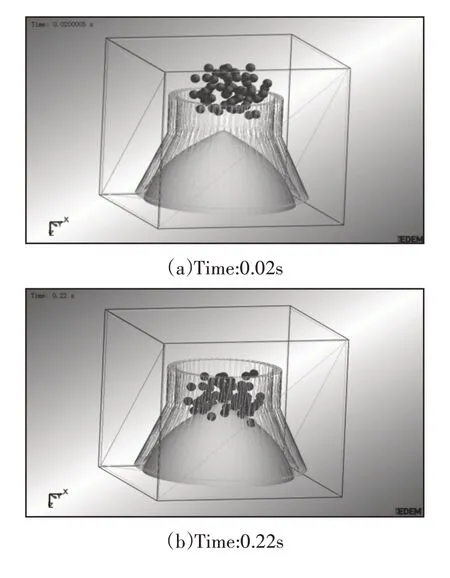

图7 不同时刻的破碎过程Fig.7 Fragmentation Process at Different Times
采取第二组优化数据物料粘结键和断裂建数目变化趋势[13-14],如图8所示。随着不同时刻的变化,物料不断发生破碎,在3s左右,破碎过程基本完成。
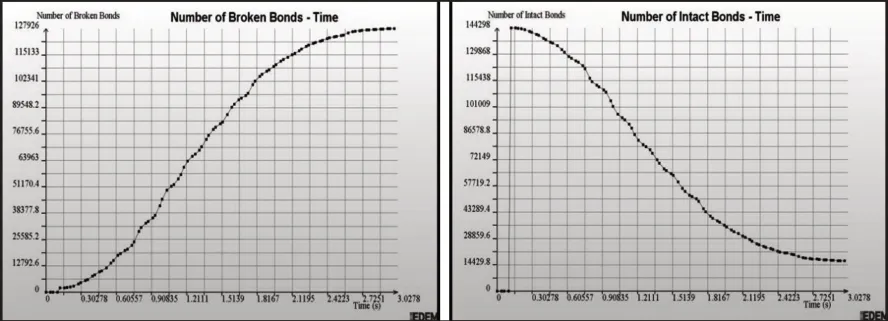
图8 物料粘结键和断裂键数目随时刻的变化Fig.8 Number of Broken Bonds and Intact Bonds-Time
物料断裂键数目N达到最大127926个,粘结键总数M破碎过程开始时刻共计生成144298个,随物料不断破碎,在物料破碎完成3s左右时刻减少到14429.8左右,即破碎百分比约为88.6%,其余各组的破碎百分比仿真结果,如表2所示。
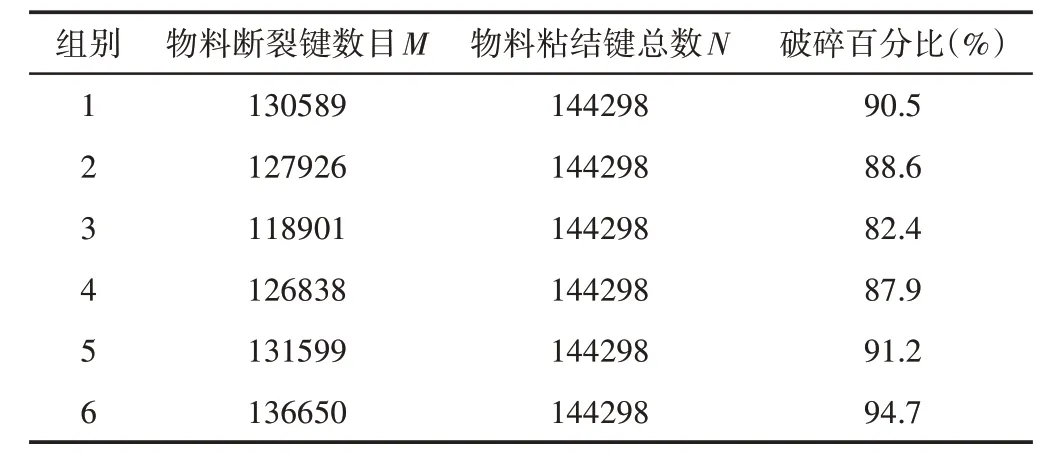
表2 破碎百分比仿真结果Tab.2 Breakage Percentage Simulation Results
根据表2,第一组到第三组是采用改变动锥底角后优化数据仿真结果。随着动锥底角的增大,破碎百分比由90.5%减少至82.6%,第四组到第五组是采用改变平行区长度后的优化数据仿真结果,随着平行区的增大,破碎百分比由87.9%增加至94.7%。通过对仿真结果的分析,进一步证明表1优化后的结构参数对破碎效果影响规律的可靠性。
5 实验验证与分析
根据客户生产要求与生产实际,现采取表1中第2组优化数据结合本文给出的腔型设计方法进行实验验证。优化后的动锥衬板实物,如图9所示。实验数据如表1表示,优化前破碎机生产率为990t/h,现场测得实际生产率最大约为1009t/h,理论优化值为1151t/h,优化后生产率提高了约2%。优化前小于闭边排料口尺寸16mm颗粒占破碎产品百分数为80%,优化后实际测得小于闭边排料口尺寸16mm颗粒占破碎产品百分数为82.1%,理论优化值是83.2%,优化后小于闭边排料口尺寸颗粒占破碎产品百分数提高了约2.1%。由于在实际生产条件下的给料速度,给料均匀性等无法达到理想状态,故实验数据均小于理论优化值。

图9 优化后动锥衬板Fig.9 Optimized Moving Cone Liner
通过分析优化前后实际破碎产品质量得到产品的粒度曲线,横坐标为粒度,纵坐标为粒级累计含量,曲线较陡部分的粒度,表示该粒度附近的粒级含量较多,对应于曲线较缓部分的粒度,表示在该粒度附近的粒级含量较少,如图10所示。由曲线可知,优化前小于闭边排料口尺寸16mm颗粒累计含量约为80%,粒度大于17mm或小于10mm的粒级含量较少,多集中于(10~17)mm间,优化后小于闭边排料口尺寸16mm颗粒累计含量约为82.1%,粒度大于15mm或小于5m的粒级含量较少,多集中于(5~15)mm之间,通过对比分析优化前后的产品粒度曲线,可知采用优化后腔型所得到的破碎产品质量较优化前有了一定程度的提高,证明了该优化设计方法的可靠性。
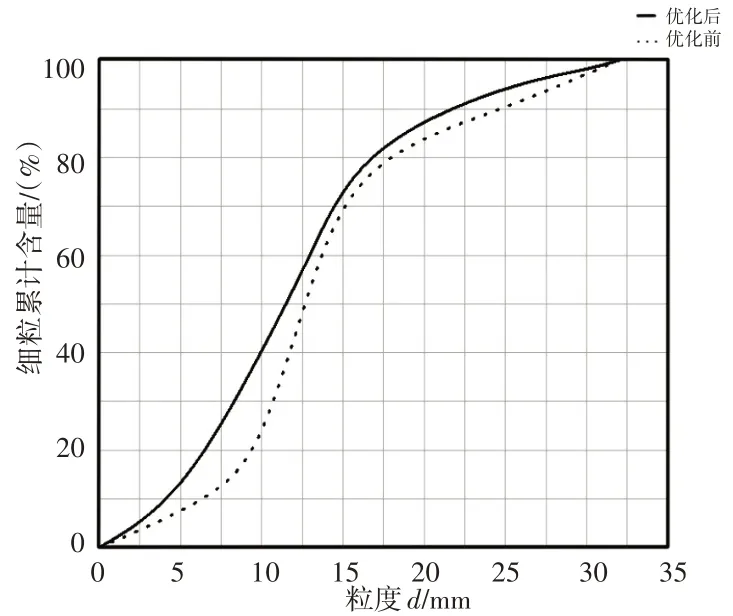
图10 产品粒度曲线Fig.10 Roduct Particle Size Curve
6 结论
(1)基于衬板耐磨曲线函数总结归纳了破碎机耐磨腔型动定锥的理论设计方法。并根据现阶段破碎机生产率的理论计算模型,考虑上拱量,推导出一种新的生产率的计算方法。
(2)建立了以生产率和破碎粒度为目标的优化模型,得到了优化后的破碎机工作参数对破碎机生产率性能的影响规律,并以EDEM仿真验证了该影响规律的可靠性,为破碎机腔型与设计参数的优化提供了依据。
(3)将该设计方法应用于实际生产中,通过实际分析得到了产品粒度曲线,破碎机性能得到了提升,为破碎机腔型优化与设计提供了一种新思路。
