立足基本图形 “圆”来如此清晰

2022-06-27江苏省南京市金陵中学仙林分校中学部丁婷婷邮编210000

中学数学教学 2022年3期

江苏省南京市金陵中学仙林分校中学部丁婷婷程冲（邮编：210000）

笔者所执教的学生在区九年级第一学期期末考试中填空最后一题遇到一道关于求圆中线段长度的问题，批改后此题学生平均得分为0.15分，因此对此题进行了深入研究，发现如果能准确识别和构造适当的基本图形，不但问题可以迎刃而解，甚至还可以一题多解. 接下来，将从3 个角度来谈谈此题的几种解法.

1 原题呈现

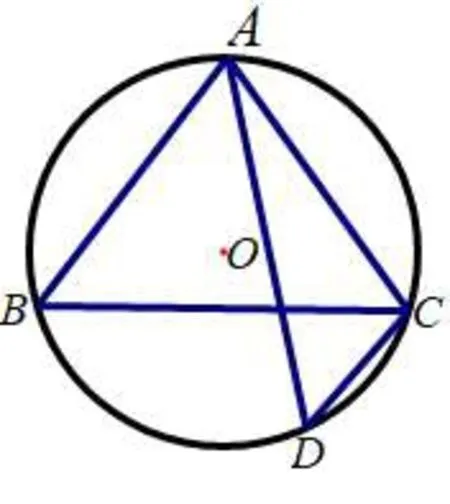
图1

2 解法研究

2.1 灵活运用模型

解法1 如图2，AD、BC相交于点F，设BF=2x，则CF=12-2x，易证△ABF∽△CDF.

图2

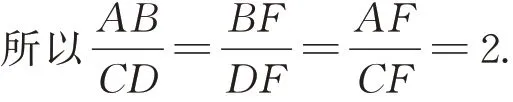
所以DF=x,AF=2(12-2x)，AD=AF+DF=24－3x.

因为∠DAC=∠FAC，∠ACF=∠ADC,

所以AD=3+2 21.

此解法不需要添加任何的辅助线，从一组相似比为2 的斜X 型相似三角形入手，表示图中线段的长，再由一组母子型相似列式求解，计算量虽然偏大，但只要学生对相似的几种常见模型A型、斜A 型、X 型、斜X 型、母子型熟悉，就很容易想到，很贴近学生思维的最近发展区.

解法2如图3，过点A作AE⊥BC，垂足为E，设EF=2x，则CF=6-2x，BF=6+2x.

图3

同解法1，可得△ABF与△CDF的相似比为2,所以AF=2CF=12-4x, DF=0.5BF=3+x，AD=15-3x.在Rt△AEF中，由勾股定理得，AE2+EF2=AF2. 即82+（2x）2=(12－4x)2，解得所以

此题中的已知条件中含有一个三边已知的等腰三角形，故而联想到作常规辅助线，底边的高线，由等腰三角形“三线合一”的性质易得出BF、CF、EF三者的关系，在Rt△AEF中利用勾股定理求解，优化了解法1 中使用的第二组母子型相似，减小了部分计算量.

2.2 巧构相似三角形

（1）构造直角相似

解法3如图4，过点A作AE⊥BC，垂足为E，过点C作CF⊥AD，垂足为F.

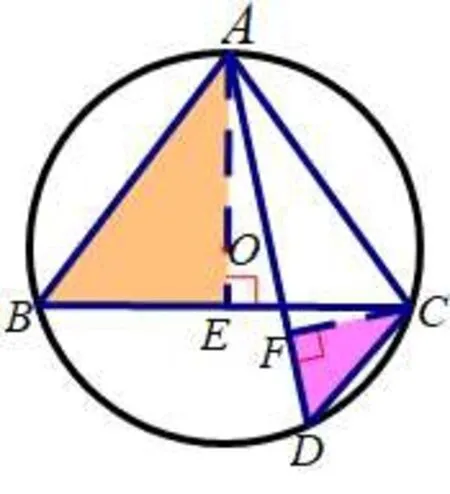
图4

在Rt△ABE中，AB=10，BE=6，AE=8，

在⊙O中∠B=∠D，易证△ABE∽△CDF.

所以可得DF=3,CF=4.

在Rt△ACF中，AC=10，CF=4，

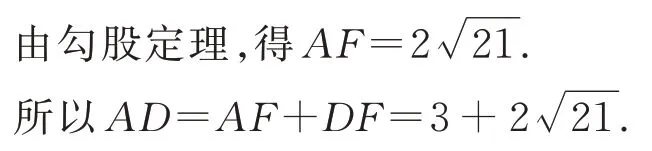
解法4如图5，过点A作AE⊥BC，垂足为E，作AF⊥CD，垂足为F.

对于任意一个已知三边的圆内接三角形，我们常利用直径所对的圆周角为直角，巧构如图6的两个相似直角三角形△ABE、△ADC求外接圆的半径. 受此启发，在图5 中，可以构造一个和Rt△ABE相似的三角形，而∠B=∠D，所以就需要构造一个包含锐角∠D的直角三角形，又已知CD=5，从而可得图4 和图5，从解法来看，图4 是将AD分成两部分来求解，但计算量很小. 而图5是将AD看成一个整体来求解，求解中用到三角形求线段长度中常用的双勾股，计算量虽大点，但只要熟悉双勾股的基本图形，此解法还是符合学生的自然认知水平.

图5

图6

（2）构造旋转相似

图7

题目中所求的AD 与△ABC构成一个爪形，而△ACD已知两边，求第三边，故将△ACD旋转，又∠B=∠D，从而可以构造一组共点旋转相似，找到对应边AD和AB的关系，再结合勾股定理求解. 旋转的解法虽然不易想到，但其实在全等图形的学习中对于有一组邻边相等的爪形图中，常构造一组共点旋转全等来实现问题的解决. 而全等是特殊的相似，可以通过类比来获得问题解决的方法.

（3）构造斜A 型相似

解法6如图8，连接BD并延长交AC的延长线于点F，过点E作BE⊥AC，垂足为E.

图8

在△ABC中，由等积法，得BE=9.6.

在Rt△BEC中，由勾股定理，得CE=7.2.

因为圆内接四边形的外角等于内对角，

在Rt△BEF中，由勾股定理，

A、B、C、D为⊙O上四点，从而可得到⊙O的内接四边形ABDC，由托勒密定理可知，求AD需求BD. 再由圆内接四边形的外角等于内对角联想到延长相交构造斜A型相似，且相似比为2，在Rt△BEF中由勾股定理求解. 较前面的几种解法，此解法复杂且计算量大，但圆内接四边形和斜A 型相似确都是圆中常见的基本图形.

2.3 利用余弦定理

初中阶段所学的锐角三角函数将直角三角形的边角关系紧密的联系了起来，是对勾股定理的一种补充. 正、余弦定理是研究任意三角形的边角关系，虽然是高中所学的内容，但确是锐角三角函数这一章必不可少的拓展和延伸，故而对于学情允许的班级可以进行适当的探究. 此题中含两个三角形，共有5 边已知，且有一角相等，用余弦定理求解应该算是本题最简洁的方法.

3 几点思考

3.1 “变化中抓不变”，唤醒解题思路

数学问题众多，如若用孤立的眼光来看，它们是不断变化的，但如若用联系的观点来看，就会发现变化问题中存在不变点. 而几何问题中常用的基本图形就可以看成是变化问题中的一个不变点. 有的问题直接利用基本图形就可以求解（如方法1，方法7），有的需要再适当添加辅助线（如方法2）或将几个基本图形叠合在一起来求解(如巧构相似三角形的几种方法).

基本图形的选择是解题思路的基础，故而这就需要我们教师在新知教学中不要求全，而在于求变，给出层层的变式问题，让学生通过问题的解决识别出基本图形并能进行灵活应用.

3.2 “不变中抓变化”，优化解题方法

虽然此题从巧构相似三角形的角度去分析有4 种解法，但解法3 将CD=5 当成直角三角形的一边来求解，不论是从问题的思考还是问题的解答来看都是这几种解法中最优的，其他方法虽然也用到了CD=5 这个已知条件，但并没有此种方法用的巧.

事实上想让学生在考场上限定的时间内完成问题的解决并使用最优的方法，这需要丰富的解题经验. 经验的积累虽可以通过课后大量的强化训练来实现，但这都没有课堂上教师有目的的训练来的快，所以这就更要求教师在课堂的问题设置上“求精”而不在于“求多”，尽可能多的给学生创造出一题多解的典型问题. 同时，多些课堂等待，让学生从题设或结论，这些关键点多角度去思考解决问题的方法，让学生的思维更舒展，从而真正获得知识的内化.